Improved Modeling of In Vivo Kinetics of Slowly Diffusing Radiotracers for Tumor Imaging

Abstract

Large-molecule tracers, such as labeled antibodies, have shown success in immuno-PET for imaging of specific cell surface biomarkers. However, previous work has shown that localization of such tracers shows high levels of heterogeneity in target tissues, due to both the slow diffusion and the high affinity of these compounds. In this work, we investigate the effects of subvoxel spatial heterogeneity on measured time–activity curves in PET imaging and the effects of ignoring diffusion limitation on parameter estimates from kinetic modeling.

Methods

Partial differential equations (PDE) were built to model a radially symmetric reaction-diffusion equation describing the activity of immuno-PET tracers. The effects of slower diffusion on measured time–activity curves and parameter estimates were measured in silico, and a modified Levenberg–Marquardt algorithm with Bayesian priors was developed to accurately estimate parameters from diffusion-limited data. This algorithm was applied to immuno-PET data of mice implanted with prostate stem cell antigen–overexpressing tumors and injected with ¹²⁴I-labeled A11 anti–prostate stem cell antigen minibody.

Results

Slow diffusion of tracers in linear binding models resulted in heterogeneous localization in silico but no measurable differences in time–activity curves. For more realistic saturable binding models, measured time–activity curves were strongly dependent on diffusion rates of the tracers. Fitting diffusion-limited data with regular compartmental models led to parameter estimate bias in an excess of 1,000% of true values, while the new model and fitting protocol could accurately measure kinetics in silico. In vivo imaging data were also fit well by the new PDE model, with estimates of the dissociation constant (K_d) and receptor density close to in vitro measurements and with order of magnitude differences from a regular compartmental model ignoring tracer diffusion limitation.

Conclusion

Heterogeneous localization of large, high-affinity compounds can lead to large differences in measured time–activity curves in immuno-PET imaging, and ignoring diffusion limitations can lead to large errors in kinetic parameter estimates. Modeling of these systems with PDE models with Bayesian priors is necessary for quantitative in vivo measurements of kinetics of slow-diffusion tracers.

Radiolabeled antibodies have shown great utility in both imaging and therapeutics, but there are obstacles to accurate quantification of these compounds in vivo (1–5). There are many antibodies approved for clinical use, with even more in phase I–III trials; however, the full kinetic activity of these compounds has yet to be completely understood quantitatively (1,6). It has long been known that although monoclonal antibodies show high specificity in target tissues, there is a divergence in spatial localization between in vivo and in vitro studies (7). Early in silico work showed that slow diffusivity of these molecules in target tissues can lead to steep concentration gradients of tracers in tissue on the subvoxel level (8). Intact antibodies (~150 kDa) are orders of magnitude larger than traditional small-molecule tracers (usually <1 kDa), and their larger size results in both reduced capillary permeability and slower rates of diffusion in tissues (9).

Another major factor leading to heterogeneous localization of these molecules is their high affinity in target tissues (10–12). Because of their high affinity, heterogeneous localization is observed even with relatively small (25 kDa) single-chain variable fragments and with small micrometastases (13,14). Understanding the simultaneous effects of imaging agent size and affinity has been further complicated by studies showing variable tumor penetration of several trastuzumab (146 kDa) derivatives and limited tumor penetration of the much smaller (0.5 kDa) doxorubicin (15,16).

These complications necessitate a new class of kinetic models that will allow for improved PET quantitation and therapeutic planning. When using these molecules as therapeutics, spatial heterogeneity on length scales less than 100 µm leads to large volumes of target tumors being completely devoid of treatment, with almost all localization close to the capillary wall (17). The ability to robustly plan treatment protocols with these compounds, with appropriate dose at all depths in tissue, is contingent on knowledge of biologic parameters such as receptor density in target tumors and full kinetic knowledge of the probes. Previously, however, to accurately measure these necessary parameters, investigators would need to use some combination of compartmental kinetic modeling or Scatchard analysis, which both assume wellmixed or uniform compartmental activity on the subvoxel level (18). As described above, in the case of large high-affinity compounds, such as labeled antibodies, these assumptions are violated. Despite these deviations from standard assumptions, some properties of labeled antibodies confer advantages and simplifications to quantification of immuno-PET. With few exceptions (e.g., antihuman epidermal growth factor receptor 2 antibodies), because of the high specificity of antibody-based imaging agents there will be little to no uptake in myocardial tissue, allowing for accurate measurements of image-derived input functions from the left ventricle. Additionally, the high specificity of tracers will lead to high signal-to-noise ratios and low background activity. Therefore, in this work we propose, implement, and test a method for accurately measuring the kinetic activity of such compounds in vivo, through a set of partial differential equations (PDEs) describing the reaction-diffusion equations governing this system. Although previous work has investigated the effect that this tissue heterogeneity will have on whole-tumor activity over time, until now there has yet to be work published on the accurate extraction of kinetic parameters from PET imaging in such situations and determining the true dose-at-depth in therapeutics for such systems (11,19).

In addition to simulation studies, we apply the results of the in silico work to in vivo imaging of the ¹²⁴I-labeled A11 (¹²⁴IA11) minibody in prostate cancer xenografts. The minibody (scFv-CH3, homodimer, 80 kDa) is an antibody fragment that helps to address the long uptake time and slow blood clearance kinetics of intact antibodies (150 kDa; half-life, days to weeks) by deleting the C_H1 and C_H2 domains to create a fragment that retains the binding strength and specificity of whole antibodies but exhibits faster blood clearance (half-life, 6–8 h), allowing for high-contrast imaging at earlier time points (20–22). The reduced size of these compounds likely contributes to increased penetration into tumors, however, they are still large enough to show depth-dependant concentration effects (13,16).

The A11 minibody is engineered for imaging prostate stem cell antigen (PSCA)–expressing tumors (23). The PSCA is cell surface protein with little normal expression throughout the body, limited to low-level expression in normal prostate, bladder, and stomach (24). However, PSCA is highly expressed in most local and metastatic prostate cancers, with expression levels correlating to Gleason score, tumor invasion, and a poor prognosis (24–27). The ability to obtain accurate measures of anti-PSCA tracer kinetics could thus be an important tool in staging and monitoring treatment response in prostate cancer. PSCA is additionally overexpressed in bladder and pancreatic cancers. Although previous work has shown that ¹²⁴I-labeled anti-PSCA minibodies exhibit high-contrast images of PSCA-expressing targets at relatively early time points (6–44 h), no work has yet been done to quantify the kinetics of these systems (28,29).

In this work, we examine theoretic models of both linear and saturable binding kinetics of large-molecule tracers and the effect of diffusion rates on measured time–activity curves from target regions. Next, we investigate the effects of naively fitting diffusion-limited data with regular compartmental models, assuming infinitely fast diffusion (i.e., well-mixed compartments), and effective methods for accurately measuring kinetics from such systems. Finally, we apply the previously discovered fitting methods to an in vivo investigation of ¹²⁴I-labeled A11 minibody in xenografts overexpressing PSCA in mice.

MATERIALS AND METHODS

Kinetic Models

PDE models were built to simulate the kinetics of a slowly diffusing radiotracer. Tissue was modeled as a nonoverlapping composite of radially symmetric cylinders with radius R. At each radius r, away from the capillary wall at r₀, tracer kinetics were modeled as a compartmental system specific to that radius, leading to a system of radially symmetric, reaction-diffusion equations. Two sets of models were built: a simpler PDE model of linear binding kinetics and a more complex nonlinear PDE model of saturable binding kinetics (Eqs. 1 and 2, respectively). Both sets of reaction-diffusion equations modeled concentration of tracer in interstitial space, bound to surface receptors, and internalized into the cell (u, v, and w, respectively). In the case of saturable binding, the concentration of unbound receptor sites at each radius (x(r,t)) was modeled as well. Both linear and nonlinear PDE models were subject to the same Neumann boundary conditions (Eq. 3). These boundary conditions ensure that there is no leak from the system due to diffusion deep in tissue (r > R), as that loss will be reciprocally matched by leaks into the system from adjacent regions. Initial conditions for all models had zero tracer in tissue, and for nonlinear models initial unbound antigen sites were at steady-state values (dens₀). A more complete derivation and explanation of these equations can be found in the supplemental materials (available at http://jnm.snmjournals.org)

$$\frac{\delta }{\delta t}u(r,t)=D[\frac{{\delta }^2}{\delta r^2}u(r,t)+\frac{1}{r}\frac{\delta }{\delta r}u(r,t)]-k_{1}u(r,t)+k_2\nu (r,t)\frac{\delta }{\delta t}\nu (r,t)=k_{1}u(r,t)-(k_2+k_3)\nu (r,t)\frac{\delta }{\delta t}w(r,t)=k_3\nu (r,t)-k_{4}w(r,t).$$ (Eq. 1)

$$\frac{\delta }{\delta t}u(r,t)=D[\frac{{\delta }^2}{\delta r^2}u(r,t)+\frac{1}{r}\frac{\delta }{\delta r}u(r,t)]-k_{1}u(r,t)x(r,t)+k_2\nu (r,t)\frac{\delta }{\delta t}\nu (r,t)=k_{1}u(r,t)x(r,t)-(k_2+k_4)\nu (r,t)\frac{\delta }{\delta t}x(r,t)=-k_{1}u(r,t)x(r,t)+k_3({\mathit{\text{dens}}}_0-x(r,t))+k_2\nu (r,t)\frac{\delta }{\delta t}w(r,t)=k_4\nu (r,t)-k_{5}w(r,t).$$ (Eq. 2)

$$-D\frac{\delta }{\delta r}u(r,t){|}_{r=r_0}=P{C}_p(t)-Pu(r_0,t)\frac{\delta }{\delta r}u(R,t)=0.$$ (Eq. 3)

The model governing linear binding kinetics was solved analytically in Laplace space and numerically inverted into the time domain. The nonlinear model cannot be solved analytically and therefore was solved numerically through a combination of fourth-order Runge–Kutta and method of lines algorithms. Solutions were integrated across all radii (including the plasma compartment), to simulate time–activity curves from the modeled tissue. For both the linear and the saturable binding kinetic models, ordinary differential equation (ODE) models were built for these systems assuming infinitely fast diffusion (i.e., regular compartmental models), which were solved using fourth-order Runge–Kutta numeric analysis.

For nonsaturable binding kinetics, the effects of slower diffusion were examined by comparing responses of ODE and PDE models (differing only in rates of diffusion) to a unit impulse. Simulated time–activity curves of saturable binding ODEs and PDEs were similarly compared; however, their simulated time–activity curves were in response to a triexponential input function because a unit impulse response would not be sufficient to describe these nonlinear systems.

In cases in which finite diffusion rates led to measurable differences in time–activity curves, simulated diffusion-limited data with gaussian noise was fit repeatedly with both finite and infinite diffusion models using standard Levenberg–Marquardt optimization. To overcome possible problems of parameter identifiability, these simulated data were also repeatedly fit using a modified Levenberg–Marquardt algorithm, incorporating weak Baysian priors on binding and disassociate rates, k_on and k_off, assuming a priori in vitro measurements. Priors for kinetic parameters were formulated as lognormal, with mean of the true parameter value and SD equal to one half an order of magnitude.

Affinity Studies

The apparent affinity of the unmodified A11 minibody was measured by quartz crystal microbalance (QCM) using an Attana Cell A200 (Attana). Human PSCA-mFc antigen (40 µg/mL) was immobilized on an LNB-carboxyl sensor chip by amine coupling. Binding experiments were performed in HEPES-buffered saline (HEPES is N-(2-hydroxyethyl)piperazine-N′-(2-ethanesulfonic acid)) 0.005% polysorbate 20 (25µL/min, 22°C). Five serial dilutions (160−5 nM) of the construct were run in triplicate in random order. The chip was regenerated using 0.1 M glycine, pH 2.5, between each sample. Buffer injections were performed before each sample injection to use as a reference in integrated Attester Evaluation software (Attana) with which the binding curves were fit using a mass transport limited binding model.

Small-Animal PET/CT

Two mice were implanted with a control 22Rv1 tumor, a prostate epithelial cell line, expressing almost no PSCA (369 ± 486 antigens/cell) and a contralateral 22Rv1 tumor transfected to overexpress PSCA (2.2 × 10⁶ antigens/cell), as described previously (24). Approximately 25 µg (4 MBq) of ¹²⁴I-A11, with a purity of 98% or more, were administered to tumor-bearing mice via tail vein injection. The iodination of the minibody was performed as described previously, with immunoreactivity of ¹²⁴I-A11 found to be 76% ± 9.7% (24,30). Before ¹²⁴I-A11 administration, thyroid and stomach uptake of radioiodine was blocked, respectively, with Lugol iodine and potassium perchlorate as described previously (23). Mice underwent an initial 2-h dynamic small-animal PET scan at the time of injection. At 20 and 44 h after injection, mice were anesthetized with 1.5% isoflurane anesthesia and imaged with 10-min acquisitions on an Inveon small-animal PET scanner (Siemens Preclinical Solutions), followed by a micro-CT scan (microCAT II; Siemens Preclinical Solutions) (31). One mouse also underwent 10-min static scans at 4, 6, 8, and 12 h after injection. All animal experiments were conducted in compliance with a protocol approved by the Institutional Animal Care and Use Committee of the University of California, Los Angeles.

Small-animal PET images were reconstructed by nonattenuation or scatter-corrected filtered backprojection and analyzed and displayed using AMIDE (A Medical Image Data Examiner) (32). Plasma activity was described by an image-derived input function, measured using a cylindric volume of interest (~ 3 mm³) covering the left ventricle. Tumor activity was measured using elliptic volumes of interest covering the tumor. Tissue activity was converted from scanner units to Molar concentration using known specific activity of injected doses and whole-body activity in the first frame of the dynamic scan. Measured activity was modeled using both ODE and PDE models of saturable binding kinetics. For both models, no intracellular compartment was included, because previous work has shown that intracellular metabolism of ¹²⁴I-A11 results in fast cleavage of the PET tracer isotope, which is subsequently free to diffuse from the tissue and is then rapidly renally excreted (33).

RESULTS

Solving the PDE system of linear binding kinetics showed only minor differences (<1%) in simulated unit impulse responses over a range of biologically feasible diffusion parameters (D > 10 µm²s⁻¹) and less than 4% difference from a regular compartmental model at very slow diffusion rates (D = 1 µm²s⁻¹). In the linear binding model, slower diffusion rates did lead to large concentration gradients in tissue, such that for biologically reasonable diffusion rates the total doses at the deepest points in tissue were 50% of regions closest to the capillary wall (Supplemental Fig. 1).

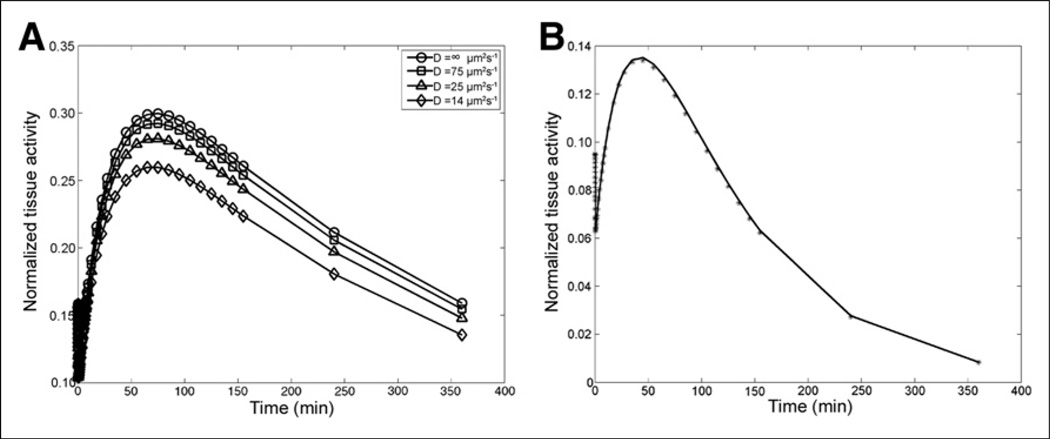
Simulated time–activity curves from the nonlinear model governing saturable binding kinetics were much more sensitive to changes in diffusion rates (Fig. 1A). As can be seen in Table 1 and Figure 1B, although in silico diffusion-limited time–activity curves (D = 14 µm²s⁻¹) could be fit well using a regular compartmental model (i.e., D = ∞ µm²s⁻¹), parameters obtained with this fitting showed large levels of bias, in excess in 1,000% of true values for some parameters.

Figure 1.

Results of simulated diffusion-limited time–activity curves. (A) Effect of diffusion rates on simulated time–activity curve. (B) Fitting of in silico time–activity curve (D = 14 µm²s⁻¹) using compartmental model (D 5 ∞ µm²s⁻¹). Data are normalized to steady-state receptor concentration in tissue.

TABLE 1.

Mean Bias and Relative SD of Fitted Parameters Using Compartmental or Diffusion-Limited Model to Fit Simulated Diffusion-Limited Time–Activity Curves with Gaussian Noise

Fitting model	k1 (kon)	k2 (koff)	k3	k4	P*	Blood volume
Compartmental (no priors)
μ	3,100%	1 × 106%	2,090%	1,660%	63%	13%
Relative SD	76%	180%	910%	860%	61%	28%
Compartmental (with priors)
μ	210%	470%	1.5 × 104%	1.7 × 103%	−7%	6%
Relative SD	100%	200%	340%	500%	16%	42%
Diffusion (no priors)
μ	31%	−30%	290%	10%	25%	8%
Relative SD	150%	140%	180%	16%	110%	25%
Diffusion (with priors)
μ	1%	−20%	210%	4%	6%	−6%
Relative SD	46%	110%	170%	8%	18%	3%

^*P is capillary permeability.

Data shown are percentage of true parameter values (for mean) and percentage of mean fitted value (for relative SD).

With the inclusion of Bayesian priors on both the binding and the unbinding rates (k₁,k₂), bias rates for both compartmental and diffusion models were reduced. However, for compartmental model fits, mean bias for some parameters without priors were increased (Table 1). Therefore, fitting with Bayesian priors, as opposed to a standard least-squares algorithm, was used for in vivo data.

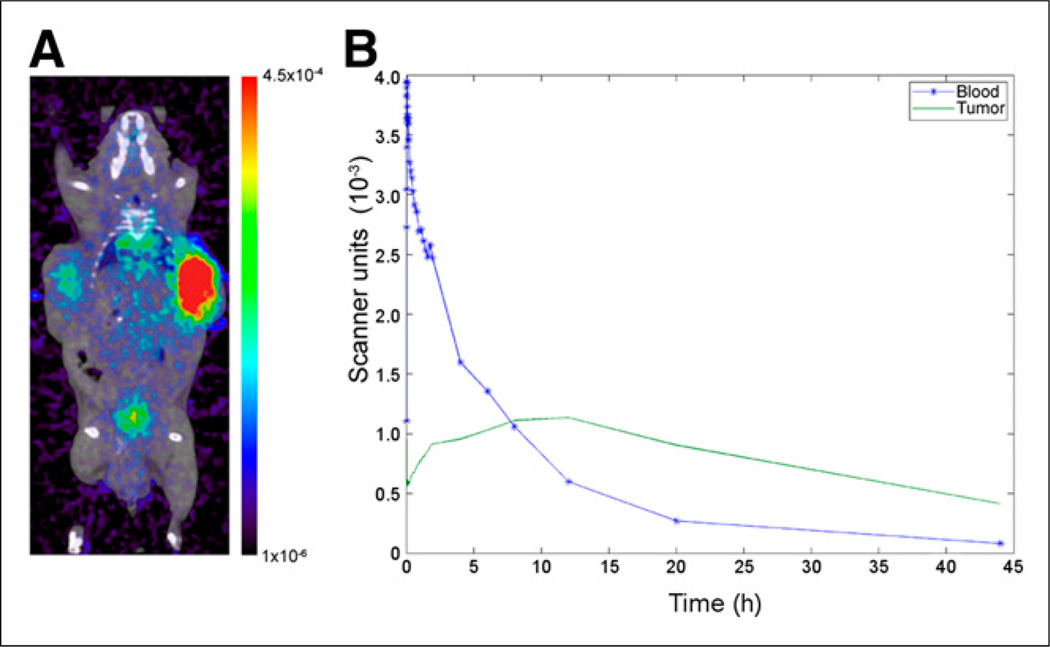
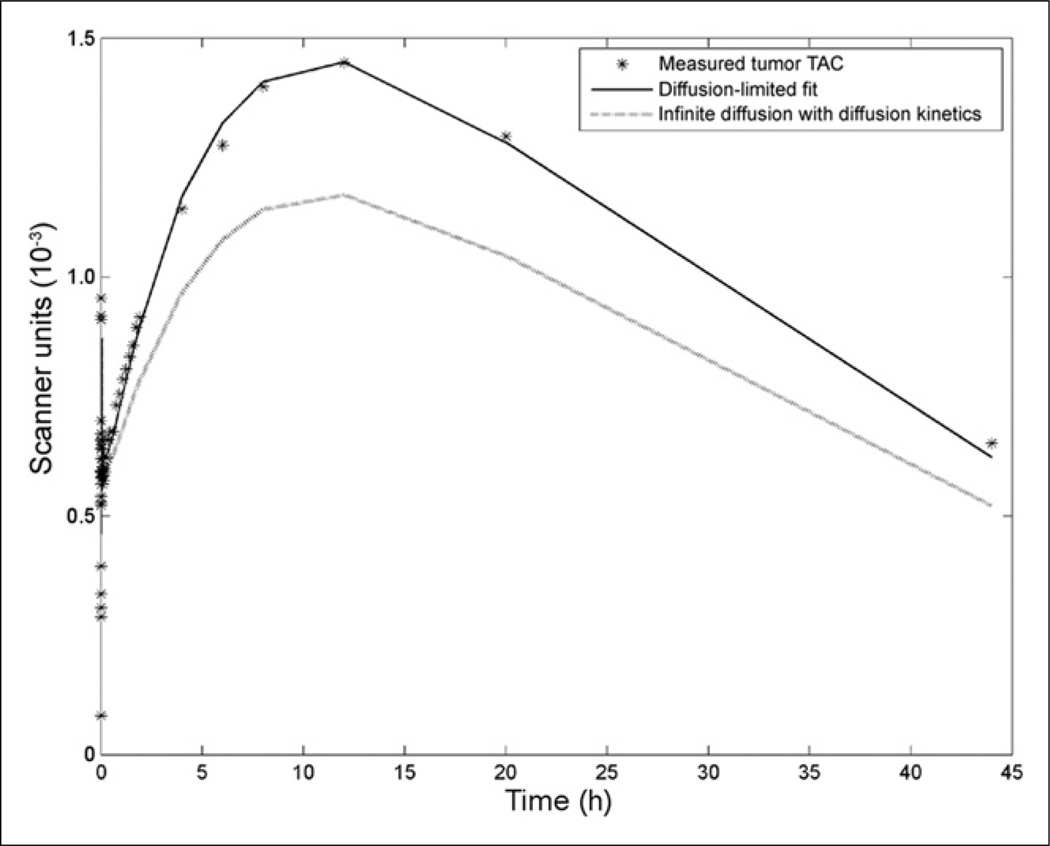
Input functions, as measured by tracer activity in the left ventricle, were well fit by a standard triexponential decay (Fig. 2). Measured time–activity curves from PSCA-overexpressing tumors were fit with compartmental and diffusion-limited models. In both cases, Bayesian priors for k₁ and k₂ were incorporated into the fitting, as determined by QCM (1.21 × 10⁵ (M·s)⁻¹ and 4.95 × 10⁻⁴ s⁻¹, respectively) (Supplemental Fig. 2). As in in silico studies, priors were formulated as lognormal distributions. Both models successfully reproduced the measured time–activity curves for the mouse with 6 static scan time points (mouse 1) but with large differences in fitted kinetic and biologic parameters between the diffusion-limited and compartmental models (Table 2). For the mouse with 2 static scan time points (mouse 2), only the diffusion-limited model was able to reproduce the measured time–activity curve. Results of fitting with the diffusion-limited model and the effects of diffusion rate on the measured time–activity curve can be seen in Figure 3. The fitted time–activity curve from the second mouse can be seen in the supplemental data (Supplemental Fig. 3).

Figure 2.

Results of in vivo imaging of A11 minibody. (A) PET/CT of mouse at 20 h after injection with 22rv1 tumor on left and 22rv1×PSCA on the right side. Color bar is in scanner units. (B) Measured time–activity curve from PSCA-positive tumor (green) and from left ventricle with fitted curve (blue).

TABLE 2.

Parameter Values for Measured Time–Activity Curves from Both Mice Using Both Compartmental and Diffusion Models with Bayesian Priors

Model	kon (M·s)−1	koff (s)−1	k3 (s)−1	k4 (s)−1	P* (m/s)	Blood volume	Ag† (nM)	D (µm2/s)
Compartmental (mouse 1)	4.1 × 104	5.3 × 10−4	7.7 × 10−6	5.1 × 10−6	4.4 × 10−9	0.17	1,031	Not applicable
Diffusion
Mouse 1	1.6 × 105	2.1 × 10−4	1.1 × 10−5	6.9 × 10−6	3.7 × 10−9	0.16	140	9
Mouse 2	1.8 × 105	4.4 × 10−4	2.6 × 10−5	8.1 × 10−6	3.7 × 10−9	0.10	161	10
Percentage difference between compartmental and diffusion models	−74%	152%	−30%	−26%	19%	6%	646%	Not applicable

^*P is capillary permeability.

^†Ag is steady-state antigen receptor concentration.

Figure 3.

Fitting results of diffusion-limited model. Measured tumor activity fit using diffusion model is shown as solid line. Simulated time–activity curve (TAC) with parameters from diffusion model fit, but using infinite diffusion, is shown as dotted line.

DISCUSSION

The results of in silico studies suggest that, in the case of linear binding kinetics, there will likely not be any measurable difference in time–activity curves of large-molecule imaging agents because differences from an infinite diffusion model were less than 5% even at diffusion rates an order of magnitude smaller than those likely for antibodies (11). Although slow diffusion of molecules does not appear to have an effect on the measured activity of imaging agents, slow diffusion does result in a steep concentration gradient of the compound in tissue, with in silico results showing that differences in dosages can be 2-fold across tissue depths. This finding has important ramifications in the planning of treatment protocols, particularly because most tumor volume is located farther away from the capillary wall where dosage will be lower. However, there are many reasons why the kinetics of the compound in vivo would deviate from the linear binding regime, such as the case of targets with low antigen expression, low-specific-activity imaging agents, blocking or coinjection studies, or large-dosage therapeutic treatments for which receptor saturation is often the goal (34). Furthermore, as shown above (Fig. 1A), even in the cases of relatively low saturation of available receptors, slow diffusion can result in large and measurable differences in time–activity curves. Therefore, it is likely that for most in vivo applications the usage of nonlinear saturable binding models will be necessary and the non–diffusion-limited linear model will show considerable error for estimates of biologic parameters despite good appearing fits of the in vivo data.

Although diffusion-limited data can be fit well with either a compartmental or a diffusion model (Fig. 1B), the large differences in fitted parameters reveal the problem of parameter identifiability when modeling these data with standard algorithms such as Levenberg–Marquardt. The results of the in silico fitting results shown in Table 1 also demonstrate that naively fitting time–activity curves of slowly diffusing compounds with high target affinity can lead to large errors (>1,000%) in important kinetic parameters. These results all suggest that although a noncompartmental model incorporating rates of diffusing is necessary to accurately model in vivo kinetics of large-molecule tracers, standard fitting techniques will not be sufficient. Adding Bayesian priors to parameters that can be measured in vitro before scanning is shown to be a viable approach in overcoming problems of parameter identifiability. Although there are still large errors in some parameter estimates when using a regular compartmental model with Bayesian priors, some parameters not constrained by a priori measurements can have low bias, such as capillary permeability and tumor blood volume. This result suggests that compartmental models could be used to provide initial parameter estimates for diffusion-limited fitting, because the ODE models are much less computationally expensive than the PDE equations governing the diffusion model.

Results of fitting in vivo imaging data of the A11 minibody largely confirm results from the initial in silico simulations. It can be seen that although time–activity curves can be fit (in terms of sum of squared errors) with a regular compartmental model, parameter estimates vary greatly from both Bayesian priors and results of diffusion-limited fitting but with only small differences in fitted values of capillary permeability and blood volume. Most notably is the divergence in predicted receptor density when diffusion limitations are ignored, with more than a 600% difference in model predictions. Because receptor density can be an important factor in staging tumor progression and evaluating the response of the tumor to therapeutic interventions, accurate estimates of this parameter is incredibly important for the utility of quantitative immuno-PET (25).

Parameters yielded from diffusion-limited models showed strong agreement between both mice scanned, even with 1 mouse having 4 fewer static scans. Additionally, parameter estimates for capillary permeability were similar to previously estimated results (3–5 × 10⁻⁹ m/s) (11). There was likewise excellent agreement between K_d as measured with QCM (4.1 nM) and as measured by kinetic modeling of the 2 mice (1.3 and 2.4 nM, respectively). Although there were small differences, these are likely explained by differing microenvironments between in vivo studies and the in vitro QCM experiment. Although the a priori measurements were performed on unlabeled compounds, previous work has shown that the iodination of the minibody used will not result in changes to K_d (24). With in vivo studies, there can be a multitude of binding cofactors that could reduce the dissociation constant that would not be present in vitro, leading to larger K_d measures in experiments such as QCM.

The results shown here, from both in silico and in vivo studies, reveal the importance of considering diffusion in the quantification of high-affinity compounds in both imaging and therapeutic planning. Fitting results demonstrate that biologic and kinetic information can be successfully extracted from immuno-PET data with physically accurate diffusion-limited models, whereas data naively fit with regular compartmental models can lead to very large errors. These large errors have important repercussions in both therapeutic planning, where proper dosages need to be delivered to the entire tumor volume, and immuno-PET applications for staging disease progression.

There are still some limitations in transitioning quantitative immuno-PET modeling into clinical usage. First, in this work we have presented fitting data of a tracer with a radioisotope that is rapidly cleaved and excreted after internalization. This phenomenon alleviates the need for an intracellular compartment and reduces the number of parameters needed for fitting. Tracers with radioisotopes that are not rapidly cleared after endocytosis (such as A11 conjugated with ⁸⁹Zr) will require more complicated models that may be more difficult to fit than those described above, even with Bayesian priors (35). Future work is in progress to model time–activity curves measured from mice implanted with 22rv1×PSCA tumors scanned with ⁸⁹Zr-A11 to confirm the utility of this model in more complex systems.

An additional barrier to this quantitative analysis in clinical use is the repeated scan times and long biologic half-life of these tracers. The minibodies used in this work show a substantial improvement over whole antibodies in biologic half-life and reduce the time over which time–activity curves need to be measured, thus lessening this barrier. However, the protocol used in this study, with 7 scans over the period of 44 h, is still much more than would be viable in clinical usage. Therefore, future work is planned on optimizing dosage and scan protocols to minimize scan numbers and durations, while maintaining parameter identifiability in kinetic analysis.

CONCLUSION

This work shows that slow diffusion of high-affinity compounds will have little effect on measured time–activity curves in immuno-PET for linear binding kinetics. However, in the likely case of saturable binding (due to low receptor expression, low labeling efficiency, blocking/coinjection studies, or therapeutic antibody doses) slow diffusion will have a strong effect on measured time–activity curves. Using regular compartmental models to estimate biologic and kinetic parameters of such diffusion-limited data can lead to large errors, which can be alleviated through the use of nonlinear PDE models and the incorporation of Bayesian priors. Future work is planned to validate the use of this fitting technique in intracellular retained tracers, such as ⁸⁹Zr-A11, and to optimize imaging protocols for such tracers to minimize scan time and retain parameter identifiability.