Value normalization in decision making: theory and evidence

Abstract

A sizable body of evidence has shown that the brain computes several types of value-related signals to guide decision making, such as stimulus values, outcome values, and prediction errors. A critical question for understanding decision-making mechanisms is whether these value signals are computed using an absolute or a normalized code. Under an absolute code, the neural response used to represent the value of a given stimulus does not depend on what other values might have been encountered. By contrast, under a normalized code, the neural response associated with a given value depends on its relative position in the distribution of values. This review provides a simple framework for thinking about value normalization, and uses it to evaluate the existing experimental evidence.

Introduction

A rapidly growing and convergent body of evidence has shown that the brain computes several types of value-related signals during decision making (for reviews, see [1–5]). Three particularly important signals are stimulus values, outcome values, and prediction errors. Stimulus values (SV) are computed at the time of choice for the purpose of guiding decisions, and reflect the anticipated value of the outcomes associated with each option, regardless of whether or not the option is chosen. Neurophysiology [6••,7–9], functional magnetic resonance imaging (fMRI) [10–13,14•,15–19] and electroencephalography (EEG) [20] studies have found signals in orbito-frontal cortex (OFC) and ventromedial prefrontal cortex (vmPFC) consistent with the encoding of SV. Outcome values (OV, sometimes called experienced utility) indicate the value of consumption experiences, and measure their desirability. Activity consistent with the encoding of OV has also been found in similar areas of OFC and vmPFC [21–26]. Prediction error (PE) signals are computed whenever individuals receive new information about their rewards, measure the change in expected rewards, and can be used to learn SV. PE signals have been most closely associated with the responses of midbrain dopamine neurons, which project to large segments of cortex [27–32]. Other important signals include the net value of taking an action (action values [33]) and the values of chosen and unchosen options (for more details see [3–5]).

A basic question is whether the SV, OV, and PE signals are computed using an absolute or a normalized code. Under an absolute code, the neural response used to represent a given value is always the same. By contrast, under a normalized code, the neural response associated with that same value depends on its relative position in the distribution of values that might be encountered. For example, consider the response of a neuron that encodes SV when a subject is deciding whether or not to accept a lottery that pays $100 with 75% probability and entails a loss of $150 with 25% probability. In particular, compare the response of this neuron in two different decision contexts: a low reward context in which most other stimuli (e.g. other lotteries) encountered by the subject have much lower values (e.g. gains of $10 and losses of $15), and a high reward context in which most other stimuli have much higher values (e.g. gains of $1000 and losses of $1500). Under an absolute code, the firing rates in the neuron encoding the SV at the time of evaluating the lottery are the same in both reward contexts. By contrast, under the type of normalized codes described here, the firing rates in the neuron are higher in the lower reward context.

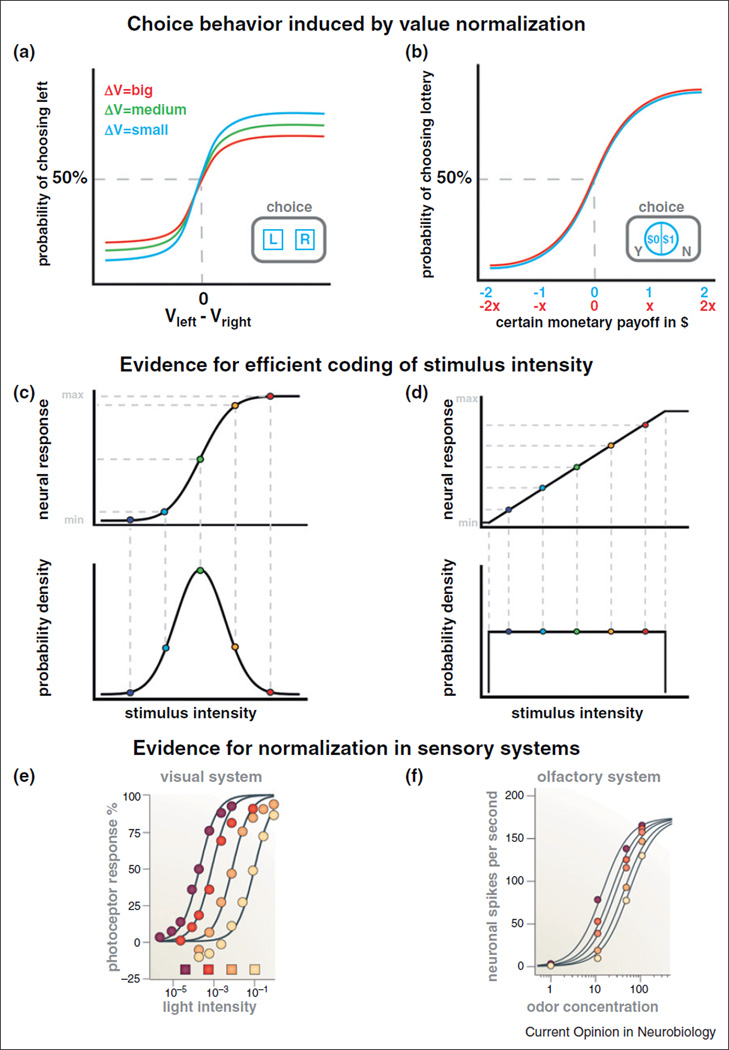
Several different motivations underlie the growing interest in value normalization. First, the presence and shape of a normalized value code has important behavioral implications. Consider a binary decision. The probability an individual chooses the item with the highest value is likely to be a function of the value of two options (V_left and V_right, Figure 1a). If choices are a stochastic function of values (e.g. as described by a logistic choice model or by the drift-diffusion model [34–37]), then the probability of choosing the left item increases with its relative value. Furthermore, under the type of value normalization schemes described below, the sensitivity of the choice curve to the relative values decreases as the range of values encountered increases during the choice task (Figure 1a.). In some settings, the psychometric choice curves are invariant to specific linear rescalings of the value of the options (i.e. multiplying all payoffs by a constant factor x > 0, Figure 1b), as a result of value normalization. Second, there is a growing belief in decision neuroscience that our ability to understand and predict choice will be greatly increased by understanding the detailed processes and mechanisms at work in value computation. We believe value normalization to be a crucial piece of the decision-making process since, as illustrated by the previous two examples, the quantitative behavioral predictions of value normalization depend on the exact functional form that it takes in different contexts.

Figure 1. Normalization in choice and sensory systems.

(a) Predicted psychometric choice curve for a choice between two target items (left and right, see inset for example task), as a function of the range of values that are being used in the overall choice task (ΔV). Some normalization models described in this review predict that the choice curve flattens (i.e. it becomes more noisy), as the value range increases (i.e. ΔV moves from blue to red, corresponding choice curves are the same color). (b) Predicted psychometric choice functions for a task in which the subject chooses between a lottery paying a fixed reward or punishment with probability of 50%, and zero otherwise, and a deterministic payoff of $0 (blue line). If subjects exhibit linear normalization (see main text) and make decisions using a logistic choice rule, then multiplying all payoffs by a common factor x > 0 will not affect choice behavior: the choice curve is unchanged (red line). (c) Normalized neural response (top) predicted by the efficient coding hypothesis for the case in which the distribution of stimulus intensities that might be encountered is Gaussian (bottom). Note that the neural signal is maximally sensitive for the stimulus intensities that are encountered most frequently. Min-max denotes the dynamic range of the neuron. A similar figure can be found in other discussions of efficient coding [40,62••]. (d) Efficient neural responses for the case of a uniform distribution of stimulus intensities. (e) Evidence for normalization in the responses of a turtle cone photoreceptor to light of increasing intensity. The intensity of the colored squares reflects the background intensity of the image (figure from [38••], original data from [45]). (f) Evidence for normalization in the responses of olfactory neurons of the antennal lobe of Drosophila to odors of increasing concentration. Darker colors represent higher concentrations of masked odorants (figure from [38••], original data from [71]).

This review provides a simple framework for thinking about value normalization, and uses it to evaluate the existing experimental evidence.

Normalization in sensory systems

Although the issue of normalization is relatively new to decision neuroscience, it has been widely investigated in sensory systems, where it has been found to be a pervasive feature of sensory coding (see [38••] for a recent review). Several convergent results and concepts from that literature provide a useful starting point for thinking about value normalization in decision making.

First, consider the problem of choosing a sensory coding scheme that maximizes the information contained in the responses of a sensory coding neuron under the constraint that it has a bounded dynamic firing range. The amount of information contained in the neural signal can be measured by its entropy, which is the inverse of the predictability of the signal values. The solution to this problem, known as the efficient coding hypothesis, states that the optimal code is the one that leads to a uniform probability over firing rates [39,40]. This implies that the normalized signals are responsive only to intensity levels that occur with positive probability, and that the exact shape of the normalization function depends on the distribution of stimulus intensities. For example, if a set of stimuli intensities is distributed normally, then the optimal normalized code for the neural responses encoding these intensities is the Gaussian cumulative distribution function, whereas if stimuli are distributed uniformly, the optimal code is linear (Figure 1c, d). Since these changes in coding are beneficial, some types of signal normalization are also often referred to as adaptive coding [41–43].

Second, studies across sensory systems and cortical regions have found sensory coding consistent with the use of a normalized code that takes a specific functional form, often called divisive normalization [38••,44]. Canonical examples are responses to light intensity and odor concentrations, in retinal and olfactory neurons (Figure 1e, f).

Third, in most experiments of sensory coding, stimulus conditions are varied across blocks, and not intermixed across trials. This design choice is justified by the fact that normalization parameters do not adapt immediately to changes in the stimulus distribution, necessitating the repetition of stimulus conditions for a few trials to reveal the form of the normalized code. For example, a classic study of normalization in light intensity signals [45] introduced a change in background luminosity for several seconds before presenting the target stimulus. In other words, although normalization can operate rapidly in many sensory systems, this adaptation is generally not instantaneous [43].

Computational framework for value normalization

In this section, we describe a simple decision-making task that dissociates SV, OV, and PE signals, and that provides a clean test of whether they exhibit absolute or normalized coding.

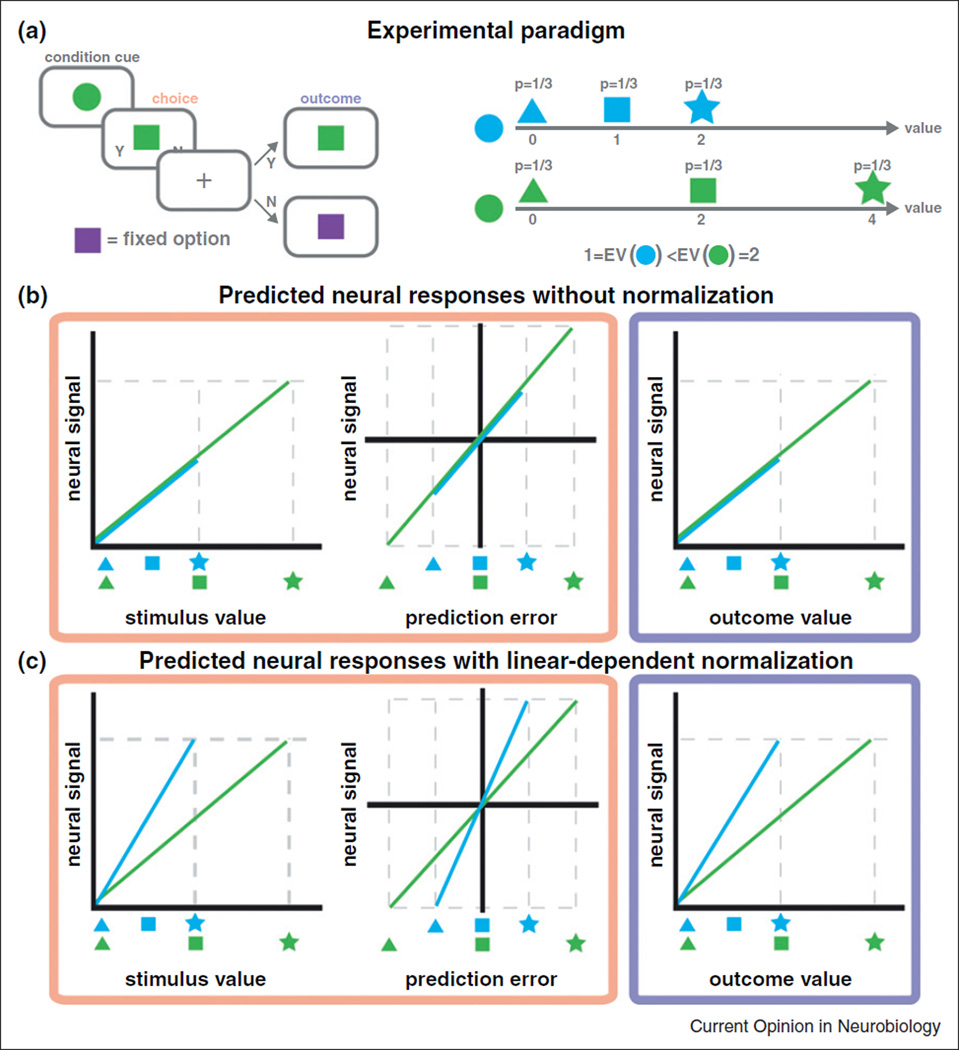
As shown in Figure 2a, subjects make choices in two different contexts (blue, green) that are held constant across long blocks of trials. In each context, the subject is shown one of three stimuli (triangle, square, star), with equal probability and has to choose between it and a fixed constant option (purple square). Subjects care about the stimuli because they are associated with a 100% probability of receiving rewards (e.g. a drop of juice if thirsty) of different value.

Figure 2. Computational and experimental framework.

(a) An example decision-making task to study value normalization. Subjects are asked to make choices in two different contexts (blue, green) that are held constant across long blocks of trials (e.g. at least 20 trials). In each context, the subject is shown one of three stimuli (triangle, square, star) and has to choose between it and a fixed constant option (purple square). The value of fixed option is within the range of other rewards. Subjects care about the choices because they are deterministically paired with rewards of different value. (b) Predicted neural responses for various value signals under absolute value coding (no value normalization). Both stimulus value and prediction errors are computed at the time of choice (faded red), whereas outcome value is computed at outcome (faded blue). (c) Predicted neural responses for various value signals in the case of linear normalization. The timing of value computations is the same as in (b). Note that the maximal neural response is the same in both the blue and green conditions in (c), but not in (b). See main text for more discussion.

Consider how the task dissociates the SV, OV, and PE signals. First, at the time the stimulus is presented, the subject computes a SV in order to make a choice, as well as a PE since the subject receives information about the rewards for the trial (e.g. seeing a star leads to a positive prediction error, while seeing a triangle leads to a negative one). Second, at the time of outcome the subject computes an OV equal to the value of the reward received, but there should not be a PE since stimuli are deterministically associated with their rewards. Figure 2b describes the predicted shape on the three signals without normalization. Figure 2c does the same under the assumption of linear normalization, which by the efficient coding hypothesis is the type of normalization that one would expect in the experiment. Regardless of the type of code (absolute versus normalized), the three signals can be dissociated: PE because they have a different shape, and SV and OV because they take place a different times.

Given this separation of different types of value signals, the task provides a straightforward test of the presence of absolute coding versus linear normalization. A careful comparison of the panels in Figure 2b, c shows that the predicted neural responses for units encoding SV, OV, and PE have a distinct response profile under both types of coding.

There are also many simple ways to modify the task. A small variation of the paradigm can also be used to study value normalization in Pavlovian (i.e. non-choice) settings. Here, individuals would be passively shown the stimuli presented in Figure 2a, but would not have to make a choice. The context and reward contingencies do not change. In this version of the task, a PE signal is coded at the time of stimulus presentation, and an OV at the time of reward delivery, but no SV are computed since no choices have to be made. Furthermore, the predicted values of the relevant signals remain as described in Figure 2b, c.

While we emphasize that this it not the only feasible paradigm providing clean tests of value normalization, some of its features are critical to avoid potential confounds. Here, we discuss three potential confounds that, as described in the next section, limit the interpretability of some existing evidence.

First, consider a task in which the contingencies between the stimuli presented at the beginning of the trial (e.g. at the time of choice) and the eventual rewards are stochastic. In this case, PE are computed at both the time of choice and the time of outcome: there is a PE at choice because the decision maker did not know the full context (i.e. the options) of the choice, and there is a PE at outcome because the chosen reward (e.g. a lottery) is stochastic. The same is true of Pavlovian tasks. Several papers in the literature (see Table 1) define a value coding neuron exhibiting normalization as one in which the response (1) increases with the absolute SV or OV, and (2) for the same unnormalized value of the signal, the neural response is larger when it is relatively more attractive (e.g. the star in blue context) than when it is relatively less attractive (e.g. the square in green context). As shown in Figure 2b, c (consider again the blue star and the green square, if a PE were also computed at outcome), this pattern is not sufficient to establish normalization because it is consistent with other combinations of PE coding and value coding. In other words, if both a PE and OV are computed at outcome, the observed neural response that satisfies the above condition (2) could be the result of PE or OV normalization, or both. This confound is not present in the proposed task, since it allows for full identification of the type of signal and the presence of normalization at outcome.

Table 1.

Summary of studies investigating the extent to which value signals exhibit range-dependent normalization. Code for signal type: SV, stimulus value; OV, outcome value; PE, prediction error; CV, chosen value. Code for brain regions: OFC, orbitofrontal cortex; vACC, ventral anterior cingulate cortex; dACC, dorsal anterior cingulate cortex; PCC, posterior cingulate cortex; vSTR, ventral striatum; fMRI, functional magnetic resonance imaging; BOLD, blood-oxygenation-level dependent.

Data type	Signal type	Study	Summary	Discussion
single unit	SV CV	Padoa-Schioppa (2009) [51••]	Task: Binary choice task with value range constant across long blocks. Finding: Normalized SV and CV signals in macaque OFC. Finding: Evidence for dynamic updating of value range.	Neural value signals in OFC are consistent with linear normalization and are sensitive to recent reward history.
single unit	CV	Cai and Padoa-Schioppa (2012) [6••]	Task: Binary choice task with value range constant across long blocks. Finding: Normalized CV signals in macaque vACC and dACC. Finding: Evidence for dynamic updating of value range.	Similar set of findings as [51••]. Neural value signals in ACC are consistent with linear normalization and are sensitive to recent reward history.
single unit	OV	Kobayashi et al. (2010) [47••]	Task: Pavlovian reward task with value range that varies across blocks of variable duration. Finding: Normalized OV signals in macaque OFC. Finding: Evidence for dynamic updating of value range.	Neural signals in OFC are consistent with value normalization and provide evidence for the temporal scale of normalization. This study also found some neurons that code value using an absolute code.
single unit	SV	Sallet et al. (2007) [52]	Task: Pavlovian reward task using two different value ranges, with value range constant within a single block. Finding: Normalized value signals in macaque ACC at time reward predictive cue shown.	Neural signals are consistent with linear value normalization. Results are also similar to [6••,51••]
single unit	PE	Tobler et al. (2005) [48]	Task: Pavlovian reward task with a larger number of potential rewards. Finding: Normalized PE signals in same area at time of reward delivery.	Neural signals are consistent with linear normalization.
fMRI	PE	Bunzeck et al. (2010) [46]	Task: Pavlovian monetary reward task. Subjects shown one of three cues associated with different lotteries over monetary payoffs, followed by the resolution of the lottery. Cues are randomly interleaved, not blocked. Finding: BOLD responses in hippocampus, vSTR, and OFC are consistent with the encoding of a normalized PE at time of reward.	Evidence is consistent with the claim of PE normalization, but is also consistent with a normalized OV signal. Also, since trials are randomly interleaved – instead of blocked – any normalization process might be cue/context dependent.
fMRI	PE	Park et al. (2012) [54•]	Task: Pavlovian monetary reward task, similar to [48]. Subjects were shown one of four cues associated with different lotteries over monetary payoffs, followed by the resolution of the lottery. Cues were randomly interleaved, not blocked. Finding: BOLD responses in vSTR are consistent with the encoding of a normalized PE at time of reward.	The cues differ on the size and probability of the potential rewards. As a consequence, their results are also consistent with the encoding of a ‘prediction error signal’ for learning the probabilistic structure of the task (i.e. the stimulus–stimulus associations). The proposed trial-to-trial normalization is more like that proposed in [48] than [53], but the same caveat for [46] applies here.
single unit	PE	Tremblay and Schultz (1999) [53]	Task: Pavlovian reward task with value range constant across blocks with different range and mean reward. Result: Normalized PE signals in macaque OFC at reward anticipation and delivery.	Neural responses are consistent with value normalization.
single unit	OV	Bermudez and Schultz (2010) [64]	Task: Pavlovian reward task with value range constant across blocks (three values per block) with different range and mean reward. Finding: Normalized OV signals in macaque amygdala at time reward-delivery.	Data are also consistent with encoding of an absolute PE signal since the mean expected reward also changes across blocks (as long as the neural response for PE=0 is not zero). This study also found some neurons that code value using an absolute code.
single unit	PE	Hosokawa et al. (2007) [72]	Task: Pavlovian reward task looking at both appetitive and aversive rewards, with value range constant across blocks. Finding: Normalized PE signals in macaque OFC at time reward-predictive cue shown.	Results extend [53] to both appetitive and aversive outcomes. However, the task does not dissociate between OV and PE.
fMRI	OV	Elliot et al. (2008) [73]	Task: Simple fMRI version of [53] with three different reward conditions. Reward pairings are randomly interleaved, not blocked. Finding: BOLD responses in OFC consistent with the encoding of a normalized reward signal at time reward-predictive cue shown.	The paradigm does not dissociate between OV and PE, so the value normalization could be taking place for either or both value signals.
fMRI	OV	Nieuwenhuis et al. (2005) [74]	Task: A Simple monetary gambling task with two conditions, ‘win’ and ‘loss’, with three possible outcomes per condition. Task condition varies from trial to trial. Finding: BOLD responses in vSTR, vmPFC, PCC consistent with the encoding of a normalized reward signal at outcome.	Data are consistent with the presence of value normalization, but the paradigm does not dissociate OV and PE.

Second, following the sensory literature, contexts are kept constant within long blocks of trials. The reason for this is the same one as in the sensory coding literature: since the normalization parameters do not adapt immediately to changes in the distribution of values that might be encountered, it is useful to keep the distribution of values that might be encountered constant for a few trials to make sure that the normalized code is fully revealed.

Third, the fact that the contingencies between the stimuli presented at the beginning of the trial (e.g. at the time of choice), and the eventual rewards are deterministic, rules out an additional potential confound. As explained above, without this feature a non-zero PE signal would also be computed at outcome. In addition, the brain would also need to learn the stimulus-reward contingencies (i.e. what is the probability of reward associated with each stimulus). This leads to a potential confound because under linear-normalization, the PE signals computed at the time of outcome would have exactly the same shape as the ‘surprise signals’ that are required to learn the stimulus-reward contingencies of the task (independently of value) [49,50].

Basic experimental tests of value normalization

A sizeable number of studies have attempted to understand how the brain normalizes SV, OV, and PE signals. Table 1 provides a detailed summary of the existing experimental evidence on value normalization, which includes monkey neurophysiology and human fMRI studies. Here, we highlight several recent macaque neurophysiology studies that have provided the strongest support to date for value normalization, as well as some studies that are subject to some of the concerns described in the previous section.

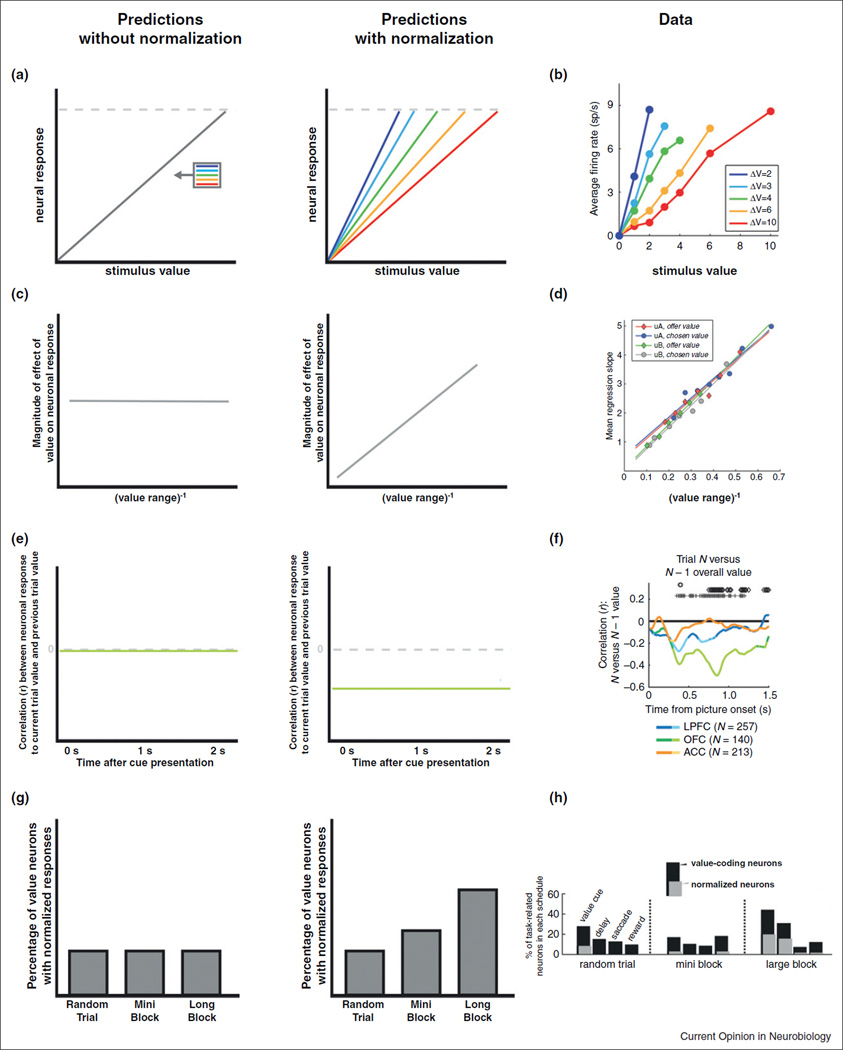
Several neurophysiology studies have provided strong evidence in favor of the existence of a normalized value code. Two studies used a decision-making paradigm that closely resembles the one described above to carry out basic tests of value normalization in OFC [51••] and anterior cingulate cortex (ACC) [6••] (Table 1). In both cases, SV coding neurons in both areas exhibited a pattern of activation with a striking resemblance to linear normalization (Figure 3a–d). The finding is remarkable, as linear normalization is predicted by the efficient coding hypothesis when SV is sampled uniformly (Figure 1d). By contrast, most studies of sensory normalization find non-linear normalization curves (with a response shape similar to the one in Figure 1c), but typically sample stimuli from non-uniform distributions [38••]. Two other studies, using Pavlovian tasks, have found neurons encoding normalized OV and PE signals in OFC, [47••,53] and normalized SV signals at the time of cue in ACC [52], and normalized PE coding in dopamine neurons at the time of reward delivery [48]. Note that while none of the tasks in these studies are identical to the one proposed here (Figure 2), their key components are similar.

Figure 3. Evidence in support of value normalization.

The left and middle columns describe the predicted neural responses without value normalization (left) and with value normalization (middle). The predictions are presented in a visual style that matches data from recent studies (right). (a, b) In this experiment, macaques make decisions among stimuli associated with rewards drawn from uniform distributions with five different value ranges (different colors of ΔV). The plots describe the predicted and actual neural responses for a unit encoding SV (data for OFC neurons from [51••]). (c, d) A different test of value normalization for the same choice task. Under normalized coding, a linear regression of neural responses on absolute value signals should decrease with the range (or increase with the inverse of the range, as shown) of stimulus values being evaluated, but should be range invariant under absolute coding. The data are again for OFC neurons from [51••]. (e, f) Basic test of dynamic tuning of the value normalization parameter during a different macaque decision-making task. Under absolute value coding (i.e. no normalization), the value of previous stimuli should not affect the neural responses to current stimuli. By contrast, under value normalization, there should be a negative correlation between the neural responses to current stimuli and previous values (since they increase the brain’s optimal estimate about the current distribution of stimuli that it might encounter). Neurons in OFC (green line) exhibited this type of dynamic tuning. Data from [55••]. (g, h) Another test of dynamic tuning of the value normalization parameters. The paradigm was a Pavlovian task in which value contexts where presented in blocks of different length. If dynamic tuning evolves gradually with time, then the theory predicts that the number of neurons exhibiting significant normalized value coding would increase with the length of the block. OFC neurons exhibited this pattern. Data from [47••].

A recent fMRI study [54•] investigated the existence of normalized PE signals using Pavlovian cues in which subjects were shown four stimuli containing explicit descriptions of different lotteries over monetary payoffs, followed by the resolution of the lottery. Using an interleaved trial structure, they found responses in ventral striatum (vSTR) at the time the uncertainty was resolved consistent with the encoding of normalized PE signals. This result would argue for a normalization of PE that is consistent with linear value normalization, a proposal that supports another neurophysiology study of normalization [48] (Table 1). The authors also found striatal coupling with both vmPFC and parts of the midbrain, which could play a role in supporting the computation of normalized PE. However, even though the task did not require any learning (i.e. the reward probabilities were stated explicitly), the PE signal found in vSTR is also exactly the signal expected by a system concerned with learning stimulus–stimulus associations. For this reason, further work is needed to fully dissociate normalized PE signals and ‘surprise signals’.

Tests of temporal properties of value normalization

A richer way to test a theory of value normalization is to also investigate how its normalization parameters evolve over time. It may be that different brain regions, such as those discussed in the previous section, have different time scales for normalization [47••]. For example, in ACC and OFC, does the distribution of values that gives shape to the normalization curve evolve quickly or slowly? Although this problem is only beginning to be investigated [6••,47••,55••], a natural hypothesis is that the normalization parameters are dynamically tuned to reflect the recent history of values.

One potential hypothesis, if reward history affects value computation, is the following: in a value-sensitive region of the brain (e.g. OFC), the neural response to a given value should be negatively correlated with the absolute value of recently encountered stimuli. Interestingly, there is evidence consistent with this prediction. A recent study [55••] had precisely this finding in OFC neurons (Figure 3e, f). Similar sensitivities of current value responses to recent previous values were also identified in a similar area of OFC, as well as in ACC [6••,51••]. A related question, then, if the range of potential values changes (e.g. a new block in an experiment), is how long does an adaptation take? Using a Pavlovian task, a recent study found that the fraction of value normalized neurons in OFC increased with block duration [47••] (Figure 3g, h), demonstrating that adaptation is not instantaneous, but occurs on the order of approximately ten to fifteen trials.

Other mechanisms through which context affects decisions

Our focus has been on a very specific type of value normalization. Here, we discuss other mechanisms through which context can affect values and choices [56]. Importantly, we view these computations as distinct from value normalization, but highlight them because of their close relationship to our discussion of normalization.

Relative versus normalized value coding

Behavioral [57,58] and neural data [14•,59,60] show that stimuli are often evaluated relative to a reference outcome (often the status-quo), or to each other. For example, a recent study of SV coding during binary choice found an area of vmPFC that at any given time encoded the value of the attended minus the value of the unattended stimulus [14•]. The computation of relative value signals entail changing the ‘zero’ of the value scale, in the sense that every SV is computed relative to the value of some other stimulus (by subtracting the value of the later). By contrast, normalized value signals entail changing the mapping from absolute values to the neural responses in value coding neurons, which look more like a change in the ‘units’ of the value scale.

Within-decision versus cross-decision value normalization

It has been proposed that SV are also subject to normalization within single-choice episodes based only on the distribution of values in the current choice set [61•,62••]. The critical distinction between this type of normalization and the one described above is the time frame at which it operates. In cross-decision normalization, the brain uses the recent history of values that it has encountered to rescale the way it encodes value signals such as SV, OV, and PE, but the value assigned to a stimulus does not depend on what other elements are in the current choice set. The opposite is true in within-decision normalization.

Value normalization versus cognitive modulation of value

Several studies have shown that the OV signals in OFC at the time of experience depend on subjects’ beliefs about its identity, independently of its physical properties [22,63]. For example, an area of OFC associated with the encoding of OV responds more strongly to the degustation of the same wine when subjects believe it to be more expensive [22]. These context effects demonstrate that ‘cognitive beliefs’ play a key role in assigning value to even basic sensory stimuli, but do not entail normalization as defined here.

Conclusion

The studies highlighted here provide support in favor of the hypothesis that neural representations of value are normalized based on the local distribution of values, that the functional form of the normalization is consistent with the efficient coding hypothesis, and that the normalization parameters are dynamically tuned. These findings point to several questions of critical importance for understanding how the brain computes subjective values.

First, despite clear evidence for value normalization, several of the studies described above also found many neurons that exhibit absolute value coding [47••,55••,64]. How do absolute and normalized value signals work in concert? For example, is the role of the absolute coding neurons to provide the distributional information that gives rise to the normalization parameters? If this is the case, how do these units handle the dynamic range problem that motivates the use of normalization in the first place?

Second, what are the exact algorithms used in the dynamic tuning of the normalization parameters? Questions of particular interest are the speed of the adaptation, the treatment of uncertainty about the underlying distribution of values that is likely to be faced, and whether context-dependent normalization parameters can be learnt when contexts are not blocked (e.g. if green and blue trials in Figure 2 are randomly intermixed). In particular, are Bayesian algorithms used to update the distributional information optimally [65–67]?

Third, a growing body of evidence suggests that SV are computed at the time of choice by estimating the attributes or characteristics of stimuli, assigning value(s) to those attributes based on previous experience or current internal and external states, and integrating them [3,68,69]. Is normalization applied at the attribute computation level or only at the integrated SV level? Owing to the complex and multi-dimensional nature of all subjective values [3,5], recent advances in understanding the integration and normalization of multi-sensory information might provide useful clues [70].

A larger goal, which we have not discussed in-depth here, is how the brain might implement value normalization computations. In general, it remains unclear to what extent normalization mechanisms for value resemble those that have been identified for the case of sensory processing, but some commonalities seem likely [38••]. Moving forward, models of subjective value computation in the brain should include testable hypotheses for plausible normalization mechanisms. Understanding the extent of normalization in the valuation process will in turn improve our understanding of how the brain makes decisions.