Abstract
The striatal dopamine signal has multiple facets; tonic level, phasic rise and fall, and variation of the phasic rise/fall depending on the expectation of reward/punishment. We have developed a network model of the striatal direct pathway using an ionic current level model of the medium spiny neuron that incorporates currents sensitive to changes in the tonic level of dopamine. The model neurons in the network learn action selection based on a novel set of mathematical rules that incorporate the phasic change in the dopamine signal. This network model is capable of learning to perform a sequence learning task that in humans is thought to be dependent on the basal ganglia. When both tonic and phasic levels of dopamine are decreased, as would be expected in unmedicated Parkinson’s disease (PD), the model reproduces the deficits seen in a human PD group off medication. When the tonic level is increased to normal, but with reduced phasic increases and decreases in response to reward and punishment respectively, as would be expected in PD medicated with L-Dopa, the model again reproduces the human data. These findings support the view that the cognitive dysfunctions seen in Parkinson’s disease are not solely due to either the decreased tonic level of dopamine or to the decreased responsiveness of the phasic dopamine signal to reward and punishment, but to a combination of the two factors that varies dependent on disease stage and medication status.
Keywords: Striatum, Dopamine, Computational model, Learning, Parkinson’s disease
Introduction
The basal ganglia (BG) are a set of interconnected, sub-cortical nuclei which form a complex network of loops integrating cortical, thalamic and brainstem information [1]. They have been primarily associated with the control of movement but recent anatomical [49] and neuroimaging data [19] have shown that they are also involved in higher cognitive functions.
Human behavioral studies have shown that subjects with Parkinson’s disease (PD) who are treated with dopaminergic medication are impaired on learning cognitive tasks [41, 3, 52, 53, 67, 68, 69, 70, 11, 12, 13, 14, 22, 23]. Furthermore, PD subjects tested after a period of medication withdrawal show different cognitive deficits on the same tasks [13, 14, 22, 69]. This raises questions about the difference between the effects on learning of PD and of the medication used to treat PD. To understand this we need to consider how the disease process of PD modifies the dopamine learning signal, and how the medication leads to different changes in the signal.
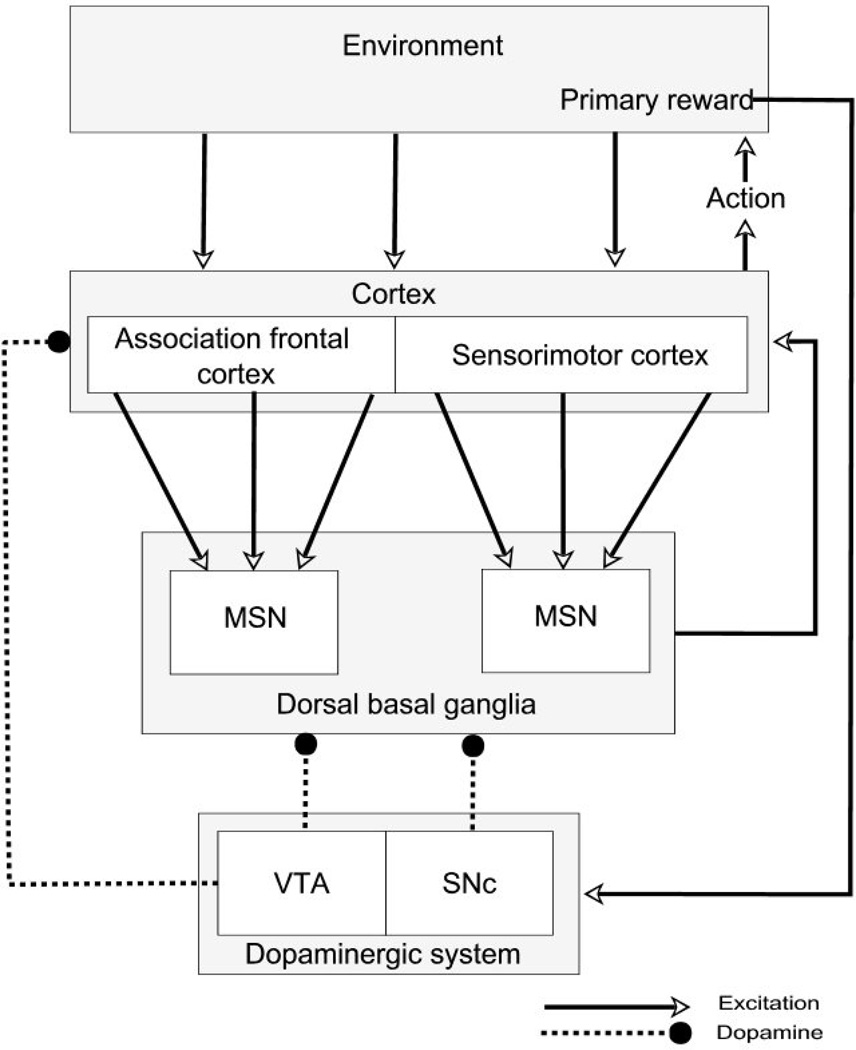
In PD, midbrain dopamine cells are lost, but those arising in the substantia nigra pars compacta (SNc) are lost to a far greater degree than those arising in the ventral tegmental area (VTA) [37]. The outputs of both nuclei project most significantly to the striatum, the principal input nucleus of the basal ganglia. Figure 1 summarizes some of the key anatomical pathways. The SNc projects principally to the dorsal striatum, which is a key structure in action selection [50]. The dorsal striatum can itself be subdivided into two major sub-areas, one with inputs from motor related cortical areas and engaged in selecting motor responses and a second with inputs from associational areas of cortex and engaged in more cognitive aspects of behavior selection.
Figure 1.
Some key anatomical components of the corticostriatal loops involving cognitive and motor areas of the dorsal striatum. Dopaminergic neurons of the SNc are lost in Parkinson’s disease, with relative sparing of the dopaminergic neurons of the VTA. In the model, the dorsal basal ganglia is represented by direct pathway medium spiny neurons. MSN – striatal medium spiny neuron; SNc – substantia nigra pars compacta; VTA – ventral tegmental area.
The best understood medication in PD is L-Dopa, a precursor of dopamine. One hypothesis is that the cognitive impairment in medicated PD is due to an overdose effect of the medication on the ventral part of the striatum where there has been less damage to the dopaminergic input [22]. Loss of SNc dopaminergic cells leads to a decrease of the steady-state background level (tonic level) of dopamine in the dorsal striatum [18]. L-Dopa is known to raise the tonic dopamine level, which would be desirable in the depleted dorsal striatum, but may not be in the less affected ventral striatum.
However, learning in the medium spiny neurons (MSNs) of the striatum has been shown to be dependent not on tonic levels of dopamine, but on pulses of dopamine, phasic changes, overlying the tonic level [85]. These phasic changes in firing of dopaminergic neurons occur in response to unexpected rewards, cues which have been learned to reliably predict reward, and the omission of reward after a reward-predicting cue [64].
The consequences of the loss of the dopaminergic cells in PD on the phasic changes, and therefore directly on learning, has proven difficult to investigate in both animal and human experiments. The use of computational modeling to simulate human learning data in PD therefore provides an alternative method for investigating the mechanisms that lead to learning impairment in PD.
There have been recent computational models of the basal ganglia that successfully simulate some behavioral tasks in which subjects with PD have performance deficits [21, 22, 23, 34]. These models have simulated the corticostriatal loops and use the phasic dopamine signal for learning. The model presented here attempts to account for changes to both the tonic and phasic aspects of the dopamine signal. The basic unit in this model is the medium spiny neuron (MSN), the principal neuron of the striatum, that has been hypothesized to play a key role in action selection [50]. This class of neuron has been shown to have currents dependent on the tonic dopamine level [35, 57, 76, 78, 79] as well as requiring phasic dopamine signals for long-term potentiation (LTP) [85]. Previous network models of the basal ganglia have not attempted to model the MSN at a level where the effect of changing both tonic and phasic dopamine can be studied. This model is therefore based on a network of MSNs that are simulated at the level of ionic currents in order to effectively study the impact of changing tonic dopamine levels occurring in PD. The learning rules in the network incorporate the phasic dopamine changes. Therefore the model is also able to simulate changes in the phasic dopamine signal that may occur in PD. This allows us simulate whether changing only the tonic or phasic dopamine is sufficient to replicate behavioral results in an action selection task, or whether a combination of tonic and changes is necessary to produce the changed behavior.
The most common role proposed for the dorsal striatum is action selection [50]. Many computational models of the striatum have used lateral inhibition to produce a ‘winner takes all’ action selection network [5, 28, 84, 43, 44, 73, 89]. This was based on the extensive recurrent dendritic field of the medium spiny neuron that potentially innervates thousands of other MSNs [56]. When demonstrated experimentally, recurrent inhibition was found to be very weak compared to feedforward inhibition [81, 42], although the absolute number of recurrent synapses is large [16, 32, 80] Combined with the very low firing rate of MSNs, it is difficult to see how lateral inhibition could be a mechanism for a “winner takes all” network in the striatum.
Without the use of lateral inhibition, one candidate mechanism for action selection in the striatum is control of the rate of change from the hyperpolarized down state to the up state of the MSN. In response to current injection, MSNs exhibit a rapid rise from the down state with a shoulder to a subthreshold plateau potential and then a gradual depolarization of the plateau potential. This provides a mechanism where small changes in strength of synaptic input could produce relatively large changes in the time that the firing threshold is crossed. The simulations presented investigate whether this mechanism is sufficient to learn to select amongst competing actions without the use of any lateral inhibition between neurons in the network and without competition between parallel corticostriatal loops in downstream nuclei of the basal ganglia.
The simulated network of model MSNs represents direct pathway striatal neurons involved in action selection. As only the direct pathway is represented, only dopamine modulation at the D1 receptor is considered [26]. The simulated task is a human cognitive sequence learning task where the subject learns to navigate through a set of rooms by choosing the one correctly colored door out of three in each room [69]. The firing of each MSN in the network represents choosing an action, in this case choosing a door by color. The network of MSNs learns the correct door in each room using a simulated dopamine signal.
The level of modeling has been chosen to be appropriate to investigate changes in both tonic and phasic dopamine levels. Tonic dopamine levels modulate currents that control the excitability of MSNs. We therefore model the neurons at the level of the ionic currents that are modulated by dopamine. Phasic dopamine changes are necessary for LTP in MSNs. We therefore develop a set of learning rules based on spike timing dependent plasticity (STDP) that incorporate phasic dopamine changes to produce realistic modification of the size of corticostriatal synapses.
We first re-analyze some of the data from the original sequence learning task for comparison with certain findings of the model. We then show that the model is capable of learning to perform the task with the same level of accuracy as human control subjects. Next, we show how changing tonic and phasic dopamine, in a manner consistent with known physiological changes leads to error levels consistent with those seen in patient groups on and off medication. We then show the effect of only varying the tonic or phasic dopamine on model performance. Finally we discuss reasons why the model does not fit the data in all areas and predictions the model makes for the performance of tasks by PD patients.
Methods
MSN Model Description
The model of the MSN used in this study is derived from work of Wilson and colleagues showing that the hyperpolarized down state of an MSN and the transition from the down state to the up state are mainly under the control of a small set of potassium currents [88]. The hyperpolarized down state is principally determined by an inwardly rectifying potassium current, IKir [39, 40, 54, 48]. At hyperpolarized membrane potentials IKir provides a current that resists depolarization and therefore stabilizes the down state, accounting for approximately 50% of resting conductance [82]. IKir activates rapidly and does not inactivate [33].
There have been three main outward rectifying potassium currents demonstrated in MSNs [54]: two transient A-type currents and a non-inactivating current [74, 75, 55].
One of the A-type currents is fast inactivating and only available above spike threshold [77]. This current is therefore excluded from this model as it does not contribute to the transitional behavior of the neuron. The second A-type current is the slowly inactivating potassium current, IKsi. This current is available at subthreshold membrane potentials and inactivates over a time course of hundreds of milliseconds to seconds [25, 74, 77]. This slow inactivation reduces the effect of IKsi gradually while the cell is in the up state, leading to a gradual ramp increase in the plateau membrane potential in the up state. . As shown by Mahon et al. (2000) [45], physiological inactivation of IKsi also leads to a reduced time to firing of the first spike if a second down to up transition occurs shortly after a first. The non-inactivating potassium current, IKrp, is also available at subthreshold membrane potentials. These two outwardly rectifying currents contribute to the plateau membrane potential of the up state by opposing the depolarizing influence of excitatory synaptic input and inward ionic currents.
It has also been shown that slowly inactivating L-type calcium currents, IL-Ca, are important in the maintenance of the plateau potential in many neurons [65, 10, 59]. This high threshold calcium current, which supplies an inward, depolarizing drive current, has been shown to be present in MSNs [4, 71] and is therefore included in this model.
The computational design of the model is based on that of Gruber et al. (2003) [29] with the neuron represented as a single, isopotential point using only those currents necessary to the behavior under examination. This provides the computational tractability to examine the behavior of a network of model neurons without the requirement for high-powered computational facilities. The main change from the model of Gruber et al. (2003) is the introduction of inactivation for IKsi.
Two of the currents used in this model are modulated by tonic dopamine levels. Both IKir [76, 57] and IL-Ca are enhanced by D1 agonists [78, 79, 35]. Later simulations show how changing the tonic dopamine level changes the up and down state membrane potentials in the model due to the effects of these two currents.
MSN Model Equations
Modified Hodgkin-Huxley techniques are used to simulate an isopotential model of an MSN. The change in membrane potential is modeled as a differential equation relating the rate of change to the ionic currents (1). The moment-to-moment membrane potential is calculated by numerical integration using a fifth order Runge-Kutta algorithm with a maximum step size of 1 ms [60].
| (1) |
where C is the membrane capacitance, Vm is the membrane potential, Is is the current due to the synaptic input, IL is the leakage current, IKir is the inwardly rectifying potassium current, IL-Ca is the L-type calcium current, IKsi is the slowly inactivating A-type potassium current, IKrp is the non-inactivating potassium current and DTonic is the neuromodulator factor, representing the tonic dopamine level, which acts as a multiplier on IKir and IL-ca. Since there is no data on the relative modulation of IKir and IL-Ca by dopamine, we use the same multiplication factor for both.
Each current, except for IL-Ca, is modeled as the product of a conductance and a linear driving force
| (2) |
where Ii is the ionic current, gi is the conductance, Vm is the membrane potential and Ei is the reversal potential for that ion. For the potassium currents the conductance is voltage dependent, and is fitted to a Boltzmann function of the form:
| (3) |
where gi is the maximum conductance for that current, Vh is the half-activation parameter, the voltage at which 50% of the current is available, and Vc controls the slope of the activation curve. Values of Vh and Vc for the inwardly rectifying potassium current [54, 48], the non-inactivating potassium current [55] and the slowly inactivating potassium current [25] have been obtained from electrophysiological recordings (Table 1).
Table 1.
MSN parameters used throughout these simulations.
| Parameter | Value |
|---|---|
| Membrane capacitance (µF/cm2) | 1 |
| Temperature (°C) | 37 |
| Excitatory reversal potential (mV) | 0 |
| Firing threshold (mV) | −45 |
| Input amplitude (µS/cm2) | 0.5 |
| Input rise time (ms) | 7 |
| Input decay time constant (ms) | 8 |
| Leakage conductance (mS/cm2) | 0.008 |
| Leakage reversal potential (mV) | −75 |
| Potassium reversal potential (mV) | −85 |
| IKir maximum conductance (mS/cm2) | 1.2 |
| IKir Vh (mV) | −110 |
| IKir Vc (mV) | −11 |
| IKsi maximum conductance (mS/cm2) | 0.5 |
| IKsi maximum variable conductance (mS/cm2) | 0.1 |
| IKsi variable conductance activation time (ms) | 1000 |
| IKsi variable conductance inactivation time (ms) | 1000 |
| IKsi Vh (mV) | −13.5 |
| IKsi Vc (mV) | 11.8 |
| Calcium concentration outside (mmol/cm3) | 0.002 |
| Calcium concentration inside (mmol/cm3) | 0.00001 |
| Calcium maximum permeability (nm/s) | 4.2 |
| Calcium Vh (mV) | −34 |
| Calcium Vc (mV) | 6.1 |
Inactivation of IKsi is represented by a 0.1% decrease in gKsi at each time step when the membrane potential is above −60mV, and, for reactivation, a 0.1% increase when Vm is below −60mV.
IL-Ca is not well modeled by a linear driving force as the low level of intracellular calcium leads to a large concentration gradient across the membrane. This leads to a non-linearity in the voltage/current relationship of the open channel. Following Hille (1992) [36], this current has therefore, been modeled using the Goldman-Hodgkin-Katz equation.
| (4) |
where z = 2, F = 9.648 × l04 C mol−1, R = 8.315 V C K−1 mol−1 and T = 273.16 +37K. [Ca]o is the extracellular calcium concentration and [Ca]i is the intracellular calcium concentration. From this the current is obtained by:
| (5) |
where PL-Ca is the membrane permeability to calcium. Bargas et al. (1994) [4] showed that the membrane permeability can be represented as a Boltzmann function of the form seen in (6).
| (6) |
where P̅L–Ca is the maximum permeability to calcium. The values used by Gruber et al. (2003) [29] for Vh and Vc for this current differ from those found experimentally. They explain that they have modified the values to account for the higher concentrations of divalent charge carrier used in the extracellular solution in the electrophysiological experiments and we have followed this.
Excitation is modeled as discrete conductance changes. Each synaptic event has a peak of 0.4nS, a rise time of 7ms and an exponential decay with half-life of 8ms. Previous simulations have suggested that a single excitatory input to a distal dendritic spine produces a peak EPSP amplitude at the soma of approximately 20mV [87]. The starting figure used here for the peak conductance change of 0.4nS produces an EPSP of 15mV which allows for growth of the synapse during learning.
The corticostriatal excitation is modeled as separate inputs, each firing at random frequency with a mean of 25Hz and a standard deviation of 2Hz (SD of firing of 10Hz was used in some simulations, but had no demonstrable effect on outcome). The time of the first spike when the excitation period starts is staggered by a random number between zero and the period of firing of the individual neuron (mean = 40ms) to allow for variable delays in activation of corticostriatal neurons as the environmental context is changed. After the first spike, there is a random amount added or subtracted to the time of each input spike, with a mean of 0ms and a maximum of 5ms. This variability is introduced to simulate the noise seen in the up state in MSNs.
There are no sodium currents in this model, so firing is simulated by use of a probabilistic function when the membrane potential is above a firing threshold.
| (7) |
Where Vf is the firing threshold and tp is the time at which the previous action potential occurred. This means that the MSN will fire immediately the firing threshold is crossed as the rise from the down state to the up state occurs and then with a minimum refractory period of 20ms thereafter.
Parameter values used in the model are shown in Table 1.
Learning rules
Learning is represented as a change in synaptic weight of each corticostriatal input. This effectively represents a change in the maximum conductance of the synapse. There are three conditions under which learning occurs.
The weight is decreased each time the neuron fires.
The weight is increased when reward is obtained.
The weight is decreased when an aversive event occurs.
This is equivalent to long term depression (LTD) occurring each time a neuron fires [9], or an aversive event occurs, and long term potentiation (LTP) occurring when reward is obtained [85]. The learning in both cases is based on spike timing dependent plasticity (STDP) rules [6, 47, 7], with a modification such that strong synapses undergo relatively less potentiation than weak synapses [83]. The LTD each time an MSN fires is calculated by:
| (8) |
where W is the current synaptic weight, Cd is the average amount of depression from one pairing, δtInput is how long before firing an excitatory input occurred at this synapse and TSTDP is the decay time constant for the synaptic input. From this rule, the weight change is proportional to the current weight. Therefore the smaller the synaptic weight the less LTD will occur from one input spike-output spike pairing.
The LTP update equation (9) proposes a three factor rule for positive striatal learning after reward is obtained [86]. The increase in synaptic weight is related to the timing of synaptic input to the synapse, timing of neuronal MSN firing and the phasic change in dopamine levels. All 3 factors are required for LTP in the model neuron and the amount of LTP is determined by the temporal proximity of the 3 factors.
| (9) |
where ΔD is the proportional dopamine change, δtfire is the time since the MS neuron fired, TSTDP is the decay time constant for the synaptic input trace and TDDP is the decay time constant for the neuron firing. TSTDP is the trace for synaptic input in both the LTP and LTD rules. This represents a process such as influx of calcium into the dendritic spine occurring after the depolarization of the dendritic spine compartment caused by an excitatory input [8]. In theory this constant should be the same in both LTP and LTD. The weight change is independent of the current weight. Therefore a synapse with a small weight will receive the same amount of potentiation as a stronger synapse which had a coincident input. But this amount of potentiation will be a greater proportion of the original synaptic weight for the smaller synapse. As shown by Van Rossum et al. (2000) [83] this tends to lead to an even distribution of synaptic weights rather than a clustering of synaptic weights at the maximum and minimum possible values. This potentiation could continue with each reinforcing event as there is no upper bound on the synaptic strength introduced by equation (9). As there is a limit to how much a synapse can grow, a constant upper bound on synaptic weight of 2 is introduced, producing a maximum EPSP amplitude of 0.8nS.
Equation (9) defines the change in synaptic weight when an action has been selected that leads to reward. A similar rule is used to model disappointment or punishment. This occurs when an action is selected that either does not lead to an expected reward or leads to an outcome that is implicitly punishing. In such a situation the dopamine level is decreased phasically and the trough level is used to calculate amount of LTD. The update rule is a cross between the 3 factor LTP rule and the STDP LTD rule. The weight decrease is proportional to the current weight as for the LTD rule. As for the LTP rule, this is three factor learning using the proportional drop in dopamine level, a synaptic trace showing how long before the neuron fired that particular synapse had an excitatory input and a back propagation trace showing how long before the dopamine pulse the neuron fired.
| (10) |
Again, TSTDP would seem to be implementing the same synaptic trace mechanism as in the earlier LTP and LTD rules, so should in theory be assigned the same value. Evidence for dopaminergic neuron firing decreasing in aversive situations is controversial [38], and it has been shown that acetylcholine levels are integral in controlling dopamine release in response to dopamine cell firing [15]. However, decreases in dopamine cell firing have been shown to lower extracellular dopamine levels in the striatum [72]. The time constant of clearance has been measured at 74ms [27], which is comparable to the time course of the rise in dopamine after burst firing that is supposedly an adequate signal for LTP. A recent model [2] of dopamine volumetric transmission suggests that the phasic dopamine signal does reach receptors very quickly. Taken together, this suggests that phasic decreases in dopamine neuron firing could provide an adequate signal for corticostriatal LTD.
The LTD rule (Equation 8) is applied every time an MSN fires, even when reward or punishment will occur. As the proportional depression from one pairing (Cd) is set to be very small (0.01), the comparative effect of LTD due to neuronal firing when reward or disappointment/punishment occurs is very small. It is included here because it is an important factor in stabilizing synaptic weights in simulations where one of either reward or disappointment/punishment do not occur at each action selection point.
Devaluation of reward/punishment signal
As has been shown by Satoh et al. (2003) [62], firing of dopamine neurons in choice tasks is related to the uncertainty of the choice leading to reward. If there are three choices and the correct choice is made on the first attempt (when there was only a one in three chance of being correct), the dopamine neurons will fire at a higher rate than when the correct choice is made on the third attempt (when the fact that reward is due is known with certainty in overtrained monkeys). Similarly, if the wrong choice is made on the first attempt, the dip in firing of dopamine neurons is less than when the wrong choice is made on the third attempt. We refer to this as RepeatDevaluation in the model (Equation 12). For the repeat devaluation, either the number of previous times correct is zero or the number of previous times wrong is zero. Thus the equation simulates the positive and negative magnitudes of the dopamine signal found when the monkey chooses correctly and incorrectly. It can also be seen from recordings published by Schultz’s group that as the response of the dopamine neurons chains back from the time of reward to the earliest predictor of reward, the magnitude of the dopamine cell response decreases [63]. We refer to this as TemporalDevaluation in the model (Equation 13). Temporal devaluation could also be considered as the number of decision points that any given decision is away from the reward/punishment when the influence of the reward/punishment on updating the synaptic weights that led to that decision is made.
| (11) |
| (12) |
| (13) |
| (14) |
where DP is the proportional devaluation, ΔDmax is the maximum pulsatile dopamine level and DTonic is the background dopamine level. The standard level for the percentage devaluation used in these simulations is 30%. ΔDmax is greater than DTonic for rewarding events and less than DTonic for disappointing/punishing events, so producing a positive and negative ΔD respectively. The size of ΔD is therefore adjusted in the model to take account of this devaluation of the reward and punishment signal as certainty increases and as the current room is further from the reward.
Whilst this concept of reward devaluation can be seen from electrophysiological studies [62, 63], it has not to our knowledge previously been applied in this manner to a computational model.
In modeling the PD disease process, the only factors that are changed are ΔDmax, DTonic and DP. All parameters in other learning equations and membrane potential equations remain the same.
Task Model
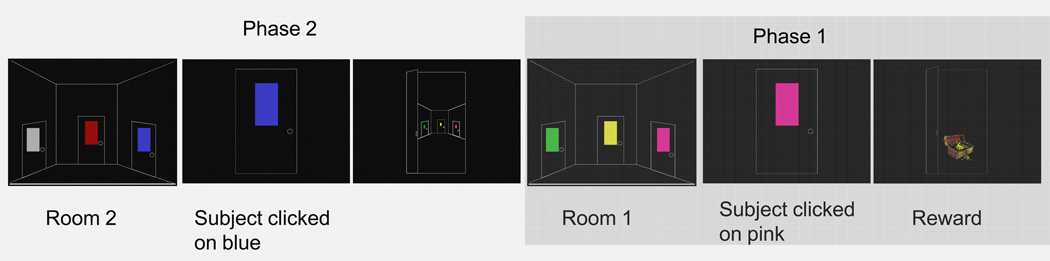
To test the model’s ability to learn sequences of action we simulated a chaining task where a subject is required to learn a sequence of choices of door colors to navigate through a set of rooms, eventually reaching the outside (Figure 2 and, for a full description, see [69]). This task was chosen because data was available for healthy controls and Parkinsonian subjects both on and off of L-Dopa with both similarities and differences in performance between the groups.
Figure 2.
Sample screen events for two phases as seen by a human subject. In acquisition phase 1 (right), the subject sees 3 colored doors and chooses one by clicking with the mouse. In this case, the subject chooses pink and gets the reward. If the subject had chosen one of the other 2 colors, the door would have been locked, the order of colors would have been shuffled and the subject would have to choose again. After choosing the correct door 5 times consecutively, the subject is started in phase 2 (left). Here the subject sees 3 different colored doors. If he chooses the wrong door, it is again locked. If, as above, he chooses the correct door, he sees the first room in the distance and is then moved to that room, where he must remember the previously learned correct door to gain the reward. After 5 consecutive successful 2 room navigations, the chain is lengthened to 3 and finally 4 rooms. If the subject learns the 4 room navigation a probe phase is started. In each room one of the incorrect door colors is replaced with a door color that is correct in another room. In the illustration above, for example, the yellow in the first room could be replaced with blue. The subject then has to navigate through the rooms 6 further times, choosing the colors in the same order as in the acquisition phases to gain the reward.
In Phase 1 the subject sees a room on the computer screen with three doors, each of a different color. The subject selects a door that either leads to the outside (which is considered rewarding) or is locked (which is considered punishing). If the subject makes an incorrect choice, the trial is repeated until the correct door is chosen and the outside is reached. Once the correct door is chosen, a new trial initiates: the display order of the three doors is shuffled and the subject has to choose again. When the correct door had been chosen five times in a row, the subject is taken to Phase 2. In this phase each trial begins in the second room in the chain and the subject is presented with a choice between a new set of doors of three different colors, all different from those seen in the first room. From the second room the incorrect doors are locked in the same manner as in the first room, and are perceived as punishing in the same manner. The correct door, selection of which is again considered rewarding, leads to the first room where the subject has to remember which door color was learned to be correct in the first phase. When the subject has selected a sequence of two doors correctly five times in a row, the chain is again lengthened by one room. This is repeated up to a four room chain length (Phase 4).
After correct learning of the four room chain, the acquisition phases are complete and the subject commences an unsignaled probe phase. In the probe phase one door color in each room is the color that has always been correct in that room; one of the previously incorrect door colors is replaced with a color that was correct in another room in the acquisition phase; the third door is the same incorrect color as it had been in the acquisition phases. The subject must then navigate through the chain 6 times, starting from room 4 and choosing the same correct doors in the same order as in the acquisition phases. In this probe phase the subject shows that they have learned to select the correct door in the correct room. This is equated with having learned the correct sequence rather than, for instance, having learned “Choose red whenever you see it”.
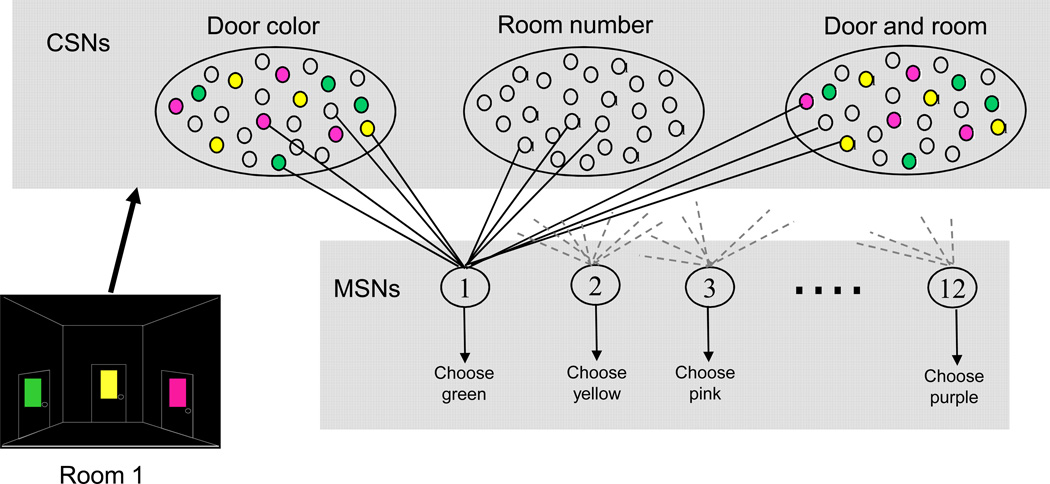
In this task, it is not possible to learn to select by position as the doors are shuffled on each trial. Therefore the subject has to learn to select based on door color (which they do during a practice session before the testing is started). We assume that each color shown excites a different ensemble of cortical neurons and that there will be some differences, but some overlap, in the ensemble of activated neurons depending on which room the color is shown in (Figure 3). Since there are 3 doors in each room and 4 rooms, there are twelve possible cortical ensembles and we use a network of 12 model MSNs to select amongst cortical ensembles. In the rat barrel cortex (an area that has input to striatum) the timing of the first spike in a single neuron contains virtually all of the information necessary to identify the whisker moved [17]. We assume that, in a similar fashion, the timing of the first spike in a striatal MSN contains sufficient information to determine which action, and therefore which door color, will be chosen. The mapping from MSN to color is set at the start of the simulations and remains constant.
Figure 3.
Model neural network. Firing of one of the 12 MSNs represents selecting a particular color. When a subject sees a room there are 3 different colored doors and an indication of which room they are in. Certain model corticostriatal neurons (CSNs) fire due to the 3 colors seen. Each CSN is randomly connected to only 1 of the 12 MSNs. Each MSN also has inputs from CSNs that are activated by colors not present in the current room, so all MSNs have active color inputs no matter what colors are currently present. There are similar connections for CSNs representing the position of the room in the sequence and a configurational representation of both color and room position. Activated CSNs start to fire with a random delay after entering a room at a frequency of 25 (s.d. 2) Hz, with a jitter of s.d. 5ms between each firing event. The randomness in CSN firing introduces noise into the membrane potential of the MSN in the up state.
Each MSN receives an equal number of inputs from each cortical ensemble, not just from the ensemble that is proposing the action that the MSN selects for. Reduction in numbers of neurons from cortex to striatum to the output nuclei of the basal ganglia is assumed to mean that each MSN only then connects back to one of the ensembles innervating it. Each MSN is therefore a link in a corticostriatal loop and selection of that MSN represents removing inhibition from one cortical ensemble. Removing this inhibition selects for the action of choosing one color. We assume that the actual motor movement necessary to click on the chosen color is selected separately, possibly in a parallel, but more dorsal, corticostriatal loop.
The excitatory inputs to the MSNs represent the various features of the environment; the current room, the colors of the doors in the room and a configuration of both room and door color (Figure 3, illustrating the activation for one room). Each corticostriatal neuron (CSN) synapses with only one, randomly chosen MSN [90] and fires when the environmental feature that it represents is present. Approximately 120 excitatory inputs with a peak excitatory conductance of 0.4nS are sufficient to take the model MSN from the down state to the up state. To have sufficient active inputs to each MSN in each environmental state therefore requires modeling approximately 11500 CSNs. We appreciate that not every MSN would have the required number of active inputs, but we are assuming that at least one MSN will in any given environmental situation, and this is the MSN that we are modeling. This random connection protocol makes the minimal assumptions of connectivity between sensory representations in the cortex and the MSNs and does not bias model MSNs for selecting any particular color.
At the start of the simulation all excitatory inputs have a synaptic weight of 1 (simulations with a SD of starting weight of 0.2 had no effect on outcome). For each trial within a room, all inputs associated with features in that room start to fire. As soon as one of the MSNs fires, the door associated with that MSN is chosen. If it is the correct door in that room, that is construed as obtaining reward. In that case the weights of all inputs to the neuron that fired are increased using the LTP learning rule in equation 9. The phasic increase in dopamine levels is delayed by 200ms to account for the activation time of the dopamine neurons after reward [51].
That trial then moves on to the next room (or outside, if it is the final room). If the door chosen is incorrect there is a phasic dip in dopamine and the weights of all inputs to the neuron that fired are decreased according to the aversive learning rule in equation 10. The trial is then repeated in the same room.
Dopamine profiles
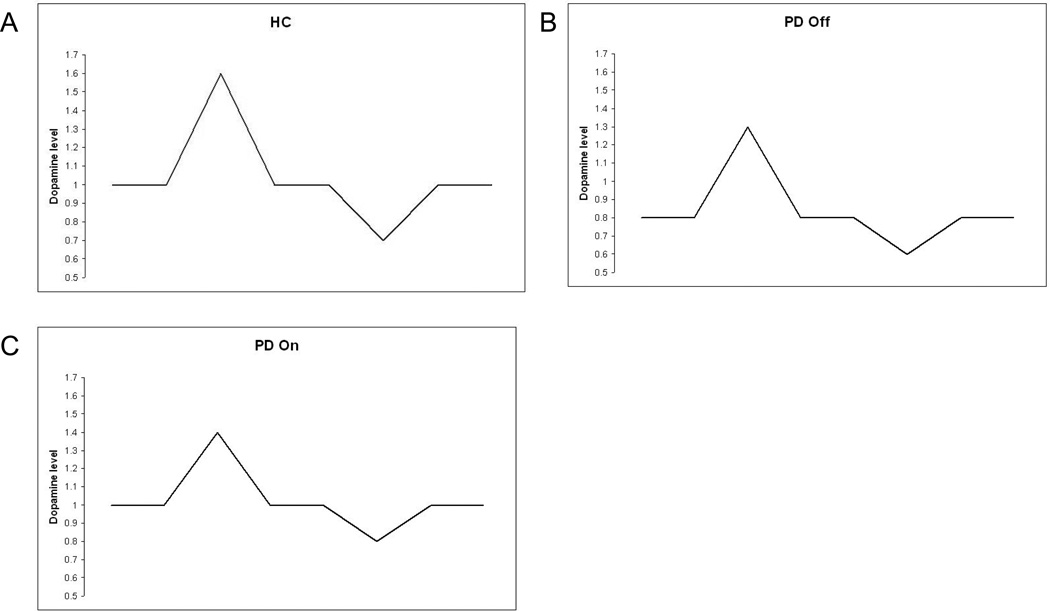
Results from 3 subject groups are modeled; Healthy controls (HC), PD patients tested on normal dopaminergic medication (PD on) and tested after overnight withdrawal of medication (PD off). To simulate the three subject groups, only the tonic and phasic dopamine levels are changed. All other parameters are kept the same. In HC, the tonic dopamine level is set at 1 as a default (Figure 4A). The tonic dopamine level is decreased to 0.8 for the PD off simulations. This is a far smaller decrease than that seen in humans in PD. However, long-term structural changes are likely to act to minimize the effect of the loss of dopaminergic neurons in humans. Modeling such changes is beyond the scope of this study, so we have chosen a figure for the reduced tonic dopamine level that reduces excitability of the model MSN, but does not make it impossible for the neuron to fire under realistic levels of excitation. For the PD on state, the dopamine level is increased back to 1 to reflect the effect of L-Dopa medication.
Figure 4.
Dopamine profiles used in the simulations. A). In healthy controls (HC), the background level is 1. The phasic rise for reward is to 1.6 and the phasic dip for disappointment is 0.7. B) To simulate PD Off the background level is reduced to 0.8 to reflect the reduction in dopaminergic neurons. The phasic rise for reward is of a similar proportion to HC, producing a lower absolute level of 1.3. Similarly, the phasic dip for disappointment is of a similar proportion, to 0.6. C). In PD On, the tonic dopamine level is restored to the HC level by L-Dopa. The phasic rise to reward is proportionately reduced to 1.4, simulating reduced capacity in the disease state. The phasic dip to disappointment is also reduced, simulating a decreased dopamine clearance.
Studies using intracranial self stimulation (ICSS) in rats have shown that a single pairing of post-synaptic potential with ICSS reward can lead to increases in PSP amplitude of up to 97% [61]. Using equation 9, with firing 200ms before reward, input to a synapse 10ms before firing and a phasic rise in dopamine of 1.6, gives a potentiation of 47% which would seem to be reasonable as opening a door would probably not be considered to be as rewarding as ICSS. The level of phasic dopamine is therefore set to 1.6 in the normal condition. In the PD off condition, the phasic rise is decreased to 1.3. This is proportionately similar the normal condition, but starts from a lower tonic level. For the PD on condition, the phasic rise in dopamine is decreased to 1.4 to reflect the decrease in the number of neurons contributing to the phasic rise.
To model disappointment, the phasic level of dopamine is decreased to 0.7 in the normal condition. In the PD off condition, this was decreased to 0.6, again reflecting the lower tonic level. In the PD on condition, the phasic dip was decreased to 0.8 to simulate evidence that PD patients on dopaminergic medication do not learn so well from disappointment [22, 23].
Results
Additional analysis of data from Shohamy et al. (2005)
In phase 1 it is possible to make 0,1 or 2 mistakes before chancing upon the correct door. This gives an average of 1 error for this phase if the subject selects only by color and then remembers the correct door. Both healthy controls and PD on groups made about 1 error in the first phase and were therefore immediately selecting by color not position. This is reasonable as they had had a practice phase in which to learn that the significant factor was door color.
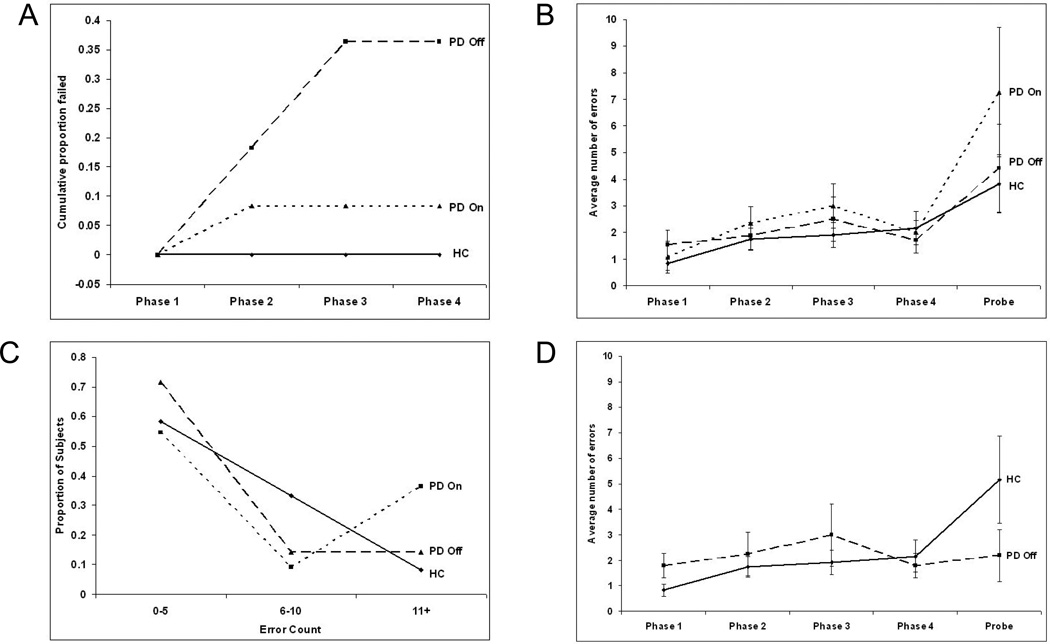
The main findings from Shohamy et al. (2005) [69] were presented in terms of the failure rates for each of the three subject groups (Figure 5A). All control subjects were able to complete all phases of the task. Of the 12 PD on subjects, one failed the second phase of the acquisition (8.5%). 4 of the 11 subjects in the PD off group (36.4%) were unable to learn the full sequence of rooms, 2 failing in phase 2 and 2 in phase 3. The data is re-represented here as the percentage failing each phase to be directly comparable to the results generated in the modeling studies.
Figure 5.
(A). Cumulative failure rates for human subjects. No control subjects failed the task. One of the 12 PD on subject failed the task on phase 2 (8.5%). 2 of the 11 PD off subjects failed the task on phase 2 and a further 2 failed on phase 3. No subjects who had completed the acquisition phases failed the probe phase. (B). Phase by phase error rates for healthy control subjects (HC), PD on and PD off subjects. Error rates in the acquisition phases do not differ significantly, but the PD on group show a higher rate of errors in the probe phase. (C). Binned error rates for the probe phase. The number of control subjects and PD off subjects falling into each bin decreases with number of errors. There is a bimodal distribution of PD on subjects, with a higher number falling into the highest probe error rate bin than into the middle bin. (D). Comparison of error rates across the phases of the task for control subjects and PD off subjects who successfully completed the task. The successful PD off subjects show a tend towards a lower rate of probe errors than controls.
Additionally error rates in each phase of the task were also measured. Due to the small sample size (especially in later phases for the PD off group), these results were not considered significant and therefore were not reported in the original paper. However, due to some correspondences with the model data, some additional analysis of the error rates for the human subjects will be given here before moving on to examine the model performance (Figure 5B).
In the human data any error counts for a single phase that were more than 2 standard deviations from the mean have been discarded. This resulted in discarding the probe error score for one healthy control and the removal of the phase 2 score for one PD off subject who then successfully completed the acquisition and probe phases.
The acquisition data were analyzed by repeated-measures ANOVA on the four learning stages with group as the factor. The probe data were analyzed by ANOVA.
There were no significant group differences across the four learning stages (repeated-measures ANOVA, F(2,26)=1.10, p=.347) and no within-subject effect of stage (F(3,78)=1.90, p=.136). On the probe data, the groups did not differ (ANOVA, F(2,26)=1.05, p=.365). Further breaking down the probe errors of the PD on group (Figure 5B) showed a bimodal distribution of errors, with 6 of the 11 subjects making less than 5 errors and 4 of the 11 subjects making more than 10 errors (Figure 5C).
Effect of tonic dopamine level on excitability of model neurons
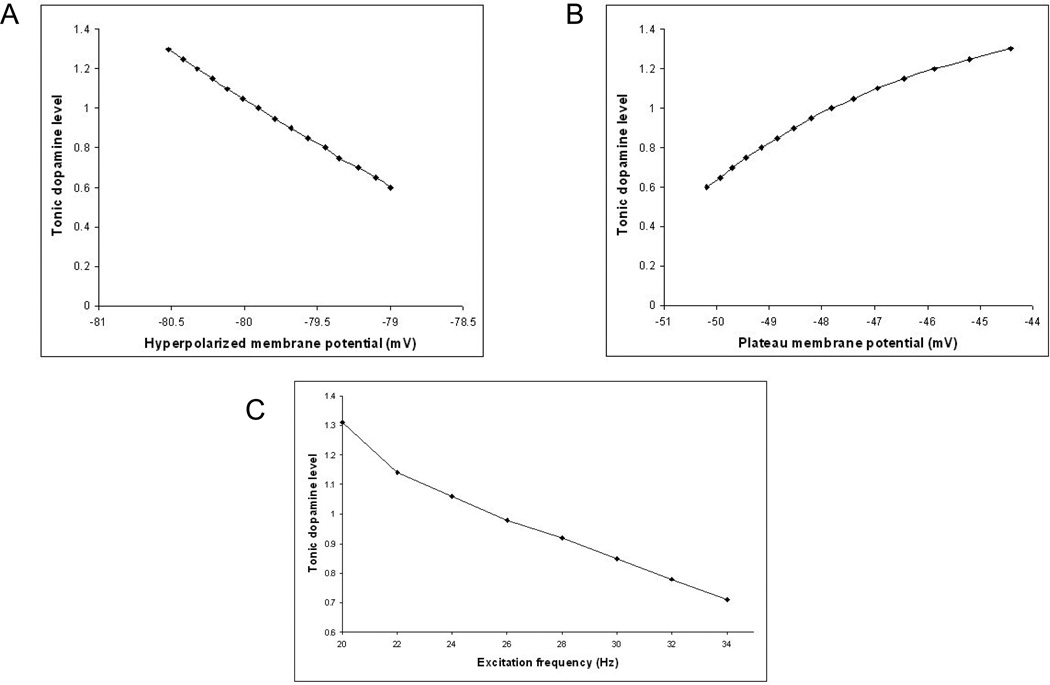
Two of the currents used in the model neuron are modulated by the tonic level of dopamine, DTonic. The inwardly rectifying potassium current, IKir, controls the voltage of the down state. Increasing this current decreases the membrane potential in the hyperpolarized down state (Figure 6A). When the neuron is in the up state, increasing the calcium current, ICa-L, increases the plateau membrane potential (Figure 6B). In the classical model of Parkinson’s disease, MSNs of the direct pathway are expected to be less excitable under conditions of reduced tonic dopamine. While MSNs have been shown to be more excitable under conditions of reduced dopamine in some experiments [20], when direct pathway MSNs are specifically identified, they have been shown to be less excitable [46].
Figure 6.
Effect of tonic dopamine on model MSN. (A). Increasing the tonic dopamine level further hyperpolarizes the membrane potential in the down state. (B). Increasing the tonic dopamine level increases the plateau membrane potential in the up state. The plateau membrane potential was measured 200ms after the start of excitation. (C). Decreasing the tonic dopamine level increases the minimum excitation frequency necessary to elicit an action potential when the neuron is in the down state.
Figure 6C shows the minimum frequency of cortical inputs that leads to firing at different levels of tonic dopamine, with120 excitatory inputs all firing at the same mean frequency. The standard tonic dopamine level of 1 would require each corticostriatal input to be firing at approximately 24Hz to cause the model MSN to fire. When the background dopamine level is decreased to 0.8, as occurs in the simulations of PD off medication, the necessary excitatory frequency increases to 32Hz.
Errors per phase
Each model simulation consisted of 100 runs with the same parameters. For each run the connection of the excitatory inputs to the model MSNs, the colors of the doors in each room and the correct doors were randomly reassigned. Data is presented as errors ± SEM.
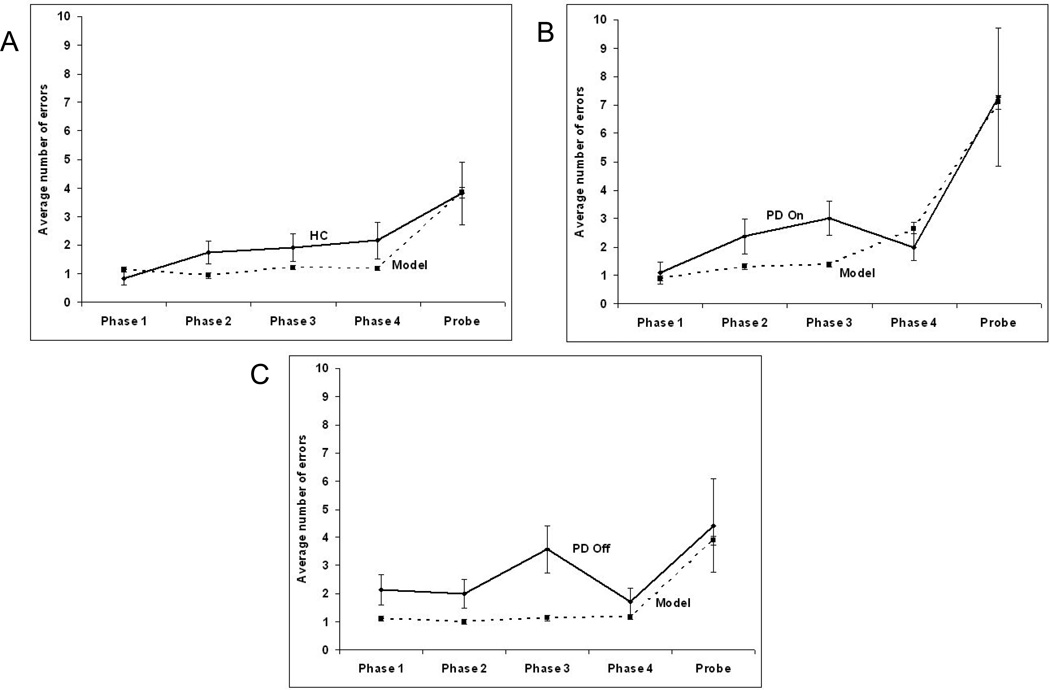
In all 3 cases the model reproduced the error rates in the probe phase but model error rates were generally slightly lower in the learning phases (Figure 7).
Figure 7.
Comparison of human data and model error rates across the phases of the task for (A) healthy controls (HC), (B) Parkinson’s disease off medication and (C) Parkinson’s disease on L-Dopa medication. Error bars represent the standard error.
Two of the factors that lead to variations in task performance in the model are reward dopamine level and the reward devaluation factor. To examine the effect of these factors in the model each was varied independently and error rates and failures measured.
Variation of phasic reward dopamine level
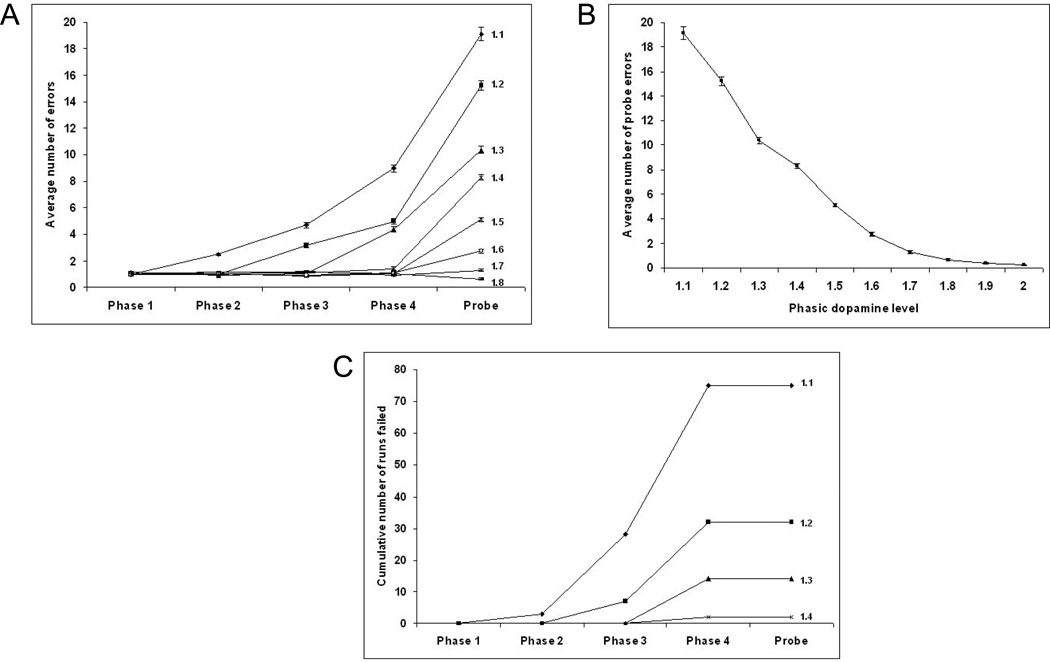
A phasic dopamine level of 1.6 with a tonic level of 1.0 was defined as “normal” in modeling the performance of the healthy control subjects. Figure 8 shows the results when the phasic reward dopamine level was varied from 1.1 to 2.0 with the tonic dopamine level remaining at 1.0. This changes the level of ΔDMax in equation 14.
Figure 8.
The effect of maximum phasic dopamine reward level on model task performance. (A). As the phasic dopamine level at time of reward is decreased from 2.0 to 1.4, there is no change in the number of acquisition phase errors. As the level is decreased below 1.4, errors in the acquisition phases start to increase, starting first in the later phases. (B). Probe error rate is inversely related to phasic dopamine level. (C). Decreasing the phasic dopamine level for reward below 1.4 leads to an increase in the failure rates in the late acquisition phases, but not in the probe phase. Phasic dopamine levels above 1.4 are not shown as no failures occurred.
As the phasic dopamine level was decreased the number of probe errors increased (Figure 8B). Also, as the phasic dopamine level was decreased below 1.3, the error rate in the acquisition phases started to rise (Figure 8A). The rates first started to rise in the last acquisition phase, phase 4 and progressed to earlier phases with lower phasic dopamine levels. Further, as the phasic dopamine level was reduced below 1.4, the number of runs failing increased (Figure 8C). As with the error rates, this first became apparent in the later phases of acquisition. There were no failures in the probe phase.
Variation of percentage devaluation
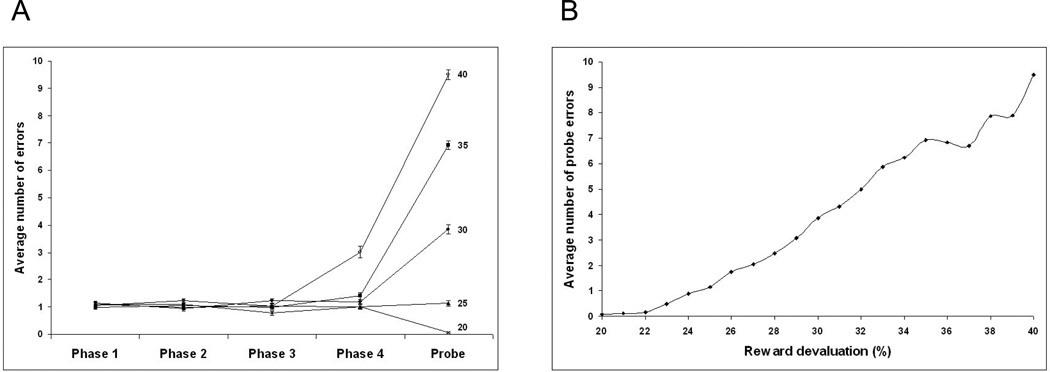
Increasing the percentage devaluation factor over a range of 20% to 40% (equation 14) resulted in an increase in probe errors with little change in errors in the acquisition phases until the reward devaluation rate was greater than 35% (Figure 9A). The increase of the probe errors as a function of reward devaluation is shown in Figure 9B.
Figure 9.
The effect of reward devaluation level on error rates in acquisition and probe phases for the model. (A) Increasing the reward devaluation from 20% to 35% does not lead to an increase in the error rates in the acquisition phase, but does lead to an increase in probe error rates. A reward devaluation rate of 40% resulted in an increased error rate in phase 4. (B) Increasing reward devaluation rates between 22% and 35% resulted in an increase in probe errors.
Failure rates
There was a zero failure rate for both the model and the human subjects in the control condition. The model had a failure rate of 12% in the PD on simulation, which was higher than the one failure in 12 PD on subjects (8.5%).
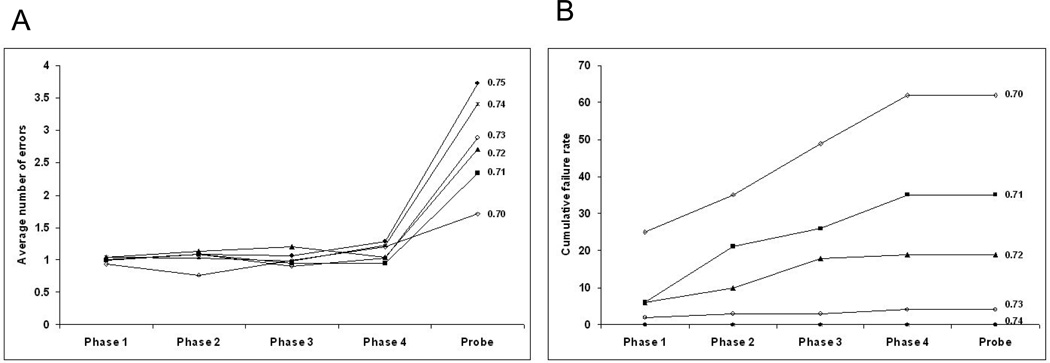
However, all failures in the model occurred in phase 4, whereas the one failure in the human PD on group occurred in phase 2. The model settings that replicated the error rates for the PD off group produced no failures, whereas the human PD off subjects had a failure rate of 4 out of 11 (36.4%) (Figure 5A). To examine the effect of tonic dopamine level on failure rate in the model, the tonic dopamine level was decreased in steps from 0.75 to 0.7. As the level was decreased below 0.74 there was a rapid increase in the failure rate at each step of the acquisition phase to reach a cumulative failure rate over the 4 acquisition phases of 62% at the lowest tonic dopamine level, 0.7 (Figure 10A). This can be compared to the human data (Figure 5A) in which the PD off group had a 36.4% cumulative failure rate over the acquisition phases. There were no failures in the probe phase in the human data or in the model data at any level of tonic dopamine examined.
Figure 10.
Variation of model cumulative failures (A) and error rates (B) as tonic dopamine level is changed. At a tonic dopamine level of 0.74, an average of 3.4 probe errors occurred, with no failures in 100 runs. As the tonic dopamine level was decreased to 0.7, the average number of probe errors decreased to 1.71 but the cumulative failure rate over the 4 acquisition phases increased to 62%.
Surprisingly, the average number of probe errors decreased from 3.72 at a tonic dopamine level of 0.75 to 1.7 at a tonic dopamine level of 0.7 (Figure 10B). This can be compared with the human data where PD off subjects who successfully completed the task had a trend towards a lower probe error rate than healthy controls (Figure 5D).
Discussion
The model presented here represents one part of the action selection circuitry of the basal ganglia. It does not contain complete corticostriatal loops for a full model of the actor in decision making. The reason for the decision to make only a partial model of the actor was to demonstrate more clearly the possible role of the membrane properties of the medium spiny neurons in action selection. In this model the steep rise from a relatively hyperpolarized membrane potential to a plateau membrane potential just below the firing threshold, coupled with a slow depolarization when the plateau membrane potential is reached, provides a mechanism that is sufficient to select between actions based on relatively small changes in the synaptic strengths of the corticostriatal afferent neurons. This leads to the possibility that the action selection is performed in the corticostriatal loop at the first possible stage, which would be the most efficient solution. This does not mean that the rest of the corticostriatal loop plays no part in action selection. Besides deciding which action to select it may be necessary to perform the action at a specific time, especially in sequences of actions, to adjust the intensity of the action and to terminate the action at a specific time. It is possible that these functions are addressed in other parts of the circuitry.
A feature of this model is the absence of lateral inhibition to produce a ‘winner takes all’ network. Unlike prior models [5, 28, 84, 43, 44, 73, 89] this network relies entirely on the membrane characteristics of the model MSNs to give adequate differentiation in firing times. These simulations show that such a mechanism would seem to be adequate for learning to select amongst a small group of actions and to learn the correct sequence of actions in a set of environmental contexts.
There have been several models of the complete corticostriatal loops that have been able to perform action selection using different mechanisms within the loops. The model of Gurney et al. (2001) [31] selected actions based on the salience of the corticostriatal input. The strongest corticostriatal input is always selected. In our model we do not make the assumption that there is any initial difference in the strength of corticostriatal inputs. It has been shown that learning in the cortex is slower than in the basal ganglia [58, 66]. We would suggest that in our model action selection is an emergent property of the network of MSNs rather than en enhancement of a pre-existing difference in cortical ensemble activations. However, these two mechanisms may play roles in action selection at different stages of learning.
Some models have also simulated behavioral tasks in Parkinson’s disease without using lateral inhibition within the striatum, but using competition between pathways for selection. Those of Frank et al [21, 22, 23, 24] demonstrate different effects in Parkinson’s patients on and off medication and on deep brain stimulation. These models are at a higher level and perform selection through interactions of the direct and indirect pathways. The task used here is clearly different from the probabilistic selection task used by Frank which makes direct comparison of model performance difficult. However, our model shows that the action selection could be accomplished in the striatum and opens up the possibility of a different function for the interaction of direct and indirect pathways. Gruber et al. have also extended their original model of the MSN [30], on which our model is based, to make a network model of working memory. This model does not use competition amongst striatal units to perform action selection as this was not required in the memory task under consideration. It does, however, show the effect of dopamine on cortical working memory robustness, and this is a factor that would need to be taken into account in a full corticostriatal loop model. A model from Leblois et al [44] has demonstrated action selection as an interaction between direct and hyperdirect pathways in two parallel corticostriatal loops. In this model, tonic dopamine depletion causes an imbalance between the two pathways that leads to oscillations. The induction of oscillations in corticostriatal loops is clearly beyond the scope of our model, but, our proposal that action selection is performed at the striatal level should not change the findings of interactions between the direct and hyperdirect pathways in a different aspect of Parkinson’s symptomatology.
The second aspect of this model is the 3-factor learning rules that are used to adjust the corticostriatal synaptic weights based on feedback learning. Previous models have based learning solely on the magnitude of the phasic dopamine signal. The learning rules presented here are a first attempt at a more biophysically detailed mechanism for learning in the striatum.
In these simulations only two factors were changed to replicate the human behavioral data of control subjects and PD patients on and off medication; the tonic and phasic dopamine levels. Results for the control and PD on groups fit well with the model, both in error rates and failure rates. For the PD off group, the model produced comparable error rates to human subjects, but without the high failure rate. We showed that, in the model, a further small decrease in the tonic dopamine level produced high failure rates, but with very low error rates when the task was completed successfully. This fit with the human data, where PD off subjects who successfully completed the task had a tendency to have lower error rates the control subjects (Figure 5D). This would suggest that, in Parkinson’s patients off medication, there is an adequate phasic dopamine signal for learning, but that, if the tonic dopamine level is decreased a small amount further, the acquisition phases of the task become increasingly difficult. As the tonic dopamine level is decreased in the model, the plateau membrane potential decreases (Figure 6B). Below a certain level the plateau is too far from the firing threshold and, even with the relatively large amounts of corticostriatal input noise used in the model, the MSN is very unlikely to fire. Tonic dopamine levels found in PD are much lower than those that cause high failure rates in the model. In humans there are probably compensatory mechanisms that allow the tonic level of dopamine to fall much further before the plateau of the MSN membrane potential is too low for the neuron to fire. It may be that the human data for the PD off group can be explained by a small inter-group variation in tonic dopamine levels.
Changing the devaluation factor in the model did not reproduce patterns of errors or failure seen in either PD group. This would suggest that discounting of the reward is not a major problem in PD.
Increasing the phasic dopamine levels in the model continued to decrease the number of probe errors, suggesting that tasks that are more rewarding produce more rapid learning. The lower number of probe phase errors in PD off patients who were able to complete the task suggests that learning from the phasic dopamine signal is not just maintained in PD off, but may even be better than in controls. However, balanced against this improved signal to noise for learning in PD off, a small further decrease in tonic dopamine leads to high failure rates. Against a background of normal tonic dopamine, as in PD on, decreases in the phasic dopamine signal decrease learning to give an increase in probe phase errors.
This suggests that, to explain the different cognitive deficits in PD on and off medication, one has to take into account changes in both the tonic and phasic levels of dopamine. In PD off medication the deficits could be mainly due to the loss of tonic dopamine and in PD on medication, the deficits could be mainly due to a decrease in the phasic dopamine signal, but that in both cases the other aspect of the dopamine signal also plays a role.
Table 2.
Tonic and phasic levels of dopamine used to simulate healthy control, PD on and PD off data. In equation 13, the tonic dopamine level is DTonic and the phasic reward and disappointment dopamine levels are ΔDMax.
| Tonic dopamine level |
Phasic reward dopamine level | Phasic disappointment dopamine level | |
|---|---|---|---|
| HC | 1 | 1.6 | 0.7 |
| PD On | 1 | 1.4 | 0.8 |
| PD Off | 0.8 | 1.3 | 0.6 |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Alexander GE, DeLong MR, Strick PL. Parallel organization of functionally segregated circuits linking basal ganglia and cortex. Annu RevNeuroscie. 1986;9:357–350. doi: 10.1146/annurev.ne.09.030186.002041. [DOI] [PubMed] [Google Scholar]
- 2.Arbuthnott G, Wickens J. Space, time and dopamine. Trends in Neurosciences. 2007;30(2):62–69. doi: 10.1016/j.tins.2006.12.003. [DOI] [PubMed] [Google Scholar]
- 3.Ashby F, Noble S, Ell S, Filoteo J, Waldron E. Category learning deficits in Parkinson’s Disease. Neuropsychology. 2003;17:133–142. [PubMed] [Google Scholar]
- 4.Bargas J, Howe A, Eberwine J, Surmeier JD. Cellular and molecular characterization of Ca2+ currents in acutely isolated, adult rat neostriatal neurons. J Neurosci. 1994;14:6667–6686. doi: 10.1523/JNEUROSCI.14-11-06667.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bar-Gad I, Bergman H. Stepping out of the box: information processing in the neural networks of the basal ganglia. Curr Opin Neurobiol. 2001;11:689–695. doi: 10.1016/s0959-4388(01)00270-7. [DOI] [PubMed] [Google Scholar]
- 6.Bell CC, Han VZ, Sugawara Y, Grant K. Synaptic plasticity in cerebellum-like structure depends on temporal order. Nature. 1997;387:278–281. doi: 10.1038/387278a0. [DOI] [PubMed] [Google Scholar]
- 7.Bi G-Q, Poo M-M. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J Neurosci. 1998;18:10464–10472. doi: 10.1523/JNEUROSCI.18-24-10464.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bonsi P, Pisani A, Bernardi G, Calabresi P. Stimulus frequency, calcium levels and striatal synaptic plasticity. NeuroReport. 2003;14:419–422. doi: 10.1097/00001756-200303030-00024. [DOI] [PubMed] [Google Scholar]
- 9.Calabresi P, Maj R, Pisani A, Mercuri NB, Bernardi G. Long-term synaptic depression in the striatum—physiological and pharmacological characterization. J Neurosci. 1992;12:4224–4233. doi: 10.1523/JNEUROSCI.12-11-04224.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Carlin KP, Jones KE, Jiang Z, Jordan LM, Brownstone RM. Dendritic L-type calcium currents in mouse spinal motoneurons: implications for bistability. Eur J Neurosci. 2000;12:1635–1646. doi: 10.1046/j.1460-9568.2000.00055.x. [DOI] [PubMed] [Google Scholar]
- 11.Cools R, Barker RA, Sahakian BJ, Robbins TW. Enhanced or impaired cognitive function in Parkinson's disease as a function of dopaminergic medication and task demands. Cerebr Cortex. 2001a;11:1136–1143. doi: 10.1093/cercor/11.12.1136. [DOI] [PubMed] [Google Scholar]
- 12.Cools R, Barker RA, Sahakian BJ, Robbins TW. Mechanisms of cognitive set flexibility in Parkinson's disease. Brain. 2001b;124:2503–2512. doi: 10.1093/brain/124.12.2503. [DOI] [PubMed] [Google Scholar]
- 13.Cools R, Barker RA, Sahakian BJ. & Robbins, T.W L-Dopa medication remediates cognitive inflexibility, but increases impulsivity in patients with Parkinson's disease. Neuropsychologia. 2003;41:1431–1441. doi: 10.1016/s0028-3932(03)00117-9. [DOI] [PubMed] [Google Scholar]
- 14.Cools R, Altimirano L, D’Esposito M. Reversal learning in Parkinson's disease depends on medication status and outcome valence. Neuropsychologia. 2006;44:1663–1673. doi: 10.1016/j.neuropsychologia.2006.03.030. [DOI] [PubMed] [Google Scholar]
- 15.Cragg SJ. Meaningful silences: how dopamine listens to the ACh pause. Trends Neurosci. 2006;29:125–131. doi: 10.1016/j.tins.2006.01.003. [DOI] [PubMed] [Google Scholar]
- 16.Czubayko U, Plenz D. Fast synaptic transmission between striatal spiny projection neurons. Neuroscience. 2002;99(24):15764–15769. doi: 10.1073/pnas.242428599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Diamond ME, Petersen RS, Harris JA, Panzeri S. Investigations into the organization of information in sensory cortex. Journal of Physiology - Paris. 2004;97:529–536. doi: 10.1016/j.jphysparis.2004.01.010. [DOI] [PubMed] [Google Scholar]
- 18.Ehringer H, Hornykiewicz O. Verteilung von noradrenalin und dopamine (3-hydroxytyramin) im gehirn des menschen und ihr verhalten bei erkrankungen des extrapyramidalen systems. Klin Wschr. 1960;38:1236–1239. doi: 10.1007/BF01485901. [DOI] [PubMed] [Google Scholar]
- 19.Feigin A, Ghilardi MF, Carbon M, Edwards C, Fukuda M, Dhawan V, Margouleff C, Ghez C, Eidelberg D. Effects of levodopa on motor sequence learning in Parkinson’s disease. Neurology. 2003;60:1744–1749. doi: 10.1212/01.wnl.0000072263.03608.42. [DOI] [PubMed] [Google Scholar]
- 20.Fino E, Venance L, Glowinski J. Effects of acute dopamine depletion on the electrophysiological properties of striatal neurons. Neuroscience Research. 2007;58(3):305–316. doi: 10.1016/j.neures.2007.04.002. [DOI] [PubMed] [Google Scholar]
- 21.Frank M, Loughry B, O'Reilly R. Interactions between frontal cortex and basal ganglia in working memory: A computational model. Cognit Affect Behav Neurosci. 2001;1:137–160. doi: 10.3758/cabn.1.2.137. [DOI] [PubMed] [Google Scholar]
- 22.Frank MJ, Seeberger LC, O’Reilly RC. By Carrot or by Stick: Cognitive Reinforcement Learning in Parkinsonism. Science. 2004;306:1940–1943. doi: 10.1126/science.1102941. [DOI] [PubMed] [Google Scholar]
- 23.Frank MJ. Dynamic Dopamine Modulation in the Basal Ganglia: A Neurocomputational Account of Cognitive Deficits in Medicated and Nonmedicated Parkinsonism. J Cognit Neurosci. 2005;17:51–72. doi: 10.1162/0898929052880093. [DOI] [PubMed] [Google Scholar]
- 24.Frank M, Semanta A, Moustafa J, Sherman S. Hold Your Horses: Impulsivity, Deep Brain Stimulation, and Medication in Parkinsonism. Science. 2007;318(5854):1309–1312. doi: 10.1126/science.1146157. [DOI] [PubMed] [Google Scholar]
- 25.Gabel LA, Nisenbaum ES. Biophysical characterization and functional consequences of a slowly inactivating potassium current in neostriatal neurons. J Neurophysiol. 1998;79:1989–2002. doi: 10.1152/jn.1998.79.4.1989. [DOI] [PubMed] [Google Scholar]
- 26.Gerfen CR, Engber TM, Mahan LC, Susel Z, Chase TN, Monsma FJ, Sibley DR. D1 and D2 dopamine receptor-regulated gene expression of striatonigral and striatopallidal neurons. Science. 1990;250:1429–1432. doi: 10.1126/science.2147780. [DOI] [PubMed] [Google Scholar]
- 27.Gonon F. Prolonged and extrasynaptic excitatory action of dopamine mediated by D1 receptors in the rat striatum in vivo. J Neurosci. 1997;17(15):5972–5978. doi: 10.1523/JNEUROSCI.17-15-05972.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Groves PM. A theory of the functional organization of the neostriatum and the neostriatal control of voluntary movement. Brain Res. 1983;286:109–132. doi: 10.1016/0165-0173(83)90011-5. [DOI] [PubMed] [Google Scholar]
- 29.Gruber AJ, Solla SA, Surmeier DJ, Houk JC. Modulation of Striatal Single Units by Expected Reward: A Spiny Neuron Model Displaying Dopamine-Induced Bistability. J Neurophysiol. 2003;90:1095–1114. doi: 10.1152/jn.00618.2002. [DOI] [PubMed] [Google Scholar]
- 30.Gruber A, Dayan P, Gutkin B, Solla S. Dopamine modulation in the basal ganglia locks the gate to working memory. J Comput Neurosci. 2006;20(2):153–166. doi: 10.1007/s10827-005-5705-x. [DOI] [PubMed] [Google Scholar]
- 31.Gurney K, Prescott T, Redgrave PA. computational model of action selection in the basal ganglia I. A new functional anatomy. Biol Cybern. 2001;84:401–410. doi: 10.1007/PL00007984. [DOI] [PubMed] [Google Scholar]
- 32.Guzman JJ, Hernández A, Galarraga E, et al. Dopaminergic Modulation of Axon Collaterals Interconnecting Spiny Neurons of the Rat Striatum. J Neurosci. 2003;23(26):8931–8940. doi: 10.1523/JNEUROSCI.23-26-08931.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hagiwara S, Miyazaki S, Rosenthal NP. Potassium current and the effect of cesium on this current during anomalous rectification of the egg cell membrane of a starfish. J Gen Physiol. 1976;67:621–638. doi: 10.1085/jgp.67.6.621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hazy T, Frank M, O'Reilly R. Banishing the homunculus: making working memory work. Neurosci. 2006;139:105–118. doi: 10.1016/j.neuroscience.2005.04.067. [DOI] [PubMed] [Google Scholar]
- 35.Hernández-López S, Bargas J, Surmeier DJ, Reyes A, Galarraga E. D1 Receptor Activation Enhances Evoked Discharge in Neostriatal Medium Spiny Neurons by Modulating an L-Type Ca2+ Conductance. J Neurosci. 1997;17:3334–3342. doi: 10.1523/JNEUROSCI.17-09-03334.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hille B. Ionic Channels of Excitable Membranes. Chapter 13. Sunderland, MA: Sinauer; 1992. [Google Scholar]
- 37.Hornykiewicz O. Biochemical aspects of Parkinson's disease. Neurology. 1998;51:S2–S9. doi: 10.1212/wnl.51.2_suppl_2.s2. [DOI] [PubMed] [Google Scholar]
- 38.Horvitz JC. Dopamine gating of glutamatergic sensorimotor and incentive motivational input signals to the striatum. Behav Brain Res. 2002;137:65–74. doi: 10.1016/s0166-4328(02)00285-1. [DOI] [PubMed] [Google Scholar]
- 39.Kawaguchi Y, Wilson CJ, Emson PC. Intracellular recording of identified neostriatal patch and matrix spiny cells in a slice preparation preserving cortical inputs. J Neurophysiol. 1989;62:1052–1068. doi: 10.1152/jn.1989.62.5.1052. [DOI] [PubMed] [Google Scholar]
- 40.Kita T, Kita H, Kitai ST. Passive electrical membrane properties of rat neostriatal neurons in an in vitro slice preparation. Brain Res. 1984;300:129–139. doi: 10.1016/0006-8993(84)91347-7. [DOI] [PubMed] [Google Scholar]
- 41.Knowlton BJ, Mangels AJ, Squire LR. A neostriatal habit learning system in humans. Science. 1996;273:1399–1402. doi: 10.1126/science.273.5280.1399. [DOI] [PubMed] [Google Scholar]
- 42.Koos T, Tepper J, Wilson C. Comparison of IPSCs Evoked by Spiny and Fast-Spiking Neurons in the Neostriatum. J Neurosci. 2004;24(36):7916–7922. doi: 10.1523/JNEUROSCI.2163-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kotter R, Wickens JR. Striatal mechanisms in Parkinson’s disease: new insights from computer modeling. Artif Intell Med. 1998;13:37–55. doi: 10.1016/s0933-3657(98)00003-7. [DOI] [PubMed] [Google Scholar]
- 44.Leblois A, Boraud T, Meissner W, Bergman H, Hansel D. Competition between Feedback Loops Underlies Normal and Pathological Dynamics in the Basal Ganglia. J Neurosci. 2006;26(13):3567–3583. doi: 10.1523/JNEUROSCI.5050-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mahon S, Deniau JM, Charpier S, Delord B. Role of a Striatal Slowly Inactivating Potassium Current in Short-Term Facilitation of Corticostriatal Inputs: A Computer Simulation Study. Learn Mem. 2000;7:357–362. doi: 10.1101/lm.34800. [DOI] [PubMed] [Google Scholar]
- 46.Mallet N, Ballion B, Le Moine C, Gonon F. Cortical Inputs and GABA Interneurons Imbalance Projection Neurons in the Striatum of Parkinsonian Rats. J Neurosci. 2006;26(14):3875–3884. doi: 10.1523/JNEUROSCI.4439-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Markram H, Lübke J, Frotscher M, Sakmann B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science. 1997;275:213–215. doi: 10.1126/science.275.5297.213. [DOI] [PubMed] [Google Scholar]
- 48.Mermelstein PG, Song W-J, Tkatch T, Yan Z, Surmeier DJ. Inwardly rectifying potassium currents are correlated with irk subunit expression in rat nucleus accumbens medium spiny neurons. J Neurosci. 1998;18:6650–6661. doi: 10.1523/JNEUROSCI.18-17-06650.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Middleton FA, Strick PL. Anatomical evidence for cerebellar and basal ganglia involvement in higher cognitive function. Science. 1994;266:458–461. doi: 10.1126/science.7939688. [DOI] [PubMed] [Google Scholar]
- 50.Mink JW. The basal ganglia: focused selection and inhibition of competing motor programs. Progr Neurobiol. 1996;50:381–425. doi: 10.1016/s0301-0082(96)00042-1. [DOI] [PubMed] [Google Scholar]
- 51.Morris G, Arkadir D, Nevet A, Vaadia E, Bergman H. Coincident but Distinct Messages of Midbrain Dopamine and Striatal Tonically Active Neurons. Neuron. 2004;43(1):133–143. doi: 10.1016/j.neuron.2004.06.012. [DOI] [PubMed] [Google Scholar]
- 52.Myers C, Shohamy D, Gluck M, Grossman S, Kluger A, Ferris S, Golomb J, Schnirman G, Schwartz R. Dissociating hippocampal versus basal ganglia contributions to learning and transfer. J Cognit Neurosci. 2003a;15:185–193. doi: 10.1162/089892903321208123. [DOI] [PubMed] [Google Scholar]
- 53.Myers CE, Shohamy D, Gluck MA, Grossman S, Onlaor S, Kapur N. Dissociating medial temporal and basal ganglia memory systems with a latent learning task. Neuropsychologia. 2003b;41:1919–1928. doi: 10.1016/s0028-3932(03)00127-1. [DOI] [PubMed] [Google Scholar]
- 54.Nisenbaum ES, Wilson CJ. Potassium currents responsible for inward and outward rectification in rat neostriatal spiny projection neurons. J Neurosci. 1995;15:4449–4463. doi: 10.1523/JNEUROSCI.15-06-04449.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Nisenbaum ES, Wilson CJ, Foehring RC, Surmeier DJ. Isolation and characterization of a persistent potassium current in neostriatal neurons. J Neurophysiol. 1996;76:1180–1194. doi: 10.1152/jn.1996.76.2.1180. [DOI] [PubMed] [Google Scholar]
- 56.Oorschot DE. Total number of neurons in the neostriatal, pallidal, subthalamic and substantia nigral nuclei of the rat basal ganglia: a stereological study using the Cavalieri and optical dissector methods. J Comp Neurol. 1996;366:580–599. doi: 10.1002/(SICI)1096-9861(19960318)366:4<580::AID-CNE3>3.0.CO;2-0. [DOI] [PubMed] [Google Scholar]
- 57.Pacheco-Cano MT, Bargas J, Hernandez-Lopez S. Inhibitory action of dopamine involves a subthreshold cs+-sensitive conductance in neostriatal neurons. Exp Brain Res. 1996;110:205–211. doi: 10.1007/BF00228552. [DOI] [PubMed] [Google Scholar]
- 58.Pasupathy A, Miller E. Different time courses of learning-related activity in the prefrontal cortex and striatum. Nature. 2005;433:873–876. doi: 10.1038/nature03287. [DOI] [PubMed] [Google Scholar]
- 59.Perrier JF, Hounsgaard J. Development and regulation of response properties in spinal cord motoneurons. Brain Res Bull. 2000;53:529–535. doi: 10.1016/s0361-9230(00)00386-5. [DOI] [PubMed] [Google Scholar]
- 60.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical recipes: The art of scientific computing. 2nd ed. Cambridge, UK: Cambridge University Press; 1992. [Google Scholar]
- 61.Reynolds JNJ, Hyland BI, Wickens JR. A cellular mechanism of reward-related learning. Experimental Neurology. 2001;413:67–70. doi: 10.1038/35092560. [DOI] [PubMed] [Google Scholar]
- 62.Satoh T, Nakai S, Sato T, Kimura M. Correlated coding of motivation and outcome of decision by dopamine neurons. J Neurosci. 2003;23:9913–9923. doi: 10.1523/JNEUROSCI.23-30-09913.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Schultz W, Apicella P, Ljunberg T. Responses of monkey dopamine neurons to reward and conditioned stimuli during successive steps of learning a delayed response task. J Neurosci. 1993;13:900–913. doi: 10.1523/JNEUROSCI.13-03-00900.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Schultz W. Getting Formal with Dopamine and Reward. Neuron. 2002;36(2):241–263. doi: 10.1016/s0896-6273(02)00967-4. [DOI] [PubMed] [Google Scholar]
- 65.Seamans JK, Gorelova NA, Yang CR. Contributions of voltage-gated Ca2+ channels in the proximal versus distal dendrites to synaptic integration in prefrontal cortical neurons. J Neurosci. 1997;17:5936–5948. doi: 10.1523/JNEUROSCI.17-15-05936.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Seger C, Cincotta C. Dynamics of Frontal, Striatal, and Hippocampal Systems during Rule Learning. Cerebral Cortex. 2006;16(11):1546–1555. doi: 10.1093/cercor/bhj092. [DOI] [PubMed] [Google Scholar]
- 67.Shohamy D, Myers C, Grossman S, Sage J, Gluck M, Poldrack R. Cortico-striatal contributions to feedback-based learning: Converging data from neuroimaging and neuropsychology. Brain. 2004a;127:851–859. doi: 10.1093/brain/awh100. [DOI] [PubMed] [Google Scholar]
- 68.Shohamy D, Myers CE, Onlaor S, Gluck MA. The role of the basal ganglia in category learning: How do patients with Parkinson's disease learn? Behav Neurosci. 2004b;118:676–686. doi: 10.1037/0735-7044.118.4.676. [DOI] [PubMed] [Google Scholar]
- 69.Shohamy D, Myers CE, Grossman S, Sage J, Gluck MA. The Role of dopamine in cognitive sequence learning: Evidence from Parkinson's disease. Behavl Brain Res. 2005;156:191–199. doi: 10.1016/j.bbr.2004.05.023. [DOI] [PubMed] [Google Scholar]
- 70.Shohamy D, Myers CE, Geghman KD, Sage J, Gluck MA. LDopa impairs learning, but not generalization, in Parkinson’s disease. Neuropsychologia. 2006;44:774–784. doi: 10.1016/j.neuropsychologia.2005.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Song WJ, Surmeier DJ. Voltage-dependent facilitation of calcium channels in rat neostriatal neurons. J Neurophysiol. 1996;76:2290–2306. doi: 10.1152/jn.1996.76.4.2290. [DOI] [PubMed] [Google Scholar]
- 72.Suaud-Chagny M, Chergui K, Chouvet G, Gonon F. Relationship between dopamine release in the rat nucleus accumbens and the discharge activity of dopaminergic neurons during local in vivo application of amino acids in the ventral tegmental area. Neuroscience. 1992;49(1):63–72. doi: 10.1016/0306-4522(92)90076-e. [DOI] [PubMed] [Google Scholar]
- 73.Suri RE, Schultz W. A neural network model with dopamine-like reinforcement signal that learns a spatial delayed response task. Neurosci. 1999;91:871–890. doi: 10.1016/s0306-4522(98)00697-6. [DOI] [PubMed] [Google Scholar]
- 74.Surmeier DJ, Foehring R, Stefani A, Kitai ST. Developmental expression of a slowly-inactivating voltage dependent potassium current in rat neostriatal neurons. Neurosci Lett. 1991;122:4l–46. doi: 10.1016/0304-3940(91)90188-y. [DOI] [PubMed] [Google Scholar]
- 75.Surmeier DJ, Xu ZC, Wilson CJ, Stefani A, Kitai ST. Grafted neostriatal neurons express a late-developing transient potassium current. Neurosci. 1992;48:849–856. doi: 10.1016/0306-4522(92)90273-5. [DOI] [PubMed] [Google Scholar]
- 76.Surmeier DJ, Kitai ST. D1 and D2 dopamine receptor modulaiton of sodium and potassium currents in rat neostriatal neurons. In: Arbuthnott GW, Emson PC, editors. Progress in Brain Research. Vol. 99. Amsterdam: Elsevier; 1993. pp. 309–324. [DOI] [PubMed] [Google Scholar]
- 77.Surmeier DJ, Wilson CJ, Eberwine J. Methods in neurosciences: methods for the study of ion channels. San Diego: Academic; 1994. Patch-clamp techniques for studying potassium currents in mammalian brain neurons; pp. 39–67. [Google Scholar]
- 78.Surmeier DJ, Bargas J, Hemmings HC, Jr, Nairn AC, Greengard P. Modulation of calcium currents by a D1 dopaminergic protein kinase phosphatase cascade in rat neostriatal neurons. Neuron. 1995;14:385–397. doi: 10.1016/0896-6273(95)90294-5. [DOI] [PubMed] [Google Scholar]
- 79.Surmeier DJ, Song W-J, Yan Z. Coordinated expression of dopamine receptors in neostriatal medium spiny neurons. J Neurosci. 1996;16:6579–6591. doi: 10.1523/JNEUROSCI.16-20-06579.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Taverna S, Van Dongen Y, Groenewegen H, Pennartz C. Direct Physiological Evidence for Synaptic Connectivity Between Medium-Sized Spiny Neurons in Rat Nucleus Accumbens In Situ. J Neurophysiol. 2004;91:1111–1121. doi: 10.1152/jn.00892.2003. [DOI] [PubMed] [Google Scholar]
- 81.Tunstall M, Oorschot D, Kean A, Wickens J. Inhibitory Interactions Between Spiny Projection Neurons in the Rat Striatum. J Neurophysiol. 2002;88:1263–1269. doi: 10.1152/jn.2002.88.3.1263. [DOI] [PubMed] [Google Scholar]
- 82.Uchimura N, Cherubini E, North RA. Inward rectification in rat nucleus accumbens neurons. J Neurophysiol. 1989;62:1280–l286. doi: 10.1152/jn.1989.62.6.1280. [DOI] [PubMed] [Google Scholar]
- 83.Van Rossum MCW, Bi GQ, Turrigiano GG. Stable Hebbian Learning from Spike Timing-Dependent Plasticity. J Neurosci. 2000;20:8812–8821. doi: 10.1523/JNEUROSCI.20-23-08812.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Wickens JR, Alexander M. Analysis of Striatal Dynamics: The Existence of Two Modes of Behaviour. J Theor Biol. 1993;163:413–438. doi: 10.1006/jtbi.1993.1128. [DOI] [PubMed] [Google Scholar]
- 85.Wickens JR, Begg AJ, Arbuthnott GW. Dopamine reverses the depression of rat corticostriatal synapses which normally follows highfrequency stimulation of cortex In vitro. Neurosci. 1996;70:1–5. doi: 10.1016/0306-4522(95)00436-m. [DOI] [PubMed] [Google Scholar]
- 86.Wickens JR. Basal ganglia: structure and computations. Netw Comput Neural Syst. 1997;8:R77–R109. [Google Scholar]
- 87.Wilson C. Passive cable properties of dendritic spines and spiny neurons. J Neurosci. 1984;4:281–297. doi: 10.1523/JNEUROSCI.04-01-00281.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Wilson CJ, Kawaguchi Y. The origins of two-state spontaneous membrane potential fluctuations of neostriatal spiny neurons. J Neurosci. 1996;16:2397–2410. doi: 10.1523/JNEUROSCI.16-07-02397.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Woodward DJ, Kirilov AB, Myre CD, Sawyer SF. Neostriatal circuitry as a scalar model: modelling and ensemble neuron recording. In: Houk JC, Davis JL, Beiser DG, editors. Models of information processing in the basal ganglia. Cambridge: MIT Press; 1995. pp. 315–336. [Google Scholar]
- 90.Zheng T, Wilson CJ. Corticostriatal Combinatorics: The Implications of Corticostriatal Axonal Arborizations. J Neurophysiol. 2002;87:1007–1017. doi: 10.1152/jn.00519.2001. [DOI] [PubMed] [Google Scholar]