Bayesian hierarchical structured variable selection methods with application to molecular inversion probe studies in breast cancer

Summary

The analysis of alterations that may occur in nature when segments of chromosomes are copied (known as copy number alterations) has been a focus of research to identify genetic markers of cancer. One high-throughput technique recently adopted is the use of molecular inversion probes (MIPs) to measure probe copy number changes. The resulting data consist of high-dimensional copy number profiles that can be used to ascertain probe-specific copy number alterations in correlative studies with patient outcomes to guide risk stratification and future treatment. We propose a novel Bayesian variable selection method, the hierarchical structured variable selection (HSVS) method, which accounts for the natural gene and probe-within-gene architecture to identify important genes and probes associated with clinically relevant outcomes. We propose the HSVS model for grouped variable selection, where simultaneous selection of both groups and within-group variables is of interest. The HSVS model utilizes a discrete mixture prior distribution for group selection and group-specific Bayesian lasso hierarchies for variable selection within groups. We provide methods for accounting for serial correlations within groups that incorporate Bayesian fused lasso methods for within-group selection. Through simulations we establish that our method results in lower model errors than other methods when a natural grouping structure exists. We apply our method to an MIP study of breast cancer and show that it identifies genes and probes that are significantly associated with clinically relevant subtypes of breast cancer.

1. Introduction

1.1. Molecular inversion probe-based arrays for copy number measurement

DNA segments in a human genome are normally present in two copies, one copy from each parent. However, various studies have revealed that the numbers of copies of DNA segments, can vary due to local changes in the genome such as duplications, deletions, inversions, and translocations, resulting in gains or losses in copy numbers. Such DNA copy number alterations (CNA) can lead to over-expression of pro-oncogenes (genes favorable to cancer) or silencing of tumor suppressor genes (genes protective against cancer), and affect cellular functions in cell division or programmed cell death (Guha et al., 2008), and hence, have been identified as important drivers in many diseases including cancer (Pinkel and Albertson, 2005). Accumulation of these DNA errors will eventually influence the development or progression of cancer; hence, chromosomal copy number analysis has the potential to elucidate tumor progression and identify genetic markers for cancer diagnosis and treatment. CNAs, as gains and losses, are frequent events in breast tumors and occur in patterns that are thought to distinguish genetic paths to tumorigenesis and influence the clinical behavior of the disease (Rennstam et al., 2003; van Beers and Nederlof, 2006).

Many techniques have been developed for the genome-wide detection of CNAs, such as array-based comparative genomic hybridization (CGH), bacterial artificial chromosome CGH, and oligonucleotide array-based CGH (Pinkel et al., 1998; Iafrate et al., 2004; Lucito et al., 2003), which detect copy number changes for DNA segments of 5–10 kilobases in size. A technique that has recently been used for measuring CNAs of single alleles is the molecular inversion probe (MIP) (Hardenbol et al., 2003; Wang et al., 2007). Compared to other copy number measuring techniques such as the CGH methods, the MIP assay has the advantage of high resolution (detecting copy numbers of DNA sequences of small sizes up to one single allele), high specificity (a lower rate of false positives in copy number measurement), lower amount of DNA sample required, and reproducibility. We refer the reader to Hardenbol et al. (2003) and Wang et al. (2007) for more detailed descriptions of the technical aspects of the MIP assays.

MIPS studies in Breast Cancer

In this paper, we focus on the analysis of a novel high-dimensional MIP dataset from 971 samples of early-stage breast cancer patients (stages I and II) collected through the Specialized Programs of Research Excellence (SPORE) at the University of Texas MD Anderson Cancer Center. DNA extracted from tumor samples and matched normal samples (from the same patients) were prepared for copy number measurement in the Affymetrix^™MIP laboratory, which was blinded to all sample and subject information. The copy numbers measured from the MIP assay were then pre-processed using standard methods. (See Thompson et al. (2011) for explicit details regarding the pre-processing steps.) The MIP data include full genome quantifications for 330,000 single alleles/probes from tumor cells of the 971 breast cancer patients.

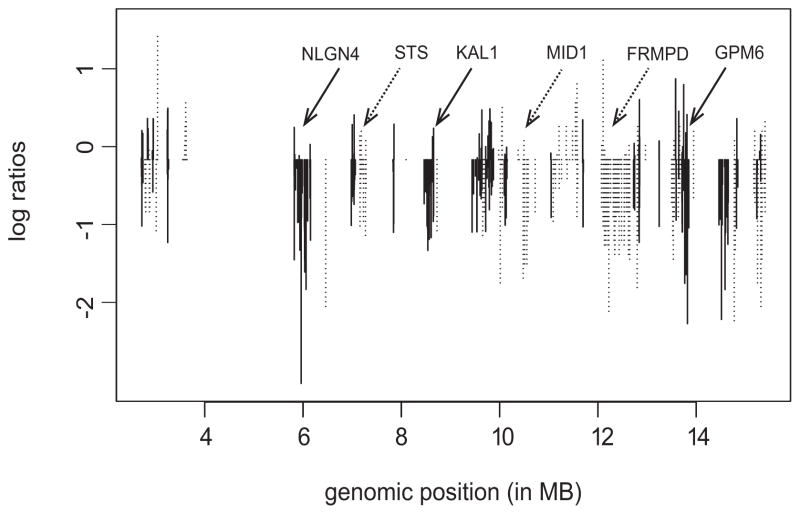
Structure of MIPS data

The data structure for downstream statistical modeling/analysis consists of log₂ intensity ratios of the copy numbers in test samples to the copy numbers in normal reference cells for all probes across the genome. Hence, for a sample with the normal probe copy number (= 2), the normalized value is log₂(2/2) = 0; for a probe with a gain of measured copy numbers (> 2) the log ratio is positive, and for a probe with a loss of copy numbers (< 2) the log ratio is negative. The magnitudes of the intensity ratios in the positive or negative direction are indicative of multiple probe-level gains and losses, respectively. The resulting data are continuous, with the distributions of the normalized values approximately symmetric around 0. Figure 1 shows an example plot of the partial MIP copy number profile for a randomly selected sample of one patient, where the x-axis is the genomic location and each vertical line is the normalized value of the copy number for an MIP probe. The different line patterns correspond to the group of probes mapped to the coding region of one gene, indicating the uniquely annotated gene structures on the chromosome. There are several features exemplified in the plot: (i) The copy number profiles have a hierarchical structure induced by biology: the contiguous probes (as per their genomic location) mapped to the coding region of a gene could be considered as a natural group of variables. (ii) There exists substantial variability, both between and within genes, primarily due to different numbers of probes mapped to each gene and different probes within the same gene contributing differently, both positively and negatively. (iii) Finally, there exists serial correlation between the copy numbers of the probes within the same gene, given their proximity by genomic location, and the correlation weakens with an increasing distance between two probes.

Fig. 1.

Copy number profile from a tumor sample. The log-ratios are plotted on the vertical axis against their genomic position (in MB). The line type patterns indicate the gene structures on the chromosome. MB: megabases; 1MB = 1,000,000 bases, where bases (or nucleobases) are structural units of DNA.

In addition to the MIP copy number profiles, non-genetic clinical information was also collected from the patients in the study, including the patient’s age, stage, tumor size, lymph node status, nuclear grade (Thompson et al., 2011). The breast tumor samples were classified into four subtypes based on immunohistochemical analysis of the tumor markers ER, PR, HER2, and Ki67: luminal A (ER⁺Ki67^low), luminal B (ER⁺Ki67^high), HER2+, and triple-negative breast cancer (TNBC) (ER⁻PR⁻HER2⁻). Our main focus in this paper is to identify probes whose CNAs are significantly associated with the clinical and pathologic characteristics of the tumors with an emphasis on clinical subtypes. In particular, we focus on the TNBC subtype, as it is among the more aggressive breast tumors for which there are no known treatment targets or prognostic factors. Discovering and validating CNAs that correlate with TNBC will identify genes and probes of high interest for further investigation as clinically useful diagnostic and treatment biomarkers.

We assume that many of the acquired chromosomal changes jointly affect the biological outcomes. Thus it is of high interest to model the joint effects of CNAs detected by the MIP assay and discover regions of the genome that exhibit significant associations with the TNBC subtype – in contrast to univariate single MIP analysis. However, inferential challenges for the MIP copy number dataset include not only its high-dimensionality but also the features of the copy number data as described above. Therefore, in our study, we aim to (i) pursue a variable selection method which incorporates the grouping/gene structures in the probe copy number profiles, (ii) identify significant genes as well as important probes within the genes that are associated with the clinical features of the patient, as both are of equal interest where genes are known as the functional units of DNA and different probes within a gene may have different predictive behaviors, and (iii) account for the serial correlation among the copy numbers of the probes within the genes. We propose a novel “hunting” approach for variable selection at the two levels, a gene (group) level and probe-within-gene (subgroup) level – leading to a statistical formulation of hierarchical structured variable selection. We start with a general model for a linear regression model assuming independent variables. We then extend the model to account for the serial correlation among the variables and for the discrete responses as in our data.

1.2. Relevant statistical literature

Variable selection is a fundamental issue in statistical analysis and has been extensively studied. Penalized methods such as the bridge regression (Frank and Friedman, 1993), the lasso regression (Tibshirani, 1996), the SCAD regression (Fan and Li, 2001), the LARS regression (Efron et al., 2004) and the OSCAR regression (Bondell and Reich, 2008) have been proposed due to their relatively stable performance in model selection and prediction. The lasso method has especially gained much attention. It utilizes an L₁-norm penalty function to achieve estimation shrinkage and variable selection. In a Bayesian framework, the variable selection problem can be viewed as the identification of nonzero regression parameters based on posterior distributions. Different priors have been considered for this purpose. Mitchell and Beauchamp (1988) propose a “spike and slab” method that assumes the prior distribution of each regression coefficient to be a mixture of a point mass at 0 and a diffuse uniform distribution elsewhere. This method is extended by George and Mc-Culloch (1993, 1997), Kuo and Mallick (1998), and Ishwaran and Rao (2005) in different settings. Other methods specify absolutely continuous priors that approximate the “spike and slab” shape, shrinking the estimates toward zero (Xu, 2003; Bae and Mallick, 2004; Park and Casella, 2008; Griffin and Brown, 2007; 2010). In particular, Park and Casella (2008) extend the frequentist lasso with a full Bayesian method by assigning independent and identical Laplace priors to the regression parameters.

These variable selection methods ignore the grouping structure that appears in many applications such as ours. The individual-level variable selection methods tend to select more groups than necessary when selection at group level is desired. To accommodate group-level selection, Yuan and Lin (2006) propose the group lasso method, in which a lasso penalty function is applied to the L₂-norm of the coefficients within each group. This method is subsequently extended by Raman et al. (2009) in a Bayesian setting. Zhao et al. (2009) generalize the group lasso method by replacing the L₂-norm of the coefficients in each group with the L_γ-norm for 1 < γ ≤ ∞. In the extreme case where γ = ∞, the coefficient estimates within a group are encouraged to be exactly the same. However, these model selection methods focus on group selection without much consideration of selection at the within-group level; that is, they only allow the variables within a group to be all in or all out of the model. More recently, some frequentist methods have been developed for selection at both the group and within-group levels. Wang et al. (2009) reparameterize predictor coefficients and selected variables by maximizing the penalized likelihood with two penalizing terms. Ma et al. (2010) propose a clustering threshold gradient-directed regularization (CTGDR) method for genetic association studies.

In this paper, we propose a Bayesian method to perform the variable selection on hierarchically structured data, given that the grouping structures are known. We propose a novel hierarchical structured variable selection (HSVS) prior that generalizes the traditional “spike and slab” selection priors of Mitchell and Beauchamp (1988) for grouped variable selection. Specifically, instead of the uniform or multivariate normal distribution of the traditional “spike and slab” methods, we let the “slab” part in the prior be a general robust shrinkage distribution such as a Laplace distribution, which leads to the well-developed lasso-type penalization formulations. Unlike other group selection methods, which usually utilize lasso penalties for group-level shrinkage and selection, our proposed method uses selection priors for group-level selection that are combined with a Laplace “slab” to obtain Bayesian lasso estimates for within-group coefficients, and thus achieves group selection and within-group shrinkage simultaneously. More advantageously, because the full conditionals of the model parameters are available in closed form, this formulation allows for efficient posterior computations, which greatly aid our analysis of high-dimensional datasets. Using full Markov chain Monte Carlo (MCMC) methods, we can obtain the posterior probability of a group’s inclusion, upon which posterior inference can then be conducted using false discovery rate (FDR)-based methods, which are crucial in high-dimensional data. Our method thresholds the posterior probabilities for group selection by controlling the overall average FDR while within-group variable selection is conducted based on the posterior credible intervals of the within-group coefficients obtained from the MCMC samples. Furthermore, we propose extensions to account for the correlation between neighboring variables within a group by incorporating a Bayesian fused lasso prior on the coefficients for within-group variable selection. Due to the conjugate nature of model formulation, our method could also be easily extended to nonlinear regression problems for discrete response variables.

The rest of the paper is organized as follows. In Section 2 we propose our hierarchical models for simultaneous variable selection at both group and within-group levels. In Section 3, we extend the hierarchical models for variable selection of generalized linear models. In Section 4, we show the FDR-based methods for group selection. Simulation studies are carried out and discussed in Section 5. We apply the models to the real MIP data analysis in Section 6 and conclude with a discussion in Section 7. All technical details are presented in Appendices available as the Supplementary Materials.

2. Probability model

Let Y = (Y₁, … , Y_n)^T denote the clinical outcomes/responses of interest from n patients/samples and X denote the n × q-dimensional covariate matrix of q probes from MIP measurements. For ease of exposition we present the model for the Gaussian case here and discuss generalized linear model extensions for discrete responses in Section 3. The model we posit on the clinical response is

$$\mathbf{Y}=U\mathit{b}+X\mathit{\beta }+\mathit{\epsilon },$$

where U denotes the non-genetic factors/confounders such as age at diagnosis, tumor size, and lymph node status with associated parameters b. We further assume that the columns of the data matrix X and the coefficients β are known to be partitioned into G groups/genes, where the g^th group contains k_g elements for g = 1, …, G and ${\sum }_{g=1}^G{k}_g=q$. We assume that a given probe occurs in only one gene (group), which is trivially satisfied for these data since the probes are grouped by genomic location and mapped to a uniquely annotated gene. Thus, we write X = (X₁, …, X_G), with β = (β₁, …, β_G) denoting the group-level coefficients and β_g = (β_g1, …, β_gkg) denoting the within-group coefficients. The error terms ε = (ε₁, … , ε_n) are assumed to be independently and identically distributed N(0, σ²) for the Gaussian responses. Our key construct of interest is the q-dimensional coefficient vector β, which captures the association between the probe measurements and the clinical outcome. Hereafter we propose a novel hierarchical prior construction based on the natural hierarchical structure of the probe measurements that simultaneously selects relevant genes and significant probes-within-genes. We first present a model in which we assume that the explanatory variables are independent. We extend the method in Section 2.2 to account for within-group correlations.

2.1. Hierarchical structured variable selection model

At the group level, we employ a “selection” prior and introduce a latent binary indicator variable γ_g for each group g with the following interpretation: when γ_g = 0, the coefficient vector β_g of the g^th group has a point mass density at zero, reflecting that all predictors in the g^th group are excluded from the regression model; conversely, when γ_g = 1, the g^th group is selected in the model. At the within-group level, we assign a robust “shrinkage” prior and use the scale mixture normal distribution for each element in β_g, conditional on γ_g = 1. That is, conditional on γ_g = 1, we assume each coefficient within the g^th group follows a normal distribution with the scale parameter of the normal distribution, instead of being a fixed value, coming from another independent distribution, called the scale mixing distribution (Andrews and Mallows, 1974; West, 1987). Our hierarchical formulation of the prior for group g’s coefficient vector can be succinctly written as

$$\begin{array}{lll}\hfill {\mathit{\beta }}_{\mathit{g}}\mid {\gamma }_g,{\sigma }^2,{\mathit{\tau }}_{\mathit{g}}^{\mathbf{2}}& ~\hfill & (1-{\gamma }_g){\delta }_{\{{\mathit{\beta }}_{\mathit{g}}={\mathbf{0}}_{{\mathbf{k}}_{\mathbf{g}}}\}}+{\gamma }_g\mathrm{N}({\mathbf{0}}_{{\mathbf{k}}_{\mathbf{g}}},{\sigma }^2{D}_{{\tau }_g}),\text{where}{D}_{{\tau }_g}=\text{diag}({\tau }_{\mathrm{g}1}^2,\dots ,{\tau }_{{\text{gk}}_{\mathrm{g}}}^2),\hfill \\ \hfill {\gamma }_g\mid p& ~\hfill & \text{Bernoulli}(p),\hfill \\ \hfill {\tau }_{gj}^2\mid {\lambda }_g& ~\hfill & \mathcal{G}(•),\hfill \end{array}$$ (2.1)

where δ_● represents the Dirac delta measure that places all its mass on zero, the τ_gj’s are the Gaussian scale parameters of the “slab” distribution, and 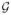(●) is a general mixing distribution for the normal scales τ_gj’s. While δ_● selects at the group level by setting all coefficients in the g^th group to zero simultaneously, the mixing distribution is applied to each element within the coefficient vector β_g, allowing for independent shrinkage of each individual coefficient at the within-group level. By setting to different mixing distributions, various shrinkage properties can be obtained. In this paper, we let 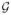(●) be an exponential distribution, ${\tau }_{gj}^2\mid {\lambda }_g~\text{Exp}({\lambda }_g^2/2)$, with a rate parameter, λ_g, for the g^th group. The exponential-scale mixture normal prior is equivalent to a Laplace distribution, and leads to well-developed lasso formulations with a (group-specific) penalty/regularization parameter λ_g for the g^th group (Park and Casella, 2008). Other formulations are possible as well, such as the normal-gamma prior of Griffin and Brown (2010) and normal-exponential-gamma prior of Griffin and Brown (2007), by using other families of scaling distributions. We call our prior in (2.1) the hierarchical structured variable selection (HSVS) prior, which has the following properties: (1) It generalizes the spike and slab mixture priors of Mitchell and Beauchamp (1988) to grouped settings, and accommodates robust shrinkage priors for the slab part of the prior, replacing the uniform slab. (2) The within-group shrinkage follows the well-developed lasso formulation, which promotes sparseness within selected groups and automatically provides interval estimates for all coefficients. (3) The hierarchy allows for the simultaneous selection and shrinkage of grouped covariates as opposed to all-in or all-out group selection (Yuan and Lin, 2006) or two-stage methods (Ma et al., 2010; Wang et al., 2009). (4) Most importantly, it is computationally tractable for large datasets since all full conditionals are available in closed form. This greatly aids our MCMC computations and subsequent posterior inference, as we show hereafter.

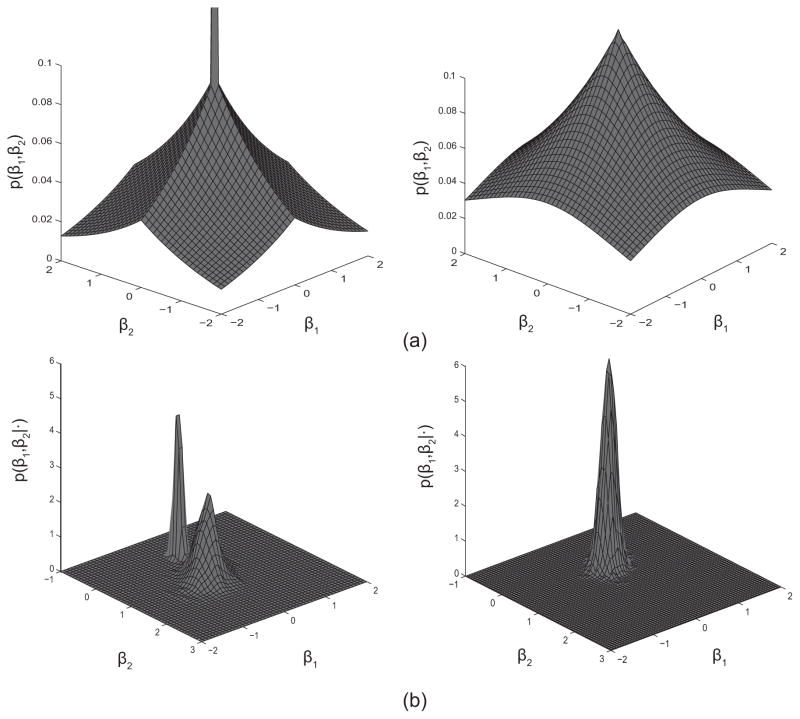
Differences with Bayesian group lasso prior

In order to gain more intuition regarding this prior, Figure 2(a) shows the schematic plot of an HSVS prior distribution versus a Bayesian group lasso prior distribution (Kyung et al., 2010), the model specification of which is as follows

Fig. 2.

Schematic plot of prior and posterior distribution of the hierarchical structured variable selection (HSVS) method. (a) Left: the density curve of an HSVS prior for a group with two variables; Right: a Bayesian lasso prior for a group with two variables. (b) Left: an example plot of the posterior distribution for a group with two variables when an HSVS prior is applied; Right: an example plot of the posterior distribution for the group of two variables when a Bayesian lasso prior is applied.

$$\begin{array}{lll}\hfill {\mathit{\beta }}_{\mathit{g}}\mid {\sigma }^2,{\tau }_g^2& ~\hfill & \mathrm{N}({\mathbf{0}}_{{\mathbf{k}}_{\mathbf{g}}},{\sigma }^2{\tau }_g^2{I}_{k_g}),\hfill \\ \hfill {\tau }_g^2& ~\hfill & \text{Gamma}(\frac{k_g+1}{2},\frac{{\lambda }^2}{2}).\hfill \end{array}$$ (2.2)

In each plot, the density of the HSVS prior and the group lasso prior is imposed on a group composed of two individual variables with coefficients β₁ and β₂. The “spike” at zero in the HSVS prior introduces group-level sparsity by simultaneously forcing both coefficients in the group to zero when β₁ and β₂ are both small in value. The Laplace distribution elsewhere in the prior independently shrinks individual coefficients within a group toward zero, which in return influences the group selection. In contrast, the Bayesian group lasso prior simultaneously shrinks β₁ and β₂ and does not lead to within-group selection. That is, the two variables in the group are either both selected or both excluded from the model. This conduct is determined by the model, as in formula (2.2), where the Bayesian group lasso employs a common variance ${\tau }_g^2$ for all coefficients in group g, shrinking the coefficients toward zero at the same rate through a Gamma mixing distribution imposed on ${\tau }_g^2$. Hence, the Bayesian group lasso selects groups but does not allow for individual variables within the group to be excluded from the regression model once a group is selected; whereas our HSVS prior results in both group and within-group variable shrinkage and selection. This is evident in Figure 2(b), which shows an example plot of the posterior distribution for the two coefficients in a group with an HSVS prior and a Bayesian group lasso prior, respectively.

To complete the prior specifications in the Gaussian case, we use a diffuse Gaussian prior N(0, cI) for the coefficients for fixed effects b, where c is some large value. For the parameter p that controls the group level selection, we use a conjugate Beta hyperprior: Beta(a, b) with (fixed) parameters a and b. We estimate the group-specific lasso parameters ${\lambda }_1^2,\dots ,{\lambda }_G^2$ and specify a common gamma mixing distribution Gamma(r, δ), ensuring their positivity. We use the improper prior density π(σ²) = 1/σ² on the error variance, which leads to a closed form of the full conditional distribution. These hyperpriors result in conjugate full conditional distributions for all model parameters, allowing for an efficient Gibbs sampler. (See Appendix A in the Supplementary Materials for the full conditional distributions and corresponding Gibbs sampling schemes.) Our full hierarchical model for the HSVS linear model can be succinctly written as

$$\begin{array}{cc}\hfill \text{Likelihood}:& \mathit{y}\mid U,X,\mathit{\beta },{\sigma }^2~\mathrm{N}(U\mathit{b}+X\mathit{\beta },{\sigma }^2{I}_n),\\ \hfill \text{Priors}:& \mathit{b}~\mathrm{N}(0,cI),\\ & {\mathit{\beta }}_{\mathit{g}}\mid {\gamma }_g,{\sigma }^2,{\mathit{\tau }}_{\mathit{g}}^{\mathbf{2}}~(1-{\gamma }_g)I\{{\mathit{\beta }}_{\mathit{g}}={\mathbf{0}}_{{\mathbf{k}}_{\mathbf{g}}}\}+{\gamma }_g\mathrm{N}({\mathbf{0}}_{{\mathbf{k}}_{\mathbf{g}}},{\sigma }^2{D}_{{\tau }_g}),\\ & \text{where}{D}_{{\tau }_g}=\text{diag}({\tau }_{\mathrm{g}1}^2,\dots ,{\tau }_{{\text{gk}}_{\mathrm{g}}}^2),\\ \hfill \text{Hyperpriors}:& {\gamma }_g\mid p~\text{Bernoulli}(p),{\tau }_{gj}^2\mid {\lambda }_g~\text{Exp}(\frac{{\lambda }_g^2}{2}),p~\text{Beta}(a,b),\\ & {\lambda }_g^2~\text{Gamma}(r,\delta ),{\sigma }^2~1/{\sigma }^2.\end{array}$$

2.2. Fused hierarchical structured variable selection model

In the above proposed HSVS construction, we utilize a group-specific binary indicator for group-level selection and a Bayesian lasso method via independent Laplace priors for within-group shrinkage, which is invariant to the permutation of the order of the group-specific variables. However, as mentioned previously, there exists serial correlation between probes within the same gene, and given their proximity by genomic location, positively correlated probes are likely to have similar effects on the response. That is, their corresponding regression coefficients also tend to be positively correlated. Similar arguments have been used in many other contexts as seen in Li and Zhang (2010), Tibshirani et al. (2005), and Huang et al. (2011). Hence, a prior introducing positive correlations between adjacent coefficients within a gene is desired in such situations where there exists a natural ordering of the variables to account for the “serial” structure of the data. In addition, in Bayesian variable selection methods with independent priors on the coefficients such as Lasso, highly positively correlated predictors would result in a negative correlation between the coefficients in the posterior, discouraging them from entering the regression model simultaneously (Kyung et al., 2010). That is, inclusion of one variable in the model would eliminate its correlated variables from the model. Such a prior with positive correlations as a priori on the coefficients would smooth the coefficient estimates toward each other in the posterior, encouraging correlated variables to be selected in the model simultaneously. For this purpose, we extend our HSVS model to accommodate these correlations via a Bayesian fused lasso formulation, as detailed below.

We first start by presenting the Bayesian version of the fused lasso by Tibshirani et al. (2005) for non-group settings, and then explain how we extend it to our HSVS setting where natural groupings exist.

Fused Lasso

Consider a regular linear regression model (without grouping structures) as

$$Y=\mathbf{X}\mathit{\beta }+\epsilon ,\epsilon ~N(0,{\sigma }^2),$$

where β = (β₁, … , β_k)′, the frequentist fused lasso estimates the regression coefficients by minimizing the penalized negative log-likelihood:

$$\widehat{\mathit{\beta }}=argmin\{\sum _i{(y_i-\sum _j{x}_{ij}{\beta }_j)}^2+{\lambda }_1\sum _{j=1}^k\mid {\beta }_j\mid +{\lambda }_2\sum _{j=1}^{k-1}\mid {\beta }_j-{\beta }_{j-1}\mid \}.$$

In comparison with the regular lasso, the fused lasso utilizes two regulation parameters. The first parameter λ₁ encourages sparsity in the coefficient estimation, and the second parameter λ₂ reduces the differences between neighboring coefficients, thus encouraging smoothness in the coefficient profiles β_j as a function of j and accounting for the adjacency structure of the data.

Bayesian Fused Lasso

From the Bayesian point of view, the fused lasso estimates could be viewed as the posterior mode estimates with the regression parameters following a Laplace prior. Specifically, Kyung et al. (2010) considered a fully Bayesian analysis using a conditional prior specification of the form

$$\pi (\mathit{\beta }\mid {\lambda }_1,{\lambda }_2,{\sigma }^2)\propto exp\left(-\frac{{\lambda }_1}{\sigma }\sum _{j=1}^k\mid {\beta }_j\mid -\frac{{\lambda }_2}{\sigma }\sum _{j=1}^{k-1}\mid {\beta }_{j+1}-{\beta }_j\mid \right),$$ (2.3)

which is the product of independent Laplace priors on β_j, j = 1, … , k, and β_j+1 − β_j, j = 1, … , k − 1. Each Laplace prior could be represented as an Exponential scale mixture of normal distributions (Park and Casella, 2008). Hence, the prior in (2.3) is equivalent to the hierarchical prior

$$\begin{array}{lll}\hfill \mathit{\beta }\mid {\sigma }^2,{\tau }_1^2,\dots ,{\tau }_k^2,{\omega }_1^2,\dots ,{\omega }_{k-1}^2& ~\hfill & N_k({\mathbf{0}}_k,{\mathrm{\sum }}_{\beta }^{-1}),\hfill \\ \hfill {\tau }_1^2,\dots ,{\tau }_k^2& ~\hfill & \prod _{j=1}^k\frac{{\lambda }_1^2}{2}exp(-{\lambda }_1{\tau }_j^2/2)d{\tau }_j^2,\hfill \\ \hfill {\omega }_1^2,\dots ,{\omega }_{k-1}^2& ~\hfill & \prod _{j=1}^{k-1}\frac{{\lambda }_2^2}{2}exp(-{\lambda }_2{\omega }_j^2/2)d{\omega }_j^2,\hfill \end{array}$$ (2.4)

where ${\mathrm{\sum }}_{\beta }^{-1}$ is a tridiagonal matrix with

$$\begin{array}{lll}\hfill \text{Main}\text{diagonal}& =\hfill & \{\frac{1}{{\tau }_j^2}+\frac{1}{{\omega }_{j-1}^2}+\frac{1}{{\omega }_j^2},j=1,\dots ,k\},\hfill \\ \hfill \text{Off}\text{diagonal}& =\hfill & \{-\frac{1}{{\omega }_j^2,j=1,\dots ,k-1}\},\hfill \end{array}$$

and $1/{\omega }_0^2$ and $1/{\omega }_k^2$ are defined as 0. This proof follows that of Kyung et al. (2010) for non-grouped settings. We extend it here for grouped settings.

Fused HSVS

In our second proposed prior, the fused-HSVS, we assign the fused lasso prior in (2.4) to each group of coefficients β_g for within-group variable selection and derive the hierarchical model as follows:

$$\begin{array}{lll}\hfill {\mathit{\beta }}_{\mathit{g}}\mid {\gamma }_g,{\sigma }^2,{\mathit{\tau }}_{\mathit{g}}^{\mathbf{2}},{\mathit{\omega }}_{\mathit{g}}^{\mathbf{2}}& ~\hfill & (1-{\gamma }_g)I\{{\mathit{\beta }}_{\mathit{g}}={\mathbf{0}}_{{\mathbf{k}}_{\mathbf{g}}}\}+{\gamma }_g\mathrm{N}({\mathbf{0}}_{{\mathbf{k}}_{\mathbf{g}}},{\sigma }^2{\mathit{\sum }}_{{\beta }_g}),\text{where}\hfill \\ \hfill {\mathrm{\sum }}_{{\beta }_g}^{-1}& =\hfill & \left[\begin{array}{ccccc}\frac{1}{{\tau }_{g1}^2}+\frac{1}{{\omega }_{g1}^2}& -\frac{1}{{\omega }_{g1}^2}& 0& \cdots & 0\\ -\frac{1}{{\omega }_{g1}^2}& \frac{1}{{\tau }_{g2}^2}+\frac{1}{{\omega }_{g1}^2}+\frac{1}{{\omega }_{g2}^2}& -\frac{1}{{\omega }_{g2}^2}& \ddots & ⋮\\ 0& -\frac{1}{{\omega }_{g2}^2}& \frac{1}{{\tau }_{g3}^2}+\frac{1}{{\omega }_{g2}^2}+\frac{1}{{\omega }_{g3}^2}& \ddots & 0\\ ⋮& \ddots & \ddots & \ddots & -\frac{1}{{\omega }_{g(k_g-1)}^2}\\ 0& \cdots & 0& -\frac{1}{{\omega }_{g(k_g-1)}^2}& \frac{1}{{\tau }_{g{k}_g}^2}+\frac{1}{{\omega }_{g(k_g-1)}^2}\end{array}\right],\hfill \\ \hfill {\gamma }_g\mid p& ~\hfill & \text{Bernoulli}(p),\hfill \\ \hfill {\tau }_{gj}^2\mid {\lambda }_{1g}& ~\hfill & \text{Exp}(\frac{{\lambda }_{1g}^2}{2}),\text{for}\mathrm{j}=1,\dots ,k_g,\hfill \\ \hfill {\omega }_{gj}^2\mid {\lambda }_{2g}& ~\hfill & \text{Exp}(\frac{{\lambda }_{2g}^2}{2}),\text{for}\mathrm{j}=1,\dots ,k_g-1,\hfill \end{array}$$

where the τ_gj’s are the variances of the individual coefficients within a group and the ω_gj’s introduce correlations between neighboring coefficients in the prior. By using the exponential hyperpriors with the regularization parameters, λ_1g’s and λ_2g’s, the hierarchy shrinks the coefficient estimates and reduces the difference in neighboring coefficients.

As with the independent HSVS model, we can assign a beta hyperprior distribution to the parameter p and diffuse gamma hyperprior distributions Gamma(r₁, δ₁) and Gamma(r₂, δ₂) to the two sets of regularization parameters {λ_1g : g = 1, …, G} and {λ_2g : g = 1, … G}, respectively. We use the same prior parameters for λ_1g’s and λ_2g’s. However, different values could be used for each set. These choices of hyperprior densities lead to conjugate conditional posterior distributions, which can then easily join the other parameters in the Gibbs sampler. The full hierarchical model with fused within-group priors is formulated as follows:

$$\begin{array}{ll}\hfill \text{Likelihood}:& \hfill \mathit{y}\mid U,X,\mathit{\beta },{\sigma }^2~\mathrm{N}(U\mathit{b}+X\mathit{\beta },{\sigma }^2{I}_n),\hfill \\ \hfill \text{Priors}:& \hfill \mathit{b}~\mathrm{N}(0,cI),\hfill \\ \hfill & \hfill {\mathit{\beta }}_{\mathit{g}}\mid {\gamma }_g,{\sigma }^2,{\mathit{\tau }}_{\mathit{g}}^{\mathbf{2}},{\mathit{\omega }}_{\mathit{g}}^{\mathbf{2}}~(1-{\gamma }_g)I\{{\mathit{\beta }}_{\mathit{g}}={\mathbf{0}}_{{\mathbf{k}}_{\mathbf{g}}}\}+{\gamma }_g\mathrm{N}({\mathbf{0}}_{{\mathbf{k}}_{\mathbf{g}}},{\sigma }^2{\mathit{\sum }}_{{\beta }_g}),\hfill \\ \hfill \text{Hyperpriors}:& \hfill {\gamma }_g\mid p~\text{Bernoulli}(p),{\tau }_{gj}^2\mid {\lambda }_{1g}~\text{Exp}(\frac{{\lambda }_{1g}^2}{2}),{\omega }_{gj}^2\mid {\lambda }_{2g}~\text{Exp}(\frac{{\lambda }_{2g}^2}{2}),\hfill \\ \hfill \hfill & p~\text{Beta}(a,b),{\lambda }_{1g}^2~\text{Gamma}(r_1,{\delta }_1),{\lambda }_{2g}^2~\text{Gamma}(r_2,{\delta }_2),{\sigma }^2~1/{\sigma }^2.\hfill \end{array}$$

2.3. Choice of hyperparameters

We discuss the hyperparameter specifications here and note that our complete posterior sampling schemes are available in Appendix A in the Supplementary Materials. For the parameters of the beta prior on p in the HSVS and fused-HSVS models, we set (a, b) = (1, 1), which is a uniform prior. This choice of prior gives that the prior probability for any specific model in which nonzero coefficients are present in exactly k of the groups is proportional to ${\left(\begin{array}{l}G\hfill \\ k\hfill \end{array}\right)}^{-1}$ (Scott and Berger, 2010), which encourages sparsity in model selection. More informative choices can be accommodated using appropriate specifications of these parameters. For the gamma priors of ${\lambda }_g^2$ in the HSVS model and of ${\lambda }_{1g}^2,{\lambda }_{2g}^2$ in the fused-HSVS model, we consider the shape parameters (r, r₁, r₂) to be 1, as in Kyung et al. (2010) and Park and Casella (2008), such that the prior densities approach 0 sufficiently fast, and we use the empirical Bayes estimator of the rate parameters (δ, δ₁, δ₂). For example, conditional on r = 1, the empirical Bayes estimator of δ in the HSVS model is ${\delta }^{(k)}=\frac{G}{{\sum }_g{\mathbf{E}}_{{\delta }^{(k-1)}}({\lambda }_g^2\mid y)}$ at the k^th iteration. We found that these choices of hyperparameters are sufficiently robust, both in our simulated and real data examples. A more detailed discussion of prior sensitivity is provided in Appendix B in the Supplementary Materials.

3. Generalized hierarchical structured variable selection model for discrete responses

Due to their conjugate construction, both the HSVS and fused-HSVS models can be extended to discrete responses using the latent variable formulations, as in Albert and Chib (1993) and Holmes and Held (2006). We present the binary case and note that extensions to multinomial and ordinal responses can be dealt with in a similar manner.

Suppose that n binary responses, Y₁, …, Y_n, are observed and that Y_i has a Bernoulli distribution with probability p_i. Following Albert and Chib (1993), we relate the explanatory variables to the responses using a probit regression model

$$\begin{array}{lll}{Y}_i\hfill & =\hfill & \{\begin{array}{ll}1,\hfill & \text{if}{Z}_i\ge 0;\hfill \\ 0,\hfill & \text{if}{Z}_i<0,\hfill \end{array}\hfill \\ Z_i\hfill & =\hfill & {\mathbf{U}}_i\mathit{b}+{\mathbf{X}}_i\mathit{\beta }+{\epsilon }_i,{\epsilon }_i~\mathrm{N}(0,1),\hfill \end{array}$$

where Z₁, …, Z_n are n independent latent variables. The prior on β parallels the developments in Sections 2.1 and 2.2 with the Y_i’s replaced by Z_i’s, giving rise to our generalized-HSVS model. The generalized-HSVS model leads to a truncated normal for the full conditional distribution of the Z_i. Hence the Z_i’s can easily be embedded in the Gibbs sampling. The posterior distribution and Gibbs sampling of the Z_i’s are detailed in Appendix A in the Supplementary Materials.

Note that we choose the probit regression model of Albert and Chib (1993) for binary responses in consideration of its computational ease. An alternative to the probit model for the binary responses is to perform logistic regression by mixing latent Gaussian models, as described by Holmes and Held (2006).

4. Model selection using false discovery rates

The posterior sampling schemes we have outlined explore the model space and result in MCMC samples of both the group indicators and the corresponding within-group coefficients at each iteration. We want to select explanatory groups that are significantly associated with the response variable. There are different ways to summarize the information in the samples for conducting model selection. One could choose the most likely set of groups (posterior mode) and conduct conditional inference on the selected model. However, this particular configuration of variable groups may appear in only a very small proportion of MCMC samples. An alternative strategy is to utilize all of the MCMC samples and average over the various models visited by the sampler. This model averaging approach weighs the evidence of significant groups using all the MCMC samples and generally results in regression models with better prediction performance (Hoeting et al., 1999; Raftery et al., 1997) – a strategy we follow here. We outline an approach to conduct model selection based on controlling the false discovery rate (FDR) (Benjamini and Hochberg, 1995) which is especially crucial in the high-dimensional settings that are of interest here.

Suppose we have T posterior samples of a parameter set from an MCMC computation. Recall that by our prior structures, for each MCMC iteration, a certain set of variable groups is included in the regression model whose group indicator ${\gamma }_g^{(t)}=1$, where ${\gamma }_g^{(t)}$ is the value of γ_g at the t^th MCMC iteration. Let p_g represent the posterior probability of including the g^th group in the model, g = 1, …, G. We can estimate p_g to be the relative number of times the g^th group is present in the model across the T MCMC samples:

$$p_g=\frac{1}{T}\sum _{t=1}^T{\gamma }_g^{(t)}.$$

We assume that for some significance threshold ϕ, any variable group with p_g > ϕ is significant, and thus is included in the regression model. Then the set of groups 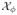_ϕ = {g : p_g > ϕ} contains all the groups considered to be significant. Note that the (1 − p_g)’s can be interpreted as the estimates of the local FDR (Storey, 2003) as they measure the probability of a false positive if the g^th group is significant but is not a predictor group in the true model. The significance threshold ϕ can be determined based on classical Bayesian utility considerations, such as in Müller et al. (2004), based on the elicited relative costs of false positive and false negative errors, or can be set to control the overall average Bayesian FDR. (See Morris et al., 2008; Baladandayuthapani et al., 2010; and Bonato et al., 2011 for detailed expositions in other settings.)

Thus, given a global FDR bound ν ∈ (0, 1), we are interested in finding the threshold value ϕ_ν for flagging the set of groups p_g > ϕ_ν as potentially relevant and labeling them as discoveries. This implies that the threshold ϕ_ν is a cut-off on the (model-based) posterior probabilities that corresponds to an expected Bayesian FDR of ν, which means that 100ν % of the groups identified as significant are expected to be false positives. The threshold ϕ_ν is determined in the following way: for all the groups g = 1, …, G, we sort p_g in descending order to yield p_(g), g = 1, … , G. Then, ϕ_ν = p_(ξ), where $\xi =max\{g\ast :{\sum }_{g=1}^{g\ast }(1-\frac{p_{(g)}}{g\ast })\le \nu \}$. Thus, the set of groups 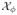_ϕν = {g : p_g > ϕ_ν} can be claimed as significant in the regression model based on an average Bayesian FDR of ν. For the within-group selection, we select individual variables (conditional on the significant groups) using the 95% two-sided credible intervals of the coefficients, which are based on the posterior probability distributions of the MCMC samples.

5. Simulation studies

We conducted two detailed simulation studies to evaluate the operating characteristics of our method in the context of a linear regression model and a probit regression model (closely mimicking our real MIPS data), as presented respectively in Sections 5.1 and 5.2 respectively.

5.1. Simulations for linear regression models

We first assumed a simple linear model,

$$\mathbf{Y}=X\mathit{\beta }+\epsilon ,$$

and considered five scenarios that portray different aspects of the data generating process, with the following specification of the covariate matrix, X.

• Model I: We first generated 21 latent random variables Z₁, …, Z₂₀ and W from independent standard normal distributions. The covariates X₁, …, X₂₀ were defined as $X_i=(Z_i+W)/\sqrt{2}$. We considered 20 variable groups for the regression model, where the i^th group, i = 1, …, 20, is composed of all the terms in a fourth-degree polynomial of X_i. The datasets were simulated from the following true model

  $$Y=\underset{}{\underbrace{X_3+\frac{1}{2}{X}_3^4}}\underset{}{\underbrace{-\frac{1}{2}{X}_6+\frac{2}{3}{X}_6^4}}\underset{}{\underbrace{+2X_9-\frac{3}{2}{X}_9^3}}+\epsilon ,$$

  where ε ~ (0, 2²). We collected 100 observations from each run. This model is similar to the settings used in Yuan and Lin (2006), where the predictors have a natural grouping structure. However, our study is different in that not all elements in a group are present in the true models, i.e., some of the within-group coefficients are set to zero. Hence, selections at both group and within-group levels are desired for the model.

• Model II: We generated the covariates X₁, …, X₂₀ as in model I. We then considered 20 variable groups for the regression model, where the i^th group, i = 1, …, 20, is composed of all the terms in a fourth-degree polynomial of X_i. However, the data were simulated from a true model with a total of 9 variable groups, each containing only 2 terms of the fourth-degree polynomial. We collected 100 observations from each run. This model has the same setting as model I except for the sparsity level in the true model, with model II being less sparse (having more variables) than model I.

• Model III: We generated 20 latent variables Z₁, …, Z₂₀ independently from a standard normal distribution. We then considered 20 groups for the regression model, with each group composed of four variables, X_ij for j = 1, …, 4. The X_ij’s were generated as $X_{ij}=(Z_i+e_{ij})/\sqrt{2}$, where e_ij ~ N(0, 1). The data were simulated from the true model

  $$Y=\underset{}{\underbrace{X_{31}+X_{32}+X_{33}}}\underset{}{\underbrace{+\frac{4}{3}{X}_{61}+\frac{1}{2}{X}_{62}}}\underset{}{\underbrace{+\frac{1}{3}{X}_{91}-X_{93}-2X_{94}}}+\epsilon ,$$

  where ε ~ N(0, 2²). We collected 100 observations from each run. In model III, the four candidate variables within the same group are correlated, with a correlation r = 0.5; whereas the variables between groups are independent. The true model includes partial elements within three groups. Hence, selections at both group and within-group levels are desired for the model.

• Model IV: We generated 20 latent variables Z₁, …, Z₂₀ independently from a standard normal distribution. We then considered 20 groups for the regression model, with each group composed of four variables, X_ij for j = 1, …, 4. The X_ij’s were generated as $X_{ij}=(Z_i+e_{ij})/\sqrt{1.01}$, where e_ij ~ N(0, 0.1²). The data were simulated from the same model as in model III. We collected 100 observations from each run. This model has the same setting as model III, except that the variables within the same group have a much higher correlation, r = 0.99.

• Model V: We generated 10 latent variables Z₁, …, Z₁₀ independently from a standard normal distribution. We then considered 10 groups for the regression model, with each group composed of 10 variables, X_ij, j = 1, …, 10. The X_ij’s were generated in the same fashion as in model III. The data were simulated from the true model

  $$Y=\underset{}{\underbrace{X_{31}+X_{32}+X_{33}+X_{34}+X_{35}+X_{36}}}\underset{}{\underbrace{-X_{61}-X_{62}-X_{63}-X_{64}}}+\epsilon ,$$

  where ε ~ N(0, 2²). We collected 100 observations from each run. Thus, model IV includes two predictive groups, each group having a block of constant nonzero coefficients. We use model IV to compare the performance of the HSVS and fused-HSVS method when collinearity between neighboring coefficients is present in a group.

For each dataset generated from models I, II, III, or IV, the HSVS, group lasso, regular lasso, and stepwise selection methods were used to estimate the coefficients. For each dataset generated from model V, the HSVS, fused-HSVS, and group lasso methods were used to estimate the coefficients. The Bayesian estimates were posterior medians using 10, 000 iterations of the Gibbs sampler after 1, 000 burn-in iterations. Significant groups were selected based on an FDR of ν = 0.10. The regular lasso and group lasso methods estimated coefficients using the lars (Efron et al., 2004) and grpreg (Breheny and Huang, 2009) packages respectively, with the tuning parameters selected using C_p-criterion and 5-fold cross validation. To evaluate the performance of each method, we use the true model error defined as

$$ME(\widehat{\mathit{\beta }})={(\widehat{\mathit{\beta }}-\mathit{\beta })}^{\prime }{X}^{\prime }X(\widehat{\mathit{\beta }}-\mathit{\beta })$$ (5.1)

Table 1 summarizes the average model errors over 200 runs, along with the number of false positive (FP) and false negative (FN) groups/individual variables selected for each method. The results show that the HSVS method has slightly smaller model errors than the group lasso method and significantly smaller model errors than the lasso and stepwise methods for models I, II and III; but it performs no better than the group lasso for model IV, where there are extremely high correlations within groups. For the group-level selection, the HSVS method is similar in performance to the group lasso method. However, the HSVS method has an obviously higher FN rate than the group lasso when the number of nonzero groups increases, as indicated in model II. For the within-group-level selection, we used the 95% posterior credible intervals based on MCMC samples to select significant variables within the FDR-based significant groups. Table 1 shows that the HSVS method performs better overall than the other methods, with lower FP rates, although at the price of a little higher FN rates. This is expected since we use the Bayesian lasso formulation, which shrinks within-group coefficients toward zero. Hence, the model tends to exclude the within-group variables that have only weak effects on the response. In our simulation study, the HSVS model has higher probabilities of obtaining FN for those variables whose true coefficients are less than 0.5 in absolute value.

Table 1.

Simulation results for models I to V. The mean model errors and the number of false positives and false negatives over 200 replications are presented in the table; standard deviations are shown in parentheses. FP: number of false positives; FN: number of false negatives. See Section 5.1 for details about the models.

	Model Error	Group of Variables		Within-group Variable
		FP	FN	FP	FN
Model I:
HSVS	0.22 (0.09)	0.00 (0.00)	0.00 (0.00)	0.14 (0.37)	0.79 (0.55)
Group Lasso	0.29 (0.15)	0.02 (0.15)	0.00 (0.00)	6.06 (0.63)	0.00 (0.00)
Lasso	0.64 (0.21)	11.41 (3.23)	0.00 (0.00)	18.42 (7.35)	0.28 (0.45)
Stepwise	1.92 (0.52)	17.00 (0.00)	0.00 (0.00)	74.00 (0.00)	0.00 (0.00)
Model II:
HSVS	0.78 (0.26)	0.00 (0.00)	0.26 (0.44)	0.65 (0.88)	4.39 (1.28)
Group Lasso	0.84 (0.25)	0.10 (0.36)	0.03 (0.16)	18.35 (1.49)	0.05 (0.31)
Lasso	1.02 (0.30)	9.19 (1.68)	0.00 (0.00)	22.97 (7.38)	0.93 (0.89)
Stepwise	1.85 (0.48)	11 (0.00)	0.00 (0.00)	62.00 (0.00)	0.00 (0.00)
Model III:
HSVS	0.47 (0.18)	0.02 (0.14)	0.00 (0.00)	0.14 (0.37)	0.71 (0.79)
Group Lasso	0.53 (0.36)	0.07 (0.33)	0.00 (0.00)	4.27 (1.31)	0.03 (0.30)
Lasso	1.36 (0.60)	10.35 (5.32)	0.00 (0.00)	19.95 (15.99)	1.13 (0.99)
Stepwise	3.33 (0.57)	17.00 (0.00)	0.10 (0.00)	72.00 (0.00)	0.00 (0.00)
Model IV:
HSVS	0.48 (0.23)	0.07 (0.25)	0.00 (0.00)	0.00 (0.00)	7.99 (0.10)
Group Lasso	0.46 (0.26)	2.29 (1.54)	0.00 (0.00)	13.16 (6.15)	0.00 (0.00)
Lasso	0.78 (0.89)	6.13 (5.52)	0.02 (0.12)	10.28 (12.68)	4.34 (1.23)
Stepwise	3.30 (0.58)	17.00 (0.00)	0.00 (0.00)	72.00 (0.00)	0.00 (0.00)
Model V:
HSVS	0.37 (0.13)	0.01 (0.07)	0.00 (0.00)	0.52 (0.68)	0.37 (0.60)
Fused-HSVS	0.29 (0.12)	0.02 (0.14)	0.00 (0.00)	0.35 (0.58)	0.21 (0.45)
Group Lasso	0.40 (0.16)	0.37 (0.48)	0.00 (0.00)	13.70 (4.84)	0.00 (0.00)

The results of model V estimation show that the fused-HSVS method has a lower mean model error than the other two. In addition, the fused-HSVS method performs better than the HSVS method in within-group-level selection, with both lower FP and FN rates. The results show that the fused-HSVS method, as expected, is better when the variables within a group have similar effects on the response. Compared to the HSVS prior, the fused-HSVS prior leads to less variation in coefficient estimates within a group, due to the constraint on the differences between neighboring coefficients.

5.2. Simulations based on real data

In this section, we conduct a second simulation study for high-dimensional generalized linear models closely mimicking our real breast cancer copy number data. Specifically, we simulated data with binary responses from the following regression model,

$$\begin{array}{lll}{Y}_i\hfill & =\hfill & \{\begin{array}{ll}1,\hfill & Z_i\ge 0;\hfill \\ 0,\hfill & Z_i<0,\hfill \end{array}\hfill \\ Z_i\hfill & =\hfill & {\mathbf{U}}_i\mathit{b}+{\mathbf{X}}_i\mathit{\beta }+{\epsilon }_i,\hfill \end{array}$$

with ε_i ~ N (0, 1), leading the probit regression model. We considered a high-dimensional dataset of 1, 800 variables composing 157 groups, with the grouping structure simulating the gene-probe architecture of a subset of genes from a randomly chosen segment on chromosome 7 in the breast cancer data. The posterior median estimates of the parameters obtained by the fused-HSVS method for the subset from the Bayesian analysis (presented in Section 6) were taken as the true values of β, which include 24 nonzero individual coefficients from 8 significant groups. The coefficients from the 8 significant groups range from −0.8 to 0.6, with the neighboring coefficients relatively close in value. The plot showing the values of the coefficient parameters is included in Figure S1 in the Supplementary Materials. One confounder variable was generated from a standard normal distribution for the matrix U with its coefficient randomly chosen from the interval (0, 1). The data matrix, X, was generated with the following two correlation structures:

• Model VI: The data matrix, X, was partitioned by columns where each submatrix X_g corresponds to the covariates of the g^th group. The grouping structures were the same as those of the breast cancer data. For each group g, the corresponding submatrix, X_g, was independently generated from N(0, Σ) with the element of Σ set as σ_ij = 0.5^|i−j|.

• Model VII: As with model VI, the data matrix, X, was partitioned by columns where each submatrix X_g corresponds to the covariates of the g^th group. The grouping structures were the same as those of the breast cancer data. For each group g, the corresponding submatrix, X_g, was independently generated from N(0, Σ). Different from model VI, the element of Σ was set as σ_ij = 0.9^|i−j|. Hence, the model has a higher level of within-group correlations in generating X than model VI.

For each model, we collected 900 observations for each run. The generalized HSVS, generalized fused-HSVS, and generalized group lasso methods were compared in estimating models VI and VII. As in Section 5.1, the Bayesian estimates were posterior medians using 10, 000 iterations of the Gibbs sampler after 1, 000 burn-in iterations. Significant groups were selected based on an FDR of ν = 0.10. The generalized group lasso method estimated coefficients using the grpreg (Breheny and Huang, 2009) package with the tuning parameters selected by 5-fold cross-validation.

The average model errors over 40 runs are presented at the bottom of Table 2, along with the number of FP and FN groups/individual variables selected for each method. We note that the fused-HSVS method has obviously lower mean model errors than the other two methods, and the mean model errors of the HSVS are a little higher than those of the group lasso method. Considering the n/q ratio and the small magnitudes of the true coefficients values (from −0.8 to 0.6), the difference in performance is probably due to that the HSVS method strongly shrinks each coefficient individually toward zero while the fused-HSVS is able to borrow strength from neighboring coefficients and prevent over-shrinking weak coefficients. The model errors of the HSVS and fused-HSVS methods increase with the serial correlations among the variables, which agrees with the simulation results of model III. For variable selection, the HSVS and fused- HSVS methods have significantly lower FP rates than the group lasso method at the price of slighter higher FN rates, both at the group and within-group levels. Compared with the group lasso method, the HSVS methods are strong variable selectors at both levels, resulting in sparser model inference, especially for data with q ≫ n. In addition, the fused-HSVS method has lower FN rates than the HSVS while maintaining low FP rates, which is consistent with their performance in model error, indicating that the fused-HSVS is better at detecting groups with consistently weak signals.

Table 2.

Simulation results for models VI and VII with binary responses. The mean model errors and the number of false positives and false negatives over 40 replications for each model are presented in the table; standard deviations are shown in parentheses. FP: number of false positives; FN: number of false negatives. See Section 5.2 for details about the models.

	Distribution of Error Term	Model Error	Group of Variables		Within-group Variable
			FP	FN	FP	FN
Model VI:
Generalized HSVS	Normal	0.85 (0.19)	0.00 (0.00)	2.10 (0.55)	0.10 (0.31)	9.00 (1.20)
Generalized Fused-HSVS		0.57 (0.06)	0.00 (0.00)	1.80 (0.48)	0.47 (0.90)	8.30 (1.79)
Generalized Group Lasso		0.82 (0.15)	7.43 (2.80)	0.33 (0.48)	66.80 (29.23)	2.13 (3.25)
Generalized HSVS	t	0.76 (0.17)	0.00 (0.00)	1.93 (0.45)	0.07 (0.25)	8.73 (1.14)
Generalized Fused-HSVS		0.52 (0.06)	0.00 (0.00)	1.66 (0.48)	0.33 (0.55)	8.10 (0.84)
Generalized Group Lasso		0.68 (0.19)	9.00 (3.03)	0.13 (0.35)	82.33 (26.35)	0.93 (2.42)
Generalized HSVS	Skew-normal	0.78 (0.17)	0.00 (0.00)	2.03 (0.61)	0.07 (0.25)	8.73 (1.31)
Generalized Fused-HSVS		0.55 (0.07)	0.00 (0.00)	1.70 (0.53)	0.43 (0.63)	7.97 (0.81)
Generalized Group Lasso		0.74 (0.17)	8.83 (3.73)	0.37 (0.56)	70.53 (34.29)	2.37 (3.41)
Model VII:
Generalized HSVS	Normal	0.93 (0.15)	0.00 (0.00)	2.93 (0.52)	0.00 (0.00)	15.63 (1.47)
Generalized Fused-HSVS		0.62 (0.12)	0.00 (0.00)	2.50 (0.63)	0.07 (0.25)	13.63 (1.65)
Generalized Group Lasso		0.85 (0.22)	5.63 (4.97)	0.90 (0.88)	82.50 (45.05)	2.27 (2.89)
Generalized HSVS	t	0.86 (0.11)	0.00 (0.00)	3.00 (0.64)	0.07 (0.25)	15.57 (1.48)
Generalized Fused-HSVS		0.57 (0.12)	0.00 (0.00)	2.20 (0.66)	0.40 (0.56)	13.10 (1.60)
Generalized Group Lasso		0.75 (0.18)	6.03 (5.26)	0.80 (0.92)	85.30 (45.02)	1.90 (2.70)
Generalized HSVS	Skew-normal	0.92 (0.13)	0.00 (0.00)	3.00 (0.37)	0.03 (0.18)	15.93 (1.20)
Generalized Fused-HSVS		0.60 (0.14)	0.00 (0.00)	2.40 (0.56)	0.30 (0.41)	13.47 (1.66)
Generalized Group Lasso		0.82 (0.20)	5.53 (3.51)	0.77 (0.78)	76.93 (31.93)	1.83 (2.51)

Robustness to model misspecifications: to test the robustness of our methods to model misspecification, we further generated data from the same models and parameter configurations, but let the error term ε_i follow a heavy-tailed distribution. We used a $t_4(0,\sqrt{\frac{1}{2}})$ and a skewed distribution $SN(-\sqrt{\frac{1}{\pi -1}},\sqrt{\frac{\pi }{\pi -1}},1)$, both of which have mean 0 and variance 1, as in the probit model. The results, as presented in Table 2 are very similar to the results of the simulations with ε_i ~ N (0, 1). We found that a moderate heavy-tail or skewness in the error distributions do not have a significant impact on the inference for our simulations.

6. Application to genomic studies of breast cancer subtype

We applied our algorithm to the MIP assay dataset to identify genes as well as probes that are significantly associated with the clinically relevant subtypes of breast cancer. The subtypes of the 971 breast cancer samples are as follows: 389 are classified as luminal A, 156 as luminal B, 158 as HER2+, 184 as TNBC, and 84 as unclassified. As mentioned previously, we elected to focus on modeling the TNBC subtype with the copy number data. Hence, we have binary response variables, with Y_i = 1 if patient i has the TNBC subtype, and Y_i = 0 otherwise. Throughout our article, we considered the error term ε_i’s to be independent and identically distributed Gaussian errors, since we treat samples/patients as replicates and any correlation between the patients is accounted for by the copy number profiles. We believe this is a reasonable assumption for our dataset, since all samples are obtained from a (somewhat) homogeneous pool of patients with early-stage breast cancer.

We modeled the binary response using the HSVS and fused-HSVS model for generalized linear models as discussed in Section 3. The candidate variables are the 167, 574 probes that are mapped to the coding regions of 16, 523 unique genes, with the probes in the same gene treated as a group. The sizes of the groups (numbers of probes in a gene) range from 1 to over 100, with an average around 10 and mode around 6. We ran our HSVS models for each chromosomal arm separately, used 10, 000 MCMC iterations with a burn-in of 1, 000 for inference and selected genes based on an FDR of ν = 0.10. The convergence of the MCMC chains was assessed based on the Geweke diagnostic test (Geweke, 1992), which tests equality of the means of two nonoverlapping parts of a chain (the first 0.1 and the last 0.5 by default). The Geweke statistic asymptotically follows a standard normal distribution if the means are truly equal. The test on the MCMC samples on a random sample of model parameters indicated stationarity of the chains since the statistics were within (−2, 2). The traceplots of three of these parameters are presented in Figure S2 in the Supplementary Materials.

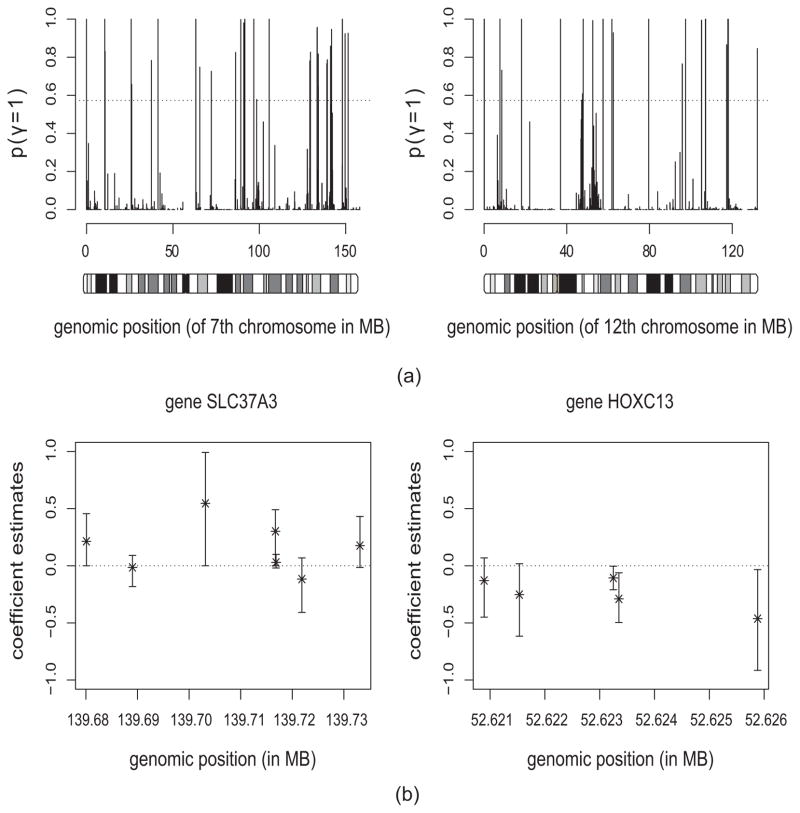
A total of 271 genes were selected by the HSVS model for further biological investigation. These genes were identified as significantly amplified (positive) or decreased (negative) in the TNBC samples compared with other subtypes. Figure 3(a) shows the posterior probabilities of the genes on two chromosomes, with the dashed line indicating the FDR threshold. A gene is considered significant if the associated probability exceeds the threshold. For each selected gene, the posterior distributions of coefficients for the gene-specific probes are also provided for detailed examination of the different impacts of the probes on a gene’s function. Figure 3(b) shows the posterior median coefficient estimates and the corresponding 95% credible intervals for the probes for two gene groups.

Fig. 3.

Data analysis results: (a) The posterior probabilities of being included in the model in MCMC samples for the genes on chromosome 7 (left panel) and 12 (right panel). The dashed line indicates the FDR threshold where genes with probabilities above the line are considered significant; (b) The posterior median estimates with 95% credible intervals for the probes in two significant genes groups. The gene names are shown on the top of each plot. MB: megabases; 1MB = 1,000,000 bases, where bases (or nucleobases) are structural units of DNA.

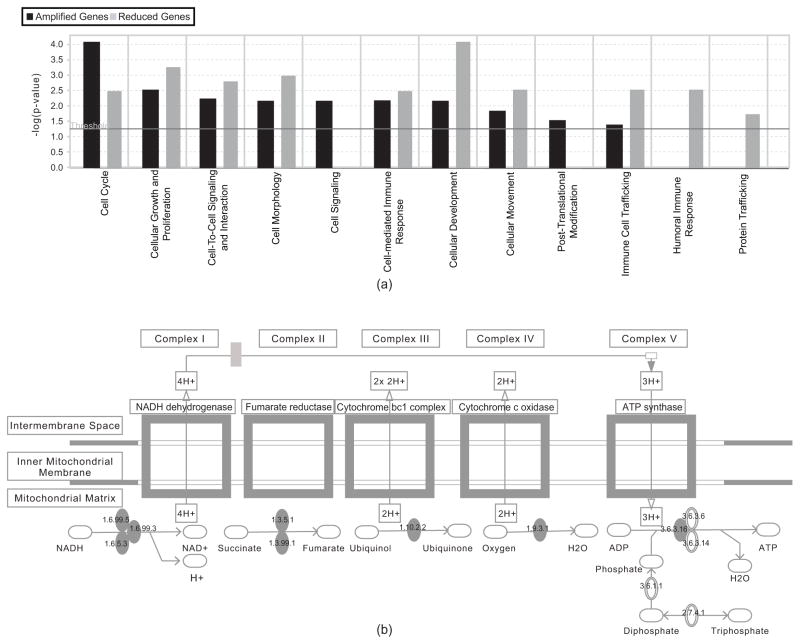
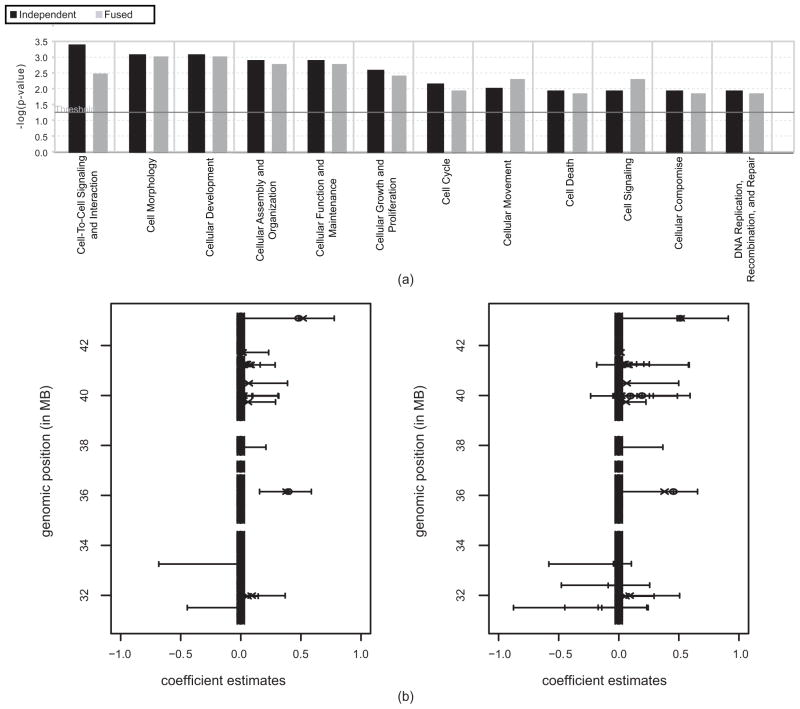
The selected genes were analyzed through the use of Ingenuity Pathway Analysis (IPA) software (Ingenuity^® Systems, www.ingenuity.com) in order to gain insight into the signaling pathways and cellular functions associated with the set of genes. The functional analysis of the selected genes identified the biological functions that were most significant to the selected genes, as displayed in Figure 4(a). The vertical axis gives the negative log ratios of the p-values of right-tailed Fisher’s exact tests, determining the probability that each functional term assigned to the set of selected genes is due to chance alone. Most interestingly, the humoral immune response is significant only in genes with decreased copy numbers in the TNBC samples, while the post-translational modification is found only in genes with increased copy numbers in the TNBC samples. This indicates that the aggressiveness of the TNBC cells may be related to a reduced immune response mediated by antibodies produced by B cells, and excessive post-translational modification of functional gene products. In addition, we find that the genes amplified in the TNBC samples include the enzymes associated with oxidative phosphorylation (as seen in Figure 4(b)). It is generally thought that cancer cells metabolize glucose by glycolysis rather than the more efficient oxidative phopshorylation. The copy number gain of the genes associated with oxidative phosphorylation may provide new clues about the TNBC tumor subtype. The copy number gain of RBBP8 also indicates an effect of the oxidative stress caused by the enhanced oxidative phosphorylation in the TNBC samples. Other genes whose identification as amplified agrees with previous biology studies include oncogenes such as PI3K (phosphoinositide-3-kinase) and SOS1 (son of sevenless homolog 1), and oncogenic transcription factor ETS1 (v-ets erythroblastosis virus E26 oncogene homolog 1-avian) (Chinnadurai, 2006; Dittmer, 2003), which are amplified in TNBC. Other genes with decreased copy numbers in the TNBC samples are BTG2 (BTG family, member 2), which correlates with increased survival in breast cancer; PLK2 (polo-like kinase 2), which is associated with checkpoint-mediated cell cycle arrest; IRS1 (insulin receptor substrate 1), a suppressor of metastasis in breast cancer; IL9 (interleukin-9) and IL13 (interleukin-13), which are associated with triggering immune response; and THBS1 (thrombospondin 1), an angiogenesis inhibiting factor (Eckerdt et al., 2005; Gibson et al., 2007; Lawler, 2002).

Fig. 4.

Functional analysis of selected genes by the Ingenuity System. (a) Ontology terms associated with the genes that have a gain or loss of copy number in the TNBC data; (b) Ingenuity pathway depicting oxidative phosphorylation. The complexes denoted by the solid ellipses show the point at which each of the five genes (enriched in copy-number) plays a role in this pathway.

The fused-HSVS model identified 294 genes that are significantly associated with the TNBC subtype, most of which (232 genes) are the same as those identified by the HSVS model. A functional analysis shows that the associated biological functions are similar across the gene sets identified by the two methods (as seen in Figure 5(a)). Most of the genes of interest mentioned above for the HSVS model were also selected by the fused-HSVS model.

Fig. 5.

Analysis results for the fused-HSVS model. (a) Comparison of the functional terms associated with the genes indicated by the HSVS (black color) and fused-HSVS (light grey color) methods. The plot is generated by the Ingenuity System; (b) Comparison of the coefficient estimates of a truncated MIP dataset for the HSVS model and fused-HSVS model. The left plot shows the posterior median estimates of the HSVS model with 95% credible intervals; the right plot shows the posterior median estimates of the fused-HSVS model with 95% credible intervals. The cross symbols in (b) are the coefficient estimates of the frequentist group lasso method.

As a comparison, we also ran the frequentist group lasso method on only the 1^st chromosome, which identified 159 genes on that single chromosome as being associated with the TNBC subtype, while the HSVS and fused-HSVS method identified only 20 and 21 genes respectively on the same chromosome. For the within-group variable level, the HSVS identified 20 probes within 11 genes as having a significant effect that should be further inspected. The fused-HSVS method identified 20 probes within 10 genes; whereas the group lasso included 2486 probes (over 98%) of the total located in the selected 159 genes. These results agree with the simulations in that the group lasso method tends to select over-dense models while the HSVS methods are favored for parsimonious modeling with a relatively small number of genes selected for further investigation. Furthermore, the group lasso includes almost all the probes within the selected genes in the model, whereas the HSVS methods select predictive probes within a significant gene, providing detailed information on the different levels of contribution of the probes within a selected gene to its functioning. Figure 5(b) shows the coefficient estimates for the HSVS methods and the frequentist group lasso method on a truncated DNA segment of 1041 probes located in the coding region of 140 genes on chromosome 1. All the genes identified by the frequentist group lasso method also showed signals based on the HSVS methods. However, only two of them were considered significant when using the FDR-based selection method. Comparing the HSVS and fused-HSVS models, the latter identified one more gene, whose group members had very small coefficient estimates (0 to 0.20). This result suggests that, compared with the HSVS method, the fused-HSVS method has a higher chance of selecting large groups of variables with consistently weak predictor members.

To conduct model diagnostics on our analysis method, we randomly split the samples such that 80% of the samples were randomly chosen as the training data and the remaining 20% as the test data. We pooled the genes selected by both the HSVS or fused-HSVS method, and re-applied the generalized HSVS, fused-HSVS, and group lasso methods to the training data, including only the selected genes for parameter estimation. The estimated models were then used to predict the binary responses for the test data. The diagnostic process of splitting the samples and running the estimations and predictions was repeated ten times. The HSVS method on average correctly classified 144.1 samples (80.96%) out of the 178 samples in the test data with the standard error to be 5.68, the fused-HSVS and group lasso methods correctly classified 147.7 (82.98%) and 148.9 (83.65%) in mean with their standard errors to be 4.85 and 3.45, respectively. A multiple comparison test shows that the misclassification rates by the three methods are not significantly different from each other. When we look at each category, the fused-HSVS correctly classified 51.66% of the TNBC patients and 90.97% of other patients on average, the group lasso 29.83% of the TNBC and 97.39% of others, and the HSVS 12.50% of the TNBC and 98.31% of others. We note that the rates of misclassifying the TNBC patients are high for all three methods (48.35% with the fused-HSVS at the lowest). This is probably due to the fact that the data have insufficient information for correct prediction of TNBC given the limited number of TNBC samples in the data. However, given the equivalent predictive performance by the three methods, the HSVS methods identify much fewer genes than the group lasso, greatly shrinking the pool of potentially relevant genes for subsequent investigation without missing important genes. In addition, we also used the CTGDR method (Ma et al., 2010) for prediction in the diagnostic test as a comparison, which assumes a logistic regression model for binary responses. The CTGDR method on average correctly classified 131.3 samples (73.76%) out of the 178 samples in the test data with the standard error to be 3.16. For each category, it correctly classified 36.48% of the TNBC and 83.36% of other patients on average. The result shows that the CTGDR method is significantly lower than the other three methods in identifying non-TNBC patients, which could be due to that the CTGDR method assumes a different generalized linear model for the binary response.

7. Discussion

In this paper, we propose a novel Bayesian method that performs hierarchical variable selection at two levels simultaneously. Compared to Wang’s hierarchical penalization method (Wang et al., 2009), which provides shrinkage at both group and within-group levels, the HSVS method conducts selection of groups and shrinkage within groups, with the significance of a group explicitly elucidated by the posterior probability of group inclusion based on MCMC samples. In addition, instead of yielding point estimates of the parameters, as in the frequentist method, the Bayesian HSVS method yields posterior distributions of the parameters, which provide the degrees of uncertainty in model inference. Finally, the HSVS model can be easily extended by implementing different “slab” priors to account for the characteristics of the data, as in the fused-HSVS model.

We conducted simulation studies under various settings to evaluate the operating characteristics of our method. We found our HSVS method to be a strong variable selector at both group and within-group levels, which satisfies the need for parsimonious model selection. The proposed method performs better overall than the group lasso and regular lasso methods when both group-level and within-group-level selections are desired. However, the performance of the HSVS method decreases when the true model is less sparse or the variables have only weak effects on the response, due to the joint effect of the spike and slab and the lasso priors used in our method. In addition, the HSVS method performs slightly worse than the group lasso method when high correlations exist within groups. This is not surprising since we use the Bayesian lasso for within-group selection, and it is not robust to such correlations.

Considering the serial correlation structure among the probes within a gene in the MIP data, we propose the fused-HSVS model by replacing the independent Laplace priors with the fused lasso priors for within-group-level selection. The implementation of the Bayesian fused lasso method encourages neighboring coefficients within a group to be close in value. This is expected in the genetic association study of the MIP data since the copy numbers of neighboring probes within a gene are positively correlated and hence are thought to have similar effects on breast cancer development.

We applied the HSVS and fused-HSVS methods to the genetic association analysis of the MIP dataset collected from patients with breast cancer. The genes selected by the two methods are mostly in common. However, the analysis suggests that the fused-HSVS prior tends to have a higher sensitivity than the HSVS prior for the genes whose probe variables have consistently weak regression coefficients.

There are several possible extensions of our HSVS-based models to more general settings in which variables have natural grouping structures. Examples of such applications include polynomial effects of the same factor, genes belonging to the same pathway, and proteins composing the same molecular complex. Another interesting extension would be in a survival context for time-to-event responses, which will address the more important biological question of finding prognostic markers for cancer progression. Finally, we can easily extend the hierarchical model by changing the “slab” part of the group prior for different purposes such as stronger within-group variable selection using various types of shrinkage priors. We leave these tasks for future consideration.