Academic Achievement and Its Impact on Friend Dynamics

Abstract

Academic achievement in adolescence is a key determinant of future educational and occupational success. Friends play an important role in the educational process. They provide support and resources and can both encourage and discourage academic achievement. As a result, the friends adolescents make may help to maintain and exacerbate inequality if friends are sorted on the basis of academic achievement. These observations prompt the question: How does academic achievement affect the friendship ties made? Using data from the high schools in the Add Health saturated sample, the author models network change using a stochastic actor-based Markov model for the co-evolution of networks and behavior. This model is carried out at the school level for each of the high schools included in the saturated sample. Results show that in the most typical American schools, similarity in academic achievement is an important and consistent predictor of friendship ties in a dynamic context. High-achieving students are more likely to extend ties to other high-achieving students, net of other sociodemographic, network, and proximity characteristics, while low-achieving students are more likely to extend ties to other low-achieving students. Adolescents respond to changes in academic achievement by changing their friendship ties.

INTRODUCTION

Academic achievement in adolescence is a key determinant of future educational and occupational success. Friends play an important role in the educational process. They provide support and resources and can both encourage and discourage academic achievement. As a result, the preferences of adolescents for friends are very important. These preferences determine the group of friends with whom adolescents spend their time and, in turn, how adolescents spend their time. If high-achieving students make high-achieving friends, their achievement is reinforced and maintained by their friendships. The advantage of already academically advantaged students is compounded, increasing the distance between the most and least advantaged and leading to a concentration of academic advantage.

Academic achievement may be an important sorting mechanism for friendships for several reasons. Although most U.S. schools are no longer formally tracked, ability grouping within subjects is common, particularly in secondary schools (Lucas 1999). Informal tracking leads to increased contact within achievement levels and decreased contact between achievement levels. Greater contact increases opportunities to meet individuals with similar levels of academic achievement and a greater likelihood of forming friendships with similarly achieving individuals (Blau 1977; Feld 1981).

In the absence of any sorting in schools, academic achievement should remain an important sorting mechanism for friendships. Friendships form between individuals with similar values, who spend time in similar ways, who understand each others’ choices and decisions (Hargreaves 1972; Newcomb 1956; Schachter 1959). A consequence of these preferences is that individuals with similar levels of academic achievement should be more likely to form friendships, even after accounting for other characteristics that may affect the formation of friendships.

Although a fundamental and important question, the vast majority of research on friends and achievement is interested in the effect of friends on achievement, ignoring the question of how individuals became friends in the first place (see e.g., Crosnoe, Cavanagh, and Elder 2003; Riegle-Crumb, Farkas, and Muller 2006). This analysis fills this gap by studying adolescent friendship tie formation, focusing on the effect of academic achievement on changes in ties. The goal is to understand the extent to which adolescents seek out similarly achieving friends, contributing to a concentration of high (and low) academic achievement within networks while accounting for the complicated relationship between friend selection and friend influence.

Recent social network methods, developed by Snijders (2001) and advanced in subsequent work (Snijders, Steglich, and Schweinberger 2007; Steglich, Snijders, and Pearson 2010), provide a way to simultaneously model how behavioral characteristics affect changes in network ties and how changes in network ties affect behavioral characteristics. These models are able to separate out the extent to which similarity between two individuals is the result of selection and the extent to which it is the result of influence. Applying these methods and using data from the National Longitudinal Study of Adolescent Health saturated sample, this article models the impact of academic achievement on changes in friendship ties within schools, separating out the effect of influence on observed similarity between friends.

This approach shows that in typical American high schools, adolescents at all achievement levels will change their friendship ties to maximize similarity between themselves and their friends. High-achieving students are more likely to extend ties to other high-achieving students while low-achieving students are more likely to extend ties to other low-achieving students. If friendships are important for academic success (and failure), these results confirm that the most academically advantaged students compound their advantage through their friendships.

In less typical small rural schools, however, academic achievement is not an important sorting mechanism of friendships. Whether because of geography, limited opportunities, or because they have grown up together in small communities, the friendships formed in these schools are not based on achievement. For these students, friendships may diminish academic inequality.

I begin this article by summarizing the most recent literature on friendship choices and dynamics. I then describe the methods and data used for this analysis. Next I provide descriptive details of each school used in the analysis, a description of changes in friendship ties across the observed time period, and changes in network structure across the observed time period. To provide a comparison, I first summarize results from a cross-sectional model of friendship choice by school. These results are compared to results from dynamic models of friendship choices by school. I conclude with a discussion of the implications of this research to our understanding of the stratification outcomes of adolescents.

BACKGROUND

The influences of friends and peers on academic achievement are frequently cited in theories explaining group differences in academic achievement, particularly across race/ethnicity and socioeconomic status (see Gamoran 2001). Frank et al. (2008) show that adolescents’ peers—defined as the group of students who take similar courses to the respondent within school—influence their math course-taking trajectory. They argue that the mechanisms for this influence are (1) the creation of norms and (2) the sharing of resources and support. Norms and resources are created and shared partially through the friendships that are formed within these local area positions. In other words, the local area positions provide adolescents with the opportunities to make friends. And these friends then influence adolescents’ academic behaviors.

Although Coleman (1988) argues that access to friends who support academic achievement is a key determinant of educational success, the actual mechanisms of friendship formation and the role academic achievement plays in friendship dynamics remain poorly measured and understood. Similarly, Frank et al. (2008) argue that peers and friends are a key academic stratifying feature of students within schools, but we do not understand how friends are made both between and within local area positions. This gap in our understanding stems largely from methodological issues; friends and achievement are endogenous to one another, and both change across the adolescent life course. Determining the effect of achievement on friend selection depends on both distinguishing the direction of the relationship between friends and achievement and incorporating dynamics into models of friend selection.

Figure 1 provides a simple illustration of the process of friend selection and influence. It works as a feedback loop, where friends affect behavior, in this case academic achievement, achievement (along with other characteristics) then influences friend preferences, and preferences combined with opportunity constraints faced within the network environment lead to the friendships we observe. Any change in achievement will potentially lead to changes in friends or changes in friends’ achievement, and any change in friends will potentially lead to changes in achievement. The underlying cause of change is a desire to maximize similarity within friendships. A result is that the already academically advantaged increase their advantage through their friendships while the academically disadvantaged are further disadvantaged by their friendships.

Figure 1.

Process of friend selection and behavioral evolution

A small literature seeks to test theories of friend selection with quantitative data. The majority of this work relies on cross-sectional models of friend selection. This work confirms that adolescents make friends with those whose characteristics mirror their own (McPherson, Smith-Lovin, and Cook 2001). Adolescents choose friends from similar racial/ethnic backgrounds (Joyner and Kao 2000; Moody 2001; Quillian and Campbell 2003; Zeng 2004), who are the same gender (Shrum, Cheek, and Hunter 1988; Tuma and Hallinan 1979), and who behave in similar ways (Billy, Rodgers, and Urdy 1984; Cohen 1977; Kandel 1978; Snijders and Baerveldt 2003).

Although research on friend selection focuses primarily on race, a few studies also consider how academic achievement impacts selection (Quillian and Campbell 2003; Tuma and Hallinan 1979; Zeng 2004). Two adolescents are more likely to be friends if they are similar with respect to academic achievement. As the achievement difference between two individuals grows, the likelihood of their being friends declines. The effect of similarity of achievement on friendship formation, however, is relatively small compared to the effect of race and ethnicity on friendship. Nonetheless, this research suggests that adolescents make friends with individuals with similar levels of academic achievement net of racial preferences and preferences for friends from similar socioeconomic backgrounds, potentially concentrating advantage and increasing the distance between the most advantaged and the least advantaged.

This cross-sectional approach to studying friendship is, however, limited in three important ways, particularly if the goal is to understand how academic achievement affects friendships and the distribution of high-achieving students across friendships. First, none of the aforementioned studies account for the effect of the full network structure on friendship ties. Measures of network structure describe how and where individuals are situated in the network. These measures include individual measures such as the number of nominated friends and popularity, dyadic measures including reciprocity and indirect connections, and global measures of the network including overall network connectedness and balance in network connections.

The influence of the network on friend selection cannot be reduced to individual or dyadic characteristics because a friendship is situated in a network composed of a multitude of individuals connected to many other individuals in complicated ways. Because tendencies toward balance¹ and reciprocity in a network are strong (Doreian et al. 1996; Hallinan and Kubitschek 1990), if initial friendships are based on similarity, the proceeding friendships will magnify similarity even if there is no preference for similarity in later friendships. For example, assume that in a network, each individual makes one friend and chooses a friend with a similar level of academic achievement. Their second friend is independent of their second friend’s achievement level but is dependent on their first friend’s ties. Because initial friendships were based on similarity of academic achievement and the second friends are based on friends’ friends, the second chosen friend will also be similar with respect to academic achievement, even though the choice was made independently of academic achievement. As a consequence of the desire for network balance, a non-network analysis of friendship is likely to overstate adolescents’ preferences for similarity in characteristics of friends.

Second, cross-sectional studies of the relationship between friendship choice and behaviors conflate selection and influence. Similarity between friends may occur because individuals make friends with people similar to themselves (the assumption of the aforementioned research) or friends may influence one another and as a result make them more similar. A cross-sectional model takes an ahistorical view of the process of friend selection. A dynamic model can account for and control for the previous friendships adolescents made and the influence that friends may have had on their academic achievement.

Finally, a cross-sectional analysis assumes that friendships are fixed, network structures are fixed, and behavioral attributes are fixed. Friendships are dynamic; they change and adapt, especially in adolescence (Bowker 2004; Snijders 2001; Steglich, Snijders, and West 2006). A cross-sectional analysis of friend selection ignores these changes and the influence of past friendships on current behaviors.

The achievement levels of adolescents also change across time. After friendships are formed, if one member of the friendship changes his or her academic achievement, will the friendship end? Network research suggests that it is easier to create a new tie than break an old tie (Van de Bunt, van Duijn, and Snijders 1999). In other words, once two individuals are friends, it takes more to end the friendship than it took to begin it. Although similarity may be important to the creation of a friendship tie, are thresholds for similarity as high for maintaining the friendship? The difference between creating ties and breaking ties suggests that if two individuals are friends, their friendship may be less sensitive to changes in academic achievement than two individuals who are not friends. As a result, dynamic models of friendships observed over time may estimate a smaller effect of academic achievement on friendship ties than estimates based on cross-sectional models.

To understand the relationship between academic achievement and adolescent friendship choices, I need to observe and model the relationship between changes in friendships, changes in network structure, and changes in academic achievement.

Dynamic Research on Friends

Recent developments in network methods have led to a class of models that can be used to model network change dynamically (Snijders 2001). Research using these models falls into two categories: research studying network evolution² (Snijders and Baerveldt 2003; van Duijn et al. 2003) and research studying the co-evolution of networks and behaviors (Knecht et al. 2010; Steglich et al. 2004, 2006). Although research using these models is limited by issues of generalizability, this work has made significant advances in our understanding of the effect of friendship network structure and delinquency on friendship network change.

The majority of this research studies one small network. However, Snijders and Baerveldt (2003) use stochastic actor-based Markov chain models to estimate the effect of delinquent behavior on friendship formation across a set of third-grade students in many schools. They model friendship evolution separately in 19 school classes and put together their results in a simple multilevel analysis. By including a large number of networks in their analysis, this work provides a more generalizable result than past studies using dynamic network models. This approach to network analysis provides a model for the analysis that follows.

Research Questions

This analysis models the change in adolescents’ friendship ties that results from changes in levels of academic achievement, accounting for the influence that friends may have on one another’s academic achievement. Answering this question provides an account of how academic achievement is distributed within a school network and, in turn, how friendship preferences help to concentrate high achievement. If adolescents respond to changes in academic achievement by changing their friendship ties, the most academically advantaged individuals remain segregated and concentrate resources and positive norms among the already advantaged.

Friend Choice?

Throughout this analysis, I implicitly (and explicitly in the model described in the following) treat a friendship between two individuals as a choice. In real life, friendships rarely feel like conscious decisions and often feel rather like the result of some combination of happenstance, similarity, and proximity. But particularly in adolescence, when one’s friends help to define one’s image, the friendships that exist may be the result of more calculated decisions. In any case, it is hardly a choice when structural constraints determine whom one comes in contact with. In the following analysis, I try to account for these structural constraints so that what we are left with are “choices” based on the characteristics of individuals and randomness. The fact that two individuals with similar levels of achievement make friends with one another does not necessarily mean that those two individuals are consciously seeking out a friend with a particular level of academic achievement, but perhaps achievement provides a signal for other, less visible personality and character traits that adolescents consciously desire in their friends.

METHOD AND DATA

A Cross-sectional Model

I begin this analysis by modeling the cross-sectional relationship between academic achievement and friend selection. I follow past cross-sectional research on friend selection and use logistic regression to model the relationship between individual characteristics, friend characteristics, potential friend characteristics, and friend selection.³ The friendship or potential friendship dyad is the unit of analysis. The dependent variable, Y, equals 1 when individual i nominates person j as a friend, and is 0 otherwise. The model compares the chosen dyads to the non-chosen but possible friendship dyads within the school. The log odds of individual i nominating individual j as a friend are:

$$\text{log}\left(\frac{\mathit{\text{pr}}(y_{\mathit{\text{ij}}}=1)}{\mathit{\text{pr}}(y_{\mathit{\text{ij}}}=0)}\right)={\mathrm{\beta }}_0+{\mathrm{\beta }}_1{X}_i+{\mathrm{\beta }}_2{X}_j+{\mathrm{\beta }}_3{X}_{\mathit{\text{ij}}},$$ (1)

where X_i represents a vector of covariates from individual i, X_j represents a vector of the same covariates from individual j, and X_ij represents the similarity between i and j on the vector of covariates X. To maintain comparability with the network models described in the following, I estimate a separate model for each school.

A Stochastic Actor-based Model for Network and Behavior Dynamics

As I discussed earlier, the cross-sectional approach suffers from several drawbacks, including ignoring network structure, conflating influence and selection, and ignoring the dynamic nature of friendship and achievement. To deal with these problems, I implement a series of stochastic actor-based Markov chain models to simultaneously estimate the effect of achievement on changes in friendship ties and the effect of friendship ties on changes in achievement. These models for network-behavior co-evolution were originally proposed by Snijders (2001) to model network evolution and elaborated in later work to incorporate behavioral evolution (Snijders et al. 2007; Steglich et al. 2010).

The underlying principle of these models is that given a series of simple assumptions about the nature of friendship tie and behavioral changes, current behaviors of actors in a network can be used to predict changes in friendship ties, and simultaneously, the current network structure can be used to predict changes in behavioral characteristics. Because changes are modeled as part of one process and a strict time ordering is assumed, I can separate the impact of behavior on friend selection and the impact of friend influence on behavior.

I begin by laying out the set of assumptions required for estimation and then describe the simulation model that results. First, assume that changes in both friendship ties and behaviors occur as a Markov process; each actor has full knowledge of the network and the behaviors of the other actors in the network and makes choices based on his or her knowledge of the current network and current behaviors of actors in the network, not earlier states. In other words, given the covariates included in the model, the probability that ties or behaviors change depends on the current state of the network or behaviors only. Second, as time moves continuously, actors in the network are randomly provided opportunities to make a change either to their network ties or to their behavior. Only one change is allowed at any moment. At time t, one actor can change a tie, change behavior (by one unit), or change nothing. In other words, actors act independently of one another and cannot coordinate changes in network ties and changes in behavior. Although potentially unrealistic, the time period between friend changes and/or behavioral changes can be infinitesimally small. Because individual changes in behaviors and friendship ties change the network environment for subsequent actors (albeit in small ways), dependence between actors occurs over time. Finally, I assume that actors control their ties to others and their behavior and make changes in order to maximize their satisfaction with their ties. This does not mean that actors are necessarily making conscious decisions about changes in behaviors or changes in ties, but rather that changes occur as a result of the actor’s characteristics and the structural limitations of actor’s contexts.

Through this series of assumptions, the model is based on single changes by one actor either in her relation to another actor or in her behavior. This single change is referred to as a micro-step. The sum of these micro-steps provides a link between the ties and behaviors I observe across time at discrete time points.

Before continuing with a description of the components of the model, I provide a more intuitive summary of the stochastic actor-based model for network and behavior dynamics for those less familiar with networks and this method of analysis. Imagine that we observe a network—for example, a school—at several points in time. We also observe the academic achievement of each actor in the network at the same discrete time points. The simulation begins with a virtual rolling of the dice. An actor in the network is chosen at random (or probabilistically based on actor and network attributes in more complicated versions of the model). That actor now has an opportunity to make a change either in her behavior (a one unit change) or to change a tie with another individual in the network. The actor evaluates the current state of the network and the characteristics of the actors in the network and herself. At this point, the actor makes a change to maximize her preferences. She does one of the following: (a) extends a tie to another actor in the network to whom she is not tied, (b) removes a tie from another actor in the network to whom she is currently tied, (c) increases her behavior by one unit, or (d) decreases her behavior by one unit. If none of these changes makes the actor “happier,” she can also choose to maintain her ties or her behavior in the current state. When the decision is made, the dice are rolled again and the process begins with a new actor and a different incarnation of the network.

Components of the SIENA Model⁴

The simulation described previously is carried out using SIENA. The network is represented by an adjacency matrix of ties between individuals, denoted by Y_ij. A tie between actor i and actor j is present if Y_ij = 1 and not if Y_ij = 0. Ties are not required to be reciprocated; Y_ij may equal 1 while Y_ji equals 0. A tie change occurs if either a tie is extended when one did not exist, or if a tie is retracted when a tie previously existed. The behavior of actors in the network is represented by a vector Z_i, which is assumed to be an ordered discrete variable. Both are time dependent.

Both network change and behavioral change are divided into three components: an objective function, an endowment function, and a rate function. The objective function for network formation describes the actor’s preferences for ties and is a function of the network structure, the focal actor’s⁵ characteristics, the characteristics of the other actors in the network,⁶ and the similarity between the two. The objective function is defined as the weighted sum of these effects,

$$f_i(\mathrm{\beta },y)=\sum _k{\mathrm{\beta }}_k{s}_{\mathit{\text{ki}}}(y),$$ (2)

where β is the estimated effect of the kth variable s for individual i. This function determines whether changes in friendship ties are made by actors and provides a numerical representation of actors’ desires or preferences.

The objective function for behavioral evolution is analogous to the objective function for network evolution (2).

$$f_i^z(\beta ,y,z)=\sum _k{\beta }_k^z{s}_{\mathit{\text{ki}}}^z(y,z),$$ (3)

where $S_{\mathit{\text{ki}}}^z(Y,Z)$ are functions of the characteristics and behaviors of the focal actor i as well as those of the actors to which she is tied and her place in the network more generally. Of course, the predictors of behavioral change are different from the predictors of network change.⁷ Because the behavior is a predictor of tie change in the evaluation function of network change and network ties are a predictor of behavioral change in the evaluation function of behavioral change, selection (tie changes) and influence (behavioral change) are distinguished from one another. The two objective functions determine a micro-step. When actor i makes a tie change or a behavioral change, she maximizes the sum of the objective function of the new state (resulting from the new tie or resulting from the new behavior) and a random term. These micro-steps are incorporated into a model of network evolution through the rate function. The rate function specifies the amount of time the actor waits until her next opportunity to change her network configuration or to change her behavior. In this analysis, actors are given opportunities to change their network ties or behavior at random moments. These moments are modeled as distinct processes for tie change and behavioral change.

For a more mathematical discussion of stochastic actor based models and SIENA, please refer to Snijders (2001) and Steglich et al. (2010). For a non-mathematical introduction to these models, refer to Snijders, van de Bunt, and Steglich (2010).

Parameters from this model are estimated using Rsiena, version 4.0 (Ripley and Snijders 2010). I estimate this model separately for each school network, leaving separate results across schools.

Data

Data for this analysis come from the National Longitudinal Study of Adolescent Health (Add Health), saturated sample (N > 3,700). In 1994–1995, Add Health surveyed 7th- through 12th-grade students in 144 schools in 80 U.S. communities. The in-school survey provided a census of students within these sampled schools. A subset of students from each school was then surveyed in the Wave 1 and Wave 2 in-home surveys conducted in the summer and fall of 1995 and 1996, respectively. In 16 schools, all students participated in all three waves of the study and were asked to nominate their five closest male friends and their five closest female friends in all three waves.^8,9 Because the complete school network is included in the survey at each wave and friendship nominations are made, this saturated sample of schools is used to describe the relationship between network change and changes in academic achievement (Bearman, Jones, and Urdy, 1997).

The Sample

The saturated sample of schools in Add Health is a unique sample of schools, overrepresenting small schools, rural schools, and private schools. Indeed, 14 of the 16 saturated schools were “saturated” because of their small size. In this analysis, 8 of the 16 schools are used to understand the relationships between friendship ties and achievement, resulting in a total sample of 3,215 adolescents.¹⁰

The analytic sample of schools is quite different from the Add Health sample of schools. Of the analysis schools, 75 percent cover the full grade span from kindergarten to 12th grade, 62 percent are rural, 37 percent are private schools, and 75 percent have fewer than 350 students in 7th through 12th grades. By contrast, fewer than 8 percent of Add Health schools are K-12 schools, only 14 percent are rural, 8 percent are private, and only 20 percent enroll fewer than 350 students in 7th through 12th grades. Furthermore, schools in the analysis sample are less racially diverse than Add Health schools generally. Nonetheless, the socioeconomic characteristics of the analysis sample do not differ dramatically from the Add Health sample.¹¹

Although the analysis sample is not a representative sample, there are two schools that may be thought of as more typical, representing particular types of schools in the United States: schools 5 and 6. These schools are large public high schools. School 6 is a racially diverse suburban high school while school 5 is a racially homogenous rural high school. Although I do not make any claims of representativeness, results from these two schools may be more suggestive of the relationship between friendship ties and achievement more generally.

Because the focus of this analysis is school networks, anyone who leaves one of the sample schools between observations leaves the network and thus leaves the analysis. Students who leave the school network account for a large portion of the missingness that occurs across waves in these eight schools.¹² Although 25 percent to 50 percent of respondents are lost between the in-school survey and the Wave 2 in-home survey, once those who leave the school network (the structurally missing) are excluded, only 2 percent to 15 percent are legitimately missing across waves. If a student falls into the legitimately missing category, the ties from earlier waves are assumed to exist in later waves. But because these observations do not change, once they go missing they do not contribute to the estimation.

Throughout the article, I refer to time points 1, 2, and 3. Time 1 refers to observations from the in-school survey, time 2 refers to observations from the Wave 1 in-home survey, and time 3 refers to observations from the Wave 2 in-home survey.

Measures

This analysis contains two parts: (1) a cross-sectional analysis of friendship choice and (2) a dynamic analysis of the co-evolution of friendship ties and academic achievement. With the exception of the network measures and the influence part of the co-evolution analysis, the cross-sectional analysis uses the same measures as the dynamic analysis.

I am primarily interested in the role of academic achievement in friend changes. Academic achievement changes across each respondent’s school career and is measured using self-reported average grades in math, science, social studies, and English from each time point.¹³ Average grades for each subject are reported in terms of letter grades. I transform letter grades into grade points (A = 4, B = 3, C = 2, D = 1) and average across subjects. The resulting achievement scale is a continuous measure. The co-evolution model used in this analysis requires that the endogenous behavioral variable be a discrete ordinal measure. I therefore transform the GPA measure into quintiles so that a one unit increase in GPA represents a movement roughly from the bottom 20 percent, for example, to the 20–40 percentile.¹⁴

In the selection equation, GPA rank is a predictor of network ties and three different measures of GPA rank are used to predict changes in friendship ties. Ego GPA rank measures the tendency for higher GPA actors to extend more ties than lower GPA actors regardless of the characteristics of those to whom they are extending ties. By contrast, alter GPA measures the tendency for actors, regardless of their achievement, to extend ties to others in the network with higher versus lower GPAs. Similarity between alter and ego GPA measures the tendency among actors to extend ties to others in the network with similar GPAs. Together, these measures provide a description of the effect of academic achievement on friendship tie changes in a school network.

Again, GPA is endogenous to network change as it may be both a cause and a consequence of tie changes. To account for this, the actor’s GPA is the dependent variable in the influence part of the co-evolution model. The average GPA of the actor’s friendship ties captures the influence that the actor’s friends have on his or her achievement.¹⁵

Additional Controls

Proximity constrains the contact that adolescents have with one another. We can only be friends with individuals with whom we have contact, and our friendship patterns are likely to change as our circumstances and contact probabilities change. Friendship choices are determined both by preferences for friends and access or exposure to possible friends (Blau 1977; Johnson 1980). Capturing exposure is particularly important when thinking about academic achievement. Course-taking patterns are intimately tied up with academic achievement; good students take more advanced courses while bad students take remedial courses. If adolescents meet their friends in their courses, and if academic tracking occurs, then what appears to be friends sorting on levels of achievement may be merely the result of exposure.

To account for the different exposure of adolescents to possible friends, I include a measure of grade in school. Adolescents generally take classes with students within their grade, or near their grade, and as a result have more contact and more opportunities to make friends with individuals in their grade or the grades similar to their own.

In small schools, grade in school is a sufficient predictor of contact and proximity. Students in these schools are not subject to tracking and often have only one or two class options available to them. In larger schools, however, grade in school does not capture the variations in contact probabilities within grades because of tracking and different course-taking trajectories. I use data from the Add Health and Academic Achievement study (AHAA) that calculates students’ local area positions in their schools based on their course-taking patterns (Riegle-Crumb et al. 2005). Two students in the same local area position are taking a similar set of courses and likely have more contact than two students in different local area positions.¹⁶ This measure is included in addition to grade in the two largest schools.

Similarly, the network structure affects contact and friend selection in important ways. Who an individual’s friends are impacts her exposure to new possible friends (through friends of friends), her desirability as a friend to others (through popularity), and the desirability of others to her (through reciprocity). Ignoring these properties of the larger social structure that friendships are embedded in tends to overstate similarities between friends within the network. Measures of number of ties, transitivity, reciprocity, and popularity are included in all network models of friend selection.

Academic achievement is correlated with many individual characteristics that may be the basis for friend choice rather than academic achievement. To accurately identify the effects of academic achievement, I control for the other characteristics that may be both correlated with academic achievement and affect friendship choice. Three of the most important of such variables are gender (Shram et al. 1988; Tuma and Hallinan 1979), socioeconomic status (Berkner, Chavez, and Carroll 1997; Campbell, Hombo, and Mazzeo 2000; Lareau 2003), and race/ethnicity (Gamoran 2001; Joyner and Kao 2000; Kao and Thompson 2003; Moody 2001; Quillian and Campbell 2003). Similarity between respondents and possible friends on all three is included in models of friend selection.^17,18

Because the focus of this article is the role of academic achievement in the friendship choices adolescents make, I present results only for GPA rank.¹⁹

RESULTS

Cross-sectional Model

Table 1 presents results from the dyadic level cross-sectional models predicting friendship nominations. To maintain comparability with the dynamic models presented later, I run models separately for each school. I also include results when all schools are combined into one model.

Table I.

Parameter Estimates from Logit Models Predicting the Effect of GPA Rank on Friend Nomination by School

Grade point average rank
School	Ego	Alter	Similarity	N
1	0.051 (0.059)	−0.040 (0.058)	1.199** (0.278)	4,970
2	0.002 (0.032)	0.1 1 1** (0.032)	0.797** (0.154)	31,862
3	0.198** (0.043)	0.046 (0.046)	0.278 (0.257)	16,002
4	0.148 (0.095)	0.210* (0.095)	0.300 (0.423)	1 1,556
5	0.060** (0.012)	0.038** (0.012)	0.729** (0.059)	570,780
6	0.053** (0.012)	0.088** (0.012)	0.936** (0.061)	2,797,256
7	0.026 (0.053)	0.1 00† (0.052)	0.404† (0.253)	10,302
8	0.080† (0.046)	0.001 (0.047)	0.083 (0.250)	6,468
All schools	0.113** (0.014)	0.120** (0.010)	0.808** (0.048)	3,450,720

Note: All models include controls for grade similarity, same gender, same race (schools 4, 5, and 6), similarity in socioeconomic background, and same Local Area Position (schools 5 and 6). Standard errors included in parentheses.

^†p < .10.

^*p < .05.

^**p < .01.

Although the effects of GPA rank on friend nominations vary significantly across schools, the pattern of results is surprisingly consistent given the variation in the characteristics of the sample schools. Adolescents are generally more likely to extend ties to individuals with higher GPAs than individuals with lower GPAs (alter effect). This effect is largest in school 4 where adolescents have odds 23 percent higher of nominating a friend in the top 20 percent of the GPA distribution compared to a friend in the 60th to 80th percentile (e^.210). In many schools, however, this effect is indistinguishable from 0 (1, 3, 7, and 8). In the two large, more typical American high schools, adolescents are significantly more likely to nominate higher achieving compared to lower achieving friends. In other words, in these schools, students in the top of the GPA distribution are more popular than students in the lower part of the GPA distribution, controlling for the race, socioeconomic status, grade, gender, and course-taking patterns of the respondent, his or her possible friends, and their similarity.

Ego’s GPA has a similarly positive and, in some cases, significant effect on friend nominations. Adolescents with higher GPAs are more likely to nominate friends, regardless of the friend’s achievement characteristics, compared to individuals with lower GPAs. In school 3, for example, adolescents in the top 20 percent of the school GPA distribution have odds more than 20 percent greater of nominating any friend compared to adolescents in the 60th to 80th GPA percentiles. Again, in the two large schools in the analytic sample (5 and 6) these results are positive and significant. In school 5, an adolescent in the top 20 percent of the GPA distribution has odds 35 percent greater of nominating a friend in school compared to an adolescent in the bottom 20 percent of the GPA distribution. In other words, the high-achievers are more social than the low-achievers.

The effect of ego and alter GPA on friend nominations is minimal compared to the impact of similarity on friend nominations. Controlling for grade level, course-taking patterns, race, gender, and socioeconomic status, similarity in academic achievement appears to structure friendships in important ways. Even within a grade and within a local area position, a high-achieving adolescent is more likely to nominate a fellow high-achieving friend over a lower achieving friend. Again, in school 5, a large public high school, an adolescent in the top 20 percent of the GPA distribution has odds more than two times greater of nominating a friend in the top 20 percent of the GPA distribution compared to a friend in the bottom 20 percent of the GPA distribution (e^.729).²⁰

Of course, this effect is not universal. In three schools, similarity in GPA quintile does not have any effect on friend nominations and the effects are borderline significant in one other school. These differences lead to significant variation in estimates of GPA effects on friend nominations across schools.

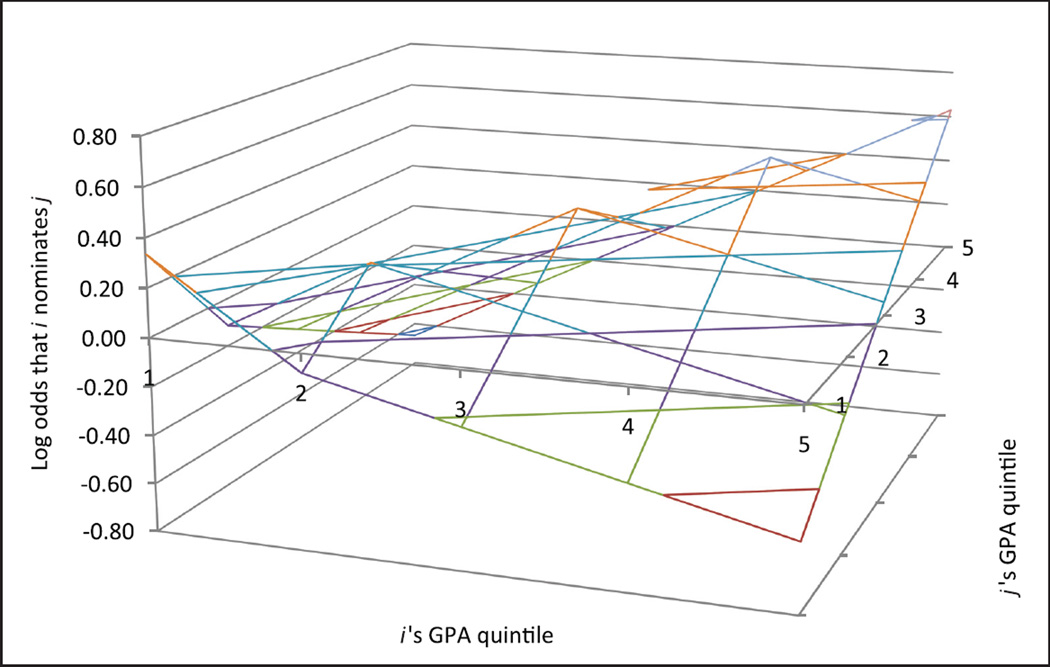
To see the full effect of achievement on friendship formation, I calculate the log odds of nominating a friend in GPA quintile x by the respondent’s GPA quintile. Figure 2 shows this relationship for school 6. Although there is a strong preference for similarly achieving friends, adolescents also prefer higher achieving friends and higher achievers are more likely to nominate friends. Together, these patterns create a peak on the diagonal leading to a high point when both alter and ego are in the highest GPA quintile.

Figure 2.

Log odds that i extends a friendship tie to j, school 6

Overall, these models suggest that GPA has a very strong impact on friendship ties. Adolescents are friends with academically similar others while also showing a preference for higher achieving friends generally. These patterns are especially strong in the two large high schools, perhaps more representative of schools in the United States more generally.

Although informative, these cross-sectional models are limited in three important ways. First, these models ignore network composition and its role in friend formation, potentially causing me to overestimate preferences for similarity between friends. Second, they treat academic achievement as an exogenous characteristic of individuals, their friends, and their possible friends. Third, they force a dynamic process into a static model, ignoring both changes in friendship ties and changes in achievement. The next section describes the changes in friendship ties and changes in achievement and then presents results from dynamic models of friend formation.

Change

Part of the motivation for this analysis is the observation that friends and achievement change across the adolescent life course. Table 2 presents data on the amount of change between time points in friendship ties and achievement. Indeed, in these eight schools, friendships change a lot over time. Although achievement changes as well, these changes take place at a slower rate. A higher proportion of respondents’ achievement stays constant across periods compared to their friendship ties. Nonetheless, the change observed is significant enough to suggest that we may miss something by focusing on a cross-section.

Table 2.

Description of Friendship Tie and Achievement Changes across Schools

	School 1	School 2	School 3	School 4	School 5	School 6	School 7	School 8
Tie changes
1→2
Add	47	146	132	86	1,239	1,480	56	108
Subtract	153	613	262	206	2,127	2,601	221	230
Same	72	191	107	80	1,167	976	64	144
2→3
Add	96	249	182	107	903	836	122	104
Subtract	51	214	105	87	1,507	1,721	50	146
Same	49	105	94	67	694	518	57	96
Achievement changes
l→2
Up	20	44	31	24	261	383	25	27
Down	14	41	26	11	164	627	24	8
Same	27	60	20	40	277	422	31	28
2→3
Up	11	41	24	13	135	405	33	18
Down	9	38	25	23	238	271	22	29
Same	27	42	26	44	175	284	23	21

The dynamic co-evolution model uses change in friendships and ties to identify effects. If few friendships change or if changes in achievement are minimal, the precision with which estimates are estimated will be low. In all cases, adolescents change their friendship ties more often than they change their achievement. As a result, my estimates of friend selection will be more powerful than my estimates of friend effects. However, particularly in the two large schools, there is sufficient change in both friendship ties and achievement across time to provide precise estimates of both friend selection and friend influence.

Testing the Markov Assumption

The changes that occur across waves can be used to shed some light on the Markov assumption. The Markov assumption states that the time 3 network is conditionally independent of the time 1 network and dependent only on the time 2 network. In other words, the probability that a tie exists at time 3 given a tie at time 1 should equal the product of the probability of a tie at time 2 given a tie at time 1 and the probability of a tie at time 3 given a tie at time 2, or

$$\mathit{\text{Pr}}(T3|T1)=\text{Pr}(T2|T1)\times \mathit{\text{Pr}}(T3|T2).$$ (4)

I calculate these probabilities in Table 3 from the tie changes presented in Table 2. To validate the Markov assumption, row 3 should equal row 4. In every school, row 4 is larger than row 3, suggesting that there are historic dependencies in friendship ties not fully captured by current friendships. This assumption, however, is conditional on the characteristics of the respondent and his or her possible friends included in the models, not just the ties. If the historical dependencies between ties are captured by the current characteristics of the network, the Markov assumption is not violated (Leenders 1995).

Table 3.

Test of Markov Assumption

	School 1	School 2	School 3	School 4	School 5	School 6	School 7	School 8
1. Pr(T2|T1)	0.32	0.24	0.29	0.28	0.35	0.27	0.22	0.39
2. Pr(T3 | T2)	0.49	0.33	0.47	0.44	0.32	0.23	0.53	0.40
3. Pr(T2|T1)×Pr(T3|T2)	0.16	0.08	0.14	0.12	0.11	0.06	0.12	0.15
4. Pr(T3|T1)	0.22	0.13	0.25	0.23	0.21	0.14	0.20	0.26
Effect of Tl on T2→T3
No covariates	1.479 (0.166)	1.492 (0.154)	1.716 (0.191)	1.788 (0.198)	0.957 (0.094)	1.170 (0.109)	2.071 (0.235)	1.389 (0.137)
All covariates	1.110 (0.177)	1.188 (0.124)	1.132 (0.208)	1.444 (0.280)	0.730 (0.123)	0.930 (0.241)	1.463 (0.292)	1.088 (0.176)

Note: Standard errors included in parentheses.

A further test of the assumption is to limit the analysis to changes in ties from time 2 to time 3, conditioning on the time 1 friendship ties. The bottom of Table 3 provides the results of this test. Confirming the ad hoc test of the Markov assumption earlier, ignoring all covariates, having a tie at time 1 with alter j increases the odds that actor i will extend a tie to j again between times 2 and 3. Controlling for the other covariates included in the analysis decreases the size of this effect, but in all cases it remains strong and significant. The size of this effect is smaller in the two large schools than in the smaller schools.

Given that the Markov assumption is violated, the important question is whether and how it affects the results of this analysis. Again, focusing on changes in friendship ties between times 2 and 3, I assess the effects of GPA rank on changes in ties, with and without a control for time 1 friendship ties. In all cases, the inclusion or exclusion of time 1 friendship ties does little to affect the size of achievement effects on friendship ties.²¹ These results provide suggestive evidence that the historical dependencies in friendship ties are at least independent of achievement and I can cautiously move forward with the analysis.

Friend Selection Controlling for Friend Influence

To estimate the effect of GPA rank on friend changes, I carry out a series of stochastic actor-based models for the co-evolution of networks and behavior. Although I build the model in a stepwise fashion, first including only the effects of GPA on network change, then adding the network structural characteristics, the measures of proximity, and finally the other covariate controls, I present results from the final model only. Results from the other models are available from the author upon request. Results from the co-evolution model are then compared to results from the cross-sectional model presented earlier.

Table 4 shows parameter estimates for the rate functions and the achievement components of the evaluation functions for both the selection and influence parts of the model. All covariates discussed earlier, including controls, are included in this model. This model provides an estimate of the effect of GPA rank on friendship tie extension, separating out the effect of friendship ties on changes in GPA rank.

Table 4.

Parameter Estimates of Selected Variables from Stochastic Actor-based Models for the Co-evolution of Network Ties and Behavior

	School 1	School 2	School 3	School 4	School 5	School 6	School 7	School 8
Selection
Rate function
Period 1	8.379** (0.968)	12.464** (0.963)	11.014** (1.189)	8.384** (1.180)	16.267** (0.528)	12.914** (0.496)	9.660** (1.069)	12.275** (1.161)
Period 2	11.497** (2.369)	13.715** (1.508)	10.972** (1.739)	6.396** (0.983)	13.545** (0.624)	8.055** (0.381)	11.470** (1.722)	11.181** (1.380)
Objective function
GPA rank
Alter	0.051 (0.062)	0.017 (0.033)	0.057 (0.050)	0.205 (0.259)	− 0.022 (0.015)	0.052 (0.020)	− 0.022 (0.079)	−0.013 (0.055)
Ego	−0.178** (0.071)	− 0.078** (0.033)	0.059 (0.051)	−0.109 (0.196)	0.024 (0.014)	0.015 (0.020)	0.074 (0.088)	0.004 (0.061)
Similarity	0.599 (0.386)	0.049 (0.207)	1.004 (0.496)	0.703 (0.964)	0.675** (0.095)	0.788** (0.150)	0.367 (0.482)	−0.350 (0.438)
Influence
Rate function
Period 1	2.005** (0.598)	1.365** (0.247)	3.405** (0.950)	1.867** (0.858)	2 797** (0.196)	3.626** (0.286)	3.338** (1.010)	1.773** (0.459)
Period 2	1.135** (0.348)	1.614** (0.335)	2.845** (0.808)	4.046** (1.682)	3.158** (0.303)	3.643** (0.264)	5.979** (2.150)	3.768** (1.400)
Objective function
GPA rank tendency	0.512** (0.175)	0.116 (0.133)	0.055 (0.121)	1.269** (0.248)	0.033 (0.029)	− 0.033 (0.025)	0.439** (0.086)	0.224 (0.133)
GPA rank tendency	− 0.078 (0.125)	− 0.048 (0.102)	− 0.178 (0.193)	0.332 (0.243)	− 0.038 (0.024)	−0.077** (0.024)	0.113** (0.055)	−0.176** (0.081)
Average alter GPA rank	− 0.057 (0.683)	0.830 (0.634)	0.682 (0.678)	0.984 (1.107)	0.396** (0.086)	0.523** (0.077)	0.052 (0.411)	− 0.042 (0.414)

Note: All models include controls for out-degree, reciprocity, transitive triplets, popularity, grade similarity, same local area position (schools 5 and 6), whether school is in session at the time of the survey, same gender, same race (schools 4, 5, and 6), and similarity in socioeconomic background in the selection equation. Standard errors included in parentheses.

^†p < .10.

^*p < .05.

^**p < .01.

Recall that the model provides actors the opportunity to change their friendship ties, one at a time at infinitesimally small time intervals. Given that an actor has an opportunity to change a tie, that actor is not required to change a tie and is permitted to maintain her ties in their current configuration, given that no other configuration is more rewarding than the current configuration of ties. When an opportunity arises for an actor to change a tie, she can do one of three things: (1) extend a new tie, (2) dissolve an old tie, or (3) maintain all current ties and make no changes.

As discussed earlier, the rate function describes how many opportunities actors have to change ties in the network (or change their behavior) between observation points. Because an actor is not required to make a change in her ties, the rate parameters do not provide a description of the amount of change in the network. In these models, all individuals in the network have an equal opportunity to change network ties.²² In school 1, for example, between times 1 and 2, students have on average 8.4 opportunities to change a tie and between times 2 and 3, they have 11.5 opportunities to change a tie.

In contrast to the rate function, the objective function describes which changes are made. Coefficients from the objective function represent the log odds ratio of the probability that actor i extends a friendship tie to actor j compared to the probability that a tie is extended to actor k. Again, I am interested in three different GPA rank effects on tie changes: the effect of the respondent’s GPA rank on whether a tie is extended (ego effect), the effect of the possible friend’s GPA rank on whether a tie is extended (alter effect), and the effect of similarity between the respondent and the possible friends’ GPA ranks.

The effect of alter’s GPA rank on tie extension represents the desire on the part of adolescents in the network to extend ties based on the alter’s GPA, net of their own GPA and similarity between them (as well as all other covariates). Positive estimated coefficients suggest that higher GPA students are more likely to be nominated as friends compared to lower GPA students. In all schools, adolescents show no preference for GPA rank when nominating alters, net of the similarity between alter and ego. In other words, students with high GPA ranks are no more attractive than students with low GPAs for tie changes, net of their similarity.

The effect of ego’s GPA rank on tie extension represents the desire of individuals with differing GPA ranks to extend ties. A positive effect suggests that higher GPA individuals are more likely to extend a tie in the network than lower GPA individuals. The effect of ego GPA rank is generally 0. In schools 1 and 2, however, individuals with higher GPAs are less likely to extend ties and therefore less likely to change their network ties than individuals with lower GPAs. In school 1, for example, an increase in GPA rank by one quintile decreases the odds of extending a tie to another person in the network 16 percent.

The effect of similarity in GPA rank on tie extension is more complicated. In the two large, more typical high schools (5 and 6), GPA rank similarity has a strong and positive effect on tie extension. In these schools, adolescents with the same GPA have odds approximately 2 times greater (e^.675, e^.788) of extending a friendship tie to someone in the same GPA quintile compared to a friend in a maximally different GPA quintile. In other words, adolescents in the bottom quintile have odds 2 times greater of making friends with someone also in the bottom quintile compared to someone in the top quintile. These results a statistically significant at the p < .05 level.

In other schools, the effect of similarity in GPA is suggestive but marginally or not at all significant. These tend to be the small private schools (with the exception of school 3). Coefficient estimates are positive with odds that vary between 1.45 and 2.72 but are not statistically significant. Because the SIENA model depends on changes in network ties to identify effects, in small networks with limited tie changes, estimates can be imprecisely estimated and this could be the cause of insignificant results in these cases rather than true non-effects, even when convergence criterion are met.

In two schools, similarity in GPA has no effect on friendship ties. These schools are both small, rural, low socioeconomic status schools. If these schools are located in truly rural areas, geography may provide an explanation for these patterns. Because of distances, the key sorting mechanism of friendships may be where one lives or which bus is taken to school. As a result, these adolescents do not have the luxury or perhaps the opportunity of making friends on the achievement dimension.

In each model, the influence that adolescents’ friends have on their achievement is controlled, ensuring that the similarities I observe between respondents and their friends are the result of selection of similar others rather than influence. Again, because few covariates are included in the influence side of the model, it is unwise to interpret the parameter estimate of the effect of the average alter’s GPA rank. Many characteristics of individuals, their families, and their schools influence their achievement. These characteristics are more than likely correlated with the characteristics of respondents’ friends. As a result, the estimated influence of friends is surely biased.

Summary of Results across Schools

Not surprisingly, there is significant variation in all achievement effects with the exception of the alter effect, which is essentially 0. Different types of schools, however, do clump together in interesting ways. In the two large public high schools, academic achievement is an important sorting mechanism for friendships. Over time, adolescents change their friendship ties to maximize similarity between themselves and their friends. These patterns remain strong even after course-taking patterns are controlled and network structure is accounted for. In these schools, the most academically advantaged students make friends with one another while the most academically disadvantaged students make friends with one another. If these schools are typical of most American high schools, this pattern of friend sorting could have important implications for inequality more generally. In the small private schools, the patterns of estimates mirror those of the two large high schools, but again are not statistically significant. By contrast, in small rural schools, academic achievement does not sort friendships. Changes in achievement do not lead to changes in friendship ties, after similarity in grade, network structure, other sociodemographic characteristics, and the influence of friends on achievement are controlled.

Comparison of Cross-sectional and Dynamic Results

Estimated effects of GPA on friend selection differ depending on methodological approach but in complicated ways. Particularly in the small and rural schools, the cross-sectional approach overstates the extent to which friendships are sorted on academic achievement. And in all schools, the cross-section suggests that higher achieving adolescents are both more popular and more social than the dynamic models suggest. These do not sound like large differences in estimated effects, but again, all three effects need to be considered together to really see the impact of estimation strategy.

Table 5 presents the calculated log odds that individual i extends a tie to individual j given i’s GPA quintile and j’s GPA quintile for schools 5 and 6. Arguably, the difference in effects across estimation strategies is smallest in these two schools. On the left side of the table is the cross-sectional result and on the right side of the table is the dynamic network result.

Table 5.

Log Odds that i Extends a Friendship Tie to j Given the GPA Quintiles of i and j

	Cross-section						Dynamic model
i\j	1	2	3	4	5	i\j	1	2	3	4	5
School 5
	0.08	−0.06	−0.21	−0.35	−0.49		0.26	0.06	−0.13	−0.32	−0.51
2	−0.04	0.18	0.04	−0.11	−0.25	2	0.11	0.26	0.07	−0.13	−0.32
3	−0.16	0.06	0.28	0.13	−0.01	3	−0.03	0.11	0.26	0.07	−0.12
4	−0.28	−0.06	0.16	0.38	0.23	4	−0.18	−0.03	0.11	0.26	0.07
5	−0.41	−0.19	0.04	0.26	0.48	5	−0.32	−0.18	−0.03	0.12	0.26
School 6
	0.34	−0.08	−0.22	−0.37	−0.52		0.32	0.02	−0.13	−0.27	−0.42
2	−0.11	0.21	0.06	−0.08	−0.23	2	−0.02	0.23	0.08	−0.06	−0.21
3	−0.30	0.03	0.35	0.20	0.06	3	−0.20	0.05	0.30	0.15	0.01
4	−0.48	−0.15	0.17	0.49	0.34	4	−0.38	−0.13	0.11	0.36	0.22
5	−0.66	−0.34	−0.01	0.31	0.63	5	−0.57	−0.32	−0.07	0.18	0.43

In both schools, preferences for high-achievers are overstated while preferences for low-achievers are understated in the cross-section. Furthermore, preferences on the diagonal, for friends in the same GPA quintile, are more evenly spread in the dynamic network models. Whereas in the cross-section it appeared that high-achievers were particularly homophilous, the dynamic network model suggests that low- and high-achievers have similar preferences for similarly achieving friends. In other words, low-achievers are more attractive friends to all adolescents than the cross-sectional models suggest, while high-achievers are generally less attractive. By understating desires among lower achievers for low-achieving friends and overstating desires among high-achievers for high-achieving friends, the cross-sectional model misstates the extent to which friend preferences based on achievement contribute to educational inequality. Although the cross-section suggests that the high-achievers are the gatekeepers who are more selective about the achievement characteristics of their friends, the dynamic approach suggests that in fact preferences for similarity are relatively constant across achievement levels.

DISCUSSION

The goal of this article was to model the changes in adolescent friendship ties that result from changes in academic achievement. This goal is complicated by the methodological difficulty of separating friend selection from friend influence. Using data from the Add Health saturated sample and new network methods to model the co-evolution of behavior and network ties, I was able to (1) show how academic achievement affects changes in friendship ties accounting for the impact that friends’ academic achievement has on changes in achievement and (2) show how traditional cross-sectional models of friend selection can misstate the role of academic achievement in observed friendship ties.

In the most typical schools in the analytic sample, GPA is an important determinant of the friends made by adolescents and helps to explain how and why friendships change. High-achieving students are more likely to extend ties to other high-achieving students and will dissolve those ties if their friends change their level of achievement. As a result, the most academically advantaged students are always friends.

Although the cross-sectional models suggest a similar amount of similarity in achievement among friends in these two typical schools, these models overstate the desire for high-achieving friends by ignoring network structure, the dynamics of friendships, and the simultaneous influence of friends on achievement. The result is that the cross-sectional model may actually understate the amount of inequality created through friendships. Preferences for achievement go in both directions. While high-achievers strive for high-achieving friends, low-achievers strive for low-achieving friends. If friends influence one another’s achievement, as the influence part of the model suggests, the differences in achievement between the high and low achievers will be exacerbated by the friends they make.

A completely different story emerges among the small and rural schools in the sample. In these schools, academic achievement plays little to no role in the sorting of friendships. There are several possible explanations for this result. Particularly in schools 1, 3, and 4, where estimated effects are comparable in size to those in the two large typical high schools, these results may be caused by the model rather than true null effects. SIENA models require a large amount of change in ties to precisely identify the relationship between academic achievement and changes in friendship ties, and the small schools in the sample may not provide enough change to identify these effects.

Alternatively, these null effects may be real. In these schools, the pool of possible friends is small. In fact, it may be so small that adolescents cannot be choosy about who their friends are, even though they may actually prefer similarly achieving friends. If these schools are truly rural, geography may play an important role in the friends they make. The geographic constraints of making friends with individuals who live far away from you may again help to trump achievement as a sorting mechanism for friendships. However, more convincing is the idea that in small communities where children have grown up together, individuals have more information about one another’s characters. In these environments, behavioral signals are less important for the friendships that develop over time. As a result, these kids may influence one another’s behaviors but their achievement characteristics will not structure their friendship choices.

Whether because their pool of possible friends is too small to be choosy, because geography limits their access to academically similar friends, or because information and historical ties make these behavioral signals less important, these friendships appear to not be structured by academic achievement. And this result is consistent with recent work suggesting that the size of the population or network will affect the extent to which homophily occurs (Grund 2010).

What are the implications of these patterns of friendship for the stratification and future inequality of adolescents as they age? Friends have important impacts on trajectories through high school and into college. The more extreme are tendencies for sorting based on academic achievement, the wider the spread of stratification outcomes will be, leading to greater privilege among the most privileged and greater deprivation among the most disadvantaged. This is in many ways an answer we expect and simultaneously dislike because the question becomes: How can we change adolescents’ preferences? Perhaps we can learn a lesson from these small rural K-12 schools. Perhaps a move toward smaller schools, tighter knit communities, and progressions through school with the same set of classmates can help to diminish the tendencies we observe among adolescents in large schools for sorting based on academic achievement.

Biography

Jennifer Flashman is a Postdoctoral Associate at the Center for Research on Inequalities and the Life Course in the Department of Sociology at Yale University. She was formerly a Postdoctoral Prize Research Fellow at Nuffield College, University of Oxford. She completed her PhD in Sociology at UCLA in 2009. Her research focuses primarily on the role of friends and schools in adolescents’ stratification outcomes.