Abstract
With the wide array of multi scale, multi-modal data now available for disease characterization, the major challenge in integrated disease diagnostics is to able to represent the different data streams in a common framework while overcoming differences in scale and dimensionality. This common knowledge representation framework is an important pre-requisite to develop integrated meta-classifiers for disease classification. In this paper, we present a unified data fusion framework, Semi Supervised Multi Kernel Graph Embedding (SeSMiK-GE). Our method allows for representation of individual data modalities via a combined multi-kernel framework followed by semi- supervised dimensionality reduction, where partial label information is incorporated to embed high dimensional data in a reduced space. In this work we evaluate SeSMiK-GE for distinguishing (a) benign from cancerous (CaP) areas, and (b) aggressive high-grade prostate cancer from indolent low-grade by integrating information from 1.5 Tesla in vivo Magnetic Resonance Imaging (anatomic) and Spectroscopy (metabolic). Comparing SeSMiK-GE with unimodal T2w, MRS classifiers and a previous published non-linear dimensionality reduction driven combination scheme (ScEPTre) yielded classification accuracies of (a) 91.3% (SeSMiK), 66.1% (MRI), 82.6% (MRS) and 86.8% (ScEPTre) for distinguishing benign from CaP regions, and (b) 87.5% (SeSMiK), 79.8% (MRI), 83.7% (MRS) and 83.9% (ScEPTre) for distinguishing high and low grade CaP over a total of 19 multi-modal MRI patient studies.
1 Introduction
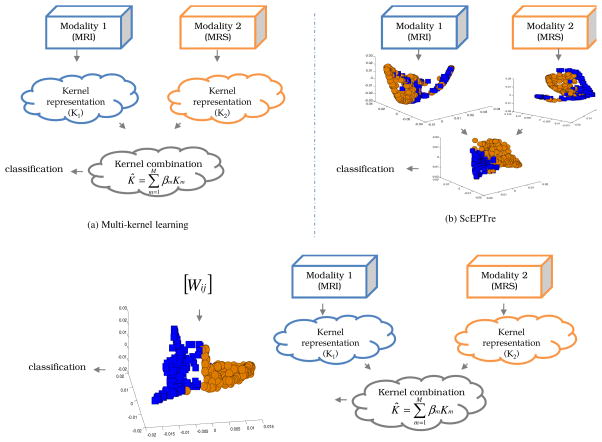
With the rapid growth of new imaging modalities and availability of multi-scale, multimodal information, data fusion has become extremely important for improved disease diagnostics. However one of the major challenges in integrating independent channels of heterogeneous information is representing them in a unified framework prior to data integration [1]. Typically, information fusing algorithms may be categorized as being either combination of data (COD) or interpretation (COI) methodologies [2]. In COD, features Fm1 and Fm2 from two disparate modalities m1 and m2 may be combined as Fm1m2 = [Fm1, Fm2]. However directly aggregating data from very different sources without accounting for differences in the number of features and relative scaling can lead to classifier bias towards the modality with more attributes. In [3], Lanckriet et al transformed data from amino acid sequences, protein complex data, gene expression data, and protein interactions into a common kernel space. Kernels are positive definite functions which capture the similarities of the input data into a dot product space such that K(F(ci), F(cj)) = 〈ΦK(F(ci), ΦK F(cj))〉, where Φ is the implicit pair-wise embedding between points F(ci) and F(cj). This multi-kernel learning (MKL) (Figure 1(a)) involves similarity matrices for kernels from individual modalities being combined and used to train classifiers (within the fused kernel space) in order to make meta-predictions. However, due to the large amount of information present in each input source, all COD methods, including MKL, suffer from the curse of dimensionality.
Fig. 1.
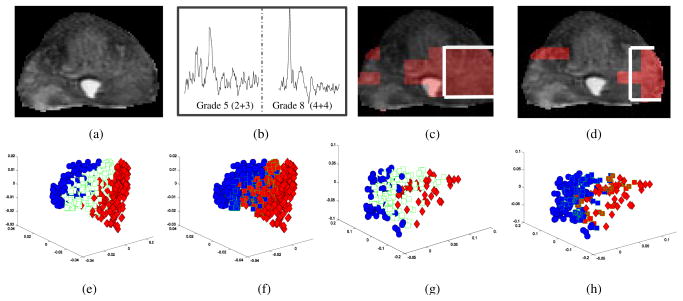
(a) MKL employs a kernel combination strategy, (b) ScEPTre-based data fusion where low dimensional embedding representations are combined, and (c) SeSMiK-GE method where MKL is performed to first combine the data in a common kernel space followed by semi-supervised GE. The two colors in each 3D embedding plot represent two different classes.
In [1], we introduced ScEPTre (Figure 1(b)) which employed graph embedding (GE) [4] to combine low dimensional data representations obtained from individual modalities. GE accounts for the non-linearities in the data by constructing a similarity graph G = (V, W), where V corresponds to the vertex between pairwise points and W is a n × n weight matrix of n data points. However GE, like most other dimensionality reduction (DR) schemes, is unsupervised and does not include any domain knowledge while transforming the data to lower dimensions which often leads to overlapping embeddings. A few supervised DR schemes such as linear discriminant analysis (LDA) employ class label information to obtain low dimensional embeddings. However obtaining labels for biomedical data is extremely expensive and time consuming. Recently semi-supervised DR (SSDR) schemes based on GE have been proposed [5], which construct a weight matrix leveraging the known labels such that higher weights are given to within-class points and lower weights to points from different classes. The proximity of labeled and unlabeled data is then used to construct the low dimensional manifold.
In this work, we present a unified data fusion DR framework called Semi Supervised Multi Kernel Graph Embedding (SeSMiK-GE), a novel data fusion and dimensionality reduction scheme that leverages the strengths of GE, semi-supervised learning, and MKL into a single integrated framework for simultaneous data reduction, fusion, and classification. Only the work of Lin et al [6], that we are aware of, has used MKL in conjunction with GE. However their approach does not leverage learning in constructing the embeddings. SeSMiK-GE involves first transforming each individual modality in a common kernel framework, followed by weighted combination of individual kernels as , where Km, m ∈ {1, 2, …, M} is the kernel obtained from each modality, βm is the weight assigned to each kernel, and M is the total number of kernels employed. DR is then performed on K̂ using semi-supervised GE (SSGE) which incorporates partial labels to provide a better low dimensional representation of the data allowing for better class separation and hence improved classification with limited training samples.
In this paper we show an application of SeSMiK-GE to combine structural information obtained from T2-weighted Magnetic Resonance (MR) Imaging (T2w MRI) and metabolic information obtained from MR Spectroscopy (MRS) for detection of high-grade prostate cancer (CaP) in vivo. The Gleason grading system is the most commonly used system world-wide for identifying aggressivity of CaP, and hence patient outcome. High Gleason scores are associated with poor outcome, while lower scores are typically associated with better patient outcome. Recently, researchers have been attempting to identify MR imaging signatures for high- and low-grade CaP in vivo [7,8].
2 Graph Embedding Framework
The aim of GE [4] is to reduce the data matrix
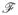 ∈ ℝD into a low-dimensional space y ∈ ℝd (D ≫ d), such that object adjacencies are preserved from ℝD to ℝd. Let
∈ ℝD into a low-dimensional space y ∈ ℝd (D ≫ d), such that object adjacencies are preserved from ℝD to ℝd. Let
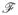 = [F(c1), F(c2), …, F(cn)] ∈ ℝD be a data matrix of n objects, i ∈ {1, …, n}, with dimensionality D, and y = [y1, y2, …, yn] be the corresponding optimal low dimensional projection matrix. y can be obtained by solving,
= [F(c1), F(c2), …, F(cn)] ∈ ℝD be a data matrix of n objects, i ∈ {1, …, n}, with dimensionality D, and y = [y1, y2, …, yn] be the corresponding optimal low dimensional projection matrix. y can be obtained by solving,
| (1) |
where W = [wij] is a similarity matrix which assigns edge weights to characterize similarities between pairwise points ci and cj, i, j ∈ {1, …, n}. The minimization of Equation 1 reduces it to an eigenvalue decomposition problem,
| (2) |
where
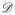 is a diagonal matrix,
is a diagonal matrix,
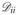 = Σi Wij. According to the Representer Theorem [9], to calculate the kernel representation K(F(ci), F(cj)) of input data, it is assumed that the optimal embedding y lies in the input space such that
. Thus, the kernel formulation of Equation 2 can be re-written as,
= Σi Wij. According to the Representer Theorem [9], to calculate the kernel representation K(F(ci), F(cj)) of input data, it is assumed that the optimal embedding y lies in the input space such that
. Thus, the kernel formulation of Equation 2 can be re-written as,
| (3) |
where K is a valid positive semi-definite kernel and α is the d dimensional eigenvector of the kernel representation in Equation 3.
3 Semi-Supervised Multi-kernel Graph Embedding (SeSMiK-GE)
Constructing Kernels for each modality: Kernel functions embed input data in the implicit dot product space, evaluating which yields a symmetric, positive definite matrix (gram matrix). A kernel gram matrix Km defining the similarities between n data points in each modality m may be obtained as Km = [K(F(ci), F(cj))] ∀i, j ∈ {1, …, n}.
- Combining Multiple kernels: A linear combination of different kernels has the advantage of also yielding a symmetric, positive definite matrix. Assuming we have M base kernel functions for M modalities, , corresponding individual kernel weights βm, the combined kernel function may be expressed as,
(4) -
Constructing the adjacency graph using partial labels: Assuming the first l of n samples are labeled ωl ∈ {+1, −1}, we can incorporate the partial known labels into the similarity matrix W = [wij]. A
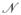 nearest neighbor graph,
nearest neighbor graph,
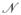 > 0, is created to obtain W such that pairwise points in
> 0, is created to obtain W such that pairwise points in
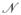 neighborhood with same labels are given high weights and points with different class labels are given low weights [5]. If the points are not in
neighborhood with same labels are given high weights and points with different class labels are given low weights [5]. If the points are not in
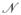 , the corresponding edges are not connected. Thus the weight matrix is,
, the corresponding edges are not connected. Thus the weight matrix is,
(5) where and σ is the scaling parameter. The weight matrix Wm obtained from each modality may be averaged to obtain .
-
Obtaining the low dimensional embedding: The combined kernel K̂ and associated weight matrix Ŵ obtained from Equations (4) and (5) can be used to reduce Equation (3) to the eigenvalue decomposition problem,
(6) where
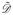 = Σj ŵji. The optimal d dimensional eigenvectors α {α1, α2, …, αn} are obtained using standard kernel ridge regression optimization as described in [10].
= Σj ŵji. The optimal d dimensional eigenvectors α {α1, α2, …, αn} are obtained using standard kernel ridge regression optimization as described in [10].
4 SeSMiK-GE for Prostate Cancer Detection and Grading
4.1 Data Description
A total of 19 1.5 Tesla (T) T2w MRI and corresponding MRS pre-operative endorectal in vivo prostate studies were obtained from the University of California, San Francisco. The 3D prostate T2w MRI scene is represented by
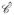 = (Ĉ, f̂), where Ĉ is a 3D grid of voxels ĉ ∈ Ĉ and f̂ (ĉ) is a function that assigns an intensity value to every ĉ ∈ Ĉ. We also define a spectral scene
= (Ĉ, f̂), where Ĉ is a 3D grid of voxels ĉ ∈ Ĉ and f̂ (ĉ) is a function that assigns an intensity value to every ĉ ∈ Ĉ. We also define a spectral scene
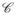 = (C, F) where C is a 3D grid of MRS metavoxels, c ∈ C, and F is a spectral vector associated with each c ∈ C. Note that multiple MRI resolution voxels are present within the region Rcd between any two adjacent MRS resolution metavoxels c, d ∈ C. An expert spectroscopist (JK) manually annotated individual MRS metavoxels across all 19 patient studies as firstly (a) CaP/benign, and secondly, (b) as low/high grade CaP. The 19 1.5 T studies comprised a total of (a) 573 CaP and 696 benign metavoxels, and (b) 175 low and 96 high grade CaP metavoxels.
= (C, F) where C is a 3D grid of MRS metavoxels, c ∈ C, and F is a spectral vector associated with each c ∈ C. Note that multiple MRI resolution voxels are present within the region Rcd between any two adjacent MRS resolution metavoxels c, d ∈ C. An expert spectroscopist (JK) manually annotated individual MRS metavoxels across all 19 patient studies as firstly (a) CaP/benign, and secondly, (b) as low/high grade CaP. The 19 1.5 T studies comprised a total of (a) 573 CaP and 696 benign metavoxels, and (b) 175 low and 96 high grade CaP metavoxels.
4.2 Feature Extraction from MRI and MRS
Feature extraction from MRS: For each c ∈ C, F(c) = [fa(c)|a ∈ {1, … U}], represents the MR spectral vector, reflecting the frequency component of each of U metabolites. The corresponding spectral data matrix is given as
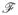 = [F1(c); F2(c), …; Fn(c)] ∈ ℝn×U where n = |C|, |C| is the cardinality of C.
= [F1(c); F2(c), …; Fn(c)] ∈ ℝn×U where n = |C|, |C| is the cardinality of C.Feature extraction from MRI: 38 texture features were extracted to define CaP appearance on in vivo T2w MRI [11]. We calculated the feature scenes
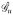 = (Ĉ, f̂u) for each
= (Ĉ, f̂u) for each
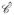 by applying the feature operators Φu, u ∈ {1, …, 38} within a local neighborhood associated with every ĉ ∈ Ĉ. 13 gradient, 12 first order statistical and 13 Haralick features were extracted at each ĉ ∈ Ĉ. We define a T2w MRI texture feature vector for each metavoxel c ∈ C by taking the average of the feature values within the corresponding metavoxel as
. The corresponding feature vector is then given as G(c) = [gu(c)|u ∈ {1, …, 38}], ∀c ∈ C, and the MRI data matrix is given as
by applying the feature operators Φu, u ∈ {1, …, 38} within a local neighborhood associated with every ĉ ∈ Ĉ. 13 gradient, 12 first order statistical and 13 Haralick features were extracted at each ĉ ∈ Ĉ. We define a T2w MRI texture feature vector for each metavoxel c ∈ C by taking the average of the feature values within the corresponding metavoxel as
. The corresponding feature vector is then given as G(c) = [gu(c)|u ∈ {1, …, 38}], ∀c ∈ C, and the MRI data matrix is given as
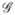 = [G1; G2; …; Gn] ∈ Rn×38.
= [G1; G2; …; Gn] ∈ Rn×38.
4.3 SeSMiK-GE for Integration of MRI and MRS
A Gaussian kernel K(F(ci),
was employed within SeSMiK-GE to obtain KMRS and KMRI from input MRS data
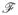 and MRI data
and MRI data
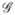 . 40% of the total samples were randomly selected to train the algorithm over 25 iterations of cross validation. WMRI and WMRS were obtained using Equation (5) and averaged to obtained the fused gram matrix Ŵ. The algorithm was evaluated over different values of β ∈ [0, 1] over intervals of 0.1 to obtain 11 embedding outputs αq, q ∈ {1, …, 11}, where α1 represents the embedding obtained purely from KMRS (β = 0) and α11 represents the embedding obtained purely from KMRI (β = 1). A probabilistic boosting tree (PBT) classifier [12], was then trained using the same set of samples exposed for SeSMiK over each iteration of 25 cross validation runs. During each iteration, the optimal αq which results in the maximum classification accuracy is selected as the final embedding result. The algorithm for SeSMiK-GE is presented below.
. 40% of the total samples were randomly selected to train the algorithm over 25 iterations of cross validation. WMRI and WMRS were obtained using Equation (5) and averaged to obtained the fused gram matrix Ŵ. The algorithm was evaluated over different values of β ∈ [0, 1] over intervals of 0.1 to obtain 11 embedding outputs αq, q ∈ {1, …, 11}, where α1 represents the embedding obtained purely from KMRS (β = 0) and α11 represents the embedding obtained purely from KMRI (β = 1). A probabilistic boosting tree (PBT) classifier [12], was then trained using the same set of samples exposed for SeSMiK over each iteration of 25 cross validation runs. During each iteration, the optimal αq which results in the maximum classification accuracy is selected as the final embedding result. The algorithm for SeSMiK-GE is presented below.
Algorithm.
SeSMiK-GE
Input:
 , ,
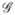 , ,
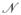 , d , d
| |
| Output: α | |
| begin | |
| 0. | Obtain KMRS ←
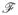 and KMRI ← and KMRI ←
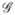
|
| 1. | Obtain WMRI and WMRS using
 ; obtain Ŵ using Equation (6) ; obtain Ŵ using Equation (6)
|
| 2. | Initialize β = 0, q = 1 |
| 3. | while β = 1, compute K̂q = β × KMRI + (1 − β) × KMRS |
| 4. | Substitute K̂q and Ŵ in Equation (3) |
| 5. | Obtain d-dimensional αq by solving Equation (7) |
| 6. | return αq |
| 7. | β = β + 0.1, q = q + 1 |
| 8. | endwhile |
| end | |
The algorithm above was applied to the problems of (a) discriminating CaP vs. benign regions, and (b) identifying high-grade CaP using multi-protocol MRI.
5 Results and Discussion
5.1 Qualitative
A PBT classifier [12] was trained on the low dimensional embedding representations obtained from application of SeSMiK-GE to the 19 MRI, MRS studies. Figure 2(a) shows a T2w MRI slice with high grade CaP, while Figure 2(b) shows signature spectra corresponding to low and high grade CaP, in turn illustrating the difficulty in visually identifying high grade CaP on in vivo MRI and MRS. Figures 2(c)–(d) show the PBT classifier prediction results (as red regions) on the same T2w MRI slice using SeSMiK-GE for identifying CaP (Figure 2(c)) and high-grade CaP (Figure 2(d)). Note the high detection accuracy obtained using SeSMiK-GE for both CaP (Figure 2(c)) and high-grade CaP (Figure 2(d)) identification. Ground truth for CaP and high-grade CaP extent is shown via a white ROI on Figures 2(c) and 2(d).
Fig. 2.
(a) Original T2w MRI, (b) MRS signatures for high/low grade CaP. Red regions on (c)–(d) show the classification results obtained using SeSMiK-GE for identifying CaP and high grade CaP on in vivo MRI, MRS. White ROI delineates the ground truth for CaP extent in (c) and high-grade CaP in (d). (e), (g) show 3D embedding plots obtained from SeSMiK-GE (with partial training labels for each class) for cancer metavoxels (red) and benign metavoxels (blue). The spectra in the evaluation (test set) are shown via green squares. (f), (h) illustrate the classification results via PBTs on the same embedding for detection of CaP ((f)), and high-grade CaP ((h)).
Embedding plots obtained from SeSMiK-GE for cancer (red)/benign (blue) and high (red)/low (blue) grade CaP are shown in Figures 2(e)–(h). Figures 2 (e), (g) show the partial labels provided to SeSMiK-GE, allowing for better separation between the classes (green squares represent the unlabeled samples). Figures 2(f), (h) show corresponding PBT classification labels for identifying CaP (2(f)) and high-grade CaP (2(h)). Note that in Figures 2(f) and (h), a majority of the unlabeled samples are accurately identified by our scheme, despite using limited partial labels for training.
5.2 Quantitative
Table 1(a) shows mean area under the ROC curve (AUC) and accuracy results averaged over 19 studies for identifying cancer vs. benign using SeSMiK-GE on (a) only MRI, (b) only MRS, and (c) in combining MRS and MRI (results shown are for optimal αq obtained at β = 0.8). We compared our results with ScEPTre [1], where GE [4] was first performed on each of
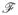 and
and
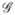 followed by concatenation of the resulting low dimensional eigenvectors. Note the high detection accuracy obtained using SeSMiK-GE for CaP (Table 1(a)) and high-grade CaP (Table 2(a)) detection. Table 1(b) shows the low variability in AUC and accuracy results over different values of reduced dimensions (d). Similar results for discriminating high and low grade CaP are shown in Table 2(b).
followed by concatenation of the resulting low dimensional eigenvectors. Note the high detection accuracy obtained using SeSMiK-GE for CaP (Table 1(a)) and high-grade CaP (Table 2(a)) detection. Table 1(b) shows the low variability in AUC and accuracy results over different values of reduced dimensions (d). Similar results for discriminating high and low grade CaP are shown in Table 2(b).
Table 1.
(a) Average AUC and accuracy for CaP detection, compared to MRI-MRS alone, and ScEPTre [1] based data fusion, averaged over a total of 19 MRI-MRS studies using the 30 top-ranked eigen values, (b) Average CaP detection accuracy and AUC results of SeSMiK-GE and ScEPTre for different dimensions d ∈ {10, 20, 30}.
| (a) | ||
|---|---|---|
| Method | AUC | Accuracy |
| T2w MRI | 66.1 ± 1.5 | 61.9 ± 1.3 |
| MRS | 82.6 ± 1.3 | 76.8 ± 1.3 |
| ScEPTre | 86.8 ± 1.26 | 78.2 ± 1.2 |
| SeSMiK-GE | 91.3 ± 0.2 | 83.0 ± 0.1 |
| (b) | ||||
|---|---|---|---|---|
| d | AUC | Accuracy | ||
| SeSMiK | ScEPTre | SeSMiK | ScEPTre | |
| 10 | 89.8 ± 0.8 | 86.8 ± 0.9 | 84.2 ± 1.1 | 80.6 ± 1.3 |
| 20 | 90.7 ± 0.9 | 87.5 ± 0.8 | 84.6 ± 0.1 | 79.1 ± 1.2 |
| 30 | 91.3 ± 0.2 | 86.8 ± 1.26 | 83.0 ± 0.1 | 78.2 ± 1.2 |
Table 2.
(a) Average AUC and accuracy for high-grade CaP detection, compared to MRI or MRS alone, and ScEPTre [1] data fusion averaged over a total of 19 MRI-MRS studies using the 10 top-ranked eigen values, (b) high-grade CaP detection accuracy and AUC results of SeSMiK-GE and ScEPTre for different dimensions d ∈ {10, 20, 30}.
| (a) | ||
|---|---|---|
| Method | AUC | Accuracy |
| T2w MRI | 79.8 ± 3.3 | 74.1 ± 4.0 |
| MRS | 83.7 ± 3.5 | 78.5 ± 3.0 |
| ScEPTre | 83.9 ± 3.5 | 76.8 ± 3.1 |
| SeSMiK-GE | 87.5 ± 2.5 | 82.5 ± 2.6 |
| (b) | ||||
|---|---|---|---|---|
| d | AUC | Accuracy | ||
| SeSMiK | ScEPTre | SeSMiK | ScEPTre | |
| 10 | 86.9 ± 2.2 | 84.4 ± 2.7 | 80.5 ± 2.6 | 79.1 ± 3.6 |
| 20 | 87.5 ± 2.5 | 83.9 ± 3.5 | 82.5 ± 2.6 | 76.8 ± 3.1 |
| 30 | 86.5 ± 2.8 | 83.8 ± 3.5 | 79.5 ± 3.3 | 77.2 ± 3.5 |
6 Conclusions and Future Work
We presented a novel semi-supervised multi-kernel (SeSMiK) scheme which is well integrated in a graph embedding framework for simultaneous data fusion and dimensionality reduction. Multi-kernel learning is first used to combine heterogeneous information from various data sources in a common kernel framework. The method leverages partial domain knowledge to create an optimal embedding from the combined data such that object classes are optimally separable. We demonstrated the application of our scheme in discriminating cancer/benign and high/low grade prostate cancer regions using metabolic information obtained from MRS and anatomic information obtained from T2w MRI. Quantitative results demonstrate a high detection accuracy in identifying cancer and high-grade prostate cancer regions, suggesting that SeSMiK can serve as a powerful tool for both computer aided diagnosis and prognosis applications. In future work we intend to explore the application of SeSMiK in other domains and problems.
Contributor Information
Pallavi Tiwari, Email: pallavit@eden.rutgers.edu.
Anant Madabhushi, Email: anantm@rci.rutgers.edu.
References
- 1.Tiwari P, et al. Spectral Embedding Based Probabilistic Boosting Tree (ScEPTre): Classifying High Dimensional Heterogeneous Biomedical Data. In: Yang G-Z, Hawkes D, Rueckert D, Noble A, Taylor C, editors. MICCAI 2009 LNCS. Vol. 5762. Springer; Heidelberg: 2009. pp. 844–851. [DOI] [PubMed] [Google Scholar]
- 2.Rohlfing T, et al. Information fusion in biomedical image analysis: Combination of data vs. combination of interpretations. In: Christensen GE, Sonka M, editors. IPMI 2005 LNCS. Vol. 3565. Springer; Heidelberg: 2005. pp. 150–161. [DOI] [PubMed] [Google Scholar]
- 3.Lanckriet G, et al. Kernel-Based Data Fusion and Its Application to Protein Function Prediction in Yeast. Pacific Symposium on Biocomputing. 2004:300–311. doi: 10.1142/9789812704856_0029. [DOI] [PubMed] [Google Scholar]
- 4.Shi J, Malik J. Normalized Cuts and Image Segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2000;22:888–905. [Google Scholar]
- 5.Zhao H. Combining labeled and unlabeled data with graph embedding. Neurocomputing. 2006;69(16–18):2385–2389. [Google Scholar]
- 6.Lin Y, et al. Dimensionality Reduction for Data in Multiple Feature Representations. Proc NIPS. 2008;21:961–968. [Google Scholar]
- 7.Zakian K, et al. Correlation of Proton MRSI with Gleason Score Based on Step-Section Pathologic Analysis after Radical Prostatectomy. Radiology. 2005;234(3):804–814. doi: 10.1148/radiol.2343040363. [DOI] [PubMed] [Google Scholar]
- 8.Wang L, et al. Assessment of Biologic Aggressiveness of Prostate Cancer: Correlation of MRI with Gleason Grade after Radical Prostatectomy. Radiology. 2008;246(1):168–176. doi: 10.1148/radiol.2461070057. [DOI] [PubMed] [Google Scholar]
- 9.Schlkopf B, et al. A Generalized Representer Theorem. Proc Computational Learning Theory. 2001:416–426. [Google Scholar]
- 10.Cai D, et al. Semi-Supervised Discriminant Analysis. Proc ICCV. 2007:1–7. [Google Scholar]
- 11.Madabhushi A, et al. Automated detection of prostatic adenocarcinoma from highresolution ex vivo mri. IEEE Transactions on Medical Imaging. 2005;24(12):1611–1625. doi: 10.1109/TMI.2005.859208. [DOI] [PubMed] [Google Scholar]
- 12.Tu Z. Probabilistic Boosting-Tree: Learning Discriminative Models for Classification, Recognition, and Clustering. Proc ICCV. 2005;2:1589–1596. [Google Scholar]