Early Numeracy Assessment: The Development of the Preschool Numeracy Scales

Abstract

Research Findings

The focus of this study was to construct and validate twelve brief early numeracy assessment tasks that measure the skills and concepts identified as key to early mathematics development by the National Council of Teachers of Mathematics (2006) and the National Mathematics Advisory Panel (2008)—as well as critical developmental precursors to later mathematics skill by the Common Core State Standards (CCSS; 2010). Participants were 393 preschool children ages 3 to 5 years old. Measure development and validation occurred through three analytic phases designed to ensure that the measures were brief, reliable, and valid. These measures included: one-to-one counting, cardinality, counting subsets, subitizing, number comparison, set comparison, number order, numeral identification, set-to-numerals, story problems, number combinations, and verbal counting.

Practice or Policy

Teachers have extensive demands on their time, yet, they are tasked with ensuring that all students’ academic needs are met. To identify individual instructional needs and measure progress, they need to be able to efficiently assess children’s numeracy skills. The measures developed in this study are not only reliable and valid, but also easy to use and can be utilized for measuring the effects of targeted instruction on individual numeracy skills.

Early Numeracy Assessment: The Development of the Preschool Early Numeracy Scales

Mathematical proficiency is an academic and economic gatekeeper that provides a key basis for achieving other academic and career skills (Baroody, Lai, & Mix, 2006; Jordan, Hanich, & Uberti, 2003)—particularly in the STEM fields (Claessens & Engle, 2013; Geary, 1994; National Mathematics Advisory Panel [NMAP], 2008). It is well known that mathematics skills develop in a cumulative fashion with early skills forming the foundation for the acquisition of later skills (Aunola, Leskinen, Lerkkanen, & Nurmi, 2004; Author, xxxx). Individual differences in early mathematics emerge early, even before formal schooling (Berch, 2005; Stevenson et al., 1990), and are predictive of later mathematics achievement and school achievement in general (Duncan et al., 2007; Ginsburg, Klein, & Starkey, 1998; Locuniak & Jordan, 2008; Mazzocco & Thompson, 2005). Children who fall behind their peers in mathematics early usually continue to develop at a slower rate than their more advanced peers and are likely to remain behind them (Aunola et al., 2004).

Developing and validating methods to enhance the mathematical performance of all children, but particularly those who enter preschool with significant deficits in their mathematical knowledge, is important for enabling them to ultimately be successful academically (Clements & Sarama, 2011a). Response to Intervention (RtI)—a multi-tiered learning difficulties prevention system—is one means that has been established to provide all children with access to appropriate instruction through age- and domain-specific screening, progress monitoring, and, where necessary, targeted intervention (Fuchs & Fuchs, 2006; Lembke, Hampton, & Beyers, 2012; Vellutino, Scanlon, Small & Fanuele, 2006). The general RtI framework of screening, progress monitoring, and targeted intervention typically can be applied across domain and age-group (Riccomini & Witzel, 2010); however, specific efforts must be undertaken to design and apply age- and domain-appropriate assessments and interventions carefully. RtI has shown broad positive impacts with at-risk elementary school students in their reading and mathematics development (Fuchs & Fuchs, 2006; Jimerson, Burns, & VanDerHeyden, 2007; Vellutino et al., 2006) and has shown promise helping to improve younger at-risk children’s early reading skills (VanDerHeyden et al., 2008). Yet, even though early mathematics achievement has been shown to be one of the strongest predictors of general academic development (Claessens & Engle, 2013; Duncan et al., 2007) and although it is clear that large individual differences in mathematics performance exist prior to formal school entry (Jordan & Levine, 2009; Starkey et al., 2004), there has not yet been a sustained effort to date to develop an RtI system designed specifically for early mathematics skills (Lembke et al., 2012).

Foundational Assessment Needs in Response to Intervention

Prior to implementation and validation of an RtI system for early mathematics, appropriate assessments tools and interventions must be developed. To ensure that children are effectively developing the wide range of competencies that form that foundation of early mathematics, it is necessary to adequately measure their progress in all aspects of early mathematics. Although teachers can generally differentiate high-performing from less well-performing students through informal observation, they need strong assessment tools to make more fine-grained differentiation (Kilday, Kinzie, Mashburn, & Whittaker, 2012)—particularly at the individual skill/concept level. Efficient and reliable assessment tools can serve a twofold purpose. First, they can be used broadly to identify which children need additional instruction and second, they can be used to identify the specific aspect(s) of mathematical knowledge in which a child needs further instruction. However, different types of assessment tools may be needed for these two purposes.

Currently Available Broad Testing Measures

Currently, a range of broad mathematical measures have been empirically validated for both diagnostic and research work with preschool children including (among others) the Test of Early Mathematics Ability – 3^rd Edition (TEMA-3; Ginsburg & Baroody, 2003), the Woodcock-Johnson III Tests of Achievement (Woodcock, McGrew, & Mather, 2001), the Child Math Assessment (Klein & Starkey, 2006), and the Tools for Assessment in Early Mathematics (TEAM; Clements, Sarama, & Wolfe, 2011). The broad measures typically provide an overall mathematics score that is intended to reflect an individual’s general mathematical ability and can be used to identify the approximate developmental level of a child in relation to same-age or same-grade peers. Broad measures such as these are critical for measuring curricular effects and children’s relative performance. However, in an RtI framework, teachers and researchers also need to be able to identify children’s performance on individual skills to identify areas of deficit or their response to instructional activities.

Although the broad mathematics tests are comprised of items that measure a wide range of early mathematical skills and concepts (e.g., one-to-one counting, comparison, story problems; see Table 1 for the breakdown of the skills assessed on each of the broad measures), the tests are not designed to measure each of these skills and concepts individually. For example, the TEMA-3 has individual items that measure one-to-one counting, numeral comparison, and number order (among many other items), but these are just individual items included in the broader measure. Although it is noted in the examiner’s manual that several items can be combined to assess a broader concept (such as counting), it is also noted that the subscales are not validated (Ginsburg & Baroody, 2003). For teachers and researchers to identify the specific aspect(s) of mathematics in which a child needs individualized interventions, efficient, reliable and valid assessment tools that have been constructed specifically to assess targeted early mathematics skills are needed.

Table 1.

Numeracy Domains Assessed Within Existing Broad and Targeted Measures of Early Numeracy

	Measures/Articles
	Broad Measures				Articles with Brief Measures a
	TEAM	CMA	TEMA-3	WJ-AP	L09	P12	R06	V04/06
Verbal Counting	X	X	X		S		S	S
One-to-one Counting	X	X	X	X	S		S	S
Cardinality	X		X	X		S
Counting Subsets	X	X	X	X
Subitizing	X		X		S		S
Number Comparison	X	X	X
Set Comparison	X		X
Number Order	X	X	X
Numeral Identification			X		S		S	S
Set-to-Numerals	X
Story Problems		X	X	X
Number Combinations	X	X	X	X

TEAM = Tools for the Assessment of Early Mathematics (Clements, Sarama, & Lui, 2008; Clements, Sarama, & Wolfe, 2011)), CMA = Child Math Assessment (Klein & Starkey, 2006), TEMA-3 = Test of Early Mathematics Ability – Third Edition (Ginsburg & Baroody, 2003), WJ-AP = Woodcock-Johnson III Applied Problems subtest (Woodcock et al., 2001).

X = skill is assessed on one or multiple items, but no subtest for that specific task is available (and/or not reliability/validity information for a possible subtest is publically available).

S = Includes a subtest for the construct that includes reliability and validity information

L09 = Lei, Wu, DiPerna, and Morgan (2009)

P12 = Polignano and Hojnoski (2012)

R06 = Reid, Morgan, DiPerna, and Lei (2006)

V04/06 = VanDerHeyden, Broussard, Fabre, Stanley, Legendre, and Creppell (2004) and VanDerHeyden, Broussard, and Cooley (2006)

^aFloyd, Hojnoski, and Key (2006) is not included in the table because their measures are fluency measures.

Specific Key Aspects of Early Mathematical Knowledge that Need to be Assessed

In developing appropriate targeted assessment tools for individual early mathematics skills in preschool, the numeracy-related skills that need to be considered generally fall into three main domains: enumeration, relations, and operations (Jordan et al., 2007; NRC, 2009). Within each of these domains, there are numerous subskills that undergo rapid and dramatic changes across the preschool years (Ginsburg et al., 1998). These specific subskills develop as a systematic and interconnected progression of knowledge (Baroody, 2003; NMAP, 2008) called a learning trajectory (Sarama & Clements, 2009; Simon & Tzur, 2004).

Specific early mathematics skills appear to develop in overlapping phases (Author, xxxx; Krajewski & Schneider, 2009). Children first begin by learning the count sequence (verbal counting), comparing small exact quantities (exact set comparison), enumerating sets by connecting number words with exact quantities (one-to-one counting, cardinality, subitizing), and even manipulating quantities through story problems. At the same time, children begin to learn numeral names—some children even begin to identify the first numerals (e.g., 1 and 2) when they are as young as 18 months (Mix, 2009; Sarama & Clements, 2009) and approximately one-quarter of children can identify the numerals 1 to 9 by the time they are four years old (Ginsburg & Baroody, 2003). However, children cannot simply learn the names of numerals (connecting number words to numerals), they must learn to connect the quantities to Arabic numerals as well (Set-to-numerals; Author, xxxx). As children acquire an understanding of the Arabic numerals and how to manipulate them for mathematical purposes, they can compare the magnitude of numerals (numeral comparison), the ordering of numerals (number order). Ultimately, all these skills build into, and are predictive of formal addition (NRC, 2009).

Failure to acquire one or more of the early competencies may result in difficulty acquiring more advanced skills because they are the developmental precursors to understanding and learning formal mathematics (Chard et al., 2005; Griffin & Case, 1997; Geary, 1994; Ginsburg, Klein, & Starkey, 1998; NMAP, 2008; NRC, 2009) and they are underlying prerequisites necessary for the mathematical knowledge children develop in kindergarten as outlined by the Common Core State Standards (CCSS; 2010). As such, it is critical to ensure that children are adequately developing each of the competencies at the appropriate time during their preschool years. Specifically, teachers need reliable measures of each of the key early numeracy skills discussed (e.g., one-to-one counting, numeral comparison).

Existing Targeted Mathematics Measures

Several research groups have begun to address the need for targeted preschool mathematics assessment tools by publishing evidence of the adequacy of a few brief measures of individual preschool mathematics skills (Floyd, Hojnoski, & Key, 2006; Lei, Wu, DiPerna, & Morgan, 2009; Polignano & Hojnoski, 2012; Reid, Morgan, DiPerna, & Lei, 2006; VanDerHeyden, Broussard, & Cooley, 2006; VanDerHeyden, Broussard, Fabre, Stanley, Legendre, & Creppell, 2004). These measures have all demonstrated strong reliability and evidence of validity and can appropriately be used in classrooms and research settings; however, they are limited in their content coverage. For example, VanDerHeyden et al., (2004; 2006) utilized six measures, but only three focused on aspects of numeracy (one-to-one counting, verbal counting, and numeral recognition). The measures constructed by Lei et al., (2009) and Reid et al., (2006) covered the same general domains as well as subitizing. Polignano and Hojnoski (2012) primarily focused on measures of geometry, shapes, and patterns (they did include one measure of cardinality). Additionally, the measures developed by Floyd et al., (2006) were fluency measures rather than performance measures for a specific domain and prior research has indicated that mathematics fluency is distinct from mathematics domain performance (Petrill et al., 2012). As can be seen in Table 1, the existing measures of individual skills are limited and do not cover the entire range skills and concepts children must master during the preschool years.

Other research groups have also developed targeted mathematical knowledge assessments for kindergarten and first grade children (Clarke & Shinn, 2004; Hampton, Lembke, Lee, Pappas, Chiong, & Ginsburg, 2012; Jordan & Glutting, 2012; Jordan, Locuniak, Ramineni, & Kaplan, 2007; Lee, Lembke, Moore, Ginsburg, & Pappas, 2012; Lembke & Foegen, 2009); however, validity of these measures has not been established for younger children. Overall, even though there are a wide range of early mathematics skills children need to develop over the course of preschool, there are few existing measures that can be used to reliably assess each individual aspect of numeracy that has been identified as important during these formative years and have been validated at the preschool ages.

Current Study

Although numerous broad mathematics measures exist and can be used in classroom and research settings, these measures are often time-consuming, costly, and are primarily intended to assess broad mathematics ability. Few brief mathematics assessment tools have been developed that can be used to measure the numerous aspects of early mathematics—particularly for use in preschool. As a result, teachers and researchers are at a significant disadvantage when they wish to identify children’s specific strengths and weaknesses in early mathematics, determine if specific skills have changed through intervention or general instruction, and understand how individual skills and concepts develop. Teachers need quick and valid ways of assessing each numeracy skill so they can plan small-group and individual instruction, as well as measure individual progress over the course of instruction. Thus, the focus of this study was to develop a set of early mathematics assessment tools that are brief, psychometrically valid, easy to administer and could be used to assess the range of early mathematics skills. Item selection for the measure development process occurred through an item response theory (IRT) framework. Reliability was assessed both through IRT standard errors and classical test theory Cronbach’s alphas. Preliminary evidence of validity was assessed both through concurrent and predictive convergent validity methods.

Method

Participants

Two overlapping samples were utilized for this study—the second sample was a large subset of the first sample. Data for Sample 1 were collected in 45 public and private preschools serving children from families with low- to middle-socioeconomic statuses. A convenience sample was used as parental consent forms were sent to parents of all eligible children by the participating schools. Signed consent forms were obtained for each participating child. The 393 children who completed the assessment were about evenly split by sex (51.7% female) and approximately representative of the demographics of the local area (55.7% White, 33.8% African-American, and 10.5% other race/ethnicity). Children ranged in age from 3.13 to 5.98 years (M = 4.75 years, SD = .75 years), were primarily English-speaking, and had no known developmental disorders. Of the participating children, 150 were in their first year of preschool and 243 were in their second year of preschool.

Data for Sample 2 came from 206 of the participants from Sample 1 who also completed the assessments one year later. Of these children 113 were in Kindergarten and 93 were in their second year of preschool. The children were evenly split by sex (51.9% female) and approximately representative of the demographics of the local area (60.2% White, 28.2% African-American, and 11.6% other race/ethnicity). In Year 2, these children ranged in age from 4.05 years to 6.83 years (M = 5.57 years, SD = .75 years). The primary reason for attrition was family mobility. However, the children who completed both testing points were not significantly different on any of the Time 1 mathematics variables than the children who did not complete the Time 2 assessment.

Measures

Early Numeracy Tasks

In the spring of both Year 1 and Year 2, children were assessed on 12 different early numeracy tasks. These tasks were: verbal counting, one-to-one counting, cardinality, counting subsets, set comparison, subitizing, numeral comparison, set comparison, number order, set-to-numerals, story problems, and number combinations. Each task is described in detail in Table 2 and an example of the administration process for the one-to-one counting task is presented in the Appendix. The tasks were developed based on the types of items and skills tested on other common measures of early mathematics assessments (Clements et al., 2008; 2011; Ginsburg & Baroody, 2003; Griffin & Case, 1997; Jordan et al., 2007; Klein et al., 2002; van de Rijt et al., 2003) and those constructs identified in the NCTM Preschool Standards and Focal Points (2006) and NMAP (2008) as central to early mathematical development. Further, these concepts and skills are considered to be the foundation of more advanced mathematical abilities identified as critical for success in elementary school by the CCSS (2010) and the NRC (2009). The initial range of items included on each task was selected to represent as broad of a range of ability as possible, without including more items than would be reasonable to assess with a preschool child. All tasks were designed to be easy to administer by using simple, straightforward instructions and scoring procedures, and minimal use of manipulatives. Other than the testing binder, only one task (counting a subset) required the use of manipulatives. In each task, children received one point for each correct response.

Table 2.

Descriptions of tasks and items for each numeracy skill.

Skill	Description	Sets
One-to-one Counting	Children were presented with a set of dots and asked to count the set.	3, 4, 6, 8, 11, 14, 16, 20
Cardinalitybce	This task was assessed in the context of the structured counting task. At the completion of each one-to-one counting item, children were asked to indicate how many dots there were in all. A correct response indicated that the child understood the last number counted means “how many.” Notably, a correct response was the last number a child counted in the counting sequence regardless of whether or not the counting sequence was correct. For example, if (for a set of 3) a child counted “1, 2, 3” for the one-to-one counting task, the correct cardinality response would be “3.” But, if a child counted “1, 2, 3, 4” for a set of 3, the correct response to the cardinality task would be “4” because it would be a demonstration that the child knew the rule.	3, 4, 6, 8, 11, 14, 16, 20
Count a subsetabcdef	Children were presented with a specific quantity of objects (e.g. 15) and asked to count out a smaller set of objects (e.g. 5) from the larger set. In the second part of this task, children were presented with a set of pictures of both dogs and cars. The child was instructed to count all of one type of picture.	Subset: 3, 4, 8, 16, 20 Category: 3, 4, 8, 16, 20
Subitizingb	Children were briefly presented (2 seconds) with a set of pictures and instructed to say how many dots or pictures were presented.	1–7
Numeral Comparisonbcdef	Children were asked to identify which of four numbers was the biggest or smallest. Half the items were presented visually with Arabic numerals and half the items were presented verbally.	Most: (Visual) 3, 4, 8, 14; (Verbal) 5, 6, 7, 13 Least: (Visual) 1, 2, 3, 6; (Verbal) 1, 3, 4, 5
Set Comparisonabef	Children were presented with four sets of dots representing different quantities. They were asked which set had the most or fewest dots.	Most: 3, 4, 8, 10, 14 Least: 1, 2, 2, 3, 6
Number Orderbcdf	Children were shown a number line with one number missing. They were asked what number comes before or after another number.	Before: 2, 5, 9 15 After: 2, 5, 9, 15
Numeral Identification	Children were presented with flashcards of all numbers from 1–15. They were shown the flashcards one at a time and asked, “What number is this?”	1 – 15
Set-to-numeralsb	On the first three items in this task, children were presented with a numeral at the top of the page and four sets of dots below. They were instructed to identify which of the sets meant the same thing as the number at the top of the page. On the last three items of this task, children were presented with a set of dots at the top of the page and four numerals at the bottom. They were instructed to identify which of the numerals meant the same thing as the set of dots at the top of the page.	Dots to numerals: 1, 3, 5, 7, 8, 12 Numerals to dots: 4, 5, 7, 8, 8, 14
Story Problems	Children were presented verbally with story problems that did not contain distracters (e.g. irrelevant information). These story problems were simple addition or subtraction problems that were appealing to children.	1+0=1; 0+2=2; 1+1=2; 1+2=3; 2+2=4; 1−1=0; 2−1=1; 3−2=1; 3−1=2; 4−1=3;
Number combinations	Children were presented with the problem (e.g., 1 + 1 =) and asked, “How much is…[stated the problem].”	1+1=1; 0+2=2; 1+1=2; 1+2=3; 2+2=4; 1+3=4
Verbal Counting	Children were asked to count as high as possible. When a child -- made a mistake, or correctly counting to 100 without making a mistake, the task was stopped.

Items were similar to an item (or items) from

^athe Early Numeracy Test (van de Rijt, van Luit, & Pennings, 2003),

^bfrom the Research-based Early Math Assessment (Clements, Sarama, & Liu, 2008),

^cthe Child Math Assessment (Starkey, Klein, & Wakeley, 2004),

^dthe Number Sense Core battery (Jordan et al., 2007),

^ethe Test of Early Mathematics Ability – Third Edition (Ginsburg & Baroody, 2003),

^fthe Number Knowledge Test (Griffin & Case, 1997).

Broad Mathematics Tasks

In the spring of Year 2, children were also assessed on the Applied Problems and Calculation subtests of the Woodcock-Johnson III Tests of Achievement. By showing that the individual early numeracy tasks are related to, and predictive of, these broader measures of numeracy, it is possible to assess the criterion validity of the early numeracy measures. These subtests are nationally normed measures of mathematics ability. The Applied Problems subtest is an untimed mathematics test where problems are visually and/or orally presented to the child and has been shown to have a median reliability of .85. The Calculation subtest is a paper and pencil test where children are asked to solve addition and subtraction problems and has a median reliability of .92 (Woodcock et al., 2001). The latter task was included to provide additional evidence of criterion validity using an assessment of a more advanced mathematical skill. Children were awarded one point for each correct answer.

Procedures

Testing Procedure

Assessments were conducted by individuals who either had completed or were working towards completion of a bachelor’s degree. These assessors engaged in two or three two-hour training sessions which were followed up by individual “testing-out” sessions (essentially a simulated testing situation for all tasks) where the first author ensured the testers could demonstrate fluency and accuracy on all assessment measures. Assessments took place in the local schools during non-instructional time in a quiet room designated by the individual preschool directors/teachers. For the early numeracy measures, children were assessed on all items of the tasks. The testing on the Applied Problems and Calculation subtests proceeded according to standard ceiling rules. The total testing time for the measure development process was approximately 60 to 90 minutes per child and was divided into three separate testing sessions typically conducted on different days. Division of testing into more sessions was done as needed.

Analytic Procedure

To construct, refine, and validate the final measures for each task, a three phase process was conducted. Each task was initially comprised of five to 15 items and the goal was to reduce the number of items on each task as much as possible by only retaining the best functioning items. The first two phases were focused on measure development and utilized participant Sample 1. Phase 1 was designed to remove any items that might perform differently (or be biased) towards particularly subgroups. Phase 2 was designed to remove overlapping or poorly-functioning items. Phase 3 was focused on providing initial evidence of concurrent and predictive validity and utilized participant Sample 2. As children’s mathematical ability undergoes rapid and dramatic changes over the preschool years, validity was evaluated for both younger (children who remained in preschool during Year 2) and older (children who were in kindergarten in Year 2) children.

Phase 1 - Differential Item Functioning

In the first phase, items were examined through a differential item functioning (DIF) test to determine if they functioned differently based on sex or race/ethnicity. Items with significant DIF are more likely to be answered correctly by an individual of one subgroup (e.g., boys) with a given latent ability than by an individual of the other subgroup (e.g., girls) with the same latent ability level. Therefore, as these items would not be reasonable to include on an assessment measure targeted for general populations, items found to have significant DIF based on these variables were removed from the measure. To test for DIF based on sex or race, a CFA-with-covariates model was conducted for each task. The CFA-with-covariates model tested whether or not the direct relation between an item and the covariate was mediated by the factor. If the direct relation between the item and the covariate was significant then the item had DIF. Significant DIF was determined by examining modification indices. Modification indices are the improvement in χ² model fit if a parameter is included in the model (e.g., including the relation of the covariate to the item and factor).

Phase 2 - Item reduction

The purpose of the second phase was to reduce the number of items that contributed to each task while maintaining the discriminating ability of each task over the ability continuum. A two-parameter logistic (2-PL) Item Response Theory (IRT) analysis was conducted on each task using Mplus (Muthén & Muthén, 2008a). IRT is a model-based method of latent trait measurement that relates the amount of an individual’s latent ability to the probability of correctly responding to an item (Embretson & Reise, 2000). IRT allows researchers to select items based on item-level characteristics. The item-level characteristics, or parameters, in a 2-PL model that describe item functioning are referred to as the difficulty parameter and the discrimination parameter. The difficulty parameter measures the point along the ability spectrum at which a specific response option would be endorsed 50% of the time for an individual with a given ability. Items with high difficulty parameters require a greater amount of latent ability to be answered correctly; hence, the item is more difficult to answer correctly than an item with a lower difficulty parameter. The discrimination parameter measures how well an item differentiates between individuals with latent abilities above and below the items difficulty parameter.

Within each task, difficulty parameters were compared to identify items that provided overlapping or comparable information. The use of multiple items that provided overlapping information is not desired because it would result in a “double-counting” of one level of item, which could inflate some children’s total scores. For example, if the test had many items with identically low difficulty parameters (i.e., easy items) then the test scores would be inflated artificially at the low end of the scale (e.g., the sum of correct answers to five easy items are not equivalent to the sum of answers on five difficult items or to the sum of answers for five items of varying difficulty). However, if the test were constructed with several items that spanned the range of mathematical ability, none of which overlapped in their information, the test would be a uniform measure of mathematics ability across the range of the latent trait. Identification and removal of similar items would result in a uniform measure of mathematics ability.

If items with overlapping difficulty parameters were identified, the discrimination parameters of those items were compared. In most cases, the item with the highest discrimination parameter was selected for retention and the other items were removed from the measure. However, in some cases, items with slightly lower (but still acceptable) discrimination parameters were selected to provide for a breadth of item type (e.g., addition vs. subtraction in the story problems). After item refinement was complete, both IRT standard error scores and classical test theory (CTT) reliability (Chronbach’s alpha) were calculated for each task. Alpha’s only provide the average reliability for a task, but the IRT standard error provides the reliability of the task across the entire ability continuum. The goal of this item-reduction phase was to reduce the number of total items for each skill while maintaining the ability to assess children over a broad range of latent abilities (i.e. retaining test-level standard error of ideally less than .316 but at least less than .546¹ over the broadest range possible of each latent trait continuum).

A separate methodology was needed to evaluate the scoring procedure for the verbal counting task because it was one item where children were asked to count as high as they could. However, simply using the total score as an indicator of a child’s verbal counting ability is misleading because once children learn the rules of the counting sequence, they are rapidly able to start counting beyond 30. Essentially, the difference in ability needed for a child to advance from being able to count to 40 to being able to count to 50 is much smaller than the difference in ability needed to count to 5 compared to being able to count to 15. To score the verbal counting task on the same metric as the other tasks, it was necessary to determine critical points at which children received credit for correctly counting to that number. To rescore this task, the task was divided into 20 separate items (e.g. correctly counted to 5, correctly counted to 10, etc.). These 20 items were then evaluated in a 1PL IRT model where the discrimination parameters were all held to be equal. A 1PL model was used rather than a 2PL model because only the discrimination parameter was of interest given that all cutoffs were scored within the context of the same item (i.e., a child could not be scored correct on counting to 20 without correctly counting to 15).

Phase 3 – Measure Validation

The final measures, developed from the analyses in Phases 1 and 2, were used in these analyses (only utilizing participant Sample 2). To provide initial evidence of predictive validity for these measures, correlations between each measure at Time 1 and the same measure Time 2 were calculated in addition to correlations between each measure at Time 1 and the two broader mathematics measures at Time 2. In addition, to provide initial evidence of concurrent validity, correlations between each early numeracy measure at Time 2 and the two broader measures at Time 2 were calculated to show that each construct was generally related to the broader construct of numeracy. All measure validation analyses were conducted separately for the younger (children in the second year who remained in preschool) and older (children in the second year who were in kindergarten) children because these skills undergo dramatic changes across the preschool years and it is necessary to support their use across ages.

Results

Phase 1 - Differential Item Functioning

To test for differential item functioning, separate CFA-with-covariate analyses, one for each task, were conducted. Modification indices for the relation between the covariate and the items were examined to determine if model fit would be improved by inclusion of the covariate in the model. The CFA-with-covariates analyses for tasks yielded no significant modification indices (a modification index of 3.84 is considered the minimum value to improve model fit; Muthén & Muthén, 2008b). Inclusion of the covariates in the model did not result in improved model fit for any of the analyses. Therefore, no DIF was detected for any items based on sex or ethnicity and no items were removed in this step of the analyses.

Phase 2 - Item reduction

The percentage of children who answered each item correctly, item-total correlations, discrimination parameters, difficulty parameters for each task, and whether or not each item was retained for the final version of the task are presented in Table 3. There were a total of 110 items across all tasks, plus the verbal counting task. For ease of discussion, the items are labeled 1 to 110 and the description of each item is listed in Table 3. Item reduction procedures for each task are discussed below. The verbal counting task was evaluated and discussed separately.

Table 3.

Psychometric Information for both Retained and Removed Items on Each Task.

	Item Detail	Percent Correct	Item-Total Correlation	Discrimination	Difficulty	Retained
One-to-one Counting
Item 1	Count 4	89	.47	1.91	−1.26	No
Item 2	Count 3	90	.49	2.41	−1.26	Yes
Item 3	Count 16	44	.69	6.50	.11	Yes
Item 4	Count 8	71	.61	1.70	−.63	No
Item 5	Count 6	75	.59	1.75	−.74	Yes
Item 6	Count 20	41	.63	3.29	.19	No
Item 7	Count 11	62	.63	1.64	−.36	Yes
Item 8	Count 14	54	.68	2.27	−.12	Yes
Cardinality
Item 9	How many 4	80	.66	3.72	−.77	No
Item 10	How many 3	83	.64	3.97	−.86	Yes
Item 11	How many 16	60	.72	3.60	−.30	Yes
Item 12	How many 8	72	.73	3.66	−.54	No
Item 13	How many 6	72	.76	3.98	−.53	Yes
Item 14	How many 20	56	.68	2.64	−.22	No
Item 15	How many 11	69	.75	3.34	−.48	No
Item 16	How many 14	60	.69	2.51	−.29	No
Counting a Subset
Give-me-n
Item 17	Count out 4	66	.67	3.11	−.42	Yes
Item 18	Count out 3	74	.62	2.95	−.69	Yes
Item 19	Count out 16	27	.58	1.82	.70	Yes
Item 20	Count out 8	55	.63	1.44	−.14	Yes
Item 21	Count out 20	27	.57	1.65	.72	No
Counting by Category
Item 22	Count 4 cars	88	.45	1.35	−1.51	No
Item 23	Count 3 dogs	89	.43	1.40	−1.53	Yes
Item 24	Count 16 cars	36	.47	1.12	.49	Yes
Item 25	Count 8 dogs	65	.49	.93	−.59	Yes
Item 26	Count 20 cars	25	.41	1.04	.94	Yes
Subitizing
Item 27	Subitize 3	73	.47	1.43	−.78	Yes
Item 28	Subitize 2	86	.44	1.65	−1.22	Yes
Item 29	Subitize 5	40	.36	.67	.48	Yes
Item 30	Subitize 1	92	.44	1.81	−1.59	Yes
Item 31	Subitize 4	59	.47	1.04	−.30	Yes
Item 32	Subitize 7	16	.31	.75	1.69	Yes
Item 33	Subitize 6	21	.39	.91	1.20	Yes
Numeral Comparison
Presented Visually
Item 34	Most – 1, 4, 3, 2	.47	.59	1.72	−.06	Yes
Item 35	Most – 3, 1, 2, 0	.48	.48	1.19	−.05	No
Item 36	Most – 5, 3, 8, 1	.43	.56	2.06	.10	Yes
Item 37	Most – 12, 7, 14, 8	.47	.51	1.37	−.04	No
Item 38	Least – 3, 6, 7, 5	.47	.54	1.66	−.01	No
Item 39	Least – 1, 3, 5, 9	.49	.50	1.83	−.08	No
Item 40	Least – 3, 6, 2, 8	.37	.37	1.15	.32	Yes
Item 41	Least – 9, 7, 6, 12	.30	.40	.96	.60	Yes
Presented Verbally
Item 42	Most – 3, 5, 1, 2	.35	.60	2.15	.20	No
Item 43	Most – 6, 3, 2, 4	.38	.34	1.85	.25	No
Item 44	Most – 5, 2, 7, 1	.37	.60	2.40	.20	Yes
Item 45	Most – 11, 6, 13, 7	.32	.50	1.17	.45	No
Item 46	Least – 1, 4, 9, 6	.35	.56	2.45	.24	No
Item 47	Least – 4, 3, 10,13	.24	.55	2.82	.48	Yes
Item 48	Least – 5, 7, 4, 12	.26	.49	1.46	.46	No
Item 49	Least – 8, 6, 5, 11	.28	.55	2.45	.45	No
Set Comparison
Item 50	Most – 1, 4, 3, 2	.67	.57	2.01	−.54	Yes
Item 51	Most – 3, 1, 2, 0	.71	.57	1.90	−.69	Yes
Item 52	Most – 5, 3, 8, 1	.81	.51	1.88	−.95	Yes
Item 53	Most – 12, 7, 14, 8	.62	.43	.99	−.40	No
Item 54	Most – 3, 7, 10, 1	.66	.47	1.24	−.53	No
Item 55	Least – 3, 6, 7, 5	.56	.58	1.82	−.31	Yes
Item 56	Least – 9, 2, 11, 7	.61	.58	2.23	−.39	Yes
Item 57	Least – 1, 3, 5, 9	.59	.54	1.66	−.35	No
Item 58	Least – 3, 6, 2, 8	.59	.50	1.39	−.27	No
Item 59	Least – 9, 7, 6, 12	.53	.44	.88	−.19	Yes
Number Order
Item 60	Number after 2	.63	.64	1.90	−.32	Yes
Item 61	Number before 2	.63	.77	6.36	−.24	Yes
Item 62	Number after 5	.57	.75	4.08	−.15	Yes
Item 63	Number before 5	.55	.77	3.59	−.08	No
Item 64	Number after 9	.40	.68	2.15	.24	No
Item 65	Number before 9	.45	.77	3.69	.14	Yes
Item 66	Number after 15	.26	.60	2.99	.63	Yes
Item 67	Number before 15	.36	.64	2.25	.33	Yes
Numeral Identification
Item 68	Identify 1	84	.57	1.95	−1.09	Yes
Item 69	Identify 2	77	.70	3.15	−.78	Yes
Item 70	Identify 3	80	.64	2.27	−.92	Yes
Item 71	Identify 4	79	.63	1.87	−.92	No
Item 72	Identify 5	80	.64	2.21	−.93	No
Item 73	Identify 6	61	.51	1.59	−.34	No
Item 74	Identify 7	64	.74	2.21	−.39	Yes
Item 75	Identify 8	67	.68	1.78	−.53	Yes
Item 76	Identify 9	53	.55	2.24	−.08	No
Item 77	Identify 10	57	.78	2.96	−.19	Yes
Item 78	Identify 11	50	.77	2.84	.01	No
Item 79	Identify 12	33	.63	1.95	.48	Yes
Item 80	Identify 13	34	.66	2.19	.45	No
Item 81	Identify 14	45	.72	2.46	.13	Yes
Item 82	Identify 15	37	.49	2.47	.37	Yes
Set-to-numerals
Item 83	Match sets of dots to the numeral 5	68	.63	2.18	−.50	No
Item 84	Match sets of dots to the numeral 3	69	.44	2.35	−.56	Yes
Item 85	Match sets of dots to the numeral 1	81	.55	2.09	−.89	Yes
Item 86	Match sets of dots to the numeral 12	68	.48	1.35	−.58	No
Item 87	Match sets of dots to the numeral 8	44	.44	1.12	.23	No
Item 88	Match sets of dots to the numeral 7	39	.57	1.57	.20	Yes
Item 89	Match numerals to a set of 5 dots	59	.38	1.82	−.37	Yes
Item 90	Match numerals to a set of 3 dots	70	.71	9.98	−.52	No
Item 91	Match numerals to a set of 8 dots	51	.54	2.08	−.14	Yes
Item 92	Match numerals to a set of 14 dots	69	.64	2.66	−.55	No
Item 93	Match numerals to a set of 8 dots	45	.50	1.69	.04	Yes
Item 94	Match numerals to a set of 7 dots	37	.52	1.47	.21	No
Story Problems
Item 95	1+0=1	55	.22	.44	−.33	No
Item 96	0+2=2	66	.39	1.00	−.59	Yes
Item 97	1+1=2	49	.49	1.00	.00	Yes
Item 98	1+2=3	39	.45	1.32	.28	No
Item 99	2+2=4	31	.47	1.14	.54	Yes
Item 100	1−1=0	38	.52	1.41	.27	Yes
Item 101	2−1=1	54	.43	1.09	−.13	Yes
Item 102	3−2=1	56	.41	.91	−.28	Yes
Item 103	3−1=2	45	.40	.91	.06	No
Item 104	4−1=3	32	.36	.99	.63	Yes
Number Combinations
Item 105	1+0=1	33	.31	.94	.56	No
Item 106	0+2=2	32	.38	1.26	.56	Yes
Item 107	1+1=2	30	.58	1.86	.60	Yes
Item 108	1+2=3	28	.57	2.15	.66	Yes
Item 109	2+2=4	22	.59	2.99	.77	Yes
Item 110	1+3=4	18	.57	2.16	.94	Yes

One-to-one counting

Items 1 and 2 had identical item difficulty parameters (b = −1.26). Item 1 was removed because Item 2 had a higher discrimination parameter (a = 2.41 vs. 1.91). Items 3 and 6 had similar item difficulty parameters (b = .11 and .19). However, Item 3 had a much higher discrimination parameter than did Item 6 (a = 6.50 vs. 3.29). Thus, Item 6 was removed from the final measure. Items 4 and 5 also had comparable difficulty parameters (b = −.63 and −.74). Item 5 had a marginally higher discrimination parameter than Item 4 (a = 1.75 vs. 1.70), and thus, Item 4 was removed from the final measure. All other items had unique difficulty parameters and thus were retained for the final measure. The items retained for this task were Items 2, 3, 5, 7, and 8. The final one-to-one counting task had an acceptable internal consistency (α = .79). This task had a standard error of less than .316 from the theta value of −.20 to .30 and a standard error of less than .548 from the theta values of −1.60 to .50.

Cardinality

This task was tied directly to the one-to-one counting task. Thus, the ideal items for this task should not only have a broad range of difficulty parameters but were included on the final one-to-one counting task. Overall, this task was fairly easy (i.e., more than 50% of children answered the hardest question correctly) and the range of difficulty was very restricted (b = −.86 to −.22). Items 9 and 10 both had comparable difficulty parameters (b = −.77 and −.86), but Item 10 had a higher discrimination parameter (a = 3.97). Item 9 was removed from the final measure. Items 11, 14, and 16 had comparable difficulty parameters (b = −.30, −.22, and −.29, respectively); however, Item 11 had the highest discrimination parameter (a = 3.60). Items 14 and 16 were removed from the final measure. Lastly, items 12, 13, and 15 all had similar difficulty parameters (b = −.54, −.53, and −.48, respectively), but Item 13 had the highest discrimination parameter (a = 3.98). Items 12 and 15 were removed from the final measure. Only three items were retained, Items 9, 11, and 13. All three of these items were also included on the structured counting task. The final cardinality task had an acceptable internal consistency (α = .75). This task had a standard error of less than .316 from the theta value of −1.00 to −.10 and a standard error of less than .548 from the theta values of −1.20 to .10.

Counting a subset

Items 19 and 21 had nearly identical difficulty parameters (b = .70 and .72), but Item 19 had a higher discrimination parameter (a = 1.82). Item 21 was removed from the final measure. Items 22 and 23 also had nearly identical difficulty parameters (b = −1.51 and −1.53), but Item 23 had a higher discrimination parameter (a = 1.40). Item 22 was removed from the final measure. All other items had unique difficulty parameters. Thus, Items 17, 18, 19, 20, 23, 24, 25, and 26 were retained for the final measure. The final counting a subset task had good internal consistency (α = .82). This task had a standard error of less than .316 from the theta value of −.90 to −.20 and a standard error of less than .548 from the theta values of −1.30 to 1.10.

Subitizing

No subitizing items had overlapping difficulty scores. All items were retained for the final measure. This task had a marginally acceptable internal consistency (α = .69). This task did not have a standard error of less than .316 at any theta value, but had a standard error of less than .548 from a theta of −1.90 to −.40.

Numeral comparison

Items 34, 35, 37, 38, and 39 all had comparable difficulty parameters (b = −.06, −.05, −.04, and −.01, respectively). All of these items, except Item 39, were “most” items. Item 39 was a “least” item. Although Item 39 (a = 1.83) had a slightly higher discrimination parameter than Item 34 (a = 1.72), Item 34 was retained so that there would be a balanced number of “most” and “least” questions. Items 35, 37, 38, and 39 were removed from the final measure. Items 42, 43, 44, and 46 all had comparable difficulty parameters (b = .20, .25, .20, and .24, respectively), but Item 44 had the highest discrimination parameter (a = 2.40). Items 42, 43, and 46 were removed from the final measure. Items 45, 47, 48, and 49 all had comparable difficulty parameters (b = .45, .48, .46, and .45, respectively), but Item 47 had the highest discrimination parameter (a = 2.82). Items 45, 48, and 49 were removed from the final measure. All other items had unique difficulty parameters and were retained for the final measure. The final number comparison task consisted of Items 34, 36, 40, 41, 44, and 47 and the task had an acceptable internal consistency (α = .74). This task had a standard error of less than .316 from the theta value of −.10 to .70 and a standard error of less than .548 from thetas of −.60 to 1.00.

Set comparison

The set comparison task was a relatively easy task because most items were answered correctly by more than 50% of the children. Items 50 and 54 had comparable difficulty parameters (b = −.54 and −.53), but Item 50 had a higher discrimination parameter (a = 2.01). Item 54 was removed from the final measure. Items 53 and 56 had comparable difficulty parameters (b = −.40 and −.39), but Item 56 had a higher discrimination parameter (a = 2.23). Item 53 was removed from the final measure. Items 55, 57, and 58 had similar difficulty parameters (b = −.31, −.35, and −.27, respectively), but Item 55 had the highest discrimination parameter (a = 1.82). Items 57 and 58 were removed from the final measure. All other items had unique difficulty parameters and were retained for the final measure. The final set comparison task consisted of Items 50, 51, 52, 55, 56, and 59 and the task had an acceptable internal consistency (α = .77). This task had a standard error of less than .316 from the theta value of −.90 to −.25 and a standard error of less than .548 from the theta values of −1.40 to .30.

Number order

Items 62 and 63 had comparable difficulty parameters (b = −.15 and −.08), but Item 62 had a higher discrimination parameter (a = 4.08). Item 63 was removed from the final measure. Items 64 and 67 also had comparable difficulty parameters (b = .24 and .33); however, Item 67 had a higher discrimination parameter (a = 2.25). Item 64 was removed from the final measure. All other items had unique difficulty parameters and were retained for the final measure. The final version of the number order task consisted of Items 60, 61, 62, 65, 66, and 67 and the task had a good internal consistency (α = .87). This task had a standard error of less than .316 from the theta value of −.55 to .70 and a standard error of less than .548 from the theta values of −.70 to 1.00.

Numeral identification

Items 70, 71, and 72 had identical difficulty parameters (b = −.92, −.92, and −.93, respectively), but Item 70 had the highest discrimination parameter (a = 2.27). Items 71 and 72 were removed from the final measure. Items 73 and 74 had very similar difficulty parameters (b = −.34 and −.39), but Item 74 had a higher discrimination parameter (a = 2.21). Item 73 was removed from the final measure. Items 76 and 77 had comparable difficulty parameters (b = −.08 and −.19), but Item 77 had the higher discrimination parameter (a = 2.96). Item 76 was removed from the final measure. Items 78 and 81 had comparable difficulty parameters (b = .01 and .13). Although Item 78 had the higher discrimination parameter (a = 2.84), Item 81 was retained because it fit better in the range of difficulty parameters. Items 79 and 80 had comparable difficulty parameters (b = .48 and .45). Even though Item 80 had a higher discrimination parameter (a = 2.19), Item 79 (a = 1.95) was retained to maximize the range of measurement because it had a slightly higher difficulty parameter. All other items had unique difficulty parameters and were retained for the final measure. The final number identification task consisted of Items 68, 49, 70, 74, 75, 77, 79, 81, and 82 and the task had a high internal consistency (α = .90). This task had a standard error of less than .316 from the theta value of −1.20 to .60 and a standard error of less than .548 from the theta values of −1.50 to .90.

Set-to-Numerals

Items 83, 84, 86, 90, and 92 had comparable difficulty parameters (b = −.50, −.56, −.58, −.52, and −.55, respectively). Even though Item 92 had the highest discrimination parameter (a = 2.66), Item 84 was selected because it also had a high discrimination parameter and balanced out the types of items in the final task (Item 84 was one of the first types of items – match number to one of the sets). Items 83, 86, 90, and 92 were removed from the final measure. Items 87, 88, and 94 had comparable difficulty parameters (b = .23, .20, and .21, respectively), but Item 88 had the highest discrimination parameter (a = 1.57). Items 87 and 88 were removed from the final measure. All other items had unique difficulty parameters and were retained for the final measure. The final numerals task consisted of Items 84, 85, 88, 89, 91, and 93 and the task had a good internal consistency (α = .80). This task had a standard error of less than .316 from the thetas of −.80 to .00 and standard error of less than .548 from thetas of −1.30 to .60.

Story Problems

Items 95 and 102 had comparable difficulty parameters (b = −.33 and −.28), but Item 102 had a much higher discrimination parameter (a = .91). Item 95 was removed from the final measure. Items 97 and 103 had comparable difficulty parameters (b = .00 and .06), but Item 97 had a higher discrimination parameter (a = 1.00). Item 103 was removed from the final measure. Items 98 and 100 had nearly identical difficulty parameters (b = .28 and .27), but Item 100 had a much higher discrimination parameter (a = 1.41). Item 98 was removed from the final measure. All other items had unique difficulty parameters and were retained for the final measure. The final task consisted of Items 96, 97, 99, 100, 101, 102, and 104 and the task had an acceptable internal consistency (α = .71). This task did not have a standard error of less than .316 at any theta value, but had a standard error of less than .548 from the theta values of −.70 to .90.

Number combinations

Items 105 and 106 had identical difficulty parameters (b = .56), but Item 106 had a higher discrimination parameter (a = 1.26). Item 105 was removed from the final version of this task. All other items had unique difficulty parameters and were retained for the final measure. The final task consisted of Items 10, 107, 108, 109, and 110 and had an acceptable internal consistency (α = .77). This task had a standard error of less than .316 from the theta value of .35 to 1.15 and a standard error of less than .548 from the thetas of .00 to 1.50.

Verbal counting

The results of the 1PL IRT analysis are presented in Table 4. Scoring cutoffs were selected so that no cutoffs had overlapping or similar difficulty parameters. The final verbal counting task score was computed in the following manner; one point each for correctly counting to 5, 10, 15, 20, 25, 40, and 100.

Table 4.

Percent correct, difficulty parameters, and whether or not the item was retained on the final measure for the Verbal Counting task

	Percent Correct	Difficulty	Retained
Count to 5	95	−1.64	Yes
Count to 10	85	−1.04	Yes
Count to 15	58	−.21	Yes
Count to 20	46	.09	Yes
Count to 25	41	.24	Yes
Count to 30	30	.51	No
Count to 35	27	.63	No
Count to 40	17	.94	Yes
Count to 45	15	1.03	No
Count to 50	12	1.18	No
Count to 55	12	1.19	No
Count to 60	11	1.24	No
Count to 65	10	1.26	No
Count to 70	10	1.27	No
Count to 75	10	1.27	No
Count to 80	9	1.36	No
Count to 85	9	1.36	No
Count to 90	8	1.41	No
Count to 95	8	1.41	No
Count to 100	7	1.51	Yes

Note. N = 393.

Summary of Measure Development

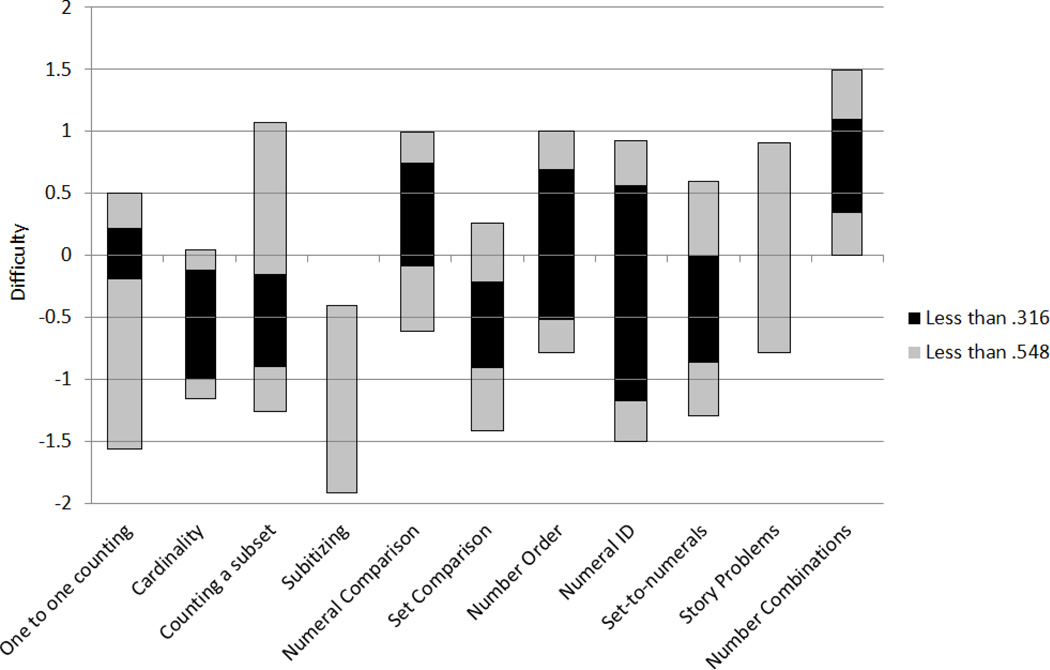
As a result of the item refinement process, all tasks were reduced to between 3 and 9 items. Children’s performance on the tasks was normally distributed with no significant skew or kurtosis (see Table 5 for final task means, standard deviations, skew, kurtosis, and alphas). All tasks had acceptable CTT reliabilities, but different tasks appeared to have better IRT standard errors at different points on the ability continuum (see Figure 1). A summary of the results of the item reduction procedure is also presented in Table 5. Additionally, all tasks were moderately correlated with one another (see Table 6).

Table 5.

Summary of Item Reduction Process and Descriptive Statistics for Final Numeracy Tasks

Task	Initial Number of Items	Final Number of Items	Mean	SD	Rangea	Skew	Kurtosis	Alpha	Theta Range of SE < .548	Theta Range of SE < .316
Verbal Counting	1	1	3.03	1.54	0 – 7	.07	−.65	--	--	--
One-to-one Counting	8	5	3.25	1.65	0 – 5	−.47	−1.05	.79	−1.60 to 0.50	−0.20 to 0.30
Cardinality	8	3	2.16	1.08	0 – 3	−.93	−.57	.75	−1.20 to 0.10	−1.00 to −0.10
Counting a subset	10	8	4.31	2.40	0 – 8	−.18	−.11	.82	−1.30 to 1.10	−0.90 to −0.20
Subitizing	7	7	3.85	1.71	0 – 7	−.22	−.18	.69	−1.90 to −0.40	--
Numeral Comparison	16	6	2.19	1.88	0 – 6	.53	−.86	.74	−0.60 to 1.00	−0.10 to 0.70
Set Comparison	10	6	3.89	1.91	0 – 6	−.41	−1.08	.77	−1.40 to 0.30	−0.90 to −0.25
Number Order	8	6	2.87	2.26	0 – 6	.03	−1.48	.87	−0.70 to 1.00	−0.55 to 0.70
Numeral Identification	15	9	5.45	3.08	0 – 9	−.41	−1.16	.90	−1.20 to 0.60	−1.50 to 0.90
Set-to-Numerals	12	6	3.45	2.00	0 – 5	−.26	−1.22	.80	−1.30 to 0.60	−0.80 to 0.00
Story Problems	10	7	3.28	2.04	0 – 7	.15	−1.01	.71	−0.70 to 0.90	--
Number Combinations	6	5	1.29	1.57	0 – 5	1.12	.10	.77	0.00 to 1.50	0.35 to 1.15

Note. Reliability scores for the Verbal Counting task is not included in this summary as it is technically only one item where cutoff criteria for scoring were identified.

^aThe range indicates both the total possible and actual range of children’s performance

Figure 1.

The difficulty range for which each task has standard errors below .316 (equivalent to a classical test theory reliability of .90) and .548 (equivalent to a classical test theory reliability of .70).

Table 6.

Correlations between the final versions of each early numeracy task

	1	2	3	4	5	6	7	8	9	10	11	12
1. Verbal Counting	-
2. One-to-one Counting	.69	-
3. Cardinality	.62	.76	-
4. Counting a Subset	.73	.76	.68	-
5. Subitizing	.52	.57	.49	.63	-
6. Numeral Comparison	.50	.47	.41	.58	.45	-
7. Set Comparison	.52	.56	.48	.64	.46	.63	-
8. Number Order	.64	.64	.58	.72	.53	.58	.64	-
9. Numeral Identification	.63	.66	.60	.70	.50	.51	.58	.70	-
10. Set-to-Numerals	.58	.63	.57	.67	.54	.56	.62	.72	.69	-
11. Story Problems	.53	.51	.48	.65	.53	.59	.63	.65	.54	.55	-
12. Number Combinations	.36	.31	.30	.39	.32	.44	.38	.44	.38	.36	.44	-

Note. N = 393. All correlations were significant at p < .01.

Preliminary Evidence of Concurrent and Predictive Validity

As seen in Table 7, with few exceptions, all tasks were significantly correlated with the same tasks given a year later. Further, the individual measures generally were related to two broad mathematics tasks (the Woodcock-Johnson III Applied Problems and Calculation tasks) given a year later suggesting that the individual measures were also measuring part of the broader construct. Only the Cardinality task was not a significant predictor of itself a year later for the younger children. This is likely due to the restricted range of the task (it only had 3 items). Nevertheless, it was one of the strongest predictors of the Applied Problems subtest a year later. The Number Combinations task was a marginally significant predictor of itself a year later in the sample of younger children. For the older children, the Cardinality task at Time 1 was only marginally significantly related to itself a year later. Once again, this was likely due to the restricted range of the task. Additionally, when assessed concurrently at Time 2, with only one exception (the correlation between the Cardinality task and the WJ-Calc task for younger children), all tasks were significantly related.

Table 7.

Correlations between the individual tasks at Time 1 and Time 2, and between the individual tasks at Time 1 and Time 2 with two broad mathematics measures at Time 2

	Time 1 tasks with			Time 2 tasks with
Task	Time 2	WJ AP	WJ CALC	WJ AP	WJ CALC
Younger Children
Verbal Counting	.48***	.43***	.37***	.49***	.29**
One-to-one Counting	.45***	.54***	.34**	.46***	.28**
Cardinality	.15	.66***	.38***	.38***	.15
Counting a Subset	.66***	.58***	.41***	.69***	.42***
Subitizing	.22*	.47***	.22*	.47***	.37***
Numeral Comparison	.44***	.41***	.32***	.55***	.41***
Set Comparison	.44***	.55***	.42***	.61***	.35**
Number Order	.41***	.40***	.31**	.70***	.49***
Numeral Identification	.72***	.55***	.33**	.60***	.32**
Set-to-Numerals	.39***	.54***	.37***	.58***	.25*
Story Problems	.51***	.46***	.40***	.58***	.40***
Number Combinations	.17+	.35***	.33**	.52***	.47***
Older Children
Verbal Counting	.43***	.48***	.34***	.55***	.41***
One-to-one Counting	.30**	.58***	.36***	.45***	.29**
Cardinality	.16+	.49***	.36***	.20*	.20*
Counting a Subset	.35***	.66***	.44***	.50***	.29**
Subitizing	.30**	.44***	.32***	.41***	.27**
Numeral Comparison	.41***	.50***	.44***	.63***	.46***
Set Comparison	.31**	.50***	.39***	.43***	.36***
Number Order	.40***	.59***	.46***	.55***	.43***
Numeral Identification	.44***	.58***	.50***	.49***	.37***
Set-to-Numerals	.32**	.53***	.33***	.42***	.24*
Story Problems	.37***	.61***	.55***	.54***	.53***
Number Combinations	.31**	.35***	.33***	.55***	.54***

Note. N Younger Children (those still in preschool in Year 2) = 93; N Older Children (those in Kindergarten in Year 2) = 113. Time 1 Task = Individual task measured in Spring of Year 1; Time 2 Task = Individual task measured in Spring of Year 2; WJ AP = Woodcock-Johnson III Applied Problems at Time 2; WJ CALC = Woodcock-Johnson III Calculation at Time 2.

^***p < .001,

^**p < .01,

^*p < .05,

⁺p < .10

Discussion

Through the measure development process in this study, 12 early numeracy skills were constructed and evidence of reliability and preliminary evidence of validity were established. These measures were designed to assess the foundational numeracy skills identified by the NCTM Standards and Focal Points (2006), the NMAP (2008), and NRC (2009) as critically important for young children’s mathematical development. The content of the measures also covers the developmental precursors of mathematical knowledge that children are expected to acquire in kindergarten, as indicated by the CCSS (2010). The final measures are brief, easy to administer, and psychometrically sound. Utilizing item response theory analyses for item selection allowed for overlapping and uninformative items to be removed from the measures, resulting in tasks that uniformly assessed the broadest possible ability range for each target skill. As a result of removing unnecessary items, each measure takes less than five minutes to administer and most take less than two or three minutes to administer. The tasks were shown to be reliable across a range of ability—albeit, the range varies by task as some tasks target more basic skills than other tasks. In addition, children’s performance on each measure during the first year of the study (with a few notable exceptions discussed later) was significantly related to performance on the same measure and broader measures of mathematics, a year later.

A wealth of evidence has supported the need for the development and implementation of RtI systems in preschool and elementary school (Fuchs & Fuchs, 2006; Jimerson, Burns, & VanDerHeyden, 2007; Vellutino et al., 2006). Yet, there is still a need to develop an RtI system for early mathematics (Lembke et al., 2012). The findings from this study address the critical first step—assessment development—in what needs to be a sustained effort to meet that purpose. Effective risk status identification and evaluation of instruction effectiveness are dependent on having appropriate assessment tools. Existing assessment tools were either broad measures designed for the assessment of general mathematics performance or targeted measures on only a limited selection of skills. The measures constructed in this study address the full range of individual skills listed in Table 1. Importantly these assessment tools have practical applications for both practitioners and researchers that can lead to important educational advances.

Practical Applications of the Measures

Classroom

As teachers have little time available in their day to focus on non-instructional components (Darling-Hammond, 2000)—particularly for learning to administer and utilizing new assessment tools—the brevity and ease of use of these measures makes them ideally suited for classroom instructional settings. Not only are these measures quick to administer, limited time would need to be spent learning to utilize these measures as they have straightforward instructions (e.g., “Count these dots” or “Which set has the most dots”) and easy to apply scoring rules (e.g., one point for each correct response). Importantly, it is not intended that a teacher would utilize all 12 assessment tasks at the same time for an individual child. They are intended to be utilized selectively when a child is developmentally ready for a specific concept or skill and to align with the general instructional goals of a classroom (or individualized instruction). For example, the number combinations measure is not intended to be utilized for a child who has very low overall mathematics skills. As children develop these individual competencies—or when they should be developing these competencies—teachers can utilize these specific tasks to measure progress, rather than simply using a broad measure that is time consuming and only provides an overall mathematics score.

Critically, there are two key related practical applications that these measures have for teachers in preschool classrooms: (a) identifying the specific areas in which a child needs further instruction and (b) to assess the effectiveness of targeted instructional efforts. As the measures were designed to assess children’s competencies in individual early mathematics skills, they can be used by teachers to individualize instruction through the identification of which specific aspects of mathematical knowledge a child needs remedial effort. Teachers could select a few tasks that align with instructional goals (or necessary precursors for the instructional goals) and assess their students to identify which children need more targeted instruction in that specific domain and which are ready for more advanced instruction. That knowledge can provide teachers with a guide for instruction and a mechanism to evaluate the effectiveness of that instruction. Similarly, a teacher could utilize the tasks in a more targeted manner to identify an area of deficit for an individual child. For example, if a teacher is concerned that an individual child is struggling with his or her counting skills, the teacher can utilize the select counting measures (verbal counting sequence, one-to-one counting, cardinal number knowledge, and counting a subset) to identify the specific aspects of counting a child has mastered and in which area a child needs further instruction. After instruction (or throughout the instructional process), the teacher can re-administer the tasks to assess a child’s progress.

Research

Beyond the classroom setting, these brief measures also have two key practical applications in research settings that apply to the development of an early mathematics RtI system: (a) improving curriculum effectiveness and (b) assessing the effectiveness of newly developed targeted interventions. Significant efforts have been undertaken to develop effective and empirically-supported preschool mathematics curricula (Clements & Sarama, 2008; Greenes, Ginsburg, & Balfanz, 2004; Klein, Starkey, Sarama, Clements, & Iyer, 2008; Starkey, Klein, & Wakeley, 2004). These curricula have generally been found to be effective at the broad level and even though these curricula are designed to improve early mathematics skills as a whole, they typically do this through targeted sequencing of instruction on individual components of early mathematics (Clements & Sarama, 2008; Starkey, Klein, & Wakeley, 2004). Unfortunately, through broad assessments, it is not possible to determine if the curricula are effective for all components of instruction. As researchers work to further refine these curricula and enhance the effects of instruction, it is necessary to identify which components of the curricula are effective and, potentially more importantly, which aspects of the curricula may need further refinement. These brief measures could be used to assess the effectiveness of components of these curricula and identify areas in which further refinement is needed. Similarly, as researchers design individual and small group interventions for targeted mathematics constructs, they need proximal assessment tools that can be used to accurately assess the effectiveness of those targeted interventions. These brief measures can serve as tools for such evaluations.

Age-based Analyses of the Measures

Although the majority of the developed tasks exhibited strong predictive relations with the same task administered one year later, there were two tasks that functioned differently than expected. The first task, the cardinality task, was not significantly correlated across time in either age group—even though for the younger children, the cardinality task, administered at Time 1, was the strongest predictor of the Applied Problems subtest administered at Time 2, and one of the strongest predictors of the Calculation task administered at Time 2. The low correlation is likely because of a restriction in the range of measurement on this task. The final cardinality task was constructed of only three items, all of which were easier items (based on difficulty parameter) and clustered in the same general difficulty range (between the three items there was, at most, a difference of .56). Such close difficulty parameters indicate that, rather than cardinality being a skill that spans a broad range of ability and children develop greater mastery over time, it is more likely a critical concept, that once grasped, the child can exhibit proficiency in regardless of the set size. For example, once a child learns the rule that the last number said in the counting sequence means “how many?” he or she can apply that rule to all counting items. Furthermore, this is a skill that rapidly develops around 4-years of age and can be generalized easily to larger quantities (Sarama & Clements, 2009). Thus, it is reasonable to expect that early performance would be highly related to broader ability because it is a critical skill in mathematical development, but that performance across this age range would not be related as children score at the ceiling on the task.

The second task that did not function ideally with younger children was the number combinations task. Not surprisingly, the year-to-year correlation for the measure was significant in the sample of older children. However, the task was only marginally correlated to the same task a year later in the sample of younger children. This low correlation was likely due to young children’s limited proficiency with this skill. The number combinations task is a relatively difficult task (all items on the task had difficulty parameters greater than .50) and children typically do not receive any formal instruction on this skill until school entry. Although there was only a marginally significant year-to-year correlation on the number combinations task for the younger sample, the correlations between Time 1 number combinations and Time 2 broader measures of mathematics, were significant. This relation suggests that, although the younger children often had limited proficiency on the task, those children who did demonstrate facility with number combinations when they were younger, went on to exhibit higher ability in overall mathematics performance. The remaining measures were all significantly correlated with themselves across time and with the broader measures of mathematics.

One of the key benefits of utilizing item response theory in the development of these measures is that the resulting IRT standard error measurement is not sample dependent (Embretson & Reise, 2000)—meaning that the reliability of these measures is not based on age, but rather ability level. The intentional selection of a broad range of non-overlapping items for each concept/skill resulted in a wide ability range for which each task had acceptable reliability. As noted earlier, it would be inappropriate to utilize the number combinations task with a child who has very low numeracy skills because any correct answers are likely to be due to chance. However, when a child is developmentally ready (regardless of age), the task is a reliable measure of basic addition skills. The use of each task needs to be done in a judicious manner when a child has acquired the necessary prerequisite skills and to align with instructional needs.

Limitations

Although the tasks were psychometrically strong and good predictors of later mathematics, several limitations should be noted. First, although no DIF was identified for either sex or race/ethnicity, other variables not measured in this study could result in DIF. One possibility is family socio-economic-status (SES). DIF could not be calculated for family SES in this study, however, because family demographic information was not collected. In future studies, SES-related DIF should be examined. Second, further evidence of validity across ages and within different subpopulations is needed. Third, the utility of the measures for being sensitive to change cannot be ascertained from the current study. One-year correlations for each task were generally strong, but short-term test-retest reliability needs to be conducted. Given the high correlations across a full year for each task, it is highly likely that shorter test-retest reliabilities will be equivalent or higher. Additionally, future work utilizing these measures to demonstrate growth over time in each domain needs to be conducted as well as analyses evaluating the developmental relations across each of the tasks. Finally, these measures cover a relatively broad range of numeracy domains that have been identified as key skills and concepts in preschool; however, there is still a need to construct and validate measures for other early mathematical domains such as geometry and patterns. Although geometry has been noted to be a critical, but often overlooked aspect of early mathematics skills (Clements & Sarama, 2011b), it has also been found to be a domain distinct from numeracy skill in preschool (Wolfe, Clements, & Sarama, 2011). The construction of geometry measures was not included in this study primarily for practical issues—namely, including assessing children on additional geometry components would have taken a significant amount of extra time and the initial measure development process already took 60 to 90 minutes per child. Subsequent work is needed to develop individual geometry measures.

Conclusions

Overall, the development of these measures provides a platform from which to build future research in early mathematics development—particularly regarding building the framework and capacity for validating an RtI system for preschool. These measures can serve to fill the need for targeted progress monitoring tools in that system. These brief measures also provide mechanisms for evaluating the effectiveness of classroom curricula and of targeted interventions. As they are brief, reliable, and easy to administer, they are ideally suited for both research and classroom purposes.

Appendix

Example process for administering the one-to-one counting task.

Materials: Testing flip-book, pen/pencil, and scoring form.

Instructions:

1. Tester brings child to testing area and says to the child, “We’re going to play a counting game. Let’s count some dots!”

2. The tester turns to the first page of the one-to-one counting task (see image below for example) and the child is presented with a series of dots in the testing material and the tester says, “Count these dots, point to each one as you count.” As the tester gives this instruction s/he runs finger across the row of dots.

   

3. If the child correctly counts the set of dots, they receive one point. If they do not count correctly (skip a dot, skip a number, double count a dot, double count a number, etc.) they receive zero points.

4. Testing continues in a similar fashion until all five items are completed.

5. After items all items have been completed, the tester either returns child to classroom or continues on with another task.

Note. All tasks follow similar general procedures with task specific directions. Copies of the test materials can be requested from Author at xxxx@xxxx.edu.