MULTI-MODAL DATA FUSION SCHEMES FOR INTEGRATED CLASSIFICATION OF IMAGING AND NON-IMAGING BIOMEDICAL DATA

Abstract

With a wide array of multi-modal, multi-protocol, and multi-scale biomedical data available for disease diagnosis and prognosis, there is a need for quantitative tools to combine such varied channels of information, especially imaging and non-imaging data (e.g. spectroscopy, proteomics). The major problem in such quantitative data integration lies in reconciling the large spread in the range of dimensionalities and scales across the different modalities. The primary goal of quantitative data integration is to build combined meta-classifiers; however these efforts are thwarted by challenges in (1) homogeneous representation of the data channels, (2) fusing the attributes to construct an integrated feature vector, and (3) the choice of learning strategy for training the integrated classifier. In this paper, we seek to (a) define the characteristics that guide the 4 independent methods for quantitative data fusion that use the idea of a meta-space for building integrated multi-modal, multi-scale meta-classifiers, and (b) attempt to understand the key components which allowed each method to succeed. These methods include (1) Generalized Embedding Concatenation (GEC), (2) Consensus Embedding (CE), (3) Semi-Supervised Multi-Kernel Graph Embedding (SeSMiK), and (4) Boosted Embedding Combination (BEC). In order to evaluate the optimal scheme for fusing imaging and non-imaging data, we compared these 4 schemes for the problems of combining (a) multi-parametric MRI with spectroscopy for prostate cancer (CaP) diagnosis in vivo, and (b) histological image with proteomic signatures (obtained via mass spectrometry) for predicting prognosis in CaP patients. The kernel combination approach (SeSMiK) marginally outperformed the embedding combination schemes. Additionally, intelligent weighting of the data channels (based on their relative importance) appeared to outperform unweighted strategies. All 4 strategies easily outperformed a naïve decision fusion approach, suggesting that data integration methods will play an important role in the rapidly emerging field of integrated diagnostics and personalized healthcare.

1. INTRODUCTION

A major challenge to overcome when quantitatively integrating heterogeneous data types (which may not be directly combined) lies in the significant differences in dimensionality and scale that exist between disparate modalities, especially imaging and non-imaging modalities. Most existing work on multi-modal data integration is targeted towards purely homogeneous image-based data (which may be directly combined), such as for the fusion of Computed Tomography (CT) and Magnetic Resonance Imaging (MRI) [1] or fusing different MRI protocols for disease characterization [2]. Combination of Interpretation (COI) [3] strategies aim to combine independent classifications made based on each modality; however, such a combination may prove sub-optimal as inter-modality dependencies are not accounted for.

A major limitation in constructing integrated meta-classifiers for imaging and non-imaging data streams is having to deal with different data representations (differing in both scale and dimensionality). A possible solution to overcome these representational differences is to first project the data streams into a space where the scale and dimensionality differences are removed; we refer to this space as a meta-space. For example, proteomics and imaging data (Figure 1) could be homogeneously represented in the format of eigenvectors in a PCA reduced meta-space [3]. A second challenge in constructing meta-classifiers from imaging and non-imaging data is to weight the relative contributions of the different channels. While one could naïvely concatenate the original (or meta-space) based representations to construct a fused attribute vector, learning strategies could be leveraged to optimally weight and then combine the individual data streams.

Fig. 1.

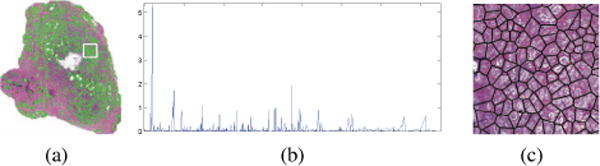
Sample image and non-image data, (a) prostate tissue specimen with a region-of-interest (ROI) outlined in white, (b) proteomic spectra associated with this ROI, (c) quantification of the image ROI with nuclear arrangement features. Note the significant differences in dimensionality (1000s of proteomic spectra vs 100s of histology features) preventing direct combination of such heterogeneous data.

The third challenge is to build a predictor based off the multi-attribute vector, following meta-space fusion. The predictor (meta-classifier) could be trained by a range of supervised, unsupervised, or semi-supervised learning strategies; the choice of training strategy usually being a function of the amount of labeled, annotated data available.

Recently, our group [3–6] and a few others [7, 8] have begun to develop multi-modal data fusion strategies with the express purpose of building such integrated meta-classifiers. In [3], Lee et al proposed the Generalized Fusion Framework (GFF) for homogeneous data representation and subsequent fusion in the meta-space using dimensionality reduction techniques. Alternatively, multi-kernel learning (MKL) schemes [7] have also been proposed where the meta-space representation is decided by choice of kernel.

The goal of this paper is twofold. Firstly we aim to describe some of the challenges in meta-space representation, fusion, and meta-classifier construction in the context of imaging and non-imaging data (Section 2). The second objective is to describe and compare 4 state of the art embedding and kernel combination-based data integration schemes and quantitatively evaluate their performance in the context of two important diagnostic and prognostic applications. In the first application, we evaluate the 4 schemes in their ability to combine multi-parametric MRI and MR spectroscopy data for prostate cancer diagnosis in vivo. The second problem is focused on quantitative fusion of imaging and proteomic signatures obtained from the tumor nodule on radical prostatectomy sections; the aim being to build meta-classifiers that can accurately distinguish between which patients are at risk for disease recurrence versus those who are not (following prostate surgery).

2. DESIGNING A MULTI-MODAL DATA INTEGRATION METHOD

In the following discussion, we define the feature descriptors associated with samples c_i and c_j for modality ϕ_m as F_m(c_i) and F_m(c_j), where i, j ∈ {1, …, N}, m ∈ {1, …, M}, N is the total number of samples, and M is the total number of modalities. After transforming the data for homogeneous representation, we will have E_m(c_i) and E_m(c_j) respectively.

2.1. Meta-Space Representation Approaches

To overcome the problem where heterogeneous data cannot be directly combined, meta-space representation (methods which transform such data into a homogeneous space), allows for direct combination of modalities.

1. Embedding Projections (EP): EP methods involve transforming the high dimensional modality feature space into a homogeneous low dimensional representation such that relative local proximities between sample points are optimally preserved. Such relative proximities are captured via a confusion matrix W, traditionally formulated as $W_m^{\mathbf{F}}(i,j)={\Vert F_m(c_i)-F_m(c_j)\Vert }_2$ for each modality ϕ_m. $W_m^{\mathbf{F}}$ then undergoes eigenvalue decomposition to result in non-linear projections (E_m(c_i)) of the input feature space.

2. Kernel space Projections (KP): Kernels allow for an implicit form of data representation where object similarities are captured in a gram matrix K formulated as a simple dot product, K_m(i, j) = 〈Φ(F_m(c_i), Φ(F_m(c_j))〉. Φ is the implicit pairwise embedding between the sample feature vectors for modality ϕ_m. Kernels may be fine tuned based on the choice of data modality, hence allowing different kernels to be employed for imaging and non-imaging data.

2.2. Meta-Space Fusion Approaches

Following meta-space representation, meta-space fusion strategies examine how to combine these homogeneous representations, such that maximal relevant information captured by each data source is preserved:

1. Confusion Matrix Combination (CC): Proximities between samples are calculated based on E_m(c_i) and E_m(c_j) for each modality ϕ_m to construct $W_m^{\mathbf{E}}$ (similar to $W_m^F$), in the homogeneous meta-space calculated via EP. These confusion matrices may then be combined in a linear or weighted manner to yield $\tilde{W}(i,j)={\displaystyle {\sum }_{m=1}^M{\beta }_m{W}_m^{\mathbf{E}}}(i,j)$, based on weights β_m. A final fused EP representation may then be calculated based on $\tilde{W}$.

2. Kernel Combination (KC): The kernel transformation of information from each modality ϕ_m results in a corresponding kernel gram matrix K_m. These may then be combined in a linear or weighted manner as $\tilde{K}(i,j)={\displaystyle {\sum }_{m=1}^M{\gamma }_m}{K}_m(i,j)$ based on weights γ_m. Re-projecting the data based on this $\tilde{K}$ yields the final fused KP data representation.

3. Embedding Concatenation (EC): The vectors obtained via EP of from each modality ϕ_m, m ∈ {1, …, M} can be directly concatenated as $\tilde{E}=[{\mathbf{E}}_1(c_i),\dots ,{\mathbf{E}}_M(c_i)]\forall c_i,i\in \{1,\dots ,N\}$. This is similar to concatenating intensity values at every pixel between registered images.

2.3. Learning Strategies for Meta-Space Classification

These learning approaches refer to the framework within which the fused meta-space representation is used to construct an integrated meta-classifier.

1. Unsupervised (U): No label information is utilized for either meta-space representation or meta-space fusion.

2. Semi-supervised (SS): This approach is utilized when partial label information is available [9]. A nearest neighbor graph, $\mathcal{N}$, is constructed for all the samples. The confusion matrix $W_m^F$ is then modified in a pairwise fashion such that points in $\mathcal{N}$ with the same class labels are given high weights and points with different labels are given low weights. If the points are not in $\mathcal{N}$, the corresponding edges are given a weight of 0 (i.e. disconnected).

3. Supervised (S): All available label information is incorporated when calculating optimal projections (for meta-space representation) or optimal weighting parameters (for meta-space fusion).

3. REVIEW OF RECENT DATA INTEGRATION METHODS

3.1. Generalized Embedding Combination (GEC)

GEC makes use of EP for homogeneous meta-space representation of the features corresponding to each modality. Meta-space fusion is then accomplished via EC of the resulting embedding representations. This technique was presented in [3] previously.

3.2. Consensus Embedding (CE)

Constructing low-dimensional embeddings directly from the individual high-dimensional modality vectors may be a suboptimal approach since the low dimensional representation may be susceptible to noise in the high dimensional data, and/or to choice of parameters. We therefore construct an ensemble of embeddings (similar in flavor to constructing an ensemble classifier in machine learning [10]). First, a number of bootstrapped feature subsets culled from the entire multi-modal feature space are constructed. These are then individually projected via EP to yield corresponding subset embeddings. Based on label information available, those subset embeddings are selected which optimally discriminate between classes in the data. Selected subset embeddings are then combined via unweighted CC, resulting in the final consensus embedding representation [4].

3.3. Semi-Supervised Multi Kernel(SeSMiK)

SeSMiK [5] leverages the interplay between EP and KP schemes, to inherently represent and combine the data in an integrated approach. First, for each modality ϕ_m, a corresponding K_m is constructed using an unique base kernel function for each of the M different modalities. Partial labels are then incorporated to construct a confusion matrix $W_m^F$associated with each modality, in a semi-supervised manner [9]. M different K_m and $W_m^F$ are then combined (via KC and CC) to yield $\tilde{K}$ and $\tilde{W}$, respectively. These are then substituted in an eigenvalue decomposition problem to yield the final homogeneously fused SeSMiK representation.

3.4. Boosted Embedding Combination (BEC)

BEC is a semi-supervised extension to GEC. This approach makes use of EP to calculate embeddings based on each modality ϕ_m. These embeddings are then combined via a weighted CC approach, where optimal weights are calculated based on the classification accuracy of these embeddings (using partially-labeled data for evaluation). The weighted confusion matrix is subsequently input to an active learning technique [6], which iteratively utilizes available partial-label information to yield the final BEC representation.

4. EXPERIMENTAL DESIGN

4.1. Multiparametric MRI classifiers for CaP detection

A total of 36 1.5 Tesla T2w MRI, MRS studies (S₁) were obtained prior to radical prostatectomy from University of California, San Francisco (UCSF). All of these studies were biopsy proven prostate cancer patient datasets that were clinically referred for a prostate cancer MR staging exam. Expert labeled regions (as cancer and benign) on a per voxel basis were used as a surrogate for the ground truth annotation. The goal of this experiment was to distinguish between CaP and benign regions on a per voxel basis, via quantitative integration of the T2w MRI and spectroscopy (MRS), where MRS is a metabolic vector (non-imaging) reflecting the concentration of key metabolites in the prostate.

Feature extraction from MRS

Radiologists typically assess presence of CaP on MRS based on the choline (A_ch), creatine (A_cr), citrate peaks (A_cit), and associated ratios. Variations in these values from predefined normal ranges (A_ch+cr/A_cit > 1) is highly indicative of the presence of CaP. A metabolic feature vector was obtained for MRS, by calculating A_ch, A_cr, and A_cit for each MRS spectrum and recording the corresponding ratios (A_ch, A_cr, A_cit, A_ch+cr/A_cit, A_ch/A_cr).

Feature extraction from T2-w MRI

36 texture features were calculated from each T2w MRI image based on responses to various gradient filters and gray level co-occurrence operators. These features were chosen based on previously demonstrated discriminability between CaP and benign regions on T2w MRI [4].

4.2. Combining histology and proteomics for CaP prognosis

A cohort of CaP patients at the Hospital at the University of Pennsylvania (UPENN) were identified, all of whom had gland resection (S₂). Half of these patients had biochemical recurrences following surgery (within 5 years) and the other half did not. For each patient, a representative histology section was chosen and the tumor nodule identified. Mass Spectrometry (MS) was performed at this site to yield a protein expression vector. The aim of this experiment was to combine quantitative image descriptors on histology of the tumor with the proteomic vector to build a meta-classifier to distinguish the patients at risk of recurrence from those who are not.

Feature extraction from Histology Images

Following an automated gland segmentation process used to define the gland centroids and boundaries, architectural and morphological image features (quantifying glandular arrangement) were extracted from histology, as described in [3].

Feature extraction from proteomic data

Protein data from a high resolution mass spectrometry procedure underwent quantile normalization, log(2) transformation, and mean and variance normalization on a per-protein basis. A t-test feature selection is then utilized to prune the protein feature set to the 10 most discriminatory proteins across the 19 patient studies.

4.3. Experimental Setup

For each method described in Section 3, we construct a 3-dimensional fused representation of the input data. Gaussian kernels were employed for kernel representation. For the semi-supervised approaches, 40% of the labeled information was used when constructing the fused meta-space representation. The Random Forest (RF) classifier [10] was then employed in conjunction with each data representation. A randomized three-fold cross validation was performed by dividing our datasets (S₁ and S₂) into three parts, where 2/3 of the dataset was used for training and 1/3 for testing. This is repeated until all the samples are classified within each dataset. This randomized cross-validation was then repeated a total of 25 times. Additionally, a COI classifier is constructed by combining individual classification results (h₁, …, h_M) from modalities ϕ₁, …, ϕ_m by invoking the independence assumption: h_d = h₁ × h₂ × … h_M. Note that M = 2 for both our datasets, S₁ and S₂. The classifier accuracy at the operating point of the ROC curve for each meta-space fusion strategy (including COI) was recorded. The mean and standard deviation of classifier AUC (μ_AUC ± σ_AUC) and accuracy values (μ_Acc ± σ_Acc) were then calculated over the 25 runs.

5. RESULTS & DISCUSSION

As may be observed in Table 2, the meta-space fusion methodologies (GEC, CE, SeSMiK, BEC) outperform a COI approach. This finding reiterates the limitation of COI strategies in that a significant loss of relevant information is probably occurring when reducing each modality to a single decision. On the other hand, transforming the data to a meta-space representation followed by fusion and classification, results in a significantly improved classification performance.

Table 2.

Quantitative results obtained via data integration methods GEC, CE, SeSMiK, BEC, and COI for S₁ and S₂.

Method	S1 (MRS + MRI)		S2 (Histology + Proteomics)
	μAUC + σAUC	μAcc + σAcc	μAUC + σAUC	μAcc + σAcc
GEC	0.88 ± 0.05	0.87 ± 0.05	0.89 ± 0.03	0.83 ± 0.01
CE	0.82 ± 0.19	0.82 ± 0.14	0.73 ± 0.03	0.70 ± 0.04
SeSMiK	0.90 ± 0.05	0.89 ± 0.05	0.89 ± 0.01	0.83 ± 0.01
BEC	0.86 ± 0.07	0.78 ± 0.11	0.88 ± 0.04	0.87 ± 0.01
COI	0.73 ± 0.19	0.79 ± 0.13	0.73 ± 0.04	0.68 ± 0.03

Amongst the data-fusion strategies, SeSMiK and BEC outperform CE. This may be due to the fact that SeSMiK and BEC strategies optimally weight the contributions from different modalities, such that the more discriminatory modality receives a higher weight. Further, since CE assumes that each modality should receive an equal contribution in meta-space, it may be unable to appropriately leverage contributions from overachieving modalities. SeSMiK and BEC also appear to have a distinct advantage over CE in that they leverage a semi-supervised approach in constructing the meta-space representation, potentially boosting discriminability. Therefore, adaptively weighting contributions of the individual modalities and incorporating partial labels when calculating the meta-space representation may play significant roles in optimal heterogeneous data fusion. GEC also outperforms CE, suggesting that perhaps there is some merit in using an unsupervised, embedding concatenation strategy.

Overall, SeSMiK was observed to perform marginally better compared to all the other data fusion methods. SeSMiK uniquely utilizes both kernel and embedding projections in an integrated fashion to produce the final fused meta-space representation. Additionally, SeSMiK leverages the semi-supervised learning approach when constructing the meta-space representation, potentially enabling greater class separability. A final unique aspect of SeSMiK is that since it combines multiple kernels, unique kernels optimized to the specific data modality could be chosen for improved discriminability.

6. CONCLUDING REMARKS

In this paper, we examined the significant challenges in quantitative, heterogeneous multi-modal data integration. Specifically, we reviewed the challenges in (1) meta-space representation, (2) meta-space fusion, and (3) learning strategies for meta-classifier construction, in the specific context of integrating imaging and non-imaging data. We also reviewed and evaluated 4 different state-of-the-art data fusion methods in the context of building meta-classifiers by: (1) combining histology with mass-spectrometry to predict prostate cancer recurrence, and (2) combining MRS with MRI data to predict prostate cancer presence. We found that methods which explicitly attempt to overcome the challenges of heterogeneous data fusion result in improved classifications as compared to a naïve COI approach. Methods such as SeSMiK, which integrate multiple representation (EP,KP) and fusion approaches (KC,CC) within a semi-supervised (SS) framework appeared to outperform all other approaches. However, it is important to note that this paper only serves to highlight recent strategies and methods which have been successful for multi-modal fusion. As can be deduced from Table 1, many potentially useful data fusion methods using unexplored combinations of strategies have yet to be developed. With the increasing relevance of fused diagnostics in personalized healthcare, it is expected that such heterogeneous fusion methods will play an important role in combining and interpreting multiple imaging and non-imaging modalities.

Table 1.

Table showing different meta-space representation, meta-space fusion and meta-classifier construction strategies used for each of GEC, CE, SeSMiK and BEC.

Method	Representation	Fusion	Learning Strategies
GEC	EP	EC	U
CE	EP	CC	S
SeSMiK	EP,KP	KC,CC	SS
BEC	EP	CC	SS

Fig. 2.

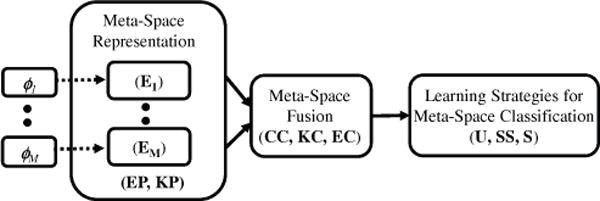
Flowchart showing various system components of the Generalized Fusion Framework. Homogeneous meta-space representations (EP or KP) of the heterogeneous modalities ϕ₁, …, ϕ_M are used to facilitate integration via meta-space fusion (CC, KC or EC). Learning strategies (U, SS, or S) are then used to construct the integrated meta-classifier.