Improving Patient Care Using the Johnson-Neyman Analysis of Heterogeneity of Treatment Effects According to Individuals' Baseline Characteristics

Abstract

Objective

Because each patient’s baseline (pre-treatment) characteristics differ (e.g., age, sex, socioeconomic status, ethnicity/race, biomarkers), treatments do not work the same for every patient-some can even cause detrimental effects. To improve patient care, it is critical to identify such heterogeneity of treatment effects. But the standard analytic approach dichotomizes baseline characteristics (low vs. high) which often leads to a loss of critical patient-care information and power to detect heterogeneity, as the results may depend strongly on the cut-points chosen. A more powerful analytic approach is to analyze baseline characteristics (i.e., covariates) measured on a continuous scale that retains all of the information available for the covariate.

Methods

In this article, we show how the Johnson-Neyman (J-N) method can be used to identify the prognostic and predictive value of baseline covariates measured on a continuous scale - findings that often cannot be determined using the traditional dichotomized approach. As an example, we used the J-N method to explore treatment effects for varying levels of the biomarker salivary mutans streptococci (MS) in a randomized clinical prevention trial comparing fluoride varnish with no fluoride varnish for 376 initially caries-free high-risk children, all of whom received oral health counseling.

Results

The J-N analysis showed that children with higher baseline MS values who were randomized to receive fluoride varnish had the poorest dental caries prognosis and may have benefitted most from the preventive agent.

Conclusion

Such methods are likely to be an important tool in the field of personalized oral health care.

To assess preventive and therapeutic benefits, modern dental research relies on clinical trials that are extremely expensive and time consuming. It is therefore critical that the greatest amount of information be extracted from them. At the same time, it is well known that the treatments evaluated in these trials, including those that are preventive and curative, do not work the same for every patient and that some may experience detrimental effects (1–6). To identify who may or may not benefit from a particular treatment, investigators frequently use subgroup analyses to evaluate 'treatment-effect heterogeneity' according to patients' baseline characteristics.

We define "subgroup analysis" here as any treatment effect evaluation for a specific end point in subgroups of study participants, while subgroups are constructed according to participants' baseline characteristics (e.g., socioeconomic status, age, sex, race/ethnicity, biomarkers). The end point is usually the primary endpoint, such as a measure of treatment efficacy or safety. The treatment effect, a comparison between the treatment groups, is either measured on the absolute scale (e.g., arithmetic difference) or relative scale (e.g., relative risk or odds ratio). Subgroup analyses are often listed as a primary or secondary study objective, and the research question usually posed may depend on how the baseline characteristic is measured: continuous versus dichotomized. Baseline characteristics measured on a continuous scale are often categorized into two (dichotomized) or more groups (e.g., salivary mutans streptococci (MS) level dichotomized as low vs. high), resulting in a loss of information and power (7), while the results from these dichotomized analyses may depend on the chosen cut-point. However, for baseline characteristics measured on a continuous scale (e.g., age, baseline MS), an investigator can ask how treatment effects vary by the levels of those characteristics.

Identifying treatment-effect heterogeneity provides critical patient information needed to tailor treatments according to an individual's characteristics and to ultimately lead to more effective oral health care delivery for personalized medicine (6). The purpose of this article is to show how baseline characteristics measured on a continuous scale can be analyzed using the Johnson-Neyman (J-N) method (8–18). This method has been applied to many different types of studies in education, psychology and medicine (19–22), but to our knowledge has not been applied to oral health. We illustrate this J-N method with an analysis of the Center to Address Disparities in Oral Health (often referred to as CAN DO) fluoride varnish trial, a randomized clinical prevention trial (RCT) that evaluated the efficacy of fluoride varnish with oral health counseling to reduce caries incidence in 376 initially caries-free high-risk children aged 6 to 44 months (23, 24). In this article, we used the J-N method for the first time in this fluoride varnish RCT to explore the predictive and prognostic value of the biomarker, salivary mutans streptococci (MS).

This article is organized as follows. In the Methods section, we first describe the standard approach that is used to evaluate treatment-effect heterogeneity. We then show how the J-N method can be used to model baseline characteristics (i.e., covariates) on a continuous scale that retains all of the available information in the covariate. In the results for Applications section, we illustrate how the J-N method can be used to evaluate treatment-effect heterogeneity in the CAN DO fluoride varnish RCT. The Discussion, with further consideration of how to avoid erroneous conclusion and other matters, is presented below. Final remarks are provided in the conclusion.

METHODS

The Standard Approach

The standard approach usually assesses treatment-effect heterogeneity, also called "interactions", "treatment-effect modification" or "moderation", by first defining (often arbitrarily) study-participant subgroups based on categorized (usually dichotomized) baseline characteristics (e.g., low MS levels vs. high MS levels). After the baseline variable is dichotomized, the results are assessed for heterogeneity by testing the statistical interaction between treatment and the dichotomized baseline characteristic for significance. But it is well known that modeling covariates on a continuous scale is more powerful than categorizing covariates into two or more groups (7), since this can diminish the effect of the baseline characteristic as a predictor of treatment effectiveness.

A common mistake is to claim heterogeneity on the basis of separate tests of treatment effects within each level of the baseline variable (2, 3). For example, testing the hypothesis that there is no treatment effect in high MS levels, and then testing it separately in study participants with low MS levels does not address the question of whether treatment differences vary according to MS levels. Another common error is to ignore the uncertainty of the estimates of the treatment effect (e.g., standard error).

The Johnson-Neyman Approach

A more accurate statistical method for assessing the heterogeneity of treatment effects is the Johnson-Neyman (J-N) approach (8–16). Recent developments to this methodology include applications to both longitudinal data with normally distributed continuous outcomes (e.g., hierarchical linear (multi-level models)) (17), as well as non-normally distributed data suitable for generalized linear (mixed) models with adjustment for multiple testing, which protects against erroneous conclusions (18). In Appendix A, we describe how the J-N method can be applied to generalized linear models (GLMs), particularly logistic regression models that assume a logit link and Bernoulli distribution (see Lazar and Zerbe (18) for additional details about the J-N method for generalized linear mixed models). Appendix B provides additional details about the J-N approach that are applicable to the CAN DO fluoride varnish trial described in the Results-Applications section. Appendix C provides a SAS macro based on SAS version 9.3 GLIMMIX procedure that can be used to perform the J-N analysis for logistic regression models with cross-sectional data. It also includes the SAS code used to perform the J-N analysis presented in the Results-Applications section.

To give a brief overview of the method to evaluate heterogeneity of treatment effects, the J-N approach compares the relationship between the treatment effect (e.g., odds ratio) and baseline characteristic (e.g., pre-treatment or pre-intervention variables that do not vary over time) of interest by evaluating whether the fitted regression curves differ significantly among treatment groups, while optionally adjusting for other characteristics. When there is evidence of a heterogeneous treatment effect, then the 'significance region' (the range of the values of the baseline characteristic that significantly differ between the fitted regression curves) can be determined. Determining the significance region involves comparing the treatment curves at each value of the characteristic, which results in statistical tests for every value of the characteristic. In dentistry studies, this can sometimes be well over 1000 tests. Rather than evaluate a potentially infinite number of tests, the J -N analysis can determine the significance region explicitly with adjustment for multiple testing that protects against erroneous conclusions (see Appendix A and Appendix B). While this 'explicit solution' assumes that the patient characteristic (or co-variate) has linear effects, an alternative solution as well as the standard dichotomized approach does not require linearity in the covariates (see Appendix A). A plot of the treatment effect against the baseline characteristic (i.e., covariate) together with the 95% confidence band graphically illustrates heterogeneity of treatment effects.

One advantage of this approach is that by evaluating the prognostic and predictive value of a co-variate, J-N can make more detailed and substantial descriptions than the standard approach. The J-N method makes statements about a significant ‘interaction’ effect and also about the values of the covariate that are significant (e.g., 'There were significant differences between treatments over the whole range of the covariate, and treatment effects increased with increasing value of the covariate'; or possibly, 'Treatment effects increased with increasing value of the covariate, and groups were significantly different for values of the covariate above' (25)). Another advantage over the standard approach that distills heterogeneity of treatment-effects to a not very intuitive p-value is that the J-N method can graphically illustrate the treatment-effects as a function of a continuous covariate.

RESULTS - APPLICATION

Dental caries in children remains a significant public health problem (WHO, 2011). Since caries incidence can be greatest in children and adolescents, dentists need various tools to predict the occurrence of new carious lesions. Some studies have shown that the number of salivary mutans streptococci (MS) is associated with caries onset and progression (26–29), but researchers have questioned whether it is a reliable predictor for dental caries risk in children (30).

Using the J-N method described in the Methods section, we can evaluate the prognostic and predictive value of MS in the CAN DO fluoride varnish study, a controlled dental examiner masked phase III RCT that evaluated the efficacy of fluoride varnish (FV) with oral health counseling versus counseling alone to reduce caries incidence in 376 initially caries-free high-risk children aged 6 to 44 months from predominantly low-income Chinese and Hispanic San Francisco families. The participants underwent dental examination at baseline prior to the intervention and at one and two years post intervention. Intent-to-treat analyses showed a fluoride varnish protective effect in caries incidence, p<0.001 (23). Caries incidence was significantly higher for counseling only (0 FV) vs. the groups assigned counseling + FV once/year (OR=2.20, 95% CI: 1.19–4.08) and twice/year (OR=3.77, 95% CI 1.88–7.58))(23).

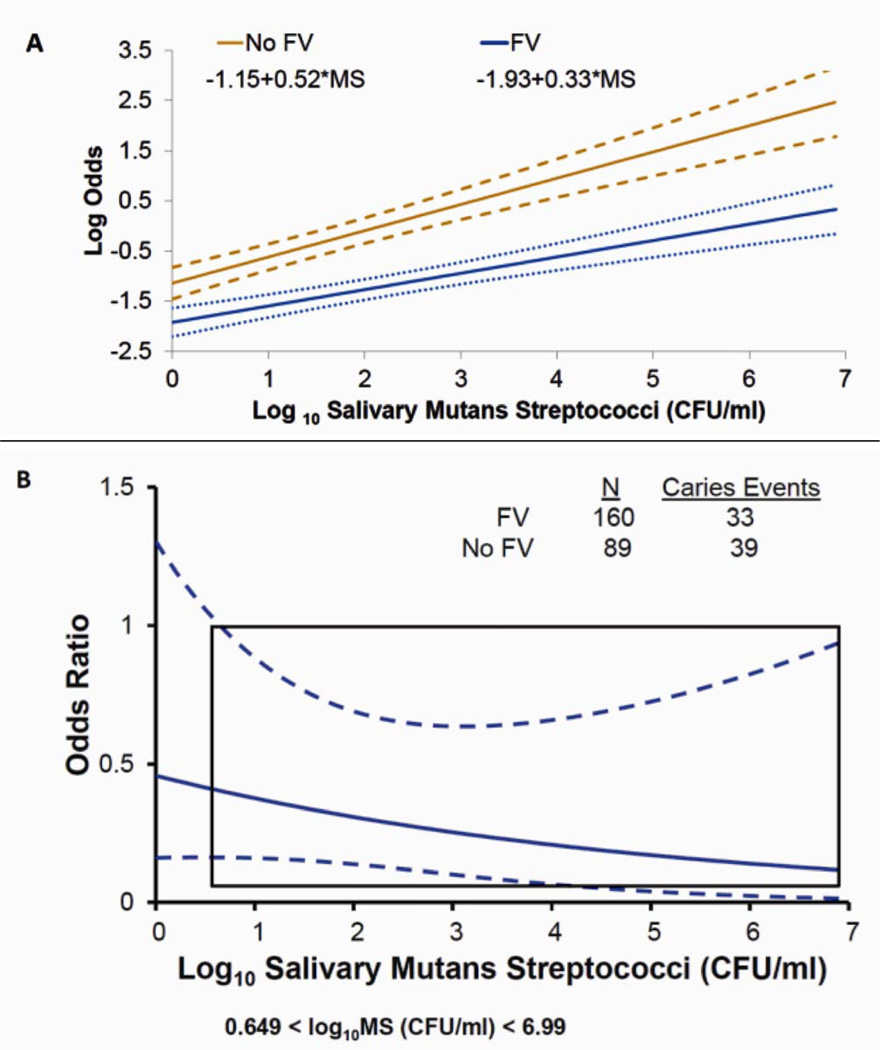
The study had baseline MS measurements (0 FV per treatment per year: n=89; 1 FV treatment per year n=78; 2 FV treatments per year n=82) for 249 caries-free children. To illustrate the J-N approach more clearly, we collapsed the two FV treatment groups into a single group. We then simultaneously fit two logistic regression curves of any caries incidence, the primary outcome, to evaluate the prognostic and predictive value of MS, which was logarithmically transformed in base 10 (log₁₀ MS). In Figure 1A, the best fitting curves of any caries incidence for the two treatment groups are:

• −1.15+0.52 log₁₀ MS (colony forming units per milliliter or CFU/ml) for no FV, and

• −1.93+0.33 log₁₀ MS (CFU/ml) for FV with associated standard error lines (dashed lines).

Figure 1.

Johnson-Neyman analysis of the treatment effect of fluoride varnish (FV) versus no fluoride varnish (No FV) treatment as measured by (A) log odds of caries incidence with standard error lines (dashed lines) (B) odds ratio (less than one indicates FV better; otherwise No FV better) with corresponding 95% confidence band using Scheffé’s method (dashed lines). The x-axis indicates the values of the children’s Log₁₀ salivary mutans streptococci (CFU/ml).

Figure 1A summarizes the log odds of caries incidence for FV compared to no FV treatments as MS increases. The figure suggests that higher log₁₀ MS levels were associated with higher log odds of caries incidence, especially for children who were randomly assigned to no FV treatment.

Using the J-N method, we can evaluate the particular values of log₁₀ MS that result in a statistically different (heterogeneous) caries incidence and, most importantly, which children may benefit most from FV treatment. This question may be particularly important, for instance, for parents who are weighing the benefits of their children receiving a treatment against any potential risks. In Appendix B, we show how to use a decision guide to determine whether caries incidence differs between the treatment groups.

Figure 1B displays the relative treatment effectiveness based on odds ratios across individual levels of log₁₀ MS. For high log₁₀ MS values, the estimated odds ratio of caries was lower for children receiving FV than for those not receiving FV (an odds ratio less than one indicates that fluoride varnish was more protective against caries than no FV). The J-N analysis results show evidence for heterogeneity of relative treatment effects (joint test or interaction test: P<0.0001, Fig 1B). We conclude that: 1) when log₁₀ MS is between 0.6 and 6.9, children assigned fluoride varnish had significantly lower odds of caries, after adjustment for multiple testing; and 2) children who had the highest values of log₁₀ MS benefitted the most from receiving preventive FV treatment.

To compare the results from the J-N method, we also evaluated treatment-effect heterogeneity using the standard approach, as described in the Methods section. Levels of the biomarker MS were dichotomized as no MS (MS = 0) vs. any (MS >0). We fit a standard logistic regression model of any caries incidence, the primary outcome, to evaluate a treatment by covariate (i.e., dichotomized MS) interaction effect. The interaction test detected borderline statistically significant heterogeneity (P = 0.06). We also evaluated MS using the same dichotomization as described in Ramos-Gomez et al.(31) (i.e., log₁₀ MS < 3 vs. log10 MS ≥ 3), and the interaction test between treatment and this dichotomized version of MS detected no statistically significant heterogeneity (P = 0.21). SAS version 9.3 GLIMMIX procedure was used to perform both the Johnson-Neyman analysis, as described in Appendix C, and the standard analysis assessing the interaction between treatment and dichotomized baseline characteristic log₁₀ MS.

DISCUSSION

The CAN DO fluoride varnish RCT example illustrates how the Johnson-Neyman analysis addresses research questions that are important for both investigators and parents. Using this method, we were able to evaluate for the first time the heterogeneity of an oral health biomarker, MS, in children enrolled in this study. Our results suggest that children with higher levels of MS who were assigned to receive no fluoride varnish had a poorer prognosis, and that these children may benefit most from fluoride varnish treatment compared with no treatment. This benefit could be explained by the fluoride concentration in saliva that works as the driving force to decrease the rate of enamel demineralization and enhance the rate of mineralization (32–34). Nevertheless, despite the biological plausibility of the observed results, the fluoride varnish protocol did not a priori specify examination of the role of MS as a predictive factor, and these results should be interpreted cautiously. As documented in the primary report of the fluoride varnish trial (23), an unexpected protocol deviation resulted in some children receiving less active fluoride varnish than assigned, and the preventive effects of FV may even be stronger.

The evaluation of treatment-effect heterogeneity has been associated with well-documented problems, such as multiple testing that can lead to erroneous conclusions. However, not presenting evaluations of treatment-effect heterogeneity is a "steep price to pay for a problem that can be remedied by more responsible analysis and reporting." as Lagakos put it (2). To protect against erroneous conclusions that can lead to over-interpreted results, researchers should use a method that accounts for multiple testing, such as Johnson-Neyman. However, the safest approach is to validate exploratory analyses using an independent data set known as "replication" or "external validation". Guidelines have also been proposed to address the challenges associated with the analysis and presentation of the results (3). While these guidelines focus on the reporting of randomized clinical trials, the issues discussed can also apply to observational studies. Therefore, these guidelines are appropriate to apply to any presentation of results that evaluates treatment-effect heterogeneity, including results generated from the Johnson-Neyman approach.

We highlighted in this article how the approach of categorizing baseline characteristics measured on a continuous scale can fail to identify the value of the baseline characteristic as a predictor of treatment effectiveness. While we focused on characteristics measured on a continuous scale, the J-N method can also be applied to other types of numeric characteristics, including discrete count or ordinal (with many categories) scaled baseline characteristics. Subgroup analyses that are properly analyzed and reported can provide useful information for the care of study participants and for future research, but only if the analytic method retains all of the information in the covariate and protects against erroneous conclusions from multiple testing, as the Johnson-Neyman method does. Most importantly, regardless of the analytic method used, exploratory results generated from these subgroup analyses need to be confirmed before the results are applied to patients in the clinical setting. Identification and confirmation of baseline characteristics that predict treatment effectiveness may ultimately lead to personalized oral health care or precision medicine that improves patient health (6).

CONCLUSION

The Johnson-Neyman method enables us to evaluate the prognostic and predictive value of a patient’s characteristics. Using methods that predict heterogeneity of treatment effects can improve treatment decisions for individual patients and is becoming an important tool in the field of personalized oral health care.

APPENDIX A

The Johnson-Neyman Approach Suitable for Logistic Regression Models

The Johnson-Neyman (J-N) approach was recently developed for the generalized linear model (GLM) and the generalized linear mixed models (GLMM) [1]. The GLM is a special case of GLMM, and it can be extended to the GLMM with the addition of random effects that account for the correlation among longitudinal responses. The methodology for the Johnson-Neyman method suitable for either the GLM and GLMM, which assumes any normal or non-normal distribution from the exponential family, can be found in Lazar and Zerbe [1]. A brief overview is described below about this particular case of the J-N approach for GLM, and this overview is directly applicable to the CAN DO fluoride varnish trial described in the Application Section, particularly logistic regression models of dichotomous outcomes with a logit link and Bernoulli distribution.

Before we provide an overview of the particular case of the J-N approach for logistic regression models for dichotomous outcomes suitable for cross-sectional data, we will first describe how to build a GLM. GLM is a broad class of models suitable for analyzing a diverse type of outcomes (e.g., Bernoulli distribution for dichotomous outcomes or Poisson distribution for counts). (See McCullagh and Nelder [2] and McCulloch and Searle [3] for more information about GLM and GLMM, respectively.) Three decisions are required to build a GLM: the distribution of the data that can be from any probability distribution of the exponential family, the systematic component of the model, and the link function. The distribution can be any member of the exponential family such as Bernoulli, Poisson, negative binomial, or Normal (Gaussian). The systematic component of the model specifies the effect of the covariate, X, on the mean of the distribution, Y. This is known as the linear predictor, η = Xβ, such that η is linear in β, the regression parameters. The link function, g(.), describes the relationship between the mean of Y or m and η, where E(Y) = m and g(m) = Xβ. Any differentiable monotonic link function can be chosen, such as the Bernoulli distribution link function, which is usually the logistic or logit link function, g(m) = log(m/(1 − m)). Logistic regression is one specific kind of GLM with Bernoulli distribution, systematic component(s), X, and logit link function.

Johnson-Neyman Approach for Comparing Logistic Regression Models

Consider two typical logistic regression models fit simultaneously with dichotomous outcomes:

$${\mathrm{\eta }}_{1j}=\text{log}\left(\frac{{\mathrm{\Pi }}_{1j}}{1-{\pi }_{1j}}\right)={\alpha }_1+{\beta }_1{x}_{1j}{\mathrm{\eta }}_{2j}=\text{log}\left(\frac{{\mathrm{\Pi }}_{2j}}{1-{\pi }_{2j}}\right)={\alpha }_2+{\beta }_2{x}_{2j,}$$ (A.1)

where x_ij denote the measurement of the jth subject for the ith treatment group (here, we consider two treatment groups i = 1 or 2 but more than two groups can be considered without loss of generality). Π_ij is the probability that the outcome y_ij = 1, such that y_ij~Bernoulli(Π_ij), η_ij is the linear predictor, and α_i and β_i are the fixed intercepts and slopes for each of the i treatment groups. The log $(\frac{{\mathrm{\Pi }}_{\mathit{\text{ij}}}}{1-{\pi }_{\mathit{\text{ij}}}})$ expression is usually referred to as the logit or log-odds.

Consider comparing the curve from treatment group 1, (α₁ + β₁x), with the curve from treatment group 2, (α₂ + β₂x), from models (A.1). The joint hypothesis of equality of the intercepts, α₁ and α₂, and slopes, β₁ and β₂, of two logistic regression curves can be expressed in terms of the difference in the intercepts and the difference in the slopes: H_k = (α₁ − α₂) + (β₁ − β₂)x_k = θ_C + θ_Ax_k, where θ_C = (α₁ − α₂) and θ_A = (β₁ − β₂), for distinct k covariate valuesx₁, x₂,x₃,….

In general, when testing a null hypothesis, ${\mathrm{H}}_0=\underset{\mathit{\text{sx}}1}{\underbrace{\theta }}=\underset{\mathit{\text{sx}}1}{\underbrace{\left(\begin{array}{c}{\theta }_C\\ {\theta }_A\end{array}\right)}}=\underset{\mathit{\text{sx}}p}{\underbrace{C}}\underset{\mathit{\text{px}}1}{\underbrace{\beta }}=0$, for a fixed contrast matrix, C, where β represents the regression parameters, a t- or F-statistic can be used. When the rank of C is one, $t(\widehat{\theta })=\raisebox{1ex}{$\widehat{\theta }$}\!\left/ \!\raisebox{-1ex}{$\sqrt{{\widehat{V}}_{\widehat{\theta }}}$}\right.$, where V̂_θ̂ = CL̂C′ and L̂ is the empirical covariance matrix of β̂ − β. The null hypothesis can be tested with an F-statistic if the rank of C is greater than or equal to one, $F(\widehat{\theta })=\raisebox{1ex}{$\left[\underset{1\mathit{\text{xs}}}{\underbrace{\widehat{\theta }\prime }}{(\underset{\mathit{\text{sxs}}}{\underbrace{{\widehat{V}}_{\widehat{\theta }}}})}^{-1}\underset{\mathit{\text{sx}}1}{\underbrace{\widehat{\theta }}}\right]$}\!\left/ \!\raisebox{-1ex}{$s$}\right.$ with s numerator degrees of freedom and v denominator degrees of freedom. The denominator degrees of freedom are often estimated from the data [4], and in some cases, v denominator degrees of freedom may be simply the sample size (n) minus the number of parameters (e.g., for comparing two logistic regression curves as described in A.1, v = n − 4). Certainly the usual model assumptions must hold to make valid inference about θ that accounts for the variance-covariance matrix selected by the investigator [5, 6]. A single null hypothesis of the form, $\underset{1\mathit{\text{xs}}}{\underbrace{h}}\underset{\mathit{\text{sx}}1}{\underbrace{\theta }}=0$, can be rejected, $\underset{1\mathit{\text{xs}}}{\underbrace{h}}\underset{\mathit{\text{sx}}1}{\underbrace{\theta }}\ne 0$, if $t(h\widehat{\theta })>\sqrt{F_{1-\alpha ,1,v}}$, where the t-statistic associated with hθ̂ is $t(h\widehat{\theta })=\raisebox{1ex}{$h\widehat{\theta }$}\!\left/ \!\raisebox{-1ex}{$\sqrt{h{\widehat{V}}_{\widehat{\theta }}h\prime }$}\right.$ and F_1−α,1,v is the 1 − α percentage point of an F distribution with 1 and v numerator and denominator degrees of freedom, respectively.

Multiple null hypotheses of the form, hθ = 0, can be rejected (hθ ≠ 0) whenever the t-statistic associated with hθ exceeds the Scheffé’s criterion, $\sqrt{s{F}_{1-\alpha ,s,v}}$,

$$t(h\widehat{\theta })>\sqrt{s{F}_{1-\alpha ,s,v}}$$ (A.2)

where F_1−α,s,v is the 1 − α percentage point of an F distribution with s and v numerator and denominator degrees of freedom, respectively. In our application, $\underset{1x2}{\underbrace{h}}\underset{2x1}{\underbrace{\theta }}=\underset{1x2}{\underbrace{h}}\underset{2x4}{\underbrace{C}}\underset{4x1}{\underbrace{\beta }}=0$, where $\theta =\left(\begin{array}{c}{\theta }_C\\ {\theta }_A\end{array}\right)=\underset{\theta }{\underbrace{\left(\begin{array}{c}{\alpha }_1-{\alpha }_2\\ {\beta }_1-{\beta }_2\end{array}\right)}}=C\beta =\underset{\theta =C\beta }{\underbrace{\underset{C}{\underbrace{\left(\begin{array}{rrrr}\hfill 1& \hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1& \hfill -1\end{array}\right)}}\underset{\beta }{\underbrace{\left(\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ {\beta }_1\\ {\beta }_2\end{array}\right)}}}}$, and null hypotheses are therefore rejected whenever $t(h\widehat{\theta })>\sqrt{2F_{1-\alpha ,2,v}}$. The vertical difference between the two logistic regression equations at any X can be expressed as $h_x\theta =\underset{h_x}{\underbrace{(1X)}}\underset{\theta }{\underbrace{\left(\begin{array}{c}{\alpha }_1-{\alpha }_2\\ {\beta }_1-{\beta }_2\end{array}\right)}}=\underset{h_x}{\underbrace{(1X)}}\underset{\theta =C\beta }{\underbrace{\underset{C}{\underbrace{\left(\begin{array}{cccc}1& -1& 0& 0\\ 0& 0& 1& -1\end{array}\right)}}\underset{\beta }{\underbrace{\left(\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ {\beta }_1\\ {\beta }_2\end{array}\right)}}}}=({\alpha }_1+{\beta }_{1}X)-({\alpha }_2+{\beta }_{2}X)$, and multiple null hypotheses can be tested simultaneously at two or more unique values of X by repeating A.2 for each value of X. Scheffé’s method for multiple comparisons controls the family-wise type I error rate for tests of all linear functions, h_xθ, at level α, and the price of multiple comparisons adjustment is always the same no matter how many values of X are tested. In our application, Scheffé’s constant is $\sqrt{2F_{1-\alpha ,2,v}}$, where s = 2, which is determined from the number of rows in the C matrix, θ is a 2 × 1 vector containing the differences in the intercepts and the differences in the slopes, and h_xθ are selected to be vertical differences between the lines at specified values of x_k’s. This solution that proposes to compare each X’s test statistic with Scheffé’s criterion does not require linearity in X. The above solution is the same solution described in Lazar and Zerbe for GLM and GLMM except in this application we focus on the special case of comparing logistic regression models.

Rather than test a potentially infinite number of hypotheses (one at each x_k) that requires a separate calculation for each x_k, we can determine the significance regions explicitly, as described in Lazar and Zerbe. By re-writing A.2, a quadratic form in X is yields $h_x[\theta \theta \prime -2F_{1-\alpha ,2,v}{V}_{\theta }]h_x^{\prime }>0$. If we let $\theta =\left(\begin{array}{c}{\theta }_C\\ {\theta }_A\end{array}\right)$, where θ_C denote the difference in the intercepts and θ_A denote the difference in the slopes and V_θ(C), V_θ(A) and Cov_θ(A)θ(C) denote the empirical error variances (V_θ) and covariance (Cov) of θ_C and θ_A, then the quadratic inequality is: $(1X)\left[\right(\begin{array}{cc}{\theta }_C^2& {\theta }_C{\theta }_A\\ {\theta }_A{\theta }_C& {\theta }_A^2\end{array})-2F_{1-\alpha ,2,v}(\begin{array}{cc}{V}_{\theta (C)}& {\text{cov}}_{\theta (C)\theta (A)}\\ {\text{Cov}}_{\theta (A)\theta (C)}& V_{\theta (A)}\end{array}\left)\right]\left(\begin{array}{c}1\\ X\end{array}\right)>0$ or Ax²+Bx+C > 0, where $\mathrm{A}={\theta }_A^2-2F_{1-\alpha ,2,v}{V}_{\theta (A)}$, B = 2(θ_Aθ_C − 2F_1−α,2,VCov_θ(A)θ(c)), $\mathrm{C}={\theta }_C^2-2F_{1-\alpha ,2,v}{V}_{\theta (C)}$, D = B² - 4AC. Here we focus on two treatments groups, but more than two groups can be compared.

After estimating A, B, C and D, one of three possible cases is used to determine the significance regions explicitly.

Case I

If A>0 (implies D>0), then the tests are significant for the X’s satisfying: $X<\left[\frac{-\mathrm{B}-\sqrt{D}}{2\mathrm{A}}\right]$ or $X>\left[\frac{-\mathrm{B}-\sqrt{D}}{2\mathrm{A}}\right]$.

Case II

If A<0 and D>0, then the tests are significant for the X’s satisfying: $[\frac{-\mathrm{B}+\sqrt{D}}{2\mathrm{A}}<X<\frac{-\mathrm{B}-\sqrt{D}}{2\mathrm{A}}]$.

Case III

If D<0 and A<0, then the tests are never statistically significant for any X. The case where A>0 and D<0 cannot occur.

The ‘explicit’ solution described above is the same solution described in Lazar and Zerbe [1], which assumes that the two regression functions are linear in X. Additional clarification about the cases is described in Lazar and Zerbe.

APPENDIX B

J-N decision guide for determining the significance regions with application to the CAN DO fluoride varnish trial

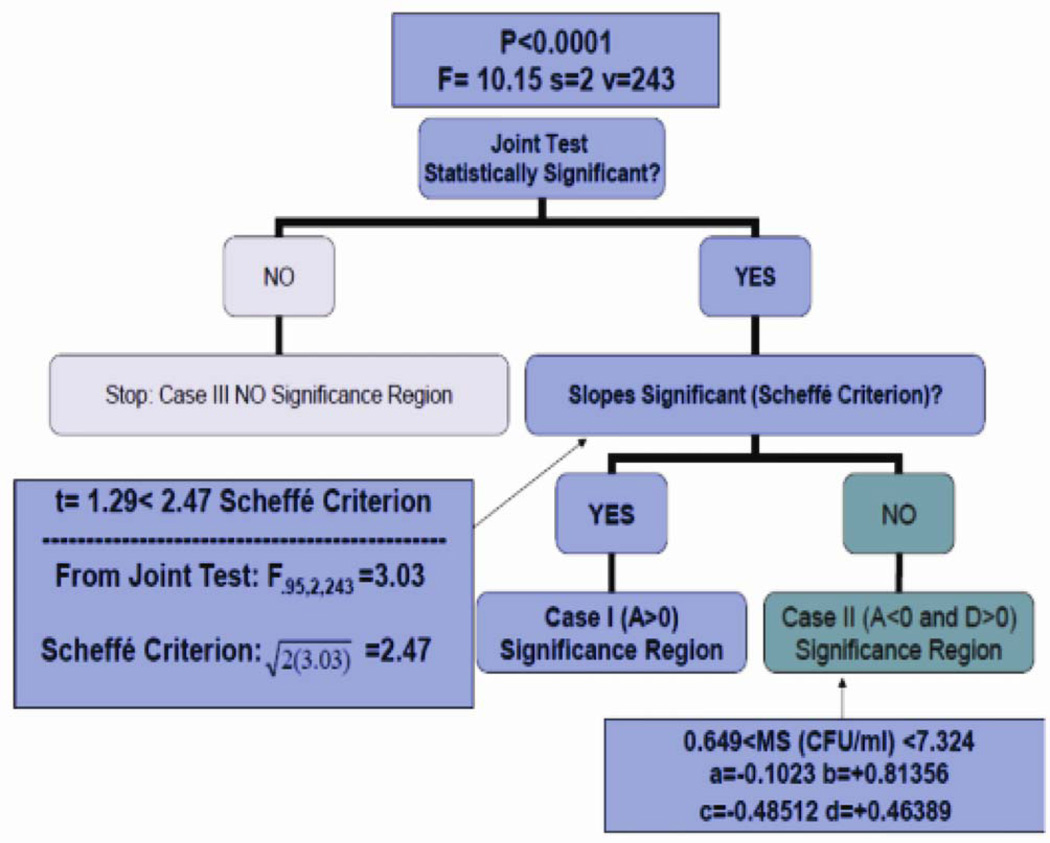
We illustrate how a decision guide useful for determining the appropriate case can be used in the fluoride varnish study (Figure 2). This guide provides a facile way to evaluate whether the curves are statistically different with adjustment for multiple comparisons and without calculation of components A, B, C, or D. In addition, this decision guide supplies additional tests to validate the selection of the appropriate case.

Figure 2.

Decision guide applied to the fluoride varnish study described in Application section.

The first step of the decision guide evaluates the joint test, which is a simultaneous test of the equality of the intercepts and the equality of the slopes. If the joint test is not statistically significant, then the lines do not differ in either intercepts or slopes. This is Case III, and it is not necessary to calculate A, B, C, or D. If the joint test is statistically significant, as in the fluoride varnish (FV) study (F-value = 10.15, s = 2, v = 243; P<0.0001), then D is greater than zero, which agrees with the results from the FV study. The next step tests whether the equality of the slopes using Scheffé’s criterion (2F_1−α,2,v) is statistically significant. Case I (A>0) occurs if, and only if, the slopes differ by Scheffé’s criterion. Case II (A<0 and D>0) occurs when the slopes do not differ by Scheffé’s criterion, and the simultaneous test of equality of the intercepts and slopes is significant by the F-test.

For the fluoride varnish study, the estimates of A, B, C and D are a = −0.1023, b = +0.81356, c = −0.48512 and d = +0.46389, respectively. Since a<0 (implies d >0), we then select Case II. Case II is verified by checking whether the slopes do not significantly differ (p > 0.05) using Scheffé’s criterion, where the |t-value| < Scheffé’s criterion: $(1.29<2.47=\sqrt{(2*3.03)})$. After plugging in a, b, c and d for Case II, as described in Appendix A, the results are 0.649 < log₁₀MS (CFU/ml)<7.324. We restrict our inference to the MS range where the data were collected. Therefore, we conclude that the results are 0.649 < log₁₀ MS (CFU/ml)< 6.99.

As shown for the fluoride varnish study, the explicit solution eliminates testing at every value of the covariate. For two or more covariates of interest, this explicit solution is thought to be intractable [7,8]. Hunka and Leighton [9] developed a solution for three covariates by casting an equation within a general linear model framework, which cannot be solved directly. Symbolic processing capabilities of computational software, such as Mathematica, can be used to provide a solution. Hunka and Leighton’s solution is limited to the analysis of covariance framework for non-correlated data and it does not consider the problem of evaluating treatment-effect heterogeneity for baseline characteristics, as described in this paper.

APPENDIX C

SAS macro for evaluating treatment-effect heterogeneity using the Johnson-Neyman methodology

The following SAS macro was used to analyze the CAN DO fluoride varnish data using the Johnson-Neyman logistic regression analysis of any caries incidence vs. no caries incidence (outcome), a dichotomous outcome with a continuous covariate of interest, MS.

The SAS Code starts on the next page.

/***************************START SAS CODE*****************************/

/* SignificanceRegion.sas

   Macro for performing Johnson-Neyman for a logistic regression model.
   (Similar SAS code adapted from the generalized linear mixed model de-
scribed by Lazar and Zerbe 2011)

     The input parameters are:
     SignificanceRegion
               datasetname = data set name
               outcome = Dichotomous outcome variable (0 or 1)
               treatment = Treatment Indicator (0 or 1)
               continuousvar= baseline continuous variable of interest

*/
%macro SignificanceRegion(datasetname,outcome,treatment,continuousvar);
proc glimmix data=&datasetname oddsratio ;
class &treatment;
model &outcome(event='1')= &treatment &treatment*&continuousvar   /s
dist=bin link=logit noint;
   /*Joint Test*/
   contrast 'contrast Fixed' &treatment 1, &treatment*&continuousvar
1 ;
  /*Difference in Slopes to Calculate A*/
  estimate 'slope' &treatment*&continuousvar −1 1;
  /*Difference in the Intercepts to Calculate C*/
  estimate 'int' &treatment −1 1 ;
  /*Used to Calculate the Covariance for B*/
  estimate 'intslope' &treatment −1 1 &treatment*&continuousvar −1 1;
/* Outputs the above information using the output delivery system*/
  ods output estimates=estimates;
/*Alternative way to determine the Significance Region is to compare
Scheffe's Constant to the t-value based on the following calculation
/*
   estimate 'check 0' &treatment 1 &treatment *&continuousvar 0/or;
   estimate 'check 3.5' &treatment 1 &treatment *&continuousvar 3.5/or;
   estimate 'check 6' &treatment 1 &treatment *&continuousvar 6/or;
    */

  run;
proc sort data=estimates;by df;
data f;set estimates;by df;
/*Denominator degrees of freedom determined from the joint test speci-
fied in the model*/
if first.df;
/*F-statistic*/
F=finv(0.95,2,df);
/*Use Scheffe to compare to the t-statistic*/
Scheffe = sqrt(2*f);
match=1;
keep f match Scheffe;
run;

proc print data=f;run;
data estimates2;set estimates;match=1;run;
data estimates3;merge f estimates2 ;by match;
data intestimates;set estimates3;
if label='int' then do;InterceptEst=estimate;IntVar=StdErr**2;
 C = (InterceptEst**2)−(2*f*IntVar);output;end;
keep C InterceptEst IntVar f;
run;
data slopeestimates;set estimates3;
if label='slope' then do;SlopeEst = estimate;SlopeVar=StdErr**2;
slopesq=SlopeEst**2;
A = (slopesq)−(2*f*SlopeVar);output;end;
keep A SlopeEst SlopeVar ;
run;
data intslope;set estimates3;if label='intslope' then do;IntSlopeEst =
estimate;IntSlopeVar=StdErr**2;output;end;
keep f IntSlopeEst IntSlopeVar;
run;
data all;merge intestimates slopeestimates intslope;
/* could calcuate cov using formula as described in Lazar & Zerbe
(2011);
Form 1: V((a1−a2)+(b1−b2))=V(a1−a2)+V(b1−b2)+2Cov((a1−a2),(b1−b2))
So Cov((a1−a2),(b1−b2)) =( V((a1−a2)+(b1−b2))−V(a1−a2)−V(b1−b2))/2

Or use this formula; same formula as described in Lazar & Zerbe (2011);
Form 2: V((a1−a2)−(b1−b2))=V(a1−a2)+V(b1−b2)−2Cov((a1−a2),(b1−b2))
So Cov((a1−a2),(b1−b2))=(V(a1−a2)+V(b1−b2)−V((a1−a2)−(b1−b2)))/2*/
covariance=(IntSlopeVar-intvar-slopevar)/2; /*using form 1*/
run;

data all1;set all;
B=2*((InterceptEst*SlopeEst)−(2*f*Covariance));
D=(B**2)−(4*A*C);
f2sqrt=sqrt(f*2);
if A>0 then do; Case1lower=((−B−sqrt(D))/(2*A));Case1upper = ((−B+sqrt
(D))/(2*A));end;
if A<0 and D>0 then do; Case2lower=((−B+sqrt(D))/(2*A)); Case2upper=((−B
−sqrt(D))/(2*A));end;
label Case1Lower= 'Case I X< ';
label Case1Upper ='Or X>';
label Case2Lower = 'Case II';
label Case2Upper = '<X< ';
F_To_Compare_to_T=sqrt(f*2);
label F_To_Compare_to_T = 'Scheffe Constant For Comparing to T-Value';;
run;
proc print data=all1 noobs label;var A B C D Case1Lower Case1Upper
Case2Lower Case2Upper F_To_Compare_to_T;run;

%mend;
/*
Macro call for CANDO fluoride varnish dataset
Intended is the name of the dataset, dfs1 is the outcome variable,
intended1 is the treatment variable, mutansStrep is the variable of in-
terest measured on a continuous scale;
*/
%SignificanceRegion(intended,dfs1,intended1,mutansStrep);
/*************************END SAS CODE*********************************/

Before using the above macro, we suggest that the appropriate model be fitted to the data using the usual model fitting criteria. Examples of the Johnson-Neyman approach for longitudinal data suitable for generalized linear mixed models using SAS GLIMMIX with associated SAS code can be found in Lazar and Zerbe (1).