Point: Proposing the Electrokinetic Model

Abstract

It is still not fully resolved how the glomerular filter works and why it never clogs. Several models have been proposed. In this review, we will compare the most widely used “pore model” to the more recent and refined “electrokinetic model” of glomerular filtration. The pore model assumes the existence of highly ordered regular pores, but it cannot provide a mechanistic explanation for several of the inherent characteristics of the glomerular filter. The electrokinetic model assumes that streaming potentials generate an electrical field along the filter surface which repels the negatively charged plasma proteins, preventing them from passing across the filter. The electrokinetic model can provide elegant mechanistic solutions for most of the unresolved riddles about the glomerular filter.

Each day, our kidneys produce about 180 L of primary filtrate, which is virtually free of plasma proteins. For this purpose, about 10 kg of plasma protein must be retained by the glomerular filter, so that less than 1 gram of protein passes into the proximal tubule from where it is reabsorbed and, in part, returned to the circulation (1). There is continuing controversy about how the glomerular filter accomplishes this extraordinary task (2). Two alternative models for glomerular filtration will be discussed here: the “pore model” and the “electrokinetic model.”

The Pore Model

In the “pore model,” the glomerular filter is regarded as a classical filter, where an impermeable wall is perforated by highly selective small and large pores. More recently, derivatives of the pore model (e.g. heteroporous model or charged fiber model) have been proposed to account for the unexpected differences in permeability of different macromolecules. These models are nevertheless based on a concept similar to the pore model. Small pores (or gaps with precisely defined diameters) allow the passage of small molecules (water and electrolytes), while the much less frequent large pores allow the passage of macromolecules (plasma proteins or tracer substances like Ficoll) (Figure 1A). In a classical filter, 2 major forces drive plasma proteins into and across the filter: convection and diffusion (Figure 1A). Convection is driven by the drag of the bulk flow (water) across the barrier and is proportional to the effective filtration pressure. Diffusion is driven by the concentration difference within the capillary lumen and the primary filtrate.

FIGURE 1 —

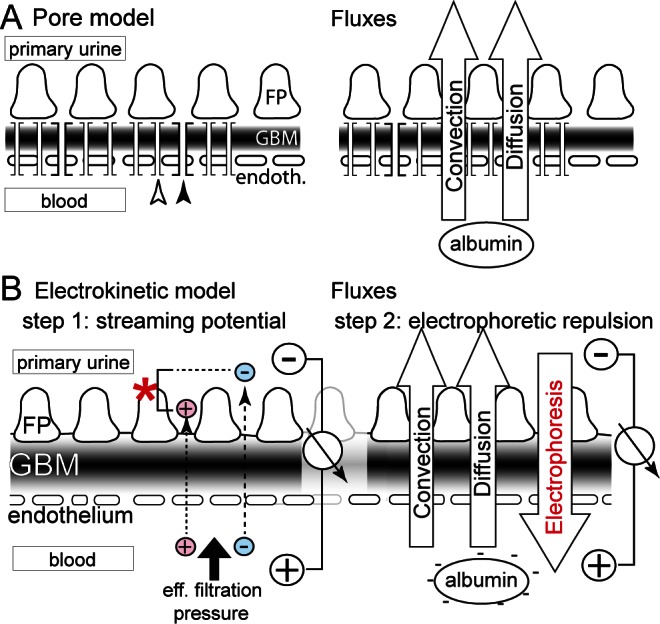
Schematic of the models for glomerular filtration. A. In the pore model, the glomerular filter is envisioned as an impermeable wall perforated by highly defined pores. Small pores (white arrow) allow the passage of water and small solutes, while rare large pores (black arrow) allow the passage of macromolecules. Two fluxes drive albumin across the barrier: convection and diffusion. Only the small size of the pores restricts albumin from passing. Proteinuria is understood as a pore-pathy, where pore diameter increases. B. In the electrokinetic model, a streaming potential (asterisk) is generated by the effective filtration pressure and slight differences in the passage of small ions (red, blue) (step 1). This electrical field acts on negatively charged albumin, preventing its passage across the barrier (step 2). Electrophoresis prevents the influx of albumin into the filter driven by convection and diffusion. FP = podocyte foot processes; GBM = glomerular basement membrane.

The recently proposed “electrokinetic model” (3) assumes that, in addition to the 2 above-described forces, an electrical field is generated across the barrier by the physical phenomenon of a “streaming potential” (step 1), which in turn prevents the negatively charged (anionic) plasma proteins from entering or passing the filter (step 2).

Step 1

Streaming potentials occur in every filtration process because small ions (and also pure water which acts as a dipole) adhere in layers of alternating charge, termed “electrical dilayers,” to the filter surface. Because the ions in these layers have different mobilities in the filtration process, either cations (e.g. sodium, potassium) or anions (e.g. chloride, bicarbonate) can pass the filter more easily when filtration pressure is applied (Figure 1B, step 1). The physical effects are explained in more detail in the supplemental paragraph “Electrical double layers.” This generates a streaming potential proportional to the effective filtration pressure. The magnitude and polarity of this electrical field depends on the electrical characteristics of the filter and cannot be predicted from theory. In general, a specific polarity is observed more commonly in a negatively charged filter (i.e. positive in Bowman’s space) but either polarity is physically possible (4,5). The polarity of the streaming potential is very important because it determines the direction in which plasma proteins will be driven by the electrical field in step 2. To resolve this important question, our group has succeeded in measuring a streaming potential across a filtering glomerular capillary by micropuncture in vivo for the first time (6). In mammalian kidneys, it is technically challenging to micropuncture glomerular capillaries due to their small diameter (about 4 – 5 μm). In Necturus maculosus (an amphibian with capillary diameter of 50 μm), a streaming potential was detected that was positive within the capillary and negative in Bowman’s space with an average field strength of 1600 V/m at mammalian filtration pressures (i.e. 0.1 – 0.7 mV across the barrier depending on the position of the microelectrode and proportional to effective filtration pressures). The uncommon polarity was later confirmed by an independent group ex vivo using an isolated basement membrane of bovine lens, which has a similar composition to the glomerular basement membrane (GBM) (7).

Step 2

The electrokinetic model predicts that the streaming potential is sufficient to repel the plasma proteins from entering the glomerular filter. Proteins are retarded by the gel-like mesh-work/matrix of the endothelial glycocalyx and GBM, where they are subject to the electrophoretic force of the streaming potential (Figure 1B, step 2). This can be imagined as a wind (i.e. the electrophoretic force) blowing plasma proteins away from the filter back into the blood. The “sails” of the plasma proteins are their negative charges.

Of note, streaming potentials are different from “charge selectivity.” A streaming potential is a dynamic electrical field across the glomerular filtration barrier that is proportional to filtration pressures. “Charge selectivity” describes the difference in permeability of macromolecules (proteins or polymeric tracers, such as dextrane) depending on their charge. It has been proposed that negatively charged macromolecules penetrate the glomerular filter less easily because they are repelled by the static negative (electrostatic, coulombic) charges of the matrix fibers (or within the pores when assuming the pore model) within the filter. In short, “charge selectivity” means that the gaps (or pores) of the glomerular filter appear smaller because of electrostatic interactions (repulsion) with the fixed negative surface charges for negatively charged macromolecules. We proposed that the phenomenon of “charge selective” filtration of proteins can also be explained by electrophoretic interactions with the streaming potential—such that electrically charged pores with precisely defined diameters are not required to explain this phenomenon.

In previous studies, albumin was shown to be excluded from the glomerular filter in a logarithmic fashion at the level of the endothelium and its glycocalyx (8,9). This logarithmic distribution can best be explained by an electrical field (generated by a streaming potential). This finding also strongly suggests that the endothelial glycocalyx is likely a major site for generation of the streaming potential (in addition to the GBM [7]). Finally, to address the relevance of the streaming potential directly, we determined the electrophoretic mobility of albumin in isolated perfused kidney. The results suggest that weak electrical fields are sufficient to influence the permeability of albumin, as predicted by the electrokinetic model (manuscript in preparation).

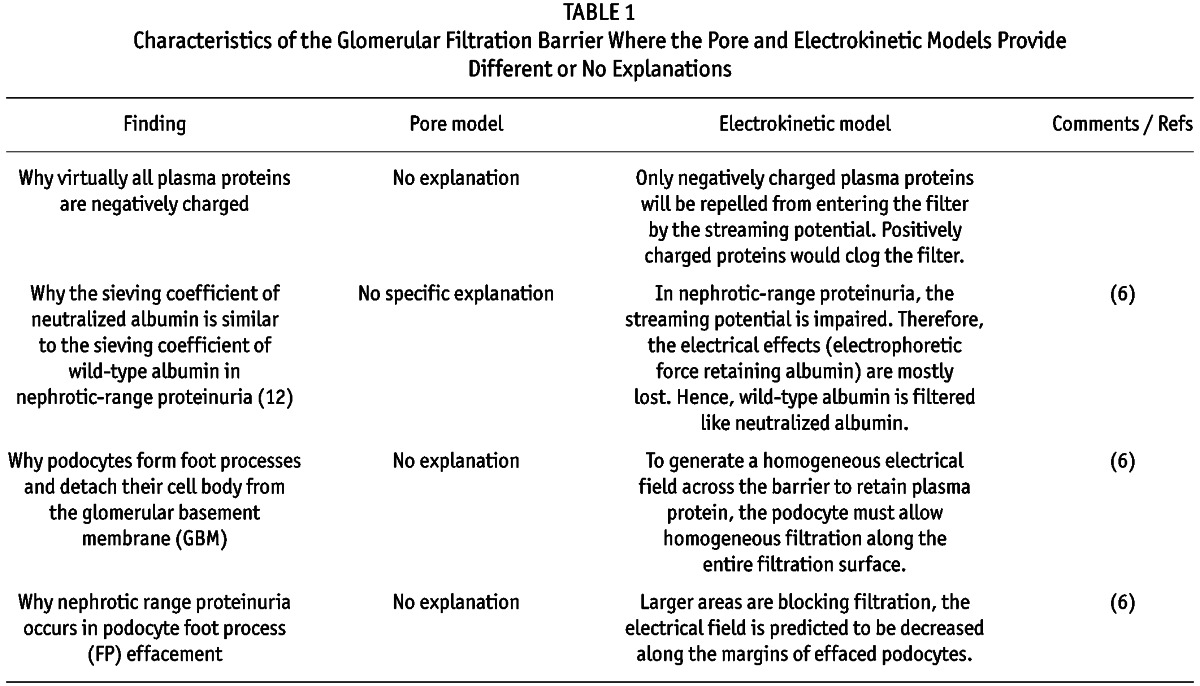
To compare the validity of both models and due to size restrictions, selected unresolved characteristics of the glomerular filtration barrier will be discussed. More points are highlighted in brief in Table 1. Specific issues raised by Rippe & Öberg are addressed in the supplemental information.

TABLE 1.

Characteristics of the Glomerular Filtration Barrier Where the Pore and Electrokinetic Models Provide Different or No Explanations

There are no Pores

According to evidence provided by electron microscopy, an impermeable barrier with highly ordered regular pores does not exist. An effort was made to describe 4 nm pores within the slit diaphragm (10,11). However, plasma proteins are excluded already at the level of the endothelium and inner aspect of the GBM (8,9). Also, in a classical stack of filters, as required by the pore model such as the glomerular filtration barrier, the most selective filter (slit) must not be positioned last, or else the retentate (proteins) accumulates before the slit within the filter and clogging occurs (12).

A Mathematical Formula Can Only Show You What You Feed into it

If the underlying physical model of a formula is incomplete, the results will be inaccurate. The pore theory considers only 2 forces governing albumin filtration; it does not consider electrical effects. The forces can be described mathematically (Figure 2A). However, since the results of this formula did not match experimental results, correction factors were introduced (“hindrance factors”) that depend on the particle-to-pore size (particle = albumin; pore size is calculated mathematically from experimental results for each individual particle). For albumin, the convective and diffusive hindrance factors are, respectively, H_C = 0.0098 and H_D = 0.000219 (13). Thus, the results are modified by 2 – 4 orders of magnitude to match experimental results. For larger molecules (e.g. immunoglobulin), the correction factors become even more significant (3 – 6 orders of magnitude) (13). Since the mathematical model is based on the existence of specific pores (which do not exist), it is likely that not all forces governing filtration of albumin are considered by the formula and that other unknown forces/factors are compensated for by the hindrance factors, for example the electrical effects such as the streaming potential.

FIGURE 2 —

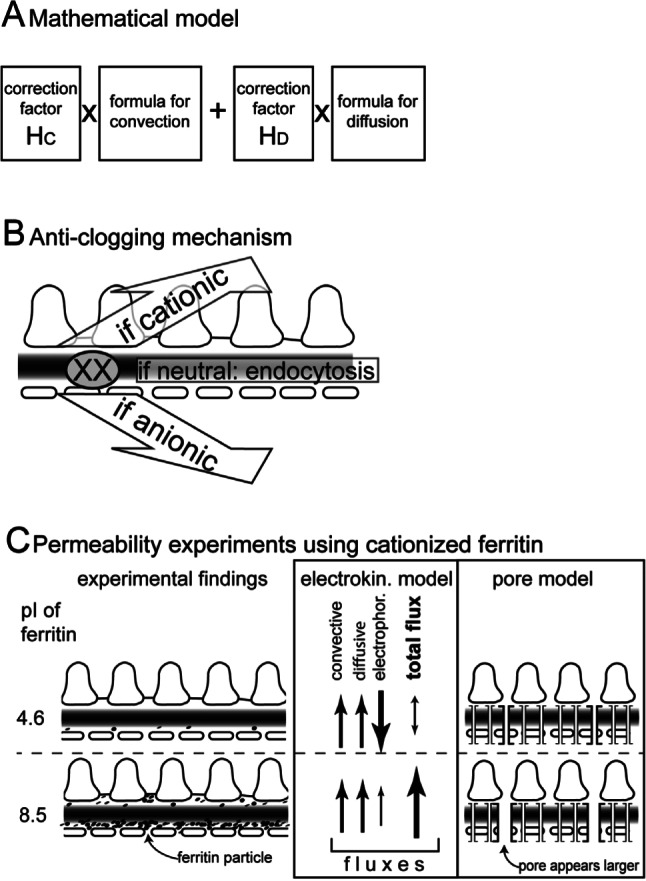
A. Schematic of the pore model formula to calculate the albumin sieving coefficient (i.e. the fraction that passes the glomerular filter). Two fluxes are added: convection and diffusion. In order to match experimental data, correction factors were introduced (“hindrance factors”) that modify the result by several orders of magnitude. B. Anti-clogging mechanism of the electrokinetic model. If a macromolecule (XX) is trapped within the filter, the electrokinetic model predicts that it will be removed by electrophoresis since macromolecules are virtually always electrically charged. A small fraction of macromolecules may not bear sufficient charges, and it is predicted they will be removed by endocytosis by endothelial cells and podocytes. C. Summary of permeability experiments using wild-type negatively charged (pI = 4.6) or neutralized/slightly positively charged ferritin (pI = 8.5). Negative ferritin is excluded from the filter, while neutral ferritin passes the filter and is partially retained by the GBM, clogging the filter. The electrokinetic model provides a consistent explanation for all of the experimental findings, since negative ferritin is repelled while neutral ferritin freely enters, passes, and clogs the filter. The pore model cannot explain why negative ferritin does not enter the filter. Regarding neutralized ferritin, the pore model predicts correctly that neutral ferritin passes the filter better (because the apparent pore diameter appears wider) but it predicts less retention and clogging, which is inconsistent with experimental results. Hc = convective hindrance factor; Hb = diffusive hindrance factor; pI = isoelectric point.

In summary, the mathematical model can be used to describe existing experimental results (e.g. by adjusting the correction factors or by introducing another pore), but it cannot be used to make predictions about how the filter behaves in a novel situation. For this reason, we recommend caution when considering any argumentation based solely on mathematical calculations.

Why the Filter does not Clog

Any classical filter system clogs unless it is actively cleaned. While the pore model does not address this problem, a simple solution is offered by the electrokinetic model. Since virtually all macromolecules are electrically charged, they will be removed by electrophoresis into the blood (if negative) or the urine (if positive) (Figure 2B) (3,13). Virtually all plasma proteins are negatively charged, so that they will be retained within the blood. Crucial experiments were performed from the 1960s to the 1980s tracing filtration of macromolecular probes (e.g. ferritin), where the charge was modified progressively from negative (anionic, i.e. low isoelectric point, pI) to positive (cationic, high isoelectric point) (14–16) (Figure 2C). The results could not be interpreted at that time. They showed consistently that when the charge of a large protein becomes more neutral and positive, it enters and passes the filter and clogs the filter progressively along the inner aspect of the GBM. Since this already happens with a neutralized protein, electrostatic adherence cannot explain this observation. This result is inconsistent with the pore model, since a neutralized (or even cationic) protein should detect wider pores because of “charge selectivity,” and pass the filter more easily with less retention in the filter and less clogging.

We agree with Dr. Rippe that the experimental evidence in favor of “charge selectivity” is convincing (17). However, the electrokinetic model may provide a better explanation for “charge selective” filtration of macromolecules as well as of the above-mentioned experiments using cationized ferritin: Positively charged ferritin is driven into the filter by electrophoresis (explaining increased permeability of cationized proteins), where it is retained in part by the GBM so that clogging of the filter occurs (Figure 2C).

Summary

The pore model has been very useful. It was the motivation for a multitude of excellent meticulous studies, the results of which are still of great value today. However, we should keep an open mind, and a large body of evidence suggests that the model for glomerular filtration needs to be refined. In our view, the electrokinetic model provides for the first time a relatively simple, consistent, and mechanistic solution for the great majority of so far unexplained issues about the filter. As with every new model, more studies are needed to validate the new concept.