Multiscale computational models in physical systems biology of intracellular trafficking

Abstract

In intracellular trafficking, a definitive understanding of the interplay between protein binding and membrane morphology remains incomplete. The authors describe a computational approach by integrating coarse‐grained molecular dynamics (CGMD) simulations with continuum Monte Carlo (CM) simulations of the membrane to study protein–membrane interactions and the ensuing membrane curvature. They relate the curvature field strength discerned from the molecular level to its effect at the cellular length‐scale. They perform thermodynamic integration on the CM model to describe the free energy landscape of vesiculation in clathrin‐mediated endocytosis. The method presented here delineates membrane morphologies and maps out the free energy changes associated with membrane remodeling due to varying coat sizes, coat curvature strengths, membrane bending rigidities, and tensions; furthermore several constraints on mechanisms underlying clathrin‐mediated endocytosis have also been identified, Their CGMD simulations have revealed the importance of PIP2 for stable binding of proteins essential for curvature induction in the bilayer and have provided a molecular basis for the positive curvature induction by the epsin N‐terminal homology (EIMTH) domain. Calculation of the free energy landscape for vesicle budding has identified the critical size and curvature strength of a clathrin coat required for nucleation and stabilisation of a mature vesicle.

1 Introduction

Numerous mutations are present in malignant cells of a tumour, however, only a subset of them have presumably been selected because they confer a fitness advantage for malignant cells in a heterogeneous tumour microenvironment [1, 2]. Such mutations are correlated with providing a gain of function in several categories of cancer cell signalling including cell adhesion and motility, signalling, transcriptional regulation, cellular metabolism and intracellular trafficking [3, 4]. Finding mechanistic links between such alterations and the hallmarks of cancers such as increased proliferation and survival, aggressive invasion and metastasis, evasion of cell death, and increased metabolism [5, 6] is a central goal in cancer biology. Elucidation of such mechanisms is expected to directly aid in biomarker development, and in identifying targets for drug therapy.

There is a growing appreciation for the importance of intracellular trafficking in cancer progression [7]. Yet, traditional methods in cell biology such as phospho‐proteomics, immuno‐precipitation, polymerase chain reaction and direct sequencing along with network‐based theories and bioinformatics are not directly amenable to membrane‐mediated phenomena such as cell adhesion, cell motility and intracellular trafficking. Integration of models from physical biology – such as those of cell membranes and curvature based on statistical mechanics, effect of tension and force because of cytoskeleton, cell–cell and cell–matrix adhesions – and models from systems biology – such as those describing signal transduction based on networks – can lead to quantitative paradigms of intracellular trafficking. This approach is complimentary to, and imposes crucial (structural as well as energetic) constraints on, mechanisms gleaned from cell‐based, high‐throughput genomic and super‐resolution microscopy experiments.

The insight obtained from this modelling approach together with experimental data can prove effective in dissecting how malignant cancer cells employ/alter/hijack intracellular trafficking mechanisms to gain a fitness advantage. Such models can also be used to explore new models/mechanisms for (altered) trafficking of growth factor receptors and how they contribute to cancer progression. Three specific examples discussed below, collectively serve as illustrations to this argument.

• (1) Preferential proliferative signalling: proteins implicated in trafficking can direct/alter the localisation of receptors in intracellular organelles such as the endosomes, which in turn, manifests in altered signalling. Altered trafficking can lead to robust changes in downstream signalling and in particular differentially alter the activation of proliferative/survival pathways, and in doing so it is poised to alter cell‐fate [8–10].

• (2) Chemokine receptor signalling and relevance to cancer progression: overexpression of chemokine receptors has been correlated with metastatic behaviour in certain breast cancers [11, 12]. An imbalance because of increased chemokine mediated migration and/or decreased cadherin‐mediated cell–cell contact can provide a stimulus for invasive behaviour. Trafficking of chemokine receptors through clathrin‐mediated endocytosis and cadherins, integrins through both clathrin and non‐clathrin pathways are central in quantifying the balance/imbalance between cell–cell adhesion and cell migration, and has been correlated with metastatic behaviour [11].

• (3) Mechanism of formation of autophagosomes: autophagy is an extreme cellular response employed by malignant cells under conditions of stress and starvation in order to remodel >70% of its proteome, re‐tread core cellular processes including metabolism and prolong cell survival. The formation of autophagosomes is correlated with large alterations in signalling and cellular metabolism in malignant cells [13]. Cell studies and genetic screens in yeast and mammalian systems have outlined the proteins and lipid components involved in the formation and maturation of autophagosomes in response to the cellular response of autophagy. The mechanisms of nucleation of double‐walled membrane vesicles characteristic of autophagosomes are not precisely known.

Molecular and membrane mediated mechanisms that can lead to changes in trafficking and localisation because of copy number variations of proteins (such as expression levels of receptors or adaptors) and because of changes in the extracellular or cellular microenvironment (such as stiffness of matrix proteins or cytoskeletal linkages), thereby providing mechanistic links between the circumstances for altered trafficking and hyper‐proliferative signalling. Altered endocytosis has been singled out as a mechanism by which a malignant cell is able to generate hyper‐proliferative signals (by modulating receptor tyrosine kinase activity) or decreased cell‐adhesion and increased motility (by altering the trafficking of adhesion proteins or chemokine receptors) [7, 14]. Hence, there is now considerable interest in defining the emerging roles for endocytosis (trafficking) and membrane curvature in mechanisms governing cancer cell signalling.

In light of the important role of these elementary cellular mechanisms in cancer progression, we focus on building a computational platform for constructing (minimal, yet predictive) models of such intracellular processes involving the membrane by integrating theoretical and computational approaches from physical biology (statistical mechanics and molecular simulations) and systems biology. In this paper, we illustrate our approach through an application to the ubiquitous trafficking pathway of clathrin‐mediated endocytosis [15, 16].

We have recently discussed, through construction of minimal models, the various components limiting clathrin coat formation [17, 18]. In particular, we introduced a three‐species inhomogeneous Potts model (cellular Potts model or CPM) representing clathrin, adaptor protein (AP‐2) and free membrane and showed that weak hydrophobic associations (of the order of a few k_B T) can capture all the relevant findings of the clathrin coat nucleation and growth both in vitro as well as in vivo [17]. In the regime corresponding to low levels of clathrin, the coat nucleates on the membrane via association with adaptors (AP‐2), to which they bind more strongly. In the absence of AP‐2, the model predicts no coat nucleation, consistent with experiments. When the clathrin concentration is increased, coat formation is rescued even in the absence of AP‐2. Adaptor‐free clathrin cages have been observed in cell‐free experiments with high levels of clathrin concentration, and in auxilin knockdown experiments where auxilin‐dependent inhibition of clathrin self‐interaction is abrogated, corresponding to the model result [17].

Recruitment of ligand‐activated receptors into the clathrin coat is thought to be essential for coat growth as it is believed that activated receptors increase levels of phosphatidylinositol 4,5‐bisphosphate (PtdIns(4,5)P₂) in a ligand dose‐dependent manner. Upon capture of these receptors by the coat, AP‐2‐receptor complexes are formed, which activate phosphatidylinositol phosphate (PIP) kinase (PIPK) type Iγ [19, 20]. The PIPK then increases local levels of PtdIns(4,5)P₂, which diffuses among other membrane phospholipids. In this way, the receptor activation can clearly affect coat size, since higher levels of PIP₂ produce a larger membrane area of enriched PtdIns(4,5)P₂ to sustain coat growth. We have modelled the synthesis, diffusion and absorption of membrane‐bound species using CPM; specifically, we showed that increasing levels of activated receptors (in particular, receptor‐AP‐2 complex) within a coat lead to larger stable coats, as predicted by the model [17]. In a subsequent extension of this model, we considered epsin proteins binding to the lattice of a growing clathrin coat through the interaction of the clathrin‐associated protein–binding (CLAP) domain of epsin with the clathrin triskelion [21]. This way, multiple epsins localised spatially and orientationally templated on the clathrin coat collectively play the role of a curvature inducing capsid. In addition, epsin serves as an adapter in binding the clathrin coat to the membrane through the interaction of its epsin N‐terminal homology (ENTH) domain with the PtdIns(4,5)P₂ molecules on the membrane [18].

However, several questions remain unaddressed pertaining to the mechanisms of the coat assembly. (1) How do clathrin coat size and vesicle size get regulated in vivo [17]? What is the critical curvature strength necessary to stabilise a budding vesicle? (2) What are the mechanisms underlying the curvature generation by epsin and by the coat assembly and what is the strength and shape profile of this induced curvature field? (3) Does the epsin‐AP‐2‐clathrin coat assembly have sufficient interaction strength to nucleate and stabilise a coated vesicle? We address these questions directly in this paper by introducing a multiscale modelling strategy.

Our modelling utilises computational methodologies to integrate coarse‐grained (CG) molecular dynamics simulations and continuum Monte Carlo (CM) field‐based approaches for cell membranes in the context of the signalling/trafficking microenvironment of relevance to clathrin‐mediated endocytosis [17]. The continuum field‐based approach to cell‐membrane deformation, curvature and energetics, enables the study of membrane morphologies under extreme curvature [18, 22–27]. The mechanisms of curvature induction by proteins are captured accurately by the near‐atomistic resolution of the CG models [26, 28–35]. We also introduce a framework to achieve a novel integration of the CG models for protein–lipid interactions with the CM models for membrane through a mapping method that defines the strength, extent and anisotropy of the local curvature field induced by the protein on the membrane. We show how our models based on physical principles can be placed within the context of the constraints placed by cellular signalling in endocytosis. This integrative modelling approach allows for quantification of mechanisms surrounding trafficking and signalling proposed in the literature and subject them to constraints based on physical–chemical interactions, energetics and cooperative phenomena. Moreover, our model is minimal and helps identify the core interactions that lead to emergent behaviour and thus allows us to focus on key sets of interactions from a dataset of high‐dimensionality arising from high‐throughput experiments.

2 Methods

2.1 Continuum (CM) and mesoscale methods to study interaction of proteins with biological membranes

Traditional multiscale modelling involves bottom‐up approaches of systematically coarse‐graining the atomistic description, in order to access the mesoscale [36]. Alternatively, a top‐down approach can be pursued, in which models are constructed at the mesoscale based on phenomenological interaction potentials, and the parameters are determined directly by independent biophysical experimentation [37]. In works published in the literature, both approaches have been extensively employed as viable avenues for pursuing models that provide physical insight as well as for enabling direct contact with experiments [17].

We have modelled the membrane energy E using the Helfrich formulation [17, 18, 38], which is parameterised by membrane elastic bending rigidities, and local mean and Gaussian curvatures of the membrane. The effect of curvature inducing proteins (such as ENTH and Bin–Amphiphysin–Rvs (BAR) domains) and scaffolds (such as the clathrin coat) are modelled through the presence of spatially varying spontaneous (or intrinsic) curvature of the membrane. Protein diffusion is modelled as probabilistic hopping events along the membrane surface. In each diffusion step, while we fix the membrane profile, we allow the protein to translate continuously on the x–y plane to a new position, then the energy change associated with such movement is calculated and this movement is rejected or accepted according to the Metropolis criteria. Background curvature induced in the membrane (such as due to presence of a clathrin coat) is modelled as static curvature fields [39].

Using our simulation methodology, we have analysed the equilibrium behaviour of bilayer membranes under the influence of curvature‐inducing proteins [40]. This study revealed how the protein diffusion and cooperativity associated with a multitude of protein–membrane interactions elicits rearrangements and new topographies in the membrane phase. Based on our model simulations, we predicted that, depending on the density of membrane‐bound proteins and the degree to which a single protein can induce intrinsic mean curvature in the membrane, a range of membrane phase behaviours can be observed including two different modes of vesicle‐bud nucleation and repressed membrane undulations. A state diagram as a function of experimentally tunable parameters to classify the underlying states was constructed [40].

At the micron scale, where a cell and its internal organelles display amazing complexity in their shape and organisation, the physical properties of a biological membrane can be better understood using phenomenological models, the well‐known being the Helfrich Hamiltonian given by [41, 42]

$${\mathcal{H}}_{\text{el}}=\int \mathrm{d}A\left\{\frac{\kappa }{2}(2H-H_0){}^2+2{\kappa }^{\prime }K+\sigma \right\}$$ (1)

Here, the membrane is approximated to a quasi‐two‐dimensional (2D) fluid, elastic sheet, with lateral dimensions large enough to neglect its thickness.

The phenomenological parameters, κ, κ′ and σ are the bending rigidity, Gaussian rigidity and surface tension of the membrane, whose surface area is A. The gauge invariants H = (c ₁ + c ₂)/2 and K = c ₁ c ₂ are, respectively, the mean and Gaussian curvature of the membrane, where c ₁ and c ₂ are the two principal radii of curvatures, and H ₀ is the spontaneous curvature (magnitude of imposed deformation) imposed on the membrane by a curvature modulating factor, which in general denotes any heterogeneity in composition of the membrane, or the presence of curvature inducing protein‐inclusions or assemblies [42].

For a membrane with fixed topology, by virtue of the Gauss–Bonnet theorem, the Gaussian rigidity term remains a constant irrespective of the membrane morphology, and is hence not included in our studies using MC methods. The effects of κ and σ are investigated in this study. Several studies employing the small slope approximations to (1) have been published [39, 40, 43], but they have the limitation of not being able to predict morphological transitions such as overhangs in the membrane structure (e.g. in vesicle budding).

Analytical and semi‐analytical techniques, based on (1) in the large slope (high curvature) limit, are only useful when the membrane under investigation has a smooth, axisymmetric shape [18, 44, 45]. However, a vast majority of naturally occurring membrane morphologies in the cellular context are influenced by thermal fluctuations that endows the membrane with non‐axisymmetric shapes. We overcome this problem and explore the entire conformational space using computations based on the dynamically triangulated MC (DTMC) technique [24]. This method has two advantages: (a) thermal fluctuations that play a key role in the self‐organisation of membranes are accounted for, and (b) the fluidity of the membrane, which makes it different from other thin film systems, is also preserved.

It has been shown that the physical properties of the triangulated membrane complements analytical results in the limit of large κ, where the membrane is fairly smooth. In DTMC, the thin sheet representing the middle plane of a membrane bilayer is discretised into N material points (vertices), denoted by { X }, and interconnected by a set of triangles (faces), denoted by { T }; with each triangle representing a planar membrane patch, see Fig. 1, with a characteristic length scale of the link between two vertices a ₀ ≤ ξ _p, where ξ _p is the persistence length of the membrane bilayer. The length‐scale a ₀ can be also thought of as the characteristic size of the material particle that forms the surface; a concrete discussion on the value of a ₀ for the specific systems we have investigated here is available in Section 3.4. A patch of the triangulated membrane is shown in Fig. 1 a.

Fig. 1.

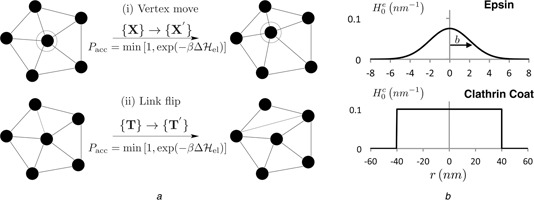
Monte Carlo moves for the membrane model and illustration of the various curvature fields

a Triangulated membrane patch‐vertex shift and link flip MC moves

b Curvature field functions for epsin and clathrin

The triangulated membrane explores all accessible equilibrium states in its phase space, corresponding to a given thermodynamic state point, through the set of MC moves, shown in Fig. 1 a. These moves include: (a) ‘vertex move’ – the position of a randomly chosen vertex is perturbed around its mean position such that { X } → { X ′} and (b) ‘link flip’ – a link shared between two triangles is flipped by reconnecting the previously unshared vertices in the two triangles: are accepted using the Metropolis scheme with a probability given by the Boltzmann factor of the energy change associated with the move.

In this framework, we quantify the surface deformations, induced by the membrane proteins, as curvature fields (Fig. 1 b) and study this phenomenon using an isotropic curvature model. Membrane deformation because of curvature‐inducing proteins such as ENTH domain containing epsin is modelled as a Gaussian function with a range b_i and magnitude C _0,i . Hence the spontaneous curvature induced at a membrane vertex v because of the i th protein at vertex v_i is

$$H_{0,i}^e(v)=C_{0,i}\exp \left(\frac{(r_v-r_i){}^2}{b_i^2}\right)$$ (2)

where r_i is the 3D position vector of vertex v_i . The net induced curvature, because of N_e proteins, is a superposition of these individual contributions

$$H_0^e(v)=\sum _{i=1}^{N_e}{H}_{0,i}^e(v)$$ (3)

We justify the choice of this field on the basis of molecular‐scale computation, see Section 3. The ENTH domain diffuses on the membrane manifold through an additional MC move – where the hopping of a protein at a vertex v to any of its neighbouring vertices is accepted using the Metropolis criterion. In addition to the mobile curvature inducing proteins described above, curvature induced by static curvature inducing entities, such as a clathrin coat is modelled as, (Fig. 1 b)

$$H_0^c(v)=C_0\mathrm{\Gamma }(r_0)$$ (4)

where Γ(r ₀) is a function that is unity within a circular domain (centred at zero) of radius r ₀ and zero otherwise; r ₀ is the linear extent (radius) of the curvature‐field induced by clathrin and C ₀ is the magnitude of clathrin‐induced curvature; the validation and parameterisation of this field is provided in Section 3.

In our simulations, the membrane is modelled as a thin sheet with fixed projected area (equal to that spanned by the x–y plane) in a cubic box with periodic boundaries in two‐dimensions (i.e. along the x–y plane). The number of vertices and the projected area of the membrane are both held constant during the simulation. Results presented in this paper are obtained for a system consisting of a 30 × 30 triangulated sheet with a link length between vertices initialised as 1.3a ₀. This sets the projected area at 1317a ₀ ² for a system of 900 vertices. Budding morphologies are attained by imposing a circular clathrin coat in the centre of the simulation box according to the step function shown in (4) and illustrated in Fig. 1 b. The radius and curvature induction strength of the clathrin coat along with the membrane elasticity parameters are variables that are controlled as described in Section 3.

Each simulation is equilibrated for 3 million MC steps, where each MC step consists of N vertex moves and L link flips. Free energy methods sample membrane conformations every 1000 MC steps, with only the second half of the trajectory used in analysis (last 1.5 million MC steps).

2.2 Calculation of relative free energies of curved membranes

We have recently developed a computational methodology for calculating relative free energies for fluid membranes subject to spatially dependent intrinsic curvature fields using the method of thermodynamic integration (TI) [39, 42]. To demonstrate the applicability of the method, we considered model systems of membrane deformations with a curvature field in accordance with (4). In the small‐deformation limit, we calculated the free energy change of the membrane [subject to a curvature field imposed by (4)] as a function of the extent of the curvature field (r ₀) as well as the magnitude of the curvature field (C ₀) using the method of TI along C ₀.

By explicitly computing the free energy changes we quantified the change in entropy accompanied with increasing membrane deformation. Based on our results, two important outcomes had emerged: (i) by explicitly computing the free energy changes and by quantifying the loss of entropy accompanied with increasing membrane deformation, we showed that the membrane stiffness increases with increasing intrinsic field, thereby, renormalising the membrane bending rigidity and (ii) we showed that the entropy of the membrane decreases with increasing magnitude of r ₀. These results quantify free energy changes when a planar membrane deforms under the influence of curvature‐inducing proteins at a finite temperature. Here, we extend this approach to the large curvature regime by performing the TI on (1) using the DTMC method [42]. In this method, the free energy is coupled to a coupling parameter λ. The derivative of the Helmholtz free energy F = −k_B T lnQ (Q is the partition function) with respect to λ is given by [46]

$$\frac{\partial F}{\partial \lambda }=⟨\frac{\partial {\mathcal{H}}_{\text{el}}}{\partial \lambda }⟩$$ (5)

and the free energy difference between the states characterised by λ = 0 and λ = 1 is calculated as

$$F_{\lambda =1}-F_{\lambda =0}={\int }_0^1⟨\frac{\partial {\mathcal{H}}_{\text{el}}}{\partial \lambda }⟩\mathrm{d}\lambda$$ (6)

The change in free energy is calculated in the TI method by running a set of simulations with a range of lambda values from 0 to 1, where the integrand in (6) is calculated and stored. The discretised data are then integrated with the trapezoid rule to obtain the free energy difference between λ = 0 and λ = 1. All results shown were obtained with a window resolution of 0.1 (or λ = 0, 0.1, 0.2, …, 1). To determine the accuracy of this window resolution, a sensitivity analysis was performed, where window sizes of 0.05 and 0.02 showed no appreciable difference in free energy. Running each simulation in triplicate and calculating the standard deviation estimated the error in the free energy calculation.

2.3 Molecular modelling and CG molecular dynamics simulations

The mesoscale models described above can be applied to a variety of scenarios if the phenomenological parameters, which connects these models to real systems, can be determined from the molecular details of the systems; see recent example on lamellipod nucleation during cell migration [26]. We achieve this feat in two steps: (1) in this section, we outline the construction of a CG molecular model to quantify the protein–membrane interactions. (2) In the next section, we develop a mapping method, which translates the structural details of the membrane at the molecular level to curvature‐field parameters at the mesoscale (1), (2)–(4).

CG molecular dynamics (CGMD) simulations are employed to resolve the shape and magnitude of the membrane curvature field induced by the curvature inducing protein epsin [35]. Applicability of CGMD techniques requires the complete characterisation of the protein force fields at both the molecular and CG scales – the proteins of interest include ENTH, Exo70 and BAR domains implicated in endo and exocytosis, as well as other membrane remodelling domains (such as PH, PX, PDZ domains, implicated in membrane recruitment and remodelling) [47, 48]. The methodology is well established so far as the structural details of the domains are available from X‐ray crystallography, which is the case for the domains summarised above. Here, we present our strategy for the ENTH domain (part of epsin) on a membrane, as the model system. A recent study reported a fully CG model of how ENTH domains can stabilise tubular geometries observed in vitro when they are mixed with phospholipid bilayers [29]. Here, we show using a dual resolution multiscale model that ENTH domains can also induce and stabilise vesicular buds.

We conduct simulations of the epsin N‐terminal ENTH domain embedded in mixed 4:1 DOPC: DOPS bilayers with physiological (<1%) concentrations of the phosphoinositide lipids, PtdIns(4,5)P₂. In performing CGMD simulations, we employ MARTINI, a CG molecular dynamics force field developed by Marrink et al. [49] to access time and length scales needed to simulate the bilayer membrane, which would be prohibitively costly with all‐atom MD. The CG methodology used in MARTINI retains relevant degrees of freedom with a minimal set of tunable parameters and common chemical building blocks. In MARTINI, groups of four heavy atoms are mapped to one interaction site or ‘bead’ with a standardised mass of four water molecules. MARTINI has been used to study many protein systems [35]. Our simulations are performed in GROMACS [50] using the standard simulation parameters outlined above and described in detail by Monticelli et al. [51]. Each model is solvated in a water box with periodic boundary conditions and with counter‐ions added to create a physiological concentration.

A CG model for the epsin‐ENTH domain was constructed from the crystal structure provided by Ford et al. [21] available in the protein data bank (PDB 1H0A, see Fig. 2 a). CG simulations were performed with the MARTINI force field in GROMACS 4.6.1 [52]. Two different systems with ENTH proteins on a bilayer were studied (Fig. 2): (a) single ENTH domain bound to the bilayer in the presence of PtdIns(4,5)P₂, and (b) four ENTH domains bound to the bilayer in the presence of PtdIns(4,5)P₂. The proteins were coarse grained from the crystal structure according to the ‘Martinize’ program [53]. Each protein was then attached to a pre‐equilibrated bilayer with 12 800 total lipids, including 1,2‐dioleoyl‐sn‐glycero‐3‐phosphocholine (DOPC) and 1,2‐dioleoyl‐sn‐glycero‐3‐phospho‐l‐serine (DOPS) in a 4:1 ratio, along with at least 700 000 water beads (representing four water molecules each) and sodium and chloride ions at a total concentration of 150 mM. After minimising the protein‐bilayer structure, a single DOPS lipid near the PtdIns(4,5)P₂ binding pocket in each ENTH domain was replaced with a PtdIns(4,5)P₂ lipid. The PtdIns(4,5)P₂ were inserted using the ‘g_membed’ utility in GROMACS [54], which iteratively inflates the inserted molecule and minimises the surrounding particles without disrupting the bilayer shape. These structures were minimised using the conjugate gradient method, and simulated under constant volume for 100 ps and constant pressure for an additional 400 ps.

Fig. 2.

Atomic and coarse grain structures of epsin‐ENTH domain with and without the membrane

a Crystal structure of ENTH domain in complex with Ins(1,4,5)P₃

b Molecular model of ENTH domain interacting with the bilayer

c Side view of four ENTH domains (lower panel) and one ENTH domain (top panel) on a bilayer

Simulations at constant pressure and temperature were then equilibrated for 100 ns (CG time) with a time‐step of 20 fs. Subsequent trajectories of 100 ns (CG time) were analysed according to the curvature estimation procedure described below. The Berendsen thermostat and barostat maintained a temperature of 310 K and semi‐isotropic pressure coupling of 1.0 bar both parallel and perpendicular to the bilayer plane with coupling time constants of 1.0 and 2.0 ps, respectively. All other parameters were set per the MARTINI force field specifications [49, 51]. All simulations were performed on supercomputing platforms at the Texas Advanced Computing Center (TACC). The CGMD simulations of the protein‐membrane system were run on parallel architectures with 48–60 processors.

Parameters for PtdIns(4,5)P₂ : Our simulations include PtdIns(4,5)P₂ lipids parameterised by estimating bead type and bond parameters according to the MARTINI formula outlined in [49, 51]. In this case, the carbon ring includes three beads of type P1 (weakly polar) attached to phosphate beads of type Qa (charged) with either a −1 or −2 charge, making the PtdIns(4,5)P₂ equivalent to the singly‐ protonated state. The stearic acid tail is comprised of four type C1 beads (apolar) while the arachidonic acid tail contains four beads of slightly less apolar type C4 followed by a single type C2 bead. These bead type selections are in general agreement with those found in a previous study of membrane protein sequestration [55]. All other bond and angle parameters are chosen to match the standard parameters for MARTINI lipids. Parameters for glycolipids including PtdIns(3,5)P₂ that are fully compatible with MARTINI have been recently published [56], and share many similarities with our parameters. In our simulations, PtdIns(4,5)P₂ binds ENTH domains and remains in the binding pocket defined by the crystal structure [21], see Fig. 2.

2.4 CG/CM interface: molecular model to curvature field mapping

The spirit of the CG/CM interface is a simultaneous and self‐consistent coupling of the CG and CM simulations. In our case, the curvature field induced by a PtdIns(3,5)P₂ ‐bound protein (such as an ENTH domain) is computed directly from CG simulations and passed on to the CM. This is distinct from assuming a constitutive relationship for the curvature fields, in which the matching procedure must be performed at each time step to enable information flow between the CG and CM scales.

Trajectories of 100 ns (CG time) sampled at 200 ps intervals were selected for analysis which is similar to that described in a previous study of curvature induction by the protein Exo70 [26] and is capable of distinguishing the deformation field from undulations in the bilayer. In this method, the bilayer mid‐plane (z ₀ (x, y)) is calculated by averaging the bilinear interpolation of the lipid phosphate group positions for each monolayer onto a regular grid with a 1 nm spacing. The resulting points are filtered by proximity to the proteins: points within 15 nm of any protein were fit to a 2D Gaussian function given by the following expression, where (x ₀, y ₀) is the location of the maximum height A ₀, and θ is the angle of the field, which has standard deviations of σ_a and σ_b in its principal directions, see below

$$\begin{array}{rl}z(x,y)& =A_0\exp \left\{-\frac{{\left[(x-x_0)\cos \theta +(y-y_0)\sin \theta \right]}^2}{2{\sigma }_a^2}\right\}\\ & \times \exp \left\{-\frac{{\left[(y-y_0)\cos \theta -(x-x_0)\sin \theta \right]}^2}{2{\sigma }_b^2}\right\}\end{array}.$$ (7)

Mean curvature was calculated within the 10 nm neighbourhood of the protein according to the expression

$$2H=\frac{(1+z_x^2)z_{yy}+(1+z_y^2)z_{xx}-2z_x{z}_y{z}_{xy}}{{\left(1+z_x^2+z_y^2\right)}^{3/2}}.$$ (8)

In (8), z_x = (∂z /∂x), z_y = (∂z /∂y), z_xx = (∂ ² z /∂x ²), z_yy = (∂ ² z /∂y ²) and z_xy = (∂ ² z /∂x∂y). Some frames contained curvatures corresponding to non‐physical radii of curvature, therefore only frames with maximum curvatures from ±0.001 to ±0.06 nm⁻¹ measured within the simulation box were included in the analysis. The fitting algorithm produced valid fits for 66–73% of the systems with ENTH domains (each consisting of 500 frames) compared to only 42% of the control simulation frames. This curvature estimation method has several useful features. First, by treating the bilayer mid‐plane heights around the proteins as a generic dimple via a 2D Gaussian function – which decays to a flat surface away from the protein – we impose minimal constraints on the shape of the induced ‘dimple’ or ‘bump’ caused by the proteins. Moreover, our 2D Gaussian height function does not assume any angle, extents, peak height or lateral location of the field. This method captures fluctuations in the location of the deformation, which indeed fluctuates around the loci of the proteins. Lastly, by approximating the mid‐plane of the membrane of the vicinity of the protein and measuring its curvature, we more effectively isolate the induced curvature from thermal undulations. In general, this method provides better resolution than other methods, such as direct measurement of the mean curvature from the mid‐plane (results not shown) with minimal assumptions about the deformation field itself.

In addition to direct fitting of the deformation field, we compute the 3D stress tensor across the membrane. This stress tensor is given by the sum of kinetic and configurational terms according to the equation

$$\begin{array}{rl}{p}_V^{\alpha \beta }& =\frac{1}{V}\sum _{i\in V}{m}_i{v}_i^{\alpha }{v}_i^{\beta }+\sum _n\frac{1}{nV}\sum _{⟨j⟩}\sum _{⟨k,l⟩}\left({\nabla }_{j_k}^{\alpha }{U}^n-{\nabla }_{j_l}^{\alpha }{U}^n\right)\frac{{\mathit{r}}_{j_l{j}_k}^{\beta }}{N}\\ & \times \sum _{\lambda =0}^N{f}_V\left({\mathit{r}}_{j_l}+\frac{\lambda }{N}{\mathit{r}}_{j_l{j}_k}\right)\end{array}$$ (9)

The computation of the terms in (9) has been implemented recently in a modified version of the GROMACS integrator [57]. In (9), the 3D stress tensor $p_V^{\alpha \beta }$ is given for a voxel V, where Uⁿ is the n ‐body potential, 〈j 〉 is a sum over all n ‐clusters, ${\mathit{r}}_{j_l{j}_k}^{\beta }$ is the distance vector between particles l and k in the β ‐direction. This formulation uses the Irving‐Kirkwood contour, which consists of a straight line between particles [58]. The resulting force between particles is divided into N bins, with those that intersect the voxel (f_V = 1) contributing to the configurational portion of the stress. Integration of the tensor across the membrane yields an expression for induced curvature (C ₀) at any lateral position: $\kappa C_0={\int }_{z_1}^{z_2}\mathrm{d}z(z-z_0)\left(p_{\mathrm{L}}(z)-p_{zz}(z)\right)$, where z ₀ is the pivotal plane, and p _L (z) and p_zz (z) are the lateral and normal components of the stress tensor. The κC ₀ map provides an alternative strategy for achieving the atom‐to‐field mapping.

The 3D stress tensor map for simulations with zero, one and four ENTH domains was computed for each frame sampled at 200 ps intervals for 100 ns (CG time) and re‐processed using the modified GROMACS [57] with a voxel size of 1 nm³. Simulation trajectories were read using the MD Analysis toolkit [59] and all subsequent calculations were carried out using an in‐house Python code. Each position in the resulting 64 × 64 grid provides an estimate for C ₀ (x, y) given the bending rigidity of κ measured from the q⁻⁴ portion of the height–height undulation spectrum, see Figure S1, supplementary material. We integrate seven voxels on either side of the ensemble‐averaged mid‐plane (z ₁ = −7 nm and z ₂ = 7 nm), since the difference in lateral and normal pressures decays to zero at normal distances beyond the bilayer itself.

We also note that other strategies for establishing the atom to field map are through the analysis of the coupling between curvature and undulations and ensuring that the nature of the coupling is preserved and identical in both CG and CM simulations. These alternative strategies will be pursued in the future.

2.5 Context of the approximations of the continuum (CM) model

Even though our CGMD models have near molecular resolution, simplified physical models and model‐parameters at the CM level introduce approximations. Specific choices of our macroscopic governing equations, such as the form for membrane free energy, the methodology for treating protein diffusion and so on have been validated by prior modelling and experimental studies. A few physical processes that have been ignored in our treatment include reorganisation of lipid structure on the membrane and membrane rupture. Non‐equilibrium effects (beyond the linear response approximation) are also not considered. Neglected effects, and avenues for including them, are summarised below:

• Interlayer‐friction and hydrodynamics: based on the Helfrich description and through theoretical formalisms and simulation algorithms, the dynamics of an elastic membrane sheet in the over‐damped limit including hydrodynamic coupling to surrounding solvent and arbitrary external forces have been introduced in previous studies [60–64]. The infinitely thin elastic sheet assumption has also been relaxed and the inter‐layer friction and slippage between the lipid monolayers have been incorporated [64–66]. In this study, the more complex bilayer continuum model based on inter‐layer friction is not pursued because the inclusion of spontaneous curvature in this model introduces additional terms, which have not yet been resolved.

• Electrostatics: the cell membrane generally consists of screened polar head groups. The contribution of this electrostatics to the membrane Hamiltonian can be included within the framework of Debye–Huckel approximation for low densities of membrane charge using the linearised Poisson–Boltzmann equation [67]. Solving for the potential we can compute the electrostatic contribution to the force on a membrane patch.

• Membrane lipid heterogeneity: in the continuum (CM) model, the membrane is assumed to have homogeneous properties over scales much larger than that of its constituting components. This assumption is justified as long as the range of interactions is smaller than the correlation length of the inhomogeneities. However, spatial distribution of lipids in the membrane can change because of curvature of the membrane. Converting the composition into area fractions, the Helfrich Hamiltonian can be appended with extra terms [68] to account for the inhomogeneity in the lipid distribution.

• Effect of cytoskeleton: presence of cytoskeleton imposes an energetic/entropic barrier on the membrane fluctuations. Cell‐based experiments [69] have demonstrated that the site of the clathrin coat nucleation (of size 36 × 10⁴ nm² of area) is depleted of cytoskeletal proteins. Hence the cytoskeleton only influences the energetics of the clathrin coat nucleation through its effect on the boundary (beyond the 36 × 10⁴ nm² area). We model the membrane patch devoid of cytoskeletal elements but subject to periodic boundaries.

3 Results

3.1 Morphology and energetics of vesicular budding

We have performed DTMC simulations for a typical membrane patch with bending rigidity κ = 10k_B T and an intrinsic curvature field H ₀ given by (4), as outlined in Section 2.1. Here the strength of the curvature field is varied from C ₀ = 0 to $C_0=1a_0^{-1}$. Using TI, see Section 2.2, we have mapped out the free energy landscape of vesicle budding as a function of the strength of the spontaneous curvature C ₀, see Fig. 3. For the clathrin coat radius of r ₀ = 4.55a ₀ [see (4)], we find that the critical strength of curvature C ₀ which sustains a bud is $C_0=0.6a_0^{-1}$. For values of $C_0>0.7a_0^{-1}$, we observe that a fully mature bud with a stabilised neck is more stable than the planar membrane (ΔF < 0), while for $C_0\le 0.6a_0^{-1}$ a neck does not form; $C_0=0.6a_0^{-1}$ also corresponds to the maximum in the free energy change (barrier height) for vesicle budding.

Fig. 3.

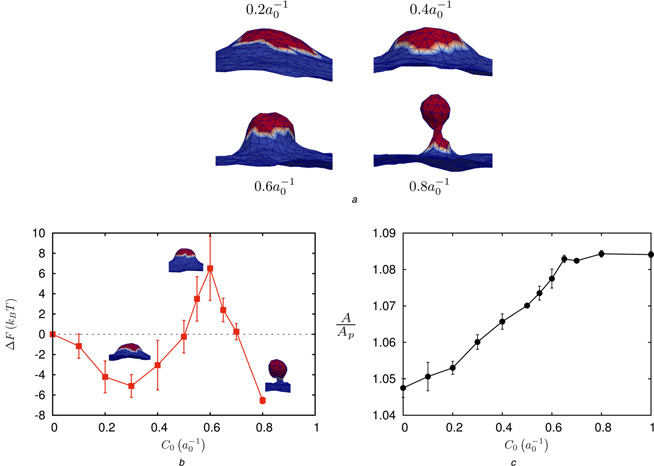
Calculations for vesicle budding using TI at κ = 10 k_B T

a Representative morphologies for varying C ₀

b Free energy change with respect to C ₀

c Change in excess membrane area with respect to C ₀

Results are reported for a coat radius of r ₀ = 4.55a ₀ in (4)

Our calculations indicate that as C ₀ increases the membrane area also increases until the neck is formed, and beyond which this increase in excess area plateaus; here the excess area (A /A _p) is defined as the curvilinear area A divided by the projected area A _p. Hence, Fig. 3 c quantifies the change in excess membrane area in the course of a planar membrane maturating into a budding vesicle in clathrin‐mediated endocytosis.

We also explored the dependence of coat radius on the morphology and the energetics of vesiculation, see Fig. 4. For a smaller coat radius of r ₀ = 3.25a ₀, the free energy landscape (especially the barrier) is lowered slightly, but the emergent morphology does not show a clear mature bud; instead, the emergent structures even under large C ₀ resemble cisternae. For a larger coat radius of r ₀ = 6.5a ₀, the coat breaks up into smaller coats to produce multiple buds and the free energy landscape shows high values of the free energy to achieve such morphologies. Thus, we conclude that there exists a lower critical coat radius below which the morphology does not resemble a mature bud even at high C ₀; similarly, there exists an upper critical coat‐radius above which multiple buds nucleate at a very high free energy cost. The optimal coat radius that is bound by these two critical coat radii is r ₀ ∼ 4.55a ₀.

Fig. 4.

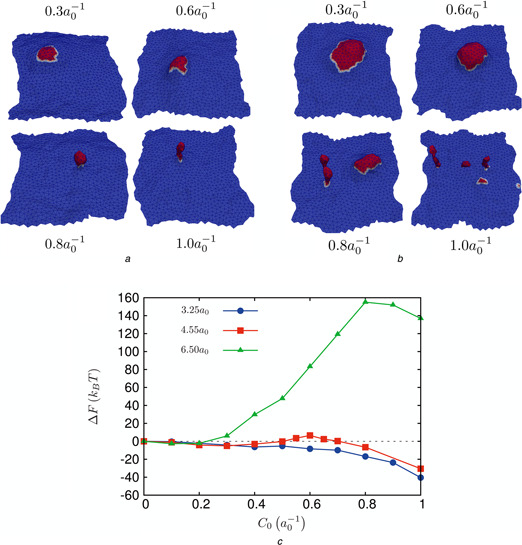
Influence of coat size on vesicle budding at κ = 10 k_B T

a Morphologies for different values of C ₀ for a coat radius of r ₀ = 3.25a ₀

b Morphologies for different values of C ₀ for a coat radius of r ₀ = 6.5a ₀

c Free energy of vesicle nucleation and its dependence on coat radius, r ₀

To estimate the dependence of budding on the bending rigidity κ, we compared the results of TI for κ = 10 and 20k_B T for an optimal coat radius of r ₀ = 4.55a ₀, see Fig. 5. While the budding morphologies for the higher κ (Fig. 5 b) were quite similar to that of the lower value (Fig. 3 a), the free energy landscape does show a distinct shift (Fig. 5 a). In particular, the free energy barrier for neck formation is absent for membranes with κ = 20k_B T and instead appears as a cusp in the free energy, suggesting that the barrier at κ = 10k_B T is entropic in origin, with significant influence from thermal undulations. For a small coat size of r ₀ = 3.25a ₀, the appearance of cisternae (Fig. 4 a) at low κ and high C ₀ is replaced by the appearance of capsids (but no budded vesicle, see Fig. 6 c) at κ = 20k_B T and $C_0=a_0^{-1}$. This strongly suggests that indeed an optimal coat radius bounded by the lower and the upper critical values is required for robust vesicle budding.

Fig. 5.

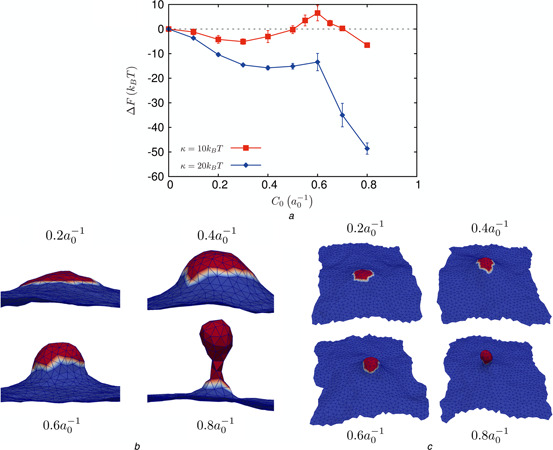
Influence of membrane bending rigidity on vesicle budding

a Free energy of vesicle nucleation and its dependence on membrane bending rigidity, κ

b Morphologies for different values of C ₀ for a coat radius of r ₀ = 4.55a ₀ and membrane bending rigidity of κ = 20k_B T

c Morphologies for different values of C ₀ for a coat radius of r ₀ = 3.25a ₀ and membrane bending rigidity of κ = 20k_B T

Fig. 6.

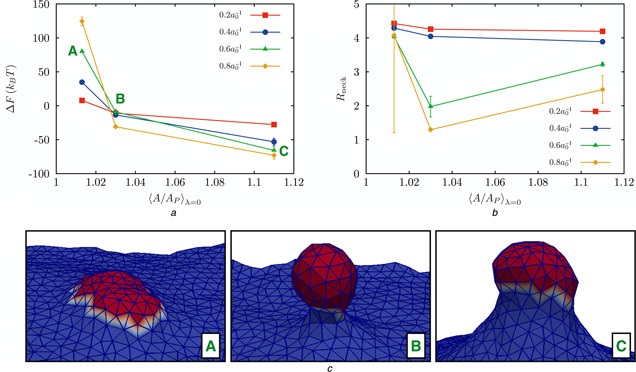
Effect of the membrane excess area on the free energy and membrane morphology

a Change in free energy as a function of excess area for four values of the induced curvature

b Radius of the neck of a bud as a function of excess area for four values of the induced curvature

c Representative snapshots of the membrane conformation for the values of A /A _p marked A, B, and C in top left panel

3.2 Effect of tension

Thus far, our results for the free energy landscape of vesiculation described above, has focused on the tensionless state of the membrane, as this is the natural state for vesicles under neutral osmotic environments. In some cellular experiments, actin engagement has been shown to be necessary to complete membrane deformation into a coated pits on apical surfaces of polarised cells and, more generally, on the surface of any cell in which the plasma membrane is under tension from osmotic swelling or mechanical stretching [70, 71]. To investigate the effect of membrane tension on the free energy landscape for endocytosis, we performed simulations by varying the membrane area (A) relative to the projected area (A _p) of the frame. Different A /A _p values correspond to different renormalised membrane tension values as changes in A /A _p profoundly influence membrane undulations [72].

We investigated three different macrostates with A /A _p values of 1.01, 1.03 and 1.1, for a membrane with κ = 20k_B T. Fitting the undulation spectra to the expression $⟨h_q{h}_{-q}⟩=k_{B}T{A}_{\mathrm{p}}^{-1}/(\kappa q^4+\sigma q^2)$ against q [42], [where h_q is the 2D Fourier transform of the membrane height z (x, y)], yields the values of σ : the resulting values of (A /A _p, σ) pairs are $(1.01,1.5k_{B}T/a_0^2)$, $(1.03,-0.4k_{B}T/a_0^2)$ and $(1.11,-0.6k_{B}T/a_0^2)$.

The effect of membrane excess area (or tension) on the free energy landscape of vesiculation, and on the emergent membrane/vesicle morphology is depicted in Fig. 6. Vesiculation is only energetically favourable in membranes under intermediate negative to zero tensions (Fig. 6 a). For large positive tensions, the free energy at large curvature strength is considerably higher than that at low curvature strength, a trend that is opposite of the other two tension states examined. Interestingly the membrane morphology resembles a mature bud only for the intermediate (negative) tension state as seen from the representative snapshots (Fig. 6 c) and from the data reporting the neck radius (Fig. 6 b). For large positive tensions, membrane does not bud even for the highest curvature strength examined, while for large negative tension, the invaginated membrane does not show a constricted neck, suggesting that formation of a mature vesicle with a constricted neck is only possible for zero to intermediate (negative) tension states.

3.3 CGMD simulations of the ENTH domain curvature induction on a bilayer

We have simulated pure dipalmitoylphosphatidylcholine (DPPC) and mixed dioleoyl‐phosphatidyl choline/ dioleoyl‐phosphatidyl serine (DOPC/DOPS) bilayers using the MARTINI CG force field for 100 ns in CG time corresponding to at least 300 ns in real time. Calculations of physical properties such as the area per headgroup (0.61 nm²) and height and thickness undulation spectra agree with experimental observations [73]. We have also verified the scaling of the height–height correlation function and the ensuing fit yields a value the bilayer bending stiffness to be κ = 21k_B T (see Figure S1, supplementary material), consistent with previous estimates [74, 75].

To describe the mechanism by which epsin stabilises positive membrane curvature, we have performed, (using the methodology described in Section 2), CGMD simulations of the membrane‐contacting ENTH domain adhered to a mixed 4:1 phosphatidylcholine and phosphatidylserine (DOPC:DOPS) lipid bilayer with a single associated PtdIns(4,5)P₂, a key binding partner. In our simulations, exclusion of the PtdIns(4,5)P₂ molecule causes the ENTH domain to dissociate from the membrane, therefore highlighting the importance of phosphoinositides in the recruitment of peripheral membrane proteins as well as in the associated mechanism of curvature induction. In the presence of PtdIns(4,5)P₂, the results, depicted in Fig. 7 compare the findings for three different systems, namely free bilayer without protein, bilayer with one ENTH domain bound, and bilayer with four ENTH domains bound.

Fig. 7.

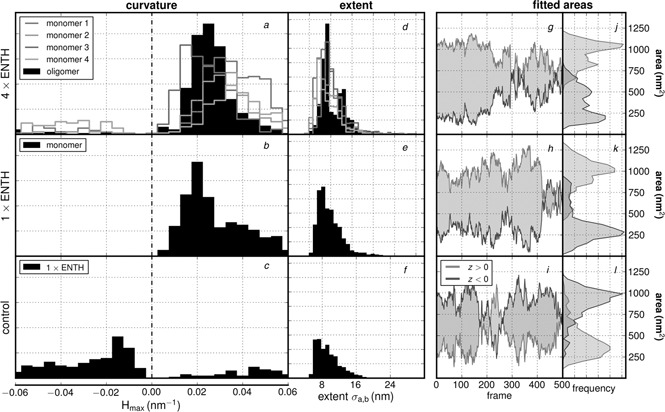
Quantification of bilayer deformation and curvature in CGMD simulations: control simulations of free bilayer without protein (c,f,i,l); simulations of bilayer with one bound ENTH domain (b,e,h,k); simulations of bilayer with four ENTH domains bound (a,d,g,j)

To characterise the anisotropy and orientation of the curvature, the angle of the field was also treated to be a fitted parameter, and hence no angle preference was imposed. Our results (Figs. 7 a –c), indicate that simulations with four ENTH domains collectively induce an average maximum mean curvature of 0.024 nm⁻¹, with individual monomers spanning a range of 0.018–0.031 nm⁻¹ while the simulation with only a single ENTH domain generates curvatures of 0.028 nm⁻¹. Curvatures calculated from the control simulation come from a very flat, broad distribution shown in Fig. 7 c which skews slightly negative due to the fact that selected points in the centre of the box (chosen to be the same size as the protein neighborhood from the ENTH simulation) were more likely to be found in a slight depression. The fact that this value is not identically zero is because of a combination of natural undulations and imperfect sampling, which results in a non‐flat average structure. Additional testing of alternate hypothetical protein positions shows that the control has no particular bias towards positive or negative curvature, and hence our measurement of −0.012 nm⁻¹ suggests that this is the limit of our effective estimate for a ‘flat’ bilayer. These calculations suggest that ENTH domains stabilise positive curvature using a cooperative mechanism. We also estimated the spatial extent of the curvature field in each of the three systems using the fitting method, described in Section 2, see Figs. 7 d –f and Table 1.

Table 1.

Estimation of curvature field parameters from CGMD simulations; our calculations always revealed that ${\sigma }_a\simeq {\sigma }_b$

System	〈H max 〉, nm−1	〈σa + σb 〉/2, nm
(four) ENTH domains	0.024	10.8
lower left	0.031	9.4
lower right	0.030	9.8
upper left	0.024	11.1
upper right	0.018	9.6
(one) ENTH domain	0.028	9.8
control (no protein)	−0.013	9.8

To ensure that the fitting procedure is robust with respect to characterising the strength and the extent of the curvature field, we quantified the area of the membrane subject to the curvature directly from the CGMD simulations, (i.e. this is quantified independent of the fits), see Figs. 7 g –l. While the control simulations show drastic fluctuations in the area, consistent with the fact that the curvature is directly a result of thermal undulations, the two systems with ENTH bound to the bilayer show very stable values for the area influenced by the proteins; this suggests that the curvature observed in the two ENTH systems is induced by the protein, rather than because of thermal undulations.

The parameters in Table 1 describe the magnitude and extents of curvature for use directly in the mesoscale model. In summary, the calculations reveal that the protein‐induced curvature is sustained and stable with weak (or little) anisotropy, and that the magnitude of the positive curvature from the four ENTH domain system is the highest among the three systems we have investigated.

Further evidence for curvature induction by ENTH can be gleaned from the spontaneous curvature maps calculated from the 3D stress tensor described in Section 2.4 and shown in Fig. 8; also see Figure S2, supplementary material. These maps show that control simulations have a relatively heterogeneous mixture of positive and negative spontaneous curvature. In contrast, systems with ENTH domains are less rugged, but show weaker opposing spikes of positive and negative curvature. However, the calculations of the stress tensor even in the longest trajectories we have harvested proved to be inherently noisy with large error bars, preventing us from using this approach to quantify the strength of the curvature field.

Fig. 8.

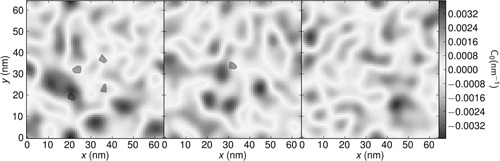
Map of spontaneous curvature (C₀) for 64 × 64 nm² bilayer systems containing either four or one ENTH domains compared to control

The colour scale describes the spontaneous curvature map over with pixel area of 10 nm²

Filled black circles represent locations of ENTH domains

3.4 Mapping the ENTH domain‐induced curvature to the curvature induced by the clathrin coat

In our model, we hypothesise that the dominant factor contributing to the intrinsic curvature H ₀ in the region where the membrane binds to the clathrin coat is the presence of epsins, bound at the CLAP‐binding sites on the coat. Here, at the CM level, we have modelled the spontaneous curvature induced by an epsin as a Gaussian function (2). That is, we have assumed that the epsin‐induced curvature decays smoothly to its far field value of zero. Such a choice of spatially varying intrinsic curvature function is justified by our CGMD simulations described in Section 3.2. Such a localised effect is also seen in other curvature‐inducing proteins such as BAR domains [26, 28–34].

From cryo‐EM studies [76, 77], the average distance between adjacent vertices of the hexagons in the clathrin cage is estimated to be 18.5 nm. The periodicity of the clathrin lattice ensures that epsins, through binding of their CLAP domains with clathrin/AP‐2, are templated spatially on the clathrin coat. We can translate the patterning of epsins on the clathrin coat to an intrinsic curvature function H ₀ of the form prescribed in (3), where the index i runs over the number of epsins on the coat separated by an average distance of 18.5 nm, the underlying periodicity of the clathrin lattice. Hence, a circularly averaged curvature field because of the epsins embedded in the clathrin coat may be obtained by assuming a central epsin bound to the coat at s _0,1 = 0, successive shells of epsins located at s _0,2 = 18.5 nm, s _0,3 = 37 nm, s _0,4 = 55.5 nm and so on, until we reach the periphery of the coat of a prescribed extent; here the coordinate s represents the curvilinear manifold along the clathrin coat. Using (2) and the results from Table 1, the averaged mean curvature because of the epsins in the clathrin coat can be approximated by

$$H(s)=\sum _{i=0}^{N}0.024{\mathrm{e}}^{-\left(((s-s_{0,i}){}^2)/(2\times {10.8}^2)\right)}{\text{nm}}^{-1}$$ (10)

where the unit of s is in nm and H in nm⁻¹. The average mean curvature is given by

$$⟨H⟩=\frac{1}{L}{\int }_0^{L}H(s)\mathrm{d}s$$ (11)

Based on (10), (11) and assuming a value of $L\gg s_{0,2}$, we find that the integral converges to $⟨H⟩$ ∼ $0.025{\text{nm}}^{-1}$.

We have shown previously [18] that the morphology of the emergent bud (not considering thermal fluctuations) is very similar between that generated by (3) and by (4), justifying the use of (4) for the curvature field in our TI method (see Section 3.1). Therefore, in summary, based on the CGMD simulations of ENTH domains interacting with the bilayer, we estimate the value of C ₀ = 2〈H 〉 for the clathrin coat [consistent with (4)] to be 0.05 nm⁻¹. Is this value sufficient to induce and stabilise a mature clathrin‐coated bud?

To address the above question, we need to complete the quantitative mapping between the CGMD and the CM simulations, by determining the value of a ₀. The area of the planar coat for a radius r ₀ = 4.55a ₀ is $\pi r_0^2$. This coat area translates into area of the neck covered by the coat in addition to the area of the vesicle. From our TI simulations, we estimate the area of the neck covered by the coat to be $31.6a_0^2$ and the average radius of the nucleated vesicle to be 1.73a ₀. In the experiments, the average radius of the clathrin‐coated vesicle in epithelial cells is 50 nm [78], from which we can map a ₀ = 50/1.73 = 28.9 nm. From Section 3.1, we determined that the critical value of C ₀ we require for the mature bud to be more stable than the planar state (i.e. ΔF < 0) is $C_0=0.7a_0^{-1}$; based on the mapping for a ₀, this critical value translates to C ₀ = 0.7/28.9 = 0.024 nm ⁻¹ . It is intriguing that this critical value (the minimum required for stable vesiculation) is considerably less than the curvature generated in the CGMD simulations, which is C ₀ = 2H = 0.50 nm ⁻¹ , suggesting that the strength and extent of curvature estimated from the CGMD simulations for ENTH domains on a bilayer are sufficient to stabilise a nucleated vesicle. Therefore the stability criteria we have established using our CM model in Section 3.1 is fully met by the strength of the induced curvature in the molecular model described in Section 3.2.

3.5 Free energy of membrane deformation against free energy of protein association

The free energy landscapes we have described in Figs. 3, 4–5, describe the energy landscape within the CM model when the orchestrating proteins are already bound. To decouple the energetics of membrane remodelling from the energetics of protein–membrane association, we transform the free energy landscape from TI in the presence of the orchestrating proteins (ΔF) to that in their absence (ΔF ₀) using the relationship [39]

$$\mathrm{\Delta }{F}_0=\mathrm{\Delta }F-⟨\int \frac{\kappa }{2}\int {\left(2H-H_0\right)}^2\mathrm{d}A⟩+⟨\int \frac{\kappa }{2}\int (2H){}^2\mathrm{d}A⟩$$ (12)

The expression for ΔF ₀ is derived based on a thermodynamic cycle as described in [39]. We plot ΔF ₀ in Fig. 8 for different coat sizes. The scale of the free energy, indicates that the large strain in free energy as the coat nucleates needs to be offset by attractive energies of the binding of orchestrating proteins to the membrane. In Fig. 8, for the coat size of r ₀ = 4.55a ₀, at the value of $C_0=0.7a_0^{-1}$, the free energy of membrane deformation is ≥200k_B T for κ = 10k_B T and almost 400k_B T for κ = 20k_B T. This has to be overcome by the attractive energy between the coat and the membrane (see Fig. 9).

Fig. 9.

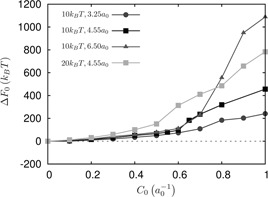
Free energy landscape ΔF₀ for different coat sizes for κ = 10 k_B T and 20 k_B T

In our model, we assume that the curvature induced in the membrane is primarily dominated by ENTH interaction with the membrane. The enthalpy of binding of the ENTH domain with Ins(1,4,5)P₃ is −14k_B T, as determined by isothermal titration calorimetry [21]. However, this does not take into account the accessibility of the PtdIns(4,5)P₂ in a bilayer setting.

Recently, the off‐rate for ENTH dissociation from a bilayer was determined from single molecule kinetics to be about k _off = 1 s ⁻¹ [79]. Given that the on‐rate is not measured, we can estimate the on‐rate based on a few assumptions:

• (1) The diffusion limit provides an estimate for the translational on‐rate to be k _diff = 6.023 × 10²³ D _ENTH (R _ENTH + R _PIP2) = 6 × 10⁷ M ⁻¹ s ⁻¹ , where D _ENTH is the diffusion coefficient of the ENTH domain which is of the order of 100 μm² /s [79], R _ENTH represents the radius of the ENTH domain (=1 nm); R _PIP2 = 0.15 nm is the radius of the PtdIns(4,5)P₂ head group which is small relative to that of the ENTH domain.

• (2) The binding of ENTH to PtdIns(4,5)P₂ requires a coil‐helix transition in the helix‐0 of the ENTH domain, for which the free energy of formation is about −3.5 kcal/mol = −6k_B T [67]; assuming that the free energy barrier for the transition is of the same order of magnitude, we obtain an additional factor of e ⁻⁶ to k _diff.

• (3) Since ENTH binding to PtdIns(4,5)P₂ is only mediated by the helix‐0, there is a contribution from rotational degrees of freedom to the on‐rate given by the ratio of the solid angles in the bound state relative to the unbound state [80], which is estimated to be (R _PIP2 /R _ENTH)/4π = 0.01.

Hence, an approximate estimate for k _on = 0.01k _diff e⁻⁶ , based on which, k_D for ENTH binding is estimated as k _off /k _on = 6 × 10 ⁻⁴ M, which translates to a free energy of binding of ΔG = −7.3k_B T for ENTH binding to PtdIns(4,5)P₂ in a bilayer. In order for the membrane remodelling free energy to be sufficiently compensated by the free energy of binding of ENTH to the bilayer, the minimum required number of ENTH domains interacting with PtdIns(4,5)P₂ is 210k_B T /7.3k_B T = 29 for a membrane with κ = 10k_B T and 400k_B T /7.3k_B T = 55 for a membrane with κ = 20k_B T.

Both these estimates for the minimum number of ENTH domains required for energetic stabilisation of a mature vesicle are less than the maximum available number of epsin binding sites in the coat, which is given by the area of the vesicular bud relative to area per CLAP binding site, and estimated as 4π (1.73a ₀)² /(π (18.5/2)²) = 115.

4 Discussion

Integration of models from physical biology and models from systems biology can lead to quantitative paradigms of intracellular trafficking. This approach explored here can impose crucial constraints on mechanisms gleaned from cell‐based experiments. In the context of endocytosis, a definitive understanding of the interplay between protein binding/migration and membrane curvature evolution is emerging but remains incomplete. Although many aspects of the fundamental processes are well characterised, especially in the domain of protein–protein interactions and increasingly in the area of protein localisation, several open questions remain, which are fundamental to a complete understanding of this fundamental cellular process.

The novel aspect of our computational approach presented here is the integration of CGMD simulations of the bilayer with proteins bound to the phosphoinositide molecule PtdIns(4,5)IP₂ with continuum CM simulations of the membrane. We have developed a mapping strategy between atomic modelling of protein–membrane interaction and the resulting curvature field strength. We also show how this mapping translates the molecular level remodelling of membrane structure into the effect it has at the cellular length‐scale, specifically in describing the energetics of vesiculation in clathrin‐mediated endocytosis.

Experimental studies [16, 69] have reported the nucleation and growth of a clathrin coat in which initiation occurred randomly, but only within subdomains 400 nm in diameter surrounded by a rim of a 200 nm dead zone devoid of cytoskeletal elements [69]. Our model consists of a finite membrane area subject to periodic boundaries, and we employ a bending rigidity κ = 10 − 20k_B T in both our CGMD and CM models, which is also consistent with experimental values [81, 82]. The response of the membrane undergoing fluctuations and acted upon by curvature‐inducing proteins is modelled at the CGMD and CM resolutions in a self‐consistent fashion through the mapping technique described in Section 2. This ensures that the predictions of the emergent vesicular morphologies at the CM level are consistent with (and constrained by) the strength of the molecular interactions in the CGMD model.

The progression to a maturing vesicle is quantified by computing the free energy of vesicle formation as outlined Section 3. The outputs from our simulations were membrane morphologies, and the free energy changes for different coat‐sizes, strength of curvature and membrane bending rigidity in the progression to vesicle budding. Several constraints emerge from the calculations outlined in Section 3, based on which quantitative paradigms in intracellular trafficking are identified, as discussed below:

• (1) The CGMD simulations have revealed the importance of PtdIns(4,5)P₂ in the stable binding and curvature induction in the bilayer. They have also provided a molecular basis for the positive curvature induction by ENTH domains and a direct means to quantify the strength and extent of the curvature to be used in the CM models. In particular, consistent with experiments [83], we find that a single ENTH domain does not induce sufficient curvature, and a tetrameric assembly of ENTH domain is able to sustainably induce sufficient curvature through a cooperative mechanism.

• (2) The calculation of the free energy landscape for vesicle budding using the TI in the CM model has identified both the critical size of the clathrin coat as well as the critical strength of the curvature field required for nucleation and stabilisation of a mature vesicle. Moreover, the dependence of the emergent morphologies and the free energy landscape for vesiculation on coat‐size as well as on the bending rigidity was delineated.

• (3) We have shown that small coat sizes (below the lower critical size) do not produce a mature bud and large coat sizes (exceeding the upper critical size) are highly energetically unfavourable leading to an automatic optimal coat size for vesicle nucleation purely on the grounds of the energetics. This constraint provides a physical mechanism as to why the coats do not grow uncontrollably to large sizes, an explanation which has hitherto been elusive in the experimental literature. In particular, we suggest that the regulation of coat size can occur purely on physical grounds (because of changes in free energy), and without any additional need for biochemical mechanisms depleting the levels of PtdIns(4,5)P₂.

• (4) Experimental estimates for membrane tension for vesicles under osmotic stress ranges from 0 to 20 μN/m and for cells grown on substrates (2D culture) ranges from 0 to 50 μN/m. In our calculations, we report the effect of membrane tension in the range −3 to +7.5 μN/m. Our free energy‐based phase diagram in Fig. 6 quantifies the range of tension values that can sustain a stable and mature vesicular bud with a well‐formed neck. Our calculations show that large positive tension hinders vesiculation by increasing the free energy barrier for membrane deformation, and moreover, the emergent membrane morphology does not translate into a well‐formed vesicular bud. While from a free energy perspective, the invaginations are easier at more negative tensions, our results show that the entropic barrier for neck formation will hinder vesiculation (see Fig. 6). Hence, in both these limits, actin may be required for vesicle stabilisation (large positive tension) [70, 71], or neck‐constriction (large negative tension) [84].

• (5) Epsins are recruited to the clathrin coat via binding through their CLAP domain, which has a free energy of binding of −9k_B T (or K_D,CLAP = 123 μM) to the coat [85]. Based on an independent binding site model [67], the fractional occupancy of epsins on the coat can be described by Θ = K_D,CLAP [epsin]/1 + K_D,CLAP [epsin], where [epsin] represents the concentration of epsins. In reality, however, the epsins expressed in the cytoplasm are targeted to the plasma–membrane through interaction with PtdIns(4,5)P₂ and hence [epsin] represents the concentration in the plasma–membrane compartment rather than the cytoplasm; a heuristic relationship can be derived [epsin]_membrane = (D /(12*R _ENTH))*[epsin]_cytoplasm, which based on a typical cell diameter of D = 20 μM (for epithelial cells) translates to [epsin]_membrane = 1667*[epsin]_cytoplasm. To produce sufficient curvature strength for stabilising a mature vesicle, our calculations in Section 3 suggest that Θ should be close to 1. This places a constraint that ${\left[\text{epsin}\right]}_{\text{membrane}}\gg K_{D,\text{CLAP}}$ [6]. In our CGMD model, an assembly of ENTH domains is identified as the functional curvature‐inducing unit with sufficient strength for stabilising a mature vesicle. In Section 3.4, we identified the minimum number of ENTH domain interactions necessary for stabilising a vesicle: The minimum number of required ENTH domain interactions are 29 and 55 for membrane bending rigidities of for κ = 10k_B T and κ = 20k_B T, respectively. Assuming that the stoichiometry of ENTH‐domain:PtdIns(4,5)P2 binding is 1:x, (where x ≥ 1), the number of PtdIns(4,5)P2 molecules necessary for a stable vesicle assembly is x times the minimum number of ENTH domains needed. These estimates for the number of PtdIns(4,5)P₂ molecules are greater than the average number of PtdIns(4,5)P₂ molecules found in the coat – for a typical PtdIns(4,5)P₂ concentration of 0.05% in the plasma membrane [47], the number of PtdIns(4,5)P2 molecules in a coat of radius 4.55a ₀ (assuming the average area per lipid is 0.65 nm²) is 41. This indicates that without active production of PtdIns(4,5)P₂ in the vicinity of the coat (e.g. because of an activated receptor recruited to the coat), the ENTH‐membrane association is unlikely to stabilise a mature vesicle. This constraint not only points to the importance of how phosphoinositide metabolism is coupled to clathrin‐mediated endocytosis, but also points to how receptor activation can directly impact and regulate clathrin‐mediated endocytosis.

Future extension of our model will serve to further delineate several of the key constraints we have highlighted above. For example, how receptor activation (in particular, for the epidermal growth factor receptor) is coupled to binding of AP‐2 and subsequent coat‐recruitment, as well as how the activated receptor spatiotemporally modulates phosphoinositide levels [17] may be explored through a spatially‐resolved, stochastic model [86, 87] in order to test specific hypothesis of the spatio‐temporal organisation of the clathrin‐coat proteins in the experimental literature [88, 89].

Extension to study the mechanisms underlining the multiple modes of receptor internalisation, such as through various clathrin‐independent mechanisms can also be tested by extending our model. This model can be used to explore molecular and membrane‐mediated mechanisms involving mutations of the associated proteins (e.g. in cancer) that can lead to changes vesicle stabilisation, thereby providing mechanistic links between the circumstances for altered trafficking and hyper‐proliferative signalling.

Another possible extension involves the incorporation of cellular‐microenvironment (such as how the effects of cytoskeletal interactions and cell–cell junctions) [70] impact the energetics of clathrin‐mediated endocytosis by redefining the constraints we have identified. The insight obtained from this modelling approach together with experimental data can prove effective in dissecting how malignant cancer cells employ/alter/hijack intracellular trafficking mechanisms to gain a fitness advantage. The particular application to endocytosis explored here will provide a direct route to discern pathological cellular trafficking fates implicated in a variety of cancers [7].