Abstract
Background
The Measles & Rubella Initiative, a broad consortium of global health agencies, has provided support to measles-burdened countries, focusing on sustaining high coverage of routine immunization of children and supplementing it with a second dose opportunity for measles vaccine through supplemental immunization activities (SIAs). We estimate optimal scheduling of SIAs in countries with the highest measles burden.
Methods
We develop an age-stratified dynamic compartmental model of measles transmission. We explore the frequency of SIAs in order to achieve measles control in selected countries and two Indian states with high measles burden. Specifically, we compute the maximum allowable time period between two consecutive SIAs to achieve measles control.
Results
Our analysis indicates that a single SIA will not control measles transmission in any of the countries with high measles burden. However, regular SIAs at high coverage levels are a viable strategy to prevent measles outbreaks. The periodicity of SIAs differs between countries and even within a single country, and is determined by population demographics and existing routine immunization coverage.
Conclusions
Our analysis can guide country policymakers deciding on the optimal scheduling of SIA campaigns and the best combination of routine and SIA vaccination to control measles.
Keywords: Measles, Immunization, Supplementary immunization activities, Low- and middle-income settings, Child health, Mathematical modeling
1. Introduction
The fourth United Nations Millennium Development Goal aims to reduce under-five mortality rates by two thirds between 1990 and 2015. Despite accelerated progress, with a decline from about 12 million deaths in 1990 to about 7–8 million deaths in 2010, the goal is unlikely to be attained at current rates of decline [1–3]. Measles has been a key contributor to this mortality. Although measles mortality has dropped globally, from up to 5% of under-five deaths in 2000 [2,4,5] to about 1–2% in 2010 [2,3], measles burden remains high in a number of countries [6]. The Measles & Rubella Initiative (www.measlesrubellainitiative.org), a broad consortium of global health agencies, has provided support to measles-burdened countries in order to sustain and achieve measles mortality reductions. It has been focusing on maintaining high coverage of routine immunization of children at about 9 or 12 months of age and supplementing it by a recommended second dose for measles vaccine [7–9]. In a large number of countries, the second dose of measles vaccine is usually included in the vaccination schedule and usually administered to children before school entry [8]. In high measles-burdened countries, often, only one dose is routinely given, but an opportunity for a second dose of measles vaccine is offered through supplemental immunization activities (SIAs) [8,9]. During SIAs, children and adolescents are targeted regardless of their previous history of measles vaccination. Periodic SIA campaigns occur nationally/sub-nationally with use of various outreach strategies [9].
World Health Organization (WHO) analysts have reported sustained decreases in measles mortality worldwide since the 2000s [6,10]; most recently, global measles-related deaths were estimated to have decreased from about 535,000 deaths in 2000 to 140,000 deaths in 2010 [6]. Despite these global reductions, measles mortality remains substantial and concentrated in a number of high measles-burdened countries [2,3,6]. For example, India accounted for almost 50% (about 65,000 deaths) of estimated measles mortality in 2010, and the WHO Africa region for almost 40% (about 50,000 deaths) [6,11]. Some of these countries have low levels of routine immunization, such as Nigeria with a 42% coverage rate for the first dose of measles vaccine (MCV1) [12]. That being said, experience from first the Pan American Health Organization (PAHO) and then sub-Saharan Africa has shown that SIAs can contribute to achieving measles control in high burden countries. Indeed, large-scale implementation of SIAs in the PAHO region since the 1990s is thought to have contributed to the elimination of the endemic transmission of measles in the Americas [13]. The same strategy has been adapted to sub-Saharan Africa and appeared as a major contributor for the reported drops in measles deaths on the African continent over the last decade [14,15]. Therefore, it is necessary to examine the optimal strategies that can be implemented in order to control measles in high burden countries; in particular, it is important to determine the appropriate use and frequency of periodic SIAs in these countries.
High measles-burden countries with limited financial resources are confronted with difficult decisions related to measles control. For example, these decisions involve sensitive trade-offs between investing in sustainable routine immunization services and implementing repeated SIAs, as part of the overall strategy. In particular, WHO recommends SIAs to be repeated every 2–4 years for those countries with MCV1 coverage below 80% [8]. In this paper, we examined the trade-offs between routine vaccination coverage and SIA coverage and inter-SIA periodicity in order to achieve measles control. Specifically, we selected countries with the highest measles mortality burden globally [2,3], and estimated the optimal scheduling of future measles SIAs in these countries, using a dynamic compartmental model of measles transmission. The aim is to inform country policymakers about the scheduling of SIAs to achieve measles control.
2. Methods
2.1. Modeling
We developed DynaMICE (Dynamic Measles Immunization Calculation Engine), an age-stratified model of measles infection transmission in vaccinated and unvaccinated individuals. The population in the model can be susceptible to measles, infected with measles or recovered from measles (and hence have lifelong immunity). The rate at which infection occurs in the susceptible population depends on the existing proportion of the population that is already infected, as well as the effective contact rate between different age groups. Individuals age discretely, in one-year increments, at the end of each year [16], between 0 and 100 years old.
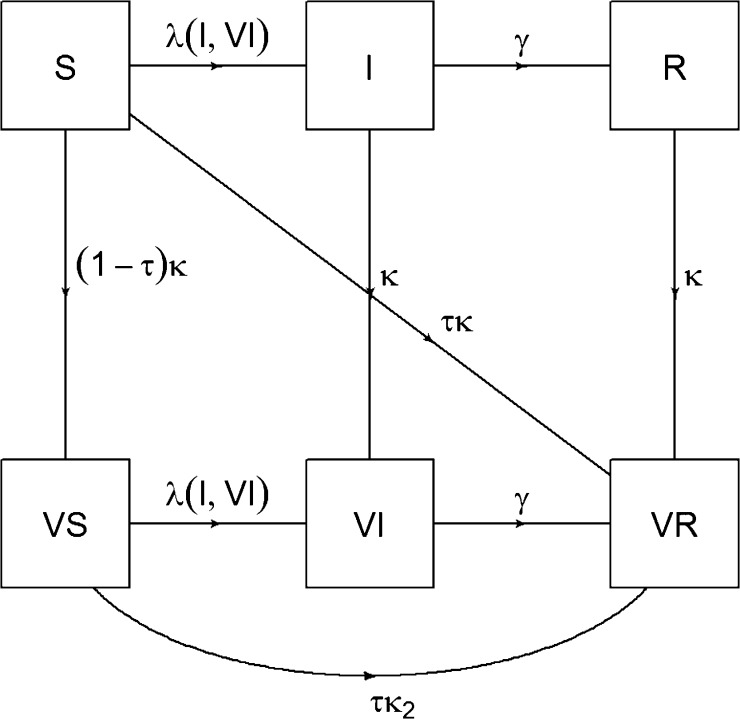
Vaccinated individuals are assumed to have a reduced risk of measles infection. Vaccine effectiveness is assumed to be 85% for the first dose when vaccinating before one year of age, 95% after one year of age and 98% for two doses, as suggested by a recent meta-analysis [17]. Vaccines are assumed to be “all or nothing” [18], so that individuals receiving the vaccine are either fully protected or not at all (Fig. 1). We assume that vaccination gives lifetime protection if it successfully elicits an immune response, and that vaccinating already infected individuals does not increase the rate of infection clearance (i.e. the vaccine has no therapeutic action).
Fig. 1.
Model of vaccine action. Note: S = susceptible, I = infected, R = recovered, VS = vaccinated susceptible, VI = vaccinated infected, VR = vaccinated recovered, λ = force of infection, γ = infectiousness period of measles, κ = coverage of measles vaccine for individuals vaccinated for the 1st time, τ = effectiveness of measles vaccine (85% for the first dose when vaccinating before one year of age, 95% after one year of age and 98% for two doses), κ2 = coverage of measles vaccine for individuals vaccinated for the 2nd time, through supplemental immunization activity (SIA) only (SIA coverage).
The model was programmed using R statistical software version 3.0.1 (www.r-project.org). Mathematical equations describing the model are provided in the Supplementary Data (Section 1). More details can be obtained from the authors upon request.
2.2. Model parameters
Dynamic models of infection transmission require data on age-dependent contact patterns in the population. However, empirical data on contacts have been published for only several European countries and Vietnam. We used well established contact survey data from Great Britain [19] corresponding to a probability of transmission per contact of about 3%, and in a sensitivity analysis, used mixing patterns from Vietnam [20]. The probability of an infected individual transmitting measles to a susceptible individual following an effective contact was set to be consistent with a basic reproduction number (R0, the number of people infected by a single infected person in a completely susceptible population) for measles of 16 [21]. We also changed R0 to the lower value of 12 in a sensitivity analysis.
The selected countries with high measles mortality burden retained were: India, Ethiopia, Nigeria, Indonesia, Mali, Afghanistan, Niger, Madagascar, and Burkina Faso. These countries were selected among the ten countries with the highest estimated burden of measles from each of two sources of estimates: the Child Health Epidemiology Reference Group of WHO and UNICEF [3] and the Institute for Health Metrics and Evaluation [2]. The population age distribution by country was sourced from the United Nations, along with crude birth rates and death rates by country [22]; these demographic parameters were assumed to be static over time (constant population growth) to simplify long-term population projections. The average infectious period of measles was assumed to be 14 days [21]. MCV1 was assumed to be delivered before the first birthday, with the SIA measles dose being given to all children between six months and five years old, assuming for simplicity that vaccination could be given as maternally derived immunity had waned. In practice, this may be an approximation since the lower age limit is commonly 9 or 12 months, which is a few months after these antibodies may have waned.1 The probability of receiving a MCV1 and SIA dose was assumed to be uncorrelated. MCV1 coverage by country was obtained from WHO and UNICEF [12]. Coverage figures for the SIAs were assumed to be of 90% among the 6–59 month-olds, a conservative estimate according to historical SIA coverage data collated by WHO [23].
2.3. Model analysis
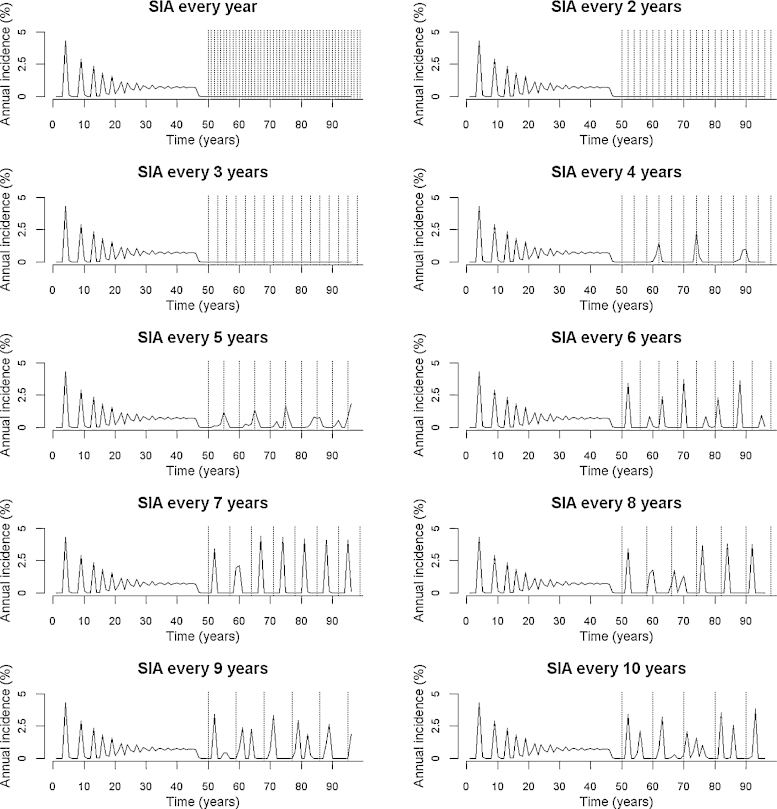
The dynamic compartmental model developed and presented above was run for 100 years with routine vaccination to reach a post-vaccination equilibrium (the last 50 years of which are shown on Fig. 2), and finally run for a further 50 years with both routine and SIA vaccination. Using country-specific inputs (e.g. MCV1 coverage), we explored the potential periodicity of SIAs required in order to achieve measles control. Disease control refers to the reduction of morbidity and mortality to locally acceptable levels [24]. Here we define measles as being controlled if the incidence of measles remains below 1 per 100,000 individuals in the entire population.
Fig. 2.
Computer model predictions of annual measles incidence pre- and post-SIA in India, under different intervals between SIAs. Each SIA is indicated by a dotted vertical line. R0 is 16 and SIAs are assumed to have 90% coverage among 6–59 month-olds. Note: The model was run for 100 years with routine vaccination to reach a postvaccination equilibrium (the last 50 years of which are shown), and finally run for a further 50 years with both routine and SIA vaccination.
2.4. Analytical approach
The computer model presented above requires considerable technical capacity and computing power. To enable policymakers to use our model for SIA planning with greater ease, we also derived a simple formula relating SIA periodicity to immunization coverage and population demographics. To do this, we simplified the system of differential equations representing the model of measles transmission (Supplementary Data, Section 1), removing age stratification in order to make the equations analytically tractable [25]. This allowed us to compute the maximum time period allowed between two consecutive SIAs that would still achieve measles control, depending on MCV1 coverage, demographic parameters, measles specific parameters, and vaccine effectiveness. The maximum inter-SIA period allowed to achieve measles control could then be estimated as (with the formula developed in Supplementary Data, Section 2):
| (1) |
where R0 is the basic reproduction number, is the birth rate adjusted for population growth (birth rate multiplied by the ratio between under-five population and 5–9-year-olds population), τR and τS are the effectiveness of MCV1 and SIA measles vaccine respectively, κR is the coverage of MCV1, and κS,eff is the effective coverage of SIA immunization (90% coverage multiplied by the fraction of measles cases among under-fives depending on MCV1 coverage and as estimated by geographical region [6]). The complete details of this approach are given in the Supplementary Data (Section 2).
3. Results
Fig. 2 shows results from the computer simulation showing change in the number of infected individuals (measles incidence) following the implementation of SIAs at regular time intervals from every single year to every 10 years (dotted vertical lines), with MCV1 coverage of 74% and with the population structure of India. In this case, we see that there is resurgence of measles (occurrence of incidence peaks after year 50) when the inter-SIA period is over three years. Furthermore, the less frequent the SIA, the larger the resurgence. Conversely, an average inter-SIA period of three years or less suffices to control measles (no occurrence of incidence peaks after year 50).
Table 1 also lists the inter-SIA periods required in order to achieve measles control, estimated computationally, for selected countries with high measles burden and 90% SIA coverage among 6–59 month-olds. We see that the maximum time period required between two consecutive SIAs depends importantly on MCV1 coverage (Pearson correlation coefficient of 0.71). For example, countries like Ethiopia and Nigeria with lower coverage of MCV1 (66% and 42%, respectively) would require SIAs about every 2 years.
Table 1.
Inter-SIA period required to achieve measles control with 90% SIA coverage and R0 of 16, as a function of routine immunization coverage for the first dose of measles vaccine and crude birth rate, for selected countries with high measles burden, and two Indian states.
| Country | Routine coverage for 1st dose of measles vaccine (%) | Crude birth rate (per 1000 population) | SIA period (years) (computational model) | SIA period (years) (analytical model) |
|---|---|---|---|---|
| Afghanistan | 68 | 36 | 2 | 2 |
| Burkina Faso | 87 | 43 | 3 | 3 |
| Ethiopia | 66 | 35 | 2 | 2 |
| India | 74 | 23 | 3 | 3 |
| State of Bihar | 58 | 29 | 2 | 3 |
| State of Uttar Pradesh | 53 | 29 | 2 | 2 |
| Indonesia | 80 | 21 | 3 | 4 |
| Madagascar | 69 | 36 | 2 | 2 |
| Mali | 59 | 49 | 2 | 2 |
| Niger | 73 | 51 | 2 | 2 |
| Nigeria | 42 | 43 | 2 | 2 |
This national picture may however mask heterogeneities at the sub-national/state level and Table 1 also lists the periodicity required between SIAs in order to achieve measles control with current level of MCV1 coverage for two Indian states, Bihar and Uttar Pradesh, where SIAs have been undertaken since 2010 and 2011, respectively. For these two states, we see that the inter-SIA period required is 2 years compared with 3 years at the national level.
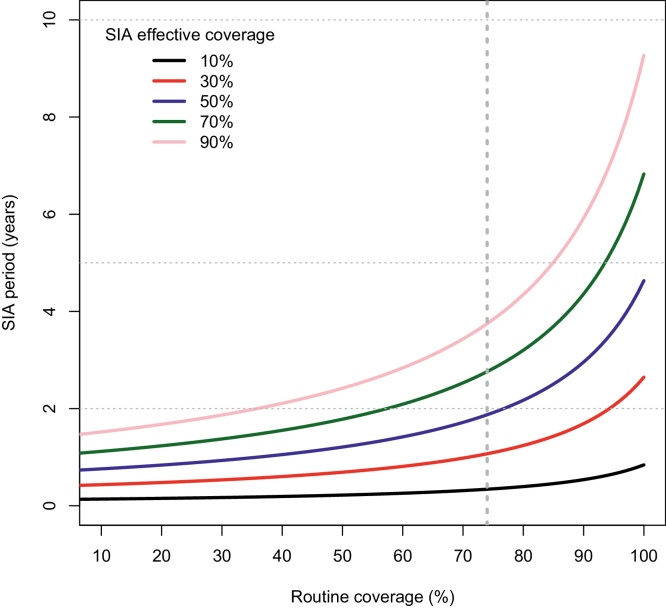
This computational analysis is further confirmed by the analytical results, also presented in Table 1. Based on Eq. (1) above, Fig. 3 shows the inter-SIA period required to achieve measles control for a range of SIA coverage levels, as a function of MCV1 coverage levels, using Indian demographic inputs and R0 of 16. In the last column of Table 1, the results are shown for the inter-SIA period required in order to achieve measles control, estimated analytically through Eq. (1) and rounded down,2 for 90% SIA coverage among 6–59 month-olds. We see that these analytical results match the simulation results closely.
Fig. 3.
Inter-SIA period (years) as a function of routine immunization coverage for the first dose of measles vaccine, for different levels of SIA coverage with Indian demographic inputs and R0 of 16. Note: the dotted vertical line depicts the current routine immunization coverage for the first dose of measles vaccine in India (74%).
Finally, in the simulation model, the use of mixing data from Vietnam [20] would lengthen the measles inter-epidemic cycles considerably and increase the height of the epidemic peaks, leading to unrealistic inter-epidemic cycles much larger than the 1–2 year cycles usually expected in low- and middle-income countries with higher birth rates and lower MCV1 coverage [21,26,27]. Although this is not clear, reasons for this difference may include less assortative mixing (due to differences in household structure and/or birth rates) or recall bias.
In addition, we varied the basic reproduction number for sensitivity analysis. Table 2 reports on the inter-SIA period required in order to achieve measles control, estimated computationally and analytically, for the selected countries with high measles burden, with 90% SIA coverage among 6–59 month-olds, and with a lower reproduction number R0 of 12, in order to highlight a better case scenario. Expectedly, we see that the inter-SIA period to achieve measles control is increased on average for all countries.
Table 2.
Supplemental immunization activity (SIA) period required to achieve measles control with 90% SIA coverage and R0 of 12, for selected countries with high measles burden, and two Indian states.
| Country | SIA period (years) (computational model) |
SIA period (years) (analytical model) |
|---|---|---|
| Afghanistan | 3 | 3 |
| Burkina Faso | 5 | 5 |
| Ethiopia | 3 | 3 |
| India | 3 | 4 |
| State of Bihar | 3 | 4 |
| State of Uttar Pradesh | 2 | 3 |
| Indonesia | 4 | 6 |
| Madagascar | 3 | 3 |
| Mali | 3 | 3 |
| Niger | 3 | 3 |
| Nigeria | 2 | 3 |
4. Discussion
Both numerical simulation and mathematical analysis indicate that a single SIA will not control measles outbreaks in any of the countries with high burden of measles. However, regular SIAs at high coverage are able to control measles transmission, with the periodicity of SIA campaigns determined by population demographics and existing MCV1 coverage.
The model also suggests that a single SIA may give the impression of having controlled measles due to a post-vaccination ‘honeymoon’ [28] (Fig. 2). Such potentially unexpected effects can have disastrous consequences on plans for national elimination or even global eradication goals. This underscores the importance of using predictive models that account for transmission events, rather than relying solely on surveillance based on reported cases, to inform decision making about vaccination.
Several models of measles transmission have been previously developed in order to explore the potential impact of different vaccination strategies [27,29–35], including the impact of mass immunization campaigns [25,36–38]. Here, we build on these models to explore the impact and optimal timing of periodic measles immunization campaigns, which have been the main focus of measles control efforts in the highest burden countries. We find that impact and optimal timing of measles SIAs varied among the highest burden countries, and even within a single country (Tables 1 and 2). This suggests that a country-specific approach to SIA timing may be most effective, with the recommended length of time between SIAs dependent on local demographics and routine coverage. Our computer model and the associated simplified analytical formula offer a way for country policymakers to determine when measles SIAs should be implemented. They can also further inform WHO guidelines on the conduct of SIAs at the country level, by recommending specific inter-SIA periods to achieve measles control at the national and sub-national levels, depending on a range of country-specific routine immunization coverage rates and demography, and including within country heterogeneities. Our analysis highlights country inter-SIA periods within the range of the 2–4 years periods recommended by WHO for countries with MCV1 coverage under 80% [8]. But, it also goes beyond these recommendations as it provides a means to weigh various combinations of coverage levels for MCV1 and SIAs with the dimension of SIA periodicity. This enables countries to identify more locally appropriate SIA scheduling in accordance with financial and operational capacity: this is especially important in the context of resource-limited settings given that SIAs can be expensive.
Nonetheless, our model has several limitations. First, we used an average estimate of the basic reproduction number of measles, and hence did not capture local variations in the intensity of measles transmission (due to differences in cultural practices and social gathering, for example). However, estimating this number separately for each setting is hindered by the lack of reliable data for measles case notifications due to underreporting and great disparity in reporting quality. As sensitivity analysis, we reported on the inter-SIA period required for the selected high burden countries with a lower reproduction number R0 of 12 (Table 2). Also, in the absence of data, we did not account for potential variations in vaccine effectiveness at the country/region level. Second, due to lack of data, the model does not take into account potential correlation between MCV1 and SIA coverage, and the fact that often children with better access to health systems and hence more likely to have received MCV1 can be easier to reach through SIA. Neither does it account for changes in immunization and birth rates into the future, as these are largely uncertain to forecast. Finally, though the model captures the conditions necessary for measles control, it is not intended to realistically model measles elimination (i.e. zero indigenous transmission events). Elimination goals depend on monitoring measles importations, vaccine coverage in hard-to-reach groups and stochastic one-off events, none of which are captured by the model (and rarely so by most models published in the literature). One could however examine the potential of an imported case to invade the population.
Despite these limitations, the broad conclusions of the model appear robust, particularly the need for regular SIAs to control measles in low routine coverage settings as in many high-endemicity countries. Models such as the one presented here are important tools for vaccination decision making, complementing existing information from surveillance systems. Our findings generally substantiate the guidance given by WHO, but most importantly can be used by country policymakers to tailor their SIA scheduling and planning to their specific setting, taking into account local demographics and routine coverage. As a result, countries with longer estimated inter-SIA periods might consider further investments in routine immunization services, whereas those with shorter inter-SIA periods may postpone such investments. Since measles control and elimination strategies are complex and require considerable financial investments, optimizing country planning of measles activities is critical. This model provides a valuable and practical tool for high measles-burdened countries toward efficient resource allocation in order to achieve measles control.
Funding
This work was supported by the WHO's Initiative for Vaccine Research. The authors alone are responsible for the views expressed in this publication and they do not necessarily represent the decisions, policy or views of the World Health Organization.
Conflicts of interest
The authors declare that they do not have any conflict of interests.
Acknowledgments
The study could not have been completed without the support of Raymond Hutubessy and the WHO's Initiative for Vaccine Research. We thank Peter Horby for providing data on contact patterns in Vietnam, and Arindam Nandi, Ashvin Ashok, Elizabeth Brouwer, and Zachary Olson for sourcing relevant data. We received valuable comments from Laurel Ohm and participants of a workshop on the broader economic benefits of vaccination (WHO, Geneva, 2012) and of the fourth meeting of the SAGE working group in measles and rubella (WHO, Geneva, 2013), particularly John Edmunds, Peter Strebel, Robert Perry and Susan Reef. SV was also partially supported by the Disease Control Priorities Network grant to the University of Washington. Finally, we would like to thank two anonymous reviewers for providing valuable and constructive comments on the manuscript.
Footnotes
This choice does not materially affect the measles dynamics studied in the paper.
Rounding down (e.g. 2.3∼2; 2.7∼2) the inter-SIA period estimated analytically leads to a more conservative estimate.
Appendix A. Supplementary data
The following are the supplementary data to this article:
References
- 1.United Nations Children's Fund . United Children's Fund; New York, NY: 2013. World Health Organization, World Bank, United Nations. Levels and trends in child mortality – Report 2013 – estimates developed by the UN Inter-agency Group for Child Mortality Estimation. [Google Scholar]
- 2.Institute for Health Metrics and Evaluation . Institute for Health Metrics and Evaluation; Seattle: 2013. Global Burden of Disease Study 2010. [Google Scholar]
- 3.Liu L., Johnson H.L., Cousens S., Perin J., Scott S., Lawn J.E. Global, regional, and national causes of child mortality: an updated systematic analysis for 2010 with time trends since 2000. Lancet. 2012;379:2151–2161. doi: 10.1016/S0140-6736(12)60560-1. [DOI] [PubMed] [Google Scholar]
- 4.Lopez A.D., Begg S., Bos E. Demographic and epidemiological characteristics of major regions, 1990–2001. In: Lopez A.D., Mathers C.D., Ezzati M., Jamison D.T., Murray C.J.L., editors. Global burden of disease and risk factors. World Bank; Washington, DC: 2006. [PubMed] [Google Scholar]
- 5.Bryce J., Boschi-Pinto C., Shibuya K., Black R.E., the WHO Child Health Epidemiology Reference Group WHO estimates of the causes of death in children. Lancet. 2005;365:1147–1152. doi: 10.1016/S0140-6736(05)71877-8. [DOI] [PubMed] [Google Scholar]
- 6.Simons E., Ferrari M., Fricks J. Assessment of the 2010 global measles mortality reduction goal: results from a model of surveillance data. Lancet. 2012;379:2173–2178. doi: 10.1016/S0140-6736(12)60522-4. [DOI] [PubMed] [Google Scholar]
- 7.Orenstein W.A., Hinman A.R., Strebel P.J. Measles: the need for 2 opportunities for prevention. Clin Infect Dis. 2006;42:320–321. doi: 10.1086/498321. [DOI] [PubMed] [Google Scholar]
- 8.World Health Organization Measles vaccines: WHO position paper. Wkly Epidemiol Rec. 2009;35(84):349–360. [PubMed] [Google Scholar]
- 9.Pan American Health Organization . Pan American Health Organization; Washington, DC: 2005. Measles elimination: field guide (Scientific and Technical Publication no. 605) [Google Scholar]
- 10.Wolfson L.J., Strebel P.M., Gacic-Dobo M., Hoekstra E.J., McFarland J.W., Hersh B.S., Measles Initiative Has the 2005 measles mortality reduction goal been achieved? A natural history modelling study. Lancet. 2007;369:191–200. doi: 10.1016/S0140-6736(07)60107-X. [DOI] [PubMed] [Google Scholar]
- 11.Morris S.K., Awasthi S., Kumar R., Shet A., Khera A., Nakhaee F. Measles mortality in high and low burden districts of India: estimates from a nationally representative study of over 12,000 child deaths. Vaccine. 2013;31(41):4655–4661. doi: 10.1016/j.vaccine.2013.07.012. [DOI] [PubMed] [Google Scholar]
- 12.World Health Organization UNICEF. World Health Organization; Geneva: 2014. WHO/UNICEF estimates of national immunization coverage. Available at: http://www.who.int/immunization_monitoring/routine/immunization_coverage/en/index4.html [accessed 29.10.14] [Google Scholar]
- 13.de Quadros C.A., Izurieta H., Venczel L., Carrasco P. Measles eradication in the Americas: progress to date. J Infect Dis. 2004;189(Suppl. 1):S227–S235. doi: 10.1086/377741. [DOI] [PubMed] [Google Scholar]
- 14.Otten M., Kezaala R., Fall A., Masresha B., Martin R., Cairns L. Public-health impact of accelerated measles control in the WHO African region 2000–2003. Lancet. 2005;366:832–839. doi: 10.1016/S0140-6736(05)67216-9. [DOI] [PubMed] [Google Scholar]
- 15.Masresha B.G., Fall A., Eshetu M., Sosler S., Alleman M., Goodson J.L. Measles mortality reduction and pre-elimination in the African region, 2001–2009. J Infect Dis. 2011;204(Suppl. 1):S198–S204. doi: 10.1093/infdis/jir116. [DOI] [PubMed] [Google Scholar]
- 16.Schenzle D. An age-structured model of pre- and post-vaccination measles transmission. Math Med Biol. 1984;1(2):169–191. doi: 10.1093/imammb/1.2.169. [DOI] [PubMed] [Google Scholar]
- 17.Sudfeld C.R., Navar A.M., Halsey N.A. Effectiveness of measles vaccination and vitamin A treatment. Int J Epidemiol. 2010;39(Suppl. 1):48–55. doi: 10.1093/ije/dyq021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Stover J., Garnett G., Seitz S., Forsythe S. Development Research Department, World Bank; Washington, DC: 2002. The epidemiological impact of an HIV/AIDS vaccine in developing countries. World Bank Policy Research Discussion Paper no. 2811. [Google Scholar]
- 19.Mossong J., Hens N., Jit M., Beutels P., Auranen K., Mikolajczyk R. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008;5(3):e74. doi: 10.1371/journal.pmed.0050074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Horby P., Thai P.Q., Hens N., Thi Thu Yen N., Mai L.Q., Thoang D.D. Social contact patterns in Vietnam and implications for the control of infectious diseases. PLoS ONE. 2011;6(2):e16965. doi: 10.1371/journal.pone.0016965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Anderson R.M., May R.M. Oxford University Press; New York, NY: 1991. Infectious diseases of humans: dynamics and control. [Google Scholar]
- 22.United Nations, Department of Economic and Social Affairs, Population Division . United Nations; New York, NY: 2011. World population prospects: the 2010 revision. [Google Scholar]
- 23.World Health Organization . 2013. Retrospective measles data on supplementary immunization activities 2000–2012. Available at: http://www.who.int/immunization_monitoring/data/data_subject/en/index.html [accessed 27.07.13] [Google Scholar]
- 24.Dowdle W.R. Perspectives for the elimination/eradication of disease with vaccines. In: de Quadros, editor. Vaccines. Preventing disease and protecting health. Pan American Health Organization; Washington, DC: 2004. [Google Scholar]
- 25.Shulgin B., Stone L., Agur Z. Pulse vaccination in the SIR epidemic model. Bull Math Biol. 1998;60:1123–1148. doi: 10.1006/S0092-8240(98)90005-2. [DOI] [PubMed] [Google Scholar]
- 26.Keeling M.J., Rohani P. Princeton University Press; Princeton: 2007. Modeling infectious diseases in humans and animals. [Google Scholar]
- 27.Earn D.J.D., Rohani P., Bolker B.M., Grenfell B.T. A simple model for complex dynamical transitions in epidemics. Science. 2000;287:667–669. doi: 10.1126/science.287.5453.667. [DOI] [PubMed] [Google Scholar]
- 28.Jit M., Brisson M. Modelling the epidemiology of infectious diseases for decision analysis. Pharmacoeconomics. 2011;29:371. doi: 10.2165/11539960-000000000-00000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Anderson R.M., May R.M. Vaccination against rubella and measles: quantitative investigation of different policies. J Hyg. 1983;90:259–325. doi: 10.1017/s002217240002893x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bolker B.M., Grenfell B.T. Chaos and biological complexity in measles dynamics. Proc R Soc Lond B. 1993;251:75–81. doi: 10.1098/rspb.1993.0011. [DOI] [PubMed] [Google Scholar]
- 31.Grenfell B.T., Kleczkowski A., Ellner S.P., Bolker B.M. Measles as a case study in nonlinear forecasting and chaos. Philos Trans R Soc Lond. 1994;348:515–530. [Google Scholar]
- 32.Keeling M.J., Grenfell B.T. Understanding the persistence of measles: reconciling theory, simulation and observation. Proc R Soc Lond B. 2002;269:335–343. doi: 10.1098/rspb.2001.1898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Conlan A.J., Grenfell B.T. Seasonality and the persistence and invasion of measles. Proc R Soc B. 2007;274:1133–1141. doi: 10.1098/rspb.2006.0030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ferrari M.J., Grais R.F., Bharti N., Conlan A.J.K., Bjornstad O.N., Wolfson L.J. The dynamics of measles in sub-Saharan Africa. Nature. 2008;451:679–684. doi: 10.1038/nature06509. [DOI] [PubMed] [Google Scholar]
- 35.Ferrari M.J., Grenfell B.T., Strebel P.M. Think globally, act locally: the role of local demographics and vaccination coverage in the dynamic response of measles infection control. Philos Trans R Soc B. 2011;368:1–7. doi: 10.1098/rstb.2012.0141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Agur Z., Cojocaru L., Mazo G., Anderson R.M., Danon Y.L. Pulse mass vaccination across age cohorts. Proc Natl Acad Sci U S A. 1993;90(24):11698–11702. doi: 10.1073/pnas.90.24.11698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nokes D., Swinton J. Vaccination in pulses: a strategy for global eradication of measles and polio? Trends Microbiol. 1997;5(1):14–19. doi: 10.1016/S0966-842X(97)81769-6. [DOI] [PubMed] [Google Scholar]
- 38.Bauch C.T., Szusz E., Garrison L.P. Scheduling measles vaccination in low-income countries: projections of a dynamic model. Vaccine. 2009;27:4090–4098. doi: 10.1016/j.vaccine.2009.04.079. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.