Lattice Light Sheet Microscopy: Imaging Molecules to Embryos at High Spatiotemporal Resolution

Abstract

Although fluorescence microscopy provides a crucial window into the physiology of living specimens, many biological processes are too fragile, too small, or occur too rapidly to see clearly with existing tools. We crafted ultra-thin light sheets from two-dimensional optical lattices that allowed us to image three-dimensional (3D) dynamics for hundreds of volumes, often at sub-second intervals, at the diffraction limit and beyond. We applied this to systems spanning four orders of magnitude in space and time, including the diffusion of single transcription factor molecules in stem cell spheroids, the dynamic instability of mitotic microtubules, the immunological synapse, neutrophil motility in a 3D matrix, and embryogenesis in Caenorhabditis elegans and Drosophila melanogaster. The results provide a visceral reminder of the beauty and complexity of living systems.

The hallmark of life is that it is animate. Every living thing is a complex thermodynamic pocket of reduced entropy through which matter and energy flow continuously. Thus, while structural imaging is certainly informative, a more complete understanding of how inanimate molecules assemble to create animate life requires high resolution imaging across all four dimensions of spacetime simultaneously.

The problem is that the twin goals of high spatial resolution to see fine structural detail and high temporal resolution to follow fast dynamical processes are mutually opposed to one another: increased spatial resolution requires more measurements, takes more time, and pumps more potentially damaging radiation into the specimen.

Fortunately, the most common tools used for in vivo molecular and organelle-specific imaging, widefield and confocal fluorescence microscopy (1, 2), leave substantial room for improvement, because they each illuminate the entire thickness of the specimen, even though high resolution information is obtained from only a single focal plane. This results in premature photobleaching and phototoxicity, limiting the duration of the imaging and altering the physiological state of the specimen.

A notable exception in this regard is light sheet microscopy (3, 4), which uses a separate excitation lens perpendicular to the widefield detection lens to confine the illumination to the neighborhood of the focal plane. This approach has proven powerful for noninvasive 4D imaging of embryos at single cell resolution (5, 6); however, conventional light sheets created with Gaussian beams (Fig. 1A) are too thick over cellular dimensions to benefit sub-cellular imaging. In response, we introduced (7) “non-diffracting” Bessel beams to light sheet microscopy (Fig. 1B): when swept across the imaging focal plane, such a beam creates a virtual light sheet of submicron thickness well-suited to noninvasive high speed 4D live cell imaging.

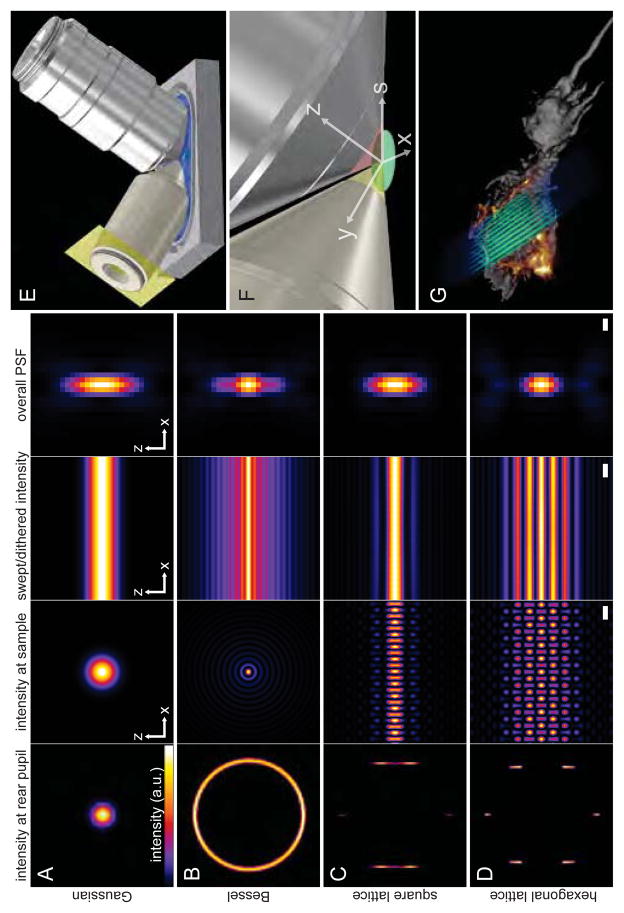
Fig. 1. Methods of light sheet microscopy.

(A) The traditional approach, where a Gaussian beam is swept across a plane to create the light sheet. (B) A Bessel beam of comparable length produces a swept sheet with a much narrower core, but flanked by sidebands arising from concentric side lobes of the beam. (C, D) Bound optical lattices (cf., movie S1) create periodic patterns of high modulation depth across the plane, greatly reducing the peak intensity and, as we have found, the phototoxicity in live cell imaging. The square lattice in (C) optimizes the confinement of the excitation to the central plane, and the hexagonal lattice in (D) optimizes the axial resolution as defined by the overall point spread function (PSF) of the microscope. The columns in (A to D) show: the intensity pattern at the rear pupil plane of the excitation objective; the cross-sectional intensity of the pattern in the xz plane at the focus of the excitation objective (scale bar, 1.0 μm); the cross-sectional intensity of the light sheet created by dithering the focal pattern along the x axis (scale bar, 1.0 μm); and the xz cross section of the overall PSF of the microscope (scale bar, 200 nm). (E) Model showing the core of our microscope, with orthogonal excitation (left) and detection (right) objectives dipped in a media-filled bath (cf., fig. S4). (F) Higher magnification view, showing the excitation (yellow) and detection (red) light cones, which meet at a common focus within a specimen that is either mounted or cultured onto a cover glass within the media. The x,y,and z directions are indicated. The s-axis defines the direction the specimen moves from image plane to image plane. (G) Representation of a lattice light sheet (blue-green) intersecting a cell (gray) to produce fluorescence (orange) in a single plane. The cell is swept through the light sheet to generate a 3D image (cf., movie S2).

In a more recent implementation (8) that exploits the principles of 3D superresolution structured illumination microscopy (SIM) (9) for further resolution enhancement, we used a linear array of seven parallel, non-interacting Bessel beams to compensate for additional acquisition time SIM requires. To our surprise, we found this multiple beam approach to be much less phototoxic than a single beam for the same total power delivered to the sample. Similar effects have been observed in spinning disk confocal microscopy (10), where the excitation is spread across many foci, greatly reducing the intensity at any single focus and in turn, reducing the effect of nonlinear photodamage mechanisms. We therefore decided to explore means to create a thin non-diffracting light sheet of low intensity, spread across a broad area, which would offer further gains in speed and noninvasiveness.

Lattice Light Sheets: Theory and Performance

Our approach begins with a 2D optical lattice. Optical lattices are periodic interference patterns in two or three dimensions created by the coherent superposition of a finite number of plane waves travelling in certain well-defined directions (11, 12), fig. S1), and have been used to trap and cool atoms (13) or to fabricate nanolithographic structures (14). Like an ideal Bessel beam, an ideal 2D lattice is non-diffracting in the sense that it propagates indefinitely in a direction y without changing its cross-sectional profile, which extends infinitely in x and z. In either case, this is accomplished by confining the illumination at the rear pupil plane of the excitation objective to points on an infinitesimally thin ring. In practice, it is necessary to replace this ring with an annulus of finite thickness, and to control the thickness of the annulus to confine the pattern in z, thereby producing a sheet rather than a block of light. However, this also reduces the extent in y over which the pattern is uniform, so there is a tradeoff between the thinness of the light sheet and its effective field of view in y. In the case of a Bessel beam restricted in y to cover the field of view of a typical cultured cell, there is enough energy remaining in side lobes concentric to the central beam to create substantial out-of-focus background in z when the beam is swept in x (Fig 1B). On the other hand, we have identified (Supplementary Note 1) numerous 2D optical lattices that, over a similar field of view, can be optimized to either: confine the excitation (15) tightly to the xy plane (Fig 1C); maximize the z resolution (Fig 1D, fig. S2) defined by the overall point spread function (PSF) of the microscope; or provide super-resolution in the xz plane by SIM (fig. S3).

To create these lattices, we started with an optical path that is (fig. S4) conceptually similar to our earlier Bessel microscope (7, 8). To this, we added a fast switching spatial light modulator (SLM) conjugated to the sample plane and placed before the annular mask. We write the xz cross-sectional electric field amplitude of the desired theoretical lattice light sheet as a binary phase pattern on the SLM (fig. S5). Incident laser light is then diffracted by the SLM, filtered by the mask, and focused by the excitation objective to produce a light sheet and corresponding PSFs in good agreement with theoretical predictions (fig. S6).

To apply such light sheets to in vivo imaging, the excitation objective and an orthogonal detection objective were suspended from above with their ends dipped in a shallow media-filled and temperature controlled bath (Fig. 1E), at an angle (Fig. 1F) in the yz plane such that their light cones of excitation (yellow) and detection (red) lie on one side of a horizontally mounted cover slip upon which the specimen rests. The lattice light sheet created in the xy plane at their common foci intersects the specimen obliquely (Fig. 1G). As the specimen is moved through the light sheet, the fluorescence thereby generated is recorded as series of 2D images on a camera. These are then assembled into a 3D image, and the process is repeated to build a 4D data set of cellular dynamics.

We operate the microscope in one of two different modes – a super-resolution SIM mode or a high speed dithered mode. In the SIM mode, we record F images at every z plane as we step the lattice light sheet in the x direction in F equal fractions of the lattice period. This data is then used to reconstruct a 3D image (9) with resolution extended beyond the diffraction limit in x and z. In the dithered mode, we use a galvanometer (fig. S4) to oscillate the lattice pattern back and forth in x at an amplitude larger than the lattice period and a speed fast compared to the camera exposure time, providing time-averaged uniform illumination across the xy plane. In this mode, we need capture only one 2D image at each z plane, but the resolution remains diffraction limited.

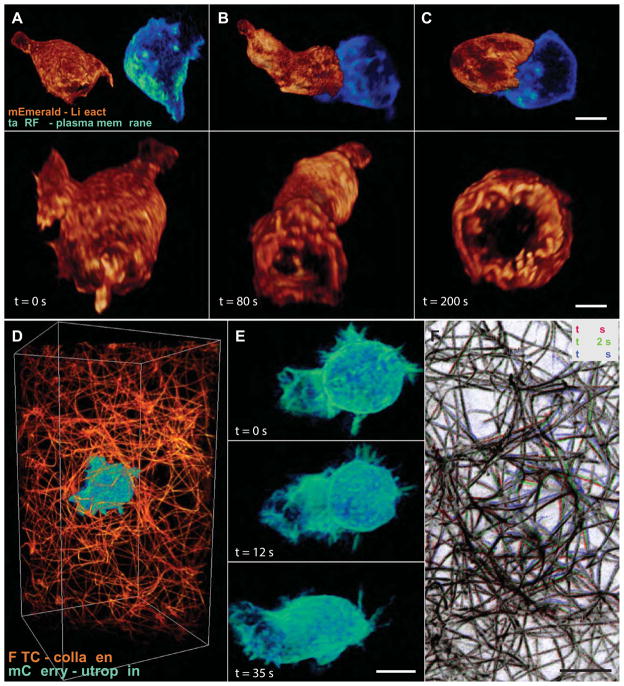
We imaged the dynamics of filopodia on HeLa cells transiently expressing mEmerald-Lifeact and found that lattice light sheet microscopy substantially outperformed our earlier Bessel beam approach. We chose cells of similar morphology and expression level for all trials, and imaged each at the same excitation power. In the SIM mode, the resolution of the two approaches (Figs. 2A, B) and the xz extension beyond the diffraction limit (Fig. 2E, F) were similar. However, in nine trials of 100 3D image volumes acquired by each approach, all cells imaged by lattice SIM exhibited minimal bleaching or changes in morphology indicative of stress, whereas all but one of the cells imaged by Bessel SIM retracted (e.g., inset, Fig. 2B), six of them within the first 50 volumes. This is likely due to the much lower intensity across the lattice light sheet, as well as the much higher signal to noise ratio (SNR) obtained due to its coherent modulation, versus the incoherent modulation produced with a stepped Bessel beam. In practice, this led to ~4× less total radiation delivered and ~3× faster imaging for patterns of similar period. It also allowed us to use finer patterns (fig. S3A) that require fewer steps F per plane. As a result, over 200 3D volumes could be acquired at 4.0 sec intervals by lattice SIM, 6.6x faster than with our previous Bessel approach.

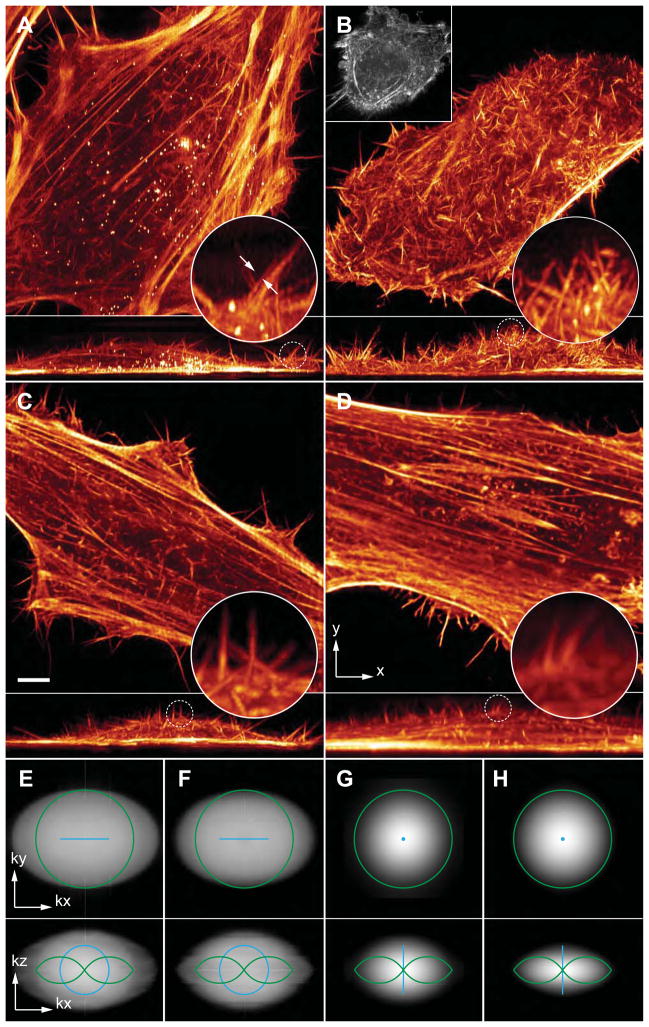
Fig. 2. Experimental comparisons of Bessel beam and lattice light sheet microscopy.

(A) 3D renderings in the xy (top) and xz (bottom) directions of the 300^th time point of a 4D data set of a living HeLa cell transfected with mEmerald-Lifeact, taken in the SIM mode with a five-phase hexagonal lattice at 7.5 sec intervals. (B) First time point from a different live HeLa cell imaged with a stepped Bessel beam and five-phase SIM at 30 sec intervals. Square inset shows the same cell, retracted at the 32^nd time point (cf., movie S3). The coherent lattice light sheet generates a pattern of much greater modulation depth (cf., movie S4), requiring less power and generating less damage to produce an image of comparable SNR. It also allows finer, three-phase patterns to be used for SIM mode imaging as fast as 4 sec per volume (cf. movie S5). (C) 300^th time point from a third HeLa cell, acquired with a hexagonal lattice in the dithered mode at 1.5 sec intervals (cf., movie S7). Scale bar, 5 μm. The low photoxicity of this mode permits even light-sensitive specimens such as D. discoideum to be imaged for long periods (cf. movies S9, S10). (D) First time point from a fourth HeLa cell, acquired with a swept Bessel beam at 1.5 sec intervals. Circular insets in (A to D) shows magnified xz views of filopodia. (E) Optical transfer functions (OTFs) in log scale showing amplitudes of spatial frequencies for the hexagonal lattice SIM mode used in (A). (F) OTFs for the Bessel SIM mode used in (B). (G) OTFs for the dithered hexagonal lattice used in (C). (H) OTFs for the swept Bessel mode used in (D). Green curves in (E to H) represent the diffraction limit of the detection. Blue curves in (E to H) represent the diffraction limit of the excitation.

In the dithered mode, we could construct low background lattices (e.g., Fig. 1C) where nearly all the excitation is within the narrow depth of focus of a high numerical aperture (NA_det = 1.1) detection objective (fig. S7). This affords high resolution, high contrast 2D imaging within multicellular specimens at up to one hundred frames per second for thousands of time points (movie S6). In comparison, a swept Bessel light sheet exhibited substantial out of focus background (Fig. 1B) over a similar field of view.

Another advantage of the dithered mode is that we can craft high resolution lattices (e.g., Fig. 1D, fig. S2) with an even more tightly confined excitation plane, although unavoidably flanked by several progressively weaker parallel planes. However, by choosing the spacing of these planes to match the nodes of the detection PSF (fig. S7), such lattices yield 3D images of substantially higher axial resolution (Fig. 2C, G) than can be obtained with a swept Bessel light sheet (Fig. 2D, H). In fact, the dithered lattice resolution (as defined by the optical transfer function (OTF)) (Fig. 2G) is 230 nm in x and ~370 nm in z, assuming GFP excitation/emission. This is only ~1.3–1.5× poorer in each direction than the 150 nm × 280 nm xz resolution we obtain in the SIM mode (Fig. 2E), yet these lattices allow us to image ~7.5× faster at comparable SNR (movie S7). Furthermore, in the dithered mode, we can image many specimens indefinitely in 3D without photobleaching or noticeable phototoxicity. This includes even notoriously light sensitive specimens such as Dictyostelium discoideum (D. discoideum), where we have imaged for hundreds of time points the rapid 3D dynamics of microtubules in multinucleate cells (16), (movie S8, 2.0 sec/volume), the contractile vacuole network - an extremely light sensitive organelle composed of interconnected tubules and bladders (17), and filamentous cortical actin (18). Thus, in practice we have found that unless the additional resolution of the SIM mode is absolutely essential, the dithered lattice light sheet is the preferred option for most biological systems.

Single Molecule Tracking and Super-resolution

The ability to detect and determine to nanometer precision the positions of single fluorescent molecules in vivo (19), either bound or diffusing, is essential to understand the molecular basis of cellular physiology. To cover cellular volumes with sufficient time resolution, widefield excitation is typically used, but the resulting out-of-focus background often limits observations to the thinner regions of single cells or confined sub-regions such as the plasma membrane. Light sheet microscopy has been applied to address this issue (20, 21), but with conventional Gaussian light sheets that are, over cellular dimensions, at least ~2–5× thicker than the depth of focus of a high NA detection objective. Consequently, the majority of the illuminated molecules are still out of focus, and produce large, blurred spots that cannot be localized precisely. Furthermore, very low molecular concentrations are needed to ensure that these out-of-focus spots do not overlap with the much smaller spots of in-focus molecules, compromising the localization of the latter. As a result, Gaussian light sheets substantially limit the number of molecules that can be studied per unit time, and therefore the density as well as the precision of the localization map obtained for a given total radiation dose to the specimen.

We used dithered lattice light sheets in the low background configuration (Fig. 1C) to overcome these problems – even over a 50 μm field of view, we can still confine the excitation to a band with a full width at half maximum (FWHM) of ~1.0 μm. This is comparable to the ~1.1 μm depth of focus of the detection objective, and thus nearly all illuminated molecules are in focus. This allowed us to study the diffusion and binding kinetics of single TMR-Halo labeled Sox2 transcription factors at high SNR not in just single isolated cells at low density (22, 23), but across a densely-labeled ~35 μm diameter spheroid of mouse embryonic stem cells (Fig. 3A, B), where epi-illumination revealed nothing and single Bessel beam plane illumination exhibited much lower SNR due to side lobe excitation. Analyzed within four nuclei (Fig. 3C), the diffusion of Sox2 fit well to a bi-exponential curve (Figs 3D, E) having a fast coefficient of 0.89 ± 0.07 μm²/sec, and a slow coefficient of 0.13 ± 0.01 μm²/sec. It has been shown previously that these two diffusion coefficients represent non-specific and DNA-specific binding interactions (22). In contrast, within the cytoplasm, high speed imaging revealed that the diffusion was tenfold greater: 8.4 ± 0.2 μm²/sec for a coefficient representing free diffusion or directed transport into the nucleus, and 0.74 ± 0.03 μm²/sec for a coefficient related to transient, non-specific interactions.

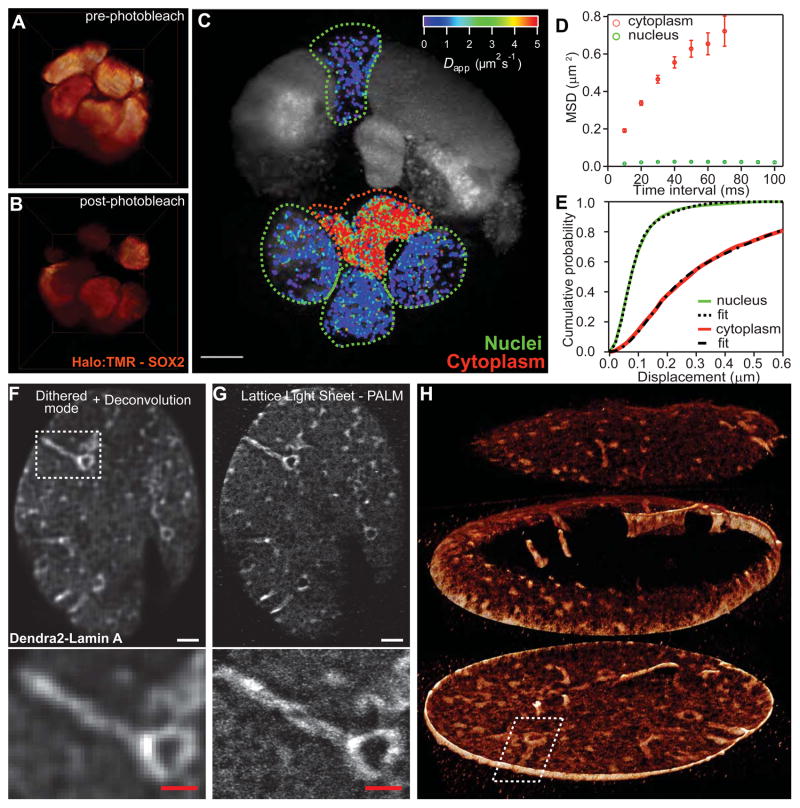
Fig. 3. Single molecule tracking and super-resolution.

(A) Lattice light sheet 3D rendering of a ~35 μm diameter spheroid of mouse embryonic stem cells containing TMR-labeled Sox2 transcription factors. (B) Same spheroid, showing bleached region after single molecule imaging with the light sheet dithered at a fixed plane (cf., movies S11, S12). (C) Local apparent diffusion coefficients of Sox2 molecules. Scale bar, 5 μm. (D) Mean square displacements (MSDs) of molecules in the nuclei (7608 trajectories) or cytoplasm (2339 trajectories) with error bars indicating the standard errors of the means. (E) Corresponding cumulative distribution functions (CDFs) representing the fraction of all tracked molecules at a given MSD or below. (F) Diffraction-limited maximum intensity projection (MIP) from a 600 nm thick slab cut through the bottom of the nuclear membrane of a fixed U2OS cell expressing Dendra2-Lamin A, taken in the dithered lattice mode. (G) Superresolution MIP from the same slab, taken with 3D PALM, where molecules in successive planes are excited with a dithered lattice light sheet. Scale bars, 2 μm in upper views of (F and G), 1 μm in zoomed boxes below. (H) Exploded view of the full 3D rendering of the nuclear envelope by PALM (cf., movie S13).

Another important application of single molecule localization is superresolution microscopy (24). As above, this has been most often applied to single cells in order to have sufficient SNR for precise localization, although Gaussian light sheets have also been used (25) to extend the approach to multicellular specimens. However, in either case, out-of-focus molecules substantially reduce the median localization precision, the localization rate, and the fraction of molecules localized rather than lost to photobleaching, which together reduce the speed and resolution of the technique. These problems are exacerbated when the method is extended to 3D, where the axial position of each molecule is inferred from the shape of its image, either directly from defocus (26), or with applied astigmatism (27). Here, even under ideal circumstances, the lateral localization precision decreases rapidly with distance from the focal plane, and minute background variations due to neighboring molecules can render the localization inaccurate in all three dimensions.

With a dithered lattice light sheet, on the other hand, we could extend 3D localization-based superresolution to thick specimens without sacrificing the localization precision, localization rate, or fraction of total molecules localized that is achievable in the optimal limit of a thin specimen. To demonstrate, we used photoactivated localization microscopy (PALM) (28) with applied astigmatism to image Dendra2-Lamin A at the nuclear envelope of a fixed U2OS cell. We scanned a region around the nucleus of the cell 31,600 times through the 1.1 μm thick light sheet in 61 steps of 0.50 μm each to ensure that every molecule would be detected at high SNR and that fluorescent bead fiducial markers would be visible across multiple steps. This allowed us to accurately assemble the narrow slab of 3D localization data from each 2D image at each sample position into a much larger 3D picture encompassing the entire field of view. At each step, we applied an 8 ms pulse of 405 nm light, and then imaged the molecules thereby activated for 95 ms under 560 nm excitation.

In the end, we localized 4.2 × 10⁶ molecules with a median emission of 645 photons to a median precision of σ_x = 0.4 nm, σ_y = 8.2 nm, and σ_z = 45.4 nm (Cramer Rao lower bound) across a volume of 51 × 26 × 30 μm³. Compared to a diffraction-limited, deconvolved 3D image acquired with the dithered lattice light sheet prior to PALM imaging (Fig. 3F), the resulting 3D PALM image (Figs. 3G, H) reveals far more structural detail in the nuclear envelope, such as a twisted braid of lamin A on the inner surface (Fig. 3G, H inset). The mean localization density within this feature is 2.2 × 10⁴ localizations/μm³, corresponding to a resolution limit defined by the Nyquist criterion of 71 nm. An exploded view in three sections (Fig. 3H) also reveals at high resolution envelope invaginations (29) that form channels spanning the entire thickness of the nucleus.

Noninvasive 3D Imaging of Intracellular Dynamics

The dividing cell is a spatially complex, highly dynamic environment. This is perhaps nowhere more evident than in the dynamic instability of microtubules (MTs), which undergo rapid stochastically-switched phases of growth and shrinkage during mitosis. Growing MT ends are decorated with the accessory protein EB1 which, when fluorescently labeled, provides a punctuate marker of the growing end (30). In interphase, it is relatively straightforward to apply 2D single particle tracking algorithms to widefield or confocal live cell data and quantify this growth in space and time. In mitosis, however, the thickness of the cell and density and speed of these puncta (movie S14) demand a much higher level of 4D spatiotemporal resolution to allow them to be isolated and tracked precisely. Such resolution is afforded by the dithered lattice light sheet.

To demonstrate, we imaged HeLa cells stably expressing GFP-EB1 and mCherry- or mTagRFP-H2B throughout mitosis, identified the stage of mitosis by the morphology of the chromosomes (from H2B) and quantified the EB1 tracks with a 2D algorithm (31) we modified for 3D. From this data, we were able to extract the 3D microtubule tip positions, growth phase lifetimes, and growth velocities across the entire cell. In a typical experiment (Fig. 4A, movie S17), we recorded ~100 two-color 3D volumes at 1.5 second intervals, waited 5–10 minutes for the cell to recover from the excitation while it advanced to a later stage, and then repeated this process through cytokinesis. Despite the extreme sensitivity of the cell during mitosis (32), we could often record ~500 3D volumes in each trial, yet still, each cell would pass through its mitotic checkpoints and divide normally. Quantification from twelve cells (fig. S8) revealed that MT growth accelerates during the early stages of mitosis, doubling by prometaphase/metaphase, and then gradually decelerates until reaching the original interphase velocity distribution in cytokinesis. Although harder to quantify, 3D images also suggest a higher mean velocity for kinetochore MT growth than astral MT growth during anaphase/telophase (fig S8, movie S17).

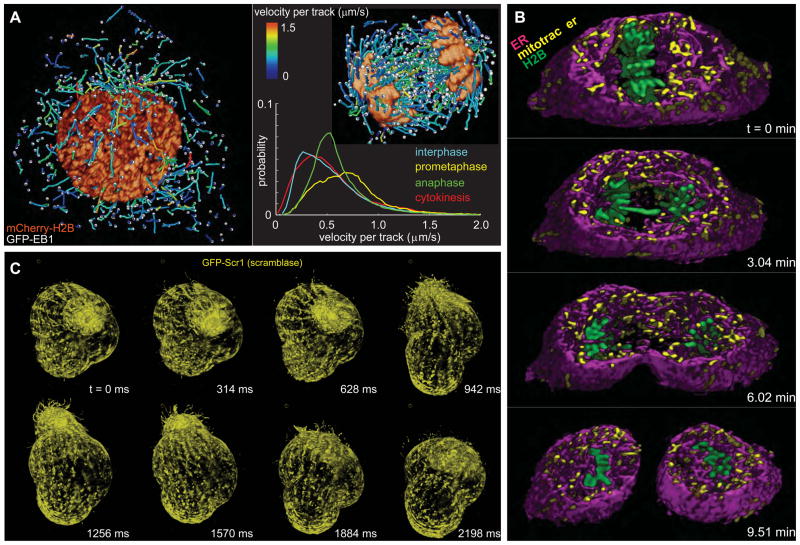
Fig. 4. Intracellular dynamics in three dimensions.

(A) Cells in prophase (left) and anaphase (right), showing histones and 3D tracks of growing microtubule ends, color coded by velocity. Color coding of each track by height (movie S15) or growth phase lifetime (movie S16) is also possible. Each image in A represents a distillation of a few time points from a 4D, two-color data set typically covering hundreds of time points per cell (cf., movie S17). Graph shows the distribution of growth rates at different stages of mitosis, averaged across nine to twelve cells (cf., figs. S8, S9). (B) 3D spatial relationship of histones (green), mitochondria (yellow), and the endoplasmic reticulum (magenta) at four time points during mitosis in a slab extracted from a larger 4D, three-color data set of HeLa cells imaged for 300 time points (cf., movie S18). (C) Volume renderings at eight consecutive time points of a single specimen of the protozoan T. thermophila taken from a 4D data set spanning 1250 time points (cf., movie S19). Imaging at 3 ms/frame in a single plane (cf., movie S20) reveals the motions of individual cilia.

We also imaged the spatiotemporal relationship of the endoplasmic reticulum (ER), mitochondria, and chromosomes during mitosis using three-color lattice light sheet microscopy. We labeled LLC-PK1 cells stably transfected with mEmerald-ER and mApple-H2B with MitoTracker® Deep Red dye (Life Technologies) and recorded 300 3D volumes in each color at 3.8 second intervals by acquiring a 2D image in each color at each z plane before moving on to the next (Fig. 4B, movie S18). As reported elsewhere, in mitosis, the mitochondria fragment (33) and the ER reorganizes into large, extended cisternae (34) with little remaining of the reticular network familiar to interphase. However, with the lattice light sheet we additionally see that the mitochondrial fragments nestle within and are corralled by the ER cisternae as they move fluidly within and between these pockets. We observed no exchange of fluorophore between the mitochondria and the ER which would be suggestive of their mutual fusion. Finally, both organelles were excluded from the region occupied by the chromosomes and the mitotic spindle during anaphase/telophase.

While our current system is capable of imaging at up to 200 planes/sec/color in multiple colors and up to 1000 planes/sec in a single color over a 100 × 20 μm xy field of view, there still exist biological systems for which even higher speed is desired. An example is the model protozoan Tetrahymena thermophila (T. thermophila) (35): we imaged a GFP-scramblase expressing specimen that was trapped in a pocket of 0.5% low melting point agarose for 1250 time points at 3.2 volumes/second (Fig. 4C, movie S19). However, the temporal resolution was insufficient to continuously follow the rapid morphological changes we observed or allay the fear of motion-induced artifacts. We then transitioned to 2D imaging of a single plane on the same specimen at 3 ms per frame. We were then able to smoothly track for 18,000 frames the motion of even the fastest processes falling within the image plane, such as the beating of motile cilia (fig. S10), raising the possibility of quantifying their bending and the forces they generate to elucidate their roles in signal transduction and locomotion. The combination of 3D and 2D imaging represented more than 200,000 images obtained from a single living, motile specimen, within the timespan of approximately 7.4 minutes. During this time, we observed no change in organism dynamics or protein distribution which would be indicative of phototoxicity.

Imaging Cell-Cell and Cell-Matrix Interactions

The vast majority of cells do not live in isolation, but rather in contact with neighboring cells or an extracellular matrix (ECM). We investigated both scenarios with the dithered lattice light sheet. In one example, we imaged the initial 3D aggregation of starved D. discoideum cells as they rapidly chemotax towards one another and begin the transition from unicellular to multicellular behavior (fig. S11). In another, we added a suspension of cytotoxic T cells expressing GFP-Lifeact to a field of peptide pulsed EL4 target cells stably expressing plasma membrane markers fused to TagRFP on a cover slip, and observed the processes of T cell/target cell engagement and the formation of the immunological synapse (36). Across dozens of trials, a stereotypic behavior emerged: a T cell, blunt at the leading end and trailing a small uropod, migrated toward a target cell while extending probing lamellipodia (Fig. 5A). Upon initial contact with the target cell, the T cell body lengthens to fill the gap and, within less than one minute, begins to establish a synapse rich in actin at its periphery but depleted elsewhere (Fig. 5B). Notably, this coincided with the initiation of an extremely rapid (> 1 μm/second) 3D flow of actin away from the synapse and along the T cell body (movie S22) that would be difficult to observe without the speed and resolution of the lattice microscope. A few minutes later, a mature synapse was established, the uropod retracted within the rounding T cell (Fig. 5C) and the fast rearward flow of actin continued unabated.

Fig. 5. Imaging cell-cell and cell-matrix interactions.

(A) T cell expressing mEmerald-Lifeact (orange) approaching a target cell expressing a plasma membrane marker fused to tagRFP (blue), as seen from the side (top) and from the viewpoint of the APC (bottom). (B) Initial contact. (C) The two cells, after the formation of a mature immunological synapse. These data represent three time points from a 4D, two-color data set spanning 400 time points. Scale bars, 4.0 μm (top), 5.0 μm (bottom). Other cell-cell interactions such as the aggregation starved D. discoideum cells can likewise be studied for extended periods (cf. movie S21). (D) Neutrophil-like human HL-60 cell expressing mCherry-utrophin in a fluorescently labeled collagen matrix. (E) Volume renderings of the cell at three time points extracted from a 4D, two-color data set of the cell and the matrix covering 250 time points (cf., movie S23). Scale bar, 5.0 μm. (F) Overlaid MIPs in three different colors of the collagen at the same three time points. Colored regions highlight local displacements of the matrix by the cell. Scale bar, 5.0 μm.

Mammalian cells typically migrate not on a 2D substrate, but through a complex 3D meshwork of ECM proteins. However, due to the limitations of conventional imaging modalities, the majority of studies of cell motility have focused on the locomotion of cells on planar surfaces (37). Recent extensions into 3D geometries have used slowly moving mesenchymal cells such as fibroblasts (~1 μm/min) (38), where the speed is amenable to current technologies. However, less is known about migration of neutrophils, which must navigate at ~10-× faster speeds (~8–12 μm/min) (39) through complex 3D microenvironments in infected tissues. We studied this process by adding neutrophil-like human HL-60 cells (40) expressing mCherry-utrophin to a 3D, fluorescently labeled collagen mesh (Fig. 5D, movie S23). Interestingly, cells embedded in the mesh migrated at speeds comparable to cells on cover slips (movie S24), despite the added physical constraints. They also exhibited a similar polarized morphology, with leading lamella and a trailing uropod (Fig. 5E). However, the embedded cells sent lamellar-like protrusions in a greater variety of directions as they probed alternative pathways through the mesh. We also recorded the displacement of the collagen filaments by the cells (Fig. 5F), and in the future this data might be combined with 3D traction force microscopy (41) to create high spatiotemporal resolution maps of the forces generated by the cells as they migrate through their surroundings.

Imaging the Subcellular Physiology of Developing Embryos

Much of our knowledge of cellular physiology comes from studies of immortalized cells cultured onto flat substrates. However, to understand the true physiological state of a cell, it must be studied within the multicellular environment in which it evolved. This is also possible with lattice light sheet microscopy, at least in the superficial layers of developing embryos where sample-induced aberrations are minimal. We demonstrated this in two model systems: the nematode Caenorhabditis elegans (C. elegans) (Fig. 6A,B), and the fruit fly Drosophila melanogaster (D. melanogaster) (Fig. 6C–F).

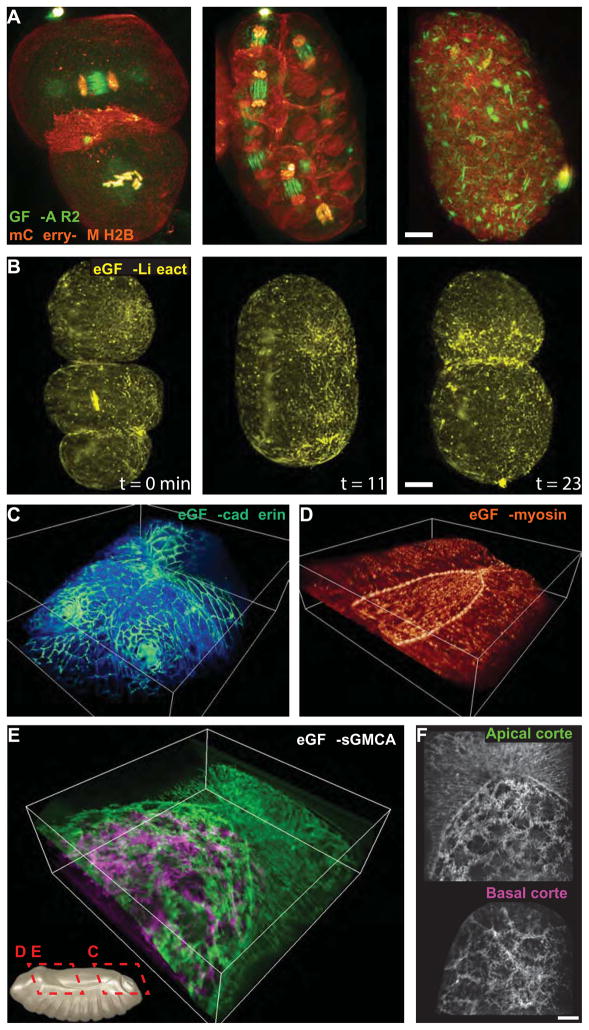
Fig. 6. Embryogenesis in three dimensions.

(A) Distribution of chromosomal passenger protein GFP-AIR-2 (green) relative to plasma membranes and histones (red) in C. elegans embryos at the two cell (left, cf. fig. S12, movie S25) through six cell developmental stages. Scale bar, 5 μm. Even late stage development of C. elegans can be studied (cf., movie S26) although muscle contractions make it difficult to follow specific features continuously. (B) xy view MIPs of the distribution of lifeact in a C. elegans embryo during pseudocleavage ingression (left), in maintenance phase just prior to the first division (center), and during the first division (right), extracted from a 4D data set covering 368 time points (cf., fig. S13, movie S27). Scale bar, 5 μm. (C) Volume rendering of DE-cadherin during dorsal closure in Drosophila development, highlighting boundaries between amnioserosa cells and the formation of spriacles, from a 4D data set containing 840 time points (cf., movie S28), bounding box, 86 × 80 × 31 μm. (D) Myosin II during dorsal closure, highlighting the myosin-rich purse string at the interface between the outer epithelium and the amnioserosa, from a 4D data set covering 1000 time points (cf., movie S29), bounding box, 80 × 80 × 26 μm. (E) sGMCA, a marker of filamentous actin at the plasma membrane, during dorsal closure, from a 4D data set covering 639 time points (cf., movie S30), bounding box, 73 × 73 × 26 μm. (F) MIPs highlighting cortical actin at the apical and basal surfaces of the amnioserosa, extracted from (E). Scale bar, 10 μm.

One challenge in such studies is that many subcellular processes occur on the time scale of seconds to minutes, whereas development from fertilization to hatching occurs over many hours to several days. However, even with the minimal invasiveness of our method, it is not possible to acquire the tens to hundreds of thousands of 3D volumes needed to follow fast subcellular dynamics over the full course of development without bleaching or damaging the specimen. Hence, it is necessary to carefully select the exact developmental stage and imaging interval to match the process of interest at the time of interest. For example, we imaged a GFP-tagged version of the Aurora B kinase homologue AIR-2, a chromosomal passenger complex protein essential for cytokinesis in C. elegans, at one minute intervals in order to follow its localization during cell division (Fig. 6A, movie S25). As seen previously in embryos (42, 43), AIR-2 localizes to metaphase chromosomes, followed by midbody microtubules in anaphase, and eventually in a persistent midbody remnant after cytokinesis. However, the thinness of our lattice light sheet allowed us to follow this process in 4D at high SNR in live embryos with remarkable detail (fig. S12). AIR-2 first associated with the chromosomes in prophase. By anaphase, it was indeed most concentrated at the spindle midzone microtubules, but some remained at the chromosomes, some at the centrosomes, and a faint residue outlined the astral microtubules. In late cytokinesis, AIR-2 was observed on the midbody remnant between the daughter cells. Although the localization of AIR-2 has been well studied in fixed samples or single 2D slices (43, 44), high spatiotemporal analysis of the 3D localization of different populations of AIR-2 may provide new insight into how it regulates cell division in developing embryos.

Other dynamic processes in C. elegans require higher time resolution. At the three-fold stage, just prior to hatching, muscle contractions make it difficult to follow specific features continuously over time, although we have recorded two color 3D snapshots across the entire embryo at 2.6 sec intervals. At the other end of the developmental spectrum, we imaged the 3D distribution of GFP-Lifeact at 4.8 second intervals for over three hundred time points from the single cell pseudocleavage stage through the division of the AB cell in an uncompressed embryo (Fig. 6B, fig. S13, movie S27). We observed an initial enrichment of actin generating the pseudocleavage furrow which progressively relaxed to create a smooth round embryo in maintenance phase. At this stage, actin became concentrated into long, bright, bundled filaments in the anterior half of the embryo. Prior to the formation of the first contractile ring, actin again spread across the entire embryo in dim filaments and bright puncta before becoming concentrated in the cleavage furrow during the first embryonic division. Just prior to the division of the AB cell, actin became enriched in the anterior portion of the P1 cell. This actin then migrated to the interface between the P1 and the ABp cells after AB division. Throughout the imaging, extremely actin-dense comets would occasionally appear and move rapidly through the cytosol. Although these comets and other stages of the cortical actin distribution have been observed previously in live embryos by spinning disk confocal microscopy (45), higher 4D resolution of both the actin dynamics and the shape of the embryo such as we demonstrate here will aid in developing physical models of how actomyosin forces lead to morphological changes in the early embryo (46), without the potential artifacts introduced by the embryo compression typically applied when using spinning disk confocal microscopy.

On a larger scale, we also studied the process of dorsal closure in D. melanogaster, the point in embryogenesis where two lateral sheets of epithelial cells converge over an eye-shaped opening to cover the amnioserosa, a thin layer of squamous cells. In embryos expressing GFP-labeled DE-cadherin to mark cell boundaries, apical shape oscillations and ingression of amnioserosa cells have been previously quantified in 2D models of the curved surface extracted from 3D spinning disk data (47). However, with lattice light sheet microscopy, we could study this process (Fig. 6C) in 4D up to twice as fast and at 5× finer z sampling in uncompressed embryos throughout the thickness of the amnioserosa and beyond. We have also imaged embryos expressing GFP-tagged myosin (Fig. 6D, movie S29) or sGMCA (Fig. 6E), a marker of filamentous actin at the plasma membrane, and observed contractile oscillations of the cytoskeleton temporally correlated to cell shape changes at the basal as well as the apical surface (Fig. 6F). Taken together, such data may facilitate the development of 4D models of the collective dynamics of dorsal closure as driven by forces in the amnioserosa and in the encroaching epithelium, with its actomyosin-rich purse string that resides near their mutual boundary.

Discussion

One limitation of lattice light sheet microscopy is that, like all forms of optical microscopy, its performance degrades increasingly with depth, due to sample-induced aberrations. Thus, depending on the optical heterogeneity of the specimen of interest, imaging beyond 20–100 μm will likely require combining the technique with adaptive optics (48) in both the excitation and detection pathways to compensate for these aberrations.

The chief benefit of lattice light sheet excitation for in vivo imaging is its exceptionally low photobleaching and phototoxicity – each of the 4D data sets presented here was distilled from tens to hundreds of thousands of raw 2D images acquired from each specimen. This is approximately an order of magnitude more images per specimen than we achieved with linear Bessel beam plane illumination (7, 8), and nearly two orders of magnitude more than in typical confocal data sets of similar specimens at similar expression levels. Thus, while excitation with a line (Bessel) is better than a point (confocal), a plane (lattice) is better than a line. The implication is that, while the total light dose delivered to the specimen is an important factor dictating its health, an even more important metric may be the peak intensity delivered to the specimen. In retrospect, this is not surprising, as photodamage mechanisms that scale supra-linearly with peak intensity have been identified for both visible (49) and two-photon (50) excitation. Given that confocal and lattice light sheet microscopy operate at similar 1–100 μW power levels in live cells, yet distribute this power over areas that differ by 10⁴–10⁵× in the focal plane, these mechanisms should be expected to yield vastly greater phototoxicty in the confocal case.

Indeed, seen in this context, confocal microscopy is far from an optimal tool for in vivo imaging – not only do the incoming and outgoing cones of excitation create premature bleaching and damage outside the focal plane, at the focal plane itself an actinic spot of light is created that leaves destruction in its wake as it sweeps through the specimen. While this damage is ameliorated in spinning disk confocal microscopes that use many foci in parallel, peak intensities are still far higher than in lattice light sheet microscopy, out-of-focus excitation remains a problem, and pinhole crosstalk can lead to artifacts and poor SNR in thick fluorescent specimens (51).

Another key advantage of our method is its speed. At 200–1000 planes/sec, it is typically an order of magnitude faster than with linear Bessel beam excitation and two orders of magnitude faster than in typical spinning disk confocal systems applied to comparable specimens. This is critical, because if we wish to follow physiological processes throughout the 3D volume of the specimen with the same or better temporal resolution as in prior 2D studies, we must image at least N-fold faster, where N is the number of 2D images comprising each 3D stack. In spinning disk confocal systems, speed limitations often makes it necessary to under sample N, trading axial resolution for temporal. However, with our approach, we can image many specimens in 3D at sub-second intervals, even though N ~ 100 – 200 planes per time point are required by the Nyquist criterion to recover the full axial resolution of which our microscope is capable (~370 nm in the dithered mode, 280 nm in the SIM mode). Achieving such high axial and temporal resolution simultaneously (which is not possible under either the spinning disk confocal or Gaussian light sheet paradigms) is essential: when imaging in 4D, the results are often only as strong as the weakest dimension - high resolution information from certain dimensions is lost when smeared across the poor resolution of others.

Together, the high speed and low photo-toxicity position lattice light sheet microscopy not only at the forefront of live cell fluorescence imaging, but also as a key enabler to bring recent advances in biology and microscopy into mainstream application. For example, genome edited cells (52) expressing endogenous levels of a targeted protein allow specimens to be studied closer to their native physiological state; however, expression levels can be far lower than in conventionally transfected specimens. This requires proportionally higher excitation intensities to yield comparable SNR at comparable speed when imaging in vivo, and will severely limit their applications with conventional microscopy. High speed also expands the application space for structured illumination microscopy which, to reconstruct artifact-free images, requires that the specimen move by less than the reconstructed voxel size in the time it takes to record the raw images contributing to that voxel. Because the elimination of out-of-focus background permits us to use shorter exposures to achieve the same SNR, we can image 3D processes that evolve at least 10× faster by lattice light sheet SIM than is possible with widefield SIM, albeit at somewhat lower resolution. In addition, we can image these processes far longer due to the elimination of out-of-focus photobleaching and photodamage and lower total light dose per time point. Finally, for other physiological processes that evolve slowly compared to the speed of our microscope, the extra bandwidth can be expended in a fifth dimension to image in more colors. Indeed, typical cells are composed of more than ten thousand unique proteins, yet they are usually imaged in vivo only one or two at a time. Using spectral unmixing (53) and/or combinatorial labeling (54–56), it may prove possible with our system to study the 4D interplay of a dozen or more proteins in the same cell at the same time, and to understand how they orchestrate complex cellular functions such as membrane trafficking or mitosis.

Materials and Methods

Microscope Optics

Seven collinear but individually modulated circular laser beams ranging in wavelength from 405 to 647 nm are passed through two pairs of cylindrical lenses to illuminate a thin stripe across the width of a ferroelectric spatial light modulator (SLM, fig. S4a, Forth Dimension Displays, SXGA-3DM). The SLM has a large number of pixels (1280 × 1024) and a fast (< 1 ms) switching time, the latter essential for rapid co-registered multicolor imaging. The remainder of the excitation optical path serves to create a demagnified image of the SLM (81.6 nm pixels) at the focal plane of the excitation objective, so that the pattern projected on the SLM (e.g., fig. S5C) creates a corresponding lattice light sheet of the desired properties (e.g., fig. S5G) within the specimen. First, a lens is used in a 2F configuration to create a diffraction pattern at its front focal plane (e.g., fig. S5D) that is the Fourier transform of the electric field reflected from the SLM. A custom opaque mask with transmissive annuli (e.g., fig. S5E, Photo-Sciences Inc.) is placed at this plane, and a specific annulus is chosen to remove the unwanted diffraction orders and enforce a limit on the minimum field of view in y. The electric field transmitted through the mask (e.g., fig. S5F) is then imaged in series onto each of a pair of galvanometers (Cambridge Technology, 6215H) and the rear pupil plane of the excitation objective. The galvanometers serve to translate the light sheet through the specimen in x and z. Finally, the field is reverse transformed by the excitation objective to create the desired lattice light sheet at its front focal plane.

The fluorescence generated within the specimen is collected by a detection objective (Nikon, CFI Apo LWD 25XW, 1.1 NA, 2 mm WD) whose focal plane is co-incident with the light sheet. Its high NA is essential to maximize the xy resolution, and to optimize the light collection for single molecule detection. The excitation objective (Special Optics, 0.65 NA, 3.74 mm WD) was custom designed to fill the remaining available solid angle above the cover slip (Figs. 1E, F), in order to optimize the z resolution, as well as the x resolution in the SIM mode, under this constraint.

A tube lens images the fluorescence from the illuminated slice within the specimen onto an sCMOS camera (Hamamatsu Orca Flash 4.0 v2) capable of frame rates down to 1 ms. A 3D image is produced from a stack of such 2D slices, either by moving the light sheet and detection objective together through the specimen (the former with the z galvo, the latter with a piezoelectric stage (Physik Instrumente, P-621.1CD)) or, far more commonly, by translating the specimen with a second piezo stage through the stationary light sheet along an axis s in the plane of the specimen cover slip (Fig. 1F, movie S2). The latter approach permits the use of more tightly confined light sheets for specimens that are thinner than they are long, such as single cultured cells. The specimen holder and specimen piezo are mounted on a trio of closed loop micropositioning stages (Physik Instrumente M-663 for horizontal motion in the cover slip plane, M-122.2DD for vertical travel). In conjunction with an epi-fluorescence view finding objective from below (fig. S4A, Olympus LUMPLFLN40XW, 0.8 NA, 3.3 mm WD), these are used to position the desired region of interest within the field of view of the light sheet. They also permit larger fields of view to be tiled together from multiple image sub-volumes, or permit multiple specimens to be imaged on the same cover slip in a repetitive loop for those cases where the dynamics occur on a time scale slow compared to the 3D imaging speed.

Complete details regarding the optical design are given in the Supplementary Note 3. Certain aspects of the design are derived from our earlier Bessel beam work, so these earlier publications (7, 8, 57) remain valuable resources as well.

Control Electronics

All analog/digital input/output signals are calculated and controlled by custom LabVIEW software (Coleman Technologies, Inc., National Instruments) and a Field-Programmable Gate Array card (FPGA, fig. S14, National Instruments, PCIe-7852R Virtex-5 LX50 R series). Analog outputs (AO) controlling galvos and piezos were conditioned by individual scaling amplifiers (SRS, SIM983 and SIM900 mainframe) to match their 16-bit resolution to the control range of each device. Instrument control and data analysis were performed on independent Supermicro workstations (Supermicro X8DTG-QF) running Windows 7 Professional 64 bit, each equipped with 2 Intel Hexa-CoreXeon X5680 processors, 96GB RAM, and an NVIDIA GeForce GTX TITAN graphics card.

The SLM runs under internal timing, and serves as the master clock for image acquisition. A series of SLM images known as a Running Order (fig. S15) is loaded into the SLM, and a hardware start signal from the FPGA triggers execution of the Running Order (fig. S16). A digital LED Enable output from the SLM is read by the FPGA, and mirrored as an output sent to the sCMOS camera (which operates in external trigger, rolling shutter mode), in order to synchronize the image acquisition to the positive/negative display states of the SLM (fig. S17). The number of transitions of LED Enable is counted to determine which SLM image in the Running Order is currently displayed, so the FPGA can send the appropriate outputs to control the AOTF, galvos, and piezos (fig. S18). The acceleration and flyback speeds of the latter two can be adjusted independently (fig. S19) to match their intrinsic response times. Control sequences exist to run the microscope in single or multiple colors in any one of four versions: objective scan, dithered mode (fig. S20); objective scan, SIM mode (fig. S21); sample scan, dithered mode (fig. S22); or sample scan, SIM mode (fig. S23). More complete details can be found in the Supplementary Note 4.

Sample Preparation and Imaging Conditions

Specimens are cultured or mounted on 5 mm diameter cover slips (Warner Instruments, 64-0700), cleaned prior to use according to our earlier protocol (7). The cover slip is clipped to the end of a long extension of the sample holder (orange, fig. S4D). This end is dipped in a shallow media-filled bath (translucent yellow, fig. S4D), while the opposite end is bolted to the sample piezo. The bath has inlet and output ports for perfusion of the media. A subassembly with the excitation and detection objectives and their translation stages is lowered from above until the ends of the objectives are dipped in the media at the distance from the cover slip appropriate for creating a lattice light sheet near its upper surface.

For operation away from room temperature (particularly for live mammalian cells at 37°C), heated or chilled water from a remote temperature-controlled reservoir is pumped through self-contained channels cut in the base of the bath, unconnected to the bowl that contains the imaging media. Asymmetric heating or cooling of the ends of the objectives creates significant optical aberrations that affect the microscope performance, as does convection of the media due to temperature gradients in the bath. Thus, additional heating/cooling blocks (translucent green and red, fig. S4D) with self-contained water channels are bolted around and close to the objectives, but not in contact. These are supplied with water from a second reservoir to maintain a circularly symmetric, uniform temperature around the objectives that matches the temperature of the bath. The temperatures of the two reservoirs needed to attain a given specimen temperature differ, but can be determined empirically.

Preparation conditions specific to each specimen are given in the Supplementary Note 5. Imaging conditions specific to each specimen, including maximum and minimum excitation NA, excitation power, imaging time, image and voxel sizes, imaging mode, fluorophores and proteins, etc., are given in table S1.

Image Processing and Visualization

Unless otherwise noted, all data acquired in the dithered mode were deconvolved using a Richardson-Lucy algorithm adapted to run on a GPU (NVIDIA, GeForce GTX TITAN), using an experimentally measured PSF for each emission wavelength. All data acquired in the SIM mode were reconstructed with an implementation of the algorithm for 3D-SIM (9) previously adapted for Bessel beam structured plane illumination microscopy (8, 57), running on the same GPU, using an OTF calculated from an experimentally measured PSF for each emission wavelength. All 3D data sets acquired via sample scan in the x,y,s coordinated system were transformed (“deskewed”) to the more conventional x,y,z coordinates in the GPU prior to visualization. Where noted (table S1), datasets were corrected for photobleaching and hot pixels using either built in Image J functions (histogram matching or exponential fitting), or by rescaling the maximum display value such that approximately 0.1 percent of all voxels (99.9^th percentile) at any given time point were saturated. Finally, processed data sets were imported into Amira (FEI) for 5D volumetric rendering.

Single Molecule Tracking and 3D PALM Imaging

Single molecule tracking within mouse embryonic stem cell spheroids (Figs. 3A–E, movies S11, S12) was performed using the particle tracking software Diatrack (v3.03, Semasopht) as described previously (58). Briefly, the software fits intensity spots with fixed-width symmetric 2D Gaussian functions. A map of local apparent diffusion coefficients was generated with code written in Igor 6.3.4 (WaveMetrics). The local apparent diffusion coefficients are evaluated in 40 nm × 40 nm grids, and are calculated from the mean square displacements originating from within a radius of 150 nm of each grid point over a timescale of 10 ms (Fig. 3C). The single-molecule trajectories were further analyzed by calculating mean square displacements (MSDs) for all possible time intervals, and cumulative distribution functions (CDFs) of all 10 ms displacements in the sample plane (Figs. 3D, E). The fit data from each CDF was best fit by a linear combination of two exponential functions, P(r)=1−[exp(−r²)/4D_appΔt], corresponding to both a fast and slow component.

Photoactivation localization microscopy (PALM) was performed with a cylindrical lens of 1000 mm focal length (Thorlabs, LJ1516RM-A) placed 40 mm before the imaging camera, to enable axial localization via the resulting astigmatism (27). The sample was scanned 31,000 times in 61 steps of 500 nm each (270 nm in the z direction), for a total of 1.83 × 10⁶ raw 2D single molecule images. For each such image, single molecules were identified and localized in 3D using a custom written maximum likelihood estimator algorithm, an experimentally measured calibration curve (for z-axis fitting), and a Levenberg-Marquardt optimization. Each 3D fit was offset by the sample-piezo position at the time of acquisition and assembled into a composite 3D image. Because a molecule could be localized at multiple image planes and across multiple image volumes, an algorithm was employed to link repeated localizations of the same molecule, as determined by a minimum spatial/temporal separation, into a single higher precision localization event in the final reconstructed image. The initial localization, fit refinement, and linking was implemented on a GPU using custom written Matlab and CUDA code. For visualization of the final dataset, a 3D Gaussian with standard deviations determined by the 3D localization precision was plotted at the centroid of each localization. The voxel size of the final reconstructed image (Figs. 3G, H, movie S13) was 10 × 10 × 20 nm.

Tracking Plus Ends of Microtubules During Mitosis

Microtubule trajectories and velocities (Fig. 4A, figs. S8, S9, movies S15–S17) were determined from the centroids of EB1 spots in each 3D dataset using a watershed algorithm, and linked between time points using a version of plusTipTracker (31) that was custom modified to accept our 4D datasets. The computed trajectories were then imported into Amira and color coded by track velocity using the Spatial Graph data class.

Supplementary Material

Movie S1

Fig. S1. Principles and definitions for two-dimensional optical lattices. (A) All wavevectors k_n of any 2D optical lattice lie on the surface of a single cone. (B) Fundamental 2D optical lattices for each of the five possible Bravais lattice symmetries. Insets show the locations (white) of the light beams in the rear pupil (red) that are needed produce the wavevectors that generate the corresponding lattice. (C) The five shortest period 2D sparse optical lattices of square symmetry. Scaling assumes 0.6 NA excitation. (D) Generation of new sparse 2D optical lattices by applying one of the symmetry transformations valid for that lattice type to an existing sparse lattice. (E) Composite lattices formed by stepwise addition of the wavevector sets from the different sparse lattices of the same symmetry and period from (D). The rightmost example shows the maximally symmetric composite lattice created by applying all symmetry operations of a square Bravais lattice to the sparse lattice at left. (F) The five shortest period 2D maximally symmetric composite lattices of square symmetry, derived from the sparse lattices in (C).

Fig. S2. Lattices optimized for the dithered mode. Calculated examples of lattices where the axial bounding has been optimized to produce high resolution in the z direction when used in the dithered lattice mode. Columns from left to right: the ideal 2D lattice in the xz plane upon which light sheet is based; the intensity pattern at the rear pupil of the excitation objective that produces the light sheet; the xz cross-sectional intensity profile of the stationary lattice light sheet at the sample; the xz cross-sectional intensity after the light sheet is dithered; and the overall point spread function (PSF) defined by the product of the dithered intensity profile and the PSF of the detection. (A) Maximally symmetric fundamental rectangular lattice, with z period = 1.5 × x period, where x period = 2.641 ×NA_exc ×λ_exc/n, and NA_exc and λ_exc are the numerical aperture and free space wavelength, respectively, of the light used to create the ideal lattice, and n is the refractive index of the imaging medium. The ideal lattice is comprised of four wavevectors. (B) Maximally symmetric fundamental square lattice, rotated to place two of the four wavevectors of the ideal lattice along the x axis. These two wavevectors become two vertical bands in the bound lattice, which are then clipped by the annulus to create four smaller vertical bands in the rear pupil. x period = 4.828 ×NA_exc ×λ_exc/n. (C) Maximally symmetric fundamental hexagonal lattice, rotated to place two of the six wavevectors of the ideal lattice along the z axis. The ideal lattice is comprised of six wavevectors. x period = 4.896 ×NA_exc ×λ_exc/n. (D) Maximally symmetric first order sparse square lattice. x period = 6.952 ×NA_exc ×λ_exc/n. (E) Maximally symmetric first order sparse square lattice, rotated 45° with respect to (D). The ideal lattice is comprised of eight wavevectors. x period = 9.485 ×NA_exc ×λ_exc/n. (F) Maximally symmetric first order sparse hexagonal lattice, x period = 20.92 ×NA_exc ×λ_exc/n. The ideal lattice is comprised of twelve wavevectors.

Fig. S3. Lattices optimized for the SIM mode. Calculated examples of lattices where the axial modulation depth and spatial frequency have been optimized to produce high resolution in the z direction when used in the structured illumination mode. Columns from left to right: the ideal 2D lattice in the xz plane; the intensity pattern at the rear pupil of the excitation objective that produces the lattice light sheet; the xz cross-sectional intensity profile of the light sheet at the sample; the optical transfer function (OTF) of the light sheet excitation in the xz plane; and the overall xz OTF defined by the convolution of the excitation and detection OTFs. (A) Fundamental hexagonal lattice, comprised of three wavevectors, rotated to place one of the wavevectors on the x axis. The pattern requires three phase-stepped images for SIM reconstruction. (B) Maximally symmetric fundamental square lattice of the same type as in fig. S2B, but with less axial confinement for optimization in the SIM mode. Five phase-stepped images are required for SIM reconstruction. (C) Maximally symmetric fundamental hexagonal lattice of the same type as in fig. S2C, but also with reduced axial confinement. Five phase-stepped images are required for SIM reconstruction. (D) Maximally symmetric first order sparse square lattice of the same type as in fig. S2D, except with reduced axial confinement. Seven phase-stepped images are required for SIM reconstruction. (E) Maximally symmetric fundamental hexagonal lattice, rotated 90° with respect to the lattice in (C). Nine phase-stepped images are required for SIM reconstruction. (F) Maximally symmetric first order sparse square lattice, of the same type and orientation as in fig. S2E. Nine phase-stepped images are required for SIM reconstruction.

Fig. S4. Schematic, mechanical design, and implementation of the lattice light sheet microscope. (A) Schematic of the optical path through the microscope. A linearly polarized circular input beam is stretched by a pair of cylindrical lenses in the x direction and compressed by another pair in the z direction, illuminating a thin stripe across the center of a binary, ferroelectric spatial light modulator (SLM), upon which the desired lattice pattern is projected. The light reflected from the SLM then passes through a transform lens, creating a Fourier diffraction pattern at an opaque mask containing a transparent annulus. The mask filters out unwanted diffraction orders and enforces maximum and minimum NA of illumination that dictate the y extent of the eventual lattice light sheet. The mask is serially conjugate to x and z galvanometers as well as the rear pupil of the excitation objective, so that the light sheet can be translated in x and z and rapid oscillated in x for the dithered mode of operation. The SLM itself is then conjugate to the sample plane, so that the lattice pattern projected on the SLM is imaged within the sample. The lattice light sheet generates fluorescence in a plane within the sample, which is imaged via a 1.1 NA detection objective and tube lens onto an sCMOS camera. Although the light sheet and objective can be translated in z to acquire a 3D volume, we more commonly use a piezoelectric flexure stage to translate the sample through the light sheet. (B) 3D solid model of the microscope. All components (except lasers) are mounted on an 18 × 24 inch breadboard which is in turn vertically mounted on an optical table. The sample itself is then horizontal in the shallow, media filled bath. (C) Photograph of the assembled microscope. (D, E) Magnified views of the sample chamber region, showing: the two objectives surrounded by temperature control blocks; the media bath; the sample holder; and the sample translation subassembly underneath.

Fig. S5. Generation of the SLM pattern for a specific lattice light sheet. (A) Real part of the electric field E of an ideal 2D lattice serving as the seed for a particular desired lattice light sheet. (B) E field of the bound lattice obtained after multiplication by a bounding function ψ(z). (C) SLM pattern created via 0/π binarization of the bound lattice E field. (D) Predicted diffraction pattern impinging upon the annular mask. (E) Annular filter mask that is conjugate to the rear pupil of the excitation objective. (F) Predicted illumination pattern at the rear pupil. (G) Predicted xz excitation cross-section of the lattice light sheet. (H) Predicted cross-section of the dithered lattice light sheet. (I) Predicted overall PSF for the lattice light sheet in the dithered mode.

Fig. S6. Experimental measurement of lattice light sheet parameters. Experimentally measured parameters for light sheets derived from three different optical lattices. Columns, from left to right: the intensity pattern at the rear pupil of the excitation objective that produces the light sheet; the xz cross-sectional intensity profile of the lattice light sheet at the sample; the overall PSF in the xz plane for the dithered mode of operation; and the overall reconstructed PSF in the xz plane in the SIM mode of operation. Data in columns two, three, and four were measured using 100 nm fluorescent beads. (A) Fundamental hexagonal lattice, comprised of three wavevectors, optimized for fast SIM (cf., fig. S3A). (B) Maximally symmetric fundamental square lattice, comprised of four wavevectors, optimized to confine excitation to a single plane, e.g., for single molecule studies (cf., fig. S2B). (C) Maximally symmetric fundamental hexagonal lattice, comprised of six wavevectors, optimized for high axial resolution in either the dithered or SIM modes (cf., figs. S2C, S3C).

Fig. S7. Axial confinement and point spread functions of two dithered lattice light sheets. (A) Maximally symmetric first sparse square lattice optimized to confine the axial excitation (green) to a single plane. (B) Maximally symmetric fundamental hexagonal lattice optimized to minimize the axial width of the overall axial point spread function (red). Both cases assume restriction of the rear pupil illumination to an NA range of 0.57 to 0.65. NA 1.1 is assumed for the axial detection PSF (blue).

Fig. S8. 3D quantification of microtubule growth during mitosis. (A) Trajectories of the endpoints of growing microtubules in HeLa cells expressing GFP-EB1 at four different time points during division of a HeLa cell, color coded by velocity, from a 4D data set covering 500 time points. (B) Distributions of the mean velocity of each growth track, collated over nine to eleven different cells at seven different stages before and during mitosis. Velocities increase from interphase to metaphase, and then decrease back to the interphase level during cytokinesis. (C) Distributions of the velocities of the endpoints as measured between successive time points. Trends are the same as in (B).

Fig. S9. Microtubule growth rates in individual cells during mitosis. Distribution of microtubule growth rates at different stages of mitosis show the same trends when compared across twelve different cells.

Fig. S10. Cilia motion in Tetrahymena. 2D imaging at a fixed plane through the protozoan T. thermophila. When the specimen is nearly at rest, imaging at 3ms intervals is fast enough to follow the shape and motion of beating cilia.

Fig. S11. Initial aggregation of starved D. discoideum. Volume renderings at three time points from a 4D data set of 300 time points showing the chemotaxis of starved amoeboid cells expressing RFP-LimE as they aggregate in the initial stages of forming a multicellular fruiting body.

Fig. S12. Distribution of AIR-2 during early embryogenesis of C elegans. (A) Volume renderings of GFP-AIR-2 localized at condensed chromosomes during prophase and metaphase at one time point from a 4D data stack covering 50 time points. Left to right: GFP-AIR-2, green channel; mCherry-H2B and PH (chromosomes and plasma membrane), red channel; overlay. (B) Volume renderings of GFP-AIR-2 present on microtubules in the spindle midzone of the AB cell and on the midbody, chromosomes, and the pericentriolar material at a slightly later time point. (C) Volume rendering of GFP-AIR-2 highlighting astral microtubules. A–C, also show AIR2, H2B, and PH localization at the polar bodies (bright spots at the top of the embryos). (D) 2D orthoslice showing the GFP-AIR-2 midbody remnant (magenta) in the extracellular space between the plasma membranes of AB and P1 cells after the first division.

Fig. S13. Distribution of actin during early embryogenesis of C elegans. Maximum intensity projections in an xy view of the top half of a developing embryo expressing GFP-Lifeact, at eight time points from a 4D data set covering 300 time points. (A) Single cell during pseudocleavage ingression, showing an intracellular actin comet. (B, C) Relaxation of the pseudocleavage furrow. (D) Bright cortical actin bundles present in maintenance phase during pronuclear meeting. (E) Smooth embryo, presumably near the time of nuclear centration or initial spindle displacement. (F) During and (G) after the first division. (H) After division of the AB cell.

Fig. S14. Control schematic for the microscope. The SLM LED Enable output is used as the master clock source, but the FPGA provides the analog/digital outputs to control most of the other electronics critical to image acquisition. Additional boards in the computer receive the data from the sCMOS and inspection cameras, and control the sample positioning stages.

Fig. S15. SLM Operation. The SLM is loaded with a series of images known as a Running Order. Once triggered, these are displayed in order, with each image displayed first in positive (0/π) and then negative (π/0) form to preserve the ferroelectric liquid crystal. The desired diffraction pattern is produced with either form, but not during the transition between them, or when the next image in the Running Order is loaded. Thus, an LED Enable digital output is provided to signal to the FPGA those times when imaging can be performed.

Fig. S16. Initialization of the SLM. The sequence of commands to load and then trigger a Running Order for the SLM.

Fig. S17. Camera Synchronization. Timing of the external trigger and exposure sequences for the sCMOS image acquisition camera relative to the image display sequences on the SLM. To optimize speed, the camera readout occurs during the load of the next SLM image in the Running Order.

Fig. S18. FPGA control signals. Galvo and AOTF control signals as synchronized to the SLM during the acquisition of a single plane of data in two colors in the dithered mode.

Fig. S19. Galvo and piezo waveforms. Acceleration, deceleration, and flyback of the galvos and piezos are controlled independently. Data acquisition occurs during the linear ramp (constant velocity) portion of the waveforms.

Fig. S20. Timing diagram for three color objective scan imaging with a dithered lattice light sheet.

Fig. S21. Timing diagram for two color objective scan imaging in the three phase SIM mode.

Fig. S22. Timing diagram for three color sample scan imaging with a dithered lattice light sheet.

Fig. S23. Timing diagram for two color sample scan imaging in the three phase SIM mode.

Fig. S24. Properties of an ideal Bessel beam. (A) Magnitude of the electric field E of an ideal Bessel beam. (B) Phase of the beam. Since E is real, the pattern consists of concentric rings of alternating opposite phase (0/π). (C) Intensity of the beam.

Fig. S25. Tightly confined light sheets derived from linear arrays of coherent Bessel-Gauss beams. The six shortest period linear arrays of Bessel-Gauss beams of either identical or alternate opposite phase that produce optimally confined light sheets (cf., movie S31). At these specific periods, the side lobes of adjacent beams are in phase in the xy plane. All cases assume a maximum NA of 0.60, and a minimum NA of 0.54.

Fig. S26. Optimally confined Bessel-Gauss beam arrays are bound 2D optical lattices. The four shortest period linear Bessel-Gauss beam arrays of optimal confinement and the corresponding bound 2D optical lattices that produce nearly identical light sheets from nearly identical rear pupil illumination patterns. (A) 0.45 μm period array of beams of alternating opposite phase, compared to a lattice light sheet derived from the maximally symmetric primitive rectangular lattice of aspect ratio 3:1. (B) 0.89 μm period array of beams of identical phase, compared to a lattice light sheet derived from the maximally symmetric fundamental square lattice. (C) 1.35 μm period array of beams of alternating opposite phase, compared to a lattice light sheet derived from the maximally symmetric first sparse square lattice. (D) 1.79 μm period array of beams of identical phase, compared to a lattice light sheet derived from the maximally symmetric fundamental hexagonal lattice.

Movie S1. Transition from an infinite 2D optical lattice to an axially bound lattice light sheet, as seen in views of the illumination pattern in the rear pupil of the excitation objective (left) and the cross-sectional intensity profile of the resulting light sheet at the specimen (right).

Movie S2. Animation of the image acquisition process, showing a lattice light sheet (blue/green) intersecting a cell (gray) to produce fluorescence (orange). As the cell is swept through the light sheet, a series of 2D images of the fluorescence are recorded to build up a 3D image of the cell. The lattice is dithered in its patterned direction to mimic a continuous light sheet.

Movie S3. Top and side view volume renderings of HeLa cells expressing mEmerald-Lifeact, demonstrating the higher speed and reduced phototoxicity of the lattice light (right) compared to Bessel beam plane illumination (left) when each is applied to super-resolution structured illumination microscopy (SR-SIM).

Movie S4. Raw 2D image frames during acquisition of a 3D data volume in the SR-SIM mode for two HeLa cells expressing mEmerald-Lifeact, demonstrating the higher modulation amplitude and lower background obtained with a lattice light sheet (right) as opposed to a stepped Bessel beam (left).

Movie S5. Side view volume rendering of filopodia dynamics at 4.0 sec intervals on the dorsal surface of a HeLa cell expressing mEmerald-Lifeact, acquired in the SR-SIM mode using a three phase hexagonal lattice light sheet.

Movie S6. Rapid muscle contractions in a C. elegans embryo in the three-fold stage, with labeled GFP-PH domains (green) and mCherry-histones (magenta), as recorded in a single 2D optical section at 50 frames/sec. Scale bar, 10 μm.

Movie S7. Top and side view volume renderings of filopodia in a HeLa cell expressing mEmerald-Lifeact, comparing the high speed of the dithered mode of lattice light sheet microscopy (left) against the high resolution of the SR-SIM mode (right).

Movie S8. Top view of microtubule dynamics in multinucleate D. discoideum cells expressing GFP-tubulin, color-coded based on their height above the substrate, over 1430 time points at 2.0 sec intervals. Rapid translational movements present in the movie represent a re-centering of the organism within the microscope field of view.

Movie S9. Volume rendering of GFP-dajumin in a D. discoideum cell, highlighting the rapid dynamics of the osmoregulatory contractile vacuole network over 400 time points at 0.6 sec intervals. A slight rocking is present in the viewer perspective during the time lapse to illustrate 3D depth.

Movie S10. Top and side view volume renderings of actin-associated GFP-LimE in a D. discoideum cell over 150 time points at 1.0 sec intervals, highlighting a transient, extremely rapid “lightning bolt” of actin-rich material in the cell cortex.

Movie S11. Single molecule tracking of TMR-labeled Sox2 transcription factors in an ~35 μm diameter spheroid of mouse embryonic stem cells, as seen by a dithered lattice light sheet at a fixed plane (top), a single Bessel beam scanned across the same plane (middle), and widefield, epi-illumination across the entire specimen (bottom).

Movie S12. SNR as a function of exposure time when tracking single TMR-labeled Sox2 transcription factors in one plane across a stem cell spheroid illuminated by a dithered lattice light sheet.

Movie S13. Orthoslices and volume renderings of the nuclear envelope of a U2OS cell labeled with Dendra2-lamin A as imaged by lattice-based super-resolution 3D PALM (left) and diffraction-limited lattice light sheet microscopy (right).

Movie S14. Top and side view maximum intensity projections after deconvolution of GFP-EB1 at growing microtubule ends (left) and TagRFP-H2B highlighting chromosomes (right) in a HeLa cell at three different stages of mitosis.

Movie S15. Maximum intensity projections and measured GFP-EB1 trajectories for a single HeLa cell in interphase. Growing microtubule endpoints and tracks are color coded by z-position above the substrate. Bounding box, 47 × 50 × 11 μm.

Movie S16. Maximum intensity projections and measured GFP-EB1 trajectories for a single HeLa cell in metaphase. Growing microtubule endpoints and tracks are color coded by growth phase lifetime. Bounding box, 29 × 36 × 26 μm.

Movie S17. Measured GFP-EB1 trajectories denoting growing microtubule endpoints, color coded by velocity, and TagRFP-H2B highlighting chromosomes, at five different stages during the division of a single HeLa cell.

Movie S18. Chromosomes (green, mCherry-H2B), mitochondria (yellow, mitotracker – deep red), and endoplasmic reticulum ( magenta, mEmerald-calnexin) in a field of dividing LLC-PK1 cells (cf., Fig. 4B). Left: individual volume renderings. Center: three-color overlay, with the imaging volume sliced in ~2 μm thick slabs to facilitate the visualization of the internal arrangement of the features. Right: magnified view of one such slab, showing mitochondrial fragments nestled in ER cisternae.

Movie S19. Rapid movements of a single cell protozoan T. thermophila expressing GFP-scramblase and confined in a small pocket in agarose (cf., Fig. 4C). Rapid translational movements present in the movie represent a re-centering of the organism within the microscope field of view. Bounding box, 53 × 53 × 51 μm.

Movie S20. Imaging T. thermophila expressing GFP-scramblase in a single 2D plane at 3 ms intervals reveals the motions of individual cilia (cf., fig. S10). Magnified view is shown at right.

Movie S21. Top and oblique view volume rendering of the mutual chemotaxis of starved D. discoideum cells expressing RFP-LimE, marking their transition from unicellular to multicellular morphology (cf., fig. S11).

Movie S22. Two-color volume rendering seen from two different orientations of the interaction of a T-cell expressing mEmerald-Lifeact (orange) with a target cell expressing a plasma membrane marker fused to tagRFP (blue) over 430 time points at 1.3 sec intervals. The target cell has been made invisible in the views in the right column (cf., Fig. 5A–C for a second example).

Movie S23. Two-color volume rendering of a neutrophilic HL-60 cell expressing mCherry-utrophin migrating through a 3D collagen matrix labeled with FITC over 250 time points at 1.3 sec intervals (cf., Fig. 5D–F).

Movie S24. Volume rendering from four different viewing angles of a neurophilic HL-60 cell expressing mCherry-utrophin migrating on a 2D glass substrate over 150 time points at 1.1 sec intervals.

Movie S25. Localization of the chromosomal passenger protein AIR-2 during the first few cell divisions of the early C. elegans embryo (cf., Fig. 6A, fig. S12).

Movie S26. Volume rendering of GFP-PH domains (green) and mCherry-H2B (orange) in a C. elegans embryo at the three-fold stage, after the onset of muscle contractions. Bounding box, 41 × 39 × 60 μm.

Movie S27. Various maximum intensity projections of the distribution of actin in the upper longitudinal half of a C. elegans embryo expressing GFP-Lifeact over 360 time points at 4.8 sec intervals, from a few minutes after fertilization to just after the division of the AB cell. Left, top view. Middle, side view. Right, MIPs in eight consecutive longitudinal slabs through the data set, designed to help distinguish cortical from cytosolic actin (cf., Fig. 6B, fig. S13)

Movie S28. Volume rendering of the amnioserosa and the encroaching epithelium during dorsal closure in a D. melanogaster embryo expressing GFP/DE-cadherin to highlight cell-cell junctions, over 840 time points at 8 sec intervals (cf., Fig. 6C). Bounding box, 86 × 80 × 31 μm.

Movie S29. Volume rendering and orthoslices of myosin II highlighting the myosin-rich purse string during dorsal closure in a D. melanogaster embryo, over 1000 time points at 6.0 sec intervals (cf., Fig. 6D). Bounding box, 80 × 80 × 26 μm.

Movie S30. Various views of dorsal closure in a D. melanogaster embryo expressing sGMCA, a marker of filamentous actin at the plasma membrane, over 639 time points at 12.0 sec intervals. Top left: orthoslice through the center of the amnioserosa. Top right: maximum intensity projection through a thin rectangular slab encompassing the apical surface of the amnioserosa. Bottom right: MIP through a similar slab encompassing the basal surface of the amnioserosa. Bottom left, volume rendering, with the apical surface in blue/green and the basal surface in orange/red (cf., Fig. 6E, F). Bounding box, 73 × 73 × 26 μm.

Movie S31. Rear pupil excitation pattern (left) and cross-sectional intensity at the sample (right) for a linear array of mutually interfering Bessel-Gauss beams, as a function of the period of the array. Top: all beams have the same phase; Bottom: adjacent beams have opposite phase.

Table S1. Imaging conditions for all experiments.