On the spatial distribution of the reflection sources of different latency components of otoacoustic emissions

Abstract

The experimental observation of long- and short-latency components in both stimulus-frequency and transient-evoked otoacoustic emissions admits a comprehensive explanation within the coherent reflection mechanism, in a linear active transmission-line cochlear model. A local complex reflectivity function associated with roughness was defined and analyzed by varying the tuning factor of the model, systematically showing, for each frequency, a multiple-peak spatial structure, compatible with the observed multiple-latency structure of otoacoustic emissions. Although this spatial pattern and the peak relative intensity changes with the chosen random roughness function, the multiple-peak structure is a reproducible feature of different “digital ears,” in good agreement with experimental data. If one computes the predicted transmission delays as a function of frequency and position for each source, one gets a good match to the latency-frequency patterns that are directly computed from synthesized otoacoustic spectra using time-frequency analysis. This result clarifies the role of the spatial distribution of the otoacoustic emission sources, further supporting the interpretation of different-latency otoacoustic components as due to reflection sources localized at different places along the basilar membrane.

I. INTRODUCTION

According to Shera and Guinan (1999), otoacoustic emissions (OAEs) are generated in the cochlea by two mechanisms, coherent linear reflection and nonlinear distortion. Recent experimental and theoretical studies (Mertes and Goodman, 2013; Sisto et al., 2013; Moleti et al., 2013), suggest that human transient-evoked otoacoustic emissions (TEOAEs) and stimulus-frequency otoacoustic emissions (SFOAEs) are mostly generated by place-fixed linear reflection. For each frequency, the main reflection should come from the peak region and be characterized by a compressive growth, approximately as p^1/3 (Sisto et al., 2013), corresponding to a p^–2/3 gain, where p is the stimulus amplitude. Other components, reflected by more basal cochlear places, would reflect the local, less-compressive, basilar membrane (BM) properties and they would therefore be expected to show a close-to-linear growth rate. These characteristic features of the more basal sources have been recently discussed by Goodman et al. (2009, 2011) and by Moleti et al. (2012a) in human TEOAE spectra. More recently, these results have been extended to SFOAEs by Sisto et al. (2013), suggesting that both TEOAEs and SFOAEs originate indeed from a linear reflection mechanism and not from nonlinear distortion. Moleti et al. (2012b) proposed an effective method, based on the wavelet transform, to separate the OAE components coming from different generation regions by filtering the waveforms (or the complex spectra) in the time-frequency domain by defining appropriate filtering regions in the t-f domain. The method is based on the assumption of the validity of linear transmission line cochlear models, in which the OAE latency is the roundtrip integral from the base to the generation region of the traveling wave (TW) inverse group velocity. In this framework, for each frequency the different components coming from different regions would be characterized by different latencies, whereas the latency of each component should approximately scale as the reciprocal of the frequency, due to the approximate cochlear global scaling symmetry. The application of the method to the TEOAE and SFOAE spectra recorded in human subjects (Sisto et al., 2013) confirmed the presence, in the time-frequency energy distribution, of a shorter-latency (SL) and faster-growth OAE component, with respect to the long-latency (LL) component, presumably reflected from the characteristic BM tonotopic region. The different I/O relations of the LL and SL components are indeed consistent with the different nonlinear properties of the BM response in the peak region and in more basal regions. Another relevant feature of the experimental SFOAE and TEOAE responses is that their energy is concentrated in a relatively small number of spots in the t-f domain. At low stimulus levels, the main SFOAE or TEOAE components belong to the LL time-frequency region, whereas at higher stimulus levels the SL components become dominant. For SFOAEs the trade-off is around 30 dB sound pressure level. At these intermediate stimulus levels, in each frequency band the most intense spot may belong either to the SL or to the LL t-f band.

Moleti et al. (2013) have also shown that in a transmission line nonlinear model directly solved in the time domain using the state-space formulation method, the SL TEOAE components disappear when the roughness is removed from the model, whereas they are still present at a very low stimulus level, in the asymptotically linear regime, suggesting that intermodulation distortion is not the main SL component generation mechanism. In particular, for each frequency, the SL component vanishes as roughness is removed from a BM region that is basally displaced with respect to the characteristic place by a typical spatial displacement, of order 0.7–3 mm, corresponding to a characteristic frequency spacing of about 10%–40%. The hypothesis of basal reflection generation for the TEOAE SL components has been further confirmed by a recent analysis of experimental TEOAE data of impaired ears of subjects exposed to firearm noise (Moleti et al., 2014). Due to the sharp gradient of the audiometric threshold level characteristic of these subjects at the lower frequency bound of their impairment range, it was possible to show a clear difference between the cutoff frequencies of the LL and SL component spectra, supporting the hypothesis that they come from different BM spatial region, with an estimated longitudinal displacement of order 0.5–1 mm.

In the present study, we will show that several experimentally observed properties of the OAE response, including the presence of basal sources, the way that the response energy tends to concentrate in spots in the t-f domain, the presence of different latency peaks in the TEOAE and SFOAE response, and the different growth rate of different latency components, are all related to an intrinsic property of the BM reflectivity function. We will define a new theoretical local reflectivity function, and show that its amplitude, computed numerically for different random roughness patterns, and varying the tuning factor of the model, is characterized by a multiple-peak spatial structure. By converting this spatial distribution into a delay distribution, using basic scaling symmetry arguments, one gets a realistic multiple-delay distribution for the OAE response, achieving good agreement with physiological results, even with a model that does not contain nonlinearities. SFOAE simulations have been systematically studied in the double-pole form of the Zweig 1-day transmission-line linear cochlear model (Shera, 2001, based on Zweig, 1991). The Wentzel-Kramer-Brillouin (WKB) approximation provides a theoretical estimate of the complex cochlear reflectivity spectrum as the convolution of a perturbative source function associated with roughness with a Green's function. The so-called reflectivity at the base is computed by performing the convolution integral over the entire length of the BM (e.g., Talmadge et al., 1998). In a smooth scale-invariant cochlea the convolution integral is negligibly small (de Boer and MacKay, 1980; Zweig and Shera, 1995). Cochlear roughness breaks the scaling symmetry so the integral is not null in a real cochlea, due to a small set of strong localized contributions.

As for the experimental SFOAE complex spectra, time-frequency analysis can be applied to the reflectivity at the base to show the presence of different latency components. In the same simulations, the new local reflectivity function was also computed, to isolate different OAE sources distributed along the BM. To do that, we integrate the reflectivity over longitudinal regions of “equal-incremental-latency” width, showing the presence of multiple peaks, localized within a region extending a few millimeters basally to the characteristic place. The absolute position and relative intensity of the peaks vary with each “individual” random roughness function, but similar spatial structures are regularly observed. These spatially distributed sources, in a transmission line model, produce OAEs of different latencies. Converting the source positions into latency, one gets time-frequency maps reproducing the latency-frequency SFOAE distributions previously obtained from the same simulations, similar to those observed in experimental and nonlinear model data of human SFOAEs and TEOAEs (Sisto et al., 2013; Moleti et al., 2013). By doing so, we will demonstrate that the experimental multiple-latency OAE response can be traced back to the spatial structure of the local reflectivity function, in a linear transmission line model.

II. MODEL

The SFOAE generation can be computed using perturbative techniques, adding the SFOAE sources as “small” perturbations on an underlying cochlear model that is both linear and smooth. The Zweig (1991) model provides a suitable framework for this study. This model is linear, which means that its response to different stimulus levels has to be roughly schematized by assuming a suitable variation of some parameter related to the sharpness of tuning. In the Zweig model, an anti-damping region slightly basal to the resonance place is present, due to the competition between an explicit anti-damping term and a stabilizing delayed stiffness term. The Zweig active model was implemented by assuming the Zweig form of the cochlear admittance (Zweig, 1991), as parametrized by Shera (2001). We used a Greenwood tonotopic map of the type (Greenwood, 1990): $\omega (x)={\omega }_1+{\omega }_0{e}^{-k_{\omega }x}$, with ω₀ = 2π·20 655 rad/s, ω₁ = 2π·165 rad/s, and k_ω = 0.138 mm⁻¹. We assumed for the wave number the form k(ω, x) = f(δ, ρ, μ, N), where {δ, ρ, μ} represent the net damping, the strength, and the delay of the stabilizing feedback force. They have been computed for each value of the quality factor (Q) of the BM transfer function, which is related to the dimensionless parameter α* of Shera (2001), representing the imaginary part of the location of the double pole of the BM admittance in the complex frequency plane. For the reader interested in reproducing these results, the relation between the BM tuning factor Q (3 dB) and the parameter α* may be accurately fitted by the empirical formula Q = 1.65/α* − 7.5, only in the parameter region explored by our analysis (Q between 4 and 20). The parameter N, which determines the approximate number of wavelengths of the TW on the BM in response to sinusoidal stimulation was set to 5.6, which is adequate for humans, and consistent with Talmadge et al. (1998).

The assumed admittance function determines the form of the smooth complex wavenumber function k(ω,x) (e.g., Talmadge et al., 1998), whose real and imaginary parts define the local transmission and absorption properties of the BM, for each frequency component ω of the forward and backward cochlear TWs. The longitudinal cochlear coordinate axis is oriented such that x = 0 at the base and x = L = 35 mm at the apex.

The backward component of the response to a scattering source distributed along the longitudinal cochlear coordinate x can be written [last term of Eq. (44) of Shera et al. (2005)] as

$$P_{\mathit{l}}(\omega ,x)=P_0\gamma \left[{\int }_x^{\infty }\epsilon (\omega ,x^{\mathrm{\prime }})k^2(\omega ,x^{\mathrm{\prime }}){\psi }_{\mathit{r}}^2(\omega ,x^{\mathrm{\prime }})d{x}^{\mathrm{\prime }}\right]{\psi }_{\mathit{l}}(\omega ,x),$$ (1)

where P₀ψ_r(ω,x) is the initial forward wave. Equation (1) represents the complex backward TW at x due to the reflectivity associated with the roughness reflection sources localized between x and the apex. The cochlear WKB basis functions ${\psi }_{l,r}$ represent, respectively, independent pressure waves moving backward and forward along the BM in a nonuniform medium [e.g., Talmadge et al., 1998, Eqs. (55) and (56)]

$${\psi }_{l,r}(\omega ,x)\cong \sqrt{\frac{k(\omega ,\hspace{0.17em}0)}{k(\omega ,\hspace{0.17em}x)}}\hspace{0.17em}\hspace{0.17em}\text{exp}\left(\pm i{\int }_0^{x}k(\omega ,x^{\mathrm{\prime }})d{x}^{\mathrm{\prime }}\right),$$ (2)

and γ is the reciprocal of their Wronskian determinant (Shera et al., 2005). The function ε(x) = dk²/k², given by Eq. (21) of Shera et al. (2005), represents the fractional wave number perturbation associated with roughness. In this study, the roughness is represented as a random fluctuation of the local resonant frequency, r(x) = δω(x)/ω(x), therefore (see also Talmadge et al., 1998)

$$\epsilon (\omega ,x)=\frac{k^2(\omega ,x){\omega }^2\left(x\right)r\left(x\right)}{8N^2{k}_{\omega }^2{\omega }^2}.$$ (3)

Equation (1), computed for x = 0 and divided by the forward initial wave P_r(ω,0), represents the first order estimate of the total roughness reflectivity at the cochlear base [Eq. (45) of Shera et al. (2005)]

$$R(\omega )=\gamma {\int }_0^{\infty }\epsilon (\omega ,x)k^2(\omega ,x){\psi }_r^2(\omega ,x)dx.$$ (4)

This reflectivity function can be compared to the SFOAE reflectivity (OAE response divided by the stimulus), by taking into account the middle ear transmission properties. Coherent reflection filtering (CRF) theory explains the observed SFOAE response as due to superposition of the elementary waves backscattered by roughness. For each frequency, the experimental SFOAE spectra result from the vector superposition of a continuum of sources distributed along the BM from the base to the characteristic place, whose local strength is represented by the integrand function in Eq. (1).

At low stimulus levels, the BM response is so sharply tuned that the peaked structure of the backscattering source term dominates the weight of the contributions to the base reflectivity in Eq. (4), so the OAE generation region is spatially narrow, and close to the characteristic place x(ω). As a consequence, the LL components dominate the OAE response. At higher stimulus levels, the BM response is not that sharp, therefore the OAE contribution for the same frequency from more basal cochlear regions (SL components) becomes relevant. In this case, the response in a given frequency band will consist of the superposition of all the contributions from a set of rather narrow cochlear regions picked up by the individual roughness distribution as preferred coherent reflection regions. It turns out that the OAE response consists of localized spots in the time-frequency domain, with distinct different-latency components in each frequency range. Indeed, for each frequency, the same preferred reflection region yields a different cochlear round-trip transmission delay, according to the approximate relation, which holds only in the scale-invariant limit [see Talmadge et al., 1998, Eq. (189)]

$$\tau (\omega ,x)\cong 2{\int }_0^{x_n}\frac{d{x}^{\mathrm{\prime }}}{v_g(\omega ,\hspace{0.17em}{x}^{\mathrm{\prime }})}=\frac{2\text{Re}\left(k\right(\omega ,x)-k(\omega ,0\left)\right)}{\omega k_{\omega }},$$ (5)

where

$$v_g(\omega ,x)={\left(\frac{\partial \text{Re}\left(k\right(\omega ,x\left)\right)}{\partial \omega }\right)}^{-1}$$ (6)

is the group velocity for a wave packet of frequency ω at the cochlear place x.

Starting from Eq. (4) a “local reflectivity” density function was defined as

$$R_{\text{local}}(\omega ,x)=\frac{\gamma }{\Delta x}{\int }_0^{\infty }g(x^{\mathrm{\prime }}-x,\hspace{0.17em}\Delta x)\epsilon \left(x^{\mathrm{\prime }}\right)k^2(\omega ,x^{\mathrm{\prime }}){\psi }_{\mathit{r}}^2(\omega ,x^{\mathrm{\prime }})d{x}^{\mathrm{\prime }},$$ (7)

where $g(x^{\mathrm{\prime }}-x,\hspace{0.17em}\Delta x)$ is a Gaussian window function centered at x, of width Δx.

This formula essentially evaluates the “local” contribution to the cochlear reflectance at frequency ω using only the roughness located in a certain region of the cochlea centered at x. The spatial integration region Δx was set according to: $\Delta x(\omega ,x)\approx v_g(\omega ,x)\Delta t(\omega )$, where Δt(ω) ≈ 2π/ω = 1/f is the best temporal resolution achievable at frequency ω, using a linear analysis tool. With this choice, one is able to separately analyze in the spatial domain the OAE sources that would appear as individual peaks in the temporal evolution of the envelope of the TEOAE response (as in Fig. 8 of Goodman et al., 2009) or as distinct spots in the time-frequency representation of the cochlear reflectivity at the base, due to their different latency.

The multiple-peak spatial structure of the reflectivity function was studied in the case of a smooth linear active model in which the reflection source associated with roughness is introduced as a perturbation. The Q was changed to roughly represent different dynamic ranges, corresponding to different stimulus levels.

The stapes reflectivity was considered null in this study. To account for finite stapes reflectivity, one would introduce multiple reflection components of multiple latency, which are an interesting part of the OAE phenomenology, but neglecting them was considered preferable in the present study because, in a model with significant stapes reflectivity, one could wonder whether the observed multiple-peaks spatial patterns were due (at least, partly) to the formation of stationary waves between the base and the characteristic place.

III. METHODS

The objective of the present study is to demonstrate that the multiple delay nature of the SFOAE response evaluated at the base can be explained by the multiple-peaked spatial structure of the cochlear reflectivity. To do that, the following method has been developed. Numerical integration of the analytical WKB perturbative solutions of the cochlear wave equations were performed for a set of M = 512 frequencies spaced by 20 Hz, over a 1-day discretized cochlea with N_el = 2000 elements, whose local characteristic frequency varied along x according to the Greenwood map.

From the same model, we computed two primary outputs:

• (1)The complex SFOAE response at the cochlear base, computed from Eq. (1) as a function of frequency, which could be directly translated into a realistic SFOAE spectrum measured in the ear canal by taking into account the transmission function through the middle ear (which is not within the scope of this study);
• (2)The SFOAE backscattering source density, or local reflectivity function, computed from Eq. (7) as a function of frequency and position.

From (1) and (2) we also computed secondary outputs applying time-frequency analysis to (1), and assuming the validity of Eq. (5) to perform position to delay conversion in (2).

In the simulations, the roughness distribution is represented by the function r(x), a random variable chosen from a Gaussian distribution with zero mean and standard deviation r. In all the simulations we used r = 0.01. Since Eq. (3) is linear in r, the results may be straightforwardly scaled to different roughness amplitudes. The cochlear complex reflectance at the base was computed in the frequency domain and then time-frequency analyzed using the wavelet method described in Moleti et al. (2012b). The time-frequency resolution of the analysis was optimized for this study by suitably choosing the dimensionless parameter β, relating frequency and bandwidth, of the wavelet basis function, of the type proposed by Tognola et al. (1997),

$$w_m\left(t\right)=\frac{\hspace{0.17em}\text{cos}\left({\omega }_{m}t\right)}{1+{\left(\beta {\omega }_{m}t\right)}^4},$$ (8)

where m = 1, 2,…, 128 is the wavelet index, and ω_m = mω₀ is the center frequency of the mth wavelet of the basis, with ω₀ = 250 rad/s. The parameter β can be adjusted to get an optimal compromise between frequency and time resolution. In this analysis β = 0.05 was used, exactly as in Tognola et al. (1997), getting (Δf ≈ 0.1 kHz; Δτ ≈ 3 ms) at 1 kHz. As in any wavelet transform, Δf/f is constant, so Δτ is proportional to 1/f. A better time resolution could be achieved, losing frequency resolution, by increasing β, if the temporal structure associated with R_local(ω,x) required it, which is not the case in this study.

The wavelet coefficients relative to a generic function y are generally defined in the time domain as the convolution between the original waveform y(t) and the wavelet basis functions w_m(t),

$$W({\omega }_m,\tau )=\int \mathit{d}\mathit{t}{w}_m(t)y(t-\tau ).$$ (9)

In our case, the complex reflectivity spectrum R is already defined in the frequency domain, so the wavelet coefficients were directly computed as the inverse Fourier transform (IFT) of the product of the Fourier transform (FT) of the wavelet basis functions, ${\tilde{w}}_m(\omega )$, by the function R(ω),

$$W({\omega }_m,\tau )=\text{IFT}({\tilde{w}}_m(\omega )R(\omega )).$$ (10)

The energy density in the time-frequency plane was computed by root mean square (rms) averaging the wavelet coefficients along the time direction, using, in each frequency bin, an integration time span scaling as the temporal resolution of the time-frequency analysis (i.e., inversely proportional to frequency). This procedure, already used in Moleti et al. (2012b), eliminates the oscillations of the wavelet coefficients at the wavelet carrier frequency while preserving the intrinsic temporal resolution of the analysis.

The integral in Eq. (7) was computed. This spatial filter allows one to isolate contributions to the overall reflectivity coming from a definite cochlear region, therefore characterized by a given phase-gradient delay (which is approximately equivalent to the round-trip transmission delay, because the coherent reflection mechanism is place-fixed). As the question that has been addressed is whether the time-frequency representation of the SFOAE response, W(ω,τ) of Eq. (10), is similar to the local reflectivity function, R_local(ω,x) of Eq. (7), and to what extent the features of one can be explained by the features of the other, the first thing to notice is that the bi-dimensional representation of Eq. (7) is in the x-f domain. To compare Eq. (10) to Eq. (7), the x-f domain in Eq. (7) was transformed to the t-f domain. To do that, the x scale was transformed into a time-delay scale by using the relation between latency and position which approximately holds in a 1-day transmission line scale-invariant cochlear model, Eq. (5). This means that, for each frequency interval (f, f + df), the reflectivity density within each time delay interval (τ, τ + dτ) was computed, using Eq. (5) to perform a frequency-dependent position-to-delay conversion. After that, a moving average was also applied along the frequency axis with a frequency-dependent integration step, matching the frequency resolution of the wavelet analysis applied to get Eq. (10).

IV. RESULTS AND DISCUSSION

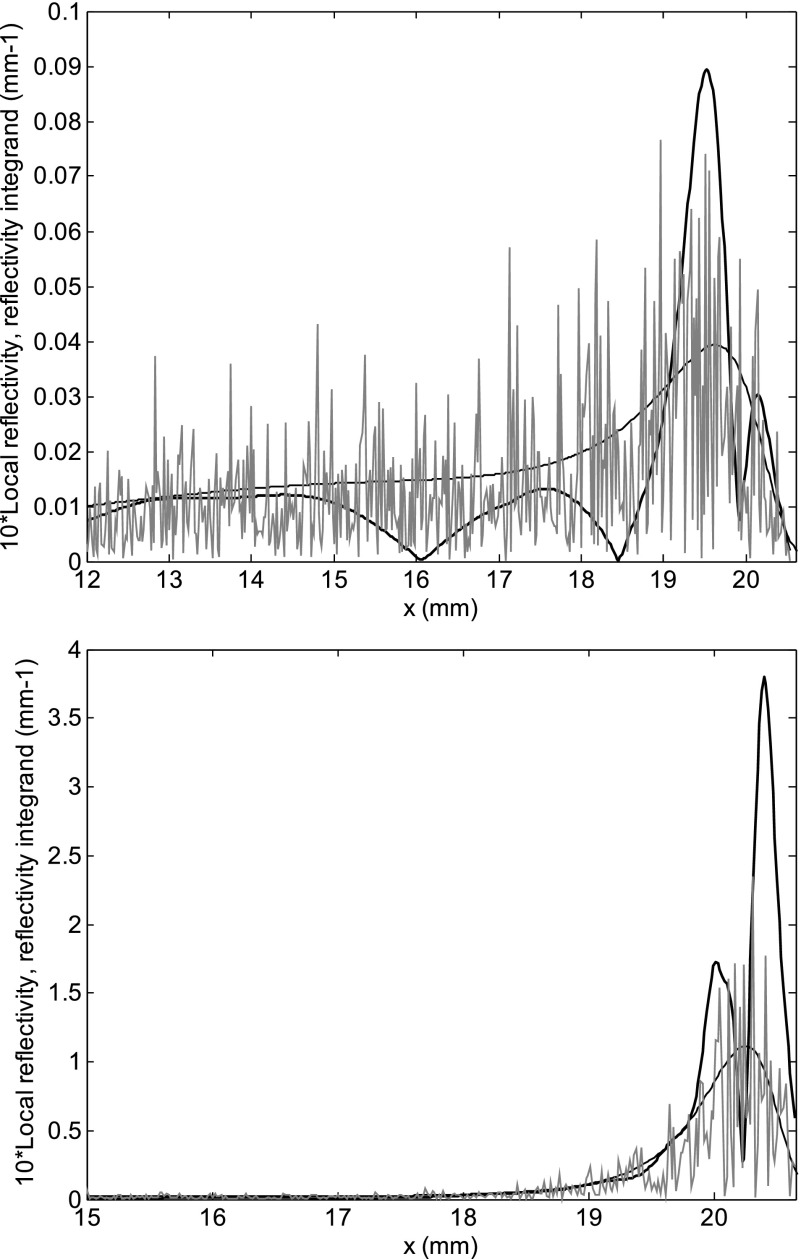
Figure 1 shows two spatial profiles of the magnitude of the local reflectivity density function of Eq. (7) (thick black lines, magnified 10 times), along with that of the integrand of Eq. (1), with (thin gray line) and without (thin black line) the random perturbation. The wave frequency is f = 1 kHz, N = 5.6, for different roughness patterns and different sharpness of the cochlear tuning [Q = 4 (top) and 12 (bottom), (corresponding to {α*, δ, ρ, μ} = {0.143, 0.105, 0.0378, 1.745} and {α*, δ, ρ, μ} = {0.0846, −0,0134, 0.0723, 1.743}, respectively). Here, and in the rest of the paper, a roughness function with fractional amplitude r = 0.01 has been used. In the perturbative WKB approach, the reflectivity is directly proportional to the roughness amplitude, so the results do not depend on this choice, apart from a scaling factor. The random nature of the roughness pattern accounts for the “rough” profile of the integrand function, with strong high-spatial-frequency oscillations. Integration yields a smoother profile, in which multiple reflectivity peaks emerge, whose details (position and relative amplitude of the main peaks) are dependent on the roughness pattern and on the sharpness of tuning.

FIG. 1.

Spatial distribution of the magnitude of the local roughness reflectivity function, Eq. (7), in linear units (thick line, magnified 10 times) at f = 1 kHz, and of the integrand of Eq. (4) with (thin gray line) and without (thin black line) the random perturbation, for a Zweig model with Q = 4, and another with Q = 12, for two different roughness patterns r(x). A number of distinct peaks appear within the resonant region.

Of course, a criticality of the definition of the local reflectivity is the choice of the width of the Gaussian window. The multiple peak structure of Fig. 1 becomes smoother as wider Gaussian windows are used in Eq. (7), ending with a single wide peak as the window becomes larger than the local wavelength. For this reason, the window width of this study was chosen independent of the model and of the spectral analysis details, being related to the best temporal resolution achievable for a signal of frequency f.

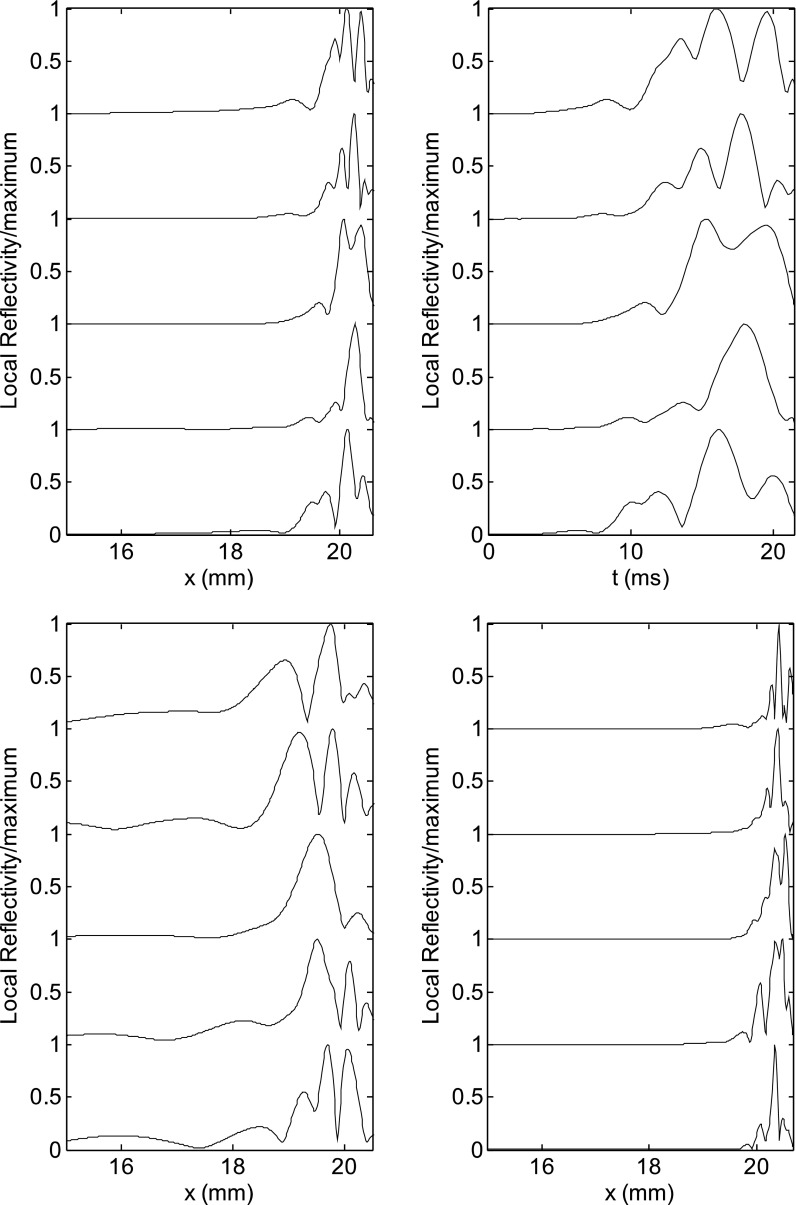
By changing the random roughness pattern one gets different characteristic generation places, as shown in Fig. 2, top left, where the local reflectivity function is plotted for a fixed frequency (1 kHz), Q = 10, and a set of five different random roughness patterns (simulating different ears). Nevertheless, multiple-peak structures are observed for almost all ears, basally to the characteristic place. If the spatial coordinate is converted into time delay using Eq. (5), and the spatial density of Eq. (7) is converted into a temporal density multiplying it by the group velocity, one gets different multiple-delay temporal profiles for different roughness patterns (Fig. 2, top right). This representation confirms the main result of Goodman et al. (2011), i.e., the peak delay distribution of the TEOAE responses of a large number of ears tends to uniformly cover a wide region along the time axis, but, for each ear, two or three main peaks at specific positions generally appear, well separated along the time axis. Figures 1 and 2 support the idea that the experimentally observed few-peak structure naturally emerges from the coherent reflection mechanism as a result of the vector superposition of a large number of elementary random backscattering sources. The same kind of plot, for very high and very low values of Q (Fig. 2, bottom), shows that for Q = 15, the reflectivity profile tends to be dominated by the shape of the resonance, and most of the reflected energy comes from within 1 mm of the resonant place. Nevertheless, distinct peaks still emerge, due to the smaller group velocity in the region close to the peak. Defining the Gaussian window width used in Eq. (7) as a function of the group velocity ensures that the narrow peaks are captured accurately. At Q = 5, in some ears, the random nature of the roughness reflectivity may significantly shift the reflectance distribution toward the base, with significant contributions from regions basally shifted by more than 3 mm (about 1 octave in terms of characteristic frequency).

FIG. 2.

(Top left) Magnitude of the local reflectivity density, normalized to its peak value, at 1 kHz, for a Zweig model with Q = 10, for five different roughness patterns (“digital ears”). (Top right) Same function plotted against the delay estimated using Eq. (5), for the same roughness patterns. A small number of peaks are present in most simulations, whose positions (or delays) change with changing the roughness pattern. (Bottom left) For Q = 5, significant contributions come from very basal regions, corresponding to a shift in characteristic frequency of order 1 octave or more. (Bottom right) For Q = 15, most of the reflected power comes from the peak of the response, yet distinct peaks still emerge, because, due to the low group velocity, even short longitudinal displacements may correspond, in the high-Q case, to measurable temporal shifts.

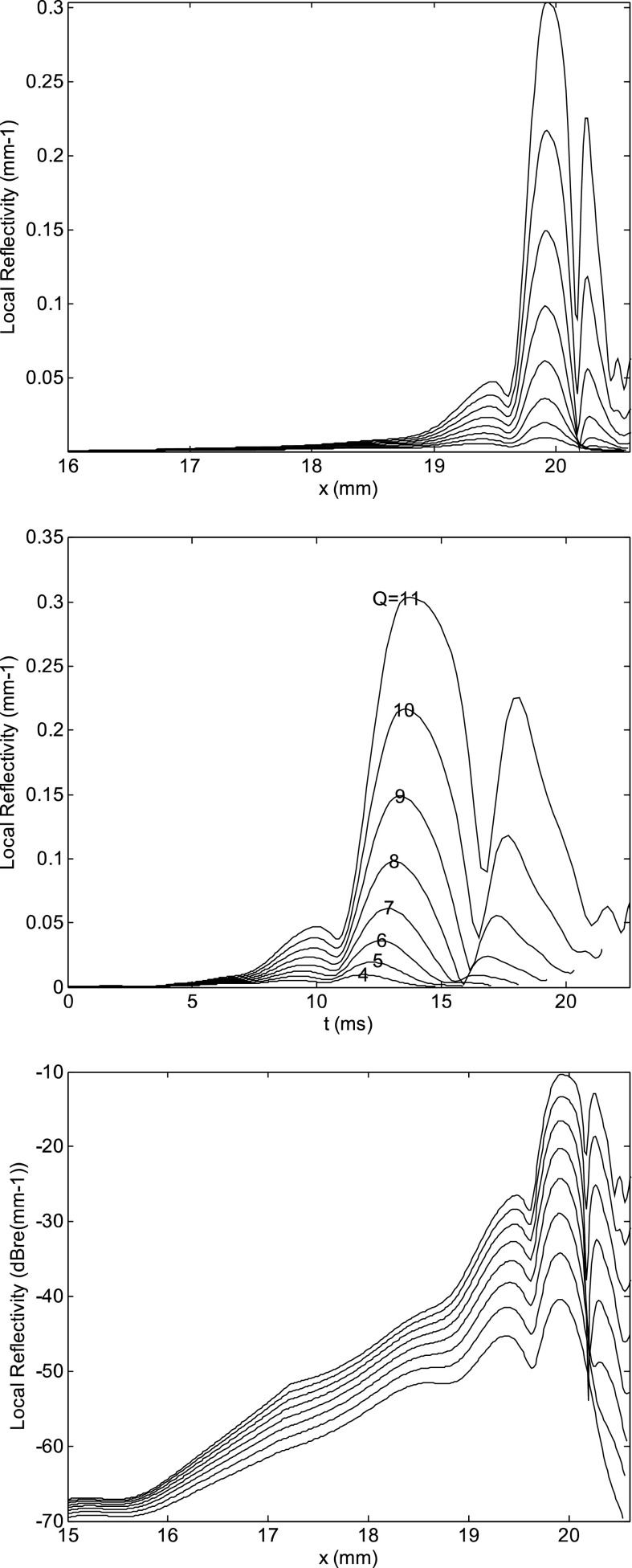
It is interesting to show how the multiple peak structure of the local reflectivity function changes as a function of Q, for the same roughness pattern (Fig. 3, top). The peak positions do not move, but their relative intensity changes, due to the change of the underlying resonant pattern. The most intense peak moves toward the base with decreasing Q. If this spatial position is converted into a delay, assuming the validity of Eq. (5), one gets the delay distributions shown in Fig. 3, middle, which can be compared with the multiple-delay bandpass filtered TEOAE responses reported in Fig. 8 of Goodman et al. (2009). The similarity between the two confirms the validity of the theoretical approach, with one notable difference. The latency of the most apical peaks significantly increases with increasing Q. Therefore, the model seems to fail in reproducing the experimentally observed insensitivity of each OAE component delay on stimulus level (e.g., Goodman et al., 2009). This issue deserves further study, to better understand whether this unexpected dependence of OAE latency on the BM Q is a characteristic of the Zweig model, or it depends on the details of our post-processing technique (e.g., having neglected the effect of roughness on the conversion from displacement to latency). In the bottom panel of Fig. 3, the same curves of Fig. 1 are reported on a dB scale, to better appreciate the different dependence on tuning of the different components. This feature is in agreement with experimental SFOAE and TEOAE measurements by Sisto et al. (2013), who showed that the LL spots (interpreted as those coming from the most apical sources) become gradually dominant as the stimulus level decreases (corresponding here to increasing Q).

FIG. 3.

(Top) Spatial distribution of the magnitude of the local reflectivity density of Eq. (7) (in linear units) at f = 1 kHz, for models with Q = 4, 6, 7, 8, 9, 10, 11, and the same roughness pattern. The spatial position of the peaks is almost independent of Q, but their relative intensity changes due to the progressive peaking of the underlying displacement basis function. At low Q the most apical peaks disappear. (Middle) Same local roughness reflectivity function, expressed in linear units as a function of the estimated transmission delay, having used Eq. (5) to convert position and frequency into delay. The latency of the most apical peaks rapidly increases with increasing Q. In the experimental bandpass filtered TEOAE data by Goodman et al. (2009), similar delay distributions were observed, but the delay of each peak was rather insensitive of the stimulus level. (Bottom) Same as in the top panel, on a vertical log scale, to better show the different dependence on Q of the different peaks.

By performing the simulation for a given roughness pattern for M = 512 frequencies, and plotting the local reflectivity density function on the x-f plane (Fig. 4) one may note that, in the low-Q case (top), a few selected cochlear places are characterized by large source density over a rather wide frequency range (which qualifies this mechanism as actually “place-fixed”). As shown in Fig. 4, the resonant form of the integrand in Eq. (7) favors the characteristic place region (which explains the observed overall regularity of the experimental OAE latency-frequency relation), particularly in the high-Q cases (bottom). Within and basally to that region, a multiple-peak spatial source structure is visible at fixed-frequency (non-monotonic intensity behavior along vertical lines).

FIG. 4.

Place-frequency distribution of the local roughness reflectivity function, for Q = 7 (top), and 12 (bottom). At moderate Q values, spatially localized OAE sources extend over a large frequency range, whereas at high Q the tonotopic relation is more strictly enforced by the peaked structure of the integrand function of Eq. (7).

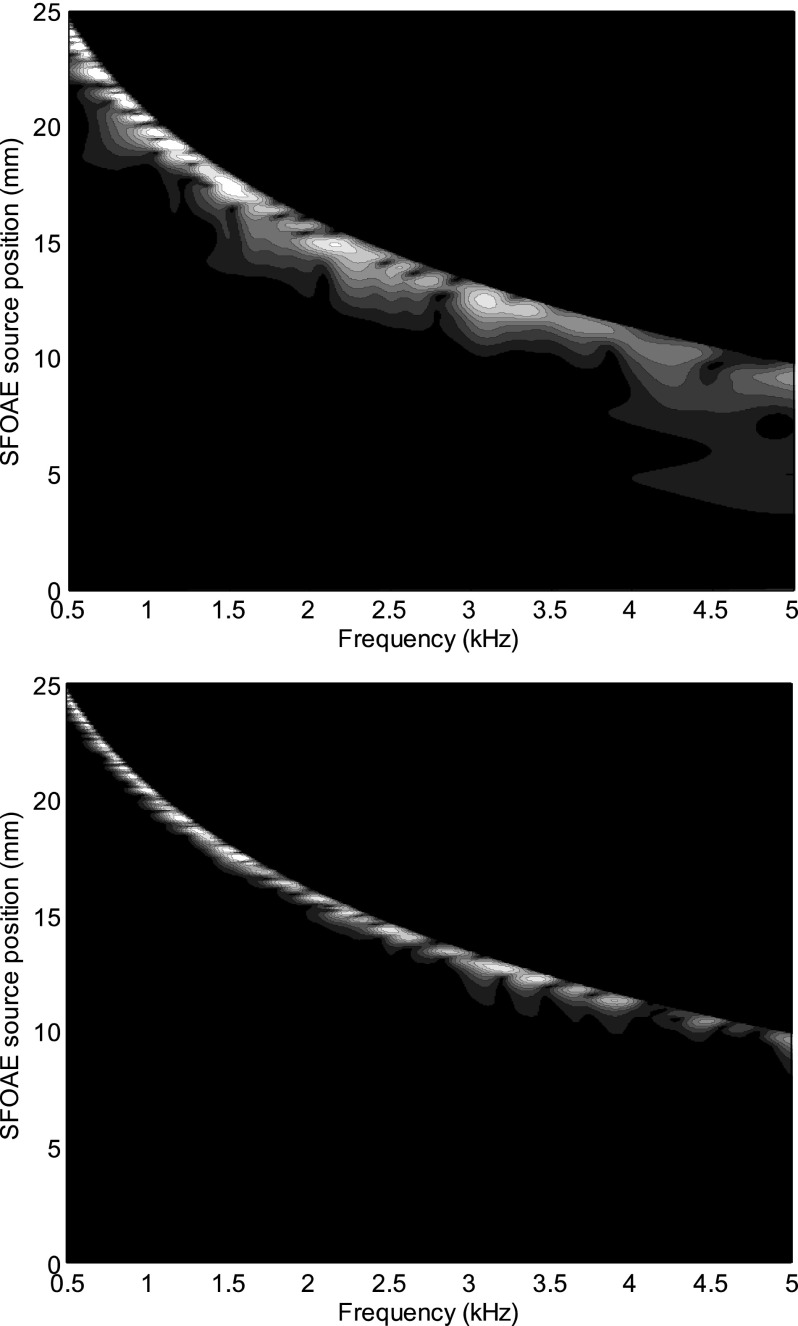
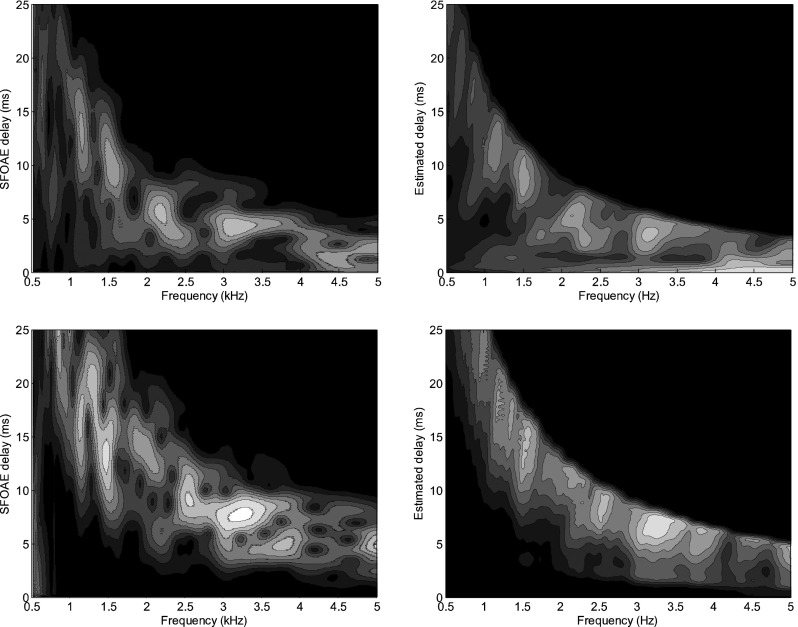
We had argued that the structure of the source position-frequency distribution was responsible for the typical multiple-latency structure observed in the experimental SFOAE and TEOAE time-frequency distributions (e.g., Sisto et al., 2013). To demonstrate that, we compute, for a given roughness pattern, the SFOAE model response at the base in the WKB approximation, and compare its time-frequency distribution with the time-frequency map obtained from the space-frequency map of the sources (Fig. 4), obtained by converting the position into latency using the scale invariant approximation to the delay path integral of Eq. (5). A good match is obtained between the two, and also with the typical time-frequency distributions of experimental SFOAE data (e.g., Sisto et al., 2013), when the quality factor is moderate (Q = 7, Fig. 5, top). At higher Q values (Q = 15, Fig. 5, bottom), the delay estimate is (in the resonant region) a very sensitive function of the position, and the reconstruction is less precise.

FIG. 5.

(Top left) Time-frequency distribution of the SFOAE response, Eq. (1), for the simulation with Q = 7 of Fig. 4, and (top right) delay-frequency representation of the source distribution obtained from Eq. (7) converting the local source position and the frequency into a time delay, using the theoretical τ(f,x) function, Eq. (5); (bottom) same plots, for a simulation with Q = 15.

Summarizing, comparison with real experimental SFOAE and TEOAE spectrograms shows that the simple model of the local cochlear reflectivity used in this study is capable of explaining the following experimental evidences, as anticipated in Sec. I:

• (1)The OAE spectrogram is concentrated in a relatively small number of “spots” of given frequency and time delay.

  In the model, this is due to the existence of a relatively small number of place-fixed coherent backscattering regions, emerging through the CRF mechanism, and producing sharp peaks in the x-f reflectivity density function.

• (2)At low stimulus levels, the main SFOAE components belong to the LL time-frequency region, whereas at higher stimulus levels the SL components become dominant. At intermediate stimulus levels, either SL or LL spots may dominate the response in each frequency band. At the highest stimulus levels, very short-latency components also appear.

  In the model, this is due to the competition between the existence of place-fixed preferred reflection regions associated with the individual roughness pattern, and the resonant form of the source term, which tends to favor the “close-to-CF-place” sources. As the stimulus level increases, the sharpness of the BM response decreases, and its maximum is basally shifted, so the relative weight of the most apical sources progressively decreases. Increasingly wider basal regions give significant contributions, from the place-fixed regions randomly selected by the individual roughness pattern.

V. CONCLUSIONS

The multiple peak nature of the local reflectivity due to roughness is sufficient to explain the presence and the phenomenology of different-latency components in the TEOAE and SFOAE spectra. This phenomenon has been studied in a 1-day transmission line cochlear model, solved in the frequency domain in the WKB approximation.

The model has been used to simulate the SFOAE complex spectra, finding a good correspondence between the latency-frequency localization of the main SFOAE components and the position of the BM regions associated with the main local reflectivity peaks.

A significant short-latency source seems to be present in the model only if the tuning factor is relatively low, which is also in agreement with experimental OAE data. Indeed, at very low stimulus levels, corresponding to sharply tuned BM response, LL components dominate the TEOAE and SFOAE response (Sisto et al., 2013).