Comparison of Three Ionic Liquid-Tolerant Cellulases by Molecular Dynamics

Abstract

We have employed molecular dynamics to investigate the differences in ionic liquid tolerance among three distinct family 5 cellulases from Trichoderma viride, Thermogata maritima, and Pyrococcus horikoshii. Simulations of the three cellulases were conducted at a range of temperatures in various binary mixtures of the ionic liquid 1-ethyl-3-methyl-imidazolium acetate with water. Our analysis demonstrates that the effects of ionic liquids on the enzymes vary in each individual case from local structural disturbances to loss of much of one of the enzyme’s secondary structure. Enzymes with more negatively charged surfaces tend to resist destabilization by ionic liquids. Specific and unique structural changes in the enzymes are induced by the presence of ionic liquids. Disruption of the secondary structure, changes in dynamical motion, and local changes in the binding pocket are observed in less tolerant enzymes. Ionic-liquid-induced denaturation of one of the enzymes is indicated over the 500 ns timescale. In contrast, the most tolerant cellulase behaves similarly in water and in ionic-liquid-containing mixtures. Unlike the heuristic approaches that attempt to predict enzyme stability using macroscopic properties, molecular dynamics allows us to predict specific atomic-level structural and dynamical changes in an enzyme’s behavior induced by ionic liquids and other mixed solvents. Using these insights, we propose specific experimentally testable hypotheses regarding the origin of activity loss for each of the systems investigated in this study.

Introduction

Lignocellulosic biomass is an important potential feedstock for the sustainable production of liquid fuels and other chemicals. Development of technologies toward effective production of biofuels from these substrates has led to the requirement of pretreatment processes to improve viability (1). Pretreatment is a general term for the processing steps used to convert raw cellulosic biomass to a form that is suitable for enzymatic hydrolysis. This includes, but is not limited to, the solubilization of cellulose and hemicellulose and the separation of lignin, which inhibits enzymatic activity (2,3). Several methods of pretreatment have been developed (e.g., steam explosion, ammonium fiber explosion, dilute acid solutions, and lime solutions), and each has advantages and disadvantages. A detailed review of pretreatment methods has been provided by Abor et al. (4). In summary, the high temperatures, high pressures, or caustic chemicals utilized in these processes are undesirable from the standpoint of capital and energy costs, safety, equipment lifetime, and environmental impact. To varying degrees, these processes also produce byproducts such as phenolic compounds and furan derivatives that interfere with enzymatic hydrolysis, degrade potentially useful secondary substrates, or cause loss of saccharides (5,6). It would be preferential to develop new pretreatment methods that run at lower temperatures, at atmospheric pressure, and with fewer hazardous chemicals. In addition, and of the most importance, such new methods should allow hydrolase activity without neutralizing or changing the solvent from step to step.

Many researchers have demonstrated that ionic liquids (ILs), organic salts that have melting temperatures near 100°C, can completely solubilize cellulosic biomass, separating the hemicellulose and cellulose from lignin while overcoming the recalcitrance of crystalline cellulose (7–9). In addition to their rare ability to dissolve crystalline cellulose, ILs are relatively benign compared to chemicals such as sulfuric acid, lime, and ammonia that are used in other pretreatment processes. The chemical and thermal stability of ILs coupled with their low vapor pressure gives them the ability to be recycled through the process many times without loss, and effective separation of ILs from biomass has been demonstrated. IL pretreatment can be done at lower temperatures and atmospheric pressures and poses less of an environmental risk than other pretreatment processes. Thus, the equipment used does not need to be as robust, and fewer safety precautions are required. Therefore, ILs have been proposed as an alternative and green pretreatment solvent (10–14).

One aspect of an IL-based pretreatment scheme is that many imidazolium-based ILs can support enzymatic catalysis at a variety of temperatures, both as pure solvents and in binary mixtures with water. When used as solvents for biochemical reactions, the right choice of IL can improve our ability to control many properties of the reaction, especially substrate and product solubility. Some hydrolases, such as chymotrypsin, retain activity in pure ILs (15), and others, such as certain lipases, exhibit enhanced thermal stability (16,17), selectivity (18), and enantioselectivity (19,20) compared to traditional solvents. Yet there are no known cellulases that can tolerate ILs at high concentrations. Instead, these enzymes tend to deactivate at much lower concentrations of IL in water. Specific examples will be discussed later. Still, the potential to dissolve cellulosic biomass while maintaining hydrolase activity in low concentrations of IL affords a unique opportunity to avoid a secondary separation step during biomass pretreatment. However, the enzyme cocktails used to hydrolyze solubilized biomass show insufficient or even no activity in many potentially useful ILs. Without either a method for improving enzyme activity in the current ILs or discovery of novel ILs that permit sufficient enzyme activity, improving the viability of biocatalytic conversion of biomass using ILs will be greatly hindered.

Glycoside hydrolase (GH) enzymes catalyze the degradation of long-chain carbohydrates such as cellulose and xylan, whose subunits are key substrates for the production of biofuels and other value-added chemicals. GHs are an important target for engineering ILs or the enzyme itself to improve their activity in the pretreatment of biomass. Recent publications from several research groups have provided important results with a view to discovering both ILs capable of supporting GH enzymes and enzymes that exhibit improved activity in ILs. In particular, Wang et al. have demonstrated up to 65% retention of activity for a cocktail of GH enzymes in 20 wt % 1-ethyl-3-methyl-imidazolium acetate ([EMIM][OAc]) in water (21). Zhang et al., in a separate publication, reported full or even enhanced activity of a cellulase (family 5 GH (GH5)) from a halophilic microbe in 20 wt % [EMIM][OAc], [EMIM][Cl], [BMIM][Cl], and [AMIM][Cl] relative to its activity in water (22). This group later demonstrated activities for three other GH family 5 cellulases that vary considerably in their ability to function within increasing concentrations of [EMIM][OAc] in water (23).

These preliminary studies offer a wealth of research opportunities to further understand the interaction between ILs and biomass-hydrolyzing enzymes. Of particular interest are results showing that structurally similar cellulases from three separate species have drastically different activity in increasing concentrations of [EMIM][OAc] (23). The three enzymes are a cellulase from Trichoderma viride, a cellulase 5A from Thermotoga maritima, and an endoglucanase from Pyrococcus horikoshii. Structures and relevant details of these enzymes, hereafter referred to as VIR, TMA, and PHO, respectively, are provided in Fig. 1, A and B. Optimal temperature and pH are taken from Datta et al (23). Surface charge is calculated as described in the Methods section. Even though the enzymes are all classified as the same family, the organisms they are extracted from belong to three different domains of life: Eukarya, Bacteria, and Archaea, respectively. VIR, an industrial benchmark for cellulase activity in water, is mesophilic; both TMA and PHO are identified as hyperthermophilic enzymes. Fig. 1 C superimposes the structures over each other. MultiSeq (24) was used to analyze the differences in the sequences and structures among the three enzymes. The root mean-square displacement (RMSD) of the coordinates of mutual residues and the percentage of identical residues are 2.3 Å and 13.1%, respectively, for VIR and TMA, 2.9 Å and 9.2%, respectively, for VIR and PHO, and 2.6 Å and 14.8%, respectively, for TMA and PHO. Twenty-five residues are conserved across the three structures, all of which are near the β-barrel that contains the catalytic residues.

Figure 1.

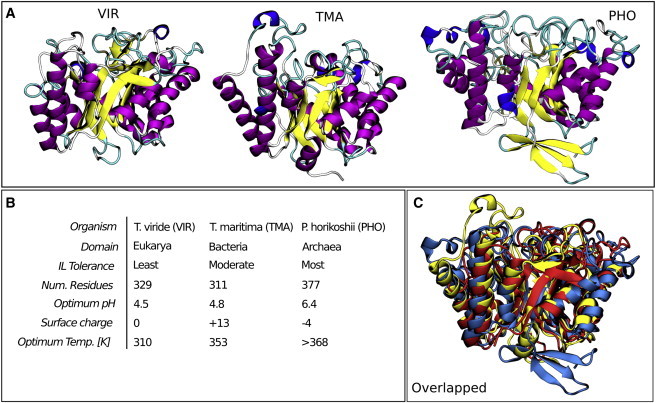
(A) Renderings of the initial configurations for each enzyme. (B) Details highlighting the differences between the enzymes. (C) Overlaid structures of PHO (blue), TMA (yellow), and VIR (red). To see this figure in color, go online.

Datta and coworkers hypothesized that thermophilic enzymes will tolerate ILs more readily than will their mesophilic relatives. The presence of a higher number of ion pairs (that is, charged amino acids) has been observed in the structures of hyperthermophilic enzymes (25). These ion pairs form salt bridges that stabilize the protein against unfolding at high temperatures. The results of the Datta et al. study provide details about the macroscopic properties of the enzymes, such as activity and melting temperatures. They identified the two thermophilic enzymes, TMA and PHO, as IL-tolerant to some degree, but their methods did not allow them to gain molecular-level insight into the structure and dynamics of the enzymes themselves. Their results provide us with the ability to connect the fine detail provided by molecular simulation with relevant macroscopic properties such as thermophilicity and IL tolerance.

Molecular simulation, in particular molecular dynamics (MD), can be used to study the effects of ILs on GHs at atomistic resolution and help to resolve several of the hypotheses previously put forth in the literature. A few MD studies have been conducted on the role that ILs play in the activity and stability of enzymes and proteins (26–30). One study compares several GH5 enzymes solvated in water using metrics taken from MD trajectories. The researchers were able to demonstrate the feasibility of MD-guided protein engineering by suggesting specific mutations that stabilized a GH5 enzyme at high temperatures (31). Based on the hypothesis of Datta and colleagues about the connection between thermal stability and IL tolerance, we determined that mutations that stabilize the protein at high temperatures are relevant to our purpose. Our previous simulations in the area of IL-enzyme compatibility analyzed the stability and fluctuations of two different hydrolases, Trichoderma longibrachiatum GH11 and Candida rugosa lipase, structures in IL-containing solvents (32,33). We suggested that the presence of IL in concentrations of up to 20 wt % does not appreciably denature the enzyme in simulations on timescales of up to 500 ns. We also suggested that the dynamics of the structure as measured by root mean-square fluctuation (RMSF) and principal component analysis could be used as a predictor for maintenance of activity of the enzyme in IL-containing solvents. In our MD study of GH11, we observed that the tested cation molecules penetrate the binding pocket of the enzyme, and we predicted that this would competitively inhibit the enzyme’s function. This hypothesis was supported by experiments in which the inhibition of a closely related GH11 by the same cation (34) was observed. Herein, we will test some of these previous hypotheses (regarding structural stability, fluctuations, and cation-catalytic residue interactions) and develop new hypotheses with different enzymes of significantly different secondary structure and a larger set of data. This will allow us to more thoroughly analyze enzyme structure and dynamics over larger timescales and to observe less common events. In this study, we focus on the observations that ILs destabilize (or even denature) the enzyme or disrupt the flexibility of the structure that is critical to the enzyme activity.

Previous simulation studies have given some insight into the relationships between IL-containing solvents and some specific enzyme structures and dynamics, but to our knowledge, a comparative study investigating IL effects across a family of enzymes has not yet been conducted. To address the disparate understanding of IL-enzyme relationships at the molecular level, we performed a series of MD simulations on a set of GH5 enzymes. Our simulations focus on the work of Datta and co-workers and seek to reproduce several of their experimental conditions at the molecular scale. Specifically, we vary the enzyme species, temperature, and IL concentration to see how each variation affects the structure and dynamics of the protein. The three enzymes share a structural motif, since they are all from the GH5 family, but they have very different activity in IL-water mixtures. These simulations will help us understand which differences in the protein structures lead to the observed loss in activity.

Materials and Methods

All simulations were performed using AMBER-compatible force fields implemented in GROMACS 4.6 (35) using the TIP3P water model (36). The enzyme forces were calculated with the AMBER99SB-ILDN force field (37), and the IL force field was adopted from our previous studies (32) and utilizes the general AMBER force field (38) and restrained electrostatic potential fitting for point charges (39) from quantum calculations using Gaussian 09 (40) at the HF/6-31g(d) level of theory. We scaled the charges by 0.8 to more accurately represent dynamic properties of the solvent, as has been demonstrated in the literature (41). Cubic boxes of the solvent and protein were generated using Packmol (42). Systems were minimized using a steepest-descent method for 10,000 steps or until machine precision was reached and then heated over 100 ps.

For our MD simulations, a time step of 2 fs was attained by constraining the bonds between hydrogens and heavy atoms using the LINCS algorithm (43). Periodic boundary conditions were applied to all dimensions. Lennard-Jones interactions were calculated over 1.0 nm and shifted to ensure that no artifacts were created from discontinuities in energy. Particle-mesh Ewald summation is used to account for the long-range electrostatic interactions. Temperature was maintained using the Parrinello stochastic velocity rescaling algorithm (44), and pressure was held at 1 bar using a Berendsen barostat (45).

We have conducted 54 total simulations: three enzymes at two temperatures in three different concentrations of IL-containing solvent in triplicate, for a total of 27 ms of simulation time. A list of all of the simulations performed is provided in Table S1 in the Supporting Material. The IL chosen for these simulations was [EMIM][OAc]. Other GHs have been shown to tolerate this IL (21,22,46). We chose three different concentrations of IL that correspond to those found by Datta et al. (23) to cause large changes in enzyme activity (0%, 15%, and 50%). Weight percent was used in our simulations, whereas volume percent was used in the experiments. This is not a perfect comparison, but the approximation can be made because the densities of the two solvents are similar and the excess volume of mixing is small (47). In this case, wt % will approximately equal vol %. These three concentrations are important for illustrating the differences in the enzymes. First, 0% was chosen as a standard. This allows us to see whether the experimental crystal structures are stable using our simulation techniques. Without this standard, we might erroneously explain destabilization of the enzyme observed in MD as being caused by the presence of IL when it might actually be caused by a less stable experimental starting structure. Second, 15% was chosen because it differentiates among the three enzymes; in 15% [EMIM][OAc], VIR loses all activity in experiments, TMA loses about half its activity, and PHO maintains nearly all of its activity. Finally, 50% was chosen because all three enzymes lose nearly all of their activity at this concentration. The two temperatures (310 K and 353 K) were chosen because the former is the optimal temperature for VIR and the latter is the optimal temperature for TMA and nearly optimal for PHO. Triplicate simulations were launched from a single minimized structure for each enzyme.

The experimental structures were taken from the Protein Data Bank (PDB) (48). VIR was modeled using an x-ray structure from Trichoderma reesei (PDB 3QR3) (49). GLU54 was mutated to ASP to match a known sequence for T. viride endoglucanase (50). TMA and PHO were modeled using x-ray structures (PDB 3AMD and 3AXX) (51,52) without mutation. PROPKA (53,54) was used to assign protonation states to the enzyme residues at the pH that optimizes cellulase activity: 4.5, 4.8, and 6.4 for VIR, TMA, and PHO, respectively. Table S2 contains a list of the charged residues for each system. The surface charge of each enzyme noted in Fig. 1 B was calculated by first enumerating all residues with solvent-accessible surface area (SASA) greater than at least 30% of the maximum possible SASA for that residue type (55,56), then counting the numbers of positive and negatively charged surface residues at the above-mentioned pH values. RMSD, RMSF, SASA, secondary structure analysis, and energetic and side-chain data were all obtained from the toolkit included with GROMACS 4.6.

Results and Discussion

General effects of IL on enzyme structure and dynamics

In this section, we first analyze general trends in the structure and dynamics of the three cellulases. This serves as a baseline for comparison among the three enzymes. Afterward, we discuss each enzyme individually and identify important observations unique to each system.

Structural evolution

The structural evolution of the systems over the 500 ns trajectories is an indicator of the stability of the enzymes in mixtures of IL and water. To provide some insights into the extent of the structural changes we observed, snapshots for the three enzymes after 500 ns of simulation in the three solvent states (0%, 15%, 50% IL) are compared to its crystallographic structures (Fig. 2). The ends of the simulations are used instead of the average structures, because the highest RMSD tends to occur near the end of the simulation. This accentuates the differences in structures to help distinguish among them. The structures are taken from simulations at 310 K for VIR and 353 K for TMA and PHO. The structures of VIR and PHO remain close to their respective crystallographic structures. Only a few largely unstructured loops (Phe-15 to Asp-43 for VIR and Lys-111 to Asp-131 for PHO) are greatly displaced in the presence of IL. TMA, on the other hand, deviates noticeably from its crystallographic structure in several regions. Several α-helices are less structured in the IL-containing systems, indicating that at least a part of the TMA structure is unfolding in the presence of ILs. Much of the deviation from the crystal structure is due to the unfolding of the α-helix at the N-terminal end. This event precedes the destabilization and unfolding of nearby structures later in the trajectory.

Figure 2.

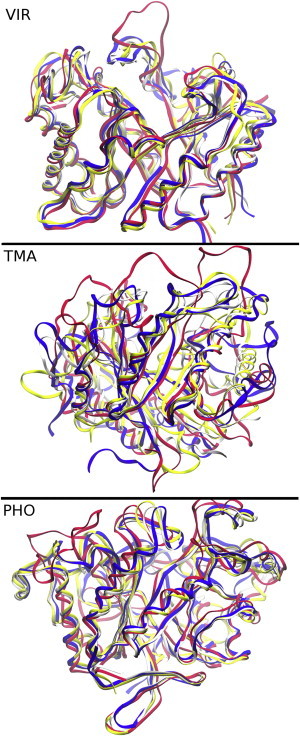
Structure of each enzyme after 500 ns of simulation compared to the crystallographic structure (white) after aligning all Cα atoms. Water (0% IL) is shown in yellow, 15% IL in red, and 50% IL in blue. To see this figure in color, go online.

Deviations of the enzyme structures from their initial configurations were analyzed over their complete trajectories using α-carbon (Cα) RMSD. In contrast to our earlier studies in ILs, several of the simulations, specifically those of the enzymes VIR and TMA, display major deviations from the starting structure over long timescales, possibly indicating the start of denaturing. The enzymes that we have previously studied with molecular simulation have very different secondary structures than these family 5 cellulases (32,33). We find that α-helices tend to be less stable than β-sheets in the presence of ILs. Fig. 3 shows plots of the Cα RMSD for each protein in different concentrations of IL and key statistics summarizing the RMSD data. The data presented in this figure are for the optimal temperature of 310 K for VIR and 353 K for TMA and PHO. The N-terminus (first 15 residues) of TMA was not included in the RMSD calculations (Figs. S1 and S2 contain all of the data for all carbons at both temperatures). This is because this region has a very high RMSD, and it might lead to the incorrect conclusion that TMA is unfolding even in the water simulations. For example, the large changes we observe in RMSD are sometimes characterized by large structural changes over relatively short time periods, occurring after significant elapsed simulation time (hundreds of nanoseconds) for multiple trajectories. That is to say, the RMSD remains low for an extended period at the beginning of the simulation, suggesting that the protein is stable. At some point later in the trajectory, a portion of the protein adopts a different structure relatively quickly. Specific examples of this behavior can be seen in Fig. 3 for TMA in water at 100 and 250 ns, for TMA in 50% IL at 200 and 400 ns, and for PHO in 15% IL at 250 ns. It should be noted that these RMSD data should be compared to the water standard in each case to determine whether there is unfolding of the protein structures. Different crystallization techniques will lead to different RMSD values. Based on the observations of the MD trajectories, it is clear that these events are indicative of at least partial protein unfolding for TMA. Without dramatically longer simulation times, it is impossible to determine whether we are observing a change in the preferred conformation of the enzyme in the ILs (i.e., solvent-induced unfolding) or high-amplitude, long-wavelength structural fluctuations (i.e., solvent-induced changes in the conformational dynamics).

Figure 3.

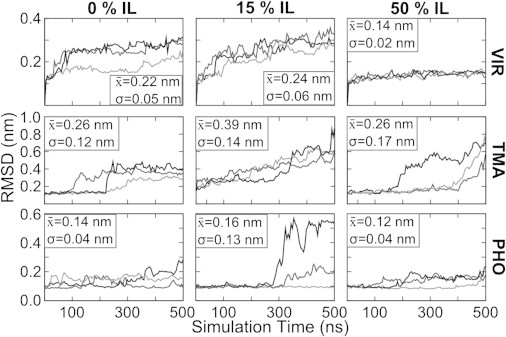
RMSD of α-carbons. Three replicas each of VIR at 310 K and TMA and PHO at 353 K. The first 15 α-carbons were excluded for TMA. The average and standard deviation of all RMSD values are shown.

The RMSD statistics for PHO, the most IL-tolerant of the three enzymes, show similar behavior among all three of the concentrations, except for those systems in 15% IL at 353 K. This difference is caused by a transition of a surface loop (Lys-111 to Asp-131) that rearranges to make contact with a different portion of the surface in one of the three replicate simulations late in the trajectory (as seen in Fig. S2). This replica was chosen for Fig. 2 to show that the maximum extent of structural disruption is limited mostly to one unstructured loop. Since the transition occurs late in the trajectory, the average remains near that of the other replicas. Taken together, these data show that the enzyme PHO maintains behavior similar to what it exhibits in water for both of the tested IL concentrations in terms of its departure from the native structure.

The two less IL-tolerant enzymes, TMA and VIR, exhibit increased deviation from the crystal structure and more varied behavior in IL mixtures. Generally, moderate deviations are seen at 310 K, whereas the largest departure from the native states is observed at 353 K. This is surprising since TMA was expected to be quite stable (melting temperature of 380 K) in water. One explanation for the deviation from the crystal structure for TMA simulations in water is the large difference in pH between the simulation conditions and the experimental crystallization conditions (4.8 vs. 8.5). VIR comes from a mesophilic organism, and it is expected to deactivate at the higher temperature—possibly suggesting that the native structure is unstable at elevated temperatures. On the other hand, TMA comes from a thermophilic organism, and its highest activity in water was reported by Datta and co-workers at 353 K. Viewing the trajectories reveals that the high RMSD of TMA can be explained by fluctuations in the N-terminal region of the protein and by the loss of secondary structure in a few key regions, details for which are provided below. For PHO and VIR, systems solvated in 50% IL exhibit more stability, even compared to the simulations of the enzymes in pure water. From our previous experience with IL-solvated proteins, this is expected. On timescales of up to 500 ns, proteins in 50%+ IL tend to have less or equal deviation from crystal structure when compared to water-solvated systems. Furthermore, in near-pure ILs, we have observed that enzymes exhibit severely diminished structural fluctuations and dynamics on the 150 ns timescale (33). This may be a consequence of the higher viscosity and lower sampling times, but experimental evidence shows that some proteins are actually stabilized over long incubation times in ionic liquids (57,58). TMA is the exception to these previous observations. TMA in 50% IL appears to be unfolding on these timescales, but that unfolding is slower than in the 15% IL system. The IL-containing TMA systems appear to still be in the process of unfolding at the end of the trajectories, as will be shown later.

The character of the RMSD plots differs from VIR to TMA. The RMSD of VIR deviates linearly with time, whereas the RMSD of TMA increases more often and with fast transitions (cf. Figs. S1 and S2). The trajectories show that these events are preceded by the breaking of key salt bridges within the protein, formation of nonnative salt bridges, and exposure of hydrophobic residues to the solvent. We hypothesize that the IL mediates this unfolding by stabilizing the exposure of charged side chains that begin internal to the protein and later rearrange to form salt bridges that are nearer the exterior of the protein. Fig. S3 shows that higher concentrations of IL correlate with higher numbers of nonnative salt bridges. The statistical entropy of the TMA side chains and the internal energy of the enzyme (discussed later) are consistent with this mechanistic interpretation.

RMSF

To analyze changes in the characteristic fluctuations of the protein backbone, Cα RMSF values of the enzymes are calculated for the last half of each trajectory and then averaged over the three replicate trajectories. The results for these calculations are shown in Fig. 4. The observations that follow hold regardless of whether individual trajectories or the aggregated/averaged data are used.

Figure 4.

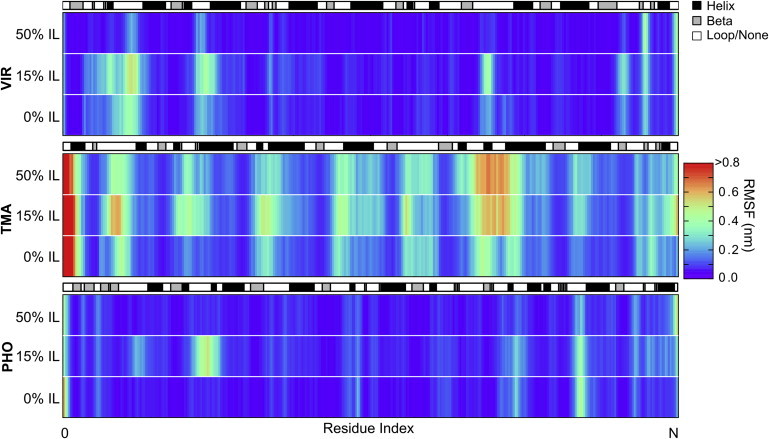
Root mean-square fluctuation (RMSF) averaged over the triplicate simulations at 310 K for VIR and 353 K for TMA and PHO. N = number of amino acids in each enzyme. The secondary structure of DSSP is shown in grayscale. To see this figure in color, go online.

The RMSF of PHO is similar across all concentrations of IL. The presence of IL affects only one region of the enzyme in a substantial way. This is due to the previously mentioned event observed in one of the three high-temperature-15%-IL simulations, where an unstructured loop (Lys-111 to Asp-131) changes contact from one section of the bulk of the protein to another. Since enzyme function can be related to dynamic motions during the binding and release of substrates, and since the catalytic function of the enzyme depends highly upon the precise arrangement of the catalytic region, we surmise that enzymes that maintain water-like character in IL-containing solvents will also maintain significant activity in those same solvents. Therefore, the retention of water-like character in increasing concentrations of IL for PHO may be indicative of its high tolerance to ILs, as observed by Datta et al. (23).

TMA and VIR, in comparison to PHO, exhibit diverse features in their RMSF at key segments in the enzyme sequence. For TMA, the presence of IL affects the magnitude of the fluctuations much more than it affects the location of the fluctuations. The N-terminus shows remarkably high fluctuations in all of the simulations. Upon inspection of the trajectories, we observe that the helix nearest the N-terminus comes undocked from the protein bulk and loses secondary structure in 15% IL. This unfolding precedes unraveling of another longer helix (Met-69 to Arg-86) and subsequent destabilization of an unstructured loop (Asn-20 to Lys-35) near the entrance to the enzyme’s binding site, both of which are connected closely linearly in the primary sequence and are in geometric proximity to the N-terminus. Similar behavior is also observed in the 50% IL simulations.

The magnitude of the fluctuations in VIR is lower than that in TMA. This is because the data presented for VIR are at 310 K, whereas those for the other two enzymes are at 353 K. The data are presented in this way because a temperature of 353 K is unnatural for VIR, and the data at 310 K better represent experimental conditions. The width of the regions of high fluctuation tend to increase from 0% to 15% IL and then decrease to relatively thin slivers as the concentration increases to 50% IL. The decrease in fluctuations in 50% IL indicates that the enzyme may be more structurally stable in these concentrations of IL at these temperatures and timescales. Inspection of the trajectories reveals that the highest fluctuations come from regions in which there are multiple salt bridges that intermittently break and reform contact.

RMSD and RMSF are useful gauges of the global average behavior of the three enzymes, but these measures can obscure important details of the trajectories. Therefore, we analyze each enzyme individually below and discuss unique aspects of the interactions between each IL-enzyme combination.

Surface charges and salt bridges

The arrangement and ratio of charged surface residues in chymotrypsin and lipase have been shown experimentally to affect the activity of these enymes in binary mixtures of IL and water (59,60). Interactions of the cations with the surface residues are hypothesized to play a role in IL tolerance by creating a shell of positive charge around the protein that cannot be penetrated by anions, which tend to disrupt protein structure more readily. Of the three enzymes studied, TMA is the only one with a positively charged surface, as predicted by the previously described SASA method. If the hypothesis about the protective properties of a layer of cations at the enzyme’s surface is true, TMA should be the most prone to attack by anions, and secondary structure should be lost more readily. We measured the average number of acetate carbonyl carbons within 0.4 nm of the protein for the natural-temperature trajectories. We then divided this count by the hydrophilic SASA of each enzyme, which averaged ∼110 nm² in all cases. The number of anions was 0.28, 0.32, and 0.23 anions/nm² for VIR, TMA, and PHO, respectively. This supports the hypothesis of more positively charged protein surfaces attracting more anions. Fig. 5 illustrates the coulombic potential at the surface of each protein for its experimental x-ray structure protonated according to predictions by PROPKA. These representations demonstrate differences in the electrostatic character of the proteins, which greatly affects the structuring of ILs around the enzymes. The number of salt bridges was enumerated to see the effect of the presence of cations and anions. Generally, higher concentrations of IL lead to higher numbers of salt bridges. This formation of additional, nonnative salt bridges is especially prevalent for TMA in 50% IL, but it can be noted in all IL systems. The evolution of salt bridges over time is visualized in Fig. S3.

Figure 5.

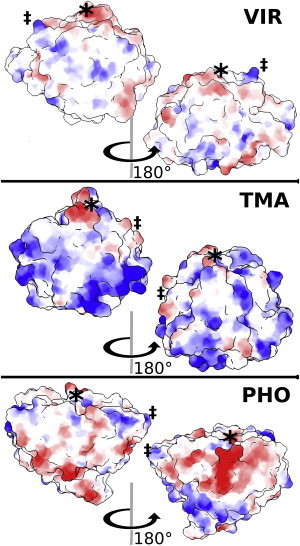
Coulombic potential surfaces for the crystallographic structures protonated by PROPKA. Red is positive. Blue is negative. Color intensity scales with potential. The asterisk and double-dagger symbols are placed to guide the eye through the rotation. To see this figure in color, go online.

Energetic and entropic contributions to cellulase/IL interactions

To gain insight into the differences in thermodynamics of the enzymes in water versus ILs, we calculated the internal energy of the protein and the statistical entropy of its side chains in each solvent. Statistical entropy of the χ₁ dihedral angle was calculated for each residue in each solvent using the definition S = R Σ Pln(P), where R is the ideal gas constant and P is the probability of the dihedral angle (33). Internal energy was calculated as the potential energy of all molecular interactions within the protein. Results of the calculations at their most optimal temperatures are presented in Figs. S4 and S5. In general, the greatest differences in χ₁ histograms between IL and water systems are observed in histidine, cysteine, and protonated aspartic acid residues. Interestingly, the presence of ILs has little effect on the positively charged lysine and arginine histograms, which are often used as targets in stabilization studies (59,60).

The effects of the solvent on the protein side-chain entropy and internal energy differ among the three enzymes. Entropy is generally reduced in the presence of ILs for VIR, indicating a significantly reduced conformational flexibility in the side chains. In 50% IL, the internal energy of the protein averaged over the last half of the trajectory is lower than that of the water system. This is consistent with structural changes that increase protein-protein interactions to reduce contact with the solvent; the RMSD of VIR in 50% IL and observation of the trajectories reveal that the protein does not exhibit any large structural changes. On the other hand, side-chain entropy is generally increased in the presence of ILs for TMA. The internal energy of the protein averaged over the last half of the trajectory is higher in IL than it is in water. These calculations indicate that the side chains are exploring more phase space and that there are fewer favorable interactions within the enzyme structure, as breaking an intramolecular protein contact will increase the internal energy, in accordance with the Lennard-Jones pairwise functions used in this study. The entropy increased especially in regions near helices, where the majority of unfolding takes place. The side-chain entropy of PHO in water is similar to that in IL. The internal energy of the protein over the last half of the trajectories is slightly higher in ILs than it is in water. In the case of 15% IL, much of the change in internal energy can be accounted for by considering the transition of the unstructured loop (Lys-111 to Asp-131), described previously. In the case of 50% IL, the increase in internal energy for PHO is much smaller than that for TMA, and the internal energy of the enzyme is close to that of water.

Enzyme-specific IL-induced changes

VIR

VIR was deactivated significantly by even the lowest experimentally tested concentration of IL (23). However, large-scale denaturation of the enzyme on the 500 ns timescale was not apparent in the RMSDs and RMSFs calculated from our simulations. Subsequently, we further investigated the trajectories for evidence of any persistent changes in the enzyme structure or other features when comparing the water simulations and the 15% IL simulations. The trajectories show specific changes in the binding pocket, which we propose may lead to deactivation (whereas the native structure is mostly maintained) even at low concentrations of IL. This analysis reveals that several events take place in the substrate-binding pocket of each of the 15% IL systems for VIR. Initially, Arg-109 and Asp-152 establish a salt bridge. Asp-20 is near this salt bridge but does not participate in it. Within the first 200 ns of each 15% IL trajectory, Asp-20, along with the nearby charged residue Lys-27, moves farther away from the bulk of the protein into more solvated states. This helps expose the loop that contains Asp-20. Interestingly, the hydrophobic Val-24 follows its two neighbors and becomes exposed to the surrounding solvent. Late in each of these trajectories (after 250 ns), Arg-109 breaks contact with Asp-152 and forms a new salt bridge with Asp-20. Altogether, these rearrangements significantly reshape the binding cleft of the enzyme and could lead to the observed deactivation. The aforementioned changes are highlighted in Fig. 4. Some salt bridges break and reform in the water-solvated trajectories, but the reproducible and significant rearrangement of contacts observed in 15% IL is not observed in water.

Conservation of the binding pocket’s structure is key to maintenance of activity in two ways. First, as a rule for biocatalysis, the alignment of the substrate near the catalytic residues can significantly affect the energy of the transition state, and thus the rate of catalysis. Second, the rate of binding and unbinding affects the turnover rate of the enzyme through its effect on the maximum rate of reaction (V_max). Fig. 6 shows disruption of the shape of the binding pocket. In its natural state, the substrate would be directed into the page in this image. Therefore, the more occluded binding pocket seen in IL systems is less accessible to natural binding of the substrate. To be clear, there are cases where a reshaping of the binding pocket can lead to higher enzyme turnover, but because of the shape of the substrate (long oligomers of carbohydrates), we suspect that steric hindrances will cause binding to be less energetically favorable in IL-containing solvent than in water. It is also possible that the substrate would have a lower rate of unbinding in IL mixtures, but we observe nothing in our simulations that would lead us to this conclusion. The relative energy of binding and unbinding of the substrate in ILs versus water could be tested by isothermal titration calorimetry, but this will not differentiate between the possibility of inhibition by the IL and reshaping of the binding pocket. Kinetic studies in very low concentrations of IL to measure inhibition constants would give even more information.

Figure 6.

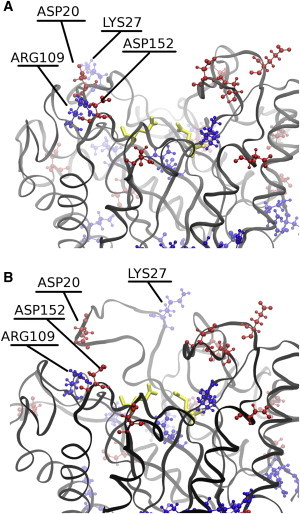
A view of the binding cleft in VIR in 15% IL. (A) Structure after minimization. (B) Structure near the midpoint of the trajectory. Positive residues are shown in blue, negative residues in red, and catalytic residue heavy atoms in yellow. To see this figure in color, go online.

TMA

Compared to VIR, TMA was deactivated less severely at low concentrations of IL (23). Complete deactivation was observed by 20% v/v IL in water. TMA is different from the other two enzymes in that it has a net positive surface charge at both neutral pH and pH 4.8, the optimal pH for enzyme activity, as observed by Datta et al. This is not characteristic of halophilic enzymes. It has been hypothesized that a negative surface charge attracts cations, thus increasing protein hydration while repelling anions that disrupt native salt bridges and hydrogen bonding (22,59). In the case of imidazolium-based ILs, the cation tends to be larger than the anion, and the charge is more dispersed on the molecule. In our system specifically, the positive charge of the cation is dispersed over the several atoms of the imidazole ring, whereas the negative charge of the anion is concentrated on the two carboxyl oxygen atoms. Following the same hypothesis, a protein with a negative surface charge will attract these large cations and be shielded from attack by the relatively small anions with high charge densities (59).

Compared to the other enzymes, TMA experiences much higher loss of secondary structure. Fig. 7 compares the α-helical content, as determined by digital shape sampling and processing (DSSP) (61), over time for each enzyme across the range of IL concentrations at the closest-to-optimal temperature for each enzyme. It can be seen that the α-helical contents of VIR and PHO remain stable throughout the simulations. On the other hand, TMA loses a majority of its α-helical character in IL-containing solvents, indicating an underlying reason for the large RMSD and RMSF values discussed above. It is interesting to note the highly positive surface charge shown for TMA (Fig. 5). In water, a highly positive surface charge appears to be not particularly detrimental to the stability of the secondary structure of the enzyme, but when anions are introduced from the IL, the enzyme denatures much more dramatically. A pH of 4.8 is optimal for activity in water, but this enzyme may need a higher pH to deprotonate the surface so that when ILs are introduced, anions do not penetrate the enzyme so readily. Similar DSSP calculations were also completed for the β-sheets and showed that this loss of secondary structure is specific to helices. β-Sheets were highly stable across all enzymes and concentrations tested. As seen in Fig. 1, the helices may shield the β-sheets from the solvent, because they form the outer surface of the protein surrounding the inner β-barrel. Although it is difficult to perform circular dichroism in imidazolium-based ILs because of the absorption spectrum of the cation and the sensitivity of the technique to even small concentrations of contaminants, we predict that IL-mediated loss in secondary structure could be observed for TMA even in concentrations as low as 15% v/v. Fourier transform infrared spectroscopy might also be suited to detect loss in secondary structure.

Figure 7.

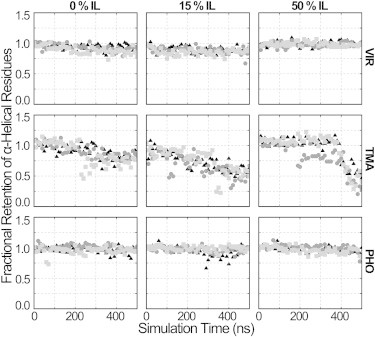
Retention of α-helical structure. Three replicate simulations are shown for each enzyme. Secondary structure content was calculated using DSSP and normalized to the cystallographic secondary structure.

PHO

PHO is surprisingly stable at all simulated concentrations of IL and both temperatures. This is consistent with the experimental observation that PHO loses relatively little activity at 20% v/v IL in water, but it is inconsistent with the experimental observation that PHO loses nearly all activity at 50% v/v IL. From the previously discussed figures, it can be seen that the water-like behavior of PHO, as measured by RMSD and RMSF and by observation of the trajectories, is maintained even in 50% w/w IL. Since the structure of the catalytic site affects catalytic activity, and since dynamic motions of the enzyme affect catalytic turnover rates, we propose that the maintenance of enzyme activity in ILs could be predicted using MD simulations to carefully screen for enzyme/IL combinations in which enzyme/water interactions like structural fluctuations are preserved. However, note that there remains the untested possibility that our simulations of PHO in high concentrations of IL were simply not long enough to observe some of the changes we noted above in the TMA and VIR systems. Still, there are several reasons why an enzyme might lose activity in IL, even when the structure and dynamics are unchanged (as in this case). The structure of the substrate might change, or the more viscous medium might lead to lower turnover rates. Yet changes in activity due to viscosity are expected to manifest themselves by a gradual decrease in activity with increasing IL concentration. This is not observed experimentally. The IL might act as a competitive inhibitor. Observation of our trajectories reveals that one of the catalytic residues (Glu-342) preferentially interacts with single imidazolium cations, trapping them within a distance of 4 Å for over 100 ns. If the cation is an inhibitor, it is not a strong inhibitor in the experiments at concentrations of up to 20% v/v. Interestingly, there is little decrease in the activity between 0% and 20% v/v IL and a sharp decrease to no activity between 20% and 50% v/v IL. We know that this range of concentrations can be an important transition point for protein stability and activity. Previous experimental findings show that denaturation of cytochrome c and human serum albumin begin to occur somewhere in the range between 25% to 50% v/v 1-butyl-3-methylimidazolium chloride (62). For human serum albumin, the structural changes lead to aggregate formations. Our previous study of a GH11 xylanase shows that aggregation occurs at similar concentrations of [EMIM][OAc] and [EMIM] ethylsulfate (32). In accordance with these previous studies, we speculate that aggregation may play a large role in the loss of activity for PHO in higher concentrations of [EMIM][OAc]. Another possibility is that the timescales of our simulations are too short to see large structural changes for PHO. Unfortunately, the computational methods employed in this study are inadequate to study aggregation, as discussed below.

Conclusions

Other considerations

Datta and co-workers previously determined the unfolding temperature of each protein in different concentrations of IL. They observed a decrease in the unfolding temperature of the proteins as the concentration of IL increased (23). However, unfolding of PHO in ILs may take place over a much longer timescale than is accessible by atomistic MD. Another possibility is that the lower melting temperature is due to new protein-protein interactions introduced with aggregation, as discussed briefly above. Based on our knowledge of how other enzymes behave in ILs, we propose that aggregation plays a role in the deactivation of PHO at high IL concentrations. Aggregation could occur as a consequence of the exposure of some portion of hydrophobic residues, or the protein could precipitate as a consequence of ILs screening the surface charges that normally keep proteins suspended as colloids (63). Some studies mention that there are limits to the solubility of certain proteins in certain ILs (63,64). There are a number of articles on the positive effects of certain ILs on the long-term stability of proteins (65,66). These studies usually focus on low or high concentrations of IL in water, and they skip over the important intermediate region where denaturation and aggregation effects have been observed previously. Still, in certain neat ILs, aggregation of other enzymes, like lipase, are observed (67). There are many factors that play a role in protein stability and aggregation in ILs, including IL species, protein structure, and temperature. Unfortunately, standard MD is not able to access timescales necessary to study aggregation. A coarser description of the protein and solvent and other methods of simulation beyond MD could help researchers access these events.

We believe that simulations of lone proteins are still useful for determining the effects of high concentrations of IL on protein structure and dynamics for the prediction of IL tolerance. We observe no unfolding in the simulations of PHO in 50% w/w IL at 353 K on the 500 ns timescale. This indicates to us that our simulations can predict high halophilicity and IL tolerance for the enzyme, but the simulation would not in and of itself predict that this enzyme is not active at this temperature and concentration. Other simulation methods and experiments would need to be employed as predictors of aggregation, precipitation, and effects on substrate-protein interactions. For example, coarse-grained simulations that predict the osmotic second virial coefficient might help us determine whether a specific protein will salt out of an IL solution (68). The outlook for future IL-protein simulations is promising. With the development of more accurate coarse-grained force fields such as the MARTINI polarizable force field and more efficient methods of enhanced sampling such as metadynamics, temperature-accelerated MD, and parallel tempering, we believe that future researchers will be able to use simulations to guide or compliment experiments in this field.

Toward improved enzyme-IL simulations

We reiterate that in addition to the limitations noted above, there remain definite areas of future work to improve enzyme-IL simulations and their use in interpreting and inspiring new experimental work. Although it is clear from the TMA simulations that large structural changes can occur after hundreds of nanoseconds, there is still essentially no way to predict a priori whether and when these transitions may occur. Future work using enhanced sampling free-energy calculations could investigate folding free energies for small model systems in an attempt to generalize some of these observations to larger systems. It is also clear that the structures are still evolving at the end of the trajectory, indicating that significantly longer timescales are needed. Emerging hardware solutions such as accelerators or special purpose MD machines could help address this in the future. Ultimately, the observations and hypotheses presented herein are meant to compliment and guide experimental studies and add some molecular-level insight into IL-protein interactions.

Causes of enzyme deactivation

We analyzed the behavior of three distinct GH5 enzymes in binary mixtures of IL and water using MD. By drawing on a previously published study on these enzymes and comparing that study’s results with our simulations, we developed the following suggested mechanisms that could prove most important in explaining loss of activity of enzymes in IL-containing solvents, and we made predictions as to how our hypotheses could be experimentally confirmed.

• 1.VIR is deactivated by deformation in the binding pocket that leads to the inability of the substrate to bind efficiently. We know from the published experimental data that the activity of this enzyme drops significantly even in very low concentrations of IL. In the absence of large structural changes in our simulations, smaller structural changes in key regions could therefore be a likely cause of the deactivation. This could be supported by isothermal titration calorimetry experiments to energetically describe binding/unbinding. Incorporating a kinetic study to determine whether competitive inhibition plays a role in substrate binding would also be useful.
• 2.TMA is deactivated by extensive loss of secondary structure in IL. The large-scale denaturation of this enzyme’s helices in the presence of ILs is obvious in our simulations. This concurs with the deactivation observed in experiments. X-ray scattering or small-angle neutron scattering could provide some detail about large changes in structure without being hindered by the unorthodox solvent. Fast Fourier infrared spectroscopy could also be used to monitor the evolution of the secondary structure. Increasing the pH of the solvent might protect the enzyme from attack by anions.
• 3.PHO shows no signs of deactivation in IL in our simulations. PHO exhibits water-like behavior in the presence of ILs, and there are no large-scale structural changes to structured portions of the enzyme or the binding pocket. We speculate that aggregation is a possible cause of the deactivation observed at 50% IL, as we have observed experimentally for another GH (32). Unfortunately, the methods employed in this study do not cover the timescales necessary to sample protein-protein interactions, but we would be able to predict high thermal stability and halophilicity. Dynamic light scattering would be able to detect large aggregates of this protein and determine the IL concentration at which it salts out.

More generally, any of these suggested experimental techniques could be applied to any of these proteins. For example, observation of PHO trajectories shows an affinity of the cation for the catalytic residues, but there is almost no deactivation for low concentrations of IL experimentally, indicating that inhibition is not a large problem. The experiments suggested for VIR could also be applied to PHO. At these timescales and temperatures, we observe a few general trends that are consistent with our previous experience in IL-enzyme simulations. Higher concentrations of IL correlate with lower RMSDs from experimental structures. High (>50%) concentrations of IL correlate with lower RMSF. It is surprising to see such a variety of character in enzymes that belong to the same family of GHs. The simulations described herein can predict the stability of enzymes in water and in IL; they can also predict local changes in the structure that cause deactivation rather than relying on heuristics based on macroscopic properties, and they can be used as a tool to better select those enzymes or mutants that tolerate ILs.