Biophysical Modeling of Phase Changes in BOLD fMRI

Abstract

In BOLD fMRI, stimulus related phase changes have been repeatedly observed in humans. However, virtually all fMRI processing utilizes the magnitude information only, while ignoring the phase. This results in an unnecessary loss of physiological information and signal-to-noise efficiency. A widely held view is that the BOLD phase change is zero for a voxel containing randomly orientated blood vessels and that phase changes are only due to the presence of large vessels. Based on a previously developed theoretical model, we show through simulations and experimental human BOLD fMRI data that a non-zero phase change can be present in a region with randomly oriented vessels. Using simulations of the model, we first demonstrate that a spatially distributed susceptibility results in a non-zero phase distribution. Next, experimental data in a finger-tapping experiment show consistent bipolar phase distribution across multiple subjects. This model is then used to show that in theory a bipolar phase distribution can also be produced by the model. Finally, we show that the model can produce a bipolar phase pattern consistent with that observed in the experimental data. Understanding of the mechanisms behind the experimentally observed phase changes in BOLD fMRI would be an important step forward and will enable biophysical model based methods for integrating the phase and magnitude information in BOLD fMRI experiments.

INTRODUCTION

Blood oxygenation-level dependent (BOLD) fMRI has been a popular tool for studying the brain noninvasively. A change in blood oxygenation level in response to local activation changes the T2* relaxation time, and subsequently changes the MRI signal. The complex-valued BOLD fMRI signal (Hoogenraad et al., 2001) contains physiologic information. However, so far, virtually all fMRI studies have analyzed only the magnitude changes. A standard approach of analysis is to correlate the time-series of the magnitude fMRI data with an assumed reference signal (Bandettini et al., 1993). This procedure completely discards the phase information in the images. If indeed useful information is being discarded, it would be quite important and interesting to utilize this information in the phase of the signal.

Due to the susceptibility difference between the intravascular (IV) blood and tissue, there is a shift in the resonance frequency of the water protons. A zero phase change from the extravascular (EV) signal contribution was predicted for a model using cylinders to represent blood vessels (Bandettini and Wong, 1995; Ogawa et al., 1993; Yablonskiy and Haacke, 1994). This result depends on the spatial symmetry of the induced magnetic field. IV signal contribution has also been considered in (Boxerman et al., 1995; Hoogenraad et al., 1998; Menon, 2002, 2003). Boxerman pointed out that the IV spins account for the majority of fMRI signal change on T2*-weighted images at 1.5 T (Boxerman et al., 1995). When the IV and EV signal contributions are considered together it was concluded that the phase changes only come from large vessels (Klassen and Menon, 2005; Menon, 2002, 2003).

Phase changes during BOLD imaging studies have been repeatedly observed. A number of these reports are concerned with voxels with larger venous to arterial blood volume fraction (Hoogenraad et al., 1998; Lee et al., 1995; Menon, 2002). There have also been a number of different post-processing approaches to utilize the phase data. For example, phase sensitive fMRI methods have been used to reduce contaminations from oriented draining veins (Klassen and Menon, 2007; Menon, 2002; Nencka and Rowe, 2007; Tomasi and Caparelli, 2007) although Tomasi and Caparelli’s model neglected to consider the sphere of Lorentz which should be considered in such vascular models (Chu, et al. 1990). All of these methods did not consider whether task related phase changes can be observed in regions absent of macro vessels. Instead, they were interested in filtering out voxels with macro-vascular contribution. We show that the proposed model predicts a task related phase change in regions absent of macro vessels. Our approach and Menon’s model (Klassen and Menon, 2005; Menon, 2002, 2003) are complementary, thus in future work we will explore the combination of those two approaches. Rowe provides a general complex fMRI model (Rowe, 2005a), and considers a number of cases of modeling the phase. A task-related phase was considered (Rowe, 2005a, b) and the phase is modeled as an arbitrary value by Rowe and Logan (Rowe and Logan, 2005) as well as using a constant value (Rowe and Logan, 2004). Furthermore, the analysis of phase-only fMRI data has been improved by adopting an angular regression model (Rowe et al., 2007). Methods, such as a complex correlation coefficient (Lai and Glover, 1997), a complex generalized likelihood ratio test (CGLRT) (Nan and Nowak, 1999; Rowe and Logan, 2004), and independent component analysis (Calhoun et al., 2002), have also been utilized to process complex-valued fMRI data. However, most of these papers focus on data processing and do not address the underlying mechanism for the phase change.

Recently, a new model for the phase change in BOLD and cerebral blood volume (CBV)-weighted fMRI was investigated by Zhao et al in (Zhao et al., 2007). CBV-weighted fMRI was performed by injecting a superparamagnetic IV contrast agent into the brain of a cat. In a related paper (Zhao et al., 2006), simulations were performed using the CBV-weighted fMRI phase change data to validate the proposed model with experimental CBV data. However, this model has not been tested in BOLD fMRI. The magnetic susceptibility effect in BOLD contrast is much smaller than that produced by exogenous intravascular contrast agents, making it more difficult to validate the model with experimental BOLD fMRI data. In addition, the results in (Zhao et al., 2007) were obtained in cats, because the CBV-weighted fMRI (as implemented in the paper (Zhao et al., 2007) with MION) can not be performed on humans due to its invasive nature. We apply Zhao’s model (Zhao et al., 2007) to BOLD fMRI experimental data for the first time. Here the signal change depends on the variation in local magnetic field inhomogeneity caused by the blood oxygenation level change.

The approaches used in most of previous literature, which model blood vessels as long cylinders, provide good insights into susceptibility contrast mechanisms. However, as pointed out in (Pathak et al., 2008), their inherent assumptions limit their applicability and cylinders may not adequately represent the micro-vessel architecture being studied. The model (Zhao et al., 2007) used in this paper calculates the magnetic field for arbitrary geometries and spatially distributed susceptibility change inside volume of activation (VOA) during the activation. We demonstrate that even for a voxel with randomly oriented micro-vessels the phase change is small, of the order of a degree, but not necessarily zero. This does not preclude the possibility that a single or more macro-vessels in a voxel can also cause similar phase changes. In addition with experimental data we demonstrate that this small phase is measurable in the presence of noise and can be used to define task related phase changes. Our intent is to better understand the observed magnitude and phase changes. The goal of our paper is to investigate this model through simulations and by comparison with experimental BOLD fMRI data in humans.

In this paper, we first present the theory for calculating the local magnetic field seen by a water proton for arbitrary geometries and inhomogeneous susceptibility changes in the VOA. Computer simulations in both frequency domain (Deville et al., 1979; Koch et al., 2006; Salomir et al., 2003) and spatial domain of the phase change caused by a series of different 3-D Gaussian volume-averaged magnetization changes provide us with insight into the properties and applicability of the theoretical model. This is done by simulation results from a simple Gaussian model showing typical quadrupolar phase effects. Here we define the term “quadrupolar” pattern as the field distribution with four lobes, two with positive and two with negative values. Next, we show a slightly more complicated simulation which produces bipolar patterns. Finally, we directly compare BOLD fMRI data with simulations and demonstrate that the model is capable of producing phase patterns quite similar to those observed in a finger tapping fMRI experiment in humans. Our expectation is that with better understanding of the observed fMRI signal phase change we will improve methods for combining phase and magnitude data in BOLD fMRI experiments.

THEORY

The phase change at a position r is given by

$$\Delta \varphi \left(\mathbf{r}\right)=-\gamma \cdot TE\cdot \Delta B\left(\mathbf{r}\right),$$

where γ is the gyromagnetic ratio, TE is the echo time, and Δ B is the change in magnetic field along B₀ at position r and MKS units are used.

Blood vessels and surrounding EV tissue can be described by a two-component model (Durrant et al., 2003; Wolber et al., 2000; Ye and Allen, 1995; Zhao et al., 2007). In each voxel, the volume-averaged magnetic susceptibility χ can be calculated from the volume-weighted average of magnetic susceptibilities of the EV tissue χ_t and the IV blood χ_b:

$$\chi =f{\chi }_b+(1-f){\chi }_t$$

where f is the relative blood volume fraction. Subsequently, the volume averaged magnetization for a voxel at position r can be written as

$$\mathbf{M}\left(\mathbf{r}\right)\approx M_z\left(\mathbf{r}\right)\stackrel{⌢}{Z}\approx \chi \left(\mathbf{r}\right)\cdot \frac{{\overrightarrow{B}}_0}{{\mu }_0},$$

Where χ(r) is volume averaged magnetic susceptibility at this position, B₀ is the external magnetic field, and μ₀ is a constant, representing the vacuum permittivity.

We now discuss the phase change model proposed in (Zhao et al., 2007), which used the Lorentz sphere concept for its derivation. The Lorentz sphere concept was originally introduced in the electrostatic and magnetostatic treatment of microscopic fields (Feynman, 1975; Lorentz, 1915). It can be used to calculate nuclear magnetic resonance (NMR) shifts induced by magnetic susceptibility changes (Chu et al., 1990; Dickinson, 1951; Haacke et al., 1999; Levitt, 1996; Springer, 1994); and in the case of a heterogeneous system like blood (Durrant et al., 2003; Wolber et al., 2000; Ye and Allen, 1995) extended the sphere of Lorentz to the size of ∼20 μm to include a number of the blood cells and tissue molecules, much larger than the classic sphere of Lorentz size (on the order of several intermolecular distances). Furthermore, this conceptual device has been adapted to the system consisting of magnetic susceptible blood vessels and EV tissue (Zhao et al., 2007; Zhao et al., 2006). The size of the sphere, in this case, is at the sub-millimeter to millimeter scale (Zhao et al., 2007; Zhao et al., 2006). In a BOLD fMRI experiment, the blood susceptibility during activation is modulated by a decrease in paramagnetic deoxyhemoglobin concentration. The magnetic field change at position r can be written as (Zhao et al., 2007)

$$\Delta \mathbf{B}\left(\mathbf{r}\right)=\Delta {\mathbf{B}}_d\left(\mathbf{r}\right)+\frac{{\mu }_0}{3}\Delta \mathbf{M}\left(\mathbf{r}\right)+\sum \Delta {\mathbf{B}}_b\left(\mathbf{r}\right),$$

where the first term is change of the demagnetizing field (B_d (r)) caused by vessels inside the VOA but outside the Lorentz cavity. And the demagnetizing field is given by (Reitz et al., 1979)

$${\mathbf{B}}_d\left(\mathbf{r}\right)=\frac{1}{4\pi }\int {\int }_{S_0}\frac{({\chi }_{\text{in}}\left({\mathbf{r}}^{\prime }\right)-{\chi }_{\text{out}}\left({\mathbf{r}}^{\prime }\right))({\mathbf{B}}_0\cdot \mathbf{n})(\mathbf{r}-{\mathbf{r}}^{\prime })}{{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }^3}d{s}^{\prime }-\frac{{\mu }_0}{4\pi }{\int }_V\int \int \frac{(\nabla {}^{\prime }\cdot \mathbf{M}\left({\mathbf{r}}^{\prime }\right))(\mathbf{r}-{\mathbf{r}}^{\prime })}{{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }^3}d{\nu }^{\prime }$$

where χ _in and χ _out are the volume-averaged susceptibility inside and outside the VOA surface, respectively. S₀ and V indicate the surface and volume of the VOA, respectively; r’ is the position on the surface for the surface integration term (the first integration) or within the VOA (excluding the Lorentz sphere) for the volume integration term (the second integration); χ_in(r’) and χ_out(r’) are the volume-averaged susceptibility inside and outside the surface at position r’, respectively; n is the unit normal vector of surface at position r’; ▽ is the divergence operator.

The second term of Eq. is the change of the Lorentz cavity field $\left(\frac{{\mu }_0}{3}\mathbf{M}\left(\mathbf{r}\right)\right)$ from the magnetization distribution on the Lorentz sphere surface, and the last term of Eq. is the change of field caused by vessels inside the Lorentz cavity (B_b (r)). The sum of the contributions from those local blood vessels to the fMRI phase change in a voxel with large vessels absent is essentially zero because of the spatial symmetry of the induced magnetic field in EV water (Ogawa et al., 1993; Yablonskiy and Haacke, 1994) and randomly orientated micro-vessels (Menon, 2002, 2003). As the result, the last term of Eq. disappears. In addition, because effectively only the component of the field change along B₀ contributes to phase change, then we have $\Delta \mathbf{B}\left(\mathbf{r}\right)\approx \Delta B_z\left(\mathbf{r}\right)\stackrel{⌢}{Z}$. Denote Δ B_dz as the z component of Δ B_d. Finally, Eq. becomes,

$$\Delta B_z\left(\mathbf{r}\right)=\Delta B_{dz}\left(\mathbf{r}\right)+\frac{{\mu }_0}{3}\Delta M_z\left(\mathbf{r}\right).$$

If we know Δ M _z (r) or, equivalently χ (r), then the above equation can be used to calculate Δ B_z (r), and subsequently from Eq. the phase change.

Next, we show the approximations made to evaluate Eq. in the spatial domain for this specific application. In fMRI experiments, by definition, the activation is negligible at the surface of the VOA denoted by S₀; subsequently, the susceptibility change at the surface S₀ is negligible, which implies that

$$\Delta {\chi }_{\text{in}}=\Delta {\chi }_{\text{out}}.$$

Thus, the first term in the demagnetizing field expressed in Eq. disappears. Now let us focus on the second term of the demagnetizing field. In our model, M(r) is parallel to z axis (Eq.), which implies that M _x = M _y = 0. Thus we have

$$\nabla {}^{\prime }\cdot \Delta \mathbf{M}\left({\mathbf{r}}^{\prime }\right)=\frac{\partial \Delta M_z\left({\mathbf{r}}^{\prime }\right)}{\partial z^{\prime }}\widehat{z},$$

and the demagnetizing field becomes

$$\Delta B_{dz}\left(\mathbf{r}\right)=-\frac{{\mu }_0}{4\pi }\int {\int }_V\int \frac{\partial \Delta M_z\left({\mathbf{r}}^{\prime }\right)}{\partial z^{\prime }}\frac{z-z^{\prime }}{{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }^3}d{\nu }^{\prime }.$$

Finally, the magnetic field change at r in Eq. can be simplified as,

$$\Delta B_z\left(\mathbf{r}\right)={\mu }_0\left[\frac{\Delta M_z\left(\mathbf{r}\right)}{3}-\frac{1}{4\pi }\int {\int }_V\int \frac{\partial \Delta M_z\left({\mathbf{r}}^{\prime }\right)}{\partial z^{\prime }}\frac{z-z^{\prime }}{{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }^3}d{\nu }^{\prime }\right]$$

Equation (10) is expressed in the spatial domain but it can be calculated in a simpler manner in the frequency domain. The frequency domain method (Deville et al., 1979; Koch et al., 2006; Salomir et al., 2003) shows that given a susceptibility distribution, the resultant magnetic field perturbations can be calculated by

$$\Delta B_z\left(\mathbf{r}\right)=B_0\cdot F{T}^{-1}[(1∕3-{K_z}^2∕K^2)\cdot FT\left(\chi \left(\mathbf{r}\right)\right)].$$

where FT and FT^-1 indicate the Fourier transform and inverse Fourier transform, K_z is the z component of k-space and K² = K_x² + K_y² + K_z².

METHODS

fMRI Experiments

All experiments were performed on a 3T Siemens TIM Trio system with a 12-channel radio frequency (RF) coil. The data is combined from the multiple channels using coil sensitivity maps obtained automatically in a separate low resolution calibration experiment. The fMRI experiment used a standard Siemens gradient-echo EPI sequence modified to store real and imaginary data separately. We used a Field-of-View (FOV) = 240 mm, Slice Thickness = 3.5 mm, Slice Gap = 1 mm, Number of slices = 32, Matrix size = 64×64, TE = 29ms, and TR = 2s. The fMRI experiment used a block design with periods of 30 s off and 30 s on. Nine healthy subjects participated in the experiment. The subjects tapped the fingers of their right hand during the on period. There were five and a half cycles, starting with off and ending with the off period. We collected 15 whole head fMRI images during each ‘on’ or ‘off’ period. The total experiment time was 5.5 minutes.

Preprocessing

Data were preprocessed using the SPM5 software package (http://www.fil.ion.ucl.ac.uk/spm/software/spm5/). The phase images were unwrapped by creating a time series of complex images (real and imaginary) and dividing each time point by the first time point, and then recalculating the phase images. Further phase unwrapping was not required. Data were motion corrected using INRIalign - a motion correction algorithm unbiased by local signal changes (Freire et al., 2002). The transformation obtained by motion correcting the magnitude image was then applied to the phase images. Both magnitude and phase images were then spatially smoothed with a 10×10×10 mm³ full width at half-maximum Gaussian kernel, and spatially normalized into the standard Montreal Neurological Institute space. Following spatial normalization, the data (originally acquired at 3.75×3.75×4.5 mm) were slightly up-sampled to 3×3×3 mm, resulting in 53×63×46 voxels. Motion correction and spatial normalization parameters were computed from the magnitude data and then applied to the phase data. Activation maps were computed using the multiple regression framework within SPM5 in which regressors are created from the stimulus onset times and convolved with the standard SPM hemodynamic response function (HRF) which is a sum of two gamma functions, one to model the activation, the other to model a small post stimulus undershoot (Friston et al., 1995). One regressor for tapping versus rest was used in addition to a constant regressor modeling the mean. A contrast was created for each individual subject for finger tapping versus rest. To compute the group maps a second level analysis was performed using the activation maps from each individual subjects and entering them into a one-sample t-test.

Simulations

We performed a computer simulation in both frequency domain and spatial domain of the phase change in order to better understand the theory described above. For our example, we assume that in the VOA the volume-averaged susceptibility or magnetization change along the direction of B₀ is 3D Gaussian. Then, the unitless volume-averaged susceptibility change is written as,

$$\Delta \chi \left(\mathbf{r}\right)=C_k\exp (-\frac{1}{2}\left[\frac{x^2}{{\sigma }_x^2}+\frac{y^2}{{\sigma }_y^2}+\frac{z^2}{{\sigma }_z^2}\right]),$$

where C_k is a scaling constant. We choose the value of C_k based on parameter values from the literature. We define Δχ’ as the susceptibility difference between completely deoxygenated and completely oxygenated red blood cells (0.264 ppm in CGS units (Spees et al., 2001)) with a hematocrit level of 0.4 (Guyton and Hall, 1996), and oxygenation level Y is the fractional oxygenation in the red cells with ΔY_cap = 0.08 (Hoogenraad et al., 2001; Hoogenraad et al., 1998). Then for a blood volume fraction f of 0.05 and ignoring the cerebral blood volume change, C_k = -f · Δ Y_cap · 4π · Δχ ’ · Hct, as the result, C is approximately -5.3×10^-9.

However, for real fMRI experiments, we usually do not have information about the volume-averaged susceptibility Δχ(r) or magnetization change ΔM(r), which poses a difficulty for us to simulate the phase change based on Eqs. and. In order to test our phase model, we make the following assumptions to approximately calculate the change in magnetization from the relative change in BOLD signal. We define S as the magnitude of the signal, and define R *₂ as the relaxation rate. Assuming the change in R *₂ is small and the proton spin density remains constant, for a fixed TE we have (Hoogenraad et al., 2001)

$$\frac{\Delta S}{S}\cong -TE\cdot \Delta {R_2}^{\ast }.$$

Under the condition that TE is greater than the characteristic time (1/δω), R₂ * is a linear function of f (χ _b - χ _t) (Yablonskiy and Haacke, 1994),

$$\Delta {R_2}^{\ast }~\Delta \left[f({\chi }_b-{\chi }_t)\right]\equiv \Delta \chi \left(\mathbf{r}\right).$$

From Eqs.,, and, we conclude that the magnitude change is approximately linearly proportional to ΔM(r) and can write

$$\frac{\Delta S}{\stackrel{‒}{S}}=A\cdot \Delta M\left(\mathbf{r}\right),$$

where A is a scaling constant.

Three simulations were performed as follows. 1) First we investigate the properties of phase change resulting from the theoretical model and understand the dependence of the phase change patterns on the spatial distribution and orientation of the susceptibility distribution. We take 3D Gaussian as an example of susceptibility distribution and show expected phase change patterns for a 3D Gaussian susceptibility distribution. Note that magnetization and susceptibility distributions are proportional. 2) However, in our fMRI BOLD experimental results the patterns tend to be bipolar. Next simulation shows how a Gaussian susceptibility distribution can be combined and modified to convert a quadrupolar to approximately a bipolar pattern. We do not claim that the chosen distribution is the only case that will produce the bipolar phase change; rather we wanted to use any simple model to test whether it was possible to produce a bipolar phase (which is not intuitive). 3) Finally, we directly compare experimental fMRI phase and magnitude data to simulation results and demonstrate that the model is capable of producing patterns quite similar to those observed in a motor finger tapping fMRI data set.

RESULTS

In Figure 1 we show expected phase change patterns for a 3D Gaussian volume-averaged susceptibility distribution from computer simulations. This is used to understand the dependence of the phase change patterns on the spatial distribution and orientation of the susceptibility distribution. These simulations show the distribution of the phase change to be typically quadrupolar, with the intensity of the positive and negative variations being dependent on the spatial distribution, shape and the orientation of the Gaussian distribution. However, in our BOLD fMRI experimental results the patterns tend to be bipolar (examples are shown in Figure 3 and Figure 4). Hence next we wanted to evaluate whether our model was capable of producing bipolar patterns. In Figure 2 we show that a quadrupolar phase pattern can look like a bipolar pattern by combining parts of two Gaussian distributions and thresholding the results to suppress low signal intensity noisy regions. Finally, we directly compared our simulated results to the patterns observed in real fMRI data by first approximating the phase pattern observed in the fMRI data and inverting through our model to produce the corresponding susceptibility pattern. These results are shown in Figure 3. Detailed results are as follows.

Figure 1.

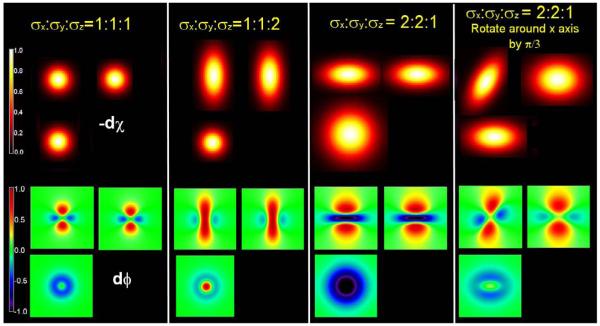
Simulation of phase change corresponding to 3D Gaussian volume-averaged susceptibility change for the cases of σ_x:σ_y:σ_z = 1:1:1, 1:1:2, 2:2:1 and 2:2:1 rotated counter-clockwise around the x-axis by π/3, respectively.

Figure 3.

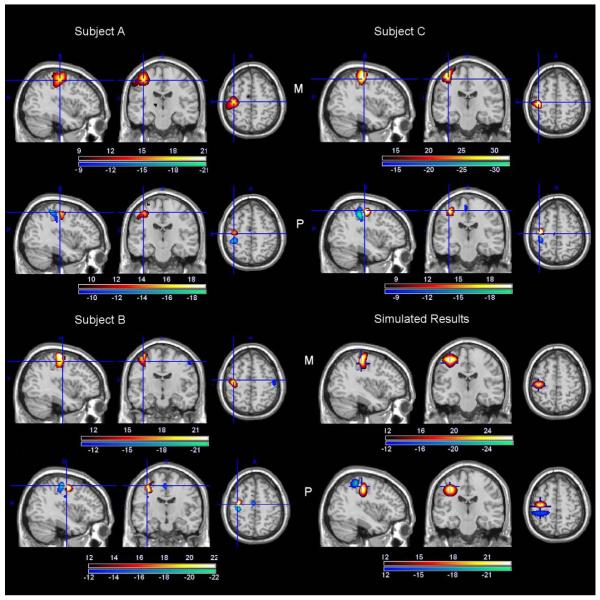
Magnitude (M) and phase (P) changes (t-values) for single subject A, B, and C together with the susceptibility and phase change of simulated results. The colorbars for the subjects show the t-value ranges. The colorbar for the simulated results indicate the relative strength of susceptibility and phase change.

Figure 4.

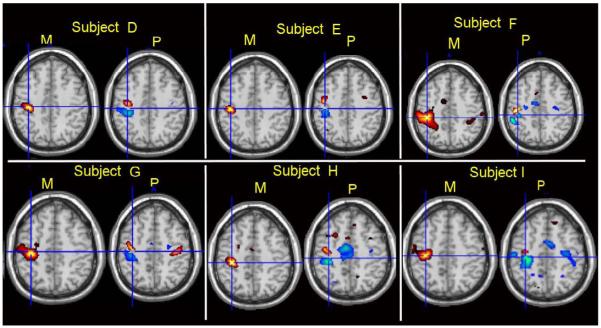
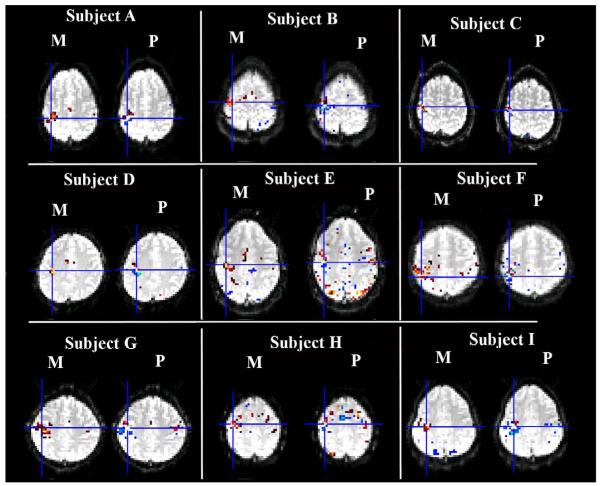
The axial slices of magnitude and phase change (t-value) for single subject D-I.

Figure 2.

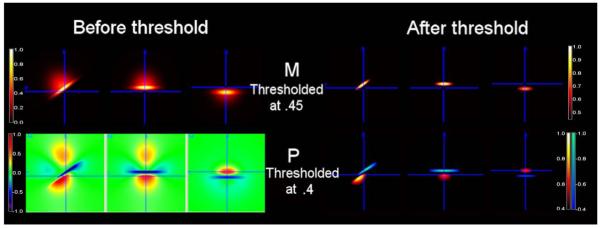
Considering the noise, the phase of quadrupolar pattern becomes bipolar for an example of asymmetric 3D Gaussian volume-averaged susceptibility change. Half of the susceptibility change has σ_x:σ_y:σ_z = 6:6:8 with the amplitude of 0.5 and another half has σ_x:σ_y:σ_z = 6:6:1 with the amplitude of 1. The total susceptibility change is rotated counter-clockwise around the x-axis by π/5.

Figure 1 shows the simulation results of phase change corresponding to 3D Gaussian volume-averaged susceptibility change for the cases of σ_x:σ_y:σ_z = 1:1:1, 1:1:2, 2:2:1 and 2:2:1 (Eq.) rotated counter-clockwise around the x-axis by π/3, respectively. Both the frequency domain and spatial domain give approximately the same results. For the value of C_k selected above, the resulting maximum simulated phase change for all of these configurations is in the order of 1°. Depending on the spatial distribution of the susceptibility changes in the VOA and the angle of the cut plane of the magnetic field change, the resulting phase shows patterns of dominantly positive, dominantly negative, or combinations of positive and negative phase changes due to the volume-averaged magnetization and demagnetization effects. More specifically, when the susceptibility change is a sphere, the resulting phase is quadrupolar, which coincides with (Haacke et al., 1999); when the long axis of the susceptibility change is parallel to the external magnetic field B₀, the volume-averaged magnetization effect dominates and the resulting phase change tends to be dominantly positive, which agrees with the results in (Wolber et al., 2000; Zhao et al., 2007); when the long axis of the susceptibility change is perpendicular to the external magnetic field B₀, the demagnetization effect plays a big role, the resulting phase change becomes more negative; in fact, the absolute value of the negative lobe of the phase is greater than the positive lobe of the phase. For the case of σ_x:σ_y:σ_z = 2:2:1 and the distribution of susceptibility change is rotated counter-clockwise around the x-axis by π/3, the resulting phase change is rotated and twisted. The positive and negative lobes are no longer 90° from each other. The resulting phase change varies according to the spatially distributed volume-averaged susceptibility change.

Figure 2 shows in the left panel that given an asymmetric 3D distribution of susceptibility change constructed by taking a part from a Gaussian distribution with σ_x:σ_y:σ_z = 6:6:8 and amplitude 0.5 and another part with σ_x:σ_y:σ_z = 6:6:1 and amplitude 1. The total susceptibility change is rotated counter-clockwise around the x-axis by π/5. For this example, the resulting phase has a pattern of asymmetric quadrupoles. Considering the real fMRI data are noisy, we threshold both susceptibility change and phase change at 0.45 and 0.4, respectively. Here the thresholds are chosen in the way that ratio of threshold over the maximum is closer to that of the real fMRI data. After the threshold is applied, the asymmetric quadrupolar phase appears bipolar.

In Figure 3, the first three panels show the magnitude and phase change of the results (t value) for subject A, subject B and subject C, respectively. The panel in the lower right corner of the figure shows the scaled susceptibility change and phase change of simulated results. Here, we assume the magnitude change is approximately linear to the volume-averaged susceptibility change. For the three subjects, the thresholds were all greater than t = 8 (p<1×10^-13), which is highly significant. The highest magnitude change was observed in the motor cortex. The phase changes all show the bipolar patterns. Further observation of Figure 3 indicates the peak of the magnitude change is not located where the phase change peaks; instead, it is closer to the sign change of the phase change. The observations above also hold true for the other subjects shown in Figure 4. The simulations to match the observed fMRI phase/magnitude changes were conducted by modeling the phase change due to a susceptibility distribution which resembles the experimentally observed BOLD fMRI magnitude change pattern, and the resulting phase change matches the experimentally observed bipolar phase patterns of fMRI after thresholding. The simulation results in the lower right corner of Figure 3 show that our model can closely match phase and magnitude change patterns observed experimentally.

Figure 5 shows the spatially unsmoothed and smoothed phase and magnitude change time courses from a single voxel (the one showing maximal phase change) for subject D, who is representative. The time evolutions of the phase and magnitude change are similar to each other, suggesting that both changes originate from the same source, the deoxyhemoglobin-induced susceptibility change. The measured voxel phase change (unsmoothed) is around 1° (0.017 radians), on the same order of 1° in the simulation results as shown in Figure 1 and Figure 2. They are both on the same order of a measured voxel phase change (no large vessel present) 0.028 radians or 1.6° in (Menon, 2002). While in the voxels with large vessels present, the phase change is relatively larger (for example, 0.085 radians in (Menon, 2002)). The spatially smoothed phase change for the same voxel is more reduced than the spatially smoothed magnitude change since the adjacent negative and positive phase changes can cancel. In this paper, we focus on modeling the phase change, in the future, a ‘smart smoothing’ approach would appear to be more important for phase change. For completeness, we present unprocessed data (no smoothing and no spatial normalization) in Figure 6 in Appendix.

Figure 5.

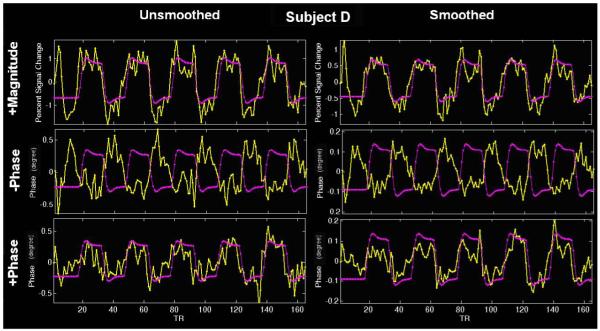
Spatially unsmoothed and smoothed phase and magnitude change time courses for subject D.

Figure 6.

Unprocessed magnitude and phase data (no smoothing and no spatial normalization) for nine subjects A-I.

Although, the principal cause of magnitude and phase change in the BOLD experiment is the susceptibility change, both magnitude and phase also depend on other factors, which includes diffusion, presence of large vessels, and physiological noise. In addition these factors affect the phase and magnitude signal in different ways. We are collecting data from a 12 channel RF coil and combining them (internally by Siemens) in an optimal manner based on coil sensitivity profiles. Under these conditions, the measurement noise in the real and imaginary channels can be correlated. Thus methods of properly combining magnitude and phase change in the presence of noise and their dependence on other previously discussed factors will prove to be useful to further improve estimates of the susceptibility change.

DISCUSSION

We begin with Zhao’s model (Zhao et al., 2007) and calculate the magnetic field change seen by a water proton at position r based on the frequency domain method (Deville et al., 1979; Koch et al., 2006; Salomir et al., 2003) and the spatial domain method described above. Zhao’s model shows that for a random distribution of micro-vessels we can do the analysis in terms of volume averaged magnetization or susceptibility. Under these assumptions we can do an analysis without the details of intra-voxel susceptibility distribution. Equation suggests that calculation of the magnetic field from magnetization depends on the demagnetizing field given by the volume integral and a Lorentz cavity field. This interpretation gives additional insight on the dependence of magnetic field change on the susceptibility distribution. The change in the Lorentz cavity field is due to the change in the volume-averaged magnetization at the measured point, while the derivatives of this volume-averaged magnetization at all other points in the direction of B₀ contribute to the change in the demagnetizing field. Depending on the relative strengths of these two fields, the net phase change will bear a dominantly positive, dominantly negative or the combination of positive and negative sign.

We next calculate susceptibility distributions that can predict the phase patterns observed experimentally in BOLD fMRI. We begin with a Gaussian spatial distribution for susceptibility and show that the phase pattern it generates can be quadrupolar. The phase is zero at the centre of the Gaussian distribution, where the susceptibility distribution is symmetric, and not zero in surrounding regions, where the susceptibility distribution is not symmetric. After combining more than one Gaussian distribution and suitable thresholding we can convert a quadrupolar phase pattern to approximately a bipolar pattern. Finally, we simulate the phase change due to a susceptibility distribution which approximates the real fMRI magnitude change pattern, and the resulting phase change matches the experimentally observed bipolar phase patterns of fMRI after thresholding. This result shows that even though the spatial patterns of the magnitude and phase change in an fMRI experiment are not similar, they can be analyzed jointly if a model is used to link a change in susceptibility to a change in the phase and magnitude of the fMRI signal. Also, in the presence of noise there can be voxels where a phase change is detectable and a magnitude change signal is not. This is a potential benefit of using the phase. Besides, the measurement noise in the phase and magnitude being statistically independent for small SNR and approximately independent for moderate to large SNR (Lei and Wehrli, 2007) is another reason for their joint analysis. Thus the joint analysis will not only improve spatial localization of activation but may also potentially let us infer intra-voxel properties, such as the presence of large vessels in a voxel. In future research, we will develop methods to infer the activation information of Δχ(r) by fitting both the magnitude and phase data to the proper magnitude model and phase model.

In the simulations discussed here we have ignored details of intra-voxel susceptibility distribution and diffusion effects. The analysis was done in terms of volume averaged magnetization, which is accurate for a random distribution of micro-vessels. In the general case, such as the presence of large vessels, the large vessels’ orientation and position will play a role in the phase change. As mentioned earlier in the paper, phase sensitive fMRI methods have been used to reduce contaminations from oriented large veins (Klassen and Menon, 2007; Menon, 2002; Nencka and Rowe, 2007; Tomasi and Caparelli, 2007). Those methods state that during the activation only the large oriented vessels produce phase changes and for randomly oriented micro-vessels, the phase change is zero. However, the approach used in our paper predicts that a voxel with randomly oriented micro-vessels can produce a non-zero phase change of the order of a degree (0.017 radians). Those methods can be used to reduce activation contributions from well oriented draining vessels. In contrast, the phase model we utilize can be used to extract useful physiologic information such as task-related activation (susceptibility change) from phase change data. Our approach and those methods are complementary, thus in future work we will explore the combination of them together. On the other hand, in order to test the phase model in the real BOLD fMRI experiments, we draw upon Yablonskiy’s result showing that, in the absence of diffusion, the magnitude change is approximately linearly proportional to the change in volume-averaged magnetization ΔM(r) so that we can approximately calculate the change in volume-averaged magnetization from the relative change in BOLD magnitude signal. The conditions when diffusion can be neglected have been discussed by Yablonskiy and Haacke (Yablonskiy and Haacke, 1994) and the simulation can follow Martindale’s method (Martindale et al., 2008), where the frequency domain method is used to calculate the magnetic field distribution from a susceptibility distribution.

Venograms will be collected in the future to detect presence of large vessels and incorporate their effect in simulations. In addition we will collect physiologic data to determine the relationship between the phase signal and physiological signals; similar to what is done for magnitude imaging (Glover et al., 2000; Kruger and Glover, 2001).

In this paper, we have demonstrated that the Lorentz sphere model for BOLD fMRI data from human subjects predicts phase change patterns observed in these experiments. At this stage we have qualitatively shown that the model is capable of producing the observed patterns. Quantitative fitting to predict change in blood susceptibility will be pursued in future work. Our approach provides strong motivation for the development of additional methods for utilizing the phase information in fMRI BOLD data.

APPENDIX

In Figure 6, we present unprocessed data (no smoothing and no spatial normalization). Here we use the first timepoint of the EPI data for the anatomical underlay.