Rate-adjusted spike-LFP coherence comparisons from spike-train statistics

Abstract

Coherence is a fundamental tool in the analysis of neuronal data and for studying multiscale interactions of single and multiunit spikes with local field potentials. However, when the coherence is used to estimate rhythmic synchrony between spiking and any other time series, the magnitude of the coherence is dependent upon the spike rate. This property is not a statistical bias, but a feature of the coherence function. This dependence confounds cross-condition comparisons of spike-field and spike-spike coherence in electrophysiological experiments.

Taking inspiration from correction methods that adjust the spike rate of a recording with bootstrapping (‘thinning’), we propose a method of estimating a correction factor for the spike-field and spike-spike coherence that adjusts the coherence to account for this rate dependence.

We demonstrate that the proposed rate adjustment is accurate under standard assumptions and derive distributional properties of the estimator.

The reduced estimation variance serves to provide a more powerful test of cross-condition differences in spike-LFP coherence than the thinning method and does not require repeated Monte Carlo trials. We also demonstrate some of the negative consequences of failing to account for rate dependence.

The proposed spike-field coherence estimator accurately adjusts the spike-field coherence with respect to rate and has well-defined distributional properties that endow the estimator with lower estimation variance than the existing adjustment method.

1. Introduction

Synchronization of rhythmic neural activity plays an important role in the function of cortical networks and the coordination of activity between local and distant neural ensembles (Buzsáki and Draguhn, 2004; Fries, 2005; Wang, 2010). One measure of neural synchrony is the coherence. The coherence is a nonparametric spectral measure of the per-frequency linear dependence between time series (Hannan, 1970), and is a commonly used descriptive statistic for neuroscientific data analysis (eg. Pesaran et al. (2002); Womelsdorf et al. (2006); Jutras et al. (2009); Anastassiou et al. (2011).

Both ordinary, and point process time series, such as spike trains, may be studied using standard coherence estimators (Bartlett, 1963; Jarvis and Mitra, 2001). This flexibility permits the use of a single metric to analyze the coupling between pairs of field rhythms like local field potentials (LFPs), between pairs of spike trains, and between spike trains and LFPs. Spike-field coherence is a particularly important metric of coordinated neuronal activity, since it indicates the degree to which individual neurons are rhythmically synchronized with bulk network activity, represented by the LFP. However, spike-field coherence is a function of the mean spike rate of the analyzed neuron (Lepage et al., 2011).

This dependence has important consequences for cross-condition comparisons of coherences when mean spike rates are not the same between conditions. Standard practice is to estimate the coherence in each of two conditions and then to determine if the coupling between spikes and LFPs differs between conditions based the difference of coherences being significantly different from zero. However, if the differences in coherences are due to the spike rate alone, and not to a change in the coupling between spikes and LFPs then, under the null hypothesis of no coupling difference, the null distribution of the differences between coherences should have non-zero mean. Thus, as we demonstrate in Section 3.4, the standard practice misspecifies the null distribution for differences in spike-LFP coupling, making it impossible to correctly specify the type-I error of the test.

One method of correcting for this confound is the so called “thinning” procedure (Gregoriou et al., 2009; Mitchell et al., 2009). In this procedure, the mean spike rate of a more rapidly firing neuron is made comparable to the spike rate of a less rapidly firing neuron by the random removal of spikes from the more rapid spike train until the mean spike rates of both spike trains are equal. This approach makes use of the assumption that the point process lacks history dependence (i.e. the process is inhomogeneous Poisson), and requires removing events from the observed point process. While the statistical properties of this procedure have not been thoroughly investigated, it is evident that the removal of spikes effectively removes information from the recording. Furthermore, the Monte Carlo approach to rate adjustment may become too computationally unwieldy when conducting analyses across a large number of channels and/or conditions. This is likely to become a more common problem as the number of simultaneous channels used to record spikes becomes large. Alternatively, rhythmic synchrony can be assessed by generalized linear modeling, which explicitly accounts for rate-dependent coupling (Lepage et al., 2013). However, the results are model-dependent and require careful interpretation.

In this paper, we propose a new method for examining spike-field coherence over a range of possible expected intensities, which is modeled after the thinning procedure, but has improved ability to detect cross-condition changes in spike-field coherence (with respect to area under the receiver operating characteristic (ROC) curve, Section 3.4).

The proposed method is developed analytically with well-defined sampling properties, precluding the need for Monte Carlo procedures which shuffle spikes, does not require the removal of data, and requires approximately the same amount of time to calculate as the conventional coherence estimator.

1.1. Background and notation

Suppose the LFP y(t) is sufficiently described as a discrete time, weak sense stationary (WSS), zero-mean process such that the auto covariance function of y(t) is given by

$$r_{\mathit{yy}}(\tau )\equiv \mathrm{E}[y(t)y(t+\tau )],$$

and the power spectral density of y is defined as

$$S_{\mathit{yy}}(f)=\mathrm{\Delta }{\displaystyle \sum _{\tau =-\infty }^{\infty }{r}_{\mathit{yy}}(\tau )e^{-i2\pi f\tau \mathrm{\Delta }}}.$$

We define the random variable n(t) as the counting process describing the number of spikes that occur on the interval [0, t). Let dn(t) = n(t+ Δ) − n(t), where Δ is a small time increment. We will define the process Λ(t) as the conditional counting process such that E[n(t)|Λ(t)] = Λ(t). In the following, we will consider Λ(t) to be an absolutely continuous random process such that

$$\mathrm{\lambda }(t)\equiv \underset{\mathrm{\Delta }\to 0}{\lim }\frac{\mathrm{\Lambda }(t+\mathrm{\Delta })-\mathrm{\Lambda }(t)}{\mathrm{\Delta }},$$

exists (Snyder and Miller, 1991), and we will call it the conditional intensity. We may then define the point process dn(t) in terms of a discrete time, doubly-stochastic Poisson (DSP) process with conditional intensity λ(t), where we choose Δ small such that P(dn(t) = 1) ≈ λ(t)Δ and $P(\mathit{dn}(t)>1)=\mathcal{O}({\mathrm{\Delta }}^2)$. We will regard λ(t) ≥ 0 as a WSS random process with E[λ(t)] = μ. We note that the expectation of dn(t) can be expressed as

$$\begin{array}{l}\mathrm{E}[\mathit{dn}(t)]=\mathrm{E}[\mathrm{E}[\mathit{dn}(t)|\mathrm{\lambda }(t)]]\\ =\mathrm{E}[P(\mathit{dn}(t)=1|\mathrm{\lambda }(t))]\\ =\mathrm{E}[\mathrm{\lambda }(t)]\mathrm{\Delta }+\mathcal{O}({\mathrm{\Delta }}^2)\\ \approx \mu \mathrm{\Delta }.\end{array}$$

Since dn(t) is WSS and DSP, the auto covariance function is a function of one variable and can be described in terms of the auto covariance function of λ(t) defined as

$$\begin{array}{l}{r}_{\mathit{nn}}(\tau )\equiv \mathrm{E}[\mathit{dn}(t)\mathit{dn}(t+\tau )]-\mathrm{E}[\mathit{dn}(t)]\mathrm{E}[\mathit{dn}(t+\tau )],\\ =\mu \mathrm{\Delta }{\delta }_{0,\tau }+{\mathrm{\Delta }}^2{r}_{\mathrm{\lambda }\mathrm{\lambda }}(\tau ),\end{array}$$ (1)

where r_λλ(τ) is the auto covariance function of λ(t), and δ₀, is the Kronecker delta function. The spike auto-spectrum is given by (Bartlett, 1963; Lepage et al., 2011)

$$\begin{array}{l}{S}_{\mathit{nn}}(f)=\mathrm{\Delta }{\displaystyle \sum _{\tau =-\infty }^{\infty }{r}_{\mathit{nn}}(\tau )e^{-i2\pi f\tau \mathrm{\Delta }}}\\ =\mathrm{\Delta }{\displaystyle \sum _{\tau =-\infty }^{\infty }(\mu \mathrm{\Delta }{\delta }_{0,\tau }+{\mathrm{\Delta }}^2{r}_{\mathrm{\lambda }\mathrm{\lambda }}(\tau ))e^{-i2\pi f\tau \mathrm{\Delta }}}\\ \approx {\mathrm{\Delta }}^2(\mu +S_{\mathrm{\lambda }\mathrm{\lambda }}(f)).\end{array}$$ (2)

the spike-field cross spectrum is similarly defined as

$$S_{\mathit{ny}}(f)\equiv \mathrm{\Delta }{\displaystyle \sum _{\tau =-\infty }^{\infty }{r}_{\mathit{ny}}(\tau )e^{-i2\pi f\tau \mathrm{\Delta }}},$$ (3)

where

$$r_{\mathit{ny}}(\tau )\equiv \mathrm{E}[\mathit{dn}(t)y(t+\tau )]$$

is the cross-correlation between dn(t) and y(t).

The coherence between y(t) and dn(t) is

$$C_{\mathit{ny}}(f)\equiv \frac{S_{\mathit{ny}}(f)}{\sqrt{S_{\mathit{nn}}(f)}\sqrt{S_{\mathit{yy}}(f)}}.$$ (4)

Note that, because λ(t) is also a WSS stochastic process, we can define the coherence between λ(t) and y(t);

$$C_{\mathrm{\lambda }y}(f)\equiv \frac{S_{\mathrm{\lambda }y}(f)}{\sqrt{S_{\mathrm{\lambda }\mathrm{\lambda }}(f)}\sqrt{S_{\mathit{yy}}(f)}},$$

which we refer to as the intensity-field coherence.

Lepage et al. (2011) showed that the spike-field coherence may be expressed as

$$C_{\mathit{ny}}(f)=C_{\mathrm{\lambda }y}(f){\left(1+\frac{\mu }{S_{\mathrm{\lambda }\mathrm{\lambda }}(f)}\right)}^{-1/2}.$$ (5)

Equation (5) explicitly shows that C_ny(f) is dependent on the mean spike rate μ. Note that this dependence is not a statistical dependence that is a property of some estimator of C_ny, but is a functional dependance derived from the definition of C_ny. When making cross-condition comparisons between estimated values of C_ny, we may erroneously conclude that the phase coupling between y(t) and the probability of spiking λ(t)Δ, embodied by Cλy(f), has changed when in fact there has only been a change in the spike rate μ. Thus, we would like to be able to distinguish between a change in C_ny that results from a change in spike tuning C_λy versus one that is simply due to a change in μ, even though we do not directly observe λ(t). The remainder of this paper is devoted to describing a strategy for achieving this end.

2. Theory

In this section, we outline the basic approach for correcting the spike-LFP coherence through thinning. We then propose a conceptually equivalent analytic procedure for rate correction that has reduced variance compared to thinning and does not require Monte Carlo trials or removal of spikes. We then describe the properties of the proposed coherence estimator.

2.1. Spike thinning

One solution to the rate-dependence confound is to correct the C_ny estimate for the spike rate by randomly removing spikes from the condition with higher spike rate such that the average number of spikes per trial will be the same between conditions (Gregoriou et al., 2009; Mitchell et al., 2009). We refer to this procedure as “thinning” due to its relation to the simulation algorithm of the same name for the generation of realizations of nonhomogenious Poisson processes (Lewis and Shedler, 1979).

Suppose the coherence is to be compared between two conditions. Let the mean spike rate of the condition with the higher spike rate be denoted as μ_H and that of the condition with the lower spike rate be μ_L. The thinning procedure works by first estimating the discrepancy in spiking probably across conditions by

$$\alpha \equiv {\mu }_L/{\mu }_H.$$

We may then generate rate-corrected trials by randomly removing (“thinning”) spikes from every trial with probability α. All of the thinned trials will then be inhomogeneous Poisson with rate μ_L and are then used as sample spike trains. This process is repeated many times and a rate-corrected estimate of C_ny is calculated using the ensemble of thinned trials. In practice, if we expect the Poisson rate to be stimulus locked, and therefore dependent on t, we may estimate μ(t) and α(t) over a short window centered at t such that the segment is approximately stationary (Jarvis and Mitra, 2001; Lepage et al., 2011) which is common practice for spectral estimates of neural signals (examples include Senkowski et al. (2005); Pesaran et al. (2008); Gregoriou et al. (2009); Buschman et al. (2012)).

2.2. Rate adjustment

In this section, we derive a theoretical rate-corrected coherence, conceptually equivalent to the thinning procedure but does not require repeated Monte Carlo trials and the removal of spikes. We will develop this procedure first in the more general context of applying a transformation of the intensity λ(t) to give an appropriate target expected intensity μ*. We will then derive expressions for the corresponding rate-adjusted spike spectrum S_n*n*(f) and spike-LFP cross spectrum S_n*y(f) from which we can obtain an expression for the rate-adjusted spike-LFP coherence.

Suppose that we have a target firing rate μ* ≠ μ. We propose the affine transformation of the conditional intensity

$${\mathrm{\lambda }}^{\ast }(t)=\alpha \mathrm{\lambda }(t)+\beta ,$$ (6)

where α represents an amplitude modulation of the original intensity process λ(t), and β represents homogeneous Poisson noise. This model is favorable because the intensity-field coherence C_λy is invariant to affine transformations of λ(t), but we retain the flexibility to assign the mean spike rate μ* = αμ + β through the parameters α and β. Therefore, we expect any difference between the spike-field coherence at the new rate C_n*y and original spike-field coherence C_ny to be due to differences in mean spiking probability, and not to differences in the underlying coupling between λ(t) and y. When β = 0, then α is equivalent to the discrepancy in spiking probability described for the thinning procedure in Section 2.1.

From (3) and (6) we find that the adjusted spike-field cross spectrum is given by

$$S_{n\ast y}(f)=\alpha S_{\mathit{ny}}(f).$$ (7)

The adjusted spike autocovariance function is given by

$$r_{n\ast n\ast }(\tau )=\mathrm{\Delta }(\alpha \mu +\beta ){\delta }_{0,\tau }+{\mathrm{\Delta }}^2{\alpha }^2{r}_{\mathrm{\lambda }\mathrm{\lambda }}(\tau ).$$ (8)

From (2) and (8) we can derive the adjusted spike auto-spectrum in terms of the unadjusted spectrum and the rate parameters,

$$\begin{array}{l}{S}_{n\ast n\ast }(f)\approx {\mathrm{\Delta }}^2(\alpha \mu +\beta +{\alpha }^2{S}_{\mathrm{\lambda }\mathrm{\lambda }}(\tau ))\\ ={\mathrm{\Delta }}^2(\alpha \mu +\beta -{\alpha }^2\mu +{\alpha }^2\mu +{\alpha }^2{S}_{\mathrm{\lambda }\mathrm{\lambda }}(\tau ))\\ ={\mathrm{\Delta }}^2((1-\alpha )\alpha \mu +\beta )+{\alpha }^2{S}_{\mathit{nn}}(f).\end{array}$$ (9)

The corresponding rate-adjusted coherence is

$$\begin{array}{l}{C}_{n\ast y}(f)=\frac{S_{n\ast y}(f)}{\sqrt{S_{n\ast n\ast }(f)}\sqrt{S_{\mathit{yy}}(f)}}\\ =\kappa C_{\mathit{ny}}(f),\end{array}$$ (10)

where

$$\kappa \equiv {\left(1+\frac{{\mathrm{\Delta }}^2((1/\alpha -1)\mu +\beta /{\alpha }^2)}{S_{\mathit{nn}}(f)}\right)}^{-1/2},$$ (11)

is the rate-adjustment factor. Rate-based adjustment of the coherence between two spike trains can be achieved as a natural extension of the spike-LFP adjustment, where a κ is determined for each spike train as

$$C_{n_1^{\ast }{n}_2^{\ast }}={\kappa }_1{\kappa }_2{C}_{n_1{n}_2},$$

where κ₁ and κ₂ correspond to rate adjustments for each spike train.

Although the proposed adjustment, including the results developed in subsequent sections regarding sample estimator properties and control of type-I error, is readily applied to spike-spike coherence, the properties of the rate-adjusted estimator are most clearly illustrated for the simpler (and far more common) single spike train – per condition case (i.e. spike-LFP coherence). Therefore, our discussion in this paper will be restricted to the case of spike-LFP coherence.

2.3. Properties of ${\widehat{C}}_{n\ast y}$

Estimates of the adjusted coherence ${\widehat{C}}_{n\ast y}(f)$ can be obtained by using (10) and (11) where the discrete time sample estimates ${\widehat{C}}_{\mathit{ny}}(f)$ and ${\widehat{S}}_{\mathit{nn}}(f)$ replace the population values of C_ny(f) and S_nn(f). In this section we will describe the sampling properties of Fisher’s z-transform (Fisher, 1921; Enochson and Goodman, 1965) of | ${\widehat{C}}_{n\ast y}(f)$|, conditional upon κ being known. Understanding these properties, such and the sampling bias and variance, will allow us to predict how the rate correction will affect the test of differences between coherences and help us to evaluate how best to apply the rate correction. The Fisher transform of | ${\widehat{C}}_{n\ast y}(f)$| is employed because it is known to converge to normal faster than | ${\widehat{C}}_{n\ast y}(f)$| (Fisher, 1921). For the remainder of this paper we will suppress the | · | for notational convenience so that all references to the coherence are exclusively to its magnitude.

Fisher’s z-transform

For a weak sense stationary pair of processes, the conventional magnitude squared coherence C_ny(f)² can be written as a squared multiple correlation (Hannan, 1970). Thus, the sampling distribution for the coherence (Goodman, 1957) is the same as that for the multiple correlation (Fisher, 1928; Wilks, 1932). This has permitted the use of classical statistical procedures for comparing correlations to be directly applied to coherences. One such procedure is the variance-normalizing transformation known as Fisher’s z-transform (Fisher, 1921; Enochson and Goodman, 1965),

$$z={\tanh }^{-1}({\widehat{C}}_{\mathit{ny}}(f)).$$

Fisher showed that, as the sample size increases, z converges to a normal distribution faster than C_ny, permitting the convenience and power of normal-distribution statistical methodology even with modest sample sizes. The z-transformed coherence has a sample variance

$${\sigma }_z^2=\frac{1}{2N}+\mathcal{O}(N^{-2}),$$ (12)

where, for coherences, N is the number of independent estimates of the spectra. This expression for the variance is particularly useful in that, unlike the variance of ${\widehat{C}}_{\mathit{ny}}(f)$, it does not depend on the unknown population parameter.

Bias and variance of the sample adjusted coherence

We will now examine expressions for the bias and variance of the rate-adjusted z so that we may identify how the rate adjustment itself modulates these quantities. In Appendix A we derive the sampling distribution for the adjusted coherence and show its relationship to the distribution of the unadjusted coherence (Goodman, 1957). As we will verify in Section 3.2, the sampling distribution of

$$z^{\ast }={\tanh }^{-1}({\widehat{C}}_{\mathit{ny}}{(f)}^{\ast })={\tanh }^{-1}(\kappa {\widehat{C}}_{\mathit{ny}}(f)),$$

is approximately Gaussian, where κ is given by (11). This being the case, the first two moments of z* are sufficient to define the distribution of z*. If we let ${\zeta }^{\ast }={\tanh }^{-1}(C_{\mathit{ny}}^{\ast })$, then we find that the expectation of z* is given by

$$\mathrm{E}[z^{\ast }]={\zeta }^{\ast }+\frac{C_{\mathit{ny}}\kappa (1-C_{\mathit{ny}}^2)}{2N(1-C_{\mathit{ny}}^2{\kappa }^2)}\left(\frac{{\kappa }^2{(1-C_{\mathit{ny}}^2)}^2}{(1-C_{\mathit{ny}}^2{\kappa }^2)}-\frac{1}{2}\right)+\mathcal{O}(N^{-2}),$$ (13)

and the sample variance of z* is given by

$${\sigma }_{z\ast }^2=\frac{{\kappa }^2}{2N}\left(\frac{1-C_{\mathit{ny}}^2}{1-C_{\mathit{ny}}^2{\kappa }^2}\right)+\mathcal{O}(N^{-2}).$$ (14)

Therefore, z* is an asymptotically unbiased and consistent estimator of ζ*. Derivations of expressions (13) and (14) are given in Appendix B. In section 3.2 we will use simulations to validate the normal-distribution assumption and the accuracy of expressions (13) and (14).

Next we will look at (13) and (14) more closely to understand how rate adjustments influence the bias and variance of the rate-adjusted estimator. We will focus exclusively on the scenario where β = 0; i.e. we are only estimating the parameter α. This is due to this scenario’s equivalence with the assumptions of the existing thinning coherence correction. Joint estimation of α and β will be left for future work.

Sensitivity to α

We can now examine how the value of α influences the values of C_n*y and ${\sigma }_{z\ast }^2$. The sensitivity of C_n*y to α is defined as the partial derivative of C_n*y with respect to α, which is given by

$$\frac{\partial C_{n\ast y}}{\partial \alpha }=C_{\mathit{ny}}\frac{\partial \kappa }{\partial \alpha },$$ (15)

where

$$\frac{\partial \kappa }{\partial \alpha }={\kappa }^3\left(\frac{{\mathrm{\Delta }}^2\mu }{2{\alpha }^2{S}_{\mathit{nn}}}\right).$$ (16)

In order to make physical sense in terms of the model (6), we must have α, κ, C_ny, S_nn ≥ 0. Thus, we find that ∂C_n*y/∂α ≥ 0 indicating that C_n*y increases with α.

We can similarly examine the sensitivity of ${\sigma }_{z\ast }^2$ to α. The partial derivative of ${\sigma }_{z\ast }^2$ with respect to α is given by

$$\frac{\partial {\sigma }_{z\ast }^2}{\partial \alpha }=\frac{\partial {\sigma }_{z\ast }^2}{\partial \kappa }\frac{\partial \kappa }{\partial \alpha }$$

with

$$\frac{\partial {\sigma }_{z\ast }^2}{\partial \kappa }=\frac{\kappa (1-C_{\mathit{ny}}^2)}{N{(1-{\kappa }^2{C}_{\mathit{ny}}^2)}^2},$$ (17)

where ∂κ/∂α is given in (16). Since 0 ≤ C_n*y < 1 and ∂κ/∂α, κ ≥ 0, we will always have $\partial {\sigma }_{z\ast }^2/\partial \alpha \ge 0$, indicating that ${\sigma }_{z\ast }^2$ increases with α. Since $\partial {\sigma }_{z\ast }^2/\partial \alpha >0$, ∀α ∈ (0, ∞), we must have, for α′ > α,

$${\sigma }_{z\ast }{(\alpha \prime )}^2{\sigma }_{z\ast }{(\alpha )}^2,$$ (18)

∀α′, α ∈ (0, ∞).

Inequality (18) has important consequences for the estimation of the difference between coherences when we compare the proposed procedure with the thinning procedure. If we define Δz ≡ z₁ − z₂ then the variance of Δz is

$$\mathrm{Var}[\mathrm{\Delta }z]=\mathrm{Var}[z_1]+\mathrm{Var}[z_2].$$

Because the proposed procedure adjusts the higher spike rate spectral estimates to match the lower spike rate, we will always have α ≤ 1. Thus, if μ₁ < μ₂ then, after adjustment,

$$\mathrm{Var}[\mathrm{\Delta }z\ast ]=\mathrm{Var}[z_1]+\mathrm{Var}[z_2^{\ast }],$$

where, for α < 1, we have $\mathrm{Var}[z_2^{\ast }]<\mathrm{Var}[z_2]$. and therefore, Var[Δz*] < Var[Δz]. Therefore, inequality (18) tells us that the variance of the adjusted coherence estimator will have lower variance than the original coherence estimator.

Alternatively, because the thinning procedure removes spikes, information about λ is lost, and the variance of the thinned coherence estimator remains the same as in (12). Therefore, because the variance of the estimator is smaller for the adjusted coherence, we have the potential for improved power in the test for cross-condition differences compared to the unadjusted test, or the test using thinning. In other words, using rate adjustment we can detect smaller differences in spike-LFP coupling than without it using the same data. Alternatively, we can use fewer trials using the proposed rate adjustment to detect similar cross-condition differences in spike-LFP coupling than would be required using thinning. We demonstrate this effect in Sec. 3.4 where we study the effects of rate adjustment on the hypothesis testing procedure.

Limiting values

We may determine the end behavior of C_n*y and ${\sigma }_{z\ast }^2$ by examining the limits of these values as α → ∞ and α → 0. We find that, because ∂C_n*y/∂α ≥ 0, the maximum of C_n*y is achieved for

$$\begin{array}{c}\underset{\alpha \to \infty }{\lim }{C}_{n\ast y}(f)=C_{\mathit{ny}}(f){(1-\frac{{\mathrm{\Delta }}^2\mu }{S_{\mathit{nn}}(f)})}^{-1/2}\\ =C_{\mathrm{\lambda }y}(f).\end{array}$$ (19)

For the variance of z*, where α → ∞ we have

$$\begin{array}{l}\underset{\alpha \to \infty }{\lim }{\sigma }_{z\ast }^2=\frac{1}{2N}{\left(1-\frac{{\mathrm{\Delta }}^2\mu }{S_{\mathit{nn}}}\right)}^{-1}\left(\frac{1-C_{\mathit{ny}}^2}{1-C_{\mathit{ny}}^2{(1-\frac{{\mathrm{\Delta }}^2\mu }{S_{\mathit{nn}}})}^{-1}}\right)+\mathcal{O}(N^{-2})\\ =\frac{1}{2N}\left(\frac{1-C_{\mathit{ny}}^2}{1-C_{\mathit{ny}}^2-\frac{{\mathrm{\Delta }}^2\mu }{S_{\mathit{nn}}}}\right)+\mathcal{O}(N^{-2})\\ =\frac{1}{2N}{\left(1-\frac{{\mathrm{\Delta }}^2\mu }{S_{\mathit{nn}}(1-C_{\mathit{ny}}^2)}\right)}^{-1}+\mathcal{O}(N^{-2}).\end{array}$$ (20)

Alternatively, we find that ${\sigma }_{z\ast }^2\to 0$ and C_n*y → ∞ 0 as α → 0. This is an intuitively appealing result when we consider that the coherence should decease as the rate of coherent spiking decreases. Therefore, we should become more certain that the coherence is going zero as μ* = αμ → 0. In contrast, as α → ∞, both the coherence estimator and its variance are maximized. Although this limit does not make sense as an observable process (infinite spike rate), it represents an upper bound on both the variability due to spiking and on the quality of inference we can draw about λ from the realized spiking process.

Sensitivity to C_ny

We now consider the impact on the adjusted sample variance due to the spike-field coherence itself. We note that the sample variance of z given by (14) is approximately independent of C_ny when α = 1 (i.e. when no adjustment is made). However, when a adjustment is made, ${\sigma }_z^2$ and C_ny are no longer independent, since C_ny appears in the expression for ${\sigma }_z^2$ in (14). The rate at which ${\sigma }_z^2$ changes with respect to C_ny is given by

$$\frac{\partial {\sigma }_{z\ast }^2}{\partial C_{\mathit{ny}}}=2{\sigma }_{z\ast }^2{C}_{\mathit{ny}}\left(\frac{{\kappa }^2}{1-{\kappa }^2{C}_{\mathit{ny}}^2}-\frac{1}{1-C_{\mathit{ny}}^2}\right).$$ (21)

Since ${\sigma }_z^2$, C_ny > 0, the sign of (21) depends on the sign of the quantity in parentheses. If we restrict ourselves to the case where κ < 1, which is always the case when α < 1, then we find immediately that ${\kappa }^2-{\kappa }^2{C}_{\mathit{ny}}^2<1-{\kappa }^2{C}_{\mathit{ny}}^2$, which we can rearrange to obtain

$$\frac{{\kappa }^2}{1-{\kappa }^2{C}_{\mathit{ny}}^2}<\frac{1}{1-C_{\mathit{ny}}^2},$$

and therefore, $\partial {\sigma }_{z\ast }^2/\partial C_{\mathit{ny}}<0$, for κ < 1. Thus, the variance of the adjusted estimator decreases as the value of the coherence for the rate-adjusted condition increases. However, for mild adjustments (κ ≈ 1) we have ${\kappa }^2/(1-{\kappa }^2{C}_{\mathit{ny}}^2)\approx 1/(1-C_{\mathit{ny}}^2)$, and therefore, $\partial {\sigma }_{z\ast }^2/\partial C_{\mathit{ny}}\approx 0$. Thus, the influence of C_ny on the variance of the rate-adjusted estimator may be negligible for small adjustments.

2.4. Estimation of α

The estimation of α is straightforward in the WSS-DSP case. Suppose dn₁(t) and dn₂(t) are independent WSS-DSP, with rates μ₁ = μ and μ₂ = αμ, respectively. The corresponding counting processes, n₁(t) and n₂(t) are therefore conditionally Poisson with parameters μ₁ = μt and μ₂ = αμt. If $\{n_{1,1},\dots ,n_{1,N_1}\}$ and $\{n_{2,1},\dots ,n_{2,N_2}\}$ are observations of n₁(t) and n₂(t) then, as shown in Appendix C, the maximum likelihood estimator (MLE) of α is given by

$${\widehat{\alpha }}_{\mathit{MLE}}=\frac{N_1{\displaystyle {\sum }_{i=1}^{N_2}{n}_{2,i}}}{N_2{\displaystyle {\sum }_{j=1}^{N_1}{n}_{1,j}}},$$

which is simply ${\widehat{\alpha }}_{\mathit{MLE}}={\widehat{\mu }}_{2,\mathit{MLE}}/{\widehat{\mu }}_{1,\mathit{MLE}}$, where ${\widehat{\mu }}_{1,\mathit{MLE}}$ and ${\widehat{\mu }}_{2,\mathit{MLE}}$ are the MLEs of μ₁ and μ₂.

A similar estimator can be used in the case of a moving window estimate of α where, on a time scale where variations in μ(t) are small, we can consider dn₁(t) and dn₂(t) to be approximately independent WSS-DSP.

3. Simulations

In this section we make use of simulated sample data to illustrate the application of the adjusted spike-field coherence, evaluate the performance of the adjusted spike field coherence estimator, and examine the accuracy of the approximate sampling distribution developed in Section 2.3. In each of four separate simulation studies, a field y(t) will be simulated by a second-order autregressive (AR(2)) process. The conditional intensity of the point process will be a log-linear function of the field such that

$$\mathrm{\lambda }(t)=\eta e^y,$$ (22)

in order to enforce its strict non-negativity. The resulting mean spike rates were specified through manipulation of the parameter η.

Spike times u_k were simulated sequentially at a sampling rate of 1000 Hz by the time rescaling method, wherein a exponential random variable τ_k ~ Exp(1) was drawn for spike k = 1, 2, …, and u_k was found by solving the equation ${\tau }_k={\displaystyle {\int }_{u_{k-1}}^{u_k}\mathrm{\lambda }(t)\mathit{dt}}$, where λ(t) is given by 22. Trial-averaged multitaper estimates of the spectra were generated with K = 2WT − 1 tapers, where WT = 5 was the time-bandwidth parameter. The multitaper coherence, and jackknife 95% confidence intervals (95%CIs), were calculated using the Chronux¹ (Mitra and Bokil, 2007) software package for Matlab (The Mathworks, Natick, MA). Chronux functions were modified for the calculation of the adjusted coherence and adjusted coherence confidence intervals. A representative realization of the simulated LFP and resulting spike train are given in Figure 1, along with the spike spectrum and coherence estimates.

Figure 1.

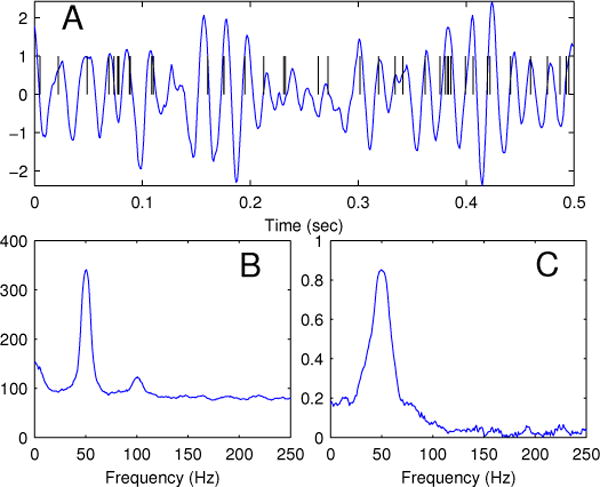
A: Representative realization of AR(2) LFP and corresponding spike times at μ = 80 spikes per second. B: Sample multitaper LFP spectral density for NW = 5, 9 tapers, and 100 trials. C: Corresponding multitaper estimate of the spike-LFP coherence.

3.1. Rate adjustment accuracy

A LFP y(t) with a single, dominant frequency was simulated by a AR(2) process with parameters (−1.911, 0.95). With a trial period of T = 1 second, realizations of spike times u₁, u₂, ⋯ < T were simulated for N = 100 trials at μ = {10, 20, …, 100} spikes per second (sps). Simulations conducted this way generate spike-field associations in which spike-field coherence C_ny will vary with μ, but the intensity-field coherence C_λy is the same for all rates. Coherences for all rates were then rate-adjusted to a variety of rates (μ* = 20, 40, 60, and 80 sps) according to (10). Adjusted coherence at peak spectral power was compared to the peak unadjusted coherence at each rate.

Estimates of |C_ny| and | $C_{\mathit{ny}}^{\ast }$| at peak spectral power, for each μ, are plotted in Figure 2 for different values of the target rate μ* = αμ. In each panel of Figure 2 we choose a different μ* (indicated by vertical line) and adjust all |C_ny|estimates to that spike rate using (10). Blue lines indicate the mean and 95% jackknife confidence interval for the unadjusted |C_ny| at each rate. We note that the unadjusted coherence increases with rate, as expected for increases in α (although this would not be the case if the rate had increased through β). Red lines indicate the mean and 95% jackknife confidence interval for | ${\widehat{C}}_{\mathit{ny}}^{\ast }$|. Horizontal lines in each panel indicate the sample unadjusted C_ny at the indicated rate, which is approximately the coherence we expect if the rate adjustment was accurate. We find that the adjusted estimates, regardless of the degree of rate adjustment, are not significantly different from the unadjusted estimates at the target rate, indicating that the rate adjustment is accurate to within the statistical precision of the presented sample.

Figure 2.

Mean (−) and jackknife 95% confidence interval (- -) for the standard (blue) and adjusted (red) spike-field coherence for simulated spike trains at different target rates μ*, but constant C_λy. The unadjusted coherence increases as the rate increases through the parameter α. Each panel displays the adjustment to a different μ* (indicated by vertical lines). Horizontal lines give the mean for the unadjusted coherence at μ = μ*.

3.2. Distribution of estimates

In this section we examine the validity of the Gaussian approximation to the sampling distribution of z, and examine the accuracy of the approximate cumulants of that distribution presented in Section 2.3. One-thousand trial-averaged estimates of the coherence were generated under the conditions given in Section 3.1 to estimate the sampling distributions of $z={\tanh }^{-1}|{\widehat{C}}_{\mathit{ny}}|$ for μ₁ = 40 sps and μ₂ = 60 sps, as well as $z\ast ={\tanh }^{-1}|{\widehat{C}}_{\mathit{ny}}^{\ast }|$ for μ₂, adjusted to μ* = μ₁.

Sample histograms, corresponding best-fitting normal distributions of sample estimates, as well as the theoretical distributions defined by Fisher transform of (10) and (14) are shown in Figure 3. The sampling distributions were not significantly different from normal (p > 0.4 for all tests) by the 1-sample Kolmogorov-Smirnov test. Sample estimates, and theoretical values, for the mean and standard deviation of the sampling distribution of z, are displayed in Table 1.

Figure 3.

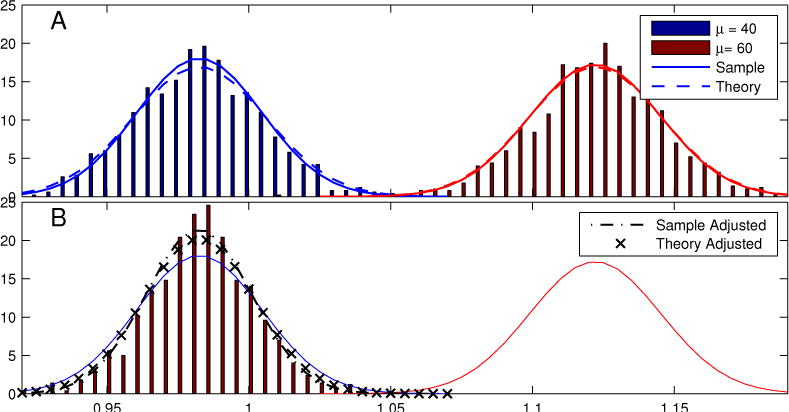
A: Sample histograms for 1000 realizations of $z={\tanh }^{-1}({\widehat{C}}_{\mathit{ny}})$, the Fisher-transformed spike field coherence, at μ₁ = 40 (blue) and μ₂ = 60 (red) with N = 100. Normal distributions are shown corresponding to the ensemble sample (−) and theoretical (- -) variance (based on (12)). B: Sample histogram and normal distributions of the higher rate condition, adjusted to the spike rate of the low-rate condition. Corresponding Gaussian distributions for the sample (− ·) and theoretical (×) distributions with adjusted mean and variance given by (13) and (14), are similar.

Table 1.

Example rate adjusted estimates at two rates with fixed C_λy. Estimates of sample mean of z = tanh⁻¹ |C_ny|, sample standard deviation ${\widehat{\sigma }}_z$, and theoretical standard deviation ${\widehat{\sigma }}_z$, for 1000 trial-averaged estimates with 100 trials (estimated by multitaper estimator with 9 tapers). The higher rate condition was adjusted to match the low-rate condition (μ₂ → μ₁).

Condition	z	${\widehat{\sigma }}_z$	${\widehat{\sigma }}_z$
μ1 = 40	0.983	0.0221	0.0236
μ2 = 60	1.122	0.0231	0.0236
μ2 → μ1	0.982	0.0186	0.0197

From Table 1 and Figure 3 we see that the mean estimates of z for the μ₁ = 40 and μ₂ = 60 conditions are significantly different, in spite of the fact that these conditions have the same C_λy. We also see that the Fisher estimates of the standard deviation ( ${\tilde{\sigma }}_z$) from (12) are quite accurate (error is less than 7% between ${\tilde{\sigma }}_z$ and ${\widehat{\sigma }}_z$). When we adjust z from the higher to the lower spike rate condition (Table 1, μ₂ → μ₁), we find that the mean of the adjusted z₂ is not significantly different from z₁. As predicted in (18), we find the sample standard deviation of the rate-adjusted estimate to be smaller than that of the un-adjusted conditions. The theoretical values for the adjusted sample standard deviation are accurate as well (less than 6% error relative to sample estimate), if not slightly conservative (Figure 3B).

3.3. Comparison with “thinning”

To demonstrate the equivalence between the proposed method and the thinning method, we simulated N = 100 trials with μ₁ = 60 and μ₂ = 40 and estimated the unadjusted coherence, and both the adjusted and thinned coherence for μ₁ → μ₂. Trial-averaged estimates are shown in Figure 4.

Figure 4.

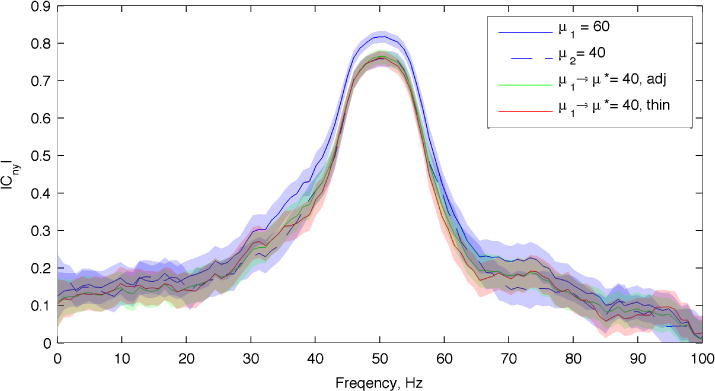
Comparison of the proposed rate adjustment with the thinning method using simulated data. Both conditions had the same C_λy, but different spike rates. Sample sizes for both conditions was N = 100. Shaded areas are jackknife 95% confidence intervals. Difference in C_ny between adjusted, thinned, and low-rate conditions are non-significant (p > .05).

The thinned, adjusted, and μ₂ estimates are all significantly different from the unadjusted μ₁ condition for a broad range of frequencies (~20–0 Hz). Conversely, both the thinned and adjusted coherences for the μ₁ condition, and the unadjusted coherence for μ₂ are statistically identical at all frequencies. Although the thinning method and proposed procedure perform similarly in this example, we show in the next sub-section an important advantage of the proposed adjustment method.

3.4. Detection of cross-condition differences

In this section, we compare the properties of the hypothesis testing procedure for cross-condition comparisons of C_ny, as a proxy for C_λy, between the proposed adjusted estimator, the thinning procedure, and the unadjusted estimator. As is most often the case for neuroscience applications, when we do not observe C_λy directly, a scientist may be inclined to simply test for differences in C_ny and assume that any differences are due to changes in C_λy. This practice precludes the proper specification of the probability of false alarm based upon the unadjusted C_ny because C_ny depends upon the average spike rate and is not the intensity field coherence. To illustrate how badly this assumption can go awry we examined three scenarios which highlight the effect that the proposed rate adjustment has on ROC.

The ROC curve is a mapping of the detection (of differences) threshold onto both the probability of a detection, given that there is in fact a difference (true positive), and the probability of a detection, given that there is in fact no difference (false positive). If the curve is unity then the detection performance is no better than guessing. The further the curve is above the diagonal, the better the performance of the detection procedure. The overall performance is often measured by the area under the ROC curve (AUC), which is .5 for guessing, and 1 for a perfect detector (Zou et al., 2007).

For each of two experimental conditions per scenario, we specified μ and C_λy, and then calculated C_ny, using (2), (5) and a sample value of a simulated S_nn from the above simulations, at peak power. The scenarios analyzed were

• (A)μ₁ < μ₂, C_λy1 < C_λy2
• (B)μ₁ > μ₂, C_λy1 > C_λy2
• (C)μ₁ = μ₂, C_λy1 = C_λy2

When the spike rates were different, we set μ1 = 10 and μ2 = 40 spikes per second. Under the alternative hypothesis we set the smaller intensity-field coherence to C_λy = .2 and the larger to C_λy = .3. We will show that adjustment procedures make the test properties invariant to the experimental scenario, where using the proposed adjustment procedure leads to a larger AUC compared to the test using the estimate obtained by the thinning procedure.

Type-I and type-II errors for the standard test

When we consider the consequences of rate-dependence for the standard procedure (testing for cross-condition differences in C_λy via differences in C_ny), we observe a serious problem with the accuracy of the test. We find that under scenarios (A) and (B), for the unadjusted estimator, the experimenter does not have control over the type-I error probability, precluding the possibility of accurately specifying the detection performance. To illustrate this, consider scenario (A). Due to the differences in rate, we will observe C_ny2 > C_ny1 even when C_λy2 = C_λy1. However, because the standard procedure is to test for differences in C_ny, the assumed null distribution for Δz has zero mean even though this distribution under H₀: C_λy2 = C_λy1, has a mean that is nonzero, making the true type-I error larger than predicted. For example, for a type-I error probability of .05 for the test C_ny1 = C_ny2, with N = 100, the type-I error probability for the test C_λy1 = C_λy2 using the unadjusted Δz is .13, meaning we will have nearly three times as many false positives as we would have otherwise tolerated. This discrepancy is illustrated in Fig. 5 for various values of the sample size and rate difference.

Figure 5.

Discrepancy between real and assumed type-I error rate for the test of cross-condition comparisons in spike-field coherence. When C_ny is used as a proxy for C_λy, then the null distribution should have non-zero mean, even while the standard practice is to assume zero mean. The x-axis indicates the type-I error rate that the experimenter thinks she is using when assuming zero-mean. The y-axis indicates the type-I error that is actually achieved for the given threshold. Solid line indicates the error rate for the adjusted test.

Figure 5 shows the relationship between the assumed type-I error rate (using the asymptotic distributions) for the test where H₀: C_ny1 = C_ny2 is used as a proxy for H₀: C_λy1 = C_λy2 for scenario (A). The black, solid line indicates an accurate type-I error rate, such as when the rate-adjusted estimator is used (i.e. the test using the rate-adjusted estimator always has the correct type-I error rate). The true type-I error rate is always larger than the assumed type-I error rate and the inaccuracy is exacerbated with increasing sample size (due to small variance) and increasing spike rate (due to differences in means). Type-II error probability can also be effected by rate differences by a similar argument.

Since the type-I error cannot be accurately controlled for the unadjusted estimators we will proceed with our ROC analysis using only the test with equal or adjusted rates.

ROC and AUC for the adjusted test

In contrast to the standard test for cross-condition differences in C_ny, the adjusted or thinned estimators accurately control type-I error rate. We defined the asymptotic distributions of the estimator of Δz, the difference in the Fisher-transformed spike-field coherence, as ${\mathrm{\Delta }}_z\sim \mathcal{N}(\mathrm{atanh}(C_{ny1})-\mathrm{atanh}(C_{ny2}),{\sigma }_{z1}^2+{\sigma }_{z2\ast }^2)$, where ${\sigma }_{z1}^2$ and ${\sigma }_{z2\ast }^2$ were determined from (14) with sample size N = 100. We then calculated the ROC curve for each scenario where spike rates are adjusted by the proposed procedure and where spike rates are adjusted by thinning. The results are summarized in Fig. 6.

Figure 6.

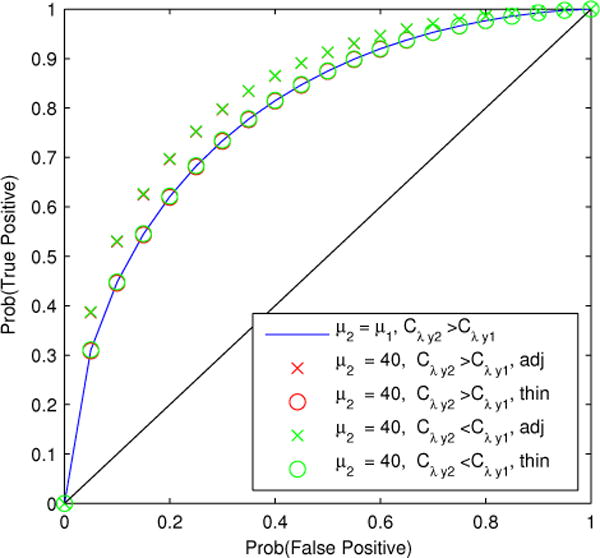
Receiver operating characteristics for the test for cross-condition differences in spike-field coherence under various conditions. Smaller rate is μ = 10 sps. Larger intensity-field coherence is C_λy = .3. Smaller intensity-field coherence is C_λy = .1. Because the proposed estimator has smaller variance than the unadjusted, or thinned estimator, the test using the proposed rate-adjusted estimator (×) always has larger AUC than the test using the thinned estimator, or the unadjusted condition with equal spike rates. Red markers are covered by green markers, since thinning and adjustment result is consistent testing properties across experimental outcomes.

Figure 6 shows in blue the ROC curve for the test of cross condition differences in z for scenario (C), where the spike rates are equal to the lower rate (μ₁ = μ₂ = 10 sps, AUC = .792). The thinning procedure maintains the test accuracy with that of the equal rates condition in the case of both scenario (A) (‘o’, AUC = .791) and scenario (B) (AUC = .793). However, the proposed adjustment procedure has improved AUC compared to the equal-rates condition, or thinning for both conditions (‘×, scenario (A), AUC = .831; scenario (B)), AUC = .832). Therefore, for all scenarios with unequal rates, rate adjustment makes the AUC of the test of cross-condition differences in coherence independent of the spike rates and the proposed adjustment has a consistently higher AUC than the thinning procedure.

4. Discussion

Prior work has indicated that the unique properties of point processes (as opposed to continuous-valued stochastic processes) must be accounted for in the analysis of rhythmic spike-field coupling (Zeitler et al., 2006; Gregoriou et al., 2009; Mitchell et al., 2009; Grasse and Moxon, 2010; Vinck et al., 2010, 2011; Lepage et al., 2011, 2013). In particular, it can be proven that the magnitude of the coherence between spikes and LFPs is dependent on the mean rate of the point process (Lepage et al., 2011). This dependence can be expressed as one part of a decomposition of the spike-field coherence (5), where one factor represents the variability in the tuning of the spiking process with respect to the field rhythm (C_λy), and the other is due to variability due to spiking only.

In the present work, we make use of the model (6) with β = 0, to examine hypothetical changes in C_ny due to changes in spike rate, while C_λy remains fixed, since C_λy is invariant to affine transformations. Thus, by adjusting C_ny in a fashion suggested by relation (6), we obtain a de facto estimator for C_λy, and can test for cross-condition differences in C_λy, without estimating C_λy directly.

The results of this paper show that the proposed estimator provides a conceptually equivalent correction to the rate adjustment of the thinning procedure described previously (Gregoriou et al., 2009; Mitchell et al., 2009) (Sec. 2.1) but does not require repeated Monte Carlo trials and has improved ROC properties for the detection of cross-condition differences. We have shown that, although lower variance is achieved by decreasing the rate via the parameter α, the rate adjustment procedure is valid for upward or downward adjustment of the rate, and it is accurate over a wide range of rates (Figure 2).

The simulation experiments in this study were restricted to be WSS and Poisson, representing the signal domain used to develop the rate-adjustment theory. Therefore, it is expected that the simulation experiments presented here would be successful and consistent with the theoretical results. However, real neuronal spike trains display history dependence (non-Poisson) and stimulus-locked variations (non-stationarity) that could influence the accuracy of the procedure. Therefore, it is still to be determined how the procedure will respond to various types of model misspecification. However, these same assumptions underlie the thinning procedure (which subtracts off time-varying mean rate, leaving only the induced activity), which is used in current practice. We are currently exploring the implications of non-stationarity and non-Poisson effects on the proposed procedure.

The properties of the rate-adjusted estimator developed in Sections 2.3 and 3.4 were developed exclusively under the assumption that β = 0 under the rate adjustment model (6). Therefore, the test and estimator properties may be quite different when β is estimated simultaneously. However, as we have shown, the procedure proposed in this paper is consistent with current practice (Gregoriou et al., 2009; Mitchell et al., 2009) and provides improved performance over existing methods (Figures 5 and 6). We have also not determined how estimation uncertainty in the rate parameter α influences the sampling distribution of the adjusted estimator. However, based on the accuracy of the approximate and simulated sampling distributions (Figure 3, Table 1), the influence appears to be negligible.

We should note that it is possible to estimate C_λy, by using (19). However, we can see from (20) that, since this approach effectively takes the asymptotic limit as α → ∞, the variance is maximized under these conditions. Therefore, the estimation of C_λy from the spiking statistics is suboptimal. In principle, it should be possible to identify the optimal test of cross-condition deferences using the coherence, in terms of AUC, by maximizing AUC with respect to a rate parameter α for each experimental condition.

In addition to the thinning procedure, alternative methods have been proposed to address the issue of rate dependence in nonparametric spectral estimators (as opposed to modeling approaches such as that of Lepage et al. (2013)) of rhythmic spike-LFP coupling. Grasse and Moxon (2010) and Vinck et al. (2011) have proposed rate correction techniques to spectral measures of spike-field synchrony but the measures used in these papers were not the standard spike-field coherence (as described by Bartlett (1963) and Jarvis and Mitra (2001)) and therefore have different interpretations and sampling properties. The pairwise phase consistency (Vinck et al., 2010) is a method that circumvents the rate-dependence problem via all-to-all pairwise comparisons between the LFP phases for every spike. However, correcting bias due to the number of trials may result in increased estimator variance (Vinck et al., 2011). Future work should include a thorough evaluation of the relative pros and cons of the available methods.

The sample coherence is classically established to be (asymptotically) the MLE for the correlation between Fourier coefficients of weak-sense stationary processes (Bartlett, 1963; Hannan, 1970; Brillinger, 1982; Kay, 1993) and as such it has a long history of theoretical development. By definition therefore, the intensity-field coherence C_λy is the correlation between Fourier representations of the spiking probability and the LFP, making it a natural quantity for the analysis of rhythmic spike-field coupling. We have taken advantage of this interpretation of the coherence by leveraging well-known properties of the sample correlation in the development of the proposed estimator and the analysis of its properties.

4.1. Control of type-I error

A critical issue associated with the rate-dependence of C_ny is the issue of setting type-I error rates (Section 3.4). If the investigator intends to test for differences in C_ny, then there is no issue. However, if the investigator intends to test for differences in C_λy by testing for differences in C_ny, then the investigator cannot test for these differences using the unadjusted C_ny’s, because the null distribution has non-zero mean when spike rates differ across conditions. As shown in Fig. 5, the accuracy of the test using unadjusted estimators actually decreases with sample size and spike rate, in both cases making the probability of false positives larger when the null distribution is miss-specified. Since the variance of the estimator of the unadjusted z (12) is not dependent on rate, but decreases with sample size, an increase in sample size decreases the variance of the estimator while holding rate bias constant. Therefore, the relative size of the rate bias is increased with respect to the variance of the difference estimator, increasing the size of the test statistic. Conversely, increased differences in spike rates can increase the bias while holding the variance constant, again increasing the size of the test statistic. Therefore, as we showed in Section 3.4, rate adjustment (either by thinning or by the proposed procedure) is essential for controlling type-I error rates.

4.2. Accuracy of approximate moments

Figure 3 and Table 1 show that the theoretical variance for the adjusted coherence estimator is slightly larger than that of the estimated variance from the sample. Overestimation of the theoretical variance of the conventional coherence has been reported previously (Jacobsen, 1993) and is likely due to truncation of terms in the Taylor series.

Empirical studies have shown that (12) is a fairly accurate estimate for the variance for large coherences (>0.4) (Enochson and Goodman, 1965). However, a problem begins to occur as the coherence becomes small, where the lower 95% confidence limit for the Gaussian approximation of z begins to cross zero. Benignus (1969) has suggested an empirical correction to this problem for very small degrees of freedom. However, this does not appear to be a problem for moderate degrees of freedom which can be reasonably expected in neuroscience applications and/or where the degrees of freedom can be appreciably increased by use of the multitaper estimator.

We should emphasize that the sample variance described in (14) is not intended to be a replacement for bootstrap / jackknife estimators of the variance often used in neuroscience applications (Thompson and Chave, 1991; Jarvis and Mitra, 2001). While we believe that (14) could, in principle, be used as a variance estimator, the primary purpose of deriving this quantity was to make predictions about how the sample variance responds to the adjustment procedure, allowing us to identify a decrease in sample variance with rate adjustment, where the decrease results in an improvement in test performance. In this respect, Fig. 3 shows the result to have suitable accuracy.

Although the variance derived from the multiple correlation seems appropriate, the bias derived from the theoretical distribution may be less accurate (Enochson and Goodman, 1965), particularly for smaller coherences. Some studies have presented alternative expressions for the bias of the coherence (Benignus, 1969; Carter et al., 1973), but all have shown the coherence estimate to be asymptotically unbiased where the bias is $\mathcal{O}(N^{-1})$. Furthermore, Nuttall and Carter (1976) showed in simulations that bias-corrected estimators have larger mean-squared error than the uncorrected estimator for degrees of freedom N > 8. The bias estimates for all of the coherences calculated in the present study via (13) have been on the order of 1% of the value of C_ny.

Leakage bias also appears to be negligible. Jacobsen (1993) has shown that leakage bias is negligibly small for conventional coherence estimates for bivariate AR(2) processes. This already small leakage bias is likely to be further mitigated by use of the multitaper estimator (Bronez, 1992; Percival and Walden, 1993). We did not observe evidence for appreciable leakage bias in the present study.

5. Conclusions

The proposed rate adjustment to the spike-field coherence estimator accurately modifies the spike-field coherence to reflect any predicted rate, given the rate difference model (6), (Figure 2), where in this work we assumed β = 0, consistent with the thinning procedure. We showed that the distribution of the inverse hyperbolic tangent of the rate-adjusted estimator is approximately Gaussian and that its sampling variance will decrease with adjustment to a lower spike rates (Figure 3, Table 1). We can exploit this property to provide a test of cross-condition differences in C_λy with improved detection properties compared to that of the thinned estimator. We also demonstrated that rate adjustment is necessary to be able to accurately control the type-I error rate of the test.

We believe that these properties indicate that the proposed rate-adjusted coherence estimator is a powerful front-line descriptive statistic to characterize rhythmic spike-LFP coupling.

Appendix A. Adjusted coherence sampling distribution

Let ( ${\widehat{S}}_{\mathit{nn}},{\widehat{S}}_{\mathit{yy}},\mathcal{R}({\widehat{S}}_{\mathit{ny}}),\mathcal{I}({\widehat{S}}_{\mathit{ny}})$), be direct sample estimators of the spike, field, and cross spectra, respectively, of a weak-sense stationary process where $\mathcal{R}$, and $\mathcal{I}$ denote the real and complex parts. For this section, we will denote the magnitude squared coherence

$$\mathrm{\gamma }\equiv {|C_{\mathit{ny}}|}^2.$$

For multi taper estimators, spectral estimates are given by

$${\widehat{S}}_{\mathit{ij}}=\frac{1}{\nu }{\displaystyle \sum _{\kappa =0}^{\nu -1}{\widehat{S}}_{\mathit{ij},k}}$$

where, i,j=(n,y), and ν is the degrees of freedom of the estimator. If, following the notation of Goodman (1957), we let

$$\begin{array}{l}a\prime =\frac{\nu }{\delta }\frac{{\widehat{S}}_{\mathit{nn}}}{2S_{\mathit{nn}}}\\ b\prime =\frac{\nu }{\delta }\frac{{\widehat{S}}_{\mathit{yy}}}{2S_{\mathit{yy}}}\\ c\prime =\frac{\nu }{\delta }\frac{\mathcal{R}({\widehat{S}}_{\mathit{ny}})}{2\sqrt{S_{\mathit{nn}}{S}_{\mathit{yy}}}}\\ d\prime =\frac{\nu }{\delta }\frac{\mathcal{I}({\widehat{S}}_{\mathit{ny}})}{2\sqrt{S_{\mathit{nn}}{S}_{\mathit{yy}}}},\end{array}$$

where δ = 1 − γ², then (a′, b′, c′, d′) will be (asymptotically) jointly distributed as a unit complex Wishart distribution with ν degrees of freedom. Noting that

$$\widehat{\mathrm{\gamma }}=\frac{{(c\prime )}^2+{(d\prime )}^2}{a\prime b\prime },\widehat{\varphi }=\arg \left\{\frac{c\prime +\mathit{id}\prime }{a\prime b\prime }\right\},$$

the joint distribution of $(a\prime ,b\prime ,\widehat{\mathrm{\gamma }},\widehat{\varphi })$ is given by (equation (4.52),(Goodman, 1957))

$$p(a\prime ,b\prime ,\widehat{\mathrm{\gamma }},\widehat{\varphi })-\frac{{\delta }^{\nu }{(a\prime b\prime )}^{\nu -1}\widehat{\mathrm{\gamma }}}{\pi \mathrm{\Gamma }(\nu )\mathrm{\Gamma }(\nu -1)}{(1-{\widehat{\mathrm{\gamma }}}^2)}^{\nu -2}\times \exp [-a\prime -b\prime -2\widehat{\mathrm{\gamma }}\sqrt{a\prime b\prime }\mathrm{\gamma }\cos (\varphi -{\varphi }_0)].$$ (A.1)

In the next section we will show how (A.1) can be used to provide the sampling distribution for the adjusted spike-field coherence estimator in (10). From (10) it can be shown that

$$\begin{array}{c}\widehat{\mathrm{\gamma }}={\left|\frac{{\widehat{S}}_{\mathit{ny}}}{{\widehat{S}}_{\mathit{nn}}{\widehat{S}}_{\mathit{yy}}}\right|}^2\\ ={\widehat{\mathrm{\gamma }}}^{\ast }\frac{a^{\prime \ast }}{a\prime },\end{array}$$ (A.2)

where

$$\begin{array}{l}{a}^{\prime \ast }=\frac{\nu }{2\delta S_{\mathit{nn}}}\left(S_{\mathit{nn}}+\mu (1/\alpha -1)\right)\\ =a\prime +\frac{n\mu (1/\alpha -1)}{2S_{\mathit{nn}}}.\end{array}$$ (A.3)

We may use (10) and (A.3) to transform (A.1) to the distribution for $(a^{\prime \ast },b\prime ,{\widehat{\mathrm{\gamma }}}^{\ast },\widehat{\varphi })$. If we define the parameter

$$\xi \equiv \frac{\nu \mu (1/\alpha -1)}{2S_{\mathit{nn}}},$$

then

$$\widehat{\mathrm{\gamma }}={\widehat{\mathrm{\gamma }}}^{\ast }{\left(1-\frac{\xi }{a^{\prime \ast }}\right)}^{-1},$$

and the Jacobian of the transformation is given by

$$J={\left(1-\frac{\xi }{a^{\prime \ast }}\right)}^{-1}.$$

The resulting joint distribution is

$$\begin{array}{l}p(a^{\prime \ast },b\prime ,{\widehat{\mathrm{\gamma }}}^{\ast },\widehat{\varphi })=\frac{{\delta }^{\nu }{((a^{\prime \ast }-\xi )b\prime )}^{\nu -1}{\widehat{\mathrm{\gamma }}}^{\ast }}{\pi \mathrm{\Gamma }(\nu )\mathrm{\Gamma }(\nu -1)}{\left(1-\frac{\xi }{a^{\prime \ast }}\right)}^{-2}{\left(1-{\widehat{\mathrm{\gamma }}}^{\ast 2}{\left(1-\frac{\xi }{a^{\prime \ast }}\right)}^2\right)}^{\nu -2}\\ \times \exp \left[-(a^{\prime \ast }-\xi )-b\prime +2{\widehat{\mathrm{\gamma }}}^{\ast }\left(1-\frac{\xi }{a^{\prime \ast }}\right)\sqrt{a^{\prime \ast }b\prime }\mathrm{\gamma }\cos (\varphi -{\varphi }_0)\right]\end{array}$$ (A.4)

Integrating out ϕ leaves

$$\begin{array}{c}p(a^{\prime \ast },b\prime ,{\widehat{\mathrm{\gamma }}}^{\ast })=\frac{2{\delta }^{\nu }{((a^{\prime \ast }-\xi )b\prime )}^{\nu -1}{\widehat{\mathrm{\gamma }}}^{\ast }}{\mathrm{\Gamma }(\nu )\mathrm{\Gamma }(\nu -1)}{\left(1-\frac{\xi }{a^{\prime \ast }}\right)}^{-2}{\left(1-{\widehat{\mathrm{\gamma }}}^{\ast 2}{\left(1-\frac{\xi }{a^{\prime \ast }}\right)}^{-2}\right)}^{\nu -2}\\ \times {\displaystyle \sum _{k=0}^{\infty }\frac{{\left[{\widehat{\mathrm{\gamma }}}^{\ast }{\left(1-\frac{\xi }{a^{\prime \ast }}\right)}^{-1}{((a^{\prime \ast }-\xi )b\prime )}^{1/2}\mathrm{\gamma }\right]}^{2k}{e}^{-(a^{\prime \ast }-\xi )b\prime }}{{\mathrm{\Gamma }}^2(k+1)}.}\end{array}$$ (A.5)

We find the marginal distribution of a′* and ${\widehat{\mathrm{\gamma }}}^{\ast }$ by integrating (A.5) over b′,

$$\begin{array}{c}p(a^{\prime \ast },{\widehat{\mathrm{\gamma }}}^{\ast })=\frac{2{\delta }^{\nu }{(a^{\prime \ast }-\xi )}^{\nu -1}{\widehat{\mathrm{\gamma }}}^{\ast }}{\mathrm{\Gamma }(\nu )\mathrm{\Gamma }(\nu -1)}{\left(1-\frac{\xi }{a^{\prime \ast }}\right)}^{-2}{\left(1-{\widehat{\mathrm{\gamma }}}^{\ast 2}{\left(1-\frac{\xi }{a^{\prime \ast }}\right)}^{-2}\right)}^{\nu -2}\\ \times {\displaystyle \sum _{k=0}^{\infty }\frac{{\left[{\widehat{\mathrm{\gamma }}}^{\ast }{\left(1-\frac{\xi }{a^{\prime \ast }}\right)}^{-1}{(a^{\prime \ast }-\xi )}^{1/2}\mathrm{\gamma }\right]}^{2k}{e}^{-(a^{\prime \ast }-\xi )}}{{\mathrm{\Gamma }}^2(k+1)}\mathrm{\Gamma }(\nu +k),}\end{array}$$ (A.6)

where $\mathrm{\Gamma }(\nu +k)={\displaystyle {\int }_0^{\infty }{(b\prime )}^{\nu +k-1}{e}^{-b\prime }\mathit{db}\prime }$ is the gamma function.

From the binomial theorem, for ν ≥ 2, we note that,

$${\left(1-{\widehat{\mathrm{\gamma }}}^{\ast 2}{\left(1-\frac{\xi }{a^{\prime \ast }}\right)}^2\right)}^{\nu -2}={\displaystyle \sum _{j=0}^{\nu -2}\left(\begin{array}{c}\nu -2\\ j\end{array}\right){(-1)}^j{\left(\frac{{\widehat{\mathrm{\gamma }}}^{\ast }}{(1-\xi /a^{\prime \ast })}\right)}^{2j}}.$$ (A.7)

Substituting (A.7) into (A.6) gives

$$\begin{array}{c}p(a^{\prime \ast },{\widehat{\mathrm{\gamma }}}^{\ast })=\frac{2{\delta }^{\nu }{(a^{\prime \ast }-\xi )}^{\nu -1}{\widehat{\mathrm{\gamma }}}^{\ast }}{\mathrm{\Gamma }(\nu )\mathrm{\Gamma }(\nu -1)}\left({\displaystyle \sum _{j=0}^{\nu -2}\left(\begin{array}{c}\nu -2\\ j\end{array}\right){(-1)}^j{\widehat{\mathrm{\gamma }}}^{\ast 2j}{(1-\xi /a^{\prime \ast })}^{-2j-2}}\right)\\ \times {\displaystyle \sum _{k=0}^{\infty }\frac{{\left[{\widehat{\mathrm{\gamma }}}^{\ast }{\left(1-\frac{\xi }{a^{\prime \ast }}\right)}^{-1}{(a^{\prime \ast }-\xi )}^{1/2}\mathrm{\gamma })\right]}^{2k}{e}^{-(a^{\prime \ast }-\xi )}}{{\mathrm{\Gamma }}^2(k+1)}\mathrm{\Gamma }(\nu +k).}\end{array}$$ (A.8)

Distributing the sum over j in equation (A.8) across the sum over k,

$$\begin{array}{c}p(a^{\prime \ast },{\widehat{\mathrm{\gamma }}}^{\ast })=\frac{2{\delta }^{\nu }{\widehat{\mathrm{\gamma }}}^{\ast }}{\mathrm{\Gamma }(\nu )\mathrm{\Gamma }(\nu -1)}{\displaystyle \sum _{k=0}^{\infty }\frac{{({\widehat{\mathrm{\gamma }}}^{\ast }\mathrm{\gamma })}^{2k}{(a^{\prime \ast }-\xi )}^{\nu +k-1}{e}^{-(a^{\prime \ast }-\xi )}}{{\mathrm{\Gamma }}^2(k+1)}\mathrm{\Gamma }(\nu +k)}\\ \times {\displaystyle \sum _{j=0}^{\nu -2}\left(\begin{array}{c}\nu -2\\ j\end{array}\right){(-1)}^j{\widehat{\mathrm{\gamma }}}^{\ast 2j}{(1-\xi /a^{\prime \ast })}^{-2k-2j-2}}.\end{array}$$ (A.9)

Noting that

$$\begin{array}{l}{(a^{\prime \ast }-\xi )}^{\nu +k-1}{(1-\xi /a^{\prime \ast })}^{-2k-2j-2}=a^{\prime \ast \nu +k-1}{(1-\xi /a^{\prime \ast })}^{\nu -k-2j-3}\\ ={\displaystyle \sum _{m=0}^{\infty }\left(\begin{array}{c}\nu -k-2j-3\\ m\end{array}\right){(-\xi )}^m}{a}^{\prime \ast \nu -1-m},\end{array}$$

we can collect all terms with a′* and integrate to get the marginal distribution of ${\widehat{\mathrm{\gamma }}}^{\ast }$

$$\begin{array}{l}p({\widehat{\mathrm{\gamma }}}^{\ast })=\frac{2{\delta }^{\nu }{\widehat{\mathrm{\gamma }}}^{\ast }{e}^{\xi }}{\mathrm{\Gamma }(\nu )\mathrm{\Gamma }(\nu -1)}{\displaystyle \sum _{k=0}^{\infty }{\displaystyle \sum _{j=0}^{\nu -2}{\displaystyle \sum _{m=0}^{\infty }\frac{{({\widehat{\mathrm{\gamma }}}^{\ast }\mathrm{\gamma })}^{2k}\mathrm{\Gamma }(\nu +k)}{{\mathrm{\Gamma }}^2(k+1)}}}}\\ \times \left(\begin{array}{c}\nu -2\\ j\end{array}\right){(-1)}^j{\widehat{\mathrm{\gamma }}}^{\ast 2j}\left(\begin{array}{c}\nu +k-2j-3\\ m\end{array}\right){(-\xi )}^m(\nu -m,\xi ),\end{array}$$ (A.10)

where $\mathrm{\Gamma }(\nu -m,\xi )={\displaystyle {\int }_{\xi }^{\infty }{a}^{\prime \ast \nu -m-1}{e}^{-a^{\prime \ast }}{\mathit{da}}^{\prime \ast }}$ is the incomplete gamma function, such that, if the lower bound on a′ is 0 then, ξ is the lower bound for the integral over a′*.

For comparison, the sampling distribution of the conventional coherence $\widehat{\mathrm{\gamma }}$ is given in Goodman (1957) as

$$p(\widehat{\mathrm{\gamma }})=\frac{2{\delta }^{\nu }\widehat{\mathrm{\gamma }}}{\mathrm{\Gamma }(\nu )\mathrm{\Gamma }(\nu -1)}{(1-{\widehat{\mathrm{\gamma }}}^2)}^{\nu -2}{\displaystyle \sum _{k=0}^{\infty }\frac{{\widehat{\mathrm{\gamma }}}^{2k}{\mathrm{\gamma }}^{2k}(\nu +k)}{{\mathrm{\Gamma }}^2(k+1)}},$$ (A.11)

which would be equivalent to (A.10) if all terms over m were zero except for when m = 0, and ξ = 0.

For the pdf under the null hypothesis H₀: γ = 0, all terms in (A.10) become zero except where k = 0. The resulting pdf is given by

$$\begin{array}{l}p({\widehat{\mathrm{\gamma }}}^{\ast }){|}_{\mathrm{\gamma }=0}=\frac{2{\widehat{\mathrm{\gamma }}}^{\ast }}{\mathrm{\Gamma }(\nu -1)}{\displaystyle \sum _{j=0}^{\nu -2}{\displaystyle \sum _{m=0}^{\infty }\left(\begin{array}{c}\nu -2\\ j\end{array}\right){(-1)}^j{\widehat{\mathrm{\gamma }}}^{\ast 2j}}}\times \left(\begin{array}{c}\nu -2j-3\\ m\end{array}\right){(-\xi )}^m\mathrm{\Gamma }(\nu -m,\xi ).\end{array}$$

Appendix B. Bias and variance of the sample rate-adjusted coherence

In this section we will derive approximate expressions for the bias and variance of the proposed rate-adjusted spike-field coherence estimator. In order to find these cumulants, we will employ the Taylor-series approach described by Hotelling (1953). We will give only a summary of the steps here (Hotelling, 1953, see for details).

The essence of Hotelling’s strategy is to find a series of z − ζ, where ζ = tanh⁻¹ (C_ny) is the transformed population coherence, as a function of increasing powers of ${\widehat{C}}_{\mathit{ny}}-C_{\mathit{ny}}$. We may then find the moments of z − ζ as a series of the moments of ${\widehat{C}}_{\mathit{ny}}-C_{\mathit{ny}}$. Here, we will treat κ as a known constant. We will suppress the | · | bars, and explicit frequency dependence for ease of notation, but it should be understood that for the remainder of this section all references to the coherences are implicitly made regarding the magnitude of the coherence, and that all estimates are dependent on the frequency at which they are evaluated.

Although the moments of ${\widehat{C}}_{\mathit{ny}}$ were first found in the so called ‘Cooperative study’ (Soper et al., 1916), Hotelling (1953) was the first to show that these moments could be expressed as a series in powers of 1/N. The first of these two moments are given by

$$\begin{array}{l}\mathrm{E}[{\widehat{C}}_{\mathit{ny}}-C_{\mathit{ny}}]=(1-C_{\mathit{ny}}^2)\left(-\frac{C_{\mathit{ny}}}{2N}+\mathcal{O}(N^{-2})\right)\\ \mathrm{E}[{({\widehat{C}}_{\mathit{ny}}-C_{\mathit{ny}})}^2]={(1-C_{\mathit{ny}}^2)}^2\left(\frac{1}{N}+\mathcal{O}(N^{-2})\right).\end{array}$$ (B.1)

The Taylor series of z* − ζ* can be expressed as

$$z^{\ast }-{\zeta }^{\ast }=\kappa ({\widehat{C}}_{\mathit{ny}}-C_{\mathit{ny}})\zeta \prime +{\kappa }^2{({\widehat{C}}_{\mathit{ny}}-C_{\mathit{ny}})}^2{\zeta }^{″}/2+\dots$$ (B.2)

where

$$\begin{array}{l}\zeta \prime =\frac{1}{1-C_{\mathit{ny}}^2{\kappa }^2},\\ \zeta ″=\frac{2C_{\mathit{ny}}\kappa }{{(1-C_{\mathit{ny}}^2{\kappa }^2)}^2},\end{array}$$

The square of (B.2) is given by

$${(z^{\ast }-{\zeta }^{\ast })}^2={\kappa }^2{({\widehat{C}}_{\mathit{ny}}-C_{\mathit{ny}})}^2{{\zeta }^{\prime }}^2+{\kappa }^3{({\widehat{C}}_{\mathit{ny}}-C_{\mathit{ny}})}^3\zeta \prime \zeta ″+\mathcal{O}\left({({\widehat{C}}_{\mathit{ny}}-C_{\mathit{ny}})}^4\right).$$ (B.3)

We can use the moments of ${\widehat{C}}_{\mathit{ny}}-C_{\mathit{ny}}$ given in (B.1) to, term by term, get the moments of (B.2) and (B.3). We may then collect the terms by order of N, to get a series for Var[z*] ≈ E[(z* − ζ*)²]. In this way, for N independent samples, we find that the expectation of z* is given by

$$\mathrm{E}\left[z^{\ast }\right]={\zeta }^{\ast }+\frac{C_{\mathit{ny}}\kappa (1-C_{\mathit{ny}}^2)}{2N(1-C_{\mathit{ny}}^2{\kappa }^2)}\left(\frac{{\kappa }^2(1-C_{\mathit{ny}}^2)2}{(1-C_{\mathit{ny}}^2{\kappa }^2)}-\frac{1}{2}\right)+\mathcal{O}(N^{-2}),$$

and the sample variance of z* is given by

$${\sigma }_{z\ast }^2=\frac{{\kappa }^2}{2N}\left(\frac{1-C_{\mathit{ny}}^2}{1-C_{\mathit{ny}}^2{\kappa }^2}\right)+\mathcal{O}(N^{-2}).$$ (B.4)

Therefore, z* is an asymptotically unbiased, and consistent estimator of ζ*. Our variance (B.4) reduces to Hotelling’s formula (12) when there is no rate adjustment (κ = 1).

Appendix C. Maximum likelihood estimator for α (β = 0)

Let n₁(t) and n₂(t) be Poisson random variables with parameters μ₁ = μt and μ₂ = αμt, respectively. If ${\overrightarrow{n}}_1=\{n_{1,1},\dots ,n_{1,N_1}\}$ and ${\overrightarrow{n}}_2=\{n_{2,1},\dots ,n_{2,N_2}\}$ are observations of n₁(t) and n₂(t), then the log likelihood of the joint observations is given by

$$\ell (\alpha ,\mu |t,{\overrightarrow{n}}_1,{\overrightarrow{n}}_2)={\displaystyle \sum _{j=1}^{N_1}{n}_{1,j}}\log (\mu t)+{\displaystyle \sum _{i=1}^{N_2}{n}_{2,i}}\log (\alpha \mu t)-N_1\mu t-N_2\alpha \mu t+C,$$

where C is a constant with respect to α and μ. The partial derivatives of $\ell (\alpha ,\mu |t,{\overrightarrow{n}}_1,{\overrightarrow{n}}_2)$ with respect to α and μ are therefore

$$\frac{\partial \ell }{\partial \alpha }=\frac{1}{\alpha }{\displaystyle \sum _{i=1}^{N_2}{n}_{2,i}-N_2\mu t},$$ (C.1)

$$\frac{\partial \ell }{\partial \mu }=\frac{1}{\mu }{\displaystyle \sum _{j=1}^{N_1}{n}_{1,i}-N_{1}t+\frac{1}{\mu }{\displaystyle \sum _{i=1}^{N_2}{n}_{2,i}-N_2\alpha t}}.$$ (C.2)

Setting ∂ℓ/∂μ = 0 and solving for μ gives

$$\mu =\frac{{\displaystyle {\sum }_{j=1}^{N_1}{n}_{1,i}+}{\displaystyle {\sum }_{i=1}^{N_2}{n}_{2,i}}}{N_{1}t+N_2\alpha t}.$$

Substituting this expression into (C.1), setting ∂ℓ/∂α = 0, and solving for α gives the MLE for α

$${\widehat{\alpha }}_{\mathit{MLE}}=\frac{N_1{\displaystyle {\sum }_{i=1}^{N_2}{n}_{2,i}}}{N_2{\displaystyle {\sum }_{j=1}^{N_1}{n}_{1,j}}}.$$

Note that the MLE’s of μ_k (k = 1, 2) are given by (Casella and Berger, 2002) ${\widehat{\mu }}_{k,\mathit{MLE}}={\displaystyle {\sum }_{i=1}^{N_k}{n}_{k,i}/N_k}$. Therefore, ${\widehat{\alpha }}_{\mathit{MLE}}={\widehat{\mu }}_{2,\mathit{MLE}}/{\widehat{\mu }}_{1,\mathit{MLE}}$.