Bridging Conditional and Marginal Inference for Spatially Referenced Binary Data

Summary

Spatially referenced binary data are common in epidemiology and public health. Owing to its elegant log-odds interpretation of the regression coefficients, a natural model for these data is logistic regression. To account for missing confounding variables that might exhibit a spatial pattern (say, socioeconomic, biological, or environmental conditions), it is customary to include a Gaussian spatial random effect. Conditioned on the spatial random effect, the coefficients may be interpreted as log odds ratios. However, marginally over the random effects, the coefficients no longer preserve the log-odds interpretation, and the estimates are hard to interpret and generalize to other spatial regions. To resolve this issue, we propose a new spatial random effect distribution through a copula framework which ensures that the regression coefficients maintain the log-odds interpretation both conditional on and marginally over the spatial random effects. We present simulations to assess the robustness of our approach to various random effects, and apply it to an interesting dataset assessing periodontal health of Gullah-speaking African Americans. The proposed methodology is flexible enough to handle areal or geo-statistical datasets, and hierarchical models with multiple random intercepts.

1. Introduction

Spatially referenced binary data abounds in the fields of epidemiology, public health, geography and image processing, among others. For valid inference on model parameters, it is important to account for correlation indexed by proximity due to the unmeasured spatial factors. While linear mixed models easily allow the incorporation of correlated random effects (REs), logistic regression and other generalized linear mixed models (GLMM) suffer an interpretation problem (i.e., a mismatch between conditional and marginal distributional shapes) due to the nonlinearity of the mean function. Because of this, researchers usually choose between a marginal model for “population-averaged” inference, or a conditional model for “subject-specific” inference for the regression parameters, primarily motivated by inferential objectives. The regression effects can be different at each level due to subject or site level variability, particularly when this variability is large, highlighting the importance of proper interpretation. While model goodness of fit is certainly an important consideration in choosing a random effects distribution, interpretability is essential. In this article, we propose a model for spatial binary data that preserves the log odds interpretation of covariate effects both conditional on and marginal over REs.

The motivating data in this article concern the periodontal health of Gullah-speaking African-American Type-2 diabetics (Fernandes et al., 2009; Bandyopadhyay et al., 2010). For each subject, the binary health status (missing/diseased) of each tooth (28 locations, excluding the 4 wisdom teeth) was recorded. The primary objective of this article was to assess the dental health of the population, and evaluate the influence of various subject-level covariates such as age and gender on the periodontal decay status of each tooth, which requires properly accounting for clustering within subjects and spatial dependence between teeth. Earlier studies (Reich, Hodges, and Carlin, 2007; Reich and Bandyopadhyay, 2010) have shown that periodontal disease markers might be spatially associated, as a diseased (or decayed) tooth (or sites within a tooth) might be influencing the periodontal health status of a set of neighboring sites or teeth. Therefore, in addition to independent subject-specific RE, we include spatially correlated RE for each tooth nested within subjects.

The usual Gaussian RE logistic regression model for spatially referenced binary data may not be well-suited here where the regression coefficients are only interpretable conditioned on the spatial REs, and thus in terms of replication at the same location for a given subject. In a more traditional disease mapping setting (with many subjects observed at each spatial location) when researchers are possibly interested in a site-specific interpretation (conditional on county of residence), these conditional parameters have meaning. However, for our data, an interpretation conditioned on tooth REs is purely hypothetical as we cannot take another replicate of the same tooth for the same subject. A similar objection arises for interpreting subject-level covariate effects such as gender, age, etc conditional on the subject. However, coefficients for certain “tooth-level” measures, such as an indicator of molar, could plausibly be interpreted conditional on a subject RE. Hence, we desire a model with interpretable parameters both conditioned on, and marginal over subject and tooth RE.

Standard modeling approaches in a GLMM choose either a marginal or conditional route for inference. For the marginal, one approach is the moment-based generalized estimating equations (GEE) framework (Liang and Zeger, 1986) accommodating a spatial covariance matrix to yield consistent regression estimates which are robust to the misspecification of the underlying correlation structure. However, the GEE not being a likelihood-based method cannot be compared to other likelihood-based methods in terms of efficiency. Likelihood-based methods include direct modeling of the binary response using the multivariate logistic distribution described by O’Brien and Dunson (2004), or the marginalized models described by Heagerty (1999) and Heagerty and Zeger (2000). Both allow for complex correlation structures. While the O’Brien and Dunson method implies correlation directly on the binary responses without using REs, the logistic-normal model of Heagerty (1999) defines the conditional mean through a convolution equation, such that the marginally specified model provides the desired marginal interpretation of the regressors. However, due to the convolution, the conditional log-odds interpretation is lost. Other existing methods focus on conditional, rather than marginal, modeling. The usual conditionally specified Gaussian REs models yields a conditional log-odds interpretation, as noted above. The marginal log-odds ratio is nonlinear and not in closed form, as will be described in Section 2, which is problematic for interpretation. Another conditional approach which has been applied to these data is the auto-logistic model (Besag, 1972; Bandyopadhyay, Reich, and Slate, 2009). In this Markovian model, the coefficients have a log-odds interpretation conditioned on a pre-defined neighbor set. Though the full conditional distributions are intuitive, they lead to a complicated joint spatial distribution (Varin, Reid, and Firth, 2011), and the marginal effects of covariates are not readily available. Further, it is unclear how to extend this model to geostatistical data defined continuously on a given spatial domain.

Wang and Louis (2003, 2004) made headway in solving the conditional-marginal dilemma for random-intercept logistic regression by proposing a new distribution (for the random intercepts), aptly named the “bridge distribution.” The marginal and conditional mean have the same form, and the marginal regression coefficients are proportional to the conditional regression coefficients. It falls under the general definition of marginalized models (Griswold and Zeger, 2004), amenable to a likelihood-based analysis through standard software, but is unique in that it retains the log-odds ratio interpretation both conditionally and marginally.

Motivated by the periodontal data, here we exploit the richness of the Wang and Louis model to study marginal/population-level covariate effects for spatially distributed binary data. This strength becomes further important in richer hierarchical models, such as the nested subject- and site-specific REs we use for the periodontal data, where the coefficients can easily be interpreted at whichever level of the hierarchy is desired. Extension to this setup for bivariate binary responses (Li et al., 2011) and a binary and continuous response (Lin et al., 2010) have been demonstrated. Here we provide a full exploration of a multivariate bridge distribution and its application in a nested REs setting. The spatial bridge distribution is derived using a Gaussian copula, and extensions to a more general t-copula are also presented. Although our model development is currently tailored towards the specific structure of dental data, it can be applied to more conventional spatial settings with a single observation at each location, or with multiple subjects observed at the same site. Our model that incorporates both subject- and site-specific REs can simultaneously estimate covariate effects conditioned on both the REs, marginally over subject-, and marginally over site-specific REs. Identification of high-risk areas through estimation of REs is possible within our unified framework, often precluded in a marginal model. Our hierarchical Bayesian scheme has computational complexity equivalent to the usual Gaussian RE model, and can easily be implemented in standard software such as OpenBUGS.

The article proceeds as follows. Section 2 introduces the spatial bridge distribution and Section 3 presents the associated MCMC computational scheme. In Section 4, we conduct simulation studies to evaluate the robustness of our methods under misspecifications of the REs. Section 5 provides analysis of the binary dental data. Section 6 concludes this study.

2. The Spatial Bridge Distribution

For notational convenience, we specify the model assuming all n subjects have observations at the same m spatial locations s₁, …, s_m. Extending to more complex designs is straightforward using our Bayesian hierarchical model. In particular, we do not require replication at each spatial location or a balanced design across subjects. The binary response Y_ij for subject i at site s_j is modeled as Y_ij |ε_ij ~ Bernoulli(π_ij), with logit(π_ij |X_ij, ε_ij) = X_ijβ^S + ε_ij, where π_ij is the Bernoulli success probability, X_ij is the design matrix of covariates, β^S is the regression vector (the superscript “S” denotes site-specific conditional parametrization of regressors), and ε_i = (ε_i1, …, ε_im)′ is the vector of spatial REs for subject i, which are independent and identically distributed.

In addition to the Bernoulli probability conditional on the REs, we are also interested in the Bernoulli probability marginal over the REs, ${\pi }_{ij}^P=\int {\pi }_{ij}g({\epsilon }_{ij})\mathrm{d}{\epsilon }_{ij}$. For most RE densities g(ε_ij), including Gaussian, this marginal probability is unknown and must be computed numerically. In the spirit of Wang and Louis (2003), to preserve the logistic shape both conditionally and marginally we allow ε_ij to follow the bridge density given by

$$g(\epsilon ;\varphi )=\frac{1}{2\pi }\frac{\text{sin}(\varphi \pi )}{\text{cosh}(\varphi \epsilon )+\text{cos}(\varphi \pi )},$$ (1)

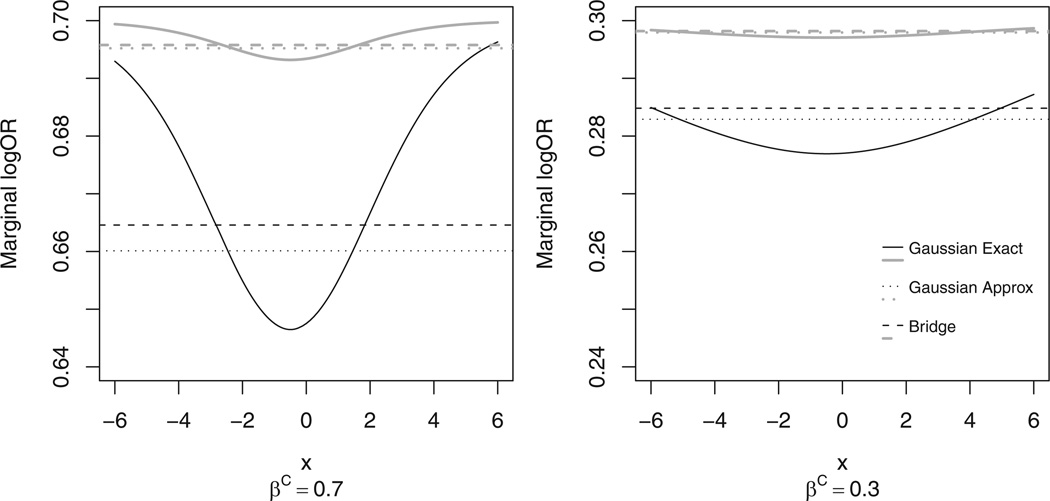
where $\text{cosh}(x)=\frac{1}{2}({\mathrm{e}}^x+{\mathrm{e}}^{-x})$. We denote this as ε ~ bridge(ϕ), where 0 < ϕ < 1 controls the variance and shape of the density. The bridge density is mean 0 and variance ${\sigma }_b^2={\pi }^2({\varphi }^{-2}-1)/3$, and like the normal distribution is symmetric and bell-shaped, though it has heavier tails. We assume ϕ to be common for all observations to assure exchangeability across the spatial units. With such a bridge structure for ε, the marginal regression model is $\text{logit}({\pi }_{ij}^P)={\mathbf{X}}_{ij}{\mathit{\beta }}^P$, where β^P is the marginal (population-level) parameter vector and is related to β^S by ${\mathit{\beta }}^P=\varphi {\mathit{\beta }}^S=1/\sqrt{1+(3/{\pi }^2){\sigma }_b^2}{\mathit{\beta }}^S$. This is a development over the marginal interpretation under the Gaussian REs model. The exact marginal log odds for Gaussian REs is nonlinear in X, with nonlinearity increasing with REs variance and the strength of conditional association, β^S. Johnson and Kotz (1970) give the approximation $\text{logit}({\pi }_{ij}^P)\approx {\mathbf{X}}_{ij}{\mathit{\beta }}^P$ where ${\mathit{\beta }}^P=1/\sqrt{1+{(16/15)}^2(3/{\pi }^2){\sigma }^2}{\mathit{\beta }}^S$. Figure 1 shows the relationship between the exact and approximate marginal log odds ratio (calculated numerically as a function of X) for a model with a single predictor. For comparison, the marginal log odds ratio that would result from assuming a bridge random effects distribution with the same variance is also shown. We observe notable differences between these curves, and that as X approaches either ∞ or −∞, the log odds for the exact Gaussian model approaches β^S.

Figure 1.

Marginal log odds ratio for unit increase from X to X + 1, when the random effects follow a Gaussian or bridge distribution. In both graphs, gray lines have random effects standard deviation σ = 0.2, and black lines have random effects standard deviation σ = 0.6.

To extend the bridge model from the exchangeable to the spatial setting, we make use of a copula (Sklar, 1953, 1973; Nelsen, 1999) to capture spatial correlation while preserving the marginal bridge distribution at each location. Let θ_i be a latent Gaussian process for subject i with zero mean, unit variance and spatial correlation function cor[θ(s), θ(s′)] = ρ(‖s − s′‖). One example of a correlation function is the the exponential correlation defined by ρ(‖s − s′‖) = e^{−‖s−s′‖/r}, where r > 0 controls the spatial range of the latent process. Marginal bridge distributions are forced via the probability integral transformation

$${\epsilon }_{ij}=G_{\varphi }^{-1}\{\mathrm{\Phi }[{\theta }_i(s_j)]\},$$ (2)

where Φ() is the cumulative distribution function (c.d.f) of N(0, 1) and $G_{\varphi }^{-1}$ is the inverse c.d.f of the univariate bridge density available in a closed form (Li et al., 2011) given by $G_{\varphi }^{-1}(y)=(1/\varphi )\text{log}[\text{sin}(\varphi \pi y)/\text{sin}(\varphi \pi (1-y))]$, for 0 < y < 1. We fix the variance of θ_i(s) at one for all s, because only the correlation structure is important in the copula specification. If θ_i(s) has a non-unit variance σ², it would be necessary to define ${\epsilon }_{ij}=G_{\varphi }^{-1}\{\mathrm{\Phi }[{\theta }_i(s_j)/\sigma ]\}$ to maintain the bridge marginal distribution, eliminating the effect of σ.

Utilizing a Gaussian copula, the joint cumulative distribution of ε_i, is given by H(ε_i1, …, ε_im) = Φ_Σr {Φ⁻¹ [G_ϕ(ε_i1)], …, Φ⁻¹ [G_ϕ(ε_im)]}, where Σ_r is the m × m covariance matrix of θ_i = (θ_i1, …, θ_im). We denote this model as ε_i ~ bridge(ϕ, Σ_r). Though motivated here from a geostatistical perspective, any valid correlation matrix, including the correlation implied by a conditionally autoregressive (CAR) model for areal data (Banerjee, Carlin, and Gelfand, 2004) could be used in place of Σ_r. Under this copula model, the random effects ε_i are non-Gaussian, but maintain the Markovian dependency structure of the CAR model.

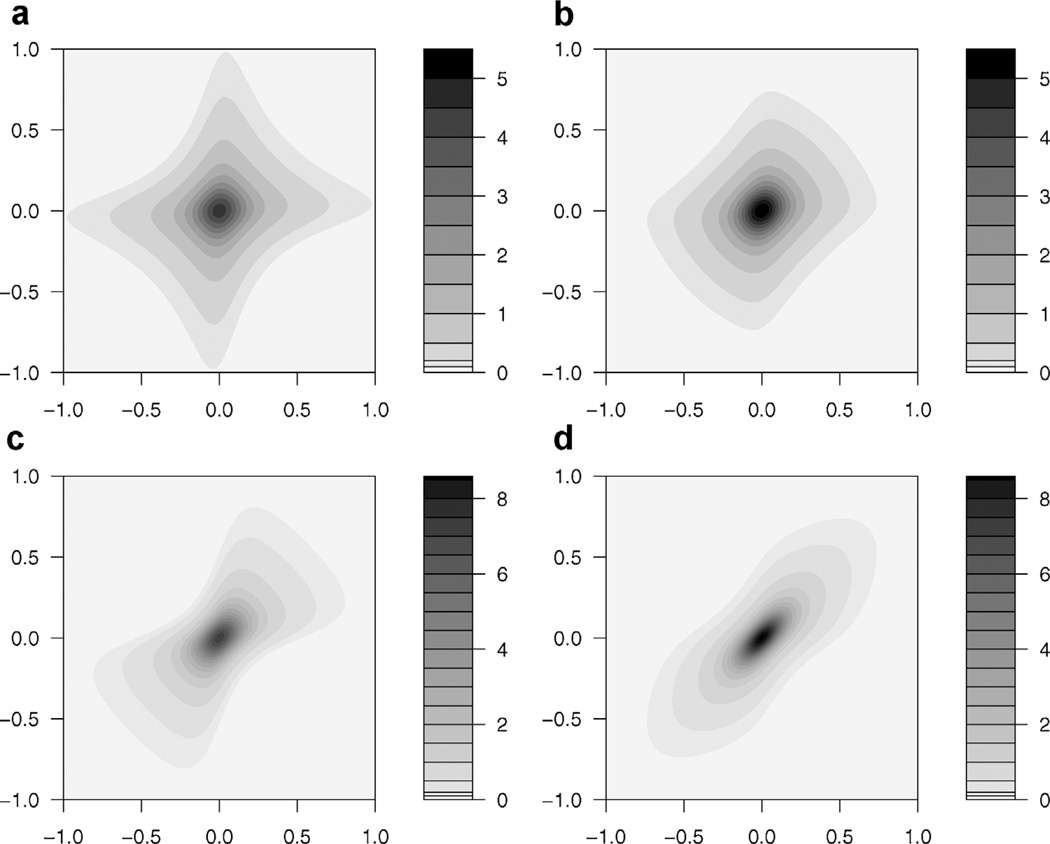
Although the Gaussian copula is an intuitive way to induce spatial correlation, it may not capture tail dependence (Demarta and McNeil, 2005). A logical alternative is the t-copula, which can be easily implemented within the Bayesian framework. The t-copula assumes that ${\mathit{\theta }}_i\stackrel{iid}{~}{t}_{\nu }(0,{\mathrm{\Sigma }}_r)$, where t_ν is the multivariate t distribution with location 0, scale matrix Σ_r and ν degrees of freedom. We can either fix ν, or assign it an additional hyperprior. Similarly as above, ${\epsilon }_{ij}=G_{\varphi }^{-1}[T_{\nu }({\theta }_{ij})]$, where T_ν is the c.d.f of a mean 0 univariate t distribution with ν degrees of freedom. Visual comparison (Figure 2) of the bivariate bridge densities for the Gaussian and t-copula at two levels of correlation reveal differences particularly in the tails. More flexible copulas such as the non-parametric copula as in Fuentes, Henry, and Reich (2012) can be used, but with the limited information available in our binary response, the parametric t-copula is likely flexible enough to capture important dependence.

Figure 2.

Bivariate density for (a) Bridge with Gaussian copula and ρ = 0.3 (b) Bridge with t-copula, ρ = 0.3 and ν = 2 degrees of freedom (c) Bridge with Gaussian copula and ρ = 0.8 and (d) Bridge with t-copula, ρ = 0.8, and ν = 2. In all graphs, ϕ = .95, for a standard deviation of σ = 0.6.

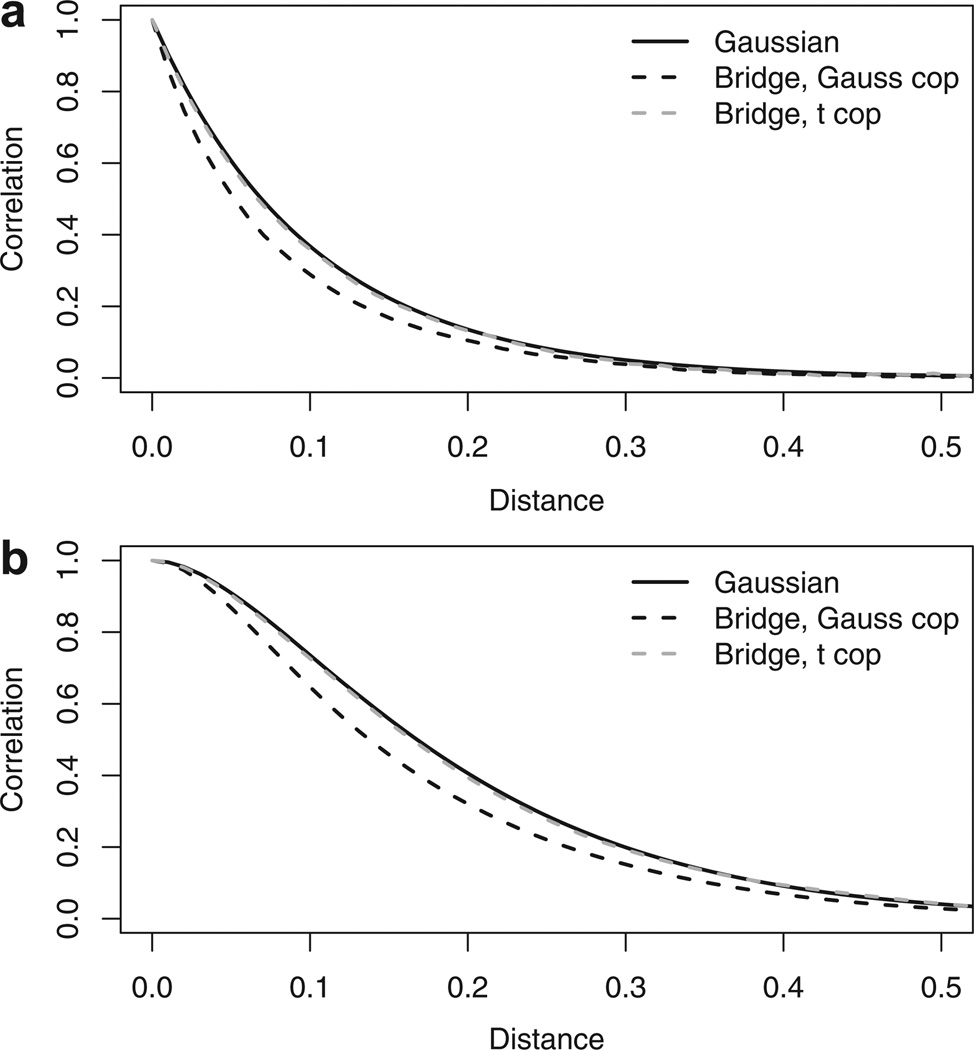
To quantify the effect on the correlation function due to the probability integral transformation, Figure 3 plots the correllogram assuming exponential and Matern spatial correlation functions, and Gaussian and t copulas. We find that for both correlation functions and copulas, the correlation function of the copula models has the same general shape as correlation function of the latent Gaussian process, but the magnitude of correlation is slightly lower. This may be useful when specifying informative priors for the spatial correlation parameters.

Figure 3.

Comparison of correlation by distance for bivariate Gaussian distribution and bridge distribution with ϕ = 0.95 using a Gaussian and t₂ copula. The plots compare (a) the exponential correlation with range 0.1 and (b) the Matern correlation with range 0.1 and smoothness 1.5.

Spatial prediction of the random effect ε_i(s₀) at prediction location s₀ follows from standard Bayesian Kriging methods. Using the Gaussian copula, we sample θ_i(s₀)|θ_i using properties of the conditional distribution of a multivariate normal, and then transform to ${\epsilon }_i({\mathbf{s}}_0)=G_{\varphi }^{-1}\{\mathrm{\Phi }[{\theta }_i({\mathbf{s}}_0)]\}$. For the t-copula, the same approach can be used after exploiting the hierarchical representation of the multivariate t. If we assume that ${\mathit{\theta }}_i|{\tau }_i~N(0,{\tau }_i^2{\mathrm{\Sigma }}_r)$, where ${\tau }_i^{-2}~\text{gamma}(\nu /2,\nu /2)$, then θ_i follows a multivariate t_ν(0, Σ_r) marginally over τ_i. Spatial interpolation can be done conditional on τ_i as with the Gaussian copula.

To accommodate the structure of the dental data, we also consider a nested REs model in which there are REs for both subjects and sites within subjects, given as:

$$\text{logit}\{P(Y_{ij}=1|{\mathbf{X}}_{ij},{\gamma }_i,{\epsilon }_{ij})\}={\mathbf{X}}_{ij}{\mathit{\beta }}^T+{\gamma }_i+{\epsilon }_{ij},$$ (3)

where γ_i are independent subject-specific REs and ε_ij are tooth-level REs. A slight complication arises with multiple REs because the bridge distribution is not additive or a scale family. As suggested by Wang and Louis (2003), we assume ${\gamma }_i={\gamma }_i^{*}/{\varphi }_2$, and that ${\gamma }_i^{*}\stackrel{iid}{~}\text{bridge}({\varphi }_1)$ and ε_i ~ bridge(ϕ₂, Σ_r). In this case we are interested in estimating the log odds at each level of the hierarchy. We let the “site-within-subject” level coefficient β^T denote the conditional log odds ratio, using “T” to signify a “tooth”-level interpretation. After integrating over the tooth REs ε_i, we have $\text{logit}\{P(Y_{ij}=1|{\mathbf{X}}_{ij},{\gamma }_i^{*})\}={\mathbf{X}}_{ij}{\mathit{\beta }}^S+{\gamma }_i^{*}$, and the coefficient β^S = ϕ₂β^T represents the “subject”-level interpretation, in that it can only be interpreted conditional on the subject REs γ_i. Finally, β^P is the “population”-level, or completely marginal coefficient, with logit{P(Y_ij = 1|X_ij)} = X_ijβ^P. The population level log odds ratios are defined by β^P = ϕ₁ϕ₂β^T. Also, we denote the total subject level standard deviation σ₁ = sd(γ_i), and the standard deviation of the bridge REs controlled by ϕ₁, ${\sigma }_1^{*}=\mathrm{s}\mathrm{d}({\gamma }_i^{*})$. Further, σ₂=sd(ε_ij) represents the standard deviation of the site-specific REs, controlled by ϕ₂. A nested RE structure is also easily implemented in other studies where perhaps γ_i are spatially correlated (e.g., county effects) and ε_ij are independent (e.g., subjects within a county).

3. MCMC Implementation

We implement the model using R (R Development Core Team, 2010) (Web Appendix A) for the simulation study, and OpenBUGS (Web Appendix B) for the dental data example. OpenBUGS coding for this model is a very simple extension from the usual Gaussian model, by treating ε_ij as a transformation of a latent Gaussian variable θ_ij. Implementation of the model with the t-copula requires the t_ν c.d.f, which, unlike the Gaussian c.d.f, is not an available function in OpenBUGS. However, this c.d.f exists in closed form for ν = 2, and so for the dental analysis with t-copula, we hold ν fixed at 2, rather than include a prior for ν. We ran 10,000 samples with 3000 burn-in for the simulated data, and visually monitored convergence by starting multiple chains from diverse starting values for a selection of datasets. For the dental data analysis, we used 25,000 iterations with 5000 burn-in.

4. Simulation Study

In this simulation study we compare marginal and conditional estimates of regression coefficients for models using Gaussian and bridge REs. Our objective is to study robustness of the coefficient estimates to misspecification of the RE distribution and identify the situations that lead to the most sensitivity. Earlier work has already considered the effect of misspecification in logistic regression models with independent, identically distributed random intercepts. Neuhaus, Hauck, and Kalbfleisch (1992) show that for a true RE distribution G, and an assumed RE distribution F, the maximum likelihood estimates under F minimize Kullback–Leibler divergence of the marginal models implied under G and F. Asymptotically and in simulation, they show that for any F and G the bias of the MLE for the conditional coefficient β^S are expected to be small, but that bias for σ may be large. It is unclear whether these results extend to a correlated intercepts setting and a Bayesian model. Furthermore, because the marginal interpretation depends directly on variance, and Neuhaus et al. (1992) show the variance is heavily biased, it is unclear how this will affect bias in the marginal estimates.

In this article, we consider n = 100 subjects, each with observations at m = 14 spatially correlated sites to mimic the structure of our dental data where each subject has 28 teeth. The fourteen spatial locations are equally spaced along a line of length one, representing the structure of one jaw. The data are generated from the nested REs model in (3). We consider p = 4 covariates, two of which are “subject level” and two of which are “site level.” The subject level covariates X₁ and X₃ take the same value for all sites for subject i, while X₂ and X₄ (the site level ones) vary across sites and subjects. All four covariates were drawn independently from standard normal distributions. The values for the conditional coefficients are β^T = (0.5, 0.5, 1, 1)^T. Thus, we can simultaneously compare the sensitivity to REs distribution for subject- and site-level covariates, and large and small coefficients. The correlation matrix of the site-specific effects is taken to be exponential with spatial range r = 0.1 or 0.4. The standard deviation of the subject REs, ${\sigma }_1^{*}$, is fixed at 1, while the standard deviation of the site-level REs is chosen to be either σ₂ = 1 or 3. The total marginal shrinkage, ϕ₁ϕ₂, is either 0.77 or 0.45. We consider four design settings for data generation:

• Design 1: Low Variance and low spatial correlation, that is, σ₂ = 1, r = 0.1.

• Design 2: Low Variance and high spatial correlation, that is, σ₂ = 1, r = 0.4.

• Design 3: High Variance and low spatial correlation, that is, σ₂ = 3, r = 0.1.

• Design 4: High Variance and high spatial correlation, that is, σ₂ = 3, r = 0.4.

At each design setting, we generate 100 datasets assuming the true REs distribution is either Gaussian or bridge. When generating the data from a Gaussian distribution, we directly generate ${\gamma }_i~N(0,{\sigma }_1^2)$. For each dataset, we fit the logistic model with Gaussian REs and bridge REs using the Gaussian copula. We also estimate the marginal effects β^P with GEE, noting only a population level interpretation is possible. We compare methods in terms of relative percent bias and root mean square error $(\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}})$, each calculated with respect to the posterior mean for β^T, β^S, and β^P. For the marginal β^P in the Gaussian REs models, the “true” value will be the approximation as in Johnson and Kotz (1970) (described in Section 2), applied twice. The model is parameterized in terms of the precision of the REs distributions, so the same priors can be used for either Gaussian or bridge REs. We assume the priors $1/{\sigma }_1^{*2}~\text{gamma}(1,0.25)$ and $1/{\sigma }_2^2~\text{gamma}(1,0.25)$. We use a normal prior with variance 100 for β, where the coefficients are independent a priori.

Table 1 presents the effect of misspecification on marginal inference. The relative percent bias in all models ranges from 0 to ±10%. As expected, when the true RE distribution is Gaussian, the Gaussian fit has slightly smaller bias and $\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}}$ than the bridge fit and vice versa. The relative $\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}}\mathrm{s}$ in Table 1c are generally closer to one in the first case where Gaussian model is true and the bridge model is misspecified, compared to the other case where the bridge model is true and the Gaussian model is misspecified. It may be that by including shape parameter ϕ the bridge distribution is more robust than the Gaussian model. The largest difference we observe is for β₁ when the bridge model is true. This is a subject-level covariate with a small coefficient; the $\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}}$ is 10–25% greater for the misspecified Gaussian model than the bridge depending on the covariance parameters. The bridge model also compares favorable to the GEE approach. Because the difference in shape of the bridge and Gaussian distribution is more pronounced as variance decreases, we expect larger differences between models for σ₂ = 1 and this is generally the case. Frequentist coverage probability (not shown) for all coefficient estimates is close to the nominal 95%. Across all model fits, we find that the $\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}}$ for the coefficients on subject specific covariates X₁ and X₃ is nearly twice that of the site specific covariates X₂ and X₄. The size of the coefficient does not appear to have an effect.

Table 1.

(a) Relative percent bias of population-level coefficients and (b) $\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}}\times 100$ when the underlying true model is Gaussian and bridge. (c) The relative MSE of the Gaussian and bridge models

	σ2 = 1						σ2 = 3
	r = 0.10			r = 0.40			r = 0.10			r = 0.40
	G	B	GEE	G	B	GEE	G	B	GEE	G	B	GEE
(a) Relative percent bias
Gaussian distribution is “true”
${\beta }_1^P$	2.13*	−2.92	0.43*	−3.57*	1.45	−0.34*	1.41*	5.22	2.18	1.47*	4.60	1.35
${\beta }_2^P$	−3.27*	−6.19	−5.45	−3.56*	−0.48	−3.19	−6.45*	−3.02	−5.82	−4.83*	−2.07	−5.37
${\beta }_3^P$	2.27*	−1.34	1.12*	−1.96*	1.97	0.99*	−3.10*	1.46	−0.22*	−1.25*	2.17	0.72*
${\beta }_4^P$	0.67	−2.03	−0.60*	−2.28*	0.54	−0.94*	−1.77*	1.54	−1.12*	−2.86*	−0.03	−2.65
Bridge distribution is “true”
${\beta }_1^P$	4.32	2.80	3.46	3.82	1.95	2.94	8.80*	5.62	6.44	6.15	4.86	4.02
${\beta }_2^P$	1.10*	−2.74	−0.58	2.91*	1.51	0.92	0.60*	−1.54	−1.67	0.81*	−1.48	−2.05
${\beta }_3^P$	3.37	3.77	2.68	3.43	2.56	2.63	4.31*	2.02	2.53	5.84*	4.25	4.40
${\beta }_4^P$	2.97*	2.77	1.83	2.20*	0.85	0.90	4.11*	2.23	1.94	3.93*	1.74	1.08*
(b) $\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}}$
Gaussian distribution is “true”
${\beta }_1^P$	11.68	11.70	11.86	13.66	13.70	13.68	11.50	11.23	11.26	13.75	13.61	13.52
${\beta }_2^P$	6.34	6.46	6.51	5.89	5.89	6.12	6.82	6.72	6.82	6.30	6.24	6.54
${\beta }_3^P$	11.13	11.18	11.35	12.08	12.31	12.22	10.35	10.63	10.40	12.48	12.95	12.70
${\beta }_4^P$	6.40	6.68	6.45	6.32	6.57	6.64	6.59	6.49	6.58	6.48	6.52	6.65
Bridge distribution is “true”
${\beta }_1^P$	11.05*	8.85	11.00*	12.91*	11.53	12.53	11.08*	10.01	10.93*	13.41*	12.11	13.13
${\beta }_2^P$	6.60	6.26	6.58	6.16	5.99	6.22	6.60	6.42	6.37	6.29	6.20	6.27
${\beta }_3^P$	10.55	11.05	10.57	11.76	11.87	11.92*	10.61	9.92	10.39*	13.19	13.60	13.35*
${\beta }_4^P$	7.75	8.19	7.58	7.22	7.06	7.23	7.26*	6.79	6.97	6.43*	6.09	6.41

(c) Ratio of MSE, Gaussian/Bridge
	Gaussian is true				Bridge is true
	σ2 = 1		σ2 = 3		σ2 = 1		σ2 = 3
	r = 0.10	r = 0.40	r = 0.10	r = 0.40	r = 0.10	r = 0.40	r = 0.10	r = 0.40
${\beta }_1^P$	1.00	1.00	1.02	1.01	1.25	1.12	1.11	1.11
${\beta }_2^P$	0.98	1.00	1.02	1.01	1.05	1.03	1.03	1.02
${\beta }_3^P$	1.00	0.98	0.97	0.96	0.95	0.99	1.07	0.97
${\beta }_4^P$	0.96	0.96	1.02	0.99	0.95	1.02	1.07	1.06

“G” indicates fit of the Gaussian model, “B” indicates the bridge model fit, and “GEE” indicates the GEE fit. The ratio of the $\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}}$ are also presented in (b). Results which show a significant difference from the bridge model are indicated with “*.”

The relatively small differences between the models should not be very surprising as both are symmetric, bell-shaped distributions, and Neuhaus et al. (1992) notes that marginal effects in particular are fairly robust with respect to different distributional assumptions for the conditional REs. In general, conditional effects are less robust compared to marginal effects, which is intuitive since more information is available for estimating marginal effects than conditional effects. It is important to carefully consider the choice of the REs distribution, but it appears little efficiency would be lost by choosing a bridge distribution for easier interpretation, even if a Gaussian distribution were the true correct choice.

5. Dental Data Example

The data consist of dental records for 260 Gullah-speaking African-Americans (Bandyopadhyay et al., 2010) in South Carolina. The location and clinical attachment level (CAL, in mm) were recorded by dental hygienists for each of the 28 adult teeth (excluding wisdom teeth), for each subject. As CAL is measured at multiple sites per tooth, we define a tooth as diseased if the mean CAL > 3 mm, indicating moderate to severe periodontitis. The response Y_ij = 1 if tooth j is missing or diseased for subject i, and 0 otherwise. The subjects range in age from 26 to 87, are mostly female (75%), and are from an under-served population with generally poor health outcomes. Over 97% of the subjects have at least one missing or diseased tooth, and 55% have 10 or more missing or diseased teeth. For each subject, age, body mass index (BMI), smoking status, and HbA1c (a measure of blood-glucose level), are recorded, in addition to their dental health records. The objective of our analysis is to assess the oral health of this under-studied population, and identify the effects of these covariates on the (binary) oral health status, both at the population and subject specific level.

We fit the nested model in (3) assuming teeth in the upper and lower jaw are independent, and within each jaw, teeth are related by a first-order Markov model (i.e., an exponential covariance). A richer model would allow correlation between jaws where neighbors between jaws and within jaws have potentially different correlation. However, initial model fits suggest the correlation between jaws is negligible after accounting for subject REs, and treating each jaw independently reduces the size of our covariance matrix by half which drastically improves the speed of computation.

We fit this model assuming a Gaussian REs distribution, a bridge REs distribution with Gaussian copula, and a bridge REs distribution with t-copula. Here we fix the degrees of freedom ν = 2 for computational purposes because of the closed form of the t₂ cdf. A richer model would allow ν to vary; however, because the t and Gaussian copulas are similar for large ν, this will also allow for more contrast in the two approaches. For comparison, we also fit these models assuming only a subject RE by setting ε_ij = 0. The prior for the coefficients ${\beta }_k^T\stackrel{iid}{\sim }N(0,100)$, for k = 0, …, p, where ${\beta }_0^T$ is the intercept term. The prior for the range parameter, r ~ logNormal(−2, 1), where the distance between teeth is standardized so the maximum distance is one unit. As in the simulation study, the prior for both standard deviations are $1/{\sigma }_k^2~\text{gamma}(1,0.25)$. In addition to the Bayesian models, we also fit a GEE model (assuming independent subjects and an unstructured working correlation matrix), where the resulting estimates are only available at the (marginal) population level.

Results for the nested REs models appear in Table 2. We compare these models using the Deviance Information Criterion (or DIC, Spiegelhalter et al., 2002), popularly used in Bayesian inference, and defined as DIC = D̅ + p_D, where D̅ is the posterior mean of the deviance and p_D is the effective number of parameters. Smaller values of DIC are preferred. A subject-only REs model appears to be inadequate here (DIC=6385 for bridge model) as expected, since we believe the implicit assumption of independent tooth effects is violated. The bridge model with both subject and tooth REs with a Gaussian copula has the lowest DIC of 4157. In addition to DIC, we calculated the Brier score, where we fit the model using 90% of the data randomly selected across teeth and subject, and estimate the posterior mean π̂_ij for the remaining 10% (hold-out set). The Brier score (Brier, 1950) is then defined by (1/N)∑_i,j(Y_ij − π̂_ij)², where N is the number of held out teeth (728). The Brier score ranges from 0 to 1, and smaller numbers are better. We further calculate the misclassification indices $\mathrm{C}{\mathrm{V}}_1=N_1^{-1}{\sum }_{(i,s)}\left\{Y_{ij}{\hat{\pi }}_{ij}\right\}$ and $\mathrm{C}{\mathrm{V}}_0=N_0^{-1}{\sum }_{(i,s)}\left\{\right(1-Y_{ij}\left){\hat{\pi }}_{ij}\right\}$, where N₁ = ∑_i,j Y_ij, or the number of held out ones, and N₀ = ∑_i,j (1 − Y_ij), or the number of held out zeros. We note that while the Brier score, CV₁ and CV₀ are similar for all three models displayed in Table 2, the Brier score is also minimized by the bridge model with Gaussian copula. To assess the statistical significance of these subtle differences in the Brier score, we repeated this test set validation ten times on a subset of 100 subjects and found the bridge model had smaller Brier score than the Gaussian model for seven of the ten splits, and a paired t-test on the difference in Brier had p-value 0.02. Also, the Brier score is higher for the subject only models (0.151 for Bridge, and 0.150 for Gaussian) than the spatial models in Table 2 (0.132 for the bridge and 0.134 for the Gaussian), again suggesting the nested REs models produce a better fit.

Table 2.

Posterior parameter estimates and 95% credible intervals (C.I.) for tooth specific (T), subject specific (S) and population level (P) fixed-effects, variance components, ϕ₁, ϕ₂ and r for the model with subject and tooth nested random effects

	Gaussian		Bridge: Gauss. copula		Bridge: t-copula		GEE
DIC	5283		4157		5490
pD	2578		1931		1692
Brier Score	0.134		0.132		0.134
CV0, CV1	0.226, 0.670		0.225, 0.670		0.223, 0.677
Int	−1.61	(−2.54, −0.66)	−1.64	(−2.72, −0.60)	−1.42	(−2.18, −0.58)
T:Age	1.17	(0.76, 1.61)*	1.48	(0.84, 2.23)*	1.14	(0.73, 1.59)*
T:Sex	−1.21	(−2.09, −0.45)*	−1.89	(−3.65, −0.80)*	−1.28	(−2.13, −0.60)*
T:BMI	−0.06	(−0.45, 0.29)	0.06	(−0.35, 0.57)	0.04	(−0.31, 0.39)
T:Smoking	0.38	(−0.08, 0.79)	0.37	(−0.14, 1.08)	0.32	(−0.05, 0.68)
T:HbA1c	0.42	(0.08, 0.88)*	0.48	(0.05, 0.97)*	0.39	(0.12, 0.71)*
T:Molar	4.12	(3.62, 4.75)*	4.96	(3.68, 7.37)*	3.78	(3.32, 4.30)*
S:Age	0.68	(0.43, 0.94)*	0.64	(0.42, 0.84)*	0.91	(0.59, 1.21)*
S:Sex	−0.71	(−1.26, −0.25)*	−0.80	(−1.26, −0.37)*	−1.17	(−1.71, −0.65)*
S:BMI	−0.04	(−0.25, 0.17)	0.02	(−0.17, 0.22)	0.02	(−0.25, 0.29)
S:Smoking	0.23	(−0.04, 0.49)	0.16	(−0.06, 0.48)	0.13	(−0.17, 0.42)
S:HbA1c	0.24	(0.05, 0.50)*	0.21	(0.02, 0.39)*	0.34	(0.08, 0.60)*
S:Molar	2.40	(2.23, 2.57)*	2.15	(1.97, 2.32)*	2.78	(2.52, 3.07)*
P:Age	0.37	(0.22, 0.53)*	0.46	(0.29, 0.60)*	0.57	(0.37, 0.76)*	0.50	(0.33,0.66)*
P:Sex	−0.39	(−0.71, −0.13)*	−0.57	(−0.92, −0.27)*	−0.74	(−1.07, −0.41)*	−0.52	(−0.92, −0.12)*
P:BMI	−0.02	(−0.14, 0.10)	0.01	(−0.12, 0.16)	0.01	(−0.16, 0.18)	−0.04	(−0.25, 0.16)
P:Smoking	0.12	(−0.02, 0.28)	0.12	(−0.04, 0.33)	0.08	(−0.11, 0.27)	−0.43	(−0.80, −0.06)*
P:HbA1c	0.13	(0.03, 0.27)*	0.15	(0.02, 0.28)*	0.21	(0.05, 0.38)*	0.19	(0.04, 0.33)*
P:Molar	1.31	(1.15, 1.46)*	1.54	(1.40,1.68)*	1.76	(1.58, 1.94)*	1.73	(1.58, 1.88)*
ϕ1	0.54	(0.48, 0.61)	0.72	(0.67, 0.76)	0.63	(0.57, 0.69)
ϕ2	0.58	(0.51, 0.65)	0.45	(0.29, 0.59)	0.63	(0.44, 0.78)
σ1	5.14	(4.02, 6.72)	4.07	(2.87, 6.17)	3.65	(2.70, 5.13)
σ2	2.69	(2.26, 3.25)	3.76	(2.49, 5.94)	2.33	(1.46, 3.71)
r	0.15	(0.12, 0.18)	0.15	(0.10, 0.18)	0.15	(0.11, 0.21)

^*95% C.I. that excludes 0. ϕ₁ controls the distribution of ${\gamma }_i^{*}$, while σ₁ is the total subject-specific effect standard deviation given by $\mathrm{s}\mathrm{d}({\gamma }_i^{*})/{\varphi }_2$. For the t-copula, there are ν = 2 degrees of freedom.

The advantage of the bridge model is that we can get an exact interpretation of the coefficients at any level. In all models, the strongest predictor is the indicator for molar. For all Bayesian models, age and HbA1c are significant, while BMI and smoking are not significant in any model. Tooth specific parameters β^T are hard to interpret here as they represent the comparison of two observations from the same tooth for the same subject, and this type of replication is not possible in the periodontal setting. After integrating over the tooth random effects, we are left with a subject specific model with coefficients denoted by “S” in Table 2. These coefficients are interpretable conditioned on the subject REs. For example, in the bridge model, we see the odds of a molar being missing or diseased are e^2.15 = 8.58 (95% credible set [7.17, 10.18]) times higher than other teeth for the same subject. Age is also interpretable at both the subject and population level. For a given individual, the odds of diseased/missing teeth increases 90% with each standard deviation increase in age- about 10.9 years. At the population level, however, the odds of a diseased/missing teeth increase by 58%, the attenuation due to averaging over between subject variability characterized by σ₁ in our model. It is important to emphasize that the subject- and population-level coefficients for the Gaussian REs model displayed in Table 2 are approximations, while in the bridge model these represent the exact log odds ratio. The GEE estimates also represent an exact marginal log odds ratio, and remain comparable to the population level estimates for both the Bayesian models. The 95% intervals for the GEE analysis are generally wider than those from bridge model with Gaussian copula, and unlike the Bayesian models the GEE analysis produces a (counterintuitive) significant protective effect of smoking on tooth loss.

Although various parameter estimates remain comparable across models, there are some notable differences. The nested REs model, the choice of RE distribution and copula has a large impact on the estimates. This is not surprising since different choices of REs/copula yield different scales, on which regression effects are estimated. For example, the population level estimate of the odds ratio corresponding to gender is e^−0.39 = 0.68 (0.49, 0.88) for the Gaussian model, as compared to 0.57 (0.40, 0.76) for the bridge model with Gaussian copula. It should be noted that the impact is mainly on the magnitude of effect estimates, though the inference remains consistent across all three models, that is, Age, Sex, HbA1c and the molar effect remain significant. Because of the relatively high degree of variation in the subject and tooth REs, there remain substantial differences in tooth-, subject-, and population-level interpretations of the coefficients. For example the estimated odds ratio for gender in the bridge model with Gaussian copula is e^βT = 0.15 at the tooth level, 0.45 at the subject level, and 0.57 at the population level. This difference in the conditional and marginal interpretations highlights the importance of correctly choosing conditional or marginal inference. There are also differences in the covariance parameter estimates across models. The between tooth variability is estimated much lower for the t-copula model than the Gaussian copula model, resulting in a lesser degree of marginal shrinkage. For the subject-and-site models, note that ${\sigma }_1={\sigma }_1^{*}/{\varphi }_2$ displayed in Table 2 is the total standard deviation of the subject REs γ_i, which depends on both ϕ₁ and ϕ₂. This is much greater than the standard deviation found in the subject only model. The range parameter is about 0.15, regardless of copula, suggesting a correlation of 0.6 between adjacent teeth.

In the Bayesian setting, we can also easily estimate the REs for each subject and tooth. This may be of particular interest in epidemiological settings, where we may, for instance, want to assess disease risk for certain states or counties, or look for areas with unusually high or low risk. To demonstrate this, Figure 4 display the estimated REs and posterior probabilities of a missing or diseased tooth at various tooth locations for an arbitrary subject. The posterior probabilities tend to be higher where teeth are missing.

Figure 4.

Posterior estimates of tooth level random effects ε_ij with central 90% credible intervals (Panel a), and posterior probability of a missing or diseased tooth at various tooth locations (Panel b) of an arbitrarily selected subject, obtained from the bridge model with Gaussian copula. The (dark) squares in the lower portion of each figure represent teeth that are missing or diseased.

6. Conclusions

In this article, we extend the bridge distribution to the spatial setting using a copula. Either a Gaussian or t-copula model can be implemented in standard software such as R or OpenBUGS. From our simulation study, we see that under REs misspecification, utilizing a bridge model did not result in a dramatic loss of efficiency. While comparing the fit to the dental dataset (see Table 2 in Section 5), the cross-validated measures (Brier score, CV₀, CV₁) are very close, although the bridge model (with the Gaussian copula) resulted in a lower DIC as compared to the Gaussian model. In any model selection problem the goodness of fit of the REs density should always remain the primary criterion in identifying the appropriate model to be utilized. However, (as in our dental data example) when both models produce similar fit, utilizing the bridge model allows for easy interpretability of regression coefficients at any level of a hierarchical model and the ability to estimate REs. In practice, there is often not enough data information to assess the distributional assumption of the (conditional) REs. Therefore, the bridge distribution may be viewed as a “vehicle” to assess and compare multilevel effects, and variations across data levels may reveal insights on level-specific heterogeneity. The information is often practically important since the source of variation is often of great interest.

A similar copula framework could be used to extend the other bridge specifications, such as for the complimentary-log-log link function for binary data (Wang and Louis, 2003), or other bridge-like distributions such as the positive stable distribution for failure time models (Hougaard, 1986), to a spatial setting. Generalizations to other copulas are also readily available. The Gaussian copula has been criticized in certain modeling applications, particularly when tail behavior is important. The copula implies symmetry of correlation - high-high combinations are as likely as low-low combinations. More concerning, extreme values are essentially independent of each other, which for binary data may impede adequately modeling large clusters of zeros or ones. There is no readily apparent way to extend the approach to models with random slope coefficients, as Wang and Louis (2003) point out for the univariate bridge distribution. It would be of interest to further explore the robustness of the bridge distribution to misspecified correlation structures or missing covariates, as well as choice of copula.

Finally, we stress that although our model was developed in the highly structured dental data setting with independent subjects and a regular grid of locations, the spatial bridge model is widely applicable to other kinds of spatial binary data. For example, a common setup in ecology is to measure the presence or absence of a species at many spatial locations. Two common objectives are to produce a spatial map of prevalence throughout the region of interest, and to estimate the effects of spatial covariates such as distance to a roadway or land-use on the presence of the species. These objectives can be addressed easily and simultaneously using the spatial bridge model, by interpolating the spatial random effects ε using standard Bayesian Kriging methods, and studying the posterior of the population parameters β^P.