A comparison of confounding adjustment methods with an application to early life determinants of childhood obesity

Abstract

We implemented 6 confounding adjustment methods: 1) covariate-adjusted regression, 2) propensity score (PS) regression, 3) PS stratification, 4) PS matching with two calipers, 5) inverse-probability-weighting, and 6) doubly-robust estimation to examine the associations between the BMI z-score at 3 years and two separate dichotomous exposure measures: exclusive breastfeeding versus formula only (N = 437) and cesarean section versus vaginal delivery (N = 1236). Data were drawn from a prospective pre-birth cohort study, Project Viva. The goal is to demonstrate the necessity and usefulness, and approaches for multiple confounding adjustment methods to analyze observational data.

Unadjusted (univariate) and covariate-adjusted linear regression associations of breastfeeding with BMI z-score were −0.33 (95% CI −0.53, −0.13) and −0.24 (−0.46, −0.02), respectively. The other approaches resulted in smaller N (204 to 276) because of poor overlap of covariates, but CIs were of similar width except for inverse-probability-weighting (75% wider) and PS matching with a wider caliper (76% wider). Point estimates ranged widely, however, from −0.01 to −0.38. For cesarean section, because of better covariate overlap, the covariate-adjusted regression estimate (0.20) was remarkably robust to all adjustment methods, and the widths of the 95% CIs differed less than in the breastfeeding example.

Choice of covariate adjustment method can matter. Lack of overlap in covariate structure between exposed and unexposed participants in observational studies can lead to erroneous covariate-adjusted estimates and confidence intervals. We recommend inspecting covariate overlap and using multiple confounding adjustment methods. Similar results bring reassurance. Contradictory results suggest issues with either the data or the analytic method.

INTRODUCTION

Valid causal inference from observational data requires at least two critical conditions: i) all confounders are measured and ii) are appropriately adjusted for in the analyses. Approaches such as instrumental variables¹ and sensitivity analyses² can sometimes be used to account for unmeasured confounders. However, instrumental variable analysis is not always possible because acceptable instrumental variables may not exist³. In this paper, we focus on the appropriate adjustment of measured confounders and do not consider issues such as unmeasured confounders, measurement error, or exposure or outcome mis-classification.

The classic confounding adjustment method is covariate-adjusted regression. However, an alternative class of methods is gaining increasing popularity⁴. These methods use the propensity score (PS), the conditional probability of receiving the exposure of interest given confounders⁵. The PS is effectively a summary score that incorporates information from multiple confounders in a single value. PSs address the “curse-of-dimensionality”⁶: a large number of confounders relative to the number of observations. Moreover, PSs can help in assessing overlap in the covariate space⁷. However, despite the increasing use of the PS-based methods and advanced methodological research in this area^8–12, understanding of how to correctly apply these methods and their potential impact is still limited^13,14.

Our purpose is to explore 6 confounding adjustment methods: covariate-adjusted regression¹⁵, PS regression¹⁶, PS stratification¹⁷, PS matching⁵, inverse-probability-weighting^18,19, and doubly-robust estimation²⁰. These are described succinctly in Table 1. Other than covariate-adjusted regression, all of these methods use PSs to adjust for confounding. To demonstrate the potential effects of adjustment, we compare results from two early life exposures that we and others have reported are associated with childhood obesity: breastfeeding status^21–24 and delivery type^25,26. In both cases, randomized trials are at best impractical, though it may be possible to use data from related trials to gain insight²⁷. Using these two examples, we review the strengths and weaknesses of the 6 confounding adjustment methods, use PSs to ensure overlap in the covariate space, examine the impact of choices made during implementation, discuss lessons learned from implementing them, and identify knowledge gaps.

Table 1.

Comparisons of the Six Confounding Adjustment Methods

Method*	Brief Summary	Strengths	Weaknesses
Covariate-adjusted regression15	Fit multivariable regression regressing the outcome on the exposure variable and confounders	Conventional approach Results relatively easy to understand and interpret Can be implemented in many statistical packages	Difficult to assess covariate overlap Limited covariates possible with rare binary outcomes
Propensity scores (applies to the five PS-based methods below)5	Fit logistic regression regressing exposure on the confounders Calculate propensity score (PS) as the probability of receiving the exposure of interest from this regression	Confounding is removed conditional on PS Facilitates the assessment of covariate overlap May be possible to adjust for multiple covariates and complex non-linear terms even with rare outcomes
PS regression16	Fit multivariable regression regressing the outcome on the exposure variable and the estimated PS		Requires PS to be correctly adjusted for in the regression model
PS stratification17	Estimate treatment effect within strata having similar PS Estimate treatment effect by combining stratum-specific effects	No additional modeling assumption	Residual confounding within strata since subjects have similar but non-identical PS
PS matching5	Construct matched pairs with subjects with similar PSs from each exposure group Conduct conditional analyses among the matched pairs to estimate treatment effect	No additional modeling assumption Can estimate either average treatment effect or average treatment effect on the treated	Residual confounding due to similar but non-identical PS within matched pair Different matching algorithms with respective advantages and disadvantages Different caliper may affect results
Inverse probability weighting18,19	Weight each subject by the inverse of the probability of receiving observed exposure Compare the outcomes between the two exposure groups in the weighted population	No additional modeling assumption Applies easily to settings with more than two exposure groups Can be extended to handle time-varying exposure and time-varying confounding	Exposed subjects with very small PSs or unexposed subjects with very large PSs have large weights and may lead to large standard errors.
Doubly robust estimation20	Combine the covariate adjusted model and the inverse probability weight using a complex augmentation term	Gives valid inference if either model is correct but not necessarily both	Complex Subjects with large weights may lead to large standard errors

^*All methods are subject to bias if covariate overlap is not present. All methods require correct specification of models. For regression, this is the relationship between the confounders and the outcome. For PS, this is the relationship between the confounders and the exposure. The exception is doubly robust estimation, for which one of these may be incorrect.

In this paper, we implement the 6 methods to adjust for baseline confounding. We do not intend to infer causality in either application example for the following two reasons. Firstly, the assumption of no unmeasured confounders is debatable. Secondly, breastfeeding during the first 6 months of life is not a one-time decision^24,28. During that period, mothers who breastfed likely considered multiple times whether to continue breastfeeding and made the decisions based on multiple factors that themselves changed over time. Some of these factors may well affect the childhood obesity outcome. To reduce difficult methodological issues raised by these relationships, we restricted our analyses to those who either exclusively breastfed or used formula-only during the first 6 months of life.

We use a continuous outcome for illustration purposes, but these methods can be applied to other types of outcomes such as binary outcomes. In fact, with binary outcomes, the PS-based approaches have more advantages over the covariate-adjusted regression approach because it is more challenging to impose a correct covariate-adjusted regression model for binary outcomes when the outcome is rare and the number of covariates is large relative to sample size.

METHODS

We begin by describing methods for covariate adjustment in more detail, then describe the two application examples.

Confounding adjustment methods

Covariate-adjusted regression

In covariate-adjusted linear regression, the outcome is regressed on the exposure variable and covariates. The validity of results depends on the correct specification of the regression model, meaning that all covariates, interactions, and quadratic, logarithmic, etc. functions affecting the exposure-outcome relationship are included. If these conditions are met, the parameter associated with the exposure is the difference in the outcome due to adding the exposure to any set of fixed values of the other covariates.

Propensity Scores

The propensity score (PS) is defined as the individual probability of receiving the exposure of interest⁵. PSs are typically estimated with a logistic regression model that regresses the exposure variable on observed confounders; PSs thus replace all of the confounders with a single value. In addition, PSs facilitate a requirement for valid covariate adjustment: overlapping covariate values, or “common support,” across the exposure groups. Common support is required to prevent extrapolation beyond the range of the data. Covariate overlap is absent, for example, when the exposure of interest group includes subjects aged 45–65 but the control group is limited to those aged 45–55. It can be challenging or tedious to detect poor covariate overlap when the ranges overlap, but the distribution in the two exposure groups differs substantially. For example, both groups might have ages between 45 and 65, but the exposed group might be 95% over age 55 and the unexposed 95% below age 55. It is quite difficult to detect this kind of differential distribution multidimesionally across a large set of covariates. However, it is relatively simple, as demonstrated below, to assess overlap using the PS.

After assessing overlap, PSs can be used to adjust for confounding in several ways: via regression, stratification, weighting, matching. The validity of each of these methods depends on a common assumption that the PS model is correctly specified, in the same sense as in the covariate-adjusted regression. The goodness-of-fit of the PS model can be assessed by comparing the distributions of the observed confounders between the exposure groups after adjusting for the estimated PSs¹⁷. The confounders should be distributed similarly between the exposure groups after adjustment. Since confounding can only affect inference if the confounders are unequally distributed between the exposure groups, valid causal inference is possible once this similarity is achieved.

Common-support regression

Common-support regression is simply covariate-adjusted regression conducted among the subset of patients within the common support. Common-support regression is generally preferred over covariate-adjusted regression as it avoids extrapolation into regions where one or the other exposure group provides little data.

PS regression

In PS regression, we regress the outcome on the exposure and the PS only. Conditional on the PS, exposure cannot be a result of confounding, so the exposure effect is un-confounded. However, analogous to covariate adjustment, the results might be biased if we do not adjust for PS appropriately in the regression model, for example if a required quadratic function of the PS is omitted¹⁶.

PS stratification

In PS stratification¹⁷, the study population is classified into strata with similar PSs. The exposure effect is estimated within each stratum and the exposure effects in each stratum are then pooled to obtain the population-wide average exposure effect. This approach does not require the additional modeling assumptions that PS regression does, but the results might be slightly biased because the PSs within strata are similar but not identical. Therefore, it is recommended to use more than 5 strata when sample size allows²⁹.

PS matching

PS matching avoids some potential issues in simpler approaches but is more complex in theory and application. In PS matching, each exposed and/or unexposed subject is matched with at least one “control” from the other exposure group with the same PS. If a matched control is found only for each exposed subject, we are estimating the average exposure effect among the treated³⁰ which sometimes is the preferred parameter of interest, but may be a biased estimate of the exposure effect in the population at large³⁰. Matching each exposed and non-exposed case ensures that the estimate is unbiased for the effect of exposure in the population at large.

Exact matching is typically infeasible, however, so in practice matches are required to have only similar PSs. We refer to the maximum allowable difference in PSs for a matched pair as the “caliper”¹⁰. Common choices of caliper include an absolute value of 0.05¹⁶ or 0.2 standard deviations of the logits of PS, i.e., of the log(PS/(1−PS))¹⁰. Subjects without eligible matches, i.e, no control with a PS within the caliper, are excluded from subsequent analyses. Conditional regression¹⁵ analyses are conducted among the matched pairs, to account for matching.

Matching can be done “with” or “without replacement”^7,31; with replacement means that, for example, a non-exposed subject may be the control for more than one exposed subject, and some subjects will likely be included in the analysis more than once. Matching with replacement reduces bias and thus is recommended, although a special variance estimator is required to appropriately account for the correlation due to duplication³².

In the sense that each PS-matched pair comprises two people with approximately equal probabilities of exposure, and one is in each exposure group, PS matching mimics randomization. Like stratification, PS matching does not require modeling the PS-outcome relationship. Residual confounding due to imperfect matching remains a concern for the validity of PS matching results.

Inverse probability weighting

In inverse-probability-weighting^18,19, each subject is weighted by the inverse of the probability of being assigned to their actual exposure group: 1/PS for exposed subjects and 1/(1 − PS) for unexposed subjects. Confounding is removed in the resulting weighted “pseudo-population” (7,8) so that linear regression applied to the pseudo-population estimates the un-confounded exposure effect.

The inverse-probability-weighting approach does not require modeling the PS-outcome relationship. In using the exact PS value, it avoids the risks of residual confounding within strata and imprecise matches. Moreover, it can be used without further modification in settings with multiple exposure groups. However, the standard error of the treatment effect may be large, due to large weights for subjects with PSs close to 0 or 1. Truncating weights or excluding subjects with extremely large weights may partially address this issue but could diminish the advantages described above and lead to estimating a different quantity than the one of interest.^16,33

Doubly-robust estimation

Doubly-robust estimation combines the PS and covariate adjustment. In covariate-adjusted regression, the association between covariates and outcome needs to be accurately modeled; in the PS-based analyses described above, the logistic regression predicting the exposure needs to be correctly modeled. Doubly-robust estimation is valid if either model is correct but not necessarily both²⁰. The original doubly-robust approach, which was proposed in Bang et al.²⁰, functions by adding to the inverse-probability-weighting estimator an augmentation term, which depends on the predicted outcome from the multivariable regression model and the PSs. This term converges to zero when the PS is correct, but offsets the bias of the inverse-probability-weighting estimator when the PS is wrong and the outcome regression function is correct. This is a complex procedure. Interested readers are referred to Bang et. al.²⁰ for technical details. A SAS macro is available to implement this method³⁴.

Table 1 summarizes each of the 6 methods and their strengths and weaknesses.

Application examples

We apply the forgoing methods to assess the associations of breastfeeding and cesarean section with body mass index (BMI) at age 3.

Study population

Study subjects were participants in Project Viva, a prospective observational cohort study of pre- and peri-natal factors and maternal and child health³⁵. Details of recruitment and retention procedures are available elsewhere³⁵.

We have previously published on the association of both breastfeeding (16) and caesarean section (17) with 3-year BMI z-score in Project Viva.

Outcome

At the 3-year Project Viva visit, we measured each child’s height with a research-standard stadiometer (Shorr Productions, Olney, Maryland, USA), and weight with a digital scale (Seca model 881, Seca Corporation, Hanover, Maryland, USA). We calculated BMI as weight in kg/(height in m)². The outcome of interest was the age- and sex-specific BMI z-score at the participant’s 3-year visit, calculated using US national reference data³⁶.

Exposure variables

Breastfeeding during the first 6 months of life was assessed by interviews at 6 months or 1 year postpartum²¹. We restricted our analyses to two subgroups: “exclusive breastfeeding” (infants whose only liquid energy source was breast milk during the first 6 months of life), and “formula only” (only formula during the first 6 months). Caesarean section versus vaginal delivery was derived from hospital medical records.

Covariates

In Tables 2 and 3, we list the potential confounders considered in the covariate-adjusted regression analyses in the original publications^21,25; not all were included in the final published models. These are all baseline covariates measured prior to either exposure.

Table 2.

Breastfeeding in First Six Months of Life (Exclusively-breastfed vs. Formula-fed Only). Characteristics Among All Subjects, Among Subjects With PS in (0.350, 0.993), and Among Matched Pairs. Data From Project Viva

		Observed data			Observed data with 0.350<PS<0.993			Matched pairs (0.350<PS<0.993, Matching caliper= 0.05)
		Exclusively breastfed (311)	Formula- fed only (126)		Exclusively breastfed (223)	Formula- fed only (53)		Exclusively breastfed (276)	Formula- fed only (276)
Maternal characteristics
		N (%)		p*	N (%)		p*	N (%)		p#
Age, years	<25 25–<35 >=35	8 (2.6) 198 (63.6) 105 (33.7)	13 (10.3) 82 (65.1) 31 (24.6)	<.01	5 (2.2) 141 (63.2) 77 (34.5)	1 (1.9) 34 (64.2) 18 (34.0)	0.98	8 (2.9) 172 (62.3) 96 (34.8)	6 (2.2) 135 (48.9) 135 (48.9)	0.48
Education level	High school or less Some college BA/BS Grad school	7 (2.3) 41 (13.2) 112 (36.1) 150 (48.3)	18 (14.3) 47 (37.3) 43 (34.1) 18 (14.3)	<.01	6 (2.7) 24 (10.8) 91 (40.8) 102 (45.7)	2 (3.8) 12 (22.6) 25 (47.2) 14 (26.4)	0.03	9 (3.3) 38 (13.8) 119 (43.1) 110 (39.9)	3 (1.1) 32 (11.6) 130 (47.1) 111 (40.2)	0.63
Race/Ethnicity	Black Hispanic Other White	25 (8.1) 9 (2.9) 26 (8.4) 250 (80.6)	19 (15.1) 6 (4.8) 6 (4.8) 95 (75.4)	0.07	13 (5.8) 8 (3.6) 14 (6.3) 188 (84.3)	3 (5.7) 2 (3.8) 1 (1.9) 47 (88.7)	0.65	15 (5.4) 17 (6.2) 18 (6.5) 226 (81.9)	10 (3.6) 20 (7.3) 5 (1.8) 241 (87.3)	0.34
US Born	Yes	260 (85.2)	117 (94.4)	0.03	199 (89.2)	51 (96.2)	0.12	242 (87.7)	233 (84.4)	0.75
House hold income>US $70,000		216 (72.9)	57 (49.1)	<.01	167 (74.9)	39 (73.6)	0.84	199 (72.1)	242 (87.7)	0.01
Pre-pregnancy BMI, kg/m2	<25 25–<30 >=30	224 (72.7) 66 (21.4) 18 (5.8)	61 (48.4) 37 (29.4) 28 (22.2)	<.01	157 (70.4) 52 (23.3) 14 (6.3)	36 (67.9) 17 (32.1) 0 (0.0)	0.10	190 (68.8) 70 (25.4) 16 (5.8)	207 (75.0) 69 (25.0) 0 (0.0)
Gestational weight gain (IOM 2009 guideline)	Inadequate Adequate Excessive	34 (11.2) 99 (32.6) 170 (56.1)	14 (11.2) 32 (25.6) 79 (63.2)	0.33	24 (10.8) 63 (28.3) 136 (61.0)	5 (9.4) 18 (34.0) 30 (56.6)	0.71	33 (12.0) 79 (28.6) 164 (59.4)	23 (8.3) 135 (48.9) 118 (42.8)	0.26
Mother herself was breastfed	Yes	129 (44.0)	17 (14.7)	<.01	92 (41.3)	11 (20.8)	<.01	110 (39.9)	112 (40.6)	0.97
Maternal glucose tolerance status	Gestational diabetes Impaired glucose tolerance Isolated hyperglycemia Normal	10 (3.3) 8 (2.6) 28 (9.1) 261 (85.0)	11 (8.8) 3 (2.4) 7 (5.6) 104 (83.2)	0.07	7 (3.1) 5 (2.2) 21 (9.4) 190 (85.2)	4 (7.6) 0 (0.0) 4 (7.6) 45 (84.9)	0.33	13 (4.7) 5 (1.8) 23 (8.3) 235 (85.1)	14 (5.1) 0 (0.0) 10 (3.6) 252 (91.3)
Smoking during pregnancy	Former During pregnancy Never	58 (19.2) 10 (3.3) 233 (77.4)	29 (23.8) 24 (19.7) 69 (56.6)	<.01	47 (21.1) 6 (2.7) 170 (76.2)	15 (28.3) 2 (3.8) 36 (67.9)	0.46	56 (20.3) 10 (3.6) 210 (76.1)	122 (44.2) 4 (1.5) 150 (54.4)	0.09
Nullipara		154 (49.5)	39 (31.0)	0.01	101 (45.3)	19 (35.9)	0.21	117 (42.4)	84 (30.4)	0.23
Paternal BMI, kg/m2	<25 25–<30 >=30	122 (40.8) 145 (48.4) 32 (10.7)	27 (22.7) 65 (54.6) 27 (22.7)	<.01	82 (36.8) 116 (52.0) 25 (11.2)	12 (22.6) 33 (62.3) 8 (15.1)	0.14	93 (33.7) 149 (54.0) 34 (12.3)	81 (29.4) 176 (63.8) 19 (6.9)	0.34
Father US born	Yes	255 (84.7)	103 (90.4)	0.14	192 (86.1)	50 (94.3)	0.10	239 (86.6)	244 (88.4)	0.82
Child characteristics
Female sex		159 (51.1)	66 (52.4)	0.81	117 (52.5)	27 (50.9)	0.84	141 (51.1)	124 (44.9)	0.58
Cesarean section		51 (16.5)	34 (27.0)	0.01	39 (17.5)	9 (17.0)	0.93	47 (17.0)	46 (16.7)	0.96
		Mean (SD)		p*	Mean (SD)		p*	Mean (SD)		p#
Birth weight for gestational age z- score		0.3 (0.9)	0.21 (0.9)	0.34	0.4 (0.9)	0.3 (0.8)	0.56	0.3 (0.9)	0.4 (0.8)	0.77
Gestational age at birth, weeks		39.8 (1.3)	39.4 (1.5)	<.01	39.9 (1.4)	39.7 (1.4)	0.25	39.9 (1.4)	39.4 (1.4)	0.13
Census-derived socio-economic status variables, expressed as percent of census tract population (Census 2000 data)
% 25 years or older with no high school diploma		9.3 (8.7)	9.2 (8.5)	0.94	7.9 (7.4)	6.6 (5.5)	0.15	8.3 (7.8)	6.5 (5.3)	0.16
% 25 years or older with college degree and above		47.2 (20.1)	31.0(15.1)	<.01	45.9 (17.9)	38.4(13.4)	<.01	43.6 (17.9)	44.7(14.5)	0.71
% below poverty line (1999 dollars)		10.4 (9.2)	6.1 (6.2)	<.01	11.1 (9.4)	7.8 (6.1)	<.01	10.3 (9.2)	9.8 (5.8)	0.17
% households with 1999 income below $20,000		16.9 (9.7)	18.7(10.3)	0.09	15.6 (8.8)	15.3 (7.9)	0.85	15.9 (9.3)	15.5 (7.3)	0.79
% household with 1999 income $150,000 and above		11 (8.6)	14.4 (9.1)	<.01	10.9 (8.2)	11.2 (5.5)	0.81	11.6 (8.8)	9.9 (5.1)	0.69

^*p-value from chi-square test or t-test

^#p-value from generalized score tests for Type III contrasts from PROC GENMOD to adjust for repeated use of the same subjects since matching was done with replacement

Table 3.

Delivery Mode (Cesarean Section vs. Vaginal Delivery). Characteristics Among All Subjects, Among Subjects With PS in (0.095, 0.530), and Among Matched Pairs. Data From Project Viva

		Observed data			Observed data (0.095<PS<0.530)			Matched pairs (0.095<PS<0.530, Matching caliper= 0.05)
		Caesarean section (280)	Vaginal Delivery (956)		Caesarean section (224)	Vaginal Delivery (710)		Caesarean section (934)	Vaginal Delivery (934)
Maternal characteristics
		N (%)		p*	N (%)		p*	N (%)		p#
Age, years	<25 25–<35 >=35	16 (5.7) 172 (61.4) 92 (32.9)	79 (8.3) 586 (61.3) 291 (30.4)	0.33	10 (4.5) 139 (62.1) 75 (33.5)	25 (3.5) 449 (63.2) 236 (33.2)	0.80	34 (3.6) 614 (65.7) 286 (30.6)	35 (3.8) 590 (63.2) 309 (33.1)	0.84
Education level	High school or less Some college BA/BS Grad school	15 (5.4) 60 (21.4) 107 (38.2) 98 (35.0)	81 (8.5) 203 (21.3) 346 (36.3) 323 (33.9)	0.39	8 (3.6) 47 (21.0) 86 (38.4) 83 (37.1)	29 (4.1) 141 (19.9) 274 (38.6) 266 (37.5)	0.97	27 (2.9) 227 (24.3) 363 (38.9) 317 (33.9)	41 (4.4) 189 (20.2) 359 (38.4) 345 (36.9)	0.60
Race	Black Hispanic Other White	38 (13.6) 17 (6.1) 29 (10.4) 196 (70.0)	114 (12.0) 59 (6.2) 82 (8.6) 698 (73.2)	0.68	23 (10.3) 13 (5.8) 19 (8.5) 169 (75.5)	58 (8.2) 38 (5.4) 47 (6.6) 567 (79.9)	0.53	77 (8.2) 55 (5.9) 78 (8.4) 724 (77.5)	89 (9.5) 44 (4.7) 80 (8.6) 721 (77.2)	0.91
US Born	Yes	219 (79.6)	783 (82.9)	0.18	182 (81.3)	595 (83.8)	0.37	780 (83.5)	777 (83.2)	0.92
House hold income >US $70,000		165 (60.7)	578 (65.2)	0.17	144 (64.3)	483 (68.0)	0.30	607 (65.0)	629 (67.3)	0.59
Pre- pregnancy BMI, kg/m2	<25 25–<30 >=30	161 (57.5) 63 (22.5) 56 (20.0)	640 (67.2) 203 (21.3) 109 (11.5)	<.01	131 (58.5) 53 (23.7) 40 (17.9)	472 (66.5) 164 (23.1) 74 (10.4)	<.01	611 (65.4) 186 (19.9) 137 (14.7)	606 (64.9) 214 (22.9) 114 (12.2)	0.56
Gestational weight gain (IOM 2009 guideline)	Inadequate Adequate Excessive	28 (10.0) 70 (25.0) 182 (65.0)	118 (12.6) 287 (30.6) 534 (56.9)	0.05	21 (9.4) 55 (24.6) 148 (66.1)	77 (10.9) 206 (29.0) 427 (60.1)	0.28	79 (8.5) 248 (26.6) 607 (65.0)	95 (10.2) 279 (29.9) 560 (60.0)	0.52
Mother herself was breastfed	Yes	24 (30.4)	122 (37.0)	0.27	90 (41.7)	278 (41.0)	0.36	394 (43.3)	366 (41.1)	0.64
Maternal glucose tolerance status	Gestational diabetes Impaired glucose tolerance Isolated hyperglycemia Normal	14 (5.1) 14 (5.1) 21 (7.6) 228 (82.3)	35 (3.7) 25 (2.6) 91 (9.6) 796 (84.1)	0.11	10 (4.5) 7 (3.1) 20 (8.9) 187 (83.5)	30 (4.2) 14 (2.0) 74 (10.4) 592 (83.4)	0.70	43 (4.6) 21 (2.3) 95 (10.2) 775 (83.0)	45 (4.8) 18 (1.9) 88 (9.4) 783 (83.8)	0.98
Smoking during pregnancy	During pregnancy Former Never	4 (4.9) 21 (25.9) 56 (69.1)	30 (8.8) 66 (19.4) 245 (71.9)	0.27	2 (3.1) 20 (30.8) 43 (66.2)	18 (6.7) 61 (22.8) 189 (70.5)	0.26	11 (3.8) 80 (27.9) 196 (68.3)	23 (6.7) 87 (25.1) 236 (68.2)	0.68
Nullipara		143 (51.1)	442 (46.2)	0.15	116 (51.8)	319 (44.9)	0.07	447 (47.9)	437 (46.8)	0.82
Paternal BMI, kg/m2	<25 25–<30 >=30	78 (29.3) 132 (49.6) 56 (21.1)	343 (37.4) 454 (49.5) 121 (13.2)	<.01	63 (28.1) 119 (53.1) 42 (18.8)	243 (34.2) 372 (52.4) 95 (13.4)	0.07	287 (30.7) 521 (55.8) 126 (13.5)	308 (33.0) 485 (51.9) 141 (15.1)	0.70
Father US born	Yes	214 (82.6)	717 (81.4)	0.65	187 (83.5)	587 (82.7)	0.78	751 (80.4)	780 (83.5)	0.41
Child characteristics
Female sex		135 (48.2)	472 (49.4)	0.73	105 (46.9)	350 (49.3)	0.52	490 (52.5)	456 (48.8)	0.44
Exclusive breastfeeding during the first 6 months		51 (18.2)	259 (6.3)	<.01	42 (18.8)	199 (28.0)	0.09	185 (19.8)	252 (27.0)	0.31
		Mean (SD)		p*	Mean (SD)		p*	Mean (SD)		p#
Birth weight for gestational age z-score		0.3 (1.0)	0.2 (0.9)	0.04	0.3 (1.0)	0.3 (0.9)	0.41	0.2 (1.0)	0.3 (0.9)	0.78
Gestational age at birth, weeks		39.6 (1.5)	39.7 (1.4)	0.44	39.6 (1.5)	39.7 (1.4)	0.52	39.4 (1.6)	39.7 (1.4)	0.08
Census-derived socio-economic status variables, expressed as percent of census tract population (Census 2000 data)
% 25 years or older with no high school diploma		8.9 (7.7)	9.5 (9.0)	0.25	8.2 (7.3)	8.1 (7.3)	0.87	8.0 (6.7)	8.3 (7.3)	0.65
% 25 years or older with college degree and above		38.5 (18.3)	40.8 (20.4)	0.07	39.2 (18.1)	41.5 (18.8)	0.10	40.6 (18.9)	41.3 (19.0)	0.71
% below poverty line (1999 dollars)		8.3 (8.3)	9.0 (8.7)	0.21	8.6 (8.3)	9.2 (8.4)	0.38	8.5 (7.7)	9.1 (8.3)	0.67
% households with 1999 income below $20,000		17.4 (9.2)	17.7 (10.5)	0.66	16.6 (8.6)	16.3 (8.8)	0.70	16.5 (8.2)	16.5 (8.8)	0.96
% household with 1999 income $150,000 and above		13.1 (8.9)	12.9 (9.8)	0.76	12.4 (8.4)	11.9 (8.1)	0.41	12.3 (8.6)	12.0 (8.0)	0.42

^*p-value from chi-square test or t-test

^#p-value from generalized score tests for Type III contrasts from PROC GENMOD to adjust for repeated use of the same subjects since matching was done with replacement

Statistical analyses

For both the breastfeeding and cesarean section examples, we implemented: 1) crude (univariate) regression; 2) covariate-adjusted regression using the covariates included in the final published models; and 3) covariate-adjusted regression with the larger set of covariates in Tables 2 and 3.

We fitted logistic regression models to estimate PSs, adjusting for the covariates listed in Tables 2 and 3. Variable selection in PS modeling is an important topic. We do not tackle this issue here. Project Viva collected a much larger set of covariates than those listed in Tables 2 and 3. In this paper, we only consider the subset of covariates that were selected by subject matter experts as potential confounders. Covariate balance was assessed using the F-test after PS stratification with quintiles¹⁷.

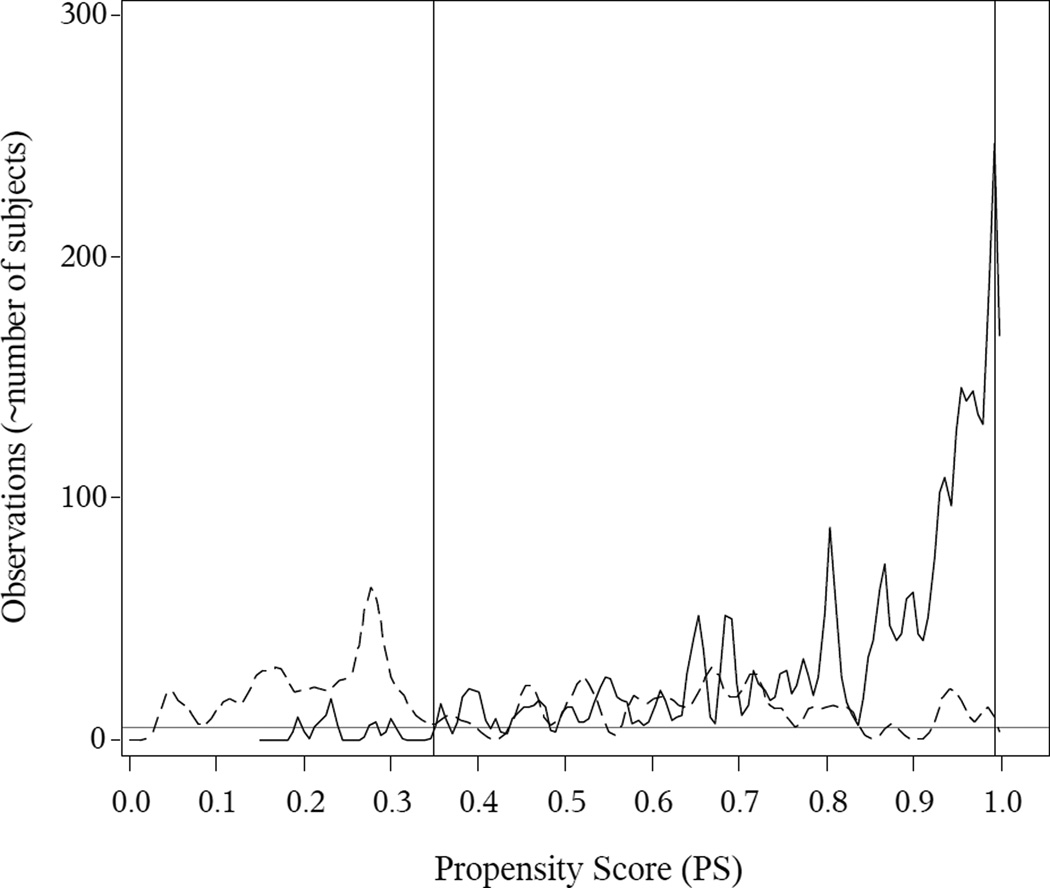
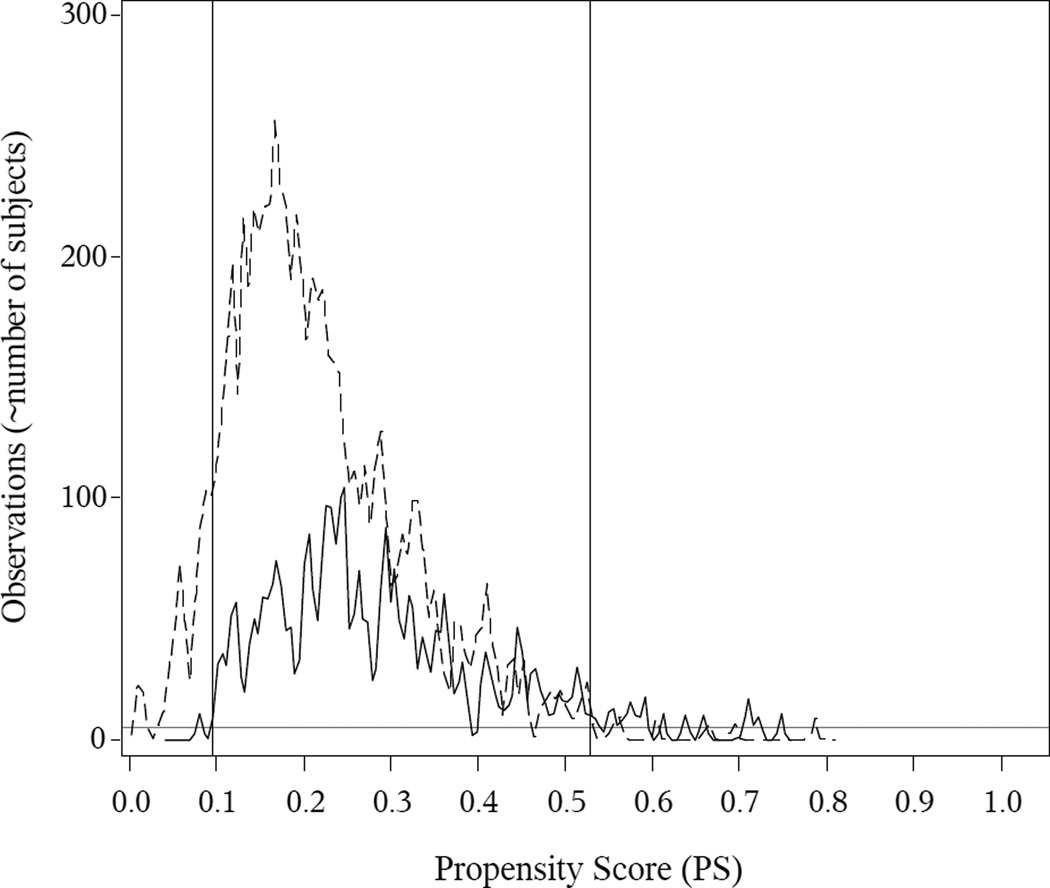
Theoretical guidance on determining the common support is not available, and we determined the common support region on an ad-hoc basis. We plotted smoothed histograms of the PSs within each group, based on kernel density estimates. These plots (Figures 1 and 2) show values of the PS for which each exposure group has at least a few observations, and we defined common support as the range of PS over which there are generally at least 5 observations in each exposure group.

Figure 1. Breastfeeding in First Six Months of Life (Exclusively-breastfed vs. Formula-fed Only): PS Kernel Density Estimates and Common Support.

The solid (exclusive breastfeeding) and dotted (exclusive formula) curves indicate the within-group smoothed histograms for the PSs, based on kernel density estimates. The grey horizontal line indicates a reference at 5 observations. The vertical lines indicate the common support, which we define as the interval on which the within-group kernel density estimates are mostly 5 or above. Here is the observed common support is (0.350, 0.993).

Figure 2. Delivery Mode (Cesarean Section vs. Vaginal Delivery): PS Kernel Density Estimates and Common Support.

The solid (C-section) and dotted (vaginal birth) curves indicate the within-group smoothed histograms for the PSs, based on kernel density estimates. The grey horizontal line indicates a reference at 5 observations. The vertical lines indicate the common support, which we define as the interval on which the within-group kernel density estimates are mostly 5 or above. Here the observed common support is (0.095, 0.530).

We implemented the three regression adjustment methods listed above and PS regression with and without considering the PS-based common support to directly assess the impact of limiting covariates to the region of common support. Observations outside the common support were excluded from other analyses.

In PS regression, we regressed the outcome on the exposure variable and the PS. Adding polynomial terms for the PS up to the 5^th order had little impact on the estimated exposure effect and variance; we report the model with linear adjustment only. For PS stratification, we used quintiles instead of higher-order quantiles due to relatively small numbers of formula-only babies and cesarean section births. In PS matching, we used two caliper values, 0.05 and 0.01. Each exposed and unexposed subject was matched to a subject in the other group, if one existed within the caliper. We used matching with replacement and accounted for this using the conservative Abadie-Imbens variance estimator³². In the breastfeeding example, we found some subjects with large weights in the inverse-probability-weighting and doubly-robust approaches, and additionally re-calculated the estimates from these two methods with PSs truncated at 0.95; truncation near 0 was unnecessary because subjects with small values had already been removed due to a lack of common support. Truncation in the cesarean section example was unnecessary after removing subjects lacking common support. In doubly-robust estimation, we considered two multivariable regression models with one including all covariates and the other including published covariates only. All analyses were done in SAS 9.3 (SAS Institute, Cary NC) except PS matching, which was implemented using the R package ‘Matching’ (R 2.15.2)³⁷.

RESULTS

For breastfeeding, there were 437 subjects in the univariate analyses; 412 had complete data on relevant variables and were included in the covariate-adjusted regression with published covariates. Sample size further decreased to 354 in the regression with a larger set of covariates. For cesarean section, the corresponding sample sizes were 1236, 1229, and 1019.

For the PS analyses, we first examined the PS overlap to determine the common support, illustrated in Figures 1 and 2. For breastfeeding, the common support region was (0.350, 0.993), i.e., subjects with PSs less than or equal to 0.35 or greater than or equal to 0.993 were excluded from further analyses. For cesarean section, the common support was (0.095, 0.530). In eTable 1 in the supplementary material, we present the descriptive statistics among those that were within the common support versus those that were outside the common support.

In Tables 2 and 3, we present the descriptive statistics for the two examples respectively. For each example, we present the statistics among the entire study population, among those within the common support region, and among the matched pairs constructed in the common support with a caliper of 0.05. Subjects outside the support were younger, less educated, more likely to be non-white, less wealthy, heavier, to have smoked during pregnancy. Due to a poorer PS overlap in the breastfeeding example than in the cesarean section example, a larger proportion of subjects fell outside the common support and thus were excluded. It appears that covariate balance was improved by restricting to subjects within the common support region and further improved by PS matching.

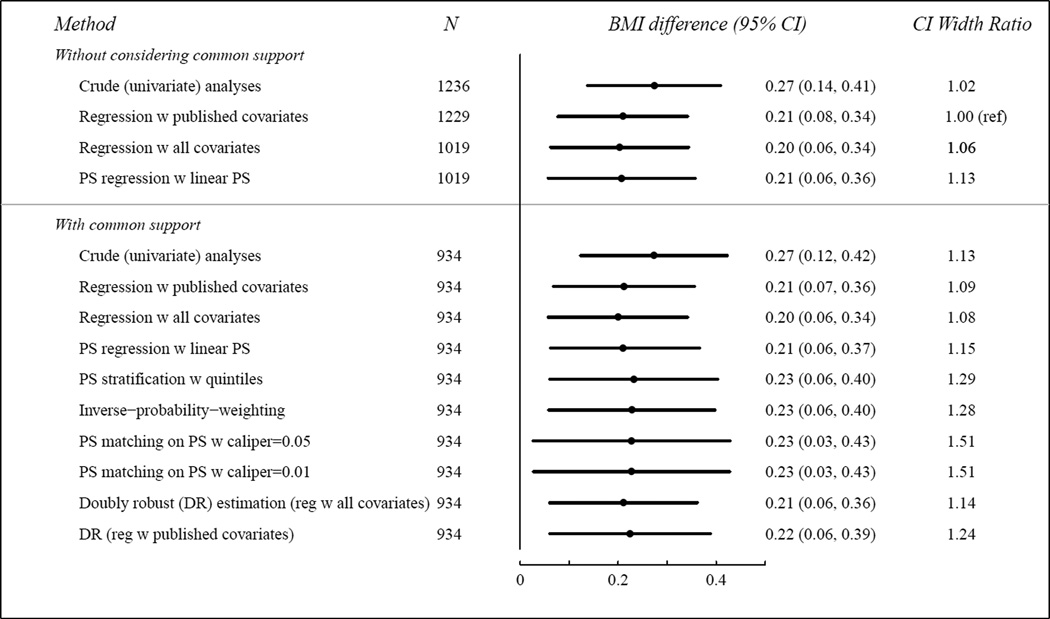
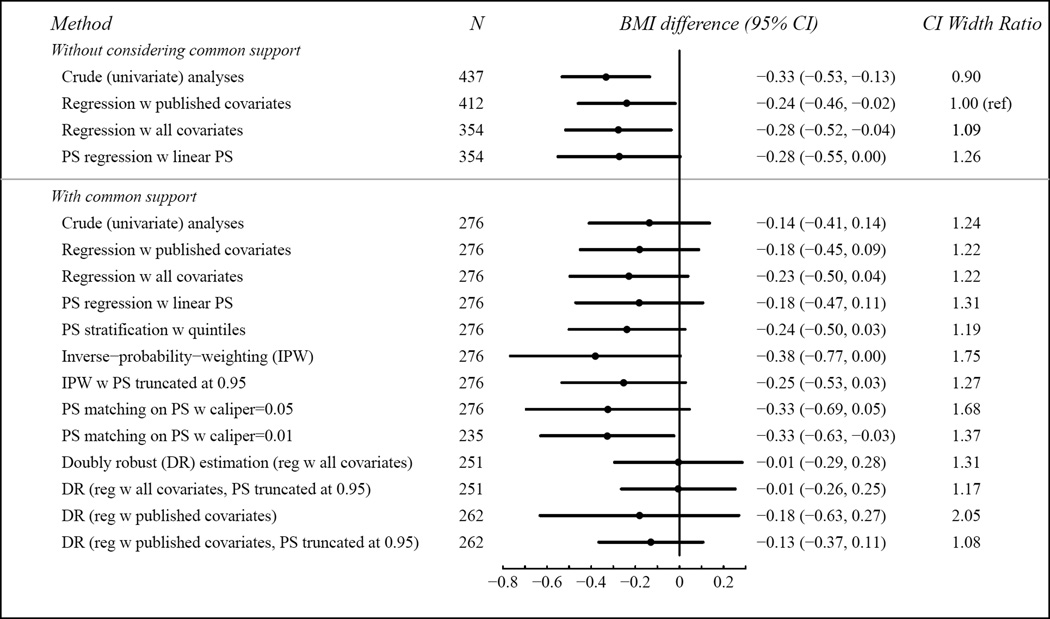
In the breastfeeding example, all analyses yielded qualitatively similar results, with the exception of the doubly-robust method with all covariates. In addition, the doubly-robust method was sensitive to the choice of covariates in that all covariates resulted in very different estimates compared to published covariates. In contrast, in multivariable regression, the other method which uses multivariable outcome regression, this choice did not materially affect the results.

Inverse-probability-weighting, PS matching with a caliper of 0.05, and doubly-robust estimation with published covariates yielded notably wider CIs than the other methods. The greater standard errors for the inverse-probability-weighting method were likely driven by the few formula-only babies whose PSs were close to 1 and whose weights were thus large. PS truncation at 0.95 helped to reduce the standard error. For PS matching, the selection of caliper affected CI width. The CI width was, surprisingly, narrower with a smaller caliper, despite a smaller sample size. A similar result was seen for the doubly-robust estimation.

For cesarean section, the estimated difference in BMI between caesarian and vaginally delivered children was remarkably consistent across adjusted methods, and the widths of the CIs differed less than in the breastfeeding example (Figure 4). The caliper choice had little impact. The CIs from PS matching were the widest, likely due to the conservative variance estimate³².

Figure 4. Delivery Mode (Cesarean Section vs. Vaginal Delivery): Difference in 3-year BMI z-score.

The last column indicates the ratio of each CI width divided by the CI width from the covariate-adjusted regression with published covariates approach.

DISCUSSION

We implemented several confounding adjustment methods to examine the associations of exclusive breastfeeding and cesarean section with 3-year BMI z-score: naïve covariate-adjusted regression, covariate-adjusted regression among all study subjects and among those within the common support, PS regression, PS stratification, PS matching, inverse-probability-weighting, and doubly-robust estimation. Each of the 6 methods has its own advantages and disadvantages and none is uniformly superior to others. Analysts need to select the method(s) that suit their data setting and pay close attention to the implementation caveats we illustrated in this paper via the two empirical examples.

One important observation is that accounting for covariate overlap can have a substantial impact, even on results from multivariable regression. In the breastfeeding example, restricting the sample to those within common support attenuated the point estimate from multivariable regression by 18%, from −0.28 to −0.23. In the cesarean section example, point estimates and CIs were more similar, presumably because the proportion of overlap was greater. In addition, the definition of the common support region may affect the results from all methods. The breastfeeding effect estimate and CI both varied widely with various definitions of the common support region (data not shown). The impact is likely to be bigger when the sample size is relatively small and PS overlap is relatively poor.

Secondly, inverse-probability-weighting and doubly-robust estimation may have large standard errors. Truncating PS at a minimum value, e.g., 0.05, and a maximum value, e.g., 0.95 may partially address this problem, but it may introduce bias. For breastfeeding, the CI width for inverse probability weighting and doubly-robust estimation with multivariable regression with published covariates decreased by 35% (from 0.77 to 0.50) and 47% (from 0.90 to 0.48) respectively after PSs were truncated at 0.95. For cesarean section, PSs were bounded away from 0 and 1 and thus the weights not large in either exposure group. The other methods do not use these weights and thus are not subject to this issue.

Thirdly, the selection of caliper is important for PS matching. For breastfeeding, the point estimate remained the same when the caliper decreased from 0.05 to 0.01, but the 95% CI width decreased by 19% (from 0.74 to 0.60). We do not recommend drawing conclusions based on an arbitrary criterion of whether the 95% CI includes or excludes the null value. But it is worth noting that if such an arbitrary criterion was used, different inference would have been obtained depending on which caliper was used.

Fourthly, the doubly-robust method in theory should result in estimates similar to either the covariate-adjusted regression or inverse-probability-weighting. In this example, however, the finite-sample performance of this method in the breastfeeding example is inconsistent with its large-sample, theoretical property. Thus, the corresponding results should not be used to derive inference in this case. The failure of the doubly-robust method here could be due to the small sample size, particularly the small number of formula-fed babies, and relatively poor overlap between the two exposure groups.

The six methods considered in this paper all assume there is no unmeasured confounding. The focus of this paper is on how to appropriately adjust for measured covariates. If residual confounding bias is a concern, there exist multiple sensitivity analyses methods^38–42 that extend these confounding adjustment methods to assess how the results may vary as the amount of residual confounding bias exists. This is beyond the scope of this paper.

In summary, we compared several of the many existing confounding adjustment methods. For cesarean section, both the point and interval estimates were remarkably robust to method selection and implementation. This finding brings reassurance but does not guarantee the accuracy or precision of the estimated mean difference. The results for breastfeeding were less similar across analyses. However, apart from doubly-robust estimation, all other analyses yielded qualitatively similar results.

We recommend assessing covariate overlap and limiting covariates to the region of common support no matter which confounding adjustment method is used. In addition, we recommend conducting analyses with multiple methods and varying implementation factors to help identify potential issues. One particular method can be pre-specified as the primary analysis and others viewed as sensitivity analyses. Consistency or inconsistency among the results should be assessed by point and interval estimates, not by whether p-values were above or below the 0.05 cut-off. More work is needed to guide implementation of each method, including how to select the common support; whether and how to truncate PS weights; and how to select the PS matching caliper.

Figure 3. Breastfeeding in First Six Months of Life (Exclusively-breastfed vs. Formula-fed Only): Difference in 3-year BMI z-score.

The last column indicates the ratio of each CI width to the CI width from the covariate-adjusted regression with published covariates approach.