Simultaneously Extracting Multiple Parameters via Fitting One Single Autocorrelation Function Curve in Diffuse Correlation Spectroscopy

Abstract

Near-infrared diffuse correlation spectroscopy (DCS) has recently been employed for noninvasive acquisition of blood flow information in deep tissues. Based on the established correlation diffusion equation, the light intensity autocorrelation function detected by DCS is determined by a blood flow index αD_B, tissue absorption coefficient μ_a, reduced scattering coefficient μ_s’, and a coherence factor β. The present study is designed to investigate the possibility of extracting multiple parameters such as μ_a, μ_s’, β, and αD_B through fitting one single autocorrelation function curve and evaluate the performance of different fitting methods. For this purpose, computer simulations, tissue-like phantom experiments and in-vivo tissue measurements were utilized. The results suggest that it is impractical to simultaneously fit αD_B and μ_a or αD_B and μ_s’ from one single autocorrelation function curve due to the large crosstalk between these paired parameters. However, simultaneously fitting β and αD_B is feasible and generates more accurate estimation with smaller standard deviation compared to the conventional two-step fitting method (i.e., first calculating β and then fitting αD_B). The outcomes from this study provide a crucial guidance for DCS data analysis.

I. INTRODUCTION

Near-infrared (NIR) light has recently been employed for noninvasive acquisition of blood flow information in deep tissues (up to several centimeters), which is referred to as NIR diffuse correlation spectroscopy (DCS) [1, 2] or diffusing-wave spectroscopy (DWS) [3-5]. Blood flow variations measured by DCS have been validated in various organs and tissues against other standards, including Doppler ultrasound [6], power Doppler ultrasound [7], laser Doppler [8], Xenon-CT [9], fluorescent microsphere flow measurement [10], and perfusion MRI [11]. DCS delivers continuous-wave (CW) coherent NIR light into tissue wherein photons encounter absorption and, more commonly, scattering events. The probabilities of these events are described by tissue optical properties: absorption coefficient μ_a and reduced scattering coefficient μ_s’. Scattered light is detected by a photodetector placed on the tissue surface at a certain distance (e.g., several centimeters) from a light source. Most photons detected experience multiple scattering events and each scattering event is associated with a random scattering phase shift. The superposition of multiple light fields with different phases creates a speckle pattern of interference.

The motions of moving scatterers, primarily red blood cells in biological tissues, cause fluctuations in light intensity, leading to changes in speckle pattern. These fluctuations/changes carry information about the dynamic properties of moving red blood cells. Time dependent light intensity fluctuations can be measured by the photodetector on the tissue surface and quantified by temporal autocorrelation functions. The electric field autocorrelation function is related to the measured light intensity autocorrelation function through the Siegert relation [12]. It has been found that the electric field autocorrelation function is governed by a correlation diffusion equation [1, 2], and blood flow index (BFI) in biological tissues can be calculated by fitting the measured autocorrelation function curve with the solution of correlation diffusion equation.

Based on the correlation diffusion equation and Siegert relation, however, the measured light intensity autocorrelation function is determined by not only blood flow, but also tissue optical properties (i.e., μ_a and μ_s’) and a coherence factor β. β relies mainly on light source and detection optics. It is thus desirable to extract as much information as possible (i.e., multiple parameters) from one single autocorrelation function. Some previous studies have chosen to use the values of μ_a and μ_s’ from literature respective to the measured tissue type (e.g., brain or muscle) for the calculation of DCS blood flow [13, 14]. These assumptions are susceptible to deviations in tissue optical properties [15]. A few of recent studies have employed hybrid instruments (NIR spectroscopy combining DCS) allowing for concurrent measurements of both μ_a and μ_s’ to extract accurate BFI [6, 16-18]. In addition, most previous studies estimated β based on the Siegert relation using the measured autocorrelation function data at the earliest correlation delay time, and then fitted BFI (i.e., two-step fitting method) [7, 19-22]. Although a few recent studies claimed fitting β and BFI simultaneously [18, 23, 24], none of them have compared the performance of the two methods (i.e., simultaneous fitting versus two-step fitting).

The present study is designed to investigate the possibility of simultaneously extracting multiple parameters such as μ_a, μ_s’, β, and BFI through fitting one single autocorrelation function curve and evaluate the performance of different fitting methods. For this purpose, computer simulations, tissue-like phantom experiments, and in-vivo tissue measurements were utilized. It is expected that the outcomes from this study will ultimately improve DCS data analysis.

II. METHODS

A. Diffuse Correlation Spectroscopy (DCS) for Flow Measurements

The flow index is quantified by a DCS flowmeter built in our laboratory. Details about DCS for flow measurements can be found elsewhere [8, 21, 22, 25, 26]. Briefly, long-coherence (> 5 meters) NIR CW light emitted from a laser diode (785 nm, ~100 mw, Crystalaser Inc., NV) enters the tissue via a 200 μm diameter multimode source fiber (Thorlabs, Inc., NJ). The transported/scattered light through tissue is collected by a ~5 μm diameter single-mode detector fiber (SM 600, Fibercore Inc., CA) connected to a single-photon-counting avalanche photodiode (APD, PerkinElmer Inc., Canada). The transistor-transistor logic (TTL) pulses are output from the APD and associated with the number of photons detected from a small area covering a single speckle on tissue surface. These signals are fed into a correlator board (correlator.com, NJ) for computing the light intensity [i.e., photon count rate with a unit of kilo counts per second (kcps)] and intensity temporal autocorrelation function [1, 2]:

$$g_2(\overrightarrow{r},\tau )=\frac{\langle I(\overrightarrow{r},t)\cdot I(\overrightarrow{r},t+\tau )\rangle }{{\langle I\rangle }^2}$$ (1)

Here $\mathrm{I}(\overrightarrow{r},t)$ is the detected light intensity at position $\overrightarrow{r}$ and time t, ⟨…⟩ denotes a time average, and τ is the autocorrelation delay time. The sampling rate for the DCS flowmeter is 1 Hz.

In highly scattering media, such as biological tissues, the electric field temporal autocorrelation function $G_1(\overrightarrow{r},\tau )=\langle \overrightarrow{E}(\overrightarrow{r},t)\cdot {\overrightarrow{E}}^{\ast }(\overrightarrow{r},t+\tau )\rangle$ satisfies the correlation diffusion equation [1, 2]:

$$\left(\mathrm{D}{\nabla }^2-\nu {\mu }_a-\frac{1}{3}\nu {\mu }_s^{\prime }{k}_0^2\alpha \langle \Delta r^2\left(\tau \right)\rangle \right)G_1(\overrightarrow{r},\tau )=-\nu S\left(\overrightarrow{r}\right)$$ (2)

Here, v is the speed of light in the medium, k₀ is the wavenumber of light in the medium, $\mathrm{S}\left(\overrightarrow{r}\right)$ is the source light distribution, α is defined as the ratio of moving scatterers to total scatterers, μ_a is medium absorption coefficient, μ_s’ is reduced scattering coefficient, D = v/3 (μ_a + μ_s’) is the photon diffusion coefficient, and <Δr²(τ)> is the mean-square displacement of moving scatterers in time τ. Intuitively, the random flow model might be considered the best model with which to fit DCS data. In practice, however, it has been observed that the diffusion model fits the autocorrelation curves rather well over a broad range of tissue types [6, 7, 10, 13, 15, 16, 19-21, 27-33]. For the case of diffusive motion, <Δr²(τ)> = 6D_Bτ, where D_B is the effective Brownian diffusion coefficient of scatterers. The combined term, αD_B, is referred to as blood flow index (BFI) in biological tissues and is commonly used to calculate the relative change of blood flow (rBF), compared to baseline BFI before physiological changes. The unit of BFI (αD_B) is cm²/s. Although this unit is different from the classical blood flow unit in biological tissues (ml/min/100ml), percentage changes in αD_B have been found to correlate well with the blood flow changes measured by many other established modalities [8-11, 34].

The homogeneous CW solution to Eq. (2) for a semi-infinite geometry is [35]

$$G_1(\rho ,\tau )=\frac{\nu S_0}{4\pi D}\left(\frac{\text{exp}(-K(\tau \left)r_1\right)}{r_1}-\frac{\text{exp}(-K(\tau \left)r_2\right)}{r_2}\right)$$ (3)

Here ρ is the source-detector separation, S₀ is source intensity, $K^2\left(\tau \right)=3{\mu }_a{\mu }_s^{\prime }+{\mu }_s^{\prime 2}{k}_0^2\alpha \langle \Delta r^2\left(\tau \right)\rangle =3{\mu }_a{\mu }_s^{\prime }+6{\mu }_s^{\prime 2}{k}_0^2\alpha D_B\tau$, $r_1={\left[{\rho }^2+{(z-z_0)}^2\right]}^{\frac{1}{2}}$, $r_2={\left[{\rho }^2+{(z+z_0+2z_b)}^2\right]}^{\frac{1}{2}}$, $z_0=\frac{1}{{\mu }_s^{\prime }}$, $z_b=\frac{2(1+R_{\mathit{eff}})}{3{\mu }_s^{\prime }(1-R_{\mathit{eff}})}$, R_eff = −1.440n⁻² + 0.710n⁻¹ + 0.668 + 0.0636n and n ≈ 1.34. The R_eff is the internal reflection coefficient which accounts for the refractive index mismatch between the medium and air, and n is the ratio of reflective indices between them.

The normalized electric field autocorrelation function $g_1(\overrightarrow{r},\tau )=\frac{G_1(\overrightarrow{r},\tau )}{G_1(\overrightarrow{r},0)}$ is related to the measured intensity autocorrelation function $g_2(\overrightarrow{r},\tau )$ through the Siegert relation [12]:

$$g_2(\overrightarrow{r},\tau )=1+\beta {\mid g_1(\overrightarrow{r},\tau )\mid }^2$$ (4)

Here β is a coherence factor and inversely proportional to the number of speckles detected. Although complete understanding of all factors that affect β needs further investigation, it is thought to mainly depend on light source and detection optics. The light source may be influenced by light coherence, laser stability and stray light while the detection optics may be affected by the detector stability and fiber-tissue coupling coefficient. Some of these factors (if not all) may change during the time course of measurements, leading to a variation in β. When a single-mode fiber is used for DCS flow detection, the maximum β value should be ~0.5 considering the two orthogonal polarization modes collected from the fiber [36]. When a polarizer is placed on the detector fiber, a β value of ~1 can be achieved. However, β will decrease when few-mode fibers (instead of the single-mode fiber) are used [37].

B. Noise Model for Simulation of Autocorrelation Functions

In order to simulate autocorrelation functions measured in real media, a proper estimate of measurement noises is needed. Previously, a noise model with single scattering limit in fluorescence correlation spectroscopy [38] has been adopted for use in diffuse correlation experiments wherein photons experience multiple scattering events [28, 37]. The phantom experiments demonstrated that the noise model provided a good estimate of DCS measurement noises in homogeneous media with infinite geometry. Briefly, the measured correlation function [g₂(τ) − 1] was assumed to decay approximately exponentially, i.e., g₂(τ)−1 = β exp(−Γτ. The experimental configuration was characterized by the correlator bin time interval T, bin index m corresponding to the delay time τ, average number of photons <n> within T [i.e., <n> = I·T, where I was the detected photon intensity], total averaging time t, and coherence factor β. The noise [standard deviation σ(τ)] of the measured correlation function [g₂(τ) − 1] at each delay time τ was estimated to be [28, 38]:

$$\sigma \left(\tau \right)=\sqrt{\frac{T}{t}}{[{\beta }^2\frac{(1+e^{-2\Gamma T})(1+e^{-2\Gamma \tau })+2m(1-e^{-2\Gamma T})e^{-2\Gamma \tau }}{(1-e^{-2\Gamma T})}+2{\langle n\rangle }^{-1}\beta (1+e^{-2\Gamma \tau })+{\langle n\rangle }^{-2}(1+\beta e^{-\Gamma \tau }\left)\right]}^{\frac{1}{2}}$$ (5)

Accordingly, the signal-noise-ratio (SNR) of DCS measurements at delay time τ was $\mathit{SNR}\left(\tau \right)=\frac{g_2\left(\tau \right)-1}{\sigma \left(\tau \right)}$, and 1/SNR(τ) can be used to estimate the noise level of DCS measurements.

For the case of diffuse reflectance measurement on medium surface, a semi-infinite geometry should be considered instead and Eq. (3) should be used to calculate [g₂(τ) − 1] rather than the assumption of exponential decay function as used in Reference [28]. However, mathematically it is difficult to derive a noise model based on the complex Eq. (3). In the present study, we designed phantom experiments to test the accuracy of this noise model [Eq. (5)] for use in homogeneous media with semi-infinite geometry. Tissue-like liquid phantoms were created with Intralipid for control of scattering (μ_s’) and particle Brownian motion (αD_B), India ink for control of absorption (μ_a), and distilled water [15]. Although temperature can affect Brownian motions (αD_B) of Intralipid particles, the room temperature was controlled constant (~23 °C) in order to obtain stable αD_B (flow). Tissue-like liquid phantoms have been commonly used for the calibration of DCS techniques [1, 15, 27]. The phantom was contained in a glass aquarium. A fiber-optic probe with a pair of source and detector fibers at a distance of 2.5 cm was secured in contact with the surface of the liquid phantom solution using a custom-designed holder. We set constant μ_s’ = 8 cm⁻¹ and vary μ_a (0.075, 0.100, 0.150 cm⁻¹) by adding ink to test the noise-model under different levels of noise. Higher μ_a was associated with lower number of photons detected (I), thus leading to higher level of noise [σ(τ)].

After the noise model was verified for semi-infinite geometry, it was used to generate the normalized intensity autocorrelation curve g₂ with noise. An autocorrelation curve (g₂) was firstly generated using Eq. (3) and Eq. (4). The standard deviation σ(τ) of [g₂(τ) − 1] was then calculated using Eq. (5), wherein the β and Γ were obtained concurrently by fitting the g₂ curve with the exponential approximation (the concurrent fitting method can be found in Section II-D), i.e., g₂(τ)−1 = β exp(−Γτ). Following a Gaussian distribution with zero mean and standard deviation σ(τ), noises that varied at different delay time τ were generated. The simulated noises were then applied on g₂(τ) to create an intensity autocorrelation curve with noise. As indicated in Eq. (5), the SNR and noise level (1/SNR) of simulated autocorrelation functions were adjusted by changing the light intensity or photon count rate (I = <n>/T).

C. Extraction of Multiple Parameters through Fitting One Single Autocorrelation Curve

Multiple parameters examined (i.e., αD_B, μ_a, μ_s’ and β) were extracted by fitting the measured autocorrelation function curve to the analytical solution of correlation diffusion equation [Eq. (3)]. The goal was to minimize the sum of squared differences (SSD) between the measured and calculated autocorrelation functions. The minimization of the objective function SSD = ∑[g_2,m(τ) - g_2,c(τ)]² was done by using Nelder-Mead simplex algorithm (fminsearch function) in Matlab (Mathwork, Inc., MA), where g_2,m(τ) was the measured intensity autocorrelation function and g_2,c(τ) was the analytical model of autocorrelation in the semi-infinite reflection geometry [Eq. (3)]. Initial guesses for these parameters were assigned randomly using the “rand” function in Matlab. The random variation ranges of these parameters were determined based on the dynamic ranges in DCS phantom experiments and in-vivo measurements: μ_a = 0.05 to 0.4 cm⁻¹, μ_s’ = 2 to 15 cm⁻¹, αD_B = 0.4 to 2 × 10⁻⁸ cm²/s, and β = 0.1 to 0.9. We set the termination tolerance for the fitted variables (TolX) at 10⁻¹¹, which is ~1000 times smaller than the value of αD_B (0.4 to 2 × 10⁻⁸ cm²/s). This termination criterion is strict enough to obtain precise results for all four parameters.

In order to determine the possibility of fitting μ_a, μ_s’ or β along with αD_B from one single autocorrelation curve, we examined the SSD change patterns by varying three pairs of the four parameters (i.e., μ_a and αD_B, μ_s’ and αD_B, β and αD_B), respectively. For this purpose, a reference light intensity autocorrelation curve without noise, g₂₀, was initially generated using Eq. (3) and Eq. (4) with the given parameters: μ_a = 0.12 cm⁻¹, μ_s’ = 8 cm⁻¹, αD_B = 10⁻⁸ cm²/s, and β = 0.45. The paired parameters were then varied to generate multiple testing autocorrelation curves. The variation ranges of these parameters were the same as those indicated above. The SSDs between the testing autocorrelation curves and the reference autocorrelation curve g₂₀ were calculated and presented in contour plots as functions of these paired parameters, respectively. Different SSD patterns (e.g., convergence or divergence) implied the possibility of extracting multiple parameters from one single autocorrelation curve.

The possibility of extracting multiple parameters was further examined by fitting the paired parameters simultaneously from the reference autocorrelation curve g₂₀ with two different levels of noise (I = 100 and 50 kcps). For each noise level, 1000 simulated curves were generated and fitted to extract the paired parameters simultaneously. The discrepancies between the fitted and given values of the paired parameters are expressed as “percentage errors”.

D. Comparison of Two Methods for Extracting β and αD_B

In most previous studies, extracting αD_B began with using Eq. (4) to determine β. Using DCS measured g₂ data at earliest τ and letting g₁ ≈ 1 [i.e., $g_1(\rho ,0)=\frac{G_1(\rho ,0)}{G_1(\rho ,0)}=1$] led to β = g₂(ρ,τ ≈ 0)−1. Using g₂(ρ,τ), β and Eq. (4), g₁(ρ,τ) was calculated for all τ. Equation (3) was then used with the unknown parameter αD_B to fit the g₁(ρ,τ) derived from DCS measurements. In addition, one could also average more g₂ datasets (i.e., several data points instead of one single data point) at early τ to reduce the noise influence for determining β.

During the study of extracting multiple parameters from one single autocorrelation curve (see Section II-C), we found it possible to simultaneously fit both β and αD_B (see Sections III-A and III-C). To compare the performance between the two methods (i.e., two-step fitting versus simultaneously fitting) for extracting β and αD_B, computer simulations, phantom experiments and in-vivo tissue measurements were utilized. For simulations, the reference autocorrelation curves g₂₀ with noise were generated based on the procedures described in Section II-B, and the levels of noise were changed by varying photon count rate from 20 to 500 kcps. At each noise level, 1000 curves were created and fitted by the two methods to examine if they were able to extract the expected values of β and αD_B from the simulated curves.

The simulation results were further verified with the data collected from the phantom experiments (see Section II-B) and in-vivo tissue measurements in forearm flexor muscle. A single-mode detector fiber was placed at a distance of 2.5 cm from the source fiber for the phantom or tissue measurement. The source and detector fibers were confined in their positions by a foam pad to form a fiber-optic probe which was placed on the surface of the measured phantom or tissue. The in-vivo measurement was taken from one healthy volunteer who signed the informed consent approved by the University of Kentucky Institutional Review Board. Before the experiment, absolute values of tissue optical properties (μ_a and μ_s’) in forearm flexor muscle were measured by a frequency-domain NIR tissue-oximeter (Imagent, ISS Inc., IL). The measured μ_a and μ_s’ were used as input parameters in calculation of β and αD_B with the two methods. To reduce the influence of physiological variations, the baseline drift of the in-vivo tissue measurement was removed using a first order high-pass Butterworth filter with a cutoff frequency of 0.05 Hz. For statistical analyses, significances of the difference between the two methods were tested using a paired t-test. The criterion for significance is p < 0.05.

III. RESULTS

A. The Noise Model can be Used in Homogeneous Media with Semi-infinite Geometry

Figure 1 shows the results from phantom experiments to verify the feasibility of applying the noise model in homogeneous media with semi-infinite geometry. During the three titrations of varying μ_a (0.075, 0.100, 0.150 cm⁻¹) while keeping μ_s’ constant (8 cm⁻¹), photon counting rates changed correspondingly (66, 41, 20 kcps). 267, 237 and 235 autocorrelation curves were collected sequentially at the three titration steps. The noise [σ(τ)] (Fig. 1a) and SNR (Fig. 1b) of the autocorrelation function at each τ were calculated and plotted (see the dots in Fig. 1). The solid curves represent the calculated noises or SNRs using Eq. (5) with the parameters obtained from the phantom experiments; β and Γ were obtained simultaneously by fitting the experimental data with the exponentially decaying function (see Sections II-C and II-D); the averaging time to obtain one correlation function curve was kept constant (t = 1 s) for all measurements; the photon count rates were recorded by the correlator board; the bin time interval T was 121 ns for the first 32 channels and doubled every 16 channels thereafter. As shown in Fig. 1, the measurement noise decreased as the delay time τ or light intensity increased, whereas the SNR increased as the light intensity increased and changed with the variation of delay time τ. These results are consistent with the predictions from Eq. (5) and suggest that the noise model provides a good estimate for DCS noises measured in homogeneous media with semi-infinite geometry.

Fig. 1.

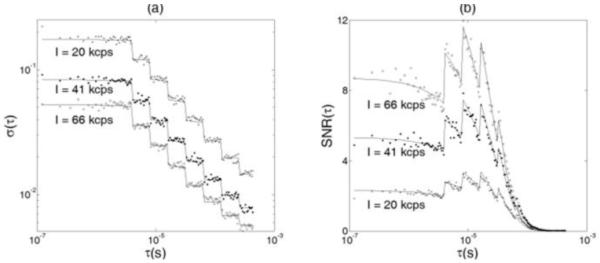
Tissue-like phantom experiments to verify the feasibility of applying the noise model in homogeneous media with semi-infinite geometry. DCS measurements were performed in three liquid phantoms with different μ_a (0.075, 0.100, 0.150 cm⁻¹) to test the noise model under different noise levels. Higher μ_a was associated with lower number of photons detected (I), thus leading to higher measurement noise [σ(τ)] and lower signal-to-noise ratio [SNR(τ)]. (a) Comparison of the measurement noises between the measured autocorrelation curves from the phantoms (dots) and calculated noises predicted by the noise model (solid curves). The measurement noise decreased as the delay time τ increased. The “steps” were due to the multi-tau arrangement of the correlator. (b) Comparison of the SNRs between the measured autocorrelation curves and model predictions. Although the measurement noise decreased as the delay time τ increased, the SNR of DCS measurement also decreased because the “signal” dropped even faster than the noise as τ increased.

We then used this noise model to generate autocorrelation curves (g₂) with three different levels of noise (I = 20, 41, 66 kcps) observed in phantom tests. Figure 2 (a, b, c) shows the results comparing the simulated and measured (from phantoms) g₂ curves with the same levels of noise. Again, the results demonstrate that the noise model works well in homogeneous media with semi-infinite geometry.

Fig. 2.

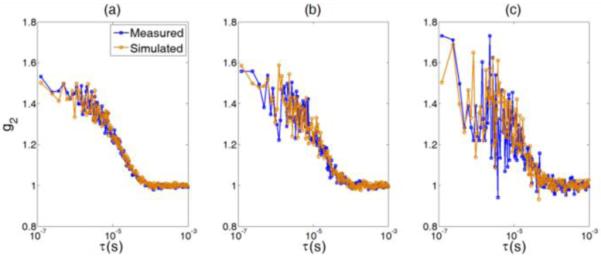
Comparison of the simulated and measured g₂ curves at three different levels of noise: (a) I = 66 kcps; (b) I = 41 kcps; and (c) I = 20 kcps. The input parameters for simulation were acquired from the phantom experiments.

B. SSD Patterns Imply the Possibility of Extracting Multiple Parameters from One Single Autocorrelation Curve

As indicated in Section II-C, a reference g₂ curve without noise was generated with the given parameters: μ_a = 0.12 cm⁻¹, μ_s’ = 8 cm⁻¹, αD_B = 10⁻⁸ cm²/s, β = 0.45. The SSDs between the reference curve g₂₀ and the testing curves generated by varying the values of paired parameters were calculated and presented in Fig. 3. The SSD values were marked on the curves.

Fig. 3.

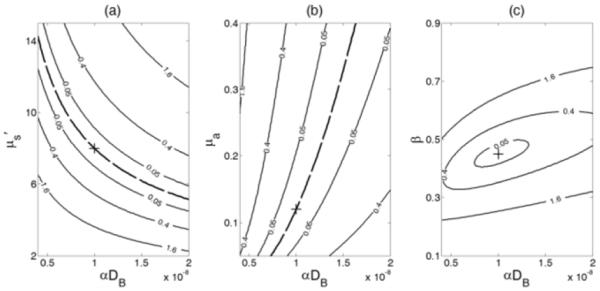
Contour plots of sum of squared differences (SSD) between a reference autocorrelation curve g₂₀ obtained with the given parameters [αD_B = 10⁻⁸ cm²/s, μ_a (785 nm) = 0.12 cm⁻¹, and μ_s’ (785 nm) = 8 cm⁻¹] and the testing curves generated by varying the values of paired parameters. The true reference values of g₂₀ are marked at the cross. (a) The SSDs obtained by varying μ_s’ from 2 to 15 cm⁻¹ and αD_B from 0.4 to 2 × 10⁻⁸ cm²/s. The dashed black curve represents the points at which local minima were achieved with compositions of μ_s’ and αD_B. (b) The SSDs obtained by varying μ_a from 0.05 to 0.4 cm⁻¹ and αD_B from 0.4 to 2 × 10⁻⁸ cm²/s. The dashed black curve illustrates the points at which local minima were achieved. (c) The SSDs obtained by varying β from 0.1 to 0.9 and αD_B from 0.4 to 2 × 10⁻⁸ cm²/s. The minimum value of SSD was reached at the true reference values of β and αD_B.

Different patterns of SSD were observed for different pairs of parameters. The curves for the pairs of μ_s’/αD_B (Fig. 3a) and μ_a/αD_B (Fig. 3b) were divergent although the proportional relationships between the two paired parameters were opposite. Large crosstalk existed between αD_B and μ_a or αD_B and μ_s’, even if when the SSDs were close to zero (see the dashed curves in Fig. 3a and Fig. 3b). Due to the fact that the SSD was a highly nonlinear function of μ_a, μ_s’, β and αD_B, the points on the dashed lines did not have exactly the same SSD value with one another, but the differences among these values were extremely small. Although the cross (+) point (with the true reference values) was the absolute minimum, there were numerous local minima along the dashed line. This made it difficult to obtain the absolute minimum at the cross point because the searching algorithm could get stuck easily in a local minimum. Conversely, the curves for the pairs of β and αD_B (Fig. 3c) were convergent. The minimum value of SSD was reached at the true reference values of β and αD_B (the cross point). In total, these results suggest that it is possible to fit β and αD_B simultaneously and precisely.

C. Simultaneously Fitting μ_a, μ_s’ or β along with αD_B from One Single Autocorrelation Curve

The results we got from Section III-B were further confirmed by simultaneously fitting the simulated autocorrelation g₂₀ curves with different levels of noise. Figure 4 shows the fitting results for extracting the three pairs of parameters simultaneously. The upper (Fig. 4a and Fig. 4b) and lower (Fig. 4c and Fig. 4d) panels represent the simulation results with two different levels of noise (I = 100 and 50 kcps). As expected, simultaneously fitting μ_a and αD_B may result in estimation errors; underestimating/overestimating μ_a of −60%/+200% led to flow index errors up to −100%/+50%. Simultaneously fitting μ_s’ and αD_B may generate even larger errors than simultaneously fitting μ_a and αD_B; underestimating/overestimating μ_s’ from −40%/+200% led to flow index errors up to +120%/−80%. These errors were mainly due to the crosstalk between the paired parameters. By contrast, when fitting β and αD_B simultaneously, the output values of fitted parameters (β and αD_B) clustered around the true values (Fig. 4b and Fig. 4d). The estimation errors for both β and αD_B at the two noise levels were smaller than 15%.

Fig. 4.

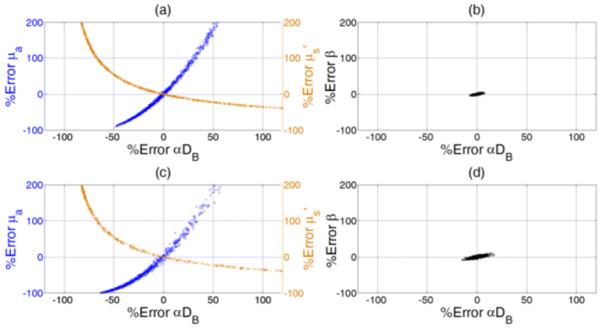
Percentage errors when simultaneously fitting three pairs of four variables respectively from the simulated autocorrelation curves (g₂₀) generated at two different levels of noise. The initial guesses of the fitted variables were assigned randomly when fitting each of the 1000 simulated g₂₀ curves._The discrepancies between the fitted and given values of the paired parameters are expressed as “% errors”. The upper (a and b) and lower (c and d) panels represent simulation results with two different levels of noise (I = 100 and 50 kcps). Higher noise level caused larger evaluation errors. The left panel (a and c) shows the results when simultaneously fitting αD_B and μ_s’ or αD_B and μ_a. Large crosstalk between the paired parameters was apparent, resulting in large estimation errors. The right panel (b and d) shows the results when simultaneously fitting β and αD_B. The estimation errors for both β and αD_B were much smaller than those shown in the left panel (a and c).

D. Results from the Comparison of Two Methods for Extracting β and αD_B

The results shown in Sections III-B and III-C indicate that β and αD_B can be simultaneously extracted by fitting one single autocorrelation curve. To compare the performance of the concurrent-fitting method with the conventional two-step fitting method (i.e., first calculating β and then fitting αD_B) for extracting β and αD_B, computer simulations, phantom experiments, and in-vivo tissue measurements were conducted in the present study.

Figure 5 shows the comparison results from the simulated g₂₀ curves with different levels of noise (i.e., photon count rate varied from 20 to 500 kcps). For the two-step method, we used either the first data point (upper panel) or averaged seven data points (lower panel) of g₂₀ at early delay time τ to estimate β. For both concurrent and two-step fitting methods, the standard deviation of fitted values increased with the increase of noise level. However, simultaneously fitting β and αD_B generated more accurate values with significantly smaller standard deviations (error bars) compared to the two-step fitting method (p < 0.001). Inaccurate estimation of β resulted in errors in fitting αD_B, which became more remarkable when the noise level increased. As expected, using one point to estimate β resulted in large standard deviations of estimation, which can be reduced by averaging more data points (7 points in this simulation) of g₂₀. Because of the decay of autocorrelation curve with τ (see Fig. 2), however, the averaging led to significant underestimations of β and αD_B (p < 0.001).

Fig. 5.

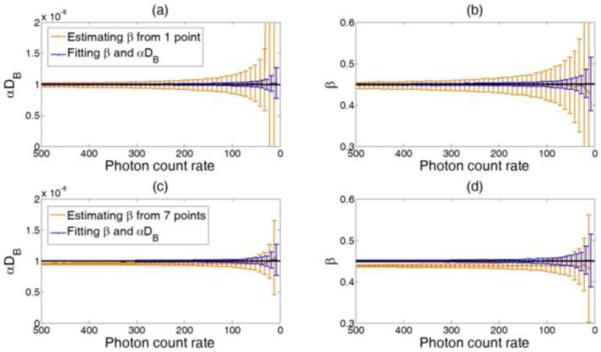
Comparison of the two methods for extracting β and αD_B from the simulated g₂₀ curves under different noise levels (i.e., the photon count rate changes from 500 kcps to 20 kcps). Dashed lines indicate the expected values (β = 0.45 and αD_B = 1 × 10⁻⁸ cm²/s). For both methods, the standard deviation (error bar) of the fitted values increased with the increase of noise level. Fitting β and αD_B simultaneously resulted in unbiased and more accurate estimation of the means and smaller standard deviations compared to the two-step fitting method. When estimating β from the first point (a and b), the standard deviations of β and αD_B were large. Estimating β from more points (c and d) reduced the standard deviations of estimation with the cost of estimation biases in β and αD_B.

These simulation results were confirmed by the phantom experiments and in-vivo tissue measurements. Figure 6a shows the estimation deviations of β and αD_B from the phantom experiments described in Section II-B. Notice that only the data from the second step of titration (μ_a = 0.10 cm⁻¹) are presented although the results from the other two steps (μ_a = 0.075 and 0.15 cm⁻¹) were similar. Since the concurrent-fitting method generated accurate estimates for β and αD_B (see simulation results above), the mean values of β and αD_B obtained by this method were assumed to be ‘true’ values of the measured phantom. The percentage deviations of β and αD_B estimated from each autocorrelation curve are presented as error bars in Fig. 6a. Compared to the concurrent-fitting method, inaccurate estimation of β by the two-step fitting method may result in significant estimation errors in αD_B (p < 0.001) and lead to larger error bars.

Fig. 6.

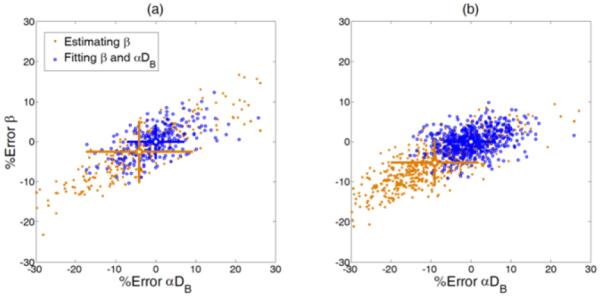
The performance of the two fitting methods evaluated with the (a) phantom test and (b) in-vivo measurement. The mean values obtained by the simultaneous fitting method were assumed as ‘true’ values, and the discrepancies between the values extracted using the simultaneously fitting method or two-step fitting method are presented as percentage errors. The error bars are shown with crosses respectively and the mean values are located at the center of the crosses.

Similarly, Figure 6b shows the estimations of β and αD_B from the data collected in in-vivo tissue measurements described in Section II-D. 574 autocorrelation curves were collected from the subject’s forearm using the DCS device. The results shown in Fig. 6b agreed with those of the simulations shown in Fig. 5 and the phantom experiments shown in Fig. 6a.

IV. DISCUSSION AND CONCLUSIONS

This study was designed to investigate the possibility of extracting multiple parameters such as μ_a, μ_s’, β, and αD_B through fitting one single autocorrelation function curve and compare the performance of different fitting methods. For this purpose, the patterns of the sum of squared differences (SSD) between the reference autocorrelation curve (g₂₀) and the testing autocorrelation curves generated by varying the values of paired parameters were examined; different SSD patterns (e.g., convergence or divergence) implied the possibility of extracting multiple parameters from a single autocorrelation curve. These results were then verified by computer simulations, phantom experiments and in-vivo tissue measurements.

For simulations with our measurement configuration, a noise model for homogeneous media with semi-infinite geometry is needed to generate autocorrelation curves with noise. Previous studies have used a noise model described in Section II-B as an approximation [28, 37], which has never been validated in semi-infinite geometry. In the present study, we designed phantom experiments to test the accuracy of this noise model for use in homogeneous media with semi-infinite geometry. The phantom experimental results agreed with the theoretical predictions from the noise model (Fig. 1a and Fig. 1b) suggesting that it provides a good estimate for DCS noises measured in homogeneous media with semi-infinite geometry. This noise model was thus used to generate autocorrelation curves with different levels of noise, and the simulated curves were compared with the curves collected from phantom measurements (Fig. 2a, Fig. 2b and Fig. 2c). The comparison results confirmed that this noise model worked well in homogeneous media with semi-infinite geometry.

To investigate the possibility of fitting μ_a, μ_s’ or β along with αD_B from one single autocorrelation curve, we examined the SSD change patterns by varying three pairs of the four parameters. According to the results, a large crosstalk between the αD_B and μ_a or αD_B and μ_s’ (Fig. 3a and Fig. 3b) existed, suggesting that it is impractical to simultaneously extract αD_B and μ_a or αD_B and μ_s’ from one single autocorrelation curve. Conversely, the SSD curves for the pairs of β and αD_B were convergent, suggesting a possibility to extract β and αD_B simultaneously. These results were then verified by simultaneously fitting the paired parameters from the simulated autocorrelation curves with noise generated by the noise model. Fitting αD_B and μ_a or αD_B and μ_s’ simultaneously caused large estimation errors (Fig. 4a and Fig. 4c) that were majorly due to the large crosstalk between the paired parameters. These simulation results (Fig. 4a and Fig. 4c) agree very well with our previous findings in phantom titration tests (see Fig. 6 in Ref. [15]). By contrast, when fitting β and αD_B simultaneously, the estimation errors for both parameters were much smaller (Fig. 4b and Fig. 4d), although they were increased with the increase of noise level.

Upon examination of the K(τ) definition [see Eq. (3)], the crosstalk between αD_B and μ_a or αD_B and μ_s’ is expected as these paired parameters can compensate each other to generate a similar autocorrelation curve. The decay of an autocorrelation curve is determined by K(τ) which can be rewritten as: $K\left(\tau \right)={\left(3{\mu }_a{\mu }_s^{\prime }+6{\mu }_s^{\prime 2}{k}_0^2\alpha D_B\tau \right)}^{\frac{1}{2}}={\left[3{\mu }_a{\mu }_s^{\prime }\left(1+2\frac{{\mu }_s^{\prime }{k}_0^2\alpha D_B}{{\mu }_a}\tau \right)\right]}^{\frac{1}{2}}$. It is apparent from this expression that the decay of an autocorrelation curve is influenced by the term of $2\frac{{\mu }_2^{\prime }{k}_0^2\alpha D_B}{{\mu }_a}\tau$ and a variation in αD_B can be compensated by a variation in μ_a μ_s’. By contrast, based on Eq. (3) and Eq. (4), β does not affect the decay of the autocorrelation curve and does not compensate the variation of αD_B. Therefore, it is possible to fit β and αD_B simultaneously without causing the crosstalk between them.

We then compared the two methods for extracting β and αD_B. All the results from the simulations (Fig. 5), phantom experiments (Fig. 6a), and tissue measurements (Fig. 6b) suggested that simultaneously fitting β and αD_B from the entire autocorrelation curve resulted in more accurate values with smaller standard deviations compared to the two-step fitting method. For the two-step fitting method, large standard deviations of estimation resulted mainly from the inaccurate β estimated using only several points at early τ of g₂ curve; limited datasets may be contaminated by noises. The estimation bias was due to the decay of autocorrelation curve with τ, which led to underestimations of β and αD_B.

In conclusion, the possibility of extracting multiple parameters (αD_B, μ_a, μ_s’ and β) via fitting one single autocorrelation function curve has not previously been investigated for DCS measurements. It is not trivial to get the answer regarding such possibility because the autocorrelation function depends on all four parameters [see Eq. (3) and Eq. (4)] and explicitly expressing the relations among them is difficult. In the present study, for the first time, we comprehensively investigated the possibility of fitting multiple parameters from one single autocorrelation curve and evaluated the performance of the two methods with computer simulations, tissue-like phantom experiments and in-vivo tissue measurements. The results from this study suggest that it is impractical to simultaneously fit αD_B and μ_a or αD_B and μ_s’ from one single autocorrelation function curve due to the large crosstalk between these paired parameters. However, simultaneous fitting of β and αD_B is feasible and generates more accurate estimation with smaller standard deviation compared to the conventional two-step fitting method.

The outcomes from this study imply that absolute values of μ_a and μ_s’ are needed for extracting accurate β and αD_B. Our laboratory has recently developed a hybrid NIR diffuse optical instrument combining a commercial frequency-domain tissue-oximeter and a DCS flowmeter, which allows for simultaneous measurements of μ_a and μ_s’ as well as β and αD_B [21]. It is expected that the use of this type of hybrid instrument and simultaneous fitting algorithms will provide accurate measurement results.