Skip to main content
PMC home page
Journal of Anatomy logoLink to Journal of Anatomy
. 2015 Feb 4;226(3):236–243. doi: 10.1111/joa.12278

A potential mechanism for allometric trabecular bone scaling in terrestrial mammals

Patrik Christen 1,*, Keita Ito 1, Bert van Rietbergen 1,✉
PMCID: PMC4337663  PMID: 25655770

Abstract

Trabecular bone microstructural parameters, including trabecular thickness, spacing, and number, have been reported to scale with animal size with negative allometry, whereas bone volume fraction is animal size-invariant in terrestrial mammals. As for the majority of scaling patterns described in animals, its underlying mechanism is unknown. However, it has also been found that osteocyte density is inversely related to animal size, possibly adapted to metabolic rate, which shows a negative relationship as well. In addition, the signalling reach of osteocytes is limited by the extent of the lacuno-canalicular network, depending on trabecular dimensions and thus also on animal size. Here we propose animal size-dependent variations in osteocyte density and their signalling influence distance as a potential mechanism for negative allometric trabecular bone scaling in terrestrial mammals. Using an established and tested computational model of bone modelling and remodelling, we run simulations with different osteocyte densities and influence distances mimicking six terrestrial mammals covering a large range of body masses. Simulated trabecular structures revealed negative allometric scaling for trabecular thickness, spacing, and number, constant bone volume fraction, and bone turnover rates inversely related to animal size. These results are in agreement with previous observations supporting our proposal of osteocyte density and influence distance variation as a potential mechanism for negative allometric trabecular bone scaling in terrestrial mammals. The inverse relationship between bone turnover rates and animal size further indicates that trabecular bone scaling may be linked to metabolic rather than mechanical adaptations.

Keywords: bone modelling and remodelling, computational modelling and simulation, metabolic rate, micro-finite element analysis, osteocyte density, osteocyte influence distance, trabecular bone scaling

Introduction

Terrestrial mammals exhibit an enormous range of size – from shrews weighing only a few grams to elephants weighing tons. Despite this variation in size, mammals evolved according to the same bauplan of bony elements that make up the vertebrate skeleton, which supports body mass and withstands forces generated during locomotion. Common to mammalian bones and independent of animal size, bones are adapted to these gravitational and locomotor loads by altering shape, mass, and microstructure (Roux, 1881; Wolff, 1892; Frost, 1987; Sugiyama et al. 2010, 2012; Barak et al. 2011; Lambers et al. 2011; Christen et al. 2012b, 2014a,b; Schulte et al. 2013). This form–function relationship is maintained by continuous bone modelling and remodelling where a network of connected osteocytes embedded in the bone senses mechanical tissue loading and accordingly triggers osteoblasts and osteoclasts on the bone surface to form and resorb bone, respectively (Roux, 1881; Crockett et al. 2011; Klein-Nulend et al. 2012; Schaffler & Kennedy, 2012; Schulte et al. 2013; Christen et al. 2014a).

Although all mammalian bone is modelled and remodelled according to the same general principle, microstructural differences dependent on animal size can occur. At the micro-scale, bone consists of small struts called trabeculae. Several studies have analysed trabecular bone structure in a variety of species. Thickness, spacing, and number of trabeculae were determined in an earlier histomorphometric study of trabecular bone in femoral heads of rat, rabbit, monkey, pig, and cow (Mullender et al. 1996). It was found that trabecular parameters differ significantly between these five mammals. Another study observed, based on an even broader group of mammals, that trabecular length and diameter scale with animal size with negative allometry (Swartz et al. 1998). More recent analyses employing micro-computed tomography further support trabecular bone scaling based on measurements of 90 mammals and bird species with body masses ranging from 0.003 to 3400 kg (Doube et al. 2011) and 34 primate species ranging from 0.06 to 130 kg (Ryan & Shaw, 2013). Both studies found that trabecular bone parameters (thickness, spacing, and number) scale with body mass with negative allometry, whereas bone volume fraction is invariant to animal size in a wide range of mammals (Doube et al. 2011) and only very weakly scales in primates (Ryan & Shaw, 2013). Primates might follow a different scaling pattern, as another primate study found that trabecular bone scales isometrically in vertebral bodies (Fajardo et al. 2013). Nevertheless, most of the studies indicate negative allometry in mammalian trabecular bone. Negative allometric scaling should not be confused with a negative correlation. The latter is an inverse relationship with a negative slope, whereas negative allometry refers to a negative deviation from isometry. As trabecular length measures change with the cubic body mass to the 1/3 power, every scaling exponent below 1/3 is regarded as negative allometry. Therefore, negative allometry of trabecular bone scaling means that smaller animals show relatively thicker, more separated, and fewer trabeculae than expected from geometric similarity, as was further confirmed in a recent extensive meta-analysis of the available literature (Barak et al. 2013).

Because bone volume fraction does not scale with animal size and trabecular thickness has been shown to increase with increased joint loading during ontogeny (Ruimerman et al. 2005; Ryan & Krovitz, 2006; Gosman & Ketcham, 2009), trabecular bone scaling could be speculated to be a strategy to cope with increased joint loading as predicted from surface/volume scaling with increasing animal size. However, the negative allometry of trabecular thickness and number (Doube et al. 2011; Ryan & Shaw, 2013) is not in agreement with this theory, as it implies relatively thinner and fewer trabeculae in larger animals than predicted by geometric scaling. It is further known that adaptations of limb posture enable differently sized animals to have similar peak bone stresses during locomotion (Biewener, 1989, 1990), providing a way to deal with the relatively higher loading in larger animals. Trabecular bone scaling in general is therefore not necessarily related to joint loading or mechanical bone stresses. Instead, as an animal's metabolism is related to its size as well, it could be that trabecular bone scaling is a consequence of metabolic adaptation. The metabolic rate is known to be inversely related to animal size, as observed in animals with sizes ranging from mice to elephants (Schmidt-Nielsen, 1984). This implicates that the activity of bone cells also follows an inverse relationship with body mass and thus affects the bone remodelling and ultimately the bone microstructure in an animal size-dependent manner. This is supported by measurements of the duration of the bone remodelling cycle in mice and rats, rabbits, dogs, and humans showing a shorter duration in smaller animals than in bigger animals (Reinwald & Burr, 2008). This would suggest that the bones of larger animals consist of relatively fewer cells or cells that expend their nutrients more slowly. And indeed, the number of osteocytes is related to animal size, as the same histomorphometric study of five mammals that measured trabecular bone parameters, also measured osteocyte densities in these animals. Osteocyte numbers ranged from 31 000 mm−3 for cows to 93 200 mm−3 for rats (Mullender et al. 1996), indicating an inverse relationship.

Besides osteocyte density, the distance an osteocyte signal is able to propagate towards osteoblasts at the bone surface, and thus its influence distance, might vary with animal size as well. Osteocytes sense the back-and-forth fluid flow within the lacuno-canalicular network, which is induced by mechanical loads acting on the bone, and release signalling molecules to regulate osteoblasts (Klein-Nulend et al. 1995a,b, 2012; Tate et al. 2000; Price et al. 2011). The reach of these signalling molecules is limited by the extent of the osteocytic network spanning the whole bone tissue and thus cannot be more than the dimensions of a trabecula in trabecular bone. No experimental results exist on the reach of these signals, but an earlier sensitivity study of this model parameter showed that the osteocyte influence distance is approximately half of the thickness of a trabecula (Mullender & Huiskes, 1995). As trabecular thickness positively correlates with animal size (Doube et al. 2011; Barak et al. 2013; Fajardo et al. 2013; Ryan & Shaw, 2013), the osteocyte influence distance is expected to correlate positively with animal size.

As the amount of osteocyte signalling molecules received by an osteoblast depends on the number of osteocytes in its vicinity and because it has been shown that osteoblasts are affected by such signals in a dose-dependent manner (Ramirez-Yanez & Symons, 2012), it is expected that the osteogenic signal received by an osteoblast increases with increasing osteocyte density and influence distance, since in both instances the number of osteocytes and thus signalling molecules affecting the osteoblast is increased. Because in vivo (Sugiyama et al. 2012; Schulte et al. 2013; Christen et al. 2014a) and in vitro (Murray & Rushton, 1990) studies indicate a linear relationship between mechanical loading and the osteogenic signal within the physiological range of loading, this would result in a positive correlation between bone volume fraction and osteocyte density and osteocyte influence distance. The finding that bone volume fraction is independent of animal size (Doube et al. 2011; Barak et al. 2013) but osteocyte density is inversely correlated with animal size (Mullender et al. 1996), further supports the positive correlation of the osteocyte influence distance with animal size.

Thus, we hypothesise that a combination of inversely related osteocyte density and positively related osteocyte influence distance with animal size can lead to bone with the same volume fraction and to negative allometric scaling. In this study, we explore this hypothesis using an established and tested computational model of bone modelling and remodelling (Huiskes et al. 2000; Ruimerman et al. 2005; Christen et al. 2012a) incorporating the microstructure of trabecular bone, the osteocyte network including cell density and influence distance, and the activities of osteoclasts and osteoblasts. Models were created mimicking six terrestrial mammals covering a wide range of body masses. With this computational model it has already been possible in previous studies to predict the forming of typical bone microstructures and their changes due to altered loading conditions during bone adaptation (Ruimerman et al. 2005), the influence of certain hormones on the remodelling process (Christen et al. 2012a), and the targeted resorption near osteocyte death and the alignment of osteons (van Oers et al. 2008), which therefore supports its application for testing our proposed hypothesis.

Materials and methods

Bone modelling and remodelling algorithm

Bone modelling and remodelling were simulated using a load-driven computational algorithm (Huiskes et al. 2000; Ruimerman et al. 2005; Christen et al. 2012a). This is based on the theory that osteocytes in the bone sense mechanical tissue loading, U, represented as strain energy density and calculated using micro-finite element analysis, and send a signal, P, to osteoblasts on the bone surface that form bone accordingly. The osteocyte signal received by an osteoblast is determined by the number of osteocytes N within the influence distance of dinf. The signal of each osteocyte at location xi exponentially decreases with increasing distance from the osteoblast at location x. With a typical decay distance of D and the osteocyte mechanosensitivity μi, the total osteocyte signal can then be calculated as:

graphic file with name joa0226-0236-m1.jpg 1

If this signal exceeds a certain threshold, k, bone tissue, Vobl, is formed over time, t, according to the formation rate, τ, and thus determined by:

graphic file with name joa0226-0236-m2.jpg 2

Bone resorption, on the other hand, is assumed to occur spatially randomly on the trabecular surface with the osteoclast activation frequency, focl. With a constant volume of bone resorbed per cavity, Vres, the total volume of resorbed bone, Vocl, over time is determined by:

graphic file with name joa0226-0236-m3.jpg 3

The mechanical tissue loading, U, is calculated using finite element analysis. The stiffness of each finite element, Eel, is calculated using the power law (Currey, 1988):

graphic file with name joa0226-0236-m4.jpg 4

where Eb is the maximum trabecular bone stiffness, Vel the normalised volume fraction of the element with a value between 0.1 for marrow and 1.0 for bone, and γ a material constant.

Bone modelling and remodelling simulations

Simulations were started from a regular lattice structure in a cubic domain of 2 × 2 × 2 mm3 (Fig.1A). By applying axial stresses of 3 MPa in each direction, simulations were then run until the bone turnover was in equilibrium, generating a typical trabecular bone structure (Fig.1B). The same loading was applied for all simulated mammals, as in vivo strain measurements showed that tissue loading is similar across species (Biewener, 1989, 1990). In a first set of analyses, the sensitivity of the bone volume fraction for changes in osteocyte density and osteocyte influence distance was investigated. A range of osteocyte densities including 2000, 10 000, 30 000, 60 000, 100 000, and 150 000 osteocytes per mm3 was defined, which well represents the values measured in mammals. Based on the relationship between osteocyte density and body mass, which was derived from species where both attributes were known (see next section for more details), this range of osteocyte densities can be associated with the following animals (body masses): Asian elephant (2991 kg) for 2000, rhinoceros (1344 kg) for 10 000, pig, donkey or cow (182 kg) for 30 000, rabbit or dog (9 kg) for 60 000, rat (0.166 kg) for 100 000, and shrew (0.001 kg) for 150 000 osteocytes per mm3.

Fig 1.

Fig 1

Open in a new tab

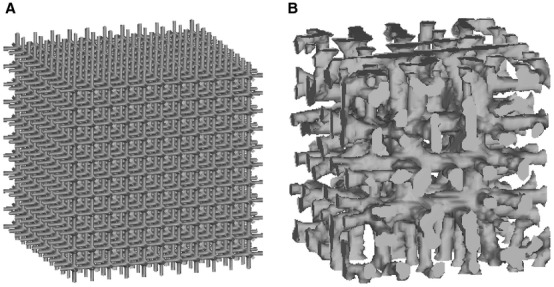
Lattice structure (A) used as initial configuration for the bone modelling and remodelling simulations and final bone structure (B) adapted to the external loading conditions and model parameters.

For each of these six osteocyte densities, simulations starting from the lattice structure and with osteocyte influence distances of 75, 112.5, 150, 225, and 300 micrometers were run. The sensitivity was then determined for each osteocyte density by calculating a linear relationship between bone volume fraction and osteocyte influence distance. Based on this relationship, the osteocyte influence distance was calculated for each osteocyte density in such a way that the resulting bone volume fraction was 20% without implementing a limit for bone volume fraction into the model. If the linear relationship did not predict the bone volume fraction within ± 1%, the influence distance was step-wise changed and new simulations were run until the target value was achieved. As skeletal elements can vary greatly with respect to bone volume fraction, this value might be set to a different level. We therefore tested whether the bone volume fraction has an influence on the scaling behaviour by running the statistical analysis on bone microstructures with bone volume fractions of 14%, 20%, 27%, and 35% that were created by changing the applied loading and based on simulations with 2000, 30 000, and 150 000 osteocytes per mm3. The regression analysis showed that the slopes for trabecular bone parameters did not differ substantially and, most importantly, that the allometric scaling is independent of the bone volume fraction. Thus we can exclude that choosing another bone volume fraction would influence our results in any way.

Using these interpolated values for the osteocyte influence distance, an additional simulation, starting again from the lattice structure, was performed for each osteocyte density such that six models with a large range in osteocyte densities and influence distances were obtained but with the same volume fraction. All the other parameters of the algorithm were kept the same for all simulations, either according to physiological values or in accordance with previous studies (Huiskes et al. 2000; Ruimerman et al. 2005; Christen et al. 2012a) (Table1).

Table 1.

Bone modelling and remodelling simulation parameters. Values were defined according to bone physiology whenever possible

Parameter Symbol Unit Value
Osteocyte density n Inline graphic Table2
Osteocyte mechanosensitivity μ Inline graphic 1.0
Osteocyte influence distance dinf μm Table2
Osteocyte decay distance D μm 100 (Mullender & Huiskes, 1995)
Bone formation threshold k 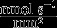Inline graphic 5.0 × 106
Bone formation rate τ 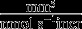Inline graphic 8.0 × 10−8
Resorption volume per cavity Vres mm3 5.6 × 10−5 (Eriksen & Kassem, 1992)
Osteoclast recruitment frequency focl 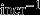Inline graphic 0.03
Loading frequency f Hz 1.0
Bone stiffness Eb GPa 5.0 (Mullender & Huiskes, 1995)
Poisson's ratio v – 0.3 (Mullender & Huiskes, 1995)
Material constant γ – 3.0 (Currey, 1988)
Open in a new tab

For the structures obtained from these last analyses, a set of bone microstructural parameters was calculated: bone volume fraction (BV/TV), trabecular thickness (Tb.Th), trabecular spacing (Tb.Sp), trabecular number (Tb.N), structural model index (SMI), and connectivity density (Conn.D) using bone microstructural analysis software (IPL, Scanco Medical AG, Switzerland). The results obtained were then used to test our hypothesis.

Statistical analysis

Reduced major axis regression based on log10-transformed variables was performed to define the scaling relationships between body mass and trabecular bone parameters as well as bone turnover rate. Body mass was determined based on the five mammals where the osteocyte density was known (Mullender et al. 1996) and the body mass available from the literature (Allison & Cicchetti, 1976) and thus an exponential function could be defined, revealing the corresponding body masses of 2991, 1344, 182, 9, 0.166, and 0.001 kg for the osteocyte densities used in the six simulations with 2000, 10 000, 30 000, 60 000, 100 000, and 150 000 osteocytes per mm3, respectively.

Results

Trabecular bone parameters

The osteocyte densities and the corresponding osteocyte influence distance used in the final analyses are specified in Table2. Bone volume fraction linearly correlated with the osteocyte influence distance in the initial simulations with osteocyte densities of 2000 (R2 = 0.920), 10 000 (R2 = 0.995), 30 000 (R2 = 0.998), 60 000 (R2 = 0.940), 100 000 (R2 = 0.827), and 150 000 (R2 = 0.667) osteocytes per mm3. In the simulations with very high osteocyte density and influence distance, a bone volume fraction of 100% was reached, indicating unrealistic combinations of values for osteocyte density and influence distance. In the present study only combinations leading to a realistic bone volume fraction of 20% were used to investigate trabecular bone scaling. Table2 also includes results for the bone microstructural parameters for the six simulations with varied osteocyte density and influence distance. SMI was not dependent on the osteocyte density. In contrast, Tb.Th, Tb.Sp, Tb.N, and Conn.D were altered (Table2, Figs2 and 3).

Table 2.

Trabecular bone parameters and bone turnover rates for the six simulations of bone modelling and remodelling with varied osteocyte density and influence distance. Please note that the osteocyte density was predefined and, in combination with it, the osteocyte influence distance chosen to lead to a BV/TV of 20%

Osteocyte density [mm−3] Osteocyte influence distance [μm] Trabecular bone parameters Bone turnover rate [BV−1]
BV/TV [%] Tb.Th [mm] Tb.Sp [mm] Tb.N [mm−1] SMI [1] Conn.D [mm−3]
2000 250 20.00 0.2042 0.5348 1.9912 2.4332 4.7760 0.0112
10 000 120 19.87 0.1533 0.3770 2.4230 2.4328 9.6197 0.0151
30 000 80 20.76 0.1382 0.3145 2.9415 2.5327 15.7167 0.0170
60 000 60 20.04 0.1162 0.2779 3.3837 2.5133 20.9330 0.0203
100 000 50 19.73 0.1017 0.2564 3.7954 2.4039 28.4526 0.0224
150 000 45 20.49 0.0939 0.2402 4.0534 2.3153 36.6496 0.0235
Open in a new tab

BV/TV, bone volume fraction; Tb.Th, trabecular thickness; Tb.Sp, trabecular spacing; Tb.N, trabecular number; SMI, structural model index; Conn.D, connectivity density.

Fig 2.

Fig 2

Open in a new tab

Cuts through the cubic domain to visualise the trabecular bone microstructure as generated by bone modelling and remodelling simulations using 100 000 (A), 60 000 (B), 30 000 (C), and 2000 (D) mm−3 osteocyte densities in the simulations with varied osteocyte density and influence distance.

Fig 3.

Fig 3

Open in a new tab

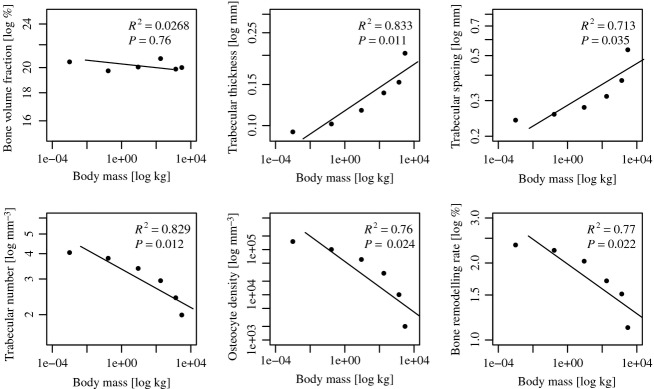
Regression analyses of trabecular bone parameters, osteocyte density, and bone turnover rate in relation to body mass. Please note that the osteocyte density was predefined and in combination with it the osteocyte influence distance chosen to lead to a bone volume fraction of 20%.

Bone turnover rates

Bone turnover rates were calculated when the amount of resorbed and formed bone was balanced and thus the bone structure was adapted to the applied loading. Our six simulations revealed that with increasing osteocyte density combined with decreasing osteocyte influence distance, the turnover rate also increases (Table2, Fig.3).

Correlations

As expected, regression showed no correlation between body mass and bone volume fraction (regression slope a = −0.003, lower and upper 95% confidence intervals CIl,95 = −0.001, CIu,95 = −0.01, R2 = 0.0268, P = 0.76) (Fig.3). In contrast, trabecular thickness (a = 0.050, CIl,95 = 0.029, CIu,95 = 0.086, R2 = 0.833, P = 0.011), trabecular spacing (a = 0.052, CIl,95 = 0.026, CIu,95 = 0.103, R2 = 0.713, P = 0.035), trabecular number (a = −0.047, CIl,95 = −0.082, CIu,95 = −0.027, R2 = 0.829, P = 0.012), osteocyte density (a = −0.280, CIl,95 = −0.529, CIu,95 = −0.148, R2 = 0.76, P = 0.024), and bone turnover rate (a = −0.048, CIl,95 = 0.091, CIu,95 = 0.026, R2 = 0.77, P = 0.022) significantly scaled with body mass with negative allometry (Fig.3).

Discussion

Our bone modelling and remodelling simulations support the proposed hypothesis: there exists a combination of osteocyte density and osteocyte influence distance for which bone volume fraction remains constant and trabecular thickness, spacing, number, and connectivity scale with negative allometry in terrestrial mammals. Negative allometric scaling of trabecular bone indicates that smaller animals show relatively thicker, more separated, fewer, and less connected trabeculae in comparison with bigger animals. This is the same scaling pattern found when measuring trabecular bone parameters in animals with a wide range of body masses (Mullender et al. 1996; Swartz et al. 1998; Doube et al. 2011; Barak et al. 2013; Ryan & Shaw, 2013). The slopes of the scaling of trabecular thickness and spacing are, however, lower than previously reported values (Doube et al. 2011; Barak et al. 2013). This difference might be due to the model parameters and assumptions used in the present study, e.g. osteocyte densities and influence distances were estimated for a certain body mass, and artificial bone structures were used. Nevertheless, interspecies variation in osteocyte density and influence distance is sufficient to explain the typical scaling of trabeculae and thus can be considered a potential mechanism for negative allometric trabecular bone scaling.

Interestingly, although showing a linear relationship, the curves in Fig.3 seem to have a parabolic or exponential shape for trabecular thickness, spacing, and number, osteocyte density, and remodelling rate. This would imply that there are certain limits to these relationships where at the extremes the curves become flat or infinitely steep. Osteocyte density, bone turnover rate, and trabecular number show a flattening of the curve where a maximum value at low body mass is defined. There is a limited take up of nutrients and thus also metabolic rate, which is related to the bone turnover rate and osteocyte density. Having more trabeculae is metabolically expensive as the bone surface where bone modelling and remodelling takes place increases. Limiting trabecular number can thus also be explained by a metabolic limit. The curves cross the x-axis at high body mass, a further indication that a metabolic minimum might constrain body mass. Trabecular thickness and spacing show flattening of the curve where a minimum value at low body mass is defined, and an infinite increase at high body mass. It is reasonable that there is a minimal thickness of trabeculae that still provides structural integrity and it is also reasonable that there is a minimal spacing between trabeculae that still provides enough space for nutrients to circulate. However, it is not reasonable to have infinitely thick trabeculae or spacing. Because trabecular number, thickness, and spacing are related to each other, it seems that the metabolically limited number of trabeculae indirectly limits trabecular thickness and spacing.

Smaller animals have a larger mass-specific body surface that requires a higher metabolic rate to keep up with the heat loss occurring at the body surface (Schmidt-Nielsen, 1984). This surface rule affects the metabolic rate and thus the total chemical energy turnover, including the number and activity of bone cells available, as suggested by the inverse relationship between osteocyte density and animal size in mammals (Mullender et al. 1996). In our computational simulations, we found that higher osteocyte densities combined with lower influence distances leads to higher bone turnover rates, which is in agreement with the surface rule for metabolic rate. This is also in agreement with the finding that the remodelling cycle is generally shorter in smaller animals, as shown by a comparison of mice and rats, rabbits, dogs, and humans (Reinwald & Burr, 2008). Trabecular bone scaling could therefore be a consequence of metabolic adaptations and is not necessarily linked to mechanical demands such as relatively higher joint loading in larger animals, which is probably mainly reduced by employing adequate locomotor limb posture (Biewener, 1989, 1990).

There are also limitations to our study. The main one is that we assumed only osteocyte density and osteocyte influence distance differ between species. Whereas there are experimental data for the former, no such data are available for the latter. Also, osteocyte densities and the related body mass are only known for five species. More osteocyte density measurements across species will be required to further support animal size-dependent osteocyte density. The present study can be viewed as guidance and justification for future studies measuring osteocyte density and influence distance across species, e.g. employing imaging techniques such as computed tomography at the nano-scale (Schneider et al. 2007; van Hove et al. 2009; Dong et al. 2014). We hope to encourage such imaging studies. Finally, although representing realistic trabecular bone structures, synthetic structures were used in the simulations.

Concluding remarks

In conclusion, using computational simulations of bone modelling and remodelling we found that animal size-dependent variation of osteocyte density and influence distance leads to negative allometric scaling of trabecular bone (thickness, spacing, number, connectivity) and constant bone volume fraction in terrestrial mammals. It is therefore a potential mechanism for negative allometric trabecular bone scaling. We also found that bone turnover rates inversely relate to animal size, indicating that trabecular bone scaling could be linked to metabolic and not necessarily mechanical adaptations.

Acknowledgments

Funding from the European Union for the Osteoporotic Virtual Physiological Human Project (VPHOP FP7-ICT2008-223865) is gratefully acknowledged.

Competing interests

Bert van Rietbergen is a consultant for Scanco Medical AG. The other authors declare that they have no competing interests.

Author contributions

P.C. developed the computational models and performed the bone remodelling simulations and regression analysis. P.C. and B.V.R. designed the study and drafted the manuscript. K.I. participated in the design of the study and helped interpret the data. All authors edited and approved the final manuscript.

References

  1. Allison T, Cicchetti DV. Sleep in mammals – ecological and constitutional correlates. Science. 1976;194:732–734. doi: 10.1126/science.982039. [DOI] [PubMed] [Google Scholar]
  2. Barak MM, Lieberman DE, Hublin JJ. A Wolff in sheep's clothing: trabecular bone adaptation in response to changes in joint loading orientation. Bone. 2011;49:1141–1151. doi: 10.1016/j.bone.2011.08.020. [DOI] [PubMed] [Google Scholar]
  3. Barak MM, Lieberman DE, Hublin JJ. Of mice, rats and men: trabecular bone architecture in mammals scales to body mass with negative allometry. J Struct Biol. 2013;183:123–131. doi: 10.1016/j.jsb.2013.04.009. [DOI] [PubMed] [Google Scholar]
  4. Biewener AA. Scaling body support in mammals – limb posture and muscle mechanics. Science. 1989;245:45–48. doi: 10.1126/science.2740914. [DOI] [PubMed] [Google Scholar]
  5. Biewener AA. Biomechanics of mammalian terrestrial locomotion. Science. 1990;250:1097–1103. doi: 10.1126/science.2251499. [DOI] [PubMed] [Google Scholar]
  6. Christen P, Ito K, Muller R, et al. Patient-specific bone modelling and remodelling simulation of hypoparathyroidism based on human iliac crest biopsies. J Biomech. 2012a;45:2411–2416. doi: 10.1016/j.jbiomech.2012.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Christen P, van Rietbergen B, Lambers FM, et al. Bone morphology allows estimation of loading history in a murine model of bone adaptation. Biomech Model Mechanobiol. 2012b;11:483–492. doi: 10.1007/s10237-011-0327-x. [DOI] [PubMed] [Google Scholar]
  8. Christen P, Ito K, Ellouz R, et al. Bone remodelling in humans is load-driven but not lazy. Nat Commun. 2014a;5:4855. doi: 10.1038/ncomms5855. [DOI] [PubMed] [Google Scholar]
  9. Christen P, Ito K, Galis F, et al. Determination of hip-joint loading patterns of living and extinct mammals using an inverse Wolff's law approach. Biomech Model Mechanobiol. 2014b doi: 10.1007/s10237-014-0602-8. DOI: 10.1007/s10237-014-0602-8. [DOI] [PubMed] [Google Scholar]
  10. Crockett JC, Rogers MJ, Coxon FP, et al. Bone remodelling at a glance. J Cell Sci. 2011;124:991–998. doi: 10.1242/jcs.063032. [DOI] [PubMed] [Google Scholar]
  11. Currey JD. The effect of porosity and mineral content on the Young's modulus of elasticity of compact bone. J Biomech. 1988;21:131–139. doi: 10.1016/0021-9290(88)90006-1. [DOI] [PubMed] [Google Scholar]
  12. Dong P, Haupert S, Hesse B, et al. 3D osteocyte lacunar morphometric properties and distributions in human femoral cortical bone using synchrotron radiation micro-CT images. Bone. 2014;60:172–185. doi: 10.1016/j.bone.2013.12.008. [DOI] [PubMed] [Google Scholar]
  13. Doube M, Klosowski MM, Wiktorowicz-Conroy AM, et al. Trabecular bone scales allometrically in mammals and birds. Proc R Soc B Biol Sci. 2011;278:3067–3073. doi: 10.1098/rspb.2011.0069. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Eriksen EF, Kassem M. The cellular basis of bone remodeling. Triangle. 1992;31:45–57. [Google Scholar]
  15. Fajardo RJ, Desilva JM, Manoharan RK, et al. Lumbar vertebral body bone microstructural scaling in small to medium-sized strepsirhines. Anat Rec (Hoboken) 2013;296:210–226. doi: 10.1002/ar.22632. [DOI] [PubMed] [Google Scholar]
  16. Frost HM. Bone mass and the mechanostat – a proposal. Anat Rec. 1987;219:1–9. doi: 10.1002/ar.1092190104. [DOI] [PubMed] [Google Scholar]
  17. Gosman JH, Ketcham RA. Patterns in ontogeny of human trabecular bone from SunWatch Village in the Prehistoric Ohio Valley: general features of microarchitectural change. Am J Phys Anthropol. 2009;138:318–332. doi: 10.1002/ajpa.20931. [DOI] [PubMed] [Google Scholar]
  18. van Hove RP, Nolte PA, Vatsa A, et al. Osteocyte morphology in human tibiae of different bone pathologies with different bone mineral density – is there a role for mechanosensing? Bone. 2009;45:321–329. doi: 10.1016/j.bone.2009.04.238. [DOI] [PubMed] [Google Scholar]
  19. Huiskes R, Ruimerman R, van Lenthe GH, et al. Effects of mechanical forces on maintenance and adaptation of form in trabecular bone. Nature. 2000;405:704–706. doi: 10.1038/35015116. [DOI] [PubMed] [Google Scholar]
  20. Klein-Nulend J, Semeins CM, Ajubi NE, et al. Pulsating fluid flow increases nitric oxide (NO) synthesis by osteocytes but not periosteal fibroblasts – correlation with prostaglandin upregulation. Biochem Biophys Res Commun. 1995a;217:640–648. doi: 10.1006/bbrc.1995.2822. [DOI] [PubMed] [Google Scholar]
  21. Klein-Nulend J, Vanderplas A, Semeins CM, et al. Sensitivity of osteocytes to biomechanical stress in vitro. FASEB J. 1995b;9:441–445. doi: 10.1096/fasebj.9.5.7896017. [DOI] [PubMed] [Google Scholar]
  22. Klein-Nulend J, Bacabac RG, Bakker AD. Mechanical loading and how it affects bone cells: the role of the osteocyte cytoskeleton in maintaining our skeleton. Eur Cell Mater. 2012;24:278–291. doi: 10.22203/ecm.v024a20. [DOI] [PubMed] [Google Scholar]
  23. Lambers FM, Schulte FA, Kuhn G, et al. Mouse tail vertebrae adapt to cyclic mechanical loading by increasing bone formation rate and decreasing bone resorption rate as shown by time-lapsed in vivo imaging of dynamic bone morphometry. Bone. 2011;49:1340–1350. doi: 10.1016/j.bone.2011.08.035. [DOI] [PubMed] [Google Scholar]
  24. Mullender MG, Huiskes R. Proposal for the regulatory mechanism of Wolff's Law. J Orthop Res. 1995;13:503–512. doi: 10.1002/jor.1100130405. [DOI] [PubMed] [Google Scholar]
  25. Mullender MG, Huiskes R, Versleyen H, et al. Osteocyte density and histomorphometric parameters in cancellous bone of the proximal femur in five mammalian species. J Orthop Res. 1996;14:972–979. doi: 10.1002/jor.1100140618. [DOI] [PubMed] [Google Scholar]
  26. Murray DW, Rushton N. The effect of strain on bone cell prostaglandin E2 release: a new experimental method. Calcif Tissue Int. 1990;47:35–39. doi: 10.1007/BF02555863. [DOI] [PubMed] [Google Scholar]
  27. van Oers RFM, Ruimerman R, Tanck E, et al. A unified theory for osteonal and hemi-osteonal remodeling. Bone. 2008;42:250–259. doi: 10.1016/j.bone.2007.10.009. [DOI] [PubMed] [Google Scholar]
  28. Price C, Zhou XZ, Li W, et al. Real-time measurement of solute transport within the lacunar-canalicular system of mechanically loaded bone: direct evidence for load-induced fluid flow. J Bone Miner Res. 2011;26:277–285. doi: 10.1002/jbmr.211. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Ramirez-Yanez GO, Symons AL. Prostaglandin E2 affects osteoblast biology in a dose-dependent manner: an in vitro study. Arch Oral Biol. 2012;57:1274–1281. doi: 10.1016/j.archoralbio.2012.03.003. [DOI] [PubMed] [Google Scholar]
  30. Reinwald S, Burr D. Review of nonprimate, large animal models for osteoporosis research. J Bone Miner Res. 2008;23:1353–1368. doi: 10.1359/JBMR.080516. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Roux W. Der Kampf der Theile im Organismus. Ein Beitrag zur Vervollständigung der mechanischen Zweckmässigkeitslehre. Leipzig: Verlag von Wilhelm Engelmann; 1881. [Google Scholar]
  32. Ruimerman R, Hilbers P, van Rietbergen B, et al. A theoretical framework for strain-related trabecular bone maintenance and adaptation. J Biomech. 2005;38:931–941. doi: 10.1016/j.jbiomech.2004.03.037. [DOI] [PubMed] [Google Scholar]
  33. Ryan TM, Krovitz GE. Trabecular bone ontogeny in the human proximal femur. J Hum Evol. 2006;51:591–602. doi: 10.1016/j.jhevol.2006.06.004. [DOI] [PubMed] [Google Scholar]
  34. Ryan TM, Shaw CN. Trabecular bone microstructure scales allometrically in the primate humerus and femur. Proc R Soc B Biol Sci. 2013;280:1–9. doi: 10.1098/rspb.2013.0172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Schaffler MB, Kennedy OD. Osteocyte signaling in bone. Curr Osteoporos Rep. 2012;10:118–125. doi: 10.1007/s11914-012-0105-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Schmidt-Nielsen K. Scaling – Why Is Animal Size so Important? Cambridge: Cambridge University Press; 1984. [Google Scholar]
  37. Schneider P, Stauber M, Voide R, et al. Ultrastructural properties in cortical bone vary greatly in two inbred strains of mice as assessed by synchrotron light based micro- and nano-CT. J Bone Miner Res. 2007;22:1557–1570. doi: 10.1359/jbmr.070703. [DOI] [PubMed] [Google Scholar]
  38. Schulte FA, Ruffoni D, Lambers FM, et al. Local mechanical stimuli regulate bone formation and resorption in mice at the tissue level. PLoS ONE. 2013;8:1–12. doi: 10.1371/journal.pone.0062172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Sugiyama T, Price JS, Lanyon LE. Functional adaptation to mechanical loading in both cortical and cancellous bone is controlled locally and is confined to the loaded bones. Bone. 2010;46:314–321. doi: 10.1016/j.bone.2009.08.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Sugiyama T, Meakin LB, Browne WJ, et al. Bones' adaptive response to mechanical loading is essentially linear between the low strains associated with disuse and the high strains associated with the lamellar/woven bone transition. J Bone Miner Res. 2012;27:1784–1793. doi: 10.1002/jbmr.1599. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Swartz SM, Parker A, Huo C. Theoretical and empirical scaling patterns and topological homology in bone trabeculae. J Exp Biol. 1998;201:573–590. doi: 10.1242/jeb.201.4.573. [DOI] [PubMed] [Google Scholar]
  42. Tate MLK, Steck R, Forwood MR, et al. In vivo demonstration of load-induced fluid flow in the rat tibia and its potential implications for processes associated with functional adaptation. J Exp Biol. 2000;203:2737–2745. doi: 10.1242/jeb.203.18.2737. [DOI] [PubMed] [Google Scholar]
  43. Wolff J. Das Gesetz der Transformation der Knochen. Berlin: Verlag von August Hirschwald; 1892. [Google Scholar]

Articles from Journal of Anatomy are provided here courtesy of Anatomical Society of Great Britain and Ireland

RESOURCES