Abstract
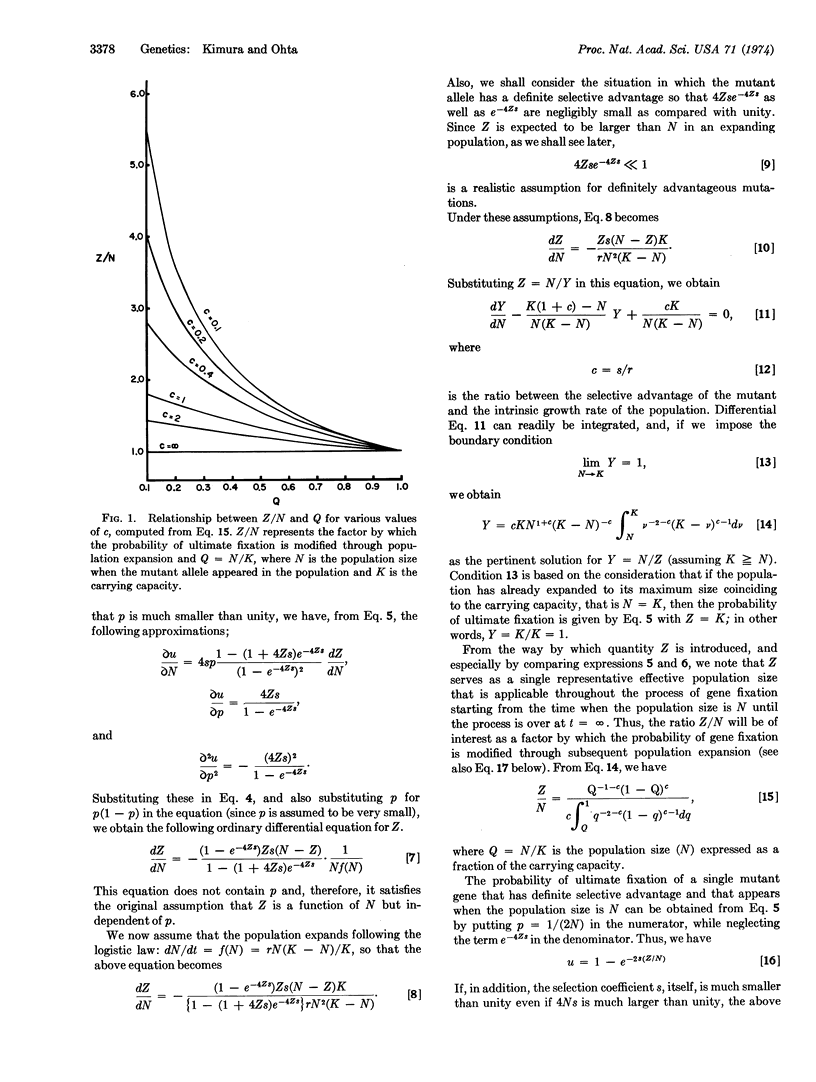
A mathematical theory was developed, based on diffusion models, that enables us to compute the probability of a rare mutant allele eventually spreading through a population when the population size changes with time. In particular, we elaborated the case in which the mutant allele has a definite selective advantage and the population expands following the logistic law. In this case, the probability of ultimate fixation of a single mutant is given by u = 2s(Z/N), where s is the selective advantage and Z/N is a factor by which the probability of fixation is modified through population expansion. Analytical expression was obtained for Z/N, and the validity of the formula for u was checked by Monte Carlo experiments.
Keywords: population genetics, diffusion model, fixation probability of mutant, logistic population
Full text
PDF

Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- KIMURA M. On the probability of fixation of mutant genes in a population. Genetics. 1962 Jun;47:713–719. doi: 10.1093/genetics/47.6.713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M., Ota T. Probability of fixation of a mutant gene in a finite population when selective advantage decreases with time. Genetics. 1970 Jul;65(3):525–534. doi: 10.1093/genetics/65.3.525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. Evolution in Mendelian Populations. Genetics. 1931 Mar;16(2):97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]


