Finite Mixtures for Simultaneously Modelling Differential Effects and Non-Normal Distributions

Abstract

Regression mixture models have been increasingly applied in the social and behavioral sciences as a method for identifying differential effects of predictors on outcomes. While the typical specification of this approach is sensitive to violations of distributional assumptions, alternative methods for capturing the number of differential effects have been shown to be robust. Yet, there is still a need to better describe differential effects that exist when using regression mixture models. The current study tests a new approach that uses sets of classes (called differential effects sets) to simultaneously model differential effects and account for non-normal error distributions. Monte Carlo simulations are used to examine the performance of the approach. The number of classes needed to represent departures from normality is shown to be dependent on the degree of skew. The use of differential effects sets reduced bias in parameter estimates. Applied analyses demonstrated the implementation of the approach for describing differential effects of parental health problems on adolescent body mass index using differential effects sets approach. Findings support the usefulness of the approach which overcomes the limitations of previous approaches for handling non-normal errors.

Finite Mixtures for Simultaneously Modelling Differential Effects and Non-Normal Distributions

Regression mixture models are a powerful tool for capturing individual differences through modeling unobserved heterogeneity in the effects of predictors on outcomes. This approach has been increasingly applied to answer research questions in the social and behavioral sciences (Ding, 2006; Dyer, Pleck, & McBride, 2012; Lanza, Kugler, & Mathur, 2011; Kaplan, 2005; Schmeige, Levin, & Bryan, 2009; Van Horn et al., 2009; Wong & Maffini, 2011). Regression mixtures are a class of finite mixture model that allows for modeling heterogeneity in the effects of covariates on an outcome across latent classes (Van Horn et al., 2009; Muthén & Asparouhov, 2009; Vermunt & Magidson, 2002; Wedel & DeSarbo, 1994; Wedel & DeSarbo, 1995). One limitation of this approach is the strong assumptions about within-class distributions of residuals (George et al., 2013; Van Horn et al., 2012). Previous work has shown that, under the typical assumption that residuals are normally distributed within classes the presence of even mild skew can severely bias model results. Strategies for dealing with error distributions that do not adhere to standard model assumptions (i.e., normally distributed within-class residuals) are needed (George et al., 2013).

In the current paper, we advance approaches for using regression mixtures to identify differential effects in the presence of data that violate distributional assumptions. First, we discuss the regression mixture model and issues with violating distributional assumptions. Next, we provide a rationale for a new approach, differential effects sets, that uses latent classes to simultaneously model differential effects and non-normality in the residual error distribution when the number of effects present is known or can be estimated. Simulations are used to examine the performance of the proposed approach when within-class residuals are skewed. Finally, we demonstrate the implementation of the differential effects sets approach to examine differential effects in the relations between parent health problems and adolescent BMI using the Longitudinal Study of Adolescent Health. Although mixture models have been previously used to study differential effects and to approximate non-normal distributions, the innovation in this paper is to incorporate both uses of mixtures into the same model.

Regression Mixture Models

Regression mixture models are a method for modeling unobserved heterogeneity in the effects of predictors on outcomes. Based on early work in economics on switching regression models (Quandt and Ramsey, 1978), regression mixtures were developed in the field of marketing (Wedel & DeSarbo, 1994; Wedel & DeSarbo, 1995) and only recently started receiving attention in the social sciences (Dyer, Pleck, & McBride, 2012; Van Horn et al., 2009). Many theories in the social and behavioral sciences provide rationale for expecting that the effects of interest differ across subpopulations. Often, researchers posit specific conditions or contexts under which an effect is stronger or weaker. When these differences can be characterized by discrete heterogeneity, regression mixtures provide a method for empirically identifying groups of individuals characterized by differential effects or differences across individuals in the relations between predictors and outcomes (Van Horn et al., 2012).

The predominant approach to identifying group differences relies on the use of statistical interaction terms. Interactions depend on observed variables to predict differential effects either by testing for differences in regression weights between groups of individuals (e.g., based on similarities in variables like gender, age, or ethnicity) or by examining whether a regression weight changes as a linear function of a predictor. Though straightforward to implement, this approach is ineffective when the predictors of differential effects are not measured and is limited when predictors are imperfectly measured or differential effects are the function of multiple variables. Accounting for complex differential effects with interactions may require many, often highly correlated, multiplicative terms. Tests of multiple interactions are likely to be underpowered, which can result in failing to find the presence of the complex differential effects that theoretically underlie the associations between variables (Boyce et al., 1998). Furthermore, when a large number of interactions are present, the interpretation of group differences can be difficult (Cohen, Cohen, West, & Aiken, 2003).

One alternative approach to modeling individual differences in effects involves the use of repeated measures data with random effects for individuals in the effects of a predictor on the outcome (Bauer, 2011), which allows direct estimates of an effect for each individual. When repeated measures are not available or the predictor does not vary greatly across short time spans, an alternative is to use regression mixture models to capture unobserved heterogeneity in effects through the use of latent classes. Using latent classes to model group differences allows for identifying groups of individuals who differ in the effect of a predictor on an outcome, even though the causes for those differences may be unknown or unmeasured. Regression mixture models differ from more commonly known mixture models (such as growth mixture models or the typical latent class analyses) in that the mixture component in a regression mixture is derived from differences between classes in the strength and/or magnitude of the effect of a predictor on an outcome, rather than differences in means and variances of the outcomes, which is often the case in traditional uses of mixture models (McLachlan & Peel, 2000). In regression mixture models, the distribution of outcomes is conditional on a set of predictor variables where the relations between predictors and outcomes are allowed to vary between classes. This allows for regression mixtures to model differences in the relations between independent and dependent variables (i.e., differential effects) by empirically deriving latent subgroups or classes of respondents based on similar patterns of relationships between variables.

Consider a sample of n individuals measured on a continuous variable, Y, where y_i is the observed value for subject i. The relations between predictor variables and the outcome, Y, are conditional on membership in latent class k for the set of P observed predictors, X = (x₁, x₂,…, x_P),expressed as

$$Y_{i|\mathbf{X},k}={\beta }_{0k}+\sum _{p=1}^P{\beta }_{pk}{x}_{ip}+{\epsilon }_{ik},{\epsilon }_{ik}\sim N(0,{\sigma }_k^2),$$ (1)

where β_0k is the intercept and ${\sigma }_k^2$ is the residual variance for class k. Differential effects are captured by β_k=(β_1k,…,β_pk), the p-dimensional vector of regression coefficients for X in latent class k. The probability density function (pdf) of the outcome given the observed predictor variables, Y|X, is

$$f(y|\mathbf{X},\phi )=\sum _{k=1}^K{\pi }_k{f}_k({\mathrm{y}}_k,{\mathbf{\theta }}_k),$$ (2)

which is a mixture, or weighted sum, of a finite number of probability densities, ƒ_k (y|θ_k). The class-specific parameters are denoted by θ_k, π=(π₁, π₂,…, π_K) are the class proportions, and ϕ=(π, θ₁,θ₂,…,θ_K) denotes the vector of all unknown parameters to be estimated. The pdfs, ƒ_k (y|θ_k), correspond to the distribution of the outcomes for K subgroups, with group membership being a latent categorical variable, C, where C = 1, 2 … K. The value of K is specified a priori, but the mixing weights, or class proportions, π, are included as parameter estimates in the model.

Regression mixture models, formulated in this way allow for the effect of the predictor on the outcome to be different for each subgroup in the population. Differential effects are evidenced by differences in these regression coefficients between groups. In this description and throughout the remainder of the manuscript, we consider only univariate outcome variables, although extensions to multivariate outcomes are straightforward.

Distributional assumptions

In general, finite mixture models with continuous variables rely on strong assumptions about within-class error distributions for the estimation of model parameters (Bauer & Curran, 2003a; Bauer & Curran, 2003b; Bauer & Curran, 2004). Finite mixtures approximate the distribution of an outcome using a specified number of classes and specific assumptions about the distribution of the outcome within each class; most often, the distribution of the outcome conditional on predictors is assumed to be normal within each class. Although latent classes are typically interpreted as representing qualitatively different groups of respondents, because there is no analytic distinction as to the cause of latent classes, evidence for multiple latent classes does not guarantee the presence of qualitatively different groups. Although latent classes may derive from underlying qualitative differences between respondents, they also may simply be the result of using latent classes to approximate a non-normal distribution for the outcome variable.

Thus, an inherent problem with finite mixtures is that the cause of latent classes is not known. If classes are assumed to represent qualitative differences between respondents, then violations of distributional assumptions within each class can impact latent class enumeration (the number of classes supported by the data) and result in biased parameter estimates (Bartolucci, 2005; Bauer & Curran, 2003a; Tofighi & Enders, 2003). Assuming normality, a mixture model will lead to empirical derivation of a specified number of classes, each with an approximate normal distribution. If one of the ‘true’ unobserved classes in fact has some non-normal distribution, this will frequently be approximated by multiple normally-distributed classes, thereby resulting in latent classes that represent qualitative differences between subjects and those that represent distributional features of the data. For example, if there are two groups of respondents in a population, one of which has a non-normal distribution of errors, a comparison of two- and three-class models may result in the selection of the three-class model because the mixture model interprets the non-normality as indicating the presence of two different classes with normal within-class distributions. Thus, the three-class model would have at least two classes differentiated by mean differences in a non-normal outcome variable (which jointly approximate the non-normal distribution), and an additional class representing a qualitative difference between classes on the effect of the predictor on the outcome.

Issues related to non-normality have been well documented with finite mixture models in general (Bauer & Curran, 2003a), but the issue has somewhat different implications for regression mixture models. The point of a regression mixture is to find discrete differences in regression weights in the population, thus the model estimates means, variances, and regression weights for each class. To date, two studies have shown that when there are discrete groups that differ in the effects of a predictor on an outcome, even small deviations from normality in the residuals within any of those groups can have large impacts on model results (George et al., 2013; Van Horn et al., 2012). These simulation studies examined the consequences of violating the assumption of normality on model results when using regression mixtures across different levels of low to highly skewed errors. As skew increased, model fit indices favored models with too many latent classes. In cases where the model with the correct number of classes was selected, estimates of regression coefficients for each class were reasonable when skew was low, but showed substantial bias with higher levels of skew.

One method that has shown promise for using regression mixtures to find differential effects in the presence of non-normal errors is the use of an ordered polytomous regression mixture model which involves transforming the outcome variable to be ordinal and then estimating a polytomous regression within each class (George et al., 2013; Van Horn et al., 2012). Simulations showed that even when error terms were highly skewed this approach was still effective at finding the correct number of classes and the correct pattern of differential effects. However, the approach was shown to have some bias in estimates of the proportion of respondents in each latent class, and is limited because the estimates from the polytomous regression are on a different scale from the observed values of the outcome. An alternative approach for estimating regression mixture models in the presence of non-normal errors within each differential effect is needed to provide more flexibility in estimating these models under conditions common in the social sciences.

Differential effects sets

We propose using differential effects sets, groups of latent classes where each group or set represents one regression weight for the predictor on the outcome, with heterogeneity in regression weights modeled between sets, to simultaneously model differential effects and non-normal error distributions when the number of effects is known. Instead of each differential effect being represented with a single class (as occurs with typical regression mixture modeling), this approach distinguishes differential effects with differing slopes across sets of classes. A similar approach has been shown to be useful for dealing with non-normal errors in univariate mixtures where multiple mixture distributions were used within each cluster with a constraint placed such that each cluster has a single mode (Bartolucci, 2005), and also in the case of growth mixture models for addressing non-normality in growth factors (Krueter & Muthén, 2008). In our case, a set of mixture components is used with the regression weight constrained to be equal for all classes within the set such that together these mixture components can approximate a non-normal distribution in errors.

The differential effects sets approach is based on the premise that mixture models can approximate a given distribution with multiple latent classes each of which is assumed to be normal with a unique mean and variance (McLachlan & Peel, 2000; Bauer & Curran, 2003a). The regression coefficient for the effect of the predictor on the outcome is equal for all classes within the differential effects set. Because the classes within a set are used solely to approximate a non-normal residual, these classes are termed residual distribution classes. Differential effects are captured by allowing regression coefficients to differ between sets. This specification captures differential effects across sets, while also capturing non-normality within a set by freely estimating intercepts and variances between residual distribution classes. Denoting the differential effects set by l=1,…,L and let m_l =1,…,M_l denote a residual distribution class in set l, this approach can be formulated as:

$$Y_{i|\mathbf{X},l,m_l}={\beta }_{0l{m}_l}+\sum _{p=1}^P{\beta }_{pl}{x}_{ip}+{\epsilon }_{il{m}_l},{\epsilon }_{il{m}_l}\sim N(0,{\sigma }_{l{m}_l}^2)$$ (3)

where ${\sigma }_{l{m}_l}^2$ is the residual variance in class m_l of differential effects set l. The result is a total of $M=\sum _{l=1}^L{M}_l$ different classes that are each allowed to have their own intercepts and variances, but where only one regression coefficient for the effect of each predictor is estimated for each set (i.e., L different regression coefficients are allowed in total). It is possible to extend this model to the multivariate case with more than one outcome; however, interpreting results under this multivariate specification will become increasingly difficult as the number of outcomes increases. By increasing the number of residual distribution classes, M_l, within a differential effect set, this model allows for increasingly complex residual distributions for the entire set. Thus, we expect that low levels of non-normality will require fewer residual distribution classes, M_l, within a set, whereas higher deviations from normality would require a higher value for M_l. The effect of X for the entire set is estimated, and differences between sets in the effect of X allow for differential effects. The intercept for the entire set can be estimated as the average of all intercepts within the set, weighted by the probability of a particular class, m_l, within that set. This model specification assumes that the effect of X is linear within each differential effect and that the residual variance is constant across all levels of X.

Although this specification posits separate error variances for each of the M classes, it is possible to constrain variances to be equal within each differential effects set or across all classes. The potential advantage of this constraint is an increase in model stability and possibly power because fewer error variances need to be estimated. Because the variance of the residuals within each distributional set is split up between multiple classes, the error variance within each differential effects set is not directly estimable, which makes determining effect sizes within each set difficult. However, a potential advantage is that heterogeneity in variance between differential effects sets can be achieved with more parsimony.

To clarify the modeling of classes in the differential effects sets approach, we consider an example with two differential effects sets of classes. A model is specified with two effects and the number of classes forming each differential effect set is determined through estimating models with an increasing number of residual distribution classes and comparing model fit. In Figure 1, the four-class model with two differential effects sets is depicted with two residual distribution classes in each effect set. The residual distribution classes in each set are constrained to have the same slope. The number of residual distribution classes in each differential effect set is not necessarily equal (e.g., it is not necessary for each effect to have two classes to account for the residual distribution in a four-class model, or for each effect to have three classes in a six-class model). In a four-class model with two differential effects sets, like in Figure 1, the two differential effects could be comprised of a 1-and-3 split of classes, with a single class for one effect and three classes in the other effect set. This is determined through comparison to the four-class model with two residual distribution classes in each set to the four-class model with one residual distribution class in one set and three in the second set. This process allows for determining the number of residual distribution classes needed to estimate the non-normality in each effect. We expect that the number of classes needed to adequately represent each effect will be a function of the degree to which the errors in that differential effects set are non-normal. In general, the percentage of respondents is not expected to be equal across classes within an effect. For example, if 50% of the respondents comprise one differential effect set, in a case with two classes representing the effect, it is not expected that each of the classes has 25% of the respondents in each class.

Figure 1.

Conceptual figure of the differential effects sets approach using a four-class model of two differential effects.

Implementing differential effects sets

Using differential effects sets in regression mixture models is much easier in practice if the number of effects is already known or estimated using a different method. This is because the number of permutations needed to find the correct number of differential effects sets and the number of residual distribution classes becomes quite large if both differential effects sets (L) and latent classes within each set (M_l) are unknown. We believe that it is possible to use differential effects sets to determine the true number of differential effects, but this greatly adds to the complexity of the model search. Therefore, we recommend that, in practice, researchers use another approach first to determine the number of effects needed to help guide the model comparisons in the differential effects sets approach. This first step could use either a strong theoretical basis that suggests a particular number of effects or an estimate of the number of differential effects from another model.

We propose using the ordered polytomous regression model for determining the number of effects, based on previous research that supports this approach for handling skewed errors (George et al., 2013; Van Horn et al., 2012). By first estimating the number of differential effects using the polytomous regression approach, the analyst can then use the differential effects sets approach as a second step to explain the non-normality within each effect set. Once the number of effects is known, model comparisons then are focused on the number of residual distribution classes needed within each differential effects set. For example, when two effects are supported, differential effects sets can be estimated where comparisons are made across models that differ in using one, two, three, or more residual distribution classes to estimate each of the two effects. If the number of effects were not treated as known, comparisons would also have to include examining models that also differ in the number of effects (L) as well as the number of classes within effects (M_l) which adds to the complexity of the process.

Study Aims

The goal of this study is to test the use of differential effects sets for estimating regression mixture models. Previous research has found polytomous regression to be an effective method for finding the number of differential effects present in a population (George et al., 2013), but this approach also was shown to poorly estimate the proportions of respondents in each latent class and is limited because estimates of regression weights are on a different scale. We extend this work by examining the use of differential effects sets to estimate regression coefficients as a second analysis step for describing differential effects. Monte Carlo simulations are used to test the efficacy of this approach in finding differential effects in the presence of skewed errors and the method is applied to data from the Longitudinal Study of Adolescent Health to examine heterogeneity in the relationship between parent health problems and adolescent BMI.

The first aim of this study is to assess the impact of increasing levels of skewed errors on parameter estimates in the standard regression mixture model with one class per differential effect. This addresses whether it is adequate to use the typical regression mixture model, given that the correct number of differential effects are known. Although previous research has examined the consequences of mild skew when using regression mixture models (Van Horn et al., 2012) and the utility of the polytomous regression approach in the presence of high skew (George et al., 2013), the consequences of a high degree of skew when the number of effects are known has not yet been investigated. We hypothesize that bias in regression coefficients, intercepts, and class proportions will increase as skew increases.

Our second aim is to evaluate the number of residual distribution classes needed for each differential effects set, given two differential effects, and to illustrate the process of finding this number via simulations. The process is simplified by treating the number of effects as known. We hypothesize that the number of classes needed to represent the distribution of the data within each differential effect set will increase as the degree of non-normality in the errors increases. For example, in a scenario in which errors are normal in one group and skewed in another group, we predicted that the differential effects set for the group with no skew will contain only one class whereas the set for the group with skew will require more than one class to represent the residual distributions. With greater degree of skew in the distribution of errors, we expected that more classes will be estimated to account for the non-normality in the effect.

The third aim of the study is to evaluate whether parameter estimates from differential effects sets accurately reflect the differential effects present in the population. We hypothesized that the use of multiple classes to approximate a normal distribution within each differential effect set will reduce bias in model parameters as compared to results of the standard regression mixture model, which only uses a single class to represent an effect.

Finally, we evaluate the application of the differential effects sets approach in examining heterogeneity in the effects of parent health problems on adolescent BMI. That is, we sought to identify different groups of adolescents for whom the effect of parent health problems differs. Given that previous research has demonstrated the complexity of processes by which parent obesity and related diseases may or may not increase risk for child obesity (Whitaker, Wright, Pepe, Seidel, & Dietz, 1997), identifying differential effects is an important first step to explain conditions under which parental health contributes to adolescent obesity. For example, Goodman and Whitaker (2002) found the number of obese parents was a strong correlate predicting adolescent obesity classification at baseline but not follow-up one year later in their investigation of the influence of adolescent depressed mood on the development and persistence of obesity. We used the Longitudinal Study of Adolescent Health (Harris et al., 2009) to further examine the heterogeneity in the effects of parent health problems on adolescent BMI. As recommended in practice, we transformed the BMI outcome into an ordered categorical variable and used polytomous regression mixture model to determine the number of effects to guide the application of the differential effects sets approach to estimate differential effects.

Methods

Simulated Data

Data generation

The first aims of this study use Monte Carlo simulations (Mooney, 1997) to examine the performance of differential effects sets. Data were generated in R (R Development Core Team, 2011), and regression mixture models were estimated using Mplus version 6 (Muthén & Muthén, 1998–2010) called in batch mode. Because this study sought to demonstrate the utility of the differential effects sets approach, we demonstrate this method with a relatively large sample size and with balanced proportions with three thousand observations in each differential effects set. The rationale for this is that we believe that regression mixtures, when defined primarily by differences between classes in regression weights of the size typically seen in behavioral research, are best thought of as a large sample technique. Several publically available datasets (such as the Add Health study used here to demonstrate differential effects sets) are available indicating that this approach can be useful at these large sample sizes.

Data were drawn from two populations in which the effects of a predictor, X, on the outcome, Y differed; X was generated from a standard normal distribution with a mean of 0 and a standard deviation of 1. Data for the first population was drawn from Y_i = 0 + .20X_i + ε_i. In the second population, the relation was either Y_i = 0 + .70X_i + ε_i or Y_i = .50 + .70X_i + ε_i. In both cases, ε was scaled so that the variance of Y would be 1. Because the variance of X and Y was fixed at 1, the regression coefficient was equivalent to a correlation. Thus, the populations differed in that in one there is a moderately week correlation between X and Y, and in the other a moderately strong correlation, with either no difference in means or with a small difference in means. The rationale for these conditions is that in the behavioral sciences, if regression mixtures are to be useful for finding differential effects, we would want them to be able to detect differences in effect sizes that are at least this large. When distributional assumptions are met, these differential effects are detectable by regression mixture models (Van Horn et al., 2012) and thus conditions of no skew in both groups are not investigated in the current study. Five hundred simulations were performed for each condition.

Data were generated under ten conditions. These conditions varied from each other in the degree of skew present in one or both of the differential effects sets and in the presence or absence of an intercept difference between the groups. Specifically, conditions were comprised of either no skew or skew of 1.0 or 1.5 in one population, and skew of 1.0 or 1.5 in the second population. Each of these conditions was evaluated with an intercept of 0 in the group with the slope of .20, and an intercept of either 0 or .5 in the group with a slope of .70. Non-normality in errors was created by adding a constant to the error to eliminate negative values and then using a power transformation of 2.76 or 4.0 to obtain the desired skewness for the condition. The resulting error was then centered such that the mean was 0 and scaled so that the standard deviation of Y was 1 for each class in every condition. The values for the power transformations were chosen as they represent major violations of distributional assumptions. We examined these conditions when there was not a difference in the intercept between differential effects sets and also when there was an intercept difference because it is expected that with real data when there is a greater slope in one group there is also at least a small mean difference between groups. No substantive differences in results were found between these two conditions; and thus, for simplicity, we present results for the five conditions in which an intercept difference was present.

Analysis models

For the current analyses, the number of differential effects is assumed to be known, which we believe is a reasonable assumption because the use of an ordered polytomous regression mixture model has been shown to be effective at finding two differential effects in similar situations (George et al., 2013). To examine the use of differential effects sets, we tested a series of seven regression mixture models across simulated conditions. The seven models ranged from a two-class model through a six-class model with different patterns of constraints on the regression coefficients across classes to represent the two differential effects. For each simulation condition we estimated models with varying numbers of residual distribution classes for each of the two differential effects sets. The seven models include: (1) a two-class model with one residual distribution class estimated for each differential effect set; (2) a three-class model with one residual distribution class estimated for differential effect set 1 and two residual distribution classes estimated for differential effect set 2; two four-class models, (3) a model with one residual distribution class estimated for differential effect set 1 and three residual distribution classes estimated for differential effect set 2, and (4) a model with two residual distribution classes estimated for each differential effect set; two five-class models (5) the first with one residual distribution class for differential effects set 1 and four for the second differential effects set, and (6) a model with two residual distribution classes estimated for differential effect set 1 and three residual distribution classes estimated for differential effect set 2, and (7) a six-class model with three residual classes estimated for each differential effect set. The six-class model was estimated only for the simulations with the greatest amount of skew for both effects.

Models were estimated as standard regression mixture models with beta coefficients constrained to be equal within each differential effects set. For example, for model 6 a five-class regression mixture model including two differential effects sets was estimated by including five classes where two of the classes were constrained to have the same beta coefficient and the other three classes were constrained to have the same beta coefficient. Regression weights between these two differential effects sets of classes were free to vary. The classes within each set were constrained to be identical to each other in regression coefficients; the intercepts of all classes were free to vary. Therefore, regardless of the number of classes estimated in the model, only two beta coefficients were estimated.

Comparisons across these seven models were conducted to identify the number of constrained residual distribution classes needed within each differential effect set (Table 1). Up to 11 comparisons were tested for each condition depending on the specific hypotheses regarding the degree of non-normality in the effects. The Bayesian information criterion (BIC) and the Adjusted Bayesian information criterion (ABIC) were used in model comparisons with lower values indicating the preferred model. The Akaike information criterion (AIC) was not used because previous research has shown that it selects too many classes in general (Naik, Shi, & Tsai, 2007; Nylund, Asparouhov, & Muthén, 2007) and when using regression mixtures specifically (Van Horn et al., 2012).

Table 1.

Model comparisons conducted for each simulated dataset under each condition

	Model A		Model B
Specific Comparison	Classes representing effect 1	Classes representing effect 2	Classes representing effect 1	Classes representing effect 2
1 (2 class vs. 3 class)	1	1	1	2
2 (3 class vs. 4 class)	1	2	1	3
3 (3 class vs. 4 class)	1	2	2	2
4 (4 class vs. 4 class)	1	3	2	2
5 (4 class vs. 5 class)	1	3	1	4
6 (4 class vs. 5 class)	2	2	1	4
7 (4 class vs. 5 class)	2	2	2	3
8 (5 class vs. 5 class)	1	4	2	3
9 (4 class vs. 6 class)	2	2	3	3
10 (5 class vs. 6 class)	1	4	3	3
11 (5 class vs. 6 class)	2	3	3	3

Note: Each comparison is a test for whether Model B improves fit over Model A.

Each model was also examined for accuracy in parameter estimates, including regression coefficients, intercepts, and the percentages of respondents in each differential effects set. Note that the standard errors of each class are not directly available for the intercepts in this approach because the intercept is a weighted average of all the intercepts of the residual distribution classes within a differential effect set. These could be obtained using bootstrapping procedures, although that introduces additional complexities such as the need to sort classes across bootstrapped datasets. It is also possible to estimate the SE for the intercept of this model using the delta approximation (Papke & Wooldridge, 2005). In this paper we report the 2.5^th and 97.5^th percentiles across Monte Carlo simulations as the confidence interval for the intercepts. Because the primary focus of regression mixture models is on regression weights which are directly estimated along with their standard errors, difficulties in estimating sampling variability for the intercepts appears to be a minor limitation. Results are reported for key comparisons¹.

Applied Data Example

We demonstrate our approach by investigating the relations between parental obesity-related health and adolescent body mass index (BMI). Adolescent obesity is a major public health concern, current estimates are that one in three adolescents is overweight, one in six is obese, and one in eight is very obese (Lobstein, Baur, & Uauy, 2004; Ogden, Carroll, Kit, & Flegal, 2012). Understanding the etiologic factors for adolescent overweight and obesity is critical as overweight adolescents not only suffer from both current and future health problems (Lobstein, Baur, & Uauy, 2004), they often experience negative social and emotional consequences such as discrimination, social isolation, and mental health problems (Vander Wal & Mitchell, 2011; Wyatt, Winters, & Dubbert, 2006). Parent obesity-related health, including diabetes, is associated with adolescent obesity (Goodman & Whitaker, 2002). Moreover, across child and adolescent development, regardless of youth obesity, having obese parents has been shown to increase the risk of youth becoming obese in adulthood (Whitaker, Wright, Pepe, Seidel, & Dietz, 1997). However, not all children who have an obese parent become obese. Examining heterogeneity in the effects of parent health problems on youth may help explain for whom and under what conditions parental health problems contribute to adolescent obesity. The current study demonstrate the utility of the differential effects set approach by examining different groups of youth for whom there is or is not an effect of parent health problems on adolescent BMI. Adolescent BMI is a good outcome for demonstrating this method as it is neither normally distributed nor does it follow a known distribution. Examining these differential effects is a first step for advancing identification of high-risk populations and psychological and behavioral risk factors for the onset of obesity (Stice, Presnell, Shaw, & Rohde, 2005).

To demonstrate the differential effects sets approach, we used wave 1 of the public use version of the National Longitudinal Study of Adolescent Health dataset, a nationally representative sample of adolescents (Harris et al., 2009). Adolescents (n = 6,504) were in grades 7–12 in the United States during the 1994-95 school year. Data were collected from in-home interviews. Parent report of biological mother’s and father’s health diagnoses was included in the current study to assess parental health problems. As part of the parent questionnaire, parents were asked to respond with “yes” or “no” to whether or not the mother or father (biological parent of the adolescent) currently has diabetes and obesity. Items pertaining to mother and father for each health item were summed, resulting in a scale of 0 = no parents with the specified health problem, 1 = one of biological parents currently have the specified health problem, or 2 = both of the biological parents currently have the specified health problem, for obesity and for diabetes (Goodman & Whitaker, 2002). This approach to quantifying the number of obese parents has been used in other studies predicting adolescent obesity measured by BMI (Whitaker, Wright, Pepe, Seidel, & Dietz, 1997) and has demonstrated predictive validity in the Add Health study (Goodman & Whitaker, 2002). Research has also provided some support for the presence of linear effects of the number of obese parents on adolescent BMI, an assumption made by the analyses presented here. Goodman & Whitaker (2002) found no differences in the effects of paternal and maternal obesity, and the persistence of elevated BMI levels has been linked to having two obese parents (Safer, Agras, Bryson, & Hammer, 2001), warranting further examination of the impact of having one or both obese parents in relation to adolescent BMI.

Adolescents were asked to report their height in feet and inches and their weight in pounds. Adolescent body mass (BMI) was then calculated using adolescents self-report of height and weight by dividing the weight in pounds by the height in inches squared multiplied by 703. This accuracy of this self-report in comparison to measured height and weight in other waves of the Add Health dataset has been documented; for example, the correlation between self-reported weight and interviewer-measure weight is .95 in wave 2 of the study (Goodman, Hinden, & Khandelwal, 2007).

Results

Simulation Study

The analyses looking at latent class enumeration reported the proportion of simulations across conditions that select a target model over a comparison model using the BIC and ABIC as criteria. The best model is not expected to be the same for every simulated condition. The presence and degree of non-normality in the condition is expected to determine which of the two models being compared best fits the data (comparisons are in Table 1). All solutions converged and the range of the smallest class size was between 10% and 49% for the two- and three-class models.

What are the impacts of skewed errors on parameter estimates from regression mixture models?

A two-class model was examined to evaluate the effects of a high degree of skew on regression mixture results when one class was estimated per differential effect. As expected, parameter estimates of this model were biased and deviated further from the population values (i.e., β₀ = 0 and β₁= .20 for differential effect 1; β₀ = .5 and β₁ = .70 for differential effect 2, and 50% of the cases in each effect) as non-normality increased in both effects. The mean of the parameter estimates based on the 500 simulated data sets are presented in Table 2. For example, in the first simulation with no skew for differential effect 1 and a skew of 1 for differential effect 2, the estimation of the regression coefficients performed reasonably well, though the intercepts were substantially biased. However, in the simulation with the greatest degree of skew (1.5) for both differential effects, the parameter estimates showed a high degree of bias (differential effect 1: β₀ = .07, β₁ = .42, 83%; differential effect 2: β₀ = 1.23, β₁ = .46, 17%).

Table 2.

Parameter estimates across Monte Carlo Simulations for the two-class model as skewed errors increase

Simulation	Condition 1		Condition 2		Condition 3		Condition 4		Condition 5
Skew in effect	0, 1		0, 1.5		1, 1		1.5, 1		1.5, 1.5
Class	1	2	1	2	1	2	1	2	1	2
Parameter (true values)	β (se)	β (se)	β (se)	β (se)	β (se)	β (se)	β (se)	β (se)	β (se)	β (se)
Intercept (.00, .50)	.19 (.04)	.34 (.02)	.27 (.01)	.23 (.02)	−.37 (.28)	.47 (.18)	−.33 (.35)	.57 (.29)	.07 (.56)	1.23 (.53)
Slope (.20, .70)	.25 (.05)	.71 (.02)	.32 (.02)	.70 (.02)	.17 (.09)	.55 (.07)	.23 (.10)	.54 (.04)	.42 (.02)	.46 (.04)
Class 1 Proportion (.50)	.57	.43	.66	.34	.28	.72	.34	.66	.83	.17

How many classes are needed to account for non-normality in each differential effects set?

Analyses were conducted for all simulations for each of the conditions described in Table 1, examining different combinations of classes to account for the residual distribution within each differential effects set. Model fit indices favored more classes in cases where there was more skew in a particular differential effect. Table 3 presents the final model selected across the majority of simulations using the BIC. With no skew in differential effect 1 and skew of 1 in differential effect 2, only two classes were selected to model the error distribution; when skew increased to 1.5, three classes were selected; and when the skew was balanced typically a balanced solution was supported. That is, when degree of skew was the same for both differential effects, a model solution that constrained an equal number of classes for each effect was typically selected. In most cases, the solution selected in table 3 was the same for all or nearly all simulations; however, in comparing a four- and five-class model for simulation condition 2, the results were not as clear. For this condition, differential effect 1 had no skew and the differential effect set 2 had skew of 1.5. As hypothesized, the four-class model with a 1 class and 3 class split provided a better fit than the three-class model (with a 1 class and 2 class split) and the four-class model with a 2 class and 2 class split, over 98% of the time. When the four-class model with a 1 class and 3 class split was compared to a five-class model with 1 class for differential effect 1 and 4 classes for differential effects set 2, the BIC supported the four-class model in 80% of the simulations while the ABIC supported the five-class model in 70% of the simulations. To understand the differences, we examined parameter estimates for both solutions. Estimates were nearly identical: the slopes for differential effect 1 were β₁ = .16 (se = .02) and β₁ = .17 (se = .02); the slopes for differential effect 2 were β₁ = .70 (se = .01) and β₁ = .69 (se = .02); and 46% and 47% of the population comprised differential effect 1 for the 4 versus 5 class solution respectively. The substantive interpretation would not change as a result of the model chosen.

Table 3.

Model selected for each scenario of skew based on model fit (BIC)

Simulation Condition		Model selected		Parameter Estimates
Parameter (population values)	Proportion in Effect 1 (.50)	Classes in Effect 1	Classes in Effect 2	Effect 1	Effect 2
				β (se)	β (se)
Condition 1 (skew = 0, 1)		1	2
Intercept (.00,.50)	.45			.00 (.05)	.46 (.05)
Slope (.20, .70)				.16 (.03)	.69 (.02)
Condition 2 (skew = 0, 1.5)
Intercept (.00,.50)	.47	1	3	.00 (.04)	.46 (.07)
Slope (.20, .70)				.16 (.02)	.70 (.01)
Condition 3 (skew = 1, 1)
Intercept (.00,.50)	.36	3*	2	−.18 (.16)	.48 (.07)
Slope (.20, .70)				.18 (.04)	.70 (.02)
Condition 4 (skew = 1.5, 1)
Intercept (.00,.50)	.39	3**	2	.07 (.17)	.50 (.07)
Slope (.20, .70)				.20 (.01)	.60 (.05)
Condition 5 (1.5, 1.5)
Intercept (.00,.50)	.45	3	3	−.10 (.28)	.55 (.13)
Slope (.20, .70)				.19 (.01)	.69 (.02)

^*Results are reported for the majority of the simulations (86%) which estimated a model with three classes representing effect 1.

^**Results are reported for the majority of the simulations (89%) which estimated a model with three classes representing effect 1.

One result of these analyses is that even in large samples with moderate levels of skew (skew = 1), only two classes were indicated using penalized information criterion to account for the non-normal residual distribution of the differential effect. This shows that this approach to modeling non-normal errors can by quite parsimonious with moderate departures from normality.

Choosing a latent class model for non-normal errors

To demonstrate the steps for selecting the best fitting model in the differential effects sets approach, we used simulation condition 5 – i.e., the condition with the greatest degree of skew in both differential effects. The results of all model comparisons across the seven models for this condition can be seen in Table 4. We began by comparing a model with few classes to one with more classes (e.g., comparison 1 examined the three-class model over the two-class model, comparisons 2 and 3 examined a four-class model over the three-class model). As expected, given the greatest degree of skew in both differential effects, for comparisons 1, 2, and 3, the target model with more classes was supported over the comparison model with fewer classes in 100% of the simulations using both the BIC and ABIC.

Table 4.

Latent class enumeration for differential effects sets for the condition with skew high in both effects

Model Comparison	1		2		3	4	5	6	7	8	9	10	11
Proportion of simulations selecting Model B (Table 1)
BIC	1.00		1.00		1.00	0.65	0.34	0.29	1.00	1.00	1.00	1.00	0.83
Adjusted BIC	1.00		1.00		1.00	0.65	0.66	0.65	1.00	1.00	1.00	1.00	0.99
Model Selected #	3 Class (1,2)		4 Class (1,3)		4 Class (2, 2)		5 Class (1, 4)		5 Class (2,3)**		6 Class
Average LL	−7185		−7131		−7130		−7118		−7092		−7072
Median Entropy	0.51		0.53		0.51		0.54		0.44		0.44
Smallest class*	.13–.22		.02–.08		.03–.12		.00–.06		.03–.10		.01–.08
Parameter (population values)	Effect		Effect		Effect		Effect		Effect		Effect
	1	2	1	2	1	2	1	2	1	2	1		2
Intercept (.00, .50)	.48	.31	−.63	.51	−.16	.40	−.42	.32	−.04	.47	−.10		.55
Slope (.20, .70)	.20	.59	.22	.58	.22	.59	.34	.50	.19	.68	.19		.69

^#The model selected by the BIC and ABIC differ for comparisons 5 and 6 with the BIC supporting the 4 Class model (2, 2)

^*The 95% range of the proportion of cases in the smallest class across all simulations; loglikelihood and entropy values are means across all simulations

^**Results are reported for the majority of the simulations (81%) which estimated a model with three classes representing effect 1.

Next, we compared models with the same number of classes and varied whether the number of classes for each differential effect was equal or unequal. In comparison 4, a solution with 1 and 3 residual distribution classes was compared to a solution with 2 and 2 residual distribution classes. We had the expectation that the model with an equal number of classes estimated for each differential effect would be selected because the skew of the residuals was equal in each differential effect. The model with 2 residual distribution classes in each differential effect set was indicated in 65% of the simulations (Table 4). In comparison 6, the simpler four-class model with equal classes was selected, as hypothesized, in 71% of the simulations using the BIC; however, the ABIC indicated the five-class model with 1 residual distribution class for differential effect 1 and 4 residual distribution classes for differential effect 2 fit best in 65% of simulations.

Additional comparisons test the need for a greater number of classes to account for the skew by comparing five-class models versus the supported four-class model with equal numbers of classes across the differential effects. Given the high degree of skew in both differential effects sets, comparisons 7 and 8 were both expected to favor the 5 class solution (with a split of 2 classes and 3 residual distribution classes) over the four-class model with a split of 2 and 2 classes) and over the four-class model (with a split of 1 class and 3 classes). This hypothesis was supported in 100% of the simulations, as seen in Table 4. The model comparisons for this condition raise an interesting complication: although the analyst specifies the split of classes for differential effects sets (a 2 and 3 split in this case), the effects for each set are determined empirically. Thus, across different simulated datasets, differential effects set 1 may include either 2 or 3 residual distribution classes. With equal skew for both effects there is no basis for a hypothesis regarding which effect will have more classes. In this case, 71% of the simulations included three classes for the effect set with a lower regression coefficient. Our method of scaling Y to determine effect sizes results in larger residual variation in the class with a lower regression coefficient, which could have contributed to this result.

The last three model comparisons (9, 10, and 11) evaluated the six-class model against the four-class model with 2 classes for each effect, and both five-class models. Given the high degree of skew in both effects in this condition, we expected that the six-class model would be selected over other models. This hypothesis was supported 100% of the time for comparisons 9 and 10 and over 80% of the time for comparison 11 (Table 4).

If this process were applied to a real data example, the interpretation of these model comparisons would typically result in a six class solution with 3 classes for each differential effects set. This supports the hypotheses that higher levels of non-normality and balanced distributions between the two differential effects will require more classes to adequately model the data and that the split of the number of classes needed will reflect differences in non-normality across the differential effects. This also illustrates the complexity of using this approach even when the number of differential effects is known; adequately modeling the shape of the error distribution requires careful consideration.

Do differential effects sets effectively estimate the differential effects?

The final aim for the simulations focused on the adequacy of parameter estimates obtained from this approach. In general, across simulations, the three-class model with two differential effects sets provided less bias in parameter estimates than the two-class model with only 1 class for each of the differential effects. This was consistent with hypotheses. The ranges of slope estimates for the effects across the scenarios were: β₁ = .16 −.28 (true β₁ = .20) for differential effect 1, and β₁ = .56 - .70 (true β₁ = .70) for differential effect two. These slopes look reasonable, but conditions with more skew or skew in both classes showed more bias in intercepts, as expected. For differential effect 1, intercepts ranged from .03 to .65 (true β₀ = .00); and for differential effect 2, intercepts ranged from −.11 to .46 (true β₀ = .50). This indicates that additional residual distribution classes were needed when skew increased.

The parameter estimates for the selected model in each condition are reported in Table 3. Intercepts and slopes for these models are reasonably well-estimated for both differential effects sets. The only case where estimates of the final intercepts and slopes differed considerably from population values was for condition 4, which had skew of 1.5 and 1 for the two differential effects. In this case, the slope of differential effect 2 was estimated as .60 rather than .70. In all other cases, estimates for both parameters were very close to the true values, and there was relatively little variation across simulations. Additionally, the estimated proportion of cases in each differential effect showed some evidence of bias with over 50% of respondents estimated to be in the class with the higher regression coefficient. This estimate should be interpreted with caution.

Applied Example

We next used the differential effects set approach for interpreting differential effects in the relationship between parental health problems and adolescent BMI, a non-normal outcome. Parental health problems were examined by including both parental obesity and parental diabetes as predictors of adolescent BMI. Because the ordered polytomous regression mixture model has been shown to be effective for identifying the number of differential effects in a relationship, we use this approach to choose the number of differential effects present. We first transformed the adolescent BMI variable into an ordered categorical variable. This was done by dividing the continuous outcome variable into six equal intervals between the 5^th and 95^th percentiles so that each respondent could be placed in the relevant category (the highest and lowest categories are inclusive of negative and positive infinity). Then, regression mixture models were estimated for a single- through a three-class model for this ordinal outcome. Indices of model fit and parameter estimates were examined to determine the number of differential effects of parental health problems on adolescent BMI present in data.

The BIC and ABIC indicated support for the two-class model (BIC: 16,145.27; ABIC: 16,097.60) in comparison to the single- (BIC: 16,161.07; ABIC: 16,138.82) and three- (BIC: 16,199.42; ABIC: 16,126.33) class models. The two classes differed in the effects of parental obesity and parental diabetes on adolescent BMI (i.e., two differential effects). One group consisted of 44% of the population and had a strong effect of both obesity and diabetes, and the other group was comprised of adolescents for whom there was no effect of parental obesity or diabetes on BMI.

Next, given support for two differential effects, we used the differential effects sets approach with the number of differential effects sets fixed to two. Seven models were examined: (1) a two-class model, (2) a three-class model, two four-class models including (3) a model with a two class and two class split across differential effects, and (4) a model with a one class and three class split across effects, and two five-class models including (5) a model with a one class and four class split, (6) a model with a two class and three class split across effects, and (7) a six-class model with three residual distribution classes in each differential effect set. The BIC and ABIC were examined for each model as well as the proportion of adolescents in each class and the substantive differences in the differential effects.

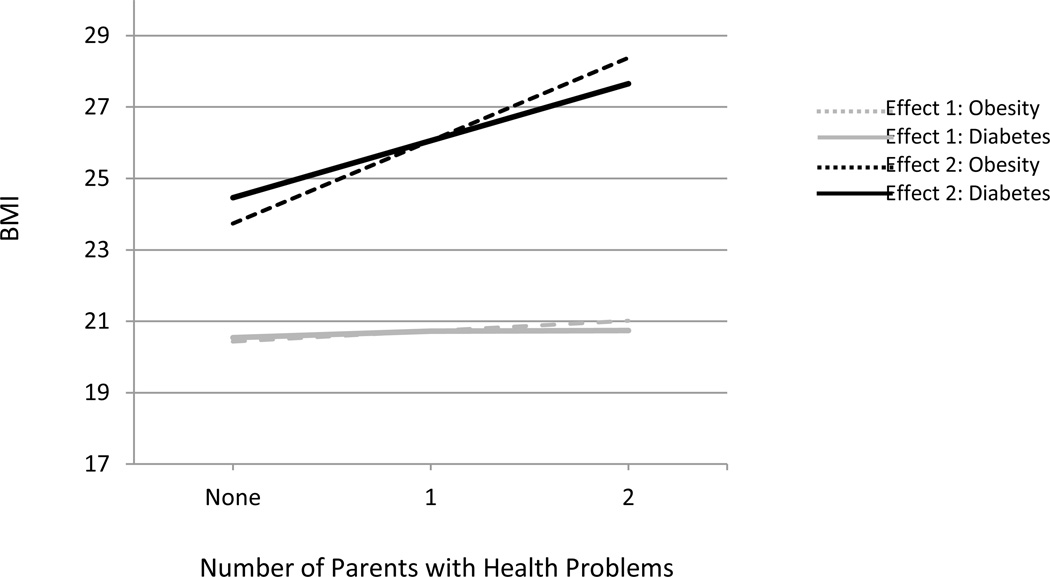
From these different models, we chose the five-class model with two classes in the smaller differential effects set and three residual distribution classes in the other. Although BIC and ABIC for the six-class models were lower, one of the residual distribution classes was estimated to have less than 1% of respondents, and the classes were substantively similar for the effects of parental obesity. Thus, we report the results of the five-class model. Table 5 presents the estimates for each of the residual distribution classes in the two differential effects sets for the indicated five-class model. In Figure 2 the two grey lines represent a differential effects set containing 80% of the sample characterized by small but positive effects of parental obesity (β₁ = .29, se = .04) and parental diabetes (β₂ = .19, se = .05) on adolescent BMI (β₀ = 20.73, se = .23), the weighted average intercept for this differential effects set is 20.72 indicating that on average individuals in this class have BMI in the normal range. The black lines represent the remaining 20% of the sample for whom there was a significant effect of both parental obesity (β₁ = 2.32, se = .25) and diabetes (β₂ = 1.59, se = .41) on adolescent BMI (β₀ = 26.06, se = .28, the weighted average intercept for this differential effects set is 26.06, indicating that on average individuals in this class are overweight, although there is significant variability in this with one (very small) residual distribution class having an intercept of 21.6, which is below the intercept of one of the residual distribution classes in the other differential effects set.

Table 5.

A five class differential effects sets model of parental health problems on adolescent BMI

Differential Effects Sets of Classes
Effect 1			Effect 2
Class (Proportion)		β (se)	Class (Proportion)		β (se)
Class 1 (.08)	Intercept	17.90 (.15)	Class 4 (.03)	Intercept	21.64 (.36)
	Obesity	.29 (.04)		Obesity	2.32 (.25)
	Diabetes	.19 (.05)		Diabetes	1.59 (.41)
Class 2 (.33)	Intercept	22.42 (.27)	Class 5 (.20)	Intercept	26.70 (.27)
	Obesity	.29 (.04)		Obesity	2.32 (.25)
	Diabetes	.19 (.05)		Diabetes	1.59 (.41)
Class 3 (.35)	Intercept	19.79 (.22)
	Obesity	.29 (.04)
	Diabetes	.19 (.05)

Figure 2.

Relationship of parental diabetes and obesity with student BMI for each differential effects set (weighted across all residual distribution classes).

Conclusions

Regression mixture models can be a useful method for identifying differential effects. However, this approach is quite sensitive to violations of distributional assumptions. This study showed that, in the context of moderate to high degree of skew, traditional regression mixtures that use only one class to represent each effect result in serious bias in parameter estimates, even when the number of classes was known. This is a new finding, as previous work demonstrated that mild departures from the assumed distribution of errors did not greatly bias estimates of differential effects, given that the correct number of differential effects was identified (Van Horn et al., 2012). This study showed that, even when the number of differential effects was known, the bias in estimates resulted in the incorrect conclusion that differential effects were not present in the population. These results support the conclusion that violating distributional assumptions when using regression mixture models leads to serious problems.

Modeling differential effects sets of classes using regression mixture models shows promise as an effective alternative for capturing differential effects when assumptions are violated. The number of classes selected to represent the non-normality in the differential effects sets approach matched the degree of skew in the effect as hypothesized in most conditions. Generally, effects without skew yielded support for a model with only one class to estimate the effect, whereas conditions with skew of 1.0 yielded two classes, and skew of 1.5 resulted in support for a model with three classes to represent the differential effect. The exception is the case of simulation 3, in which we found support for three classes representing a differential effect with skew of 1.0, showing that additional classes may be needed even with moderate amounts of skew. The use of additional classes to model non-normal residual distributions was effective and resulted in less bias in estimates of the differential effects in comparison to the standard regression mixture which relies on only one class to model each effect.

Selecting the best-fitting differential effects sets regression mixture model for the data was straightforward in most conditions using the BIC or ABIC. When there was disagreement among model fit indices the estimates of the effects were virtually identical regardless of the model selected. Because multiple classes of differential effects are used solely to account for non-normality (and the analyst need not substantively interpret these classes), the number of classes selected is not a major concern so long as they result in adequate estimates of differential effects. In all cases, the use of differential effects sets when non-normal errors were present greatly decreased bias in parameter estimates as compared to using one class per differential effect. Even in the condition of the highest degree of skew in both effects, the estimates were not only substantively correct, but mirrored the effects in the population. Conversely, a standard regression mixture with the number of effects known failed to provide support for the presence of differential effects.

We propose that the differential effects sets approach can be used in practice as a second step to the polytomous regression mixture model, which has been shown to be robust to skew for finding the number of differential effects (George et al., 2013; Van Horn et al., 2012). Although differential effects sets can be used on their own, model search is less complex when guided by the number of effects present. This investigation has shown that using this approach will uncover the underlying regression parameters within each of the differential effect sets and preserves the metric of the original dependent measure.

The applied example was used to demonstrate the differential effects sets approach in practice. We first established the number of effects empirically using the polytomous regression model and then used differential effects sets to clarify heterogeneity in the relations between parental health problems and adolescent BMI. This approach supported the presence of two differential effects, a large group for whom there was a small effect of parental obesity and diabetes and a second group for whom there was a very large effect of both parental health problems. The smaller group includes children who, on average, have BMI in the ‘overweight’ range, although there is substantial overlap between these groups. This example is limited by the measurement of the parental health indicators. The example is suggestive of some interesting heterogeneity in the effect of parental health on adolescent health, but in general indicators with only three levels provide weak evidence for heterogeneous effects and they make the assumption that effects are linear for each differential effect. Although there is some reason to believe that the assumption holds in this case, a more thorough examination of the effects found in this example is warranted.

The current study shows that regression mixture models with differential effects sets can be an effective approach for describing differential effects when error distributions are not likely to be normal. A number of limitations, however, should be acknowledged. First, this study tested the differential effects sets approach in a setting that was in some ways ideal: with large sample sizes and a 50/50 split in the proportion of respondents in each differential effects set. The purpose of the study was to show that differential effects sets are effective at dealing with non-normality rather than thoroughly exploring the conditions under which the models work. Very little research has examined sample size requirements for regression mixture models in general. Two studies in the marketing area show that the models can be effective with only a couple of hundred subjects (Papke & Wooldridge, 2005; Sarstedt & Schwaiger, 2008); however, these studies were conducted under scenarios that are unlikely to be seen in the social sciences (R² = .60 – .95 and large differences between classes in intercepts). Preliminary research using conditions closer to those observed in the social sciences suggests that under ideal conditions these models may be effective with sample sizes as low as 1500 (Smith, Van Horn, & Zhang, 2012), but that the models tend to be unstable and produce spurious results at lower samples. As expected, preliminary evidence suggests that the polytomous regression approach requires larger samples than continuous outcomes. More research is needed to examine sample sizes required for estimating differential effects sets; we hypothesize that for differences in effects similar to those reported in these simulations, sample sizes greater than 1500 will be required. Sample size requirements should decrease as more information is included in the model (such as including multiple outcomes, multiple predictors, and predictors of class membership).

Another limitation of this study is that we examined only one type of non-normality (skewed errors created using power terms). Because mixtures may be used to approximate a wide range of distributions, this approach should generalize to other types of non-normal distributions; however, this was not evaluated in this study. Additionally, we believe that this approach will not be robust if the shape of the residual distribution is not constant across levels of X. If the error variance increases or decreases as a function of the predictor, the bivariate distribution should be approximated by multiple distributions with different regression lines. We hypothesize that heterogeneity in the error distribution as a function of the predictors will result in too many differential effects sets being recovered. The polytomous regression approach should be somewhat more robust to heterogeneity of variance since the variance is not directly modeled, so it may be possible to detect this situation by differences in results between differential effects sets and the polytomous regression mixture model.

A third limitation is that the method works best when the number of effects present in the population is known. Although we used a polytomous regression mixture model for determining the number of effects, this is not the only method available, and other means for identifying the number of effects present may be used. Using a sequence of model comparisons across multiple models to determine the final model selected may not always be straightforward and could be difficult when relying on a large number of model comparisons.

We see regression mixture models as a useful exploratory method for modeling differential effects, when heterogeneity can be described by typical patterns in the relationship between a predictor and an outcome. Nearly all implementations of this approach assume that relationships are linear within latent classes, or differential effects sets, although it is possible to capture non-linear relationships across multiple classes (Bauer & Curran, 2004). The use of differential effects sets to simultaneously model differential effects and non-normal error distributions is a novel approach for addressing the sensitivity of regression mixture models to non-normal errors which brings a good deal of flexibility for approximating ‘ugly’ error distributions. More work needs to be done to better understand the cost of this approach in terms of sample size and its sensitivity to error distributions that are not constant across levels of the predictor variables.