Spatial cluster analysis of early stage breast cancer: a method for public health practice using cancer registry data

Abstract

Objectives

Cancer registries are increasingly mapping residences of patients at time of diagnosis, however, an accepted protocol for spatial analysis of these data is lacking. We undertook a public health practice–research partnership to develop a strategy for detecting spatial clusters of early stage breast cancer using registry data.

Methods

Spatial patterns of early stage breast cancer throughout Michigan were analyzed comparing several scales of spatial support, and different clustering algorithms.

Results

Analyses relying on point data identified spatial clusters not detected using data aggregated into census block groups, census tracts, or legislative districts. Further, using point data, Cuzick-Edwards’ nearest neighbor test identified clusters not detected by the SaTScan spatial scan statistic. Regression and simulation analyses lent credibility to these findings.

Conclusions

In these cluster analyses of early stage breast cancer in Michigan, spatial analyses of point data are more sensitive than analyses relying on data aggregated into polygons, and the Cuzick-Edwards’ test is more sensitive than the SaTScan spatial scan statistic, with acceptable Type I error. Cuzick-Edwards’ test also enables presentation of results in a manner easily communicated to public health practitioners. The approach outlined here should help cancer registries conduct and communicate results of geographic analyses.

Introduction

Advances in spatial technology enable epidemiologists to create detailed maps and employ spatial cluster statistics to garner insights about patterns of disease [1, 2]. Many of the early disease clustering studies focused on cancer and attempted to shed light on spatially varying risk factors [3–5]. In recent years, however, etiologic cancer cluster studies have been criticized for failing to consider the extended latency between exposure and disease, often embodied in a neglect of residential, occupational, and other forms of mobility [6–9].

In light of the challenges associated with the etiologic mapping of cancer, spatial epidemiologists have begun to map and analyze stages of cancer incidence to reveal factors about health care availability and demography that influence stage of diagnosis. In demonstrating the utility of this approach, clusters have been detected using data aggregated into (a) zip codes in a study of breast cancer in situ in Wisconsin [10], (b) census tracts in studies of prostate cancer in New Jersey [11] and colorectal cancer in Massachusetts [12], and (c) census block groups in studies of breast cancer in Florida [13] and prostate cancer in Maryland [14]. In addition, clusters were detected using geocodes (without aggregation) in studies of colorectal cancer in California [15] and Iowa [16]. In majority of these studies, factors associated with clusters were revealed, including age, race, ethnicity, socio-economic status, urbanicity, proximity to screening facilities, and average rate of screening facility usage. These studies have helped to support a relationship between living in close proximity to mammography screening centers and early stage breast cancer diagnosis [10, 13].

Despite the progress in analyzing spatial clusters of cancer using stage of diagnosis, different scales of spatial support and distinct analytical approaches are often adopted, making it difficult to compare results across studies. Cancer registries are a valuable resource for investigating influence of spatial support and analytic methodology seeing that geocoding is becoming common practice at cancer registries around the country. This article presents a protocol for spatial cluster analysis of residence at time of cancer diagnosis using cancer registry data, and grew out of a cross-disciplinary collaboration between health geographers, spatial statisticians, epidemiologists, and the Michigan Cancer Surveillance Program (which includes the state cancer registry). Given the challenges in making etiologic inferences in spatial analyses based on residence at time of diagnosis [6–9], we chose to focus on early stage breast cancer as our endpoint because of the influence of more temporally proximate factors such as access to health care and screening facilities. The overall goal is to determine an acceptable protocol for identifying regions with statistically elevated rates of early stage breast cancer. There was special interest from cancer registry staff to identify a reliable method for identifying clusters in small geographic areas, and for determining an approach that could be implemented in a straightforward fashion by public health and cancer control professionals.

Geographers have long known that results and inferences may vary due to change of scale in spatial units, and this is referred to as the modifiable area unit problem (or MAUP, for short) [17]. These inconsistencies arise as a result of the aggregation of point data into administrative boundaries; points near one another may be split into separate groupings, and similarly points somewhat far apart may be grouped together. A consequence of MAUP is the tendency for different statistical results to be obtained from the same set of data when the information is grouped at different levels of spatial resolution [17]. Therefore, one cannot claim that results of spatial studies are independent of the units selected. Although this phenomenon is widely known in the geography literature, it has not been well explored in the epidemiologic literature. One set of detailed simulation studies found that, when used in cluster studies, point data do not necessarily have greater statistical power than aggregated data [18]. This is attributable to the nature of the clustering methods themselves (e.g., a point-based method with poor statistical power will not out-perform a good area-based method), and whether the assumptions of the methods are valid in different applied settings. More recent studies have suggested that analyses of point data are more valid than those performed on aggregated data [19, 20]; however another analysis found choice of spatial unit not to influence the results [21]. No study has examined whether clustering of cancer cases by stage is consistent when using point data versus aggregated data (e.g., census block groups, census tracts, zip codes, legislative districts, etc.). The first objective of this article is to examine whether spatial clusters of early stage breast cancer persist when using different spatial units of analysis.

In addition, while several studies have examined the performance of local spatial clustering methods on aggregated data (for example, see [22–25]), only a handful of studies have compared the performance of local clustering approaches using point data [26–29], and not one of these studies concluded that one method was better than another. The second objective of this article is to compare local clustering of geocoded points of early stage breast cancer residences using two popular easy-to-use local clustering algorithms: SaTScan’s spatial scan statistic [30] and Cuzick-Edwards’ nearest neighbor local clustering test [31].

Methods

The Michigan Cancer Surveillance Program (MCSP) compiles cancer records for the State. External estimates designate a completeness percentage of 95% or higher on the population-based data collected for the state of Michigan since 1985. MCSP is funded in part by the National Program of Cancer Registries within the Centers for Disease Control and is nationally certified by the North American Association of Central Cancer Registries at its highest level. From 1994 to 2002, 67,136 women were diagnosed with breast cancer in Michigan. Cancer cases were defined as early stage (67%), late stage (22%), or unknown (10%) as derived from the SEER General Summary Stage classification [32, 33]. Early stage consisted of local and in situ cases; late stage consisted of regional and distant metastatic cancer.

Approximately 92% of breast cancer cases were successfully geocoded at residence at time of diagnosis under the oversight of the Michigan Cancer Surveillance Program. The geocoded dataset for analysis contained 42,670 early stage cases and 14,150 late stage cases. The percentage of addresses successfully geocoded did not differ by stage or year of diagnosis.

In the first cluster analysis, data were considered at different spatial scales, including individual geocode (n = 56,820), and aggregated into census block groups (n = 8,409), census tracts (n = 1,748), and state legislative districts (n = 110) across all of Michigan. A range of spatial scales was selected to compare results from the precise (individual geocode) to the coarse (state legislative districts). SaTScan spatial scan statistic v7.0.3, a popular freeware often adopted in epidemiologic studies [11–15], was used to identify spatial clusters of early stage cancer cases. This spatial scan statistic can be applied to polygons to identify clusters in rates of disease (e.g., areas with high rates of early stage cancer) or to point data to compare ratios of early stage and late stage cancers. Using geocoded point data, the Bernoulli model is recommended, and was used to examine the ratio of early-to-late stage breast cancer in Michigan. With polygon data the Poisson model is available, and the numerator was specified to represent early stage cancers while the denominator was defined as early plus late stage cancers. The Poisson model was run on data aggregated into census block groups, census tracts, and state legislative districts.

SaTScan constructs numerous circular areas over each map and determines whether the probability distribution of early stage breast cancer inside each circular area differs from that of the State as a whole. The size of these search windows varies from 0% to a specified maximum. For all models, a maximum circular search window equivalent to 4% of the population size was selected. This maximum size was selected because cancer registry staff were interested in identifying clusters within small geographic areas. This maximum window size is more than twice as large as the most populated state legislative district, more than eight times as large as the most populated census tract, and more than twenty times as large as the most populated census block group; therefore, the cluster algorithm would be able to detect a cluster in any of the scales of analysis, should one exist. A purely spatial analysis was run 999 times for each spatial scale; the Bernoulli model took nearly 10 h to examine clustering in the geocoded dataset. Significance of results was tested within the software using Monte Carlo simulation. We chose to display overlapping circular clusters so long as no pairs of centers are both in each other’s cluster, which results in amoeba-like clusters that are more plausible than isolated circular clusters. Results were visually presented using Space Time Intelligence System (STIS v1.5; Terraseer, Inc., Ann Arbor, MI).

Different algorithms for identifying local clusters using point data were also compared. Given the 10-h processing time required for SaTScan on the 1994–2002 geocoded data, these analyses were limited to only three years of data: 2000–2002 (n = 14,728 early stage breast cancer cases and 4,750 late stage cases). As described above, SaTScan’s Bernoulli model was used to scan the geocoded data for clusters. As a second method, Cuzick-Edwards’ k nearest neighbor local clustering algorithm was selected (STIS). To implement this nearest neighbor algorithm, the user specifies a number of k nearest neighbors, and the method then calculates the proportion of early stage cases surrounding each early stage case using the specified k locations nearest to each case. Similar to SaTScan, this method determines whether the probability distribution of early stage breast cancer inside each k nearest neighbor search window differs from that of the State as a whole. Given interest by Cancer Registry staff of finding clusters within small geographic areas, we elected to use k = 200 nearest neighbors, yielding a search window of ~1% of the total population; similar results were observed for k = 100 and k = 300 nearest neighbors. Cuzick-Edwards’ test took 4 min to run in STIS, compared with more than 2 h for SaTScan.

Given that we were using real data with an unknown spatial pattern, it was important to assess whether or not the clusters were believed to be credible. The plausibility of the clusters was assessed using (1) known factors associated with early stage breast cancer and (2) simulations using results from the original data. First, logistic regression analyses were conducted in STIS, investigating the relationship between early stage breast cancer clusters (dependent variable: member of cluster or not) and distance from mammography clinics (2006 locations), race (black or white), and percent of population in poverty in 2000 Census Tracts (socioeconomic measure recommended by Krieger [34]). Second, simulation studies that were founded on the observed data and geography were used.

The problem often arises in disease clustering of determining the type I and type II error, and statistical power of a disease clustering method. This is accomplished to compare methods and also to evaluate, for a given disease in a specific instance, the performance of a method or set of methods. Two approaches are commonly used to address this problem. First, the analyst might take one instance of a disease (say breast cancer at stage of diagnosis in Michigan) and analyze this single map using several different methods in order to evaluate their performance. This is the first approach described above, but has the drawback in that the analyst has no idea what the true underlying disease risk actually might be. Any observed differences in the behaviors of the methods thus may be due to vagaries of the approaches themselves, or could be due to correct detection of true (but unobservable) differences in underlying risk. The second approach relies on designed simulations to evaluate statistical performance of clustering techniques for simulated disease patterns for which the underlying true risk has been created by the analyst. Here the underlying “truth” is known, but the scope of inference regarding statistical behavior of the methods analyzed is limited to the simulation experiment. We have modified this second approach using observed data, as now described.

We are interested in determining whether Cuzick-Edwards’ test correctly detects “true” members of clusters characterized by a given level of relative risk (RR). The objective of the simulation is to evaluate type I and type II errors, using the observed population at risk and a given disease pattern. The following framework was adopted in the present article:

1. Evaluate clustering on the observed map of geocoded data (i.e., breast cancer stage at diagnosis in Michigan) using the method M of interest, Cuzick-Edwards.

2. For the same dataset, assign to each geocoded location a local rate computed as the proportion of breast cancer cases at an early stage of diagnosis within the k-neighbors (e.g., k = 200). The resulting map R will be considered as the true risk map for the quantification of false positives and false negatives.

3. Evaluate the sensitivity and specificity of method M using the Receiver Operating Characteristic (ROC) curve for a given level of elevated risk. See Goovaerts [35] for details on calculation of ROC curves, as now summarized. First, specify a given RR, e.g., 1.2, and compute the RR for each location by dividing the local rate by the area-wide rate. Identify all locations on map R with a RR ≥ 1.2; these are defined to be “true” members of clusters. The ROC curve plots the probability of false positive versus the probability of detection. The y-axis represents the proportion of correctly detected clusters (in our example the number of locations with a local RR ≥ 1.2 that have been classified as a cluster member by the method M), while the x-axis represents the proportion of true clusters that have been wrongly declared significant. This is repeated for different significance levels (identified with the p-values of the tests) to generate an ROC curve.

The approach assumes that the observed geographic distribution of cases at the different stages of diagnosis is a reasonable estimate of the “true”, underlying risk of stage at diagnosis. It gives us some idea of the statistical performance of the method being considered given the method’s parameters (e.g., k), the actual disease geography (e.g., Michigan), the observed spatial distribution of cases (e.g., the geocoded locations), and the observed heterogeneity in local disease risk. By applying this approach using different levels of RR, we are able to statistically evaluate the ability of the method (e.g., tradeoff between detection and type 1 error) to detect true clusters defined by a given RR for that specific disease geography under consideration.

Results

From 1994 to 2002, the percentage of early stage breast cancer cases in Michigan increased from 72% to 77%, with an average equal to 75% over the entire time period. Across census block groups and census tracts, the percentage ranged from 0% to 100% early stage, reflecting a wide range of values across the State (Table 1). In State House legislative districts, however, there was less variation with proportions of early stage breast cancer ranging from 64% to 80%.

Table 1.

Rates of early stage breast cancer using different spatial supports in Michigan

	Minimum	10th Percentile	Median	90th Percentile	Maximum
Census block group	0.00	0.40	0.75	1.00	1.00
Census tract	0.00	0.59	0.75	0.88	1.00
State legislative district	0.65	0.70	0.75	0.78	0.80

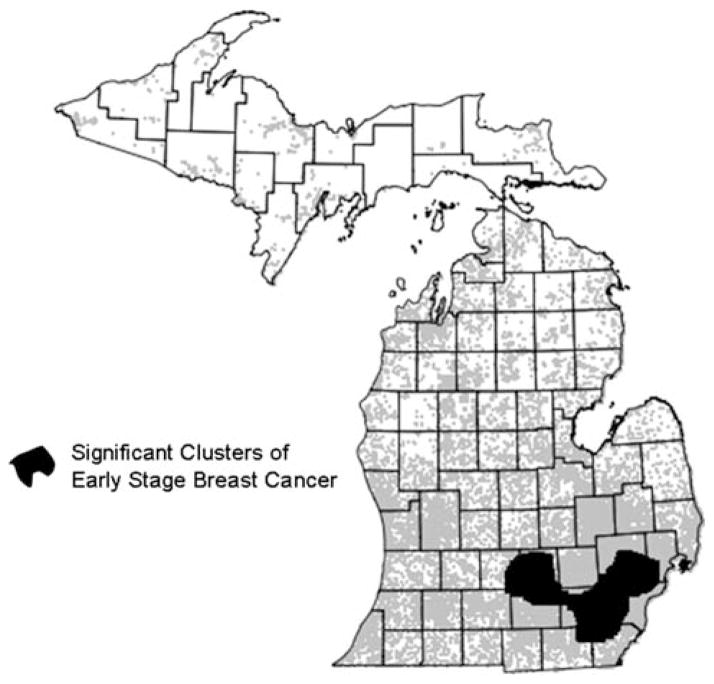
Using breast cancer cases from 1994–2002, SaTScan identified spatial clusters of early stage breast cancer using individual geocodes, but not with any of the sets of aggregated data (census block groups, census tracts, and State House legislative districts). Significant clusters were located in southeastern Michigan, and included the areas surrounding Detroit, Jackson, and Lansing, as well as the city of Ann Arbor (Fig. 1).

Fig. 1.

Significant clusters of early stage breast cancer cases 1994–2002. Results of SaTScan Bernoulli clustering model applied to geocoded points

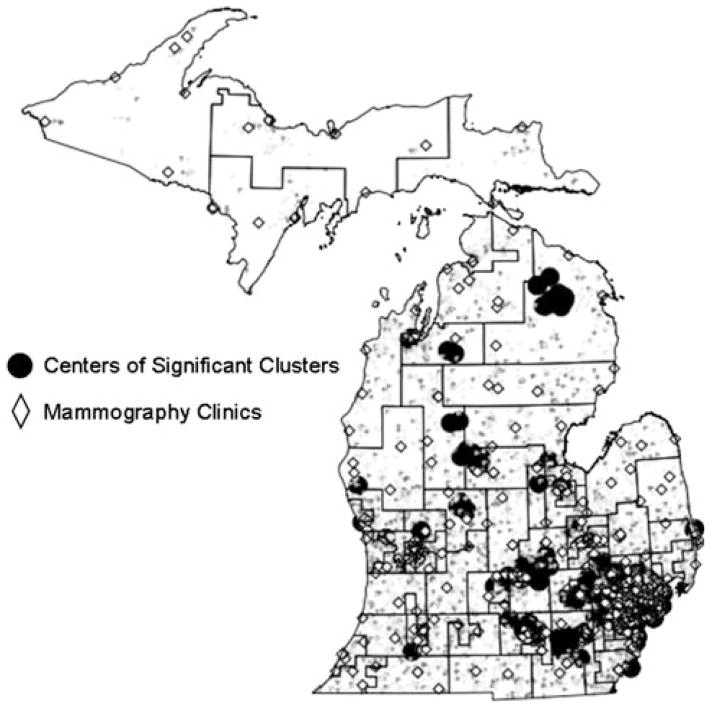
In light of significant findings using geocoded points, another popular local clustering algorithm for point data was adopted: Cuzick-Edwards’ test. The performances of SaTScan and Cuzick-Edwards’ test were compared using geocoded breast cancer cases in Michigan from 2000–2002. Using only three years of data, SaTScan no longer identified any significant clusters; however Cuzick-Edwards’ test found significant clusters in several parts of the State (Fig. 2), including the southeastern section identified by SaTScan using the data from 1994–2002 (Fig. 1).

Fig. 2.

Centers of clusters of early stage breast cancer 2000–2002; Results of Cuzick-Edwards’ test

The Cuzick-Edwards’ results were examined for plausibility, first by investigating whether parameters usually associated with early stage breast cancer were associated with the clusters. In a fully adjusted logistic regression model, clusters of early stage breast cancer were negatively associated with distance from mammography clinics (using 5 km increments: OR = 0.93; CI: 0.90, 0.95), black race (compared to white: OR = 0.47; CI: 0.39, 0.56), and percent of population in poverty in 2000 Census Tracts (for every one percent increase in poverty: OR = 0.92; CI: 0.91, 0.93).

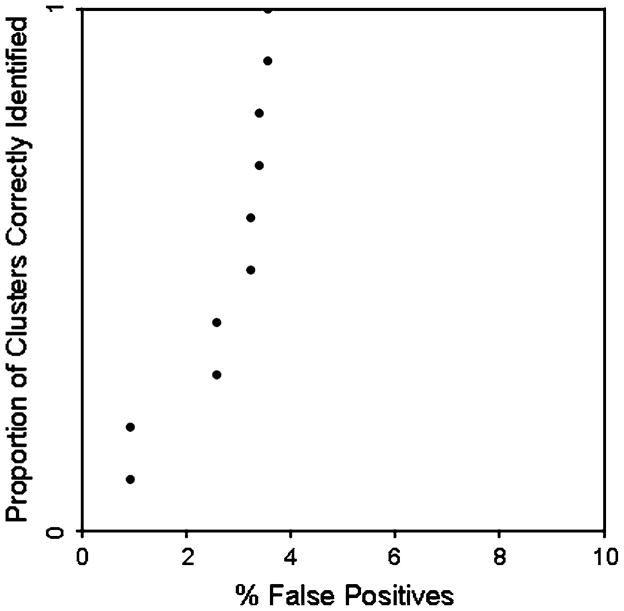
Plausibility of the Cuzick-Edwards’ results was also examined using the simulation approach based on ROC curves, as described in the section “Methods.” Here we used the observed disease map to define areas that are elevated at specific relative risk thresholds, and then assess the ability of the Cuzick-Edwards’ test to correctly identify these areas as cluster constituents. If we use results based on a RR = 1.2 (equivalent to a probability of early stage diagnosis = 0.9 for this dataset), we see fewer than 5% false positives regardless of the proportion of clusters correctly identified (ranging from 0–100%) (Fig. 3). Similar results are obtained for the case RR = 1.1. This suggests the Cuzick-Edwards’ clusters are real, since the method is capable of correctly identifying true clusters defined by relatively small increases in risk (RR = 1.1 or higher).

Fig. 3.

Receiver operating characteristic curve for relative risk ≥1.2; simulation using Cuzick-Edwards’ test

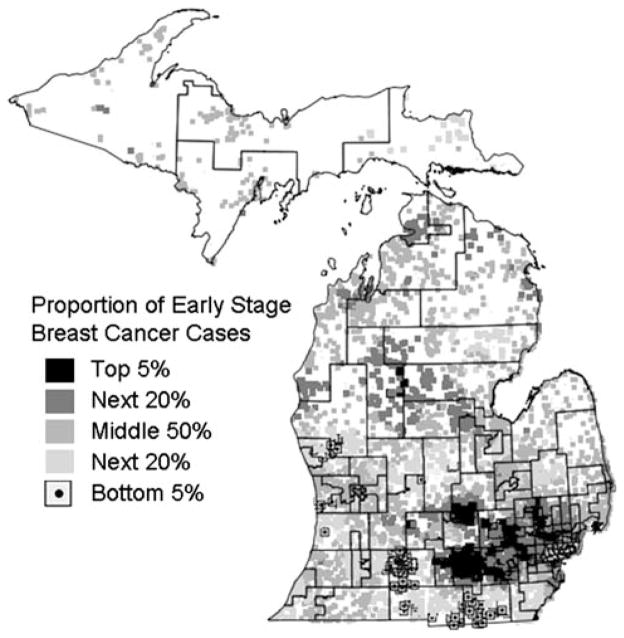
In addition to identifying significant clusters, the Cuzick-Edwards’ test generates a value for each early stage breast cancer case that reflects the proportion of early stage cases among its 200 nearest neighbors. Cancer registry officials felt overlaying these proportions on top of state legislative districts was helpful for visually depicting and communicating which regions have the highest and lowest proportions of early stage cases (Fig. 4).

Fig. 4.

Distribution of proportion of early stage breast cancer cases generated by Cuzick-Edwards’ test using k = 200 nearest neighbors

Discussion

This article results from a collaboration between researchers and cancer registry practitioners and presents three significant findings for analyzing and displaying cancer registry data. First, spatial analyses of early stage breast cancer conducted at the individual-level have the potential to identify patterns missed using data aggregated within geographical units, even when such units are small (e.g., census block groups). Second, relative to the SaTScan spatial scan statistic, Cuzick-Edwards’ test is more sensitive for identifying early stage breast cancer clusters while having acceptably low Type I error. Third, Cuzick-Edwards’ test allows presentation of areas with high and low proportions of disease, facilitating communication to public health practitioners.

Spatial cluster analyses of disease have traditionally been used to address etiologic questions; however, given concerns about latency and mobility, spatial epidemiologists are increasingly turning their attention to spatial factors about health care availability and demography that influence disease diagnosis [13, 15, 36]. A number of studies have investigated clusters of early and late stage diagnosis of different cancers [10–16]; however, analyses were generally conducted at only one spatial scale. As MAUP implies and our results illustrate, analyses of early stage breast cancer in Michigan produce conflicting results when conducted on different spatial scales; this may be attributable to the diminishing variance between regions that results from aggregating data into larger and larger geographic units (Table 1). Further, given the preference for individual-level data in epidemiologic studies and concerns about the ecologic fallacy [37], results using geocoded points are preferred.

Earlier comparison studies of local clustering approaches using point data have not demonstrated the superiority of one clustering algorithm [26–29]. In our analyses, Cuzick-Edwards’ test identified clusters of early stage breast cancer not detected by SaTScan, and those clusters were considered to be important because simulations demonstrated that the method had few false positives at even small levels of elevated risk. Further, the clusters found were associated with established factors predictive of early stage breast cancer (race, poverty, and mammography screening facilities), and thus are etiologically plausible.

Few spatial epidemiologic studies have incorporated analyses of geocoded data, at least in part as a result of patient confidentiality concerns. The Health Insurance Portability and Accountability ACT (HIPAA) is vague with regard to the release of geographic identifiers, which has resulted in many health agencies adopting the safe approach and not sharing their geocoded data [38]. However, as demonstrated here, it is clearly in the interest of public health to forge research–practice partnerships that permit the sharing of geocoded data. Spatial masks that jiggle geocoded locations in small area studies are increasingly being used [39], and secure servers that allow data to be accessed and analyzed on the server side (over the internet) rather than on the client side may be a future solution [38]. At present, data sharing agreements, human subjects training, and Institutional Review Board (IRB) approval have proven satisfactory when using data from pre-existing cohort or case–control studies, and can also be implemented for secure data sharing with cancer registries (as we accomplished in this collaboration).

One major strength of this study is that the numerator (early stage cases) and the denominator (early plus late stage cases) come from the same cancer registry dataset, precluding the need for census-derived estimates of population at risk. Failure to account for error in census-derived denominators has confounded studies for decades, with geographic analyses only the latest victim [40–42]. For example, the rapid increase in breast cancer incidence in Marin County, California during the 1990s [43], turned out to be an artifact caused by census-derived population estimates [44].

The work presented here has several additional strengths. Multiple factors were considered in these analyses, including spatial scale, local clustering algorithms, Type I error, and association between significant clusters and known predictive factors. In doing so, this work takes several steps to support the use of Cuzick-Edwards’ test in spatial clustering analyses of point datasets. Further, by overlaying different geographic regions onto the Cuzick-Edwards’ estimate of high and low proportions of early stage breast cancer cases, cancer registry practitioners felt confident they could communicate results easily, effectively, and in a straightforward manner with the public.

Notwithstanding the strengths of this work, both the data and methods have a few limitations. Stage at diagnosis was unknown for 10%of the cases and 8% were not successfully geocoded. Geocoding accuracy diminished in northern Michigan, including the Upper Peninsula; however, the percentage of addresses successfully geocoded did not differ by stage or year of diagnosis. In the aggregated analyses, the Poisson model is the only option in SaTScan, and given that the outcome (proportion of early stage breast cancer cases) does not follow a Poisson distribution, it is possible that this model misspecification influenced the results. Another concern is whether tests of significance, as opposed to effect measures (e.g., odds ratios), are suitable for determining differences between the results from SaTScan analyses conducted on different spatial scales. We chose to use statistical significance because (a) sample size remained large when aggregating to census block groups (n = 8,409) or tracts (n = 1,748), and (b) tests of significance are used almost exclusively in spatial analyses because of multiple testing concerns associated with evaluating potential clustering around each case. Along similar avenues concerning significance testing, Cuzick-Edwards’ test requires user-specification of the number of k nearest neighbors, raising possibility of significance as a result of multiple testing when using several different levels of k, or missing important clusters that are not significant using the chosen k. These concerns, however, were not found to be important here, as we observed similar results for k = 100, 200, and 300 nearest neighbors, and limited Type I error in the simulation analyses. Although the predictive variables in the regression analysis were significant, demonstrating the clusters’ plausibility, the census-derived poverty measure, and the as-a-bird-flies measure of proximity to screening facilities are surrogate estimates of individual-level income and screening experiences, respectively. No data were available on individual income or screening practices. In addition, the locations of the screening facilities were from 2006, a slight temporal mismatch from the 2000–2002 breast cancer dataset. Lastly, while some may find concern with a comparative study using real as opposed to simulated data, we believe, like others [28], that it is important to compare algorithms using real datasets because they contain variances and nuances seldom found in simulated datasets. This study’s coupling of analyses of real data with simulations based on real data is an important innovation.

This study focused on developing an approach for identifying spatial clusters of early stage breast cancer using registry data. Another spatial analysis that could be accomplished with these data might, more directly, incorporate spatial regression models and potential spatial confounding. For example, one may wish to focus on what is causing high rates of early stage breast cancer in parts of Michigan. The regression model presented here explains part of the spatial pattern using surrogate measures of income and screening practices and race. This study does not investigate neither why white race is associated with early stage breast cancer nor whether additional factors could further explain the spatial patterns in early stage breast cancer. This type of spatial regression analysis is ground for future work, and would best be served if individual-level information on health care access, use of screening clinics, socio-economic position, racial/ethnic sub-grouping, etc., were routinely collected by cancer registries.

Collaborating in this research–practice partnership enabled us to identify and illustrate a practical approach for spatial analysis of geocoded cancer registry data. The researchers embarked on this project striving to develop an appropriate methodological protocol. Cancer registry practitioners desire maps that are accurate, easy to create, and easy to explain. The methodology selected uses the actual geocoded data points, and does not require data to be aggregated into arbitrarily chosen administrative units, thereby saving time and effort in the data management process (especially cumbersome if aggregating multiple years of data). The resulting Cuzick-Edwards’ analysis of geocoded data produces maps of statistically significant clusters of early stage breast cancer (Fig. 2) and areas with high and low proportions of early stage breast cancer (Fig. 4). Different geographies may be easily added to the background of these maps (e.g., legislative districts, census districts, zip codes, counties, etc.) for assistance when communicating findings to legislators and community members.

In conclusion, in light of MAUP along with our findings of differences between analyses of point and aggregated data, we encourage researchers and cancer registry practitioners to jointly establish acceptable protocols for sharing confidential geocoded data. The approach illustrated here can be easily adopted to help understand and communicate about public health factors that are responsible for spatial patterns in stage at diagnosis, cancer survival, and other measures of relevance to cancer control.