Abstract
Methods for obtaining cardiomyocytes from human embryonic stem cells (hESCs) are improving at a significant rate. However, the characterization of these cardiomyocytes is evolving at a relatively slower rate. In particular, there is still uncertainty in classifying the phenotype (ventricular-like, atrial-like, nodal-like, etc.) of an hESC-derived cardiomyocyte (hESC-CM). While previous studies identified the phenotype of a cardiomyocyte based on electrophysiological features of its action potential, the criteria for classification were typically subjective and differed across studies. In this paper, we use techniques from signal processing and machine learning to develop an automated approach to discriminate the electrophysiological differences between hESC-CMs. Specifically, we propose a spectral grouping-based algorithm to separate a population of cardiomyocytes into distinct groups based on the similarity of their action potential shapes. We applied this method to a dataset of optical maps of cardiac cell clusters dissected from human embryoid bodies (hEBs). While some of the 9 cell clusters in the dataset presented with just one phenotype, the majority of the cell clusters presented with multiple phenotypes. The proposed algorithm is generally applicable to other action potential datasets and could prove useful in investigating the purification of specific types of cardiomyocytes from an electrophysiological perspective.
Index Terms: Stem Cells, Cardiac Electrophysiology, Spectral Grouping, Cardiomyocyte
I. INTRODUCTION
The application of stem cells in the field of cardiology has been exciting and rapidly evolving in the last decade. Methods for cardiac differentiation of human pluripotent stem cells have been constantly improving since it was first reported using human embryonic stem cells (hESCs) [1]. Cardiomyocytes (CMs) can be obtained by differentiating natural or forced aggregates of hESCs (termed human embryoid bodies, hEBs), as hESC monolayers, or through co-culture with END2 cells [1]–[3]. The efficiency of differentiation has also been greatly improved, as seen in both the quantity and quality of hESC derived cardiomyocytes (hESC-CMs). For example, in hEB-based methods, contraction can be observed in over 90% of hEBs starting as early as 9 days after initiating differentiation [4], and in monolayer-based methods, greater than 85% cardiomyocyte purity has been reported [5]. Combined with both genetic- [6] and non-genetic- [7], [8] based purification methods, it is now possible to generate large populations of high purity hESC-CMs. These advances in stem cell biology have greatly expanded the applications of these human cardiomyocytes from in vitro sources, especially in regenerative medicine [9]–[12] and drug models [13], [14].
The applications of hESC-CMs depend on their biological properties, especially whether and how well they faithfully represent native CMs. Generally, hESC-CMs have been found to be immature in both cellular structure and electrophysiology [5], [15], [16]. The cells usually have a small and rounded morphology, less organized sarcomere [5] and possess immature calcium handling mechanisms [17].
In addition to their immaturity, hESC-CMs are also heterogeneous. The variability of hESC-CMs is usually described by categorizing their APs into different electrophysiological phenotypes, usually referred to as nodal (or pacemaker)-like, atrial-like and ventricular-like hESC-CMs [18]–[22], which correspond to the three major native CM phenotypes. The development of hESC-CMs into multiple phenotypes during differentiation is considered to recapitulate embryonic heart development [18]. Phenotypes of hESC-CMs are typically determined by parameters obtained from microelectrode or patch clamp recordings of APs, such as resting potential (or maximum diastolic potential for spontaneously beating cells), action potential duration (APD), action potential amplitude, and upstroke velocity. However, the criteria for assigning phenotypes by these AP parameters in different research labs are most often subjective in nature, and only rarely quantitatively defined, as in [23], [24]. The manual assessment of features to determine the phenotype of a cardiomyocyte is near impossible to scale to large datasets, or to remain consistent across research labs, as AP morphologies of hESC-CMs differ when using different differentiation protocols [13], [18], [23]–[25]. Confounding the analysis further, the APs of hESC-CMs have generally been spontaneously active even among cells believed to represent the ventricular phenotype, which could lead to classifications that can change over time, as the hESC-CMs mature. In addition, most AP parameters vary with beating rate, which is highly variable [18], making it problematic for phenotype identification.
In this paper, we propose a new, automated framework for separating a population of hESC-CMs into different groups, which we hope will lead to more objective and biologically relevant methods for studying electrophysiological phenotypes of hESC-CMs. Our framework relies on signal processing and machine learning techniques that have been successfully used in other biological fields, such as neurophysiology [26], genomics and proteomics [27], and epidemiology [28]. However, to the best of our knowledge, they have not been applied to discriminate cardiac APs. We operate under the hypothesis that APs belonging to the same phenotype will have more similar shapes than APs belonging to different phenotypes, and that this similarity can be captured by machine learning algorithms. Specifically, we collected an original dataset of APs using optical mapping and used signal processing techniques to transform paced electrical activities at each recording site into representative APs. These representatives were aligned by activation time and compared using the Euclidean distance to define the similarity between APs. The similarities were used as the input to a spectral grouping algorithm to determine an objective separation of populations of cardiac APs with distinct phenotypes. Model selection techniques were then used to determine the optimal number of groups that represent that population. Our work, partially outlined in [29], shows the viability of automated methods for determining electrophysiologically related groups among populations of cardiac APs.
II. METHODS AND MATERIALS
This section describes our framework for grouping APs of hESC-CMs. §II-A describes the acquisition protocol used to collect our optical mapping dataset. §II-B describes signal processing methods used to obtain a representative AP at each site of each optical map. §II-C describes the algorithm used to group these APs into different phenotypes. §II-D describes model selection criteria used to determine the number of phenotypes. The overall processing pipeline is illustrated in Figure 1.
Fig. 1.

Schematic drawing of the proposed method. (a) Raw measured signals were obtained over 16 second intervals at a sampling rate of 500Hz. (b) From these 16 second traces, we obtained a representative AP by averaging over the individual APs. (c) These serve as input data for the spectral grouping algorithm, which treats the signals as vertices on a graph. Two vertices were connected by a weight defined by the integral of the squared difference between the corresponding signals. (d)–(e) The grouping of the data was obtained by finding the cut that minimizes a normalized sum of the weights.
A. Signal Acquisition
The H9 line of human embryonic stem cells was differentiated into cardiomyocytes using a previously described hEB-based protocol [30]. The hEBs usually start beating around Day 9 after the initiation of differentiation. Beating areas of hEBs were mechanically dissected on Day 15–16 of differentiation, and plated on gelatin-coated plastic coverslips as cardiac cell clusters for optical mapping. Cardiac cell clusters were stained with 10μM voltage-sensitive dye di-4-ANEPPS (Invitrogen, Grand Island, NY), and 50μM myosin II inhibitor blebbistatin (Sigma-Aldrich, St. Louis, MO) was applied throughout experiments to inhibit motion. Action potentials were recorded using a MiCAM Ultima-L CMOS camera (100 × 100 pixels, 16μm/pixel) at 500 frames per second (fps). A pair of platinum electrodes was used to deliver fixed 90 beat per minute (bpm) pacing to the clusters, and 16 second recordings containing multiple APs were obtained from each cluster. Figure 1(a) illustrates the recordings obtained with this protocol. Note that the resulting optical recordings are normalized to be in the range [0,1].
B. Signal Processing
To improve signal-to-noise ratio, we processed the optical recordings of cardiac cell clusters into one representative AP for each pixel within the each cluster (each pixel represents 16 μm × 16 μm area of the cluster). Let I(x,t) be the input optical recording, and let g(x) be a 5 × 5 boxcar filter. First, we generate a spatially averaged image by convolution of the input image with the boxcar filter in space:
| (1) |
Then, let T be the period of the pacing cycle. is condensed into a one cycle recording by averaging temporally over the period:
| (2) |
for t ε [0, T). is a single AP indicative of the cardiomyocytes in a neighborhood around each pixel. The APs from different averaged pixels were then aligned by their activation time, which was calculated to be the time point with maximal upstroke slope:
| (3) |
where
| (4) |
This alignment allows us to compare signals from different regions of the cell cluster that may be offset due to differences in activation time owing to electrical conduction of the AP wavefront through the cell cluster. Alignment is done post spatial averaging because the increased signal-to-noise ratio allows us to determine a more accurate , and experimentally we have found that the local misalignment is negligible compared to misalignment from different regions of the cell cluster. These aligned APs serve as our data elements for the machine learning framework. Figure 1(b) illustrates typical representatives obtained by this method.
C. Spectral Grouping
Once signals have been processed, the spectral grouping method of [31] is used to obtain the segmentation of the dataset into multiple groups. This algorithm represents the dataset with a graph , where is the set of nodes and is the set of edges. Each node represents the i-th signal in the dataset, xi. Each edge (i, j) ε connects nodes i and j, i ≠ j, with a weight w(i,j) ≥ 0 that depends on the similarity between the signals xi and xj. Specifically, two similar signals are connected with a higher weight than two dissimilar signals. This weight is defined as
| (5) |
where
| (6) |
is the Euclidean distance between the APs xi and xj, T is the AP cycle length, and σ > 0 is a scaling parameter. By convention, there is no edge connecting node i with itself. This means the weight w(i, i) = 0, .
The selection of the scaling parameter σ has an important effect in the final grouping. On the one hand, a high σ makes all the weights closer to zero, which encourages each AP to form its own group. On the other hand, a low σ makes all the weights closer to one, which encourages all APs to form a single group. A good balance is obtained when σ is chosen to be in the typical range of the pairwise distances between APs. For this study, σ is chosen to be the mean of the squared pairwise distances,
| (7) |
where | | is the number of edges in .
Once the weights have been computed, the goal is to group the nodes into K groups , i.e. to decompose as where for all k ≠ k′. Since low weights correspond to low similarities, one possible criterion is to minimize the average over the K groups of the sum of the weights between signals in group k and signals not in group k, i.e., . However, this criterion can lead to unbalanced groupings, as shown in [32]. To avoid this issue, [32] proposes to normalize each term of the Cut criterion by the sum of the weights of every signal in group k to every other signal, i.e.,
| (8) |
Since finding the set of groups that minimizes (8) is a combinatorial problem, the spectral grouping methods in [31], [32] find an approximate solution from the eigenvectors of a matrix built from the weights. In this paper we use the spectral grouping approach of [31]. Once the grouping of the graph has been found, the phenotype of a signal is decided by the group to which the corresponding node in the graph belongs.
D. Model Selection
Spectral grouping requires the number of groups K to be known beforehand. To determine K, we need a measure of the quality of a segmentation as a function of K.
1) Normalized Cut Cost (NCC)
The first measure that is considered is the objective function of our grouping method in (8). For well separated clusters, the numerator will be very small, while the denominator will be large, because signal pairs of the same group will be well connected while signal pairs of different groups will be poorly connected. Thus a good grouping will have a low normalized cut cost.
2) Davies-Bouldin Index (DBI)
The other measure considered is a cluster distance between pairs of groups [26], [27], [33]. Given two groups, and , the DBI distance between the groups is defined as follows:
| (9) |
where Sk and Sk′ are values for the dispersion or spread within each group, and Mkk′ is a measure between groups. For our work, Sk is defined as the average of the distances of the signals within one group to the average signal of that group, while the measure Mkk′ is the distance between the average signals of the two groups:
| (10) |
| (11) |
where,
| (12) |
For well separated, tight clusters, the dispersion for each group is very small, since the distances to the mean will be small, while the measure Mkk′ between groups will be large because the means are well separated from each other. Therefore, a lower DBI indicates better grouping. For K groups, the average DBI over all pairs of groups is chosen to be the group measure:
| (13) |
where К = {k, k′ ε 1, …,K, k < k′}.
III. RESULTS
Using the methods in §II-A and §II-B, we obtained a dataset of 6940 APs from 9 cardiac cell clusters paced at 90 bpm. To quantify the differences in morphology between two APs, we computed the weight in (5) for all pairs of APs. Figure 2(a) shows these weights for a subset of all pairs. Specifically, from each cell cluster we define a reference line and plot the weights for pairs of pixels in this line. We use red to indicate high similarity (w > 0.9) between the action potentials (low distance) and blue to indicate low similarity (w < 10−3). We observe in Figure 2(b) that the similarity between cell clusters 1 and 9 (counting from left to right) was low, as indicated by the two large blue blocks in Figure 2(b). Thus, we expected these two cell clusters to separate into different groups. In Figure 2(c), we see that the similiarity between cell clusters 2 and 3 is high in some regions, as the left part of cell cluster 2 shared high similarity with the right part of cell cluster 3 and vice versa. We can also observe variability within the clusters, as the left part of cell cluster 2 had low similiarity with the right part of that cluster.
Fig. 2.
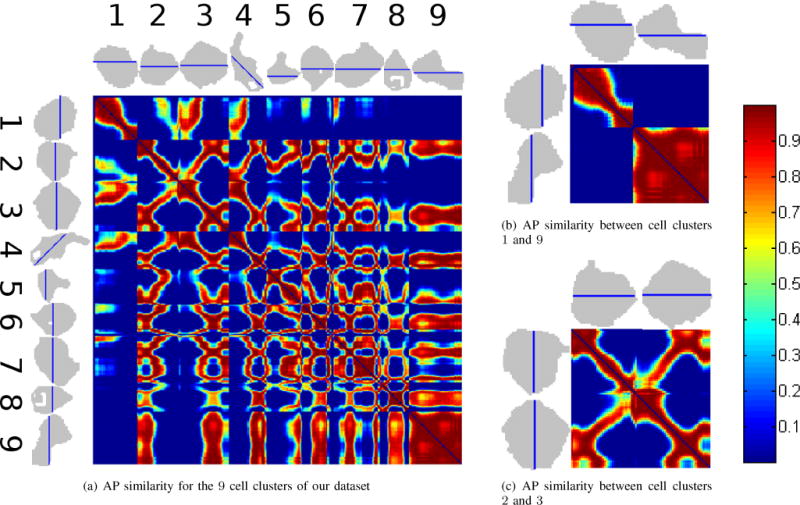
Observed Weight Matrices. (a) AP similarity for a subset of our dataset. The silhouettes of the 9 cell clusters (black regions) are shown on the top and rotated 90 degrees on the left. The subset of pixels being analyzed from each cell cluster is marked by the blue lines crossing each cluster. The similarity between the signals at pixels i and j in a line is measured by the weight w(i, j) defined in (5). Red indicates high weight and blue indicates low weight. Weights along the diagonal are 0 by convention of spectral grouping. Areas with high weight should belong to the same group, and areas with low weight to belong to different groups. (b) AP similarity for a subset of cell clusters 1 and 9. Since the weights relating these two clusters are blue (see the top right and bottom left areas of the submatrix), they should be in different groups. (c) AP similarity for a subset of cell clusters 2 and 3. In contrast with (b), there are high similarities between the left part of cluster 2 and the right part of cluster 3 and vice versa, as well as low similarity between the left and right parts of each of the clusters individually. The left side of cell cluster 2 should group with the right side of cell cluster 3 and the right side of cluster 2 should group with the left side of cluster 3.
Figure 3 shows the results of applying spectral grouping to this dataset using 2, 3 and 4 groups. Notice that cell clusters 1 and 9 presented with predominantly one phenotype, while the other 7 cell clusters showed varying degrees of mixed phenotypes. Notice also that, even though the grouping algorithm did not incorporate spatial regularization, the resulting groupings are spatially smooth, suggesting that the grouping algorithm to identify phenotype was robust. In the rightmost column, the temporal average of APs for each phenotype is presented. We see that the two group results produce two distinct AP phenotypes, while increasing number of groups produce intermediate APs that are increasingly less distinct. This conclusion is supported by the NCC and DBI numbers, which suggest an optimal segmentation into 2 groups (NCC = 0.1457 and DBI = 1.1655).
Fig. 3.

Grouping Visualizaton. The first 9 columns show the results of applying spectral grouping to all the APs in our dataset for 2 (top row), 3 (middle row), and 4 (bottom row) groups with corresponding NCC and DBI measures listed underneath. Scale bars indicate 200 μm. Some cell clusters present with primarily one phenotype, while others present a mixture of phenotypes. Both NCC and DBI suggest that K = 2 gives the best grouping fitness. The average AP of each phenotype as determined by spectral grouping is shown on the last column. Scale bar indicates 100 ms. The average 2-group APs suggest different phenotypes, while for 3 and 4 groups, pairs of phenotypes (phenotypes 2 and 3 for 3 groups, phenotypes 1 and 2 and phenotypes 3 and 4 for 4 groups) have similar shapes.
To further evaluate the characteristics of the obtained groups, we also computed the distributions of commonly used AP features [18], [19], [23], [24]. In particular, Figure 4 shows the distributions of APD30, APD80, triangulation (APD90–APD30), and normalized triangulation for the groups determined by spectral grouping and visualized in Figure 3. For the case of 2 groups, APD30 and APD80 histograms were fitted well as distinctly separated subpopulations. However, triangulation, a parameter indicative of a proarrhythmic substrate when prolonged, had a wide range in both groups, with substantial overlap. By normalizing triangulation to APD90, we obtained a shape parameter that showed better discrimination of AP morphology between the two groups, and that the group with shorter APD30 and APD80 had greater triangulation. With increased number in groups (3 and 4 groups), we observed increased overlap in all AP features among different groups, especially in normalized triangulation. This increased overlap suggests that APs in different groups are similar in shape, thus increasing difficulty in discriminating the groups by such features. Overall, these results suggest that grouping the population based on standard AP features would be possible for 2 groups, while using the entire AP waveform is effective for 2, 3, or 4 groups.
Fig. 4.
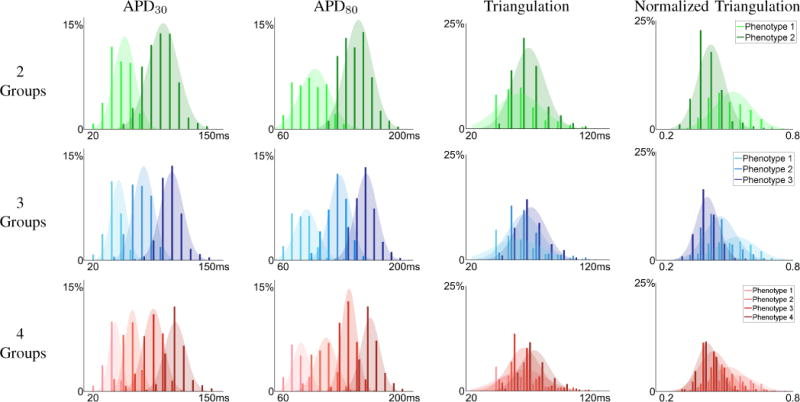
Morphological Feature Distributions. Distribution APD30 (first column), APD80 (second column), triangulation (APD90 – APD30) (third column), and normalized triangulation , rightmost column), for the spectral grouping result using 2 (top row), 3 (middle row), and 4 (bottom row) groups. The two group segmentation suggest two unique phenotypes in APD30, APD80, and normalized triangulation.
IV. DISCUSSION
In order to provide objective phenotype identification of hESC-CMs based on their electrophysiology, we have introduced a framework for automated grouping of their APs and tested it using optical mapping data obtained from hESC-CM cardiac cell clusters. In contrast to conventional subjective criteria for phenotype classification, our automated algorithm relies entirely on raw signal information from the dataset. The grouping of signals is made based on the similarities between all pairs of signals in the dataset. This leads to an unbiased and reproducible method for discrimination that is also widely applicable to larger populations of cells. We believe that objective and consistent phenotype classification algorithms are important in understanding the biology of hESC-CMs, and our results show that applying methods developed in signal processing and machine learning is a viable approach.
A. Spatial Distribution and AP Variability of cell clusters
The weight matrix used for spectral grouping analysis also provides visualization of the similarity among APs within the dataset. The existence of both similar and dissimilar regions within some cardiac cell clusters indicates that more than one phenotype may coexist within a single cluster, consistent with previous work [16]. Our results show that while there were cell clusters in our dataset that expressed primarily one phenotype, the majority of the cell clusters presented with multiple phenotypes. For the clusters with more than one phenotype, even though the grouping method did not enforce spatial regularity, continous regions of cell clusters with only one phenotype were obtained. Further, we observed smoothly varying AP shape across the boundary separating phenotypes. This is partly because of the spatial averaging performed during preprocessing, but it primarily reflects that APs vary as a continuum from one phenotype to another. Thus, it is particularly important to develop automated algorithms to maintain a consistent decision boundary across datasets.
B. Biological Interpretation
The clear differences in AP shapes and parameters between groups suggest that our algorithm is capable of distinguishing morphological differences of APs within a dataset, which is also the main goal of widely used subjective methods for phenotype identification. In our two-group classification results, APs were either less triangular (as quantified by normalized triangulation) with long APD, or more triangular with short APD. This can be interpreted as ventricular-like and nonventricular-like APs, respectively. However, definitive biological interpretation remains to be validated by further investigations. Possible avenues include phenotype-related biomarkers and patch clamp studies of phenotype-specific currents. It should also be noted that the global gene expression profile of hESC-CMs generally differs from both adult and fetal CMs [34], [35], and should also be taken into consideration. In addition, unlike most studies of spontaneously beating hESC-CMs [18], [19], we specifically controlled the beating rate to 90 bpm by delivering an external stimulus. The fixed pacing rate eliminated rate-dependent variations in AP morphology and exposed intrinsic differences in electrophysiology, which we believe are due to true phenotypic differences, and can provide insights into the mechanisms of variability among APs.
C. Adaptability of the Framework
A key feature of the proposed framework is that the pieces are generalizable. We used optical mapping recordings for our dataset, but because the spectral grouping and fitness evaluation operate with a processed action potential signal, they are amenable to action potential recordings obtained from other techniques, and thus could be used to investigate variability in current methods for purification of specific phenotypes of hESC-CMs [24], [36], [37]. Also, we used a very basic signal distance measure, the Euclidean distance, which assesses AP differences equally at every time point. This could be modified to emphasize AP differences in different segments of the action potential (e.g., more weight on the depolarization and repolarization phases of the AP and less on phase 4 resting potential), or to forgo the Euclidean distance altogether for other distances between AP shapes [38], [39]. Future work could investigate these other metrics and how the resulting groupings compare to this work. Another possiblity is to operate with other representations of the action potential such as the phase plot representation. A benefit to phase plot analysis is that the need to align the signals temporally is no longer necessary. However, appropriate measures to compare and quantify the differences between the phase plots, so that electrophysiological phenotypes can be identified.
V. CONCLUSION
We have introduced a framework for automated grouping of action potentials of cardiomyocytes derived from human embryonic stem cells together with a dataset with which future methods can be evaluated. Our results on this dataset showed that the groups obtained by our algorithm reflect phenotype differences in electrophysiology of hESC-CMs. We believe that the proposed framework provides a landmark first step into using machine learning techniques in the classification of stem cell-derived cardiomyocyte phenotypes by their action potentials.
Acknowledgments
This work was supported by NIH grants R21 HL108210, S10 RR025544, and U01 HL099775, and the Maryland Stem Cell Research Fund 2011-MSCRF-II-0008-00.
References
- 1.Kehat I, Kenyagin-Karsenti D, Snir M, Segev H, Amit M, Gepstein A, Livne E, Binah O, Itskovitz-Eldor J, Gepstein L. Human embryonic stem cells can differentiate into myocytes with structural and functional properties of cardiomyocytes. Journal of Clinical Investigation. 2001;108(3):407–414. doi: 10.1172/JCI12131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Burridge PW, Keller G, Gold JD, Wu JC. Production of de novo cardiomyocytes: human pluripotent stem cell differentiation and direct reprogramming. Cell Stem Cell. 2012;10(1):16–28. doi: 10.1016/j.stem.2011.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mummery CL, Zhang J, Ng ES, Elliott DA, Elefanty AG, Kamp TJ. Differentiation of human embryonic stem cells and induced pluripotent stem cells to cardiomyocytes: a methods overview. Circulation Research. 2012;111(3):344–58. doi: 10.1161/CIRCRESAHA.110.227512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Burridge PW, Thompson S, Millrod MA, Weinberg S, Yuan X, Peters A, Mahairaki V, Koliatsos VE, Tung L, Zambidis ET. A universal system for highly efficient cardiac differentiation of human induced pluripotent stem cells that eliminates interline variability. PloS One. 2011;6(4) doi: 10.1371/journal.pone.0018293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lundy SD, Zhu W-Z, Regnier M, Laflamme MA. Structural and Functional Maturation of Cardiomyocytes Derived from Human Pluripotent Stem Cells. Stem Cells and Development. 2013;22(14) doi: 10.1089/scd.2012.0490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Anderson D, Self T, Mellor IR, Goh G, Hill SJ, Denning C. Transgenic enrichment of cardiomyocytes from human embryonic stem cells. Molecular Therapy. 2007;15(11):2027–36. doi: 10.1038/sj.mt.6300303. [DOI] [PubMed] [Google Scholar]
- 7.Dubois NC, Craft AM, Sharma P, Elliott DA, Stanley EG, Elefanty AG, Gramolini A, Keller G. SIRPA is a specific cell-surface marker for isolating cardiomyocytes derived from human pluripotent stem cells. Nature Biotechnology. 2011;29(11):1011–8. doi: 10.1038/nbt.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hattori F, Chen H, Yamashita H, Tohyama S, Satoh Y-S, Yuasa S, Li W, Yamakawa H, Tanaka T, Onitsuka T, Shimoji K, Ohno Y, Egashira T, Kaneda R, Murata M, Hidaka K, Morisaki T, Sasaki E, Suzuki T, Sano M, Makino S, Oikawa S, Fukuda K. Nongenetic method for purifying stem cell-derived cardiomyocytes. Nature Methods. 2009;7(1):61–6. doi: 10.1038/nmeth.1403. [DOI] [PubMed] [Google Scholar]
- 9.Caspi O, Gepstein L. Myocardial regeneration strategies using human embryonic stem cell-derived cardiomyocytes. Journal of controlled release : official journal of the Controlled Release Society. 2006;116(2):211–8. doi: 10.1016/j.jconrel.2006.06.027. [DOI] [PubMed] [Google Scholar]
- 10.Gepstein L. Cardiovascular therapeutic aspects of cell therapy and stem cells. Annals of the New York Academy of Sciences. 2006;1080:415–25. doi: 10.1196/annals.1380.030. [DOI] [PubMed] [Google Scholar]
- 11.Habib M, Caspi O, Gepstein L. Human embryonic stem cells for cardiomyogenesis. Journal of molecular and cellular cardiology. 2008;45(4):462–74. doi: 10.1016/j.yjmcc.2008.08.008. [DOI] [PubMed] [Google Scholar]
- 12.Laflamme MA, Chen KY, Naumova AV, Muskheli V, Fugate JA, Dupras SK, Reinecke H, Xu C, Hassanipour M, Police S, O’Sullivan C, Collins L, Chen Y, Minami E, Gill EA, Ueno S, Yuan C, Gold J, Murry CE. Cardiomyocytes derived from human embryonic stem cells in pro-survival factors enhance function of infarcted rat hearts. Nature Biotechnology. 2007;25(9):1015–24. doi: 10.1038/nbt1327. [DOI] [PubMed] [Google Scholar]
- 13.Braam SR, Tertoolen L, van de Stolpe A, Meyer T, Passier R, Mummery CL. Prediction of drug-induced cardiotoxicity using human embryonic stem cell-derived cardiomyocytes. Stem Cell Research. 2010;4(2):107–16. doi: 10.1016/j.scr.2009.11.004. [DOI] [PubMed] [Google Scholar]
- 14.Mordwinkin NM, Burridge PW, Wu JC. A review of human pluripotent stem cell-derived cardiomyocytes for high-throughput drug discovery, cardiotoxicity screening, and publication standards. Journal of Cardiovascular Translational Research. 2012;6(1):22–30. doi: 10.1007/s12265-012-9423-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lieu DK, Turnbull IC, Costa KD, Li Ra. Engineered human pluripotent stem cell-derived cardiac cells and tissues for electrophysiological studies. Drug Discovery Today: Disease Models. 2012;9(4):209–217. doi: 10.1016/j.ddmod.2012.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Blazeski A, Zhu R, Hunter DW, Weinberg SH, Boheler KR, Zambidis ET, Tung L. Electrophysiological and contractile function of cardiomyocytes derived from human embryonic stem cells. Progress in biophysics and molecular biology. 2012;110(2–3):178–195. doi: 10.1016/j.pbiomolbio.2012.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Satin J, Itzhaki I, Rapoport S, Schroder EA, Izu L, Arbel G, Beyar R, Balke CW, Schiller J, Gepstein L. Calcium handling in human embryonic stem cell-derived cardiomyocytes. Stem cells. 2008;26(8):1961–72. doi: 10.1634/stemcells.2007-0591. [DOI] [PubMed] [Google Scholar]
- 18.He J-Q, Ma Y, Lee Y, Thomson JA, Kamp TJ. Human embryonic stem cells develop into multiple types of cardiac myocytes: action potential characterization. Circulation research. 2003;93(1):32–9. doi: 10.1161/01.RES.0000080317.92718.99. [DOI] [PubMed] [Google Scholar]
- 19.Moore JC, Fu J, Chan Y-C, Lin D, Tran H, Tse H-F, Li RA. Distinct cardiogenic preferences of two human embryonic stem cell (hESC) lines are imprinted in their proteomes in the pluripotent state. Biochemical and biophysical research communications. 2008;372(4):553–8. doi: 10.1016/j.bbrc.2008.05.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lee Y-K, Ng K-M, Lai W-H, Chan Y-C, Lau Y-M, Lian Q, Tse H-F, Siu C-W. Calcium homeostasis in human induced pluripotent stem cell-derived cardiomyocytes. Stem Cell Reviews. 2011;7(4):976–86. doi: 10.1007/s12015-011-9273-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang K, Terrenoire C, Sampson KJ, Iyer V, Osteen JD, Lu J, Keller G, Kotton DN, Kass RS. Biophysical properties of slow potassium channels in human embryonic stem cell derived cardiomy-ocytes implicate subunit stoichiometry. The Journal of Physiology. 2011;589(Pt 24):6093–104. doi: 10.1113/jphysiol.2011.220863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lieu DK, Fu J-D, Chiamvimonvat N, Tung KC, McNerney GP, Huser T, Keller G, Kong C-W, Li Ra. Mechanism-based facilitated maturation of human pluripotent stem cell-derived cardiomy-ocytes. Circulation Arrhythmia and Electrophysiology. 2013;6(1):191–201. doi: 10.1161/CIRCEP.111.973420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Peng S, Lacerda AE, Kirsch GE, Brown AM, Bruening-Wright A. The action potential and comparative pharmacology of stem cell-derived human cardiomyocytes. Journal of pharmacological and toxicological methods. 2010;61(3):277–86. doi: 10.1016/j.vascn.2010.01.014. [DOI] [PubMed] [Google Scholar]
- 24.Fu J-D, Rushing S, Lieu D, Chan C, Kong C-W, Geng L, Wilson K, Chiamvimonvat N, Boheler K, Wu J, Keller G, Hajjar R, Li R. Distinct roles of microRNA-1 and -499 in ventricular specification and functional maturation of human embryonic stem cell-derived cardiomy-ocytes. PloS One. 2011;6(11) doi: 10.1371/journal.pone.0027417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mummery C, Ward-van Oostwaard D, Doevendans P, Spijker R, van den Brink S, Hassink R, van der Heyden M, Opthof T, Pera M, de la Riviere AB, Passier R, Tertoolen L. Differentiation of human embryonic stem cells to cardiomyocytes: role of coculture with visceral endoderm-like cells. Circulation. 2003;107(21):2733–40. doi: 10.1161/01.CIR.0000068356.38592.68. [DOI] [PubMed] [Google Scholar]
- 26.Farrow K, Masland R. Physiological clustering of visual channels in the mouse retina. Journal of Neurophysiology. 2011;(January 2011):1516–1530. doi: 10.1152/jn.00331.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ahmad N, Alahakoon D, Chau R. Cluster identification and separation in the growing self-organizing map: application in protein sequence classification. Neural Computing & Applications. 2010:531–542. [Google Scholar]
- 28.Dasgupta A, Sun YV, König IR, Bailey-Wilson JE, Malley JD. Brief review of regression-based and machine learning methods in genetic epidemiology: the Genetic Analysis Workshop 17 experience. Genetic Epidemiology. 2011;35(Suppl 1):S5–11. doi: 10.1002/gepi.20642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gorospe G, Zhu R, Millrod MA, Zambidis ET, Tung L, Vidal R. Automated Analysis of action potentials from cardiac cell clusters derived from human embryonic stem cells. (abstr.). Poster presented at AHA Scientific Sessions; Los Angeles. 2012. [Google Scholar]
- 30.Weinberg S, Lipke EA, Tung L. In Vitro Electrophysiological Mapping of Stem Cells. Methods in Molecular Biology. 2010;660:215–237. doi: 10.1007/978-1-60761-705-1_14. [DOI] [PubMed] [Google Scholar]
- 31.Ng A, Jordan M, Weiss Y. On spectral clustering: Analysis and an algorithm. Advances in Neural Information Processing Systems. 2002:849–856. [Google Scholar]
- 32.Shi J, Malik J. Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2000;22(8):888–905. [Google Scholar]
- 33.Davies D, Bouldin D. A cluster separation measure. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1979;1(2):224–227. [PubMed] [Google Scholar]
- 34.Liu J, Fu JD, Siu CW, Li RA. Functional sarcoplasmic reticulum for calcium handling of human embryonic stem cell-derived cardiomyocytes: insights for driven maturation. Stem cells. 2007;25(12):3038–44. doi: 10.1634/stemcells.2007-0549. [DOI] [PubMed] [Google Scholar]
- 35.Gupta MK, Illich DJ, Gaarz A, Matzkies M, Nguemo F, Pfannkuche K, Liang H, Classen S, Reppel M, Schultze JL, Hes-cheler J, Sarić T. Global transcriptional profiles of beating clusters derived from human induced pluripotent stem cells and embryonic stem cells are highly similar. BMC Developmental Biology. 2010;10:98. doi: 10.1186/1471-213X-10-98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhang Q, Jiang J, Han P, Yuan Q, Zhang J, Zhang X, Xu Y, Cao H, Meng Q, Chen L, Tian T, Wang X, Li P, Hescheler J, Ji G, Ma Y. Direct differentiation of atrial and ventricular myocytes from human embryonic stem cells by alternating retinoid signals. Cell research. 2011;21(4):579–87. doi: 10.1038/cr.2010.163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhu W-Z, Xie Y, Moyes KW, Gold JD, Askari B, Laflamme MA. Neuregulin/ErbB signaling regulates cardiac subtype specification in differentiating human embryonic stem cells. Circulation research. 2010;107(6):776–86. doi: 10.1161/CIRCRESAHA.110.223917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Trouvé A, Younes L. Metamorphoses Through Lie Group Action. Foundations of Computational Mathematics. 2005;5(2):173–198. [Google Scholar]
- 39.Xing E, Ng A, Jordan M, Russell S. Distance metric learning, with application to clustering with side-information. Advances in Neural Information Processing Systems. 2002;15:505–512. [Google Scholar]


