Spherical Topic Models for Imaging Phenotype Discovery in Genetic Studies

Abstract

In this paper, we use Spherical Topic Models to discover the latent structure of lung disease. This method can be widely employed when a measurement for each subject is provided as a normalized histogram of relevant features. In this paper, the resulting descriptors are used as phenotypes to identify genetic markers associated with the Chronic Obstructive Pulmonary Disease (COPD). Features extracted from images capture the heterogeneity of the disease and therefore promise to improve detection of relevant genetic variants in Genome Wide Association Studies (GWAS). Our generative model is based on normalized histograms of image intensity of each subject and it can be readily extended to other forms of features as long as they are provided as normalized histograms. The resulting algorithm represents the intensity distribution as a combination of meaningful latent factors and mixing co-efficients that can be used for genetic association analysis. This approach is motivated by a clinical hypothesis that COPD symptoms are caused by multiple coexisting disease processes. Our experiments show that the new features enhance the previously detected signal on chromosome 15 with respect to standard respiratory and imaging measurements.

1 Introduction

In this paper, we employ the Spherical Topic Model[1] (which is one of the variants of the latent topic models) to extract imaging features for genetic association studies. It is common in classical Genome-Wide Association Studies (GWAS) to perform statistical association between genetic measurements and a few quantities such as diagnosis. Imaging features provide rich information about the disease phenotype and promise to enhance the sensitivity of the genetic studies. Using individual voxels as a phenotype is not informative and due to the noisy nature of imaging measurements induces high false positive rate. Therefore, summarizing imaging features into meaningful quantities (i.e., dimensionality reduction) improves the association and facilitate interpretation of the results. In this work, we build on a variant of topic models to perform this step of dimensionality reduction.

COPD is characterized by chronic and progressive difficulty in breathing, and is one of the leading causes of death in the United States [2]. The disorder is believed to be a mixture of multiple disease processes including the destruction of the air sacs (emphysema) and inflammation of the airways (airway disease). Each process consists of multiple subtypes [3]. In this paper, we focus on emphysema which manifests itself as changes in intensity of the lung in Computed Tomography (CT) images [3]. Therefore, we use image intensity of the lung as a unit of measurements for each subject. The goal is to summarize this information into meaningful features. Similar to the idea of bag of words in natural language processing, later also adopted in computer vision [4], we view a histograms as a document and subtypes of the disease as different topics. This approach assumes that every patient (document) contains multiple portions of the disease subtypes (topics) and those disease subtypes, i.e., topics, are shared across subjects. The goal of this paper is not to diagnose COPD since a test of lung function via forced exhalation has been the gold standard of COPD diagnosis for decades [5]. Our aim is to use imaging features to characterize the phenotype and the underlying genetic causes of the disease.

The search for genetic variants that increase the risk of a disorder is one of the central challenges in medical research, and has been traditionally performed via GWAS. Standard GWAS identifies correlations between genetic variants and a single phenotype (e.g., mostly disease vs. control). Although such analysis identified several variants relevant to COPD (e.g., IREB2 on chromosome 15 [6]), such studies are likely incomplete. First, COPD is a mixture of diseases and therefore is unlikely to be explained by a single factor. Second, the effect of the genetic variants may be scattered across the lung volume but their cumulative effect is manifested in the respiratory signal [7]. Imaging can help to address both challenges. Image features that capture the amount of emphysema have been previously demonstrated to reflect disease pathology and predict outcomes in COPD [7]. We seek to extract features from images that capture heterogeneous manifestations of the disease and enrich detection of genetic markers associated with COPD.

The standard approach to quantify emphysema is to apply an intensity threshold within the volume of the lung to compute a surrogate measure for the volume of emphysema [7]. Clinical studies suggest that lungs of COPD patients present symptoms of different subtypes of emphysema [7, 5]. Recent work exploits spatial patterns of intensity to classify emphysema into subtypes. Examples include the use of Kernel density estimation [8], combination of Local Binary Pattern (LBP) and intensity histogram [9], and Multi-coordinate Histogram of Oriented Gradient (MHOG) descriptors [10] for subtype classification of image patches in CT. Importantly, none of the method above characterizes how the underlying biological processes overlap with radiologic categorization.

Imaging genetics associates image phenotype with genetic markers relevant for the disease of interest. The objective is to characterize clinical heterogeneity of the disease and to detect novel genetic markers associated with COPD [11]. Most methodological innovations in imaging genetics to date have been demonstrated in the context of neuro-degenerative diseases [12, 13, 14], where image features are typically computed in a common coordinate system and are assumed to be spatially consistent across subjects. Unfortunately, such coordinate system does not exist for the lung, presenting an additional challenge for creating image-based descriptors that can be compared across subjects.

In this paper, we build a generative model that encodes the clinical assumption that COPD symptoms are caused by multiple coexisting biological processes. We assume that every subject is a mixture of latent disease factors, that are shared across the population. This approach is referred to as topic modeling in machine learning (e.g., LDA [15]). The contribution of each latent factor for a particular subject becomes a new feature that can be used as an intermediate phenotype for detecting genetic associations. To integrate the resulting features into genetic analysis, we employ a method that views the genotype as the dependent variable and uses all the latent features simultaneously to find the genetic association. We demonstrate that the new features enhance the signal on chromosome 15 by improving the sensitivity of detection.

2 Topic Modeling for Feature Extraction

Previous studies have shown the intensity of lung to be highly informative for characterization of COPD [8, 9]. Therefore, we use global histogram of image intensity of the lung as a unit of measurement for each subject. The goal is to reduce a set of histograms to a set of meaningful features that enhance subsequent statistical analysis. Histogram data can in general encode richer features such as sophisticated localized descriptors (e.g., Histogram of Oriented Gradients (HOG)), but to focus on the model, we limit ourselves to image histograms which have been shown to be informative for COPD [8, 9]. Here, we adopt the Spherical Admixture Model [1] that views each histogram as a point on a hypersphere. The advantage of this model is that it can handle unit-less (normalized) representations of the histograms. This property allows us to normalize the features by the volume of the lung.

We assume an image of subject n in a study is represented by a distribution ${\mathbf{y}}_n\in {ℝ}^D({\sum }_{d=1}^D{y}_{nd}=1)$. With a change of the variables $y_{nd}:=z_{nd}^2$, we map the intensity distribution to a unit hypersphere, z_n ∈ 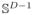. Motivated by the clinical hypothesis that COPD is a mixture of diseases, we assume that each data point (subject) is a normalized sum of K disease factors Φ = [ϕ₁ · · · ϕ_K] ∈ ℝ^D×K. The factors are shared across the population and each factor is also a distribution, ϕ_k ∈ (1 ≤ k ≤ K). The generative model can be summarized as follows[1]:

$$\begin{array}{l}\mathit{\mu }~\text{vMF}(\mathbf{m},{\kappa }_0),\\ {\mathit{\varphi }}_k~\text{vMF}(\mathit{\mu },\xi ),\\ {\mathbf{x}}_n~\text{Dirichlet}(\mathit{\alpha }),\\ {\mathbf{z}}_n~\text{vMF}\left(\frac{\mathit{\Phi }{\mathbf{x}}_n}{{\left|\right|\mathit{\Phi }{\mathbf{x}}_n\left|\right|}_2},\kappa \right)\end{array}$$ (1)

where vMF(·) and Dirichlet(·) denote the von Mises-Fisher (vMF) [16] and Dirichlet distributions respectively. vMF distribution is a natural distribution, akin to a multivariate Normal distribution, for directions on a sphere. μ is a latent variable that controls the mean of the disease factors (topics), m and κ₀ are hyper-parameters that define the mean and concentration of μ respectively. x_n is a normalized latent distribution that defines a portion of each disease factor (topic) represented in subject n. Since x_n is normalized (sums to one), Dirichlet distribution is a reasonable prior choice; α is the multivariate shape parameter of the Dirichlet distribution. $\frac{\mathit{\Phi }{\mathbf{x}}_n}{{\left|\right|\mathit{\Phi }{\mathbf{x}}_n\left|\right|}_2}$ maps the weighted sum of the topics back to the sphere and serves as a noiseless representation of the observation z_n. To accommodate possible noise, the observation is modeled as a von Mises-Fisher perturbation of the noiseless representation, parameter κ controls the concentration of the noise. For notational convenience, we define Ω = {μ, Φ, X} to be the set of the latent variables and γ = {α, ξ, κ, κ₀} to represent the set of hyper-parameters. The generative model is illustrated in Fig. 1a.

Fig. 1.

(a) Schematic visualization of the generative model. Each data point (blue) is a noisy mixture of latent disease factors (red arrows). (b) Graphical model for the spherical topic model in [1]. The open gray and white circles are the observed and the latent random variables respectively. The full circles are the hyper-parameters.

The join probability p(Z, Ω; γ) can be written as follows:

$$p(\mathbf{Z},\mathit{\Omega };\mathit{\Upsilon })=\prod _{n=1}^{N}p({\mathbf{z}}_n\mid \mathit{\Phi },{\mathbf{x}}_n;\mathit{\Upsilon })p({\mathbf{x}}_n;\mathit{\Upsilon })\prod _{k=1}^{K}p({\mathit{\varphi }}_k\mid \mathit{\mu };\mathit{\Upsilon })p(\mathit{\mu };\mathit{\Upsilon })$$ (2)

Reisinger et al. [1] proposed to use variational mean-field method to approximate the posterior distribution of the latent variables in this model with a fully factorized function as follows:

$$q(\mathit{\mu },\mathit{\Phi },\mathbf{X}\mid \stackrel{\sim }{\mathit{\mu }},\stackrel{\sim }{\mathit{\Phi }},\stackrel{\sim }{\mathbf{m}};\mathit{\Upsilon })=q(\mathit{\Phi }\mid \stackrel{\sim }{\mathit{\mu }},\xi )q(\mathbf{X}\mid \stackrel{\sim }{\mathit{\alpha }})q(\mathit{\mu }\mid \stackrel{\sim }{\mathbf{m}},{\kappa }_0),$$ (3)

where Σ = {μ̃, Φ̃, m̃} are the parameters of the approximate posterior distribution q(·). Note that Σ and Ω are not identical since the former is the set containing parameters of the approximate posterior distribution while the latter is the set of latent variables in the original model. The variational method minimizes the KL-divergence between the approximating distribution and the join probability distribution to find the optimal setting of the parameters:

$$({\mathit{\sum }}^{\ast },{\mathit{\Upsilon }}^{\ast })=arg\underset{\mathit{\sum },\mathit{\Upsilon }}{min}{\mathbb{E}}_q[logp(\mathbf{Z},\mathit{\Omega };\mathit{\Upsilon })-logq(\mathit{\Omega };\mathit{\Upsilon })].$$ (4)

Computing the derivatives with respect to Σ and γ and setting them to zero, the mean field method reduces to a set of fixed-point update equations (see [1] for detail).

We seek to estimate the posterior means of the latent features x̂_n := [x_n], which serve as a low-dimensional representation of subject n, and are used to infer associated genetic markers of the disease as described in Section 3. Estimates x̂_n can be viewed as a K-dimensional histogram defined over K latent factors. Indeed, we reduce the original D-dimensional histograms of image intensities to the K-dimensional histograms of the latent factors. Other quantities of interest are the latent factors, ϕ̃_k, which are D-dimensional histograms that describe each latent factor in the intensity space. The hyper-parameters, γ, and the parameters of the approximate posterior distribution, Σ, are estimated during learning (i.e., Eq. 4). The main parameter of the method is number of topics K.

Unlike traditional Factor Analysis methods such as PCA, this approach yields normalized factors and coefficients (i.e., both can be interpreted as histograms). This is advantageous for interpretation of the results because the Φ can be viewed the same way as the input histograms and mixing weights x_n can be viewed as the proportions of each factor in subject n.

3 From Image Features to Genetic Markers

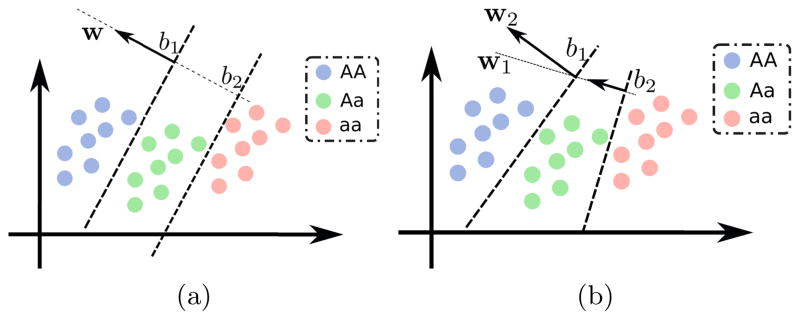
In addition to the image features x̂_n, each subject is characterized by a vector of S genetic markers (g_ns ∈ {0, 1, 2}, 1 ≤ s ≤ S). g_ns represents the allele count in the locus s of the genetic measurement for subject n. Standard GWAS builds a regression model x̂_nk = b_s,k + w_skg_ns + ε_nsk for each Single Nucleotide Polymorphism (SNP) g_ns and the phenotype x̂_nk separately. The detection procedure aims to reject the null hypothesis of no association (w_sk = 0) by performing t-test. Contrary to the standard GWAS that models phenotype as a dependent variable, we use a previously proposed method that considers the genotype as the dependent variable and uses all phenotypes features simultaneously [17]. The algorithm employs proportional odds (ordinal) logistic regression to model the allele count. Unlike multi-class logistic regression, ordinal logistic regression assumes the classes (i.e., g_ns = 0, 1, 2) are ordered, the hyperplanes separating the classes are parallel, and the difference between classes is captured by the intercepts as illustrated in Fig. 2b,2a. Ordinal logistic regression is more restrictive than a more general multi-class logistic regression and exhibits fewer degrees of freedom. The ordinal method is more appropriate when a natural ordering can be imposed on class labels. This is certainly the case here since g_ns counts the number of minor alleles and we assume an additive effect. The cumulative probability is modeled as the logistic function:

$$\mathbb{P}(g_{ns}\le j)=\psi ({\mathbf{w}}_s^T{\widehat{\mathbf{x}}}_n-b_{s,j})=\frac{1}{1+exp({\mathbf{w}}_s^T{\widehat{\mathbf{x}}}_n-b_{s,j})},$$ (5)

where j ∈ {0, 1, 2}. For the allele j in locus s, we estimate one weight w_s and two intercepts b_s,1 and b_s,2. Fitting the model reduces to maximizing the log-likelihood of data to find the best parameters (w_s, b_s,1, b_s,2) for each SNP g_ns:

$$\mathcal{L}({\mathbf{w}}_s,b_{s,1},b_{s,2};\widehat{\mathbf{x}})=\sum _{n=1}^{N}log(\psi ({\mathbf{w}}_s^T{\widehat{\mathbf{x}}}_n-b_{s,(g_n+1)})-\psi ({\mathbf{w}}_s^T{\widehat{\mathbf{x}}}_n-b_{s,g_n})),$$ (6)

where b_s,0 = −∞ and b_s,3 = +∞.

Fig. 2.

(a) Ordinal vs. (b) Multi-class logistic regression. In the ordinal regression, the separating hyperplanes are parallel (same w) and classes differ by intercepts.

We compute the likelihood ratio of the model with combination of covariates and x̂ ( ) versus only the covariates ( 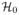). χ² distribution with degrees of freedom equal to the difference in dimensionality is used to compute the p-value [17]. Covariates are defined in the next section.

4 Experiments

Experiments in this section are organized as follows. We first qualitatively evaluate the new features x̂_n and the estimated latent factors ϕ̃_k (Fig. 3). Next, we select a few important SNPs to study the sensitivity of the algorithm with respect to the model size K (Fig. 4). Finally, we study how much the new features enrich our genetic findings versus the traditional measurements such as airflow (Fig. 5 and Fig. 6).

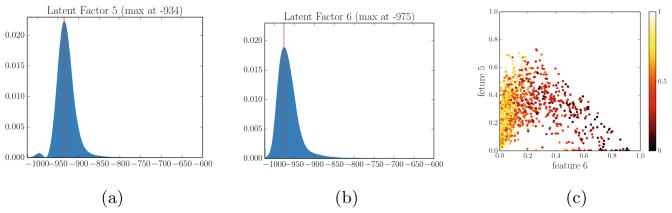
Fig. 3.

Estimated latent model estimated. (a),(b) Examples of latent factors for K = 6. (c). Scatter plot of latent features colored by FEV₁/FVC (severity of COPD). Hotter colors represent higher values (healthier subjects). The scatter plots show that new features successfully delineate the severity of the disease.

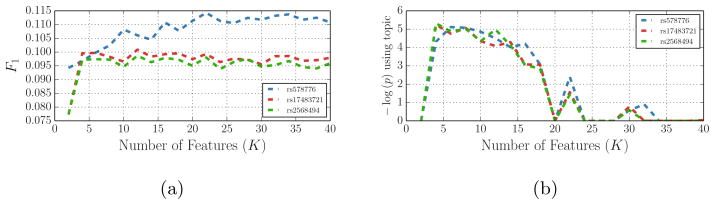
Fig. 4.

Prediction accuracy (F₁-measure) for 5-fold cross validation and quality-of-fit (− log (p)) as a function of the model size K for three important genetic markers. F₁ is defined as 2(precision × recall)/(precision + recall). We note the improvements in prediction accuracy in (a). As the model becomes more complex (higher K), the number of degrees of freedom in χ² distribution increases, which explains the initial increases and decreases in the p-value in (b).

Fig. 5.

Comparison of different feature sets. For K = 4 and for different combination of features, A > B indicates how many more SNPs are detected in one setting (A) versus the other (B) and how they were distributed in the different chromosomes.

Fig. 6.

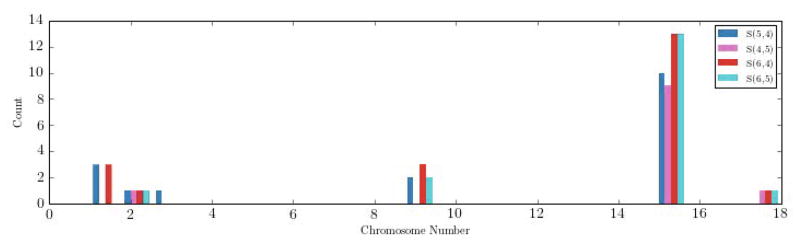
Fine-scale regional maps for the region of significance on chromosome 15. Blue, purple and green lines represent latFtr, sumImg, and Resp respectively.

Data

We demonstrate the method on a large COPD study of 6,670 subjects. The respiratory measurements include: percent predicted, forced expiratory volume in one second (F EV₁) that is used as an indicator of COPD severity, and the ratio of F EV₁ over forced vital capacity (F EV₁/F V C), used as a measure of airflow obstruction for COPD diagnosis. We will refer to the respiratory measures as Resp. We also evaluate summary measurements computed from lung CT. These include percent emphysema, defined as the percentage of lung tissue below −950 Hounsfield units; percent gas trapping, defined as the percentage of lung tissue below −910 Hounsfield units after exhalation, and the wall thickness of an airway with an internal perimeter of 10mm (Pi₁₀). We will refer to these measures as sumImg. The subjects were genotyped by Illumina on the HumanOmniExpress array. We employ standard quality control for genetic data, including missing-ness, excess heterozygous, gender mismatch, cryptic relatedness, population outliers, marker concordance, and Hardy-Weinberg equilibrium. We computed 6 principal components from the genotype to correct for population heterogeneity, and included them in the covariate set along with age, Body Mass Index (BMI) and number of aggregate packs smoked per year.

Qualitative Evaluation

Fig. 3 shows examples of the derived latent disease factors (ϕ̃_k) and the corresponding latent features (x̂) in the patient cohort. As shown in Fig. 3a and Fig. 3b, every factor is a proper distribution. In effect, the classical method is based on a single threshold that divides a histogram into two bins: lower or higher bins. There is a debate in the COPD community on what the optimal threshold should be. In contrast to the traditional approach, one can view the proposed method as an adaptive way of histogram binning with no need to specify the threshold explicitly. Nevertheless, it is interesting to see that the latent factors are located at the values that are close to −950 Hounsfield units (−950 is commonly used to define percentage of emphysema in the COPD community).

Fig. 3c presents a scatter plot of pairs of new features (x̂) in the cohort. The color in the scatter plot indicates the value of F EV₁/F V C. Higher values correspond to subjects without COPD. The scatter plot suggests that the new features successfully characterize the severity of the disease. Notice the smooth variation across the population. We also performed linear regression between new features (K = 6) and respiratory measurement FEV₁ (R² = 0.67), FEV₁/FVC (R² = 0.74), and the percent of emphysema (R² = 0.96).

Sensitivity Analysis

We chose around 500 SNPs with the lowest p-values identified in previous studies. Many of these SNPs are from regions that have been frequently reported in the genetic and respiratory literature in connection to lung cancer genes or nicotine receptors areas. We first examine the behavior of the algorithm on the smaller set of 2,441 subjects. In order to study the sensitivity of the method with respect to the main parameter (the number of the latent factors K), we choose three SNPs associated with COPD (rs578776 [18]), nicotine dependence (rs17483721 [19]), and lung cancer (rs2568494 [6]), and evaluate the significance of the model fit for different values of K.

The cross-validation accuracy of the model saturates very fast (Fig. 4a) implying that few topics summarize the dataset successfully. As K grows, so does the number of degrees of freedom in the χ² distribution that is used to evaluate the significance of the fit in Fig. 4b. Unless the fit improves substantially, we expect the significance (− log(p)) to increase at first and then to decline. The plots in Fig. 4b spike down at K = 20, 24, 34 because the features become so collinear that the optimization of the cost function of the ordinal logistic in Eq. (5) does not converge (Hessian in Eq. (6) become ill-conditioned). An alternative way to choose K is to use the variational lower bound which is not explored in this paper.

Association Study

To test if the new features enrich the association, we examined different combinations of topic features, summary image features (sumImg) and the respirometry measurement (Resp) for the set of selected SNPs. Fig. 5 reports the pair-wise comparison of different feature sets. A > B indicates how many more SNPs are detected in one setting (A) versus the other (B) and how they were distributed across different chromosomes. Almost every combination with latFtr improves with respect to the second row (sumImg). We conclude that the extracted features are correlated with previously identified clinical image-based measures, but also offer complementary detections for genetic studies. Another important message from Fig. 5 is that adding the most important clinical measurement (Resp) improves the results.

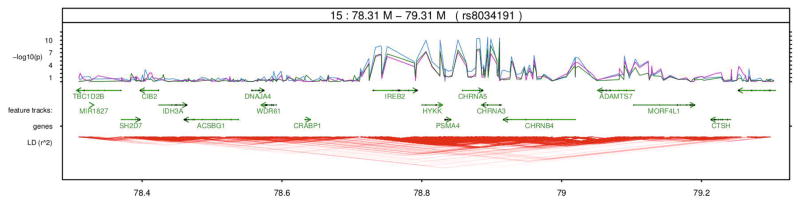
We also extracted features for the whole set of 6,670 subjects and applied regression on the genome-wide scale. Fig. 6 shows the regional maps on the chromosomes 15. Blue, purple and green lines represent new features (latFtr), sumImg, and Resp features. On the chromosomes 15, the new features (latFtr) enhanced the detection with respect to the other two feature sets by about 4 orders of magnitude in the corresponding p-values. On the chromosome 4, there is signal that is only detected effectively by the respiratory features but not by sumImg or latFtr (see Fig. 7). This suggests there is some information in the respiratory signal that is not reflected in the images.

Fig. 7.

Fine-scale regional maps for the region of significance on chromosome 4. Blue, purple and green lines represent latFtr, sumImg, and Resp respectively. There is signal that is only detected effectively by the respiratory features but not by sumImg or latFtr.

5 Conclusion

Traditional approaches to CT analysis in lung disease often rely on a single threshold or set of thresholds, and ignore the effects of genetic variants. We present a method to extract image features using topic modeling from lung CT images. Bins of the histogram are viewed as words in a dictionary or codebook. Our experiments show that new features correlate well with clinical measures of physiology (spirometry) and generalize commonly used measures for emphysema. The new features promise to improve the power of genetic associations for genetic causes of COPD. The proposed method is general and can be applied to any distribution. Including texture and lobe information to better characterize different subtypes of emphysema is a clear important and promising direction of future research.