RNAMotifScanX: a graph alignment approach for RNA structural motif identification

Abstract

RNA structural motifs are recurrent three-dimensional (3D) components found in the RNA architecture. These RNA structural motifs play important structural or functional roles and usually exhibit highly conserved 3D geometries and base-interaction patterns. Analysis of the RNA 3D structures and elucidation of their molecular functions heavily rely on efficient and accurate identification of these motifs. However, efficient RNA structural motif search tools are lacking due to the high complexity of these motifs. In this work, we present RNAMotifScanX, a motif search tool based on a base-interaction graph alignment algorithm. This novel algorithm enables automatic identification of both partially and fully matched motif instances. RNAMotifScanX considers noncanonical base-pairing interactions, base-stacking interactions, and sequence conservation of the motifs, which leads to significantly improved sensitivity and specificity as compared with other state-of-the-art search tools. RNAMotifScanX also adopts a carefully designed branch-and-bound technique, which enables ultra-fast search of large kink-turn motifs against a 23S rRNA. The software package RNAMotifScanX is implemented using GNU C++, and is freely available from http://genome.ucf.edu/RNAMotifScanX.

INTRODUCTION

Noncoding RNAs (ncRNAs) are attracting recent research focus with their amazing and versatile cellular functions (Eddy 2001; Storz 2002; Amaral et al. 2011; Wan et al. 2011; Rinn and Chang 2012), and many of them have significantly enriched our understanding of the molecular mechanisms. In many cases, the ncRNA functions are strongly tied to their specific three-dimensional (3D) structures, making the analysis of their 3D structure a key step in elucidating their functions and associating them with their molecular basis. Decades of analysis of the 3D structures point out that many of their subcomponents are recurrent. These subcomponents can be found in different locations or even different RNA structures. The so-called RNA structural motifs, or the “building blocks” of the RNA architecture (Moore 1999; Hendrix et al. 2005; Leontis et al. 2006), are highly modulated components with conserved 3D geometries and molecular functions. These features make them critically important in analyzing RNA 3D structures in a well-organized manner. In this sense, an RNA 3D structure can be considered as a collection of functional motifs, which are well organized and positioned by the scaffolding A-form helices (Reinharz et al. 2012).

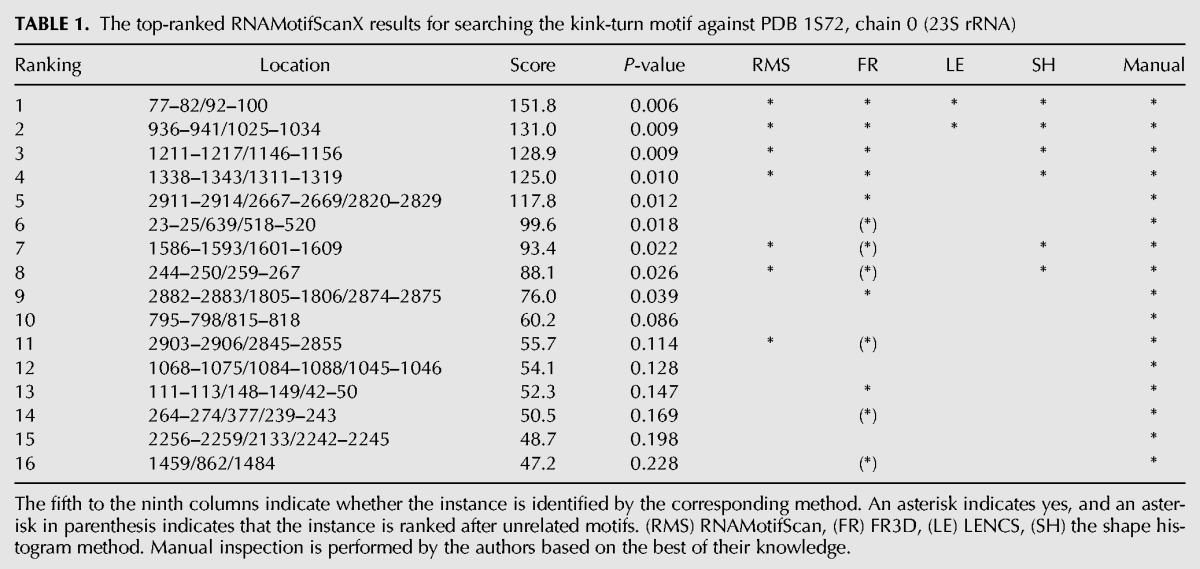
However, it remains challenging to automatically identify all known motif instances within a resolved RNA structure. Take PDB (Protein Data Bank) 1S72 (Klein et al. 2004) for example, which was resolved with a high resolution of 2.4 Å and has been released for a decade. Thirteen kink-turn motif instances have been identified from the 23S rRNA (chain “0”) subunit of this structure (see Table 1 for a list of known kink-turn instances in the subunit), either because they are predicted by at least one of the existing motif search tools or because they are manually inspected and confirmed. However, a sole motif search tool with the best performance can only identify seven out of the 13 instances perfectly (ranked on the top without including any unrelated instances). Therefore, a comprehensive motif search pipeline usually integrates the results of many state-of-the-art search tools, followed by a manual inspection/confirmation of the search results. Such a pipeline is tedious and time consuming, especially since the manual inspection step is infeasible for large-scale screening of the RNA structures. In this case, developing a new automated RNA structural motif search tool with higher accuracy and sensitivity is of crucial importance to annotate the fast-accumulating RNA structure repertoire.

TABLE 1.

The top-ranked RNAMotifScanX results for searching the kink-turn motif against PDB 1S72, chain 0 (23S rRNA)

Many of the existing motif search tools aim at detecting structural components with a similar geometry (i.e., the root mean square deviation) or backbone trajectory with the query motif. Examples of the 3D geometry-based tools include NASSAM (Harrison et al. 2003), PRIMOS (Duarte et al. 2003), ARTS (Dror et al. 2005), DIAL (Ferrè et al. 2007), FR3D (Sarver et al. 2008), and the shape histogram method (Apostolico et al. 2009) etc. Other tools try to find conserved base-interaction patterns between the query and motif, such as MC-Search (Hoffmann et al. 2003), FR3D symbolic search (Sarver et al. 2008), and RNAMotifScan (Zhong et al. 2010) etc. Based on the core alignment modules of these tools, there also exist clustering pipelines for de novo motif discovery, e.g., COMPADRES (Wadley and Pyle 2004), LENCS (Djelloul and Denise 2008), and RNAMSC (Zhong and Zhang 2012).

Despite the success of these tools, how to model the variations of the RNA structural motifs still remains as a key issue. The variations can happen at either the residue level (nucleotide insertion/deletion) or at the base-interaction level (nonisosteric mutation of base pairs). The reason is either evolutionary adaptation, or simply due to inadequate resolution of the RNA structure. For example, we discovered that the loop region of the kink-turn motif is highly variable, which may contain variation as small as a single nucleotide deletion (Zhong et al. 2010), to variation as large as a 31-nt insertion (Zhong and Zhang 2012). Existing search tools try to account for these variations with different heuristic approaches, but none of them solve the problem completely and optimally. For example, a geometry-based method FR3D (Sarver et al. 2008) requires the user to input the conserved residues when constructing the query, and only compute the geometry discrepancy on these conserved residues. Variations on the nonconserved residues are thus overlooked. The base-interaction-based method LENCS (Djelloul and Denise 2008) adopts a similar idea; but it automatically defines the conserved residues as those involved in (or directly adjacent to) the noncanonical interactions. RNAMotifScan (Zhong et al. 2010), another base-interaction-based method, aims at considering all possible variations (residue and base pair insertion/deletion/substitution) with a secondary structure alignment style algorithm (Bafna et al. 2006). However, it uses a heuristic algorithm to handle crossing base interactions due to the intrinsic limitation of its underlying alignment algorithm (Jiang et al. 2002). Incomplete consideration of all types of variations is one of the major reasons for the low sensitivity of the existing RNA structural motif search tools.

To solve this issue we introduce RNAMotifScanX, an accurate and efficient RNA structural motif search tool that optimally handles all types of variations. Variations found in the RNA structural motifs usually disrupt the complete base-interaction pattern of the motifs, and lead to “partially” conserved motif instances. To account for these partial motifs, RNAMotifScanX is designed as a “local” motif search tool that enables the identification of partially matched motifs in addition to the perfectly conserved ones. Meanwhile, to ensure the accuracy of the identified partial motifs, RNAMotifScanX performs extensive simulation on alignment-score distribution with respect to the query model, and computes the P-values of the partial matches to assess their statistical significance. Importantly, the search of the partial motifs is fully automatic, and it does not require a manual refinement of the query model based on a priori knowledge regarding variations that may present in the motif family.

These new features of RNAMotifScanX are rendered by the novel graph alignment algorithm developed in this work. Algorithmically, an RNA structural motif is modeled as a graph, where the vertices represent the residues and the edges represent base interactions between the corresponding residues (called an “interaction graph”). The proposed graph alignment algorithm aligns the two interaction graphs (one for the query and one for the target) and identifies all statistically significant matches (either partial or complete) between these graphs. Along with such an algorithmic improvement, we further introduce base-stacking information into the alignment, which is ignored by most of the motif search algorithms but largely affects the 3D structure (folding) of the structural motif. The resulting tool RNAMotifScanX is both computationally efficient, and capable of searching motif instances with significantly improved accuracy and sensitivity.

We benchmarked RNAMotifScanX with four state-of-the-art motif search tools, including RNAMotifScan (Zhong et al. 2010), FR3D (Sarver et al. 2008), LENCS (Djelloul and Denise 2008), and the shape histogram method (Apostolico et al. 2009). We used five well-studied motif families (kink-turn, C-loop, sarcin–ricin, reverse kink-turn, and the bacterial E-loop motif) with their complete sets of residues and interactions. The benchmarking results show that RNAMotifScanX achieves significantly improved overall sensitivity and specificity. We also identified several potential novel kink-turn related instances from the search results. We further observed that RNAMotifScanX can achieve the above performance with extremely fast computation time and low memory consumption. In summary, we anticipate that the accurate, efficient, and lightweight motif search tool RNAMotifScanX will significantly promote the study of RNA 3D structures and lead to novel discoveries within the field.

RESULTS

Notations and basic definitions

Let A and B be the two motif instances that are being aligned (each can be manually defined or automatically extracted from a large RNA structure). Denote the sequence of A as S^A, and its length as |S^A|. Denote the ith character of S^A as S^A[i], and a substring that begins with S^A[i] and ends with S^A[j] as S^A[i, j], inclusively. Let p^A(i, j) denote a base pair formed between S^A[i] and S^A[j]. Define a base-stacking interaction t^A(i, j) accordingly. Let P^A = {p^A} be the set of all base pairs in A, and let |P^A| denote its cardinality. Define T^A and |T^A| accordingly for base-stacking interactions.

The objective of the RNAMotifScanX algorithm is to compute the optimal “local alignment” between A and B. A local alignment M is defined by two augmented sequences M^A and M^B that are constructed by inserting gaps into substrings S^A[k, l] and S^B[k′, l′], respectively. Both M^A and M^B have the same length (however, it is not necessarily true that S^A[k, l] and S^B[k′, l′] have the same length) and characters within are aligned with one-to-one correspondence. Denote the original index for M^A[i] in S^A as i^M,A, and further simplify it as i^A when M is clear in the context. At least one of M^A[i] and M^B[i] corresponds to a nongap character for any valid alignment, where 1 ≤ i ≤ |M^A|. To ensure the completeness of the identified motifs, it is further required that the output does not contain any dangling nucleotides. Formally speaking, for the aligned substring S^A[k, l], it is ensured that p^A(k, x) ∈ P^A and p^A(y, l) ∈ P^A for some k ≤ x, y ≤ l, and a similar constraint applies to S^B[k′, l′] as well.

The goodness of an alignment M is evaluated by its corresponding “alignment score” F(M). With the consideration of base-pairing, base-stacking, and sequence conservation, define F(M) as follows:

$$F(M)={\displaystyle \sum _{i,j}\{w^P\cdot F^P(i,j)+w^T\cdot F^T(i,j)\}}+{\displaystyle \sum _i\{w^N\cdot F^N(i)\}}$$

Here, F^P, F^T, and F^N are functions to compute the matching scores for base-pairing interactions, base-stacking interactions, and individual nucleotides in the given alignment, respectively. And w^P, w^T, w^N represent weights associated with each of these categories, respectively. F^P(i, j) computes the score of the base pair matching at the alignment columns i and j, i.e., between the two potential base pairs p^A(i^A, j^A) and p^B(i^B, j^B). If p^A(i^A, j^A) ∉ P^A and p^B(i^B, j^B) ∉ P^B then F^P(i, j) is assigned a score of 0 to indicate that no base pair exists in either of the structures. For the second case, if p^A(i^A, j^A) ∉ P^A and p^B(i^B, j^B) ∈ P^B, it is taken as a “base pair insertion” case and corresponding penalty score is applied (“base pair deletion” defined similarly). Finally, if p^A(i^A, j^A) ∈ P^A and p^B(i^B, j^B) ∈ P^B, it is taken as a “base pair matching” or “substitution” case; the corresponding matching score is retrieved from a two-dimensional look-up table (defined based on isostericity [Leontis et al. 2002b; Stombaugh et al. 2009]; see Materials and Methods for details). Similarly, F^T(i, j) computes the score for the base-stacking matching at the alignment columns i and j, i.e., between the two potential base-stacking interactions t^A(i^A, j^A) and t^B(i^B, j^B); and F^N(i) computes the score of the nucleotide matching at the alignment column i, i.e., between the two nucleotides S^A[i^A] and S^B[i^B].

The RNAMotifScanX algorithm

The objective of the RNAMotifScanX algorithm is to compute the alignment M that maximizes the alignment score F(M) under the defined object function. Recall that RNA structural motif is represented as an interaction graph; thus optimally aligning RNA structural motifs is equivalent to optimally aligning the interaction graphs. It is proven that finding the optimal alignment between two interaction graphs (which allow arbitrary base interaction crossing patterns) requires exponential time (Jiang et al. 2002). Therefore the challenge is to find an efficient way to reduce the search space and maintain a reasonable running time.

RNAMotifScanX is developed based on a base-interaction “guided” approach; base-interaction matchings will partition the alignment into a set of loop regions, whose similarities can be computed efficiently as pure sequence alignments (F^N) using a dynamic programming algorithm (Needleman and Wunsch 1970). For example, if the alignment columns i and j correspond to a base pair matching, the sequence M^A will be partitioned into three subsequences, i.e., M^A[1, i − 1], M^A[i + 1, j − 1], and finally M^A[j + 1, |M^A|]. Such a partition applies to M^B as well. What follows is to sum the sequence alignment scores of these partitions, i.e.,

$${\displaystyle \sum _{k=1}^{i-1}\{F^N(k)\}+}{\displaystyle \sum _{k=i+1}^{j-1}\{F^N(k)\}+}{\displaystyle \sum _{k=j+1}^{\left|M^A\right|}\{F^N(k)\}},$$

and add it to F^P(i, j) and compute the final alignment score. (Computation of the nucleotide matching between S^A[i^A], S^B[i^B] and between S^A[j^A], S^B[j^B] is immediate and therefore eliminated from the formula for simplicity. The associated weights are eliminated as well for the same reason.) This example shows how the alignment score is computed when only one base pair matching is considered. In real cases, the RNAMotifScanX algorithm enumerates all combinations of possible base-interaction matchings, and computes all corresponding alignment scores to guarantee the optimality of the solutions.

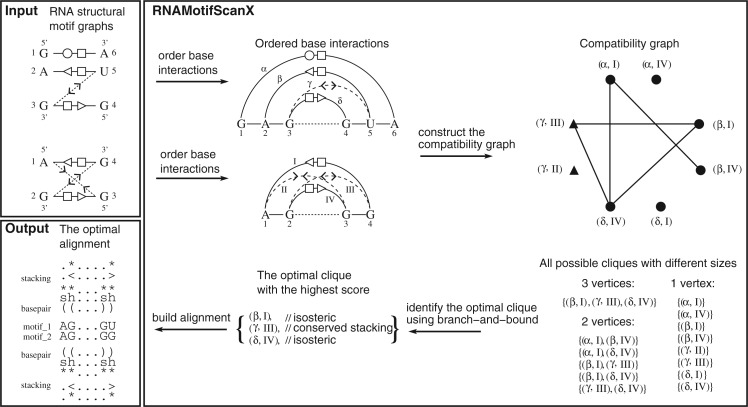
The RNAMotifScanX algorithm is outlined in Figure 1. A key observation for efficient base-interaction matching enumeration is that not all matchings are compatible (based on our definition of a valid alignment), and therefore the incompatible ones can be avoided to speed up the algorithm. A simple example of two incompatible matchings is when a base-triple (treated as two individual base pairs that share one common residue) is aligned with two base pairs (such that the one-to-one correspondence rule is violated). To detect such incompatibilities, first concatenate individual strands in the motif instance if necessary (all possible concatenation orders are enumerated to ensure optimality, see Zhong et al. 2010 for more details). Label each nucleotide in the concatenated motif with an order from its 5′ end to 3′ end. Base pairs in P^A can then be partially ordered with the following relationship: p^A(i, j) is ordered before p^A(k, l) if i < k, or i = k and j < l (see Fig. 1, “order base interactions”). Based on such an ordering, six relation groups are defined to detect incompatibility (see Fig. 2). The base pair matching formed between p^A(i, j) and p^B(i′, j′) is consistent with the one formed between p^A(k, l) and p^B(k′, l′), if and only if the relation group in which p^A(i, j) and p^A(k, l) are classified is equivalent to the relation group in which p^B(i′, j′) and p^B(k′, l′) are classified.

FIGURE 1.

The RNAMotifScanX's algorithmic framework demonstrated by aligning two artificial motif instances. The output of the algorithm is the optimal alignment between the two input motifs in terms of a weighted combination of base-pairing, base-stacking, and primary sequence similarity.

FIGURE 2.

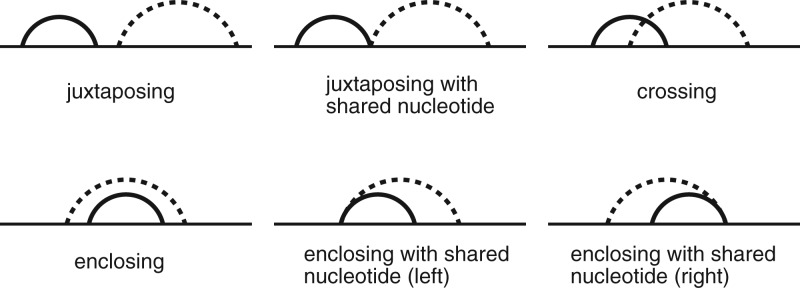
The six relation groups defined in RNAMotifScanX for base-interaction matching compatibility evaluation. The horizontal lines indicate the RNA primary sequences and the arcs represent the corresponding base interactions. Solid arc-labeled interactions are partially ordered before the broken arc-labeled interactions.

With the above definition, all base-interaction matchings can be summarized into a “compatibility graph” (see Fig. 1). Each vertex in the compatibility graph corresponds to a base-interaction matching, and each edge indicates that the corresponding base-interaction matchings are compatible. Because base-pairing interaction is not allowed to match with base-stacking interaction, the resulting size of the graph is thus |P^A|*|P^B| + |T^A|*|T^B|. Note the distinction between the interaction graph and the compatibility graph; the sole compatibility graph is summarized from two interaction graphs. For any valid alignment, any pair of base-interaction matchings must be compatible with each other, which implies that the corresponding vertices form a “clique” (completely connected subgraph) in the compatibility graph. In this case, enumerating all base-interaction matching is equivalent to finding all cliques in the compatibility graph. (The high-level objective of the problem is similar to R3D Align [Rahrig et al. 2010], but it is solved with a new algorithm that guarantees the optimal solution.)

Finding all possible cliques in a graph can be solved by using the Bron and Kerbosch algorithm (Bron and Kerbosch 1973). Although many more details and proofs can be found in the original paper, the major idea is reintroduced here for completeness. The algorithm maintains two vertex sets, namely U and V. The first set U contains all vertices that have been recruited as a part of the current clique, and V contains all candidate vertices that can potentially expand the current clique. Iteratively, each vertex in V is used to expand U. Say v ∈ V is picked for the iteration such that V′ = V − {v} and U′ = U + {v}. To ensure that V′ still holds valid candidates to expand U′, all v′ ∈ V′ that are not connected with v are subsequently removed from the set V′. Clique expansion proceeds with the updated sets U′ and V′. Iteration terminates when V′ = Ø. Alignment score is evaluated for each valid vertex set U. In this step, all possible cliques are implicitly traversed (see Fig. 1, “all possible cliques with different sizes”).

Finally, a branch-and-bound technique is further integrated into the algorithm to detect other early termination criteria. Recall that the cliques in the compatibility graph are expanded iteratively. Intuitively, if the current matching corresponds to a very low alignment score and future expansions are unlikely to make the amendment, the algorithm should terminate immediately. Define a “lower bound” to be the score that can be achieved by an existing set of base-interaction matchings, and an “upper bound” to be the score that is computed based on an optimistic forecast of the future expansion. The lower bound can be computed by simply taking the best alignment score seen so far. When computing the upper bound, note that if there are k vertices in V to be recruited into U, there should be at least k(k − 1)/2 edges formed between the vertices in V. Therefore, through counting the number of edges in V, the maximum number of possible matchings can be determined. The upper bound can then be computed accordingly. The algorithm terminates when the upper bound drops below the lower bound. After traversing all possible cliques, the recorded best solution (Fig. 1, “the optimal clique with the best score”) will be used to construct the alignment, which outputs conserved base interactions and primary sequences between the input motifs.

Search results of the kink-turn motif family

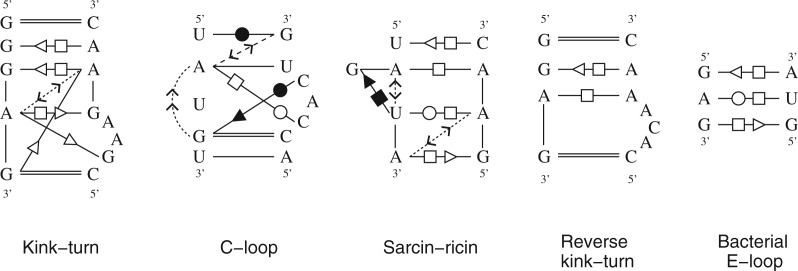
Here RNAMotifScanX was used to search the kink-turn motif (Klein et al. 2001) against the Haloarcula marismortui 23S rRNA (PDB ID: 1S72, chain “0”). The structure was chosen for benchmark purpose because it has been well studied and many of its true motif instances are known. The kink-turn motif is an asymmetric internal loop that induces a sharp turn of its two connecting helices, with its longer bulge showing a kink at the turning point. The search pattern of the kink-turn motif is shown in Figure 3, which is a consensus structure summarized by Lescoute et al. (2005). The default set of RNAMotifScanX parameters were used to conduct the search (more details in Materials and Methods). The results of the other tools were used “as is” from the corresponding publications and summarized in Table 1.

FIGURE 3.

Consensus base-interaction patterns of the five motif families that are used as the queries. The base pair notations follow those proposed by Leontis and Westhof (2001). The base-stacking interactions notations follow those proposed by Major and Thibault (2007).

In Table 1, motif instances were ranked based on the alignment scores computed by RNAMotifScanX. The last column of the table indicates manual inspection results for the motif instances; all top predictions made by RNAMotifScanX are kink-turn related motifs. The majority (13/16, 81%) of them are consistent with predictions from other tools. The other three instances that were uniquely identified by RNAMotifScanX (i.e., the tenth, twelfth, and the fifteenth instances) correspond to potentially novel motif instances (detailed in the following paragraphs). In comparison, RNAMotifScan identified seven, FR3D identified 11, LENCS identified two (note that it is a de novo clustering approach that aims for optimized specificity but not sensitivity), and the shape histogram identified six true instances. All except FR3D show significantly lower sensitivity. FR3D, on the other hand, includes unrelated predictions in its top list. For example, the eighth instance in the FR3D top list, i.e., 952–955/1012–1015, does not exhibit a sharp turn between two connecting helices, and in fact is annotated as part of a sarcin–ricin motif (see Table 2). In this case, RNAMotifScanX shows higher sensitivity and specificity than the other search tools for the kink-turn search.

TABLE 2.

The top-ranked RNAMotifScanX results for searching the C-loop motif against PDB 1S72, chain 0 (23S rRNA)

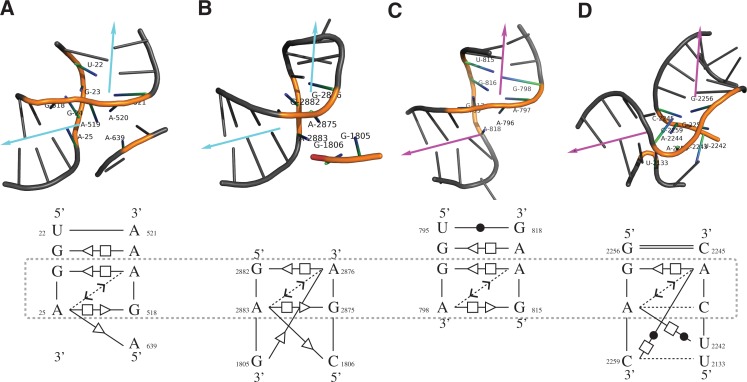
The sixth and ninth instances (Fig. 4A,B) show high similarity to the tenth and fifteenth instances (Fig. 4C,D) in terms of both geometry and base-interaction patterns. The most significant feature shared among these motif instances is the sharp turn between their connecting helices (as indicated by the arrows), a characteristic feature for the kink-turn motif. However, unlike a regular kink-turn motif, all instances lack a “kink” at the connecting region. Due to the lack of the “kink,” the sixth and ninth instances were considered (by the FR3D authors) as “kink-turn related” but not canonical kink-turn motifs (Sarver et al. 2008). Using RNAMotifScanX, such discovery can be reaffirmed by bringing in additional conservation of their base-interaction patterns. The tenth and fifteenth instances were newly discovered by RNAMotifScanX but not included by FR3D. The identification of conserved base-interaction patterns (see Fig. 4, lower panel) from geometrically divergent homologous motif instances demonstrates the power of base interactions in modeling and searching RNA structural motifs. This class of motif instances, which shows sharp turns but no kink, should be further studied with experimental evidence to confirm their relationship with the kink-turn motif family.

FIGURE 4.

The 3D structures (upper) and core base-interaction patterns (lower) of four predicted kink-turn related motif instances. All RNA 3D structure figures were generated using PyMol (http://www.pymol.org). These instances are ranked at the sixth (A), ninth (B), tenth (C), and fifteenth (D) in the RNAMotifScanX top list. All instances show sharp turns between the helices, but no significant kinks. The arrows shown in the top panel indicate the directions of the two helices, where the sharp turn between them is a key feature of the kink-turn motif. Motif instances shown in A and B are rediscovered from FR3D's predictions (cyan arrows), while motif instances shown in C and D are newly discovered by RNAMotifScanX (magenta arrows). Even though these instances share similar 3D structures, their base-interaction patterns vary. The lower panel shows the core interactions (which correspond to the colored residues in the upper panel) of the instances that are locally aligned to the query. The aligned interactions are different among the four instances, but all of them share a core that consists of two shared pairs and a connecting outward stacking interaction (boxed regions).

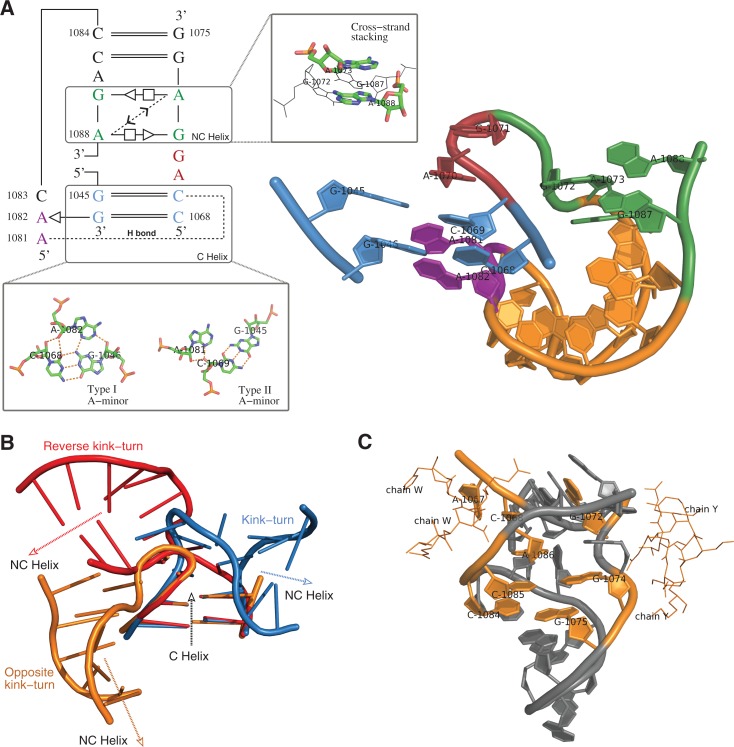
The twelfth instance predicted by RNAMotifScanX (Fig. 5) represents a potential new member of the kink-turn motif family, as supported by three key observations. First, the C helix (Fig. 5A, blue) contains two canonical G–C base pairs and the NC helix (Fig. 5A, green) contains two G–A sheared base pairs, both of which are consistent with the canonical kink-turn motif. Second, this motif instance is also stabilized through the cross-strand A–A stacking in the NC helix and the A-minor interaction in the C helix. Third, the kink region is formed by two bulged nucleotides (A1070 and G1071) (Fig. 5A, red). The superimposition of this motif instance, a typical kink-turn, and a typical reverse kink-turn motif highlights the turning direction of this motif (Fig. 5B). The bend induced by this motif is even sharper than those for the other two motifs, leaving an ∼180° angle between the two adjacent helices. Finally, the motif instance is interacting with two ribosomal proteins L30P (1S72, chain W) and L32E (1S72, chain Y) through majority of its nucleotides in the NC helix (Fig. 5C), which is also consistent with kink-turn's binding potential that is granted by the flattened minor groove of its NC helix (Klein et al. 2001).

FIGURE 5.

The twelfth motif instance identified by searching the kink-turn motif using RNAMotifScanX. (A) The base-interaction pattern and the 3D structure of this motif instance. Color labels: green—the NC helix where the cross-strand A–A stacking is found; red—the bulge loop that corresponds to the kink region of the motif instance; blue—the C helix where two A-minor interactions are found (a type I and a type II A-minor interaction); purple—the adenine residues that participate in the two A-minor interactions. (B) Superimposition of the C helices of a kink-turn (blue), a reverse kink-turn (red), and this motif instance (orange). The NC-helix turns toward neither left nor right, but to the opposite direction. (C) Interacting residues (highlighted in orange) of this motif with the ribosomal proteins L30P (1S72, chain W) and L32E (1S72, chain Y).

Finally, one motif instance was missed by RNAMotifScanX due to its higher degree of variation. The instance was identified by FR3D search, but it was ranked last (twentieth) at the FR3D prediction list. None of the annotation tools used in this study (i.e., MC-Annotate and RANVIEW) identifies any conserved base pairs from this motif instance. The motif instance is not included in RNAMotifScanX's top list.

Search results of the C-loop, sarcin–ricin, reverse kink-turn and the bacterial E-loop motif families

In addition to the kink-turn motif family, four other major RNA structural motif families, i.e., the C-loop, sarcin–ricin, reverse kink-turn, and bacterial E-loop motif families, were also searched using RNAMotifScanX (pattern summarized in Fig. 3). The detailed search results are listed in Table 2 (C-loop), Table 3 (sarcin–ricin), Table 4 (reverse kink-turn), and Table 5 (bacterial E-loop). For all searches, RNAMotifScanX identified the majority of true hits and ranked them in its top lists. While the kink-turn search has led to the discovery of many potentially new kink-turn related motif instances, the search of these motif families has shown significant performance improvements. These improvements demonstrate advantages of the new RNAMotifScanX algorithm and the incorporation of the base-stacking information.

TABLE 3.

The top-ranked RNAMotifScanX results for searching the sarcin–ricin motif against PDB 1S72, chain 0 (23S rRNA)

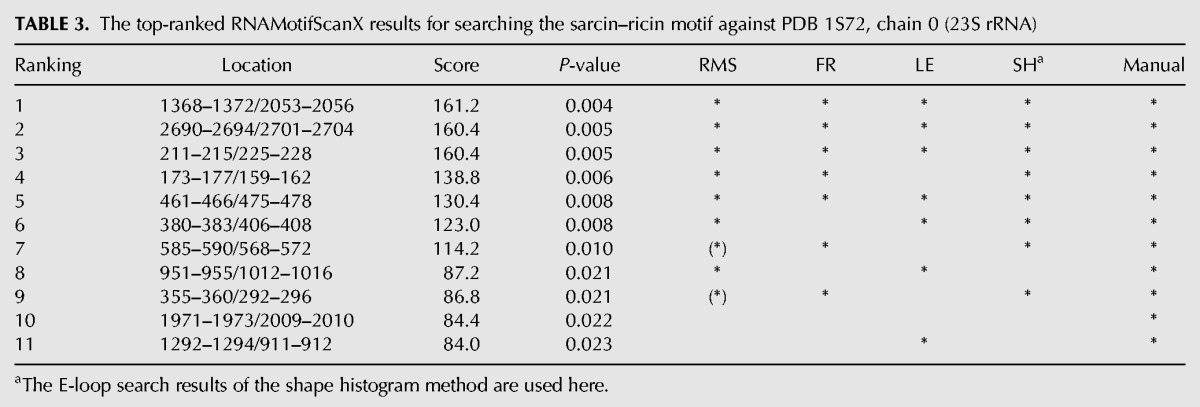
TABLE 4.

The top-ranked RNAMotifScanX results for searching the reverse kink-turn motif against PDB 1S72, chain 0 (23S rRNA)

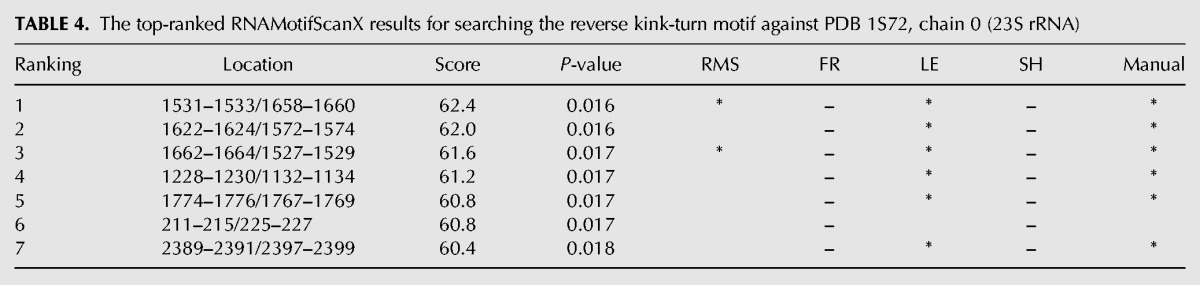
TABLE 5.

The top-ranked RNAMotifScanX results for searching the bacterial E-loop motif against PDB 1S72, chain 0 (23S rRNA)

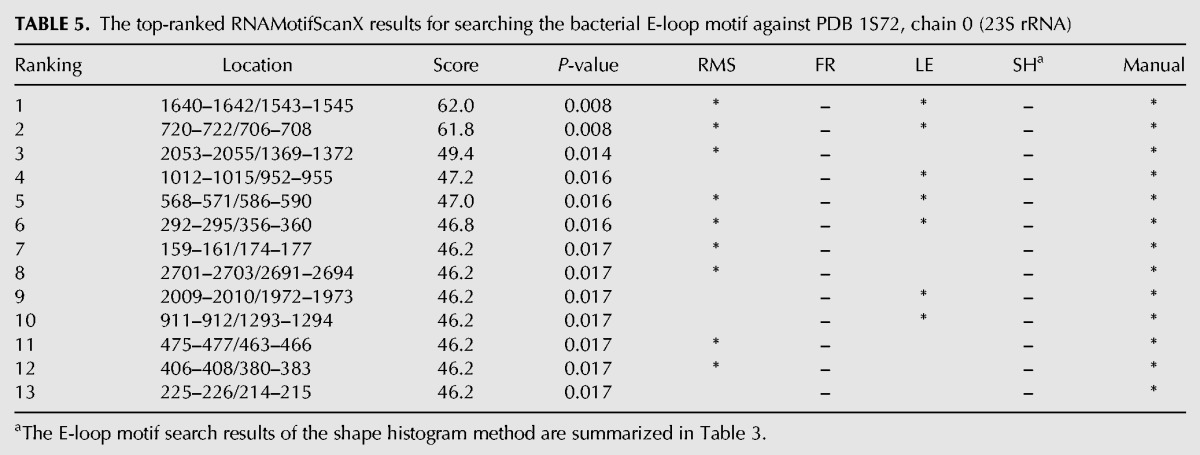
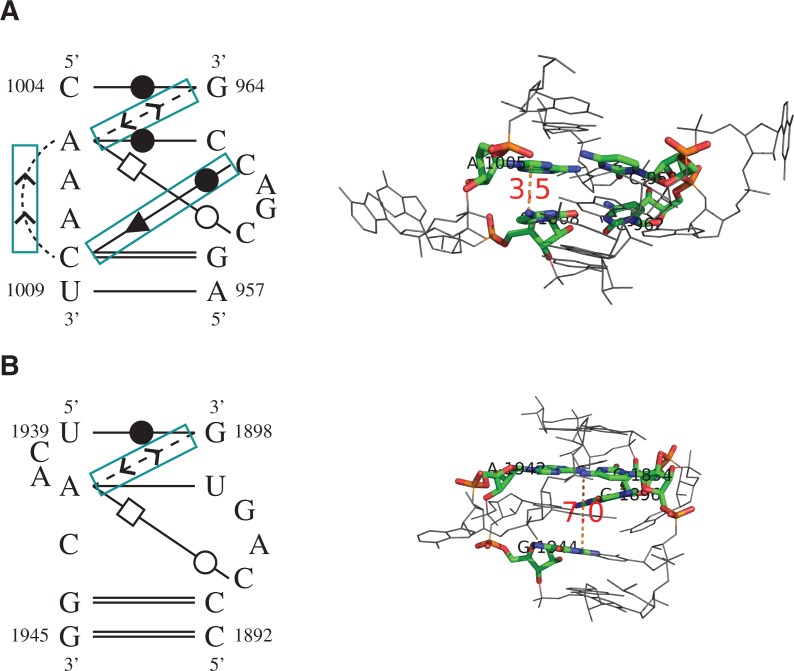
Table 2 shows the search results for the C-loop motif. RNAMotifScanX improves the prediction of RNAMotifScan by ranking all true instances on the very top of the prediction list. The first instance shown in Table 2 is a true C-loop instance, but was ranked below an unrelated motif instance by RNAMotifScan (indicated by the parenthesized asterisk in Table 2). The first instance and the unrelated instance are shown in Figure 6A and B, respectively. RNAMotifScanX identified a conserved crossing noncanonical base-pairing interaction (A1005–C1008) and a conserved base-stacking interaction (C966–C1008) from the motif instance shown in Figure 6A, but it did not identify their counterparts in the instance shown in Figure 6B. In this case, RNAMotifScanX is capable of correcting the ranking of these two motif instances. The identification of the conserved crossing base pair is due to the improvement of the novel graph alignment algorithm, which permits any type of crossing base interactions to be optimally aligned. Identification of the conserved base-stacking interaction is due to our consideration of such information in the new tool RNAMotifScanX. These newly identified interactions by RNAMotifScanX are crucial to form the C-loop core structure; in the unrelated instance shown in Figure 6B that lacks such interactions, the corresponding nucleotides (A1942 and G1944) are distant from each other, thus fail to extrude the unpaired nucleotide (C1943) between them. RNAMotifScanX also shows higher sensitivity than LENCS, as LENCS is a de novo clustering tool that favors higher specificity.

FIGURE 6.

The base-interaction patterns (left panel) and 3D structures (right panel) of (A) a true C-loop motif instance and (B) an unrelated motif instance. RNAMotifScan ranks A below B; however, RNAMotifScanX is capable of correctly ranking A above B. RNAMotifScanX corrects the ranking by considering the stacking interactions and the crossing base pair. In the left panel, conserved base interactions that are uniquely aligned by RNAMotifScanX are highlighted using the cyan boxes. The right panel shows that the lack of these interactions in B leads to significant structural changes of the core nucleotides (colored, with distance measures to highlight the variation between the same-strand stacked nucleotides, i.e., A1005, C1008 in A and A1942, G1944 in B) as well as the entire structure.

The search results of the sarcin–ricin motif family are shown in Table 3. RNAMotifScanX perfectly identified all 11 known sarcin–ricin motif instances. FR3D only identified seven out of the 11 known instances by using the same 9-nt sarcin–ricin search model shown in Figure 3. The FR3D authors further showed that based on existing knowledge regarding the conserved nucleotides in the sarcin–ricin motif, they can refine the 9-nt model into a smaller 5-nt model, and subsequently identify all 11 known instances. Similarly, the shape histogram identified eight out of 11 known instances using a 7-nt search model that contains the complete AUGA bulged strand of the sarcin–ricin motif (although the query is termed “E-loop motif” by the authors of the shape histogram method [Apostolico et al. 2009]). The results indicate that both FR3D and the shape histogram method focus on searching perfectly matched motif instances, and may require careful preparation of the query model in order to reach the optimal performances. RNAMotifScanX, on the other hand, can perfectly identify all of the 11 known instances simply by using the complete 9-nt search model. Such search results were generated fully automatically and required no a priori knowledge. This advantage of RNAMotifScanX is due to the carefully designed graph alignment algorithm that can automatically detect all high-scoring partial matches.

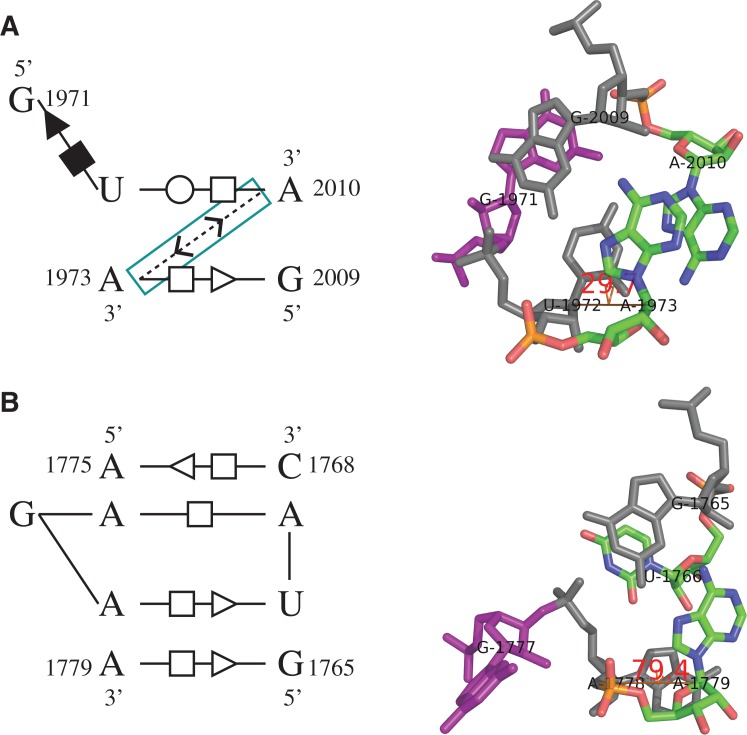
RNAMotifScanX improves the RNAMotifScan search results for the sarcin–ricin motif family by correcting rankings of the true instances (see the seventh and the ninth instances in Table 3). More importantly, RNAMotifScanX identified two more true instances (see the tenth and the eleventh instances in Table 3). Take the tenth instance (shown in Fig. 7A) for example, it is missed by RNAMotifScan because it has a lower score than several unrelated motif instances (one of these unrelated instances is shown in Fig. 7B). By considering the base-stacking information, one additional conserved base-stacking interaction is detected by RNAMotifScanX from the instance shown in Figure 7A, which improves its alignment score and leads to the identification of this true instance. Lack of such a conserved base-stacking interaction in the motif instance shown in Figure 7B can lead to structural change of the adjacent residues, and potentially the loss of its protein binding activity. The dihedral angle between the same-strand residues (U1972 and A1973 in Fig. 7A) is increased from 29.7° to 79.4° for those of the second instance (A1778 and A1779 in Fig. 7B). Such a variation leads to the different orientations of the bulged guanine residues (magenta residues in Fig. 7), which is crucial for the recognition of its associated protein (Gluck and Wool 1996; Munishkin and Wool 1997; Yang et al. 2001).

FIGURE 7.

The base-interaction patterns (left panel) and 3D structures (right panel) of (A) a true sarcin–ricin motif instance and (B) an unrelated motif instance. RNAMotifScan ranks A below B and does not identify A in its top list. However, RNAMotifScanX is capable of identifying A and ranking it in the very top of its prediction list by aligning one additional base-stacking interaction (highlighted using cyan box in left panel). The right panel shows that lack of such stacking interaction in the second instance leads to significant changes in the dihedral angle between the corresponding nucleotides (U1972, A1973 in A and A1778, A1779 in B). Such change further leads to different orientations of the bulged guanine residues (magenta).

The search results of the reverse kink-turn motif families are summarized in Table 4. The top 5 instances predicted by RNAMotifScanX correspond to true hits, while the sixth one is an unrelated motif. This motif instance overlaps with a well-characterized sarcin–ricin motif (ranked third in Table 3). The two noncanonical base pairs shared between the reversed kink-turn and the sarcin–ricin motifs (i.e., the trans S/H and trans H/H pairs, see Fig. 3) are detected for the prediction of this motif. RNAMotifScanX also misses a true hit that has been shown by the LENCS method, i.e., 2298–2300/2307–2310, because additional interactions were predicted for this instance that trigger the base pair deletion penalty. Nevertheless, RNAMotifScanX is still capable of improving the performance of RNAMotifScan by predicting five true hits compared with two at the 100% specificity level.

Finally, the bacterial E-loop search results are shown in Table 5. RNAMotifScanX predicts 13 instances in its top list. The first two motif instances perfectly match the bacterial E-loop search pattern, while the rest (the third to the thirteenth) motif instances are partial matches. These partially matched motifs were also identified by the previous experiment of searching the sarcin–ricin motif, because they share two conserved noncanonical base pairs (the trans W/H pair and the trans H/S pair shown in Fig. 3) with the sarcin–ricin query model. The strong overlap between RNAMotifScanX's sarcin–ricin and bacterial E-loop search results is also consistent with their close relationship: Both the sarcin–ricin motif and the bacterial E-loop motif can be identified from the 5S rRNA loop-E region, except that the sarcin–ricin motif is prevalently found in archaeal and eukaryotic 5S rRNAs loop-E region (Wimberly et al. 1993; Szewczak and Moore 1995) while the bacterial E-loop motif is found in bacterial 5S rRNAs loop-E region. The tool with the second best performance for this motif, RNAMotifScan, outputs 10 (one of them is missed by RNAMotifScanX and therefore only nine are shown in the Table 5) true hits without unrelated instances. RNAMotifScanX again shows significantly improved sensitivity. RNAMotifScanX missed one motif instance, i.e., 663–666/680–683, because of the insertion of 2 nt. However, such an instance is still ranked relatively high with a P-value of 0.021 (data not shown). In summary, RNAMotifScanX outperforms the other state-of-the-art motif search tools in almost all experiments (except that the LENCS method shows higher performance for the reverse kink-turn motif).

Estimating family-specific P-value cutoffs

An important unbiased measure that facilitates automatic downstream analysis is the P-value for the raw alignment scores. Generally, the P-value indicates the possibility that the null hypothesis is accepted; lower P-value indicates a higher structural similarity between the motif instances. Because motif families have largely variable sizes and different permissiveness for variations, suggesting a universal P-value cutoff for all families is difficult (Zhong et al. 2010). For example, FR3D and the shape histogram methods apply different geometric discrepancies for different motif families, while RNAMotifScan empirically suggests family-specific P-value cutoffs.

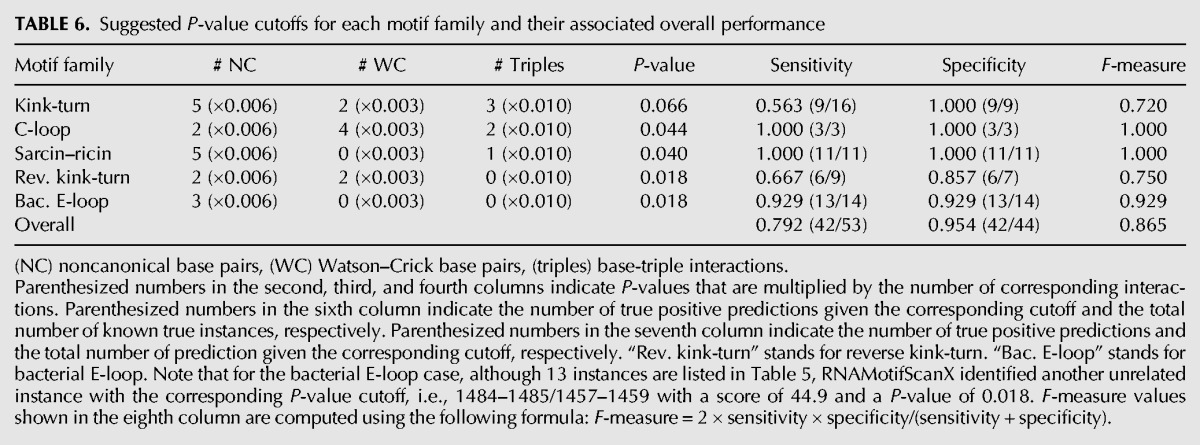
Here in RNAMotifScanX, family-specific P-values for the raw alignment scores are suggested based on the base-interaction features of the families. The raw alignment scores relate strongly with the number of base pairs in the query, because base pair matchings are usually assigned with higher weights. The raw alignment scores also depend on the number of base-triples in the query, as bonus is assigned for their matching to honor the rareness. A simple linear model is used to compute family-specific P-value cutoffs based on the number of base pairs (canonical and noncanonical) and base triples (see Table 6). Applying the automatically computed cutoff leads to an overall performance of 86.5% F-measure. Note that such performance can be achieved fully automatically, and the actual performance of RNAMotifScanX is much higher when manual inspection is applied (to simply identify the first unrelated instance as the cutoffs).

TABLE 6.

Suggested P-value cutoffs for each motif family and their associated overall performance

Computational efficiency of RNAMotifScanX

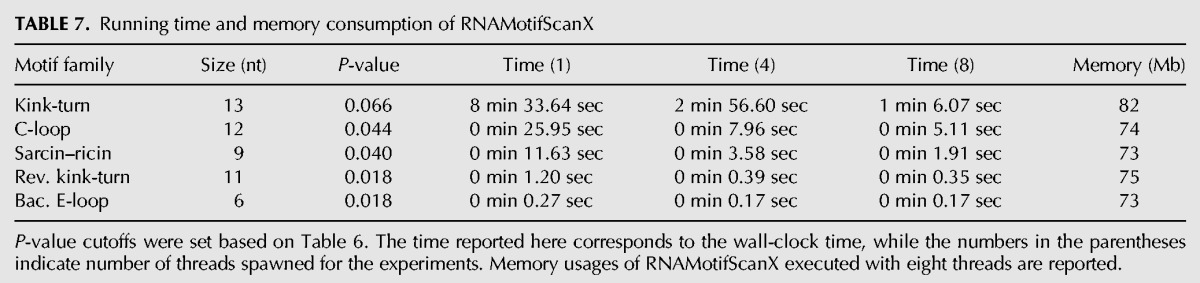
Although the running time of the RNAMotifScanX algorithm, in the worst case scenario, may grow exponentially with the input size, our carefully designed algorithm with the compatibility graph and the branch-and-bound technique makes it practical and run extremely fast for all experiments presented here. RNAMotifScanX is further empowered by parallel computing with multithreaded execution mode enabled. The running time for all searches is summarized in Table 7. Note that the relatively longer running time for the kink-turn search is required because of its larger size and the consideration of its composite instances (instances that involve up to three strands are allowed). Compared with FR3D, which requires 58.7 sec to search for the 9-nt sarcin–ricin motif query (see Fig. 3), RNAMotifScanX can finish the search within 11.6 sec (with single thread). The significant running time improvement and low memory consumption makes RNAMotifScanX an idea tool for large data set analysis.

TABLE 7.

Running time and memory consumption of RNAMotifScanX

CONCLUSIONS AND DISCUSSION

In this paper, we presented a novel local graph alignment algorithm for RNA structural motif comparison and search. We applied the algorithm to the RNA structural motif interaction graphs and computed their optimal alignments. We designed the algorithm based on a clique finding algorithm with a branch-and-bound search technique. We also incorporated the base-stacking information in our modeling of RNA structural motifs, which has been shown to significantly improve the performance of the search. We implemented the alignment algorithm into the search tool called RNAMotifScanX. We observe the following major advantages of RNAMotifScanX:

• “Sensitive and accurate”: RNAMotifScanX shows high sensitivity and specificity, and outperforms other state-of-the-art search tools for the majority of the search experiments.

• “Automatic”: RNAMotifScanX requires no a priori knowledge regarding the query, and can automatically detect the conserved regions disregarding whether they are partial or complete. Also, RNAMotifScanX outputs P-values and suggests cutoffs for each motif family. Both characteristics make automatic analysis of a large collection of RNA structures possible and convenient.

• “Fast and lightweight”: RNAMotifScanX achieves ultra-fast running time through both algorithmic improvements and parallel computing. RNAMotifScanX only requires minimum physical memory (<100 Mb) that can be easily satisfied by a personal computer.

We note that RNAMotifScanX is an ideal tool to search new motif families, as it can automatically identify the conserved local patterns between the query and the target. This feature is extremely important when the set of conserved nucleotides are unknown because of the lack of comparative studies. (We expect that RNAMotifScanX can also benefit from such information, and in the future we will enable profile-based query using either a position-specific scoring function or a hidden Markov model.) We anticipate another important use of RNAMotifScanX for large-scale PDB survey, which is made possible by RNAMotifScanX's high computational efficiency. Last but not least, we have previously demonstrated a clustering pipeline developed based on RNAMotifScan, and its application on ribosomal RNAs led to the discovery of many new instances and a novel motif family (Zhong and Zhang 2012). We expect to further expand this work by using RNAMotifScanX as the aligner and applying it to all RNA structures in the PDB.

During the search of the five RNA structural motif families, several partially conserved base-interaction patterns were identified. For example, all the kink-turn instances shown in Figures 4 and 5 share a core structure of two tandem sheared pairs connected by a cross-strand outward stacking interaction. Such a strong correlation suggests that these conserved interaction patterns can be used to aid RNA 3D modeling. The idea is very similar to the Nucleotide Cycle Motif (Lemieux and Major 2006; Parisien et al. 2009; Reinharz et al. 2012). However, the core patterns automatically detected by RNAMotifScanX are expected to be the maximally conserved regions, which could be more biologically meaningful and computationally easier to incorporate. Moreover, these core structures contain base-stacking interactions that were not considered for de novo identification of RNA structural motifs in the multiple sequence alignments (Cruz and Westhof 2011), and the identification of conserved base-stacking interaction will provide additional information for this application and lead to more accurate discoveries.

MATERIALS AND METHODS

Data preparation

Five RNA structural motif families were used as the queries. The query motifs (as shown in Fig. 3) were taken from existing analysis of their consensus patterns. The five motif families and their corresponding references are listed as the following: kink-turn (Lescoute et al. 2005), C-loop (Leontis and Westhof 2003), sarcin–ricin (Leontis et al. 2002a), reverse kink-turn (Leontis et al. 2006), and the bacterial E-loop motif (Leontis et al. 2002a). Redundant boundary canonical base pairs were removed to simplify the search. Base-stacking information was then added to the patterns. The resulting query patterns are summarized in Figure 3.

The target H. marismortui 50S rRNA structure 1S72 was downloaded from the PDB (Berman et al. 2000). The structure was annotated by MC-Annotate (Gendron et al. 2001) and RNAVIEW (Yang et al. 2003) for its base-pairing and base-stacking interactions. The annotations made by MC-Annotate and RNAVIEW were combined (union). Conflicting annotations (i.e., two different types of interactions are annotated for the same pair of residues) were resolved by taking the MC-Annotate predictions.

Individual target motif instances were automatically extracted using an anchoring approach (in-house script distributed along with the RNAMotifScanX package). For each noncanonical base pair in the query, its corresponding isosteric counterparts in the target structure were used as anchors. For each anchor, its adjacent residues were teased out to match (two excessive adjacent residues are included in each strand to account for potential insertions in the target) the size of the query motif. Only a predefined number of strands are considered. When more strands are involved, the anchoring strands (where the anchoring base pair resides) were automatically accepted, while the remaining ones were selected (to meet the predefined number for maximum allowed strands) based on how strongly they interact with the anchoring strands (sorted based on the number of interactions with the anchoring strands). The finalized set of nucleotides was further refined by removing the unpaired flanking residues to make the motif a complete loop. Finally, the accepted strands were concatenated with all possible orders as described in RNAMotifScan (Zhong et al. 2010) to form the final set of candidate target motifs.

Base-stacking information processing

Base-stacking interaction involves London dispersion intermolecular interaction (Major and Thibault 2007), and in addition to base-pairing interaction it also serves as one of the major forces that contributes to the thermodynamic stability of the RNA/DNA molecules (Batey et al. 1999; Leontis et al. 2002a, 2006; Leontis and Westhof 2003; Yakovchuk et al. 2006). Different types of stacking interactions can be classified into four categories, namely “inward,” “outward,” “upward,” and “downward.” Such information can be retrieved from MC-Annotate or RNAVIEW annotations. Base-stacking interactions are further classified as either adjacent or nonadjacent. By adjacent/nonadjacent we mean that the two residues that form the base-stacking interaction are directly adjacent/nonadjacent to each other in the primary sequence. Nonadjacent base-stacking interactions matches are also associated with higher weights because they usually indicate specific 3D geometry (a single weight for stacking, w^T, was shown in the object function for the sake of simplicity, yet two different weights are actually applied here; see more details in the “Default Parameters”). Matches of nonadjacent base-stacking interactions are summarized into the compatibility graph together with base-pairing matches; and the RNAMotifScanX algorithm enumerates all possible matches of base-pairing and nonadjacent stacking interactions between the two RNA structural motif instances.

Adjacent base-stacking interactions can be aligned together with loop regions using a modified sequence alignment algorithm (i.e., they are not summarized into the compatibility graph). Specifically, recall that the loop alignment algorithm adopts the traditional Needleman–Wunsch algorithm (Needleman and Wunsch 1970). Let S^A[k, l] and S^B[k′, l′] be the sequences of the two closed loops that are being aligned. The dynamic programming algorithm uses a two-dimensional table D to store the intermediate results. D[i + 1, i′ + 1] stores the optimal alignment between sequences S^A[k, k + i − 1] and S^B[k′, k′ + i′ − 1]. To compute D[i + 1, i′ + 1], three entries in the table are referred to, i.e., D[i, i′ + 1], D[i + 1, i′], and D[i, i′]. Besides these three entries, the algorithm is modified to refer to scores in all entries D[i, i′ − x′], where 0 < x′ < i′ and all entries D[i − x, i′] where 0 < x < i as well. The idea is to consider the cases where either S^A[k + i − 1] or S^B[k′ + i′ − 1] participates in an adjacent base-stacking interaction (note that the case where both of them correspond to adjacent base-stacking interaction is considered when referring to D[i, i′]). While referring to, say, entry D[i, i′ − x′], the matching score between the adjacent stacking interaction t^A(k + i − 2, k + i − 1) and the stacking interaction t^B(k′ + i′ − x′ − 2, k′ + i′ − 1) (which is either adjacent when we refer to D[i, i′] or nonadjacent when 0 < x′ < i′) is also evaluated. Corresponding base-stacking insertion/deletion penalty is applied similar to those for the base pairs if either of the above stacking interactions is not formed.

Default parameters

All experiments were run on an Intel Xeon E5-2640 2.5GHz workstation. Three substitution matrices are used in RNAMotifScanX for base-pairing, base-stacking, and nucleotide substitution, respectively. For base pairs, all isosteric base pair (see definition in Leontis et al. 2002b; Stombaugh et al. 2009) matches are scored 12.0, except the canonical (Watson–Crick) base pair substitutions, which are only scored 5.0 for their prevalence in RNA structures. Nonisosteric base pair substitutions are scored 1.5. Deletion of a noncanonical base pair in the query is penalized with a score of −12.0, and in the target with a score of −1.2. Canonical base pair deletions are not penalized. For base-stacking interactions, matches within the same category are scored 3.0, and 0.0 otherwise. Deletion of a base-stacking interaction in the query is penalized with a score of −8.0, and in the target for −0.8. For nucleotides, matches of the same nucleotides are scored 3.0; if different nucleotides are matched it is penalized with a score of −1.0. Deletion of a nucleotide is penalized with a score of −1.5 (for both query and target). These scores are further weighted to account for their different impacts in shaping RNA 3D structures. The weight for base pair scores (w^P) is set to 2.0, for nonadjacent base-stacking 1.0 and for adjacent base-stacking scores 0.2 (both stacking weights were summarized as w^T for the sake of simplicity), and for nucleotide scores (w^N) 0.1. Note that nucleotide insertion/deletion is weighted using w^P because it might lead to strong distortion of the local geometry (nucleotide substitutions are still weighted by using w^N). A base triple is modeled as two individual base interactions that share a single residue, and two base triples are considered conserved if both corresponding base-interaction matches are isosteric (for base pair interactions) or within the same category (for base-stacking interactions). Matches of conserved base triples are rare, and strongly indicate motif homology. In this case, a bonus score of 3.0 (such score is not weighted) is added for each pair of conserved base triples.

Random structure shuffling for P-value computation

P-values reported in RNAMotifScanX are estimated with a simulation-based approach. A given query motif is randomly shuffled a large number of times (default 1000). Specifically, each base interaction (including both base-pairing and stacking) is randomly mutated according to the background frequencies of all observed base interactions the PDB. Alignment score distribution associated with the given query is simulated by aligning the query against all of its shuffled structures. Under such an alignment score distribution, the P-values for any given alignment scores can be computed by using the Chebyshev's inequality.

Software availability

The software package RNAMotifScanX was implemented using GNU C++ and the BOOST C++ libraries (http://www.boost.org). The Linux 64-bit executable of RNAMotifScanX is freely available from http://genome.ucf.edu/RNAMotifScanX. Source code for cross-platform compilation is also available by contacting the authors.