Quantitative Analysis of TDLUs using Adaptive Morphological Shape Techniques

Abstract

Within the complex branching system of the breast, terminal duct lobular units (TDLUs) are the anatomical location where most cancer originates. With aging, TDLUs undergo physiological involution, reflected in a loss of structural components (acini) and a reduction in total number. Data suggest that women undergoing benign breast biopsies that do not show age appropriate involution are at increased risk of developing breast cancer. To date, TDLU assessments have generally been made by qualitative visual assessment, rather than by objective quantitative analysis. This paper introduces a technique to automatically estimate a set of quantitative measurements and use those variables to more objectively describe and classify TDLUs. To validate the accuracy of our system, we compared the computer-based morphological properties of 51 TDLUs in breast tissues donated for research by volunteers in the Susan G. Komen Tissue Bank and compared results to those of a pathologist, demonstrating 70% agreement. Secondly, in order to show that our method is applicable to a wider range of datasets, we analyzed 52 TDLUs from biopsies performed for clinical indications in the National Cancer Institute’s Breast Radiology Evaluation and Study of Tissues (BREAST) Stamp Project and obtained 82% correlation with visual assessment. Lastly, we demonstrate the ability to uncover novel measures when researching the structural properties of the acini by applying machine learning and clustering techniques. Through our study we found that while the number of acini per TDLU increases exponentially with the TDLU diameter, the average elongation and roundness remain constant.

1. INTRODUCTION

Terminal duct lobular units (TDLUs) of the breast are the histological structures that give rise to nearly all breast cancers. As healthy women age, TDLUs involute, reflected in a reduced number of constituent acini (main sub-unit) and a reduction in TDLU number. Data suggest that epidemiological breast cancer risk factors may be associated with the level of TDLU involution and women whose TDLUs do not involute with aging may be at increased breast cancer risk.^1–4 To date, research related to TDLU involution has relied mainly on subjective visual assessment. Accordingly, estimation of objective measurements would offer opportunities to automatically quantify longitudinal changes and to provide new variables that can be used to better study the associations between morphological properties and important factors related to breast cancer risk.

In this paper, we outline a three-step process to extract and analyze quantitative image features of TDLUs. First, we focus on developing a method to automatically extract these morphological measurements of the TDLUs. Secondly, we apply machine learning techniques to these measurements to characterize three distinct types of acini. Lastly, we relate acini measurements to TDLU diameter, from which we conclude that the morphometric features of acini that we assessed were not strongly related to TDLU size.

In this study we analyzed 1,325 acini belonging to 51 different TDLUs from seven subjects of the Komen Tissue Bank study of normal breast tissues and 52 TDLUs from eight subjects in the BREAST Stamp Project. Images were prepared by digitizing routinely hematoxylin and eosin (H&E) stained tissue sections.

2. TECHNIQUE AND APPROACH

In order to analyze the images to extract morphological features, a series of preprocessing steps were performed to prepare the image for quantification. Figure 1 shows an example of these steps applied to a representative TDLU image.

Figure 1.

Examples of image processing steps applied to the TDLU. (1) The image is converted to the HSB color space and the Brightness component is utilized. (2) A Gaussian blur is applied to the Brightness channel. (3) Histogram equalization is performed on the blurred image. (4) Tsai’s thresholding method is applied. (5 and 6) A series of erosions and dilations are performed to reveal the acini. (7) The acini are fully revealed and the statistics can be computed for each acini. (8) An example of the acini outlines on top of the original TDLU image.

First, the image was split into the Hue, Saturation, and Brightness (HSB) color space. The Hue and Saturation components were discarded and only the Brightness component was utilized. The Brightness component contained the most contrast relative to the acini and nuclei.

A Gaussian blur was applied to the Brightness component to discard high frequency data. Since we were only interested in the morphological changes to the structure of the TDLU, a Gaussian blur can remove high frequency noise that would otherwise distort the quantification of the TDLU.

Histogram equalization was then applied to the blurred image, which increased the global contrast of the image by spreading the most frequently exhibited intensity values across the full range of Brightness values. By automatically adjusting the distribution of intensity values, we increased local regions of contrast to exhibit a higher level of contrast. The higher level of contrast aides in acinus analysis.

After equalizing the image, the image was thresholded to reveal the acini in the image. The thresholding step was accomplished using Tsai’s moment processing method. In this method moments of the grayscale input image are computed and the threshold values for the output image are automatically selected in such a way that the moments are unchanged.⁵ After thresholding, each acinus appeared as a black “blob” on a white background.

A series of erosions and dilations was then applied to the thresholded image. First, the erosions attempted to disconnect adjacent acini that would otherwise appear as a single larger acinus. Secondly, the erosions also removed smaller blobs in the image that are not an acinus but might be confused as one. Finally, a series of dilations was used to regrow the eroded regions to estimate their original shape.

Lastly, the “blobs” in the image were analyzed and the area, elongation, perimeter, and roundness of each blob were computed. These statistics served as a morphological representation of each acinus.

After extracting the acini statistics from all TDLUs, we clustered acini together using X-Means – a robust version of K-Means.⁶ A typical problem when clustering data using K-Means is determining the appropriate number of clusters to generate. X-Means uses Bayesian Information Criterion (BIC) to automatically determine the optimal number of clusters. Section 3 details our findings when clustering acini.

3. SUSAN G KOMEN TISSUE BANK ANALYSIS

Seven subjects from the Susan G. Komen Tissue Bank were examined and a total of 51 TDLUs and 1,325 acini were analyzed. TDLUs were manually cropped from the original image and then our automatic image analysis method was applied to the cropped area. To validate the accuracy of our system, our results were compared to the annotations of a pathologist rendered by visual assessment aided by an electronic ruler (microns).

The number of acini in each TDLU was visually assessed categorically. These five groupings are represented by the discretization function D and the number of acini x.

$$D(x)=\{\begin{array}{rr}\hfill 1\hfill & \hfill :0\le x\le 10\\ \hfill 2\hfill & \hfill :11\le x\le 20\\ \hfill 3\hfill & \hfill :21\le x\le 30\\ \hfill 4\hfill & \hfill :31\le x\le 50\\ \hfill 5\hfill & \hfill :x>50\end{array}$$

For each TDLU, our automatic analysis was considered to be accurate if our discrete mapping of the acini counts matched the visual assessment. Overall, we obtained 70.59% agreement with the visual evaluation. After analyzing the 29.41% errors, we found that most of the discrepancies were caused by acini that could be correctly characterized as one large acinus or two acini close together, and by stain artifacts.

Next, we applied X-Means using BIC to automatically determine the optimal number of acini groupings. We found there are three optimal groupings for the acini, where the centroids are detailed in Table 1. By examining the table, we can see three distinct types of acini determined statistically that make intuitive sense: the smaller acini are less elongated, but more round, whereas larger acini are more elongated and less round. These clusters of acini concisely show that as the area of the acini increases, elongation will increase and roundness will decrease.

Table 1.

X-Means and Bayesian Information Criterion were utilized to determine the optimal number of acini groupings. Examining the table we can see three distinct types of acini: the smaller acini are less elongated, but more round, whereas larger acini are more elongated and less round. These three clusters demonstrate that as the area of acini increases, elongation will increase, thus decreasing roundness.

Area	Elongation	Perimeter	Roundness	# of Acini in Cluster
1181.58	0.48	118.26	0.84	363 (28%)
1368.51	0.60	135.23	0.66	510 (38%)
2031.45	0.98	200.85	0.43	452 (34%)

Figure 2 contains three plots visualizing the acini clusters. The first plot is almost a perfect exponential decay of the elongation vs. the roundness of the acini. Because roundness is the inverse of elongation, this plot serves to validate the accuracy of our approach. The second plot displays the area of the acini vs. the roundness, where we can see that area has little effect on roundness. The third plot shows area vs. elongation. Similar to roundness, the area of the acini has little effect on the elongation, although there are some instances where larger acini are more elongated.

Figure 2.

Left: An almost perfect exponential decay of elongation vs. roundness is displayed. Since roundness is the inverse of elongation, this figure validates the accuracy of our approach. Middle: Area vs. the roundness is displayed. We can see that area has little effect on roundness. Right: Area vs. elongation is shown. Similar to roundness, the area of the acini has little effect on elongation.

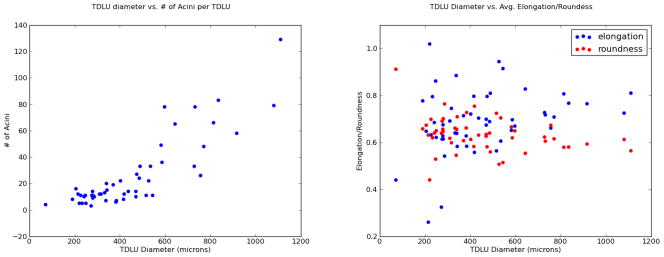
Finally, we examined the distribution of the number of acini per TDLU. The first plot in Figure 3 demonstrates, quite intuitively, that the larger the diameter of the TDLU, the more acini are present. However, the second plot shows that the average elongation and roundness of the acini are not significantly correlated with the diameter of the TDLU. The larger TDLUs still contain acini that are structurally similar to the acini in smaller TDLUs.

Figure 3.

Left: This plot intuitively shows that the larger the diameter of the TDLU, the more acini are present. Right: However, the average elongation and roundness of the acini have no correlation with the diameter of the TDLU. The larger TDLUs still contain acini that are structurally similar to the acini in smaller TDLUs.

4. BREAST STAMP PROJECT ANALYSIS

In order to demonstrate that our method is applicable to a wider range of breast tissue studies, we analyzed eight patient images from the BREAST Stamp Project. For each of the eight images we used our method detailed in Section 2 to count the total number of acini. We then calculated the mean, median, and maximum acini in each image. Table 2 compares the results from our method (“M”) to the results by the expert pathologist (“E”). As the table demonstrates, our method performs comparably with the expert annotations.

Table 2.

Comparison of expert annotations (“E”) versus our method (“M”). For each of the eight BREAST Stamp Project images we analyzed the total acini count and computed the mean, median, and maximum and applied the discretization function D. As this table demonstrates, our method performs comparably with the expert annotations.

Study ID	E. Mean	M. Mean	E. Median	M. Median	E. Max	M. Max
1	1.5	1.5	1.5	1.5	2	2
2	2.5	3.5	2.5	3.5	3	4
3	1.6	1.7	2	2	2	3
4	1.5	1.8	1.5	3	2	3
5	2.8	3	3	3	5	5
6	2	1.3	2	1	2	2
7	2	2.5	2	3	3	3
8	1.6	1.3	1.5	1	3	2

Finally, Table 3 details the correlation between our method results and the expert pathologist for the mean, median, and maximum acini counts. This table demonstrates that we were able to obtain over 70% correlation with the expert pathologist for each statistic.

Table 3.

In order to demonstrate that our method correlates with the expert pathologist, we computed the correlation between the mean, median, and maximum acini counts for the eight BREAST Stamp Project images. In each case we obtained over 70% correlation with the expert pathologist.

	Correlation
Mean	0.82
Median	0.7
Max	0.77

5. FUTURE WORK

In future work we wish to extend our clustering methods and determine if the clusters generated correlate with involution risk factors. In order to generate the clusters, we would use the bag-of-words model. X-means would be applied to the acini features, generating k clusters. Then, for each TDLU, we would assign each acinus in the TDLU to the closest centroid in the k clusters. The resulting histogram would detail the distribution of the acini in the TDLU. We expect to see that different bag-of-words acini distributions would correlate with involution risk factors, thus making it easier to detect and track risk factors over time.

6. CONCLUSION

In this paper we have presented a method to automatically quantify the morphology of the TDLUs within normal breast tissue H&E images. It has been suggested that the morphometric features of TDLUs in breast tissues are associated with breast cancer risk.^1–4 Using the methods detailed in this paper, the quantitative morphological measures can be extracted and then applied to studies of breast cancer and intermediate endpoints associated with breast cancer. Secondly, we have shown that it is possible to characterize and classify the distribution of acini by applying machine learning to the area, elongation, perimeter, and roundness of the acini. Our analysis has shown that according to Bayesian Information Criterion, there are optimally three distinct groupings of acini. Finally, we have compared the distribution of the number of acini per TDLU with the average elongation and roundness per TDLU. While the number of acini grow exponentially with diameter of the TDLU, the elongation and roundness were not correlated with diameter in this preliminary dataset.