Accuracy of gastrocnemius muscles forces in walking and running goats predicted by one-element and two-element Hill-type models

Abstract

Hill-type models are commonly used to estimate muscle forces during human and animal movement —yet the accuracy of the forces estimated during walking, running, and other tasks remains largely unknown. Further, most Hill-type models assume a single contractile element, despite evidence that faster and slower motor units, which have different activation-deactivation dynamics, may be independently or collectively excited. This study evaluated a novel, two-element Hill-type model with “differential” activation of fast and slow contractile elements. Model performance was assessed using a comprehensive data set (including measures of EMG intensity, fascicle length, and tendon force) collected from the gastrocnemius muscles of goats during locomotor experiments. Muscle forces predicted by the new two-element model were compared to the forces estimated using traditional one-element models and to the forces measured in vivo using tendon buckle transducers. Overall, the two-element model resulted in the best predictions of in vivo gastrocnemius force. The coefficient of determination, r², was up to 26.9% higher and the root mean square error, RMSE, was up to 37.4% lower for the two-element model than for the one-element models tested. All models captured salient features of the measured muscle force during walking, trotting, and galloping (r² = 0.26 to 0.51), and all exhibited some errors (RMSE = 9.63 to 32.2% of the maximum in vivo force). These comparisons provide important insight into the accuracy of Hill-type models. The results also show that incorporation of fast and slow contractile elements within muscle models can improve estimates of time-varying, whole muscle force during locomotor tasks.

Introduction

Muscle models that accurately reproduce time-varying muscle forces are crucial for evaluating motor performance and key to interpreting muscle-driven simulations of movement. Hill-type models, which estimate a muscle’s force based on length-tension and force-velocity properties (e.g., Zajac, 1989; Winters, 1990), are arguably one of the most widely-used tools in biomechanics — yet the accuracy of the forces predicted by Hill-type models during walking, running, and other motor tasks remains largely unknown. In this study, we examined the ability of several different Hill-type models to reproduce in vivo gastrocnemius forces measured in goats during locomotion.

Rigorous validation of Hill-type models requires experimental measures of fascicle lengths and muscle excitations, which are typically used to drive the models, as well as direct measures of muscle or tendon force. Most previous tests of muscle models have relied on in situ stimulation experiments in animals, where the neural excitation and fascicle strain values are not generally representative of in vivo dynamic behavior (e.g., Brown and Loeb, 1999, 2000). Only a few studies have assessed the performance of Hill-type models under more realistic conditions (Sandercock and Heckman, 1997; Perreault et al., 2003). Varying results in the errors in force prediction by muscle models, and the paucity of validation studies based on in vivo data, warrant further investigation. In particular, models must be tested during dynamic tasks that involve time-varying excitations, both to refine interpretation and to identify limitations that need to be addressed.

One limitation of traditional Hill-type models is their failure to account for different mechanical properties of the fiber types recruited. Muscles are comprised of different types of muscle fibers, broadly classified as slow to fast, that have different activation-deactivation rates, and force development. Most previous Hill-type models assume either that fiber type within the muscle is homogeneous (e.g., Zajac, 1989) or that orderly recruitment occurs (e.g. Umberger et al. 2003; van Soest and Bobbert, 1993). However, previous analyses of motor unit recruitment in rats (Hodson-Tole and Wakeling, 2009), humans (Wakeling 2004), and goats (Lee et al., 2013) have revealed that the recruitment patterns of slow and fast fibers can vary depending on the motor task. Recently, we showed that a Hill-type model could more accurately predict gastrocnemius forces in goats during in situ isometric contractions when the model incorporated both fast and slow contractile elements, and when the contractile elements were activated in a manner consistent with measured electromyographic (EMG) recordings (Wakeling et al. 2012). Some other muscle models have incorporated different fiber-type properties, but have also been limited to simulations of isometric contractions (Bol et al., 2011; Fuglevand et al., 1993). Therefore, a secondary aim of this study was to test — for in vivo locomotor tasks — whether a Hill-type model with fast and slow contractile elements (i.e., a “two-element model” or “differential” model) yields more accurate predictions of whole muscle force than traditional one-element models. We compared our recently developed, two-element model (Wakeling et al. 2012) to three commonly used Hill-type models that have been applied in a wide range of biomechanics applications. In situ and in vivo experiments were conducted on the lateral and medial gastrocnemius (LG and MG) muscles of goats, as these muscles are known to comprise both slow and fast fibers (Lee et al., 2013). These experiments yielded simultaneous recordings of fascicle length, excitation, and time-varying tendon force, providing a comprehensive and informative data set for testing the predictive accuracy of the different models. The models in this study relied on measured fascicle lengths, rather than on scaled fiber lengths derived from the muscle-tendon lengths (e.g., Zajac et al., 1989); this allowed us to evaluate modeling assumptions related to properties of the fiber types recruited, which was our main goal, while minimizing uncertainty in the models’ force-length properties, which also influence the predicted force.

Methods

Six African pygmy goats (Capra hircus L; 3 males, 3 females; age 21.0 ± 15.5 months, mass 25.85 ± 6.20 kg) were tested at Harvard University’s Concord Field Station. The experimental protocol involved four main steps over a three-day period: surgical implantation of transducers, in vivo testing, surgical implantation of nerve cuffs, and in situ testing. All experimental protocols are described elsewhere (Lee et al., 2011, Wakeling et al., 2012, Lee et al., 2013; also see supplementary materials) and are reviewed here in brief:

Experimental data collection

1. Goats were trained to walk, trot and gallop on a motorized treadmill, and they performed these gaits on level and inclined surfaces as part of a larger study. Our previous analysis showed that the level trials elicited the most pronounced differences in recruitment (Lee et al., 2013). Thus, the level trials were used in the current study to test the different muscle models.

2. The MG and LG were instrumented with fine-wire EMG electrodes to measure muscle excitation (Lee et al., 2011), sonomicrometry crystals to measure fascicle length (resolution = 0.3μm Lee et al., 2011), and “E”- shaped tendon buckle transducers on the Achilles tendon were used to measure tendon force (calibration yielded r² > 0.99, Biewener & Baudinette, 1995). In vivo lateral and medial tendon forces were estimated from the total in vivo tendon force, measured by the single tendon buckle on the tendon, using the ratio of the maximum forces measured from the in situ recordings of the lateral and medial gastrocnemius muscles from the two tendon buckles (see below). Tendon forces were normalized by the maximum force recorded during incline trotting, F_max, consistent with previous analyses (Lee et al., 2013).

3. In vivo recordings were made while goats walked, trotted, and galloped on the treadmill. Between 15 and 20 strides were recorded for each condition, and data were recorded at 5000 Hz (Lee et al., 2013). Sufficient rest was given between trials to ensure the goats could complete the experiments.

4. An additional force transducer was surgically attached on the medial portion of the Achilles tendon prior to the in situ experiments. In situ recordings were made to measure the muscles’ active and passive force-length relationships, using tetanic stimulation, for a range of ankle angles and muscle lengths. A series of different nerve stimulation protocols were used to elicit twitches from different motor units, enabling identification of the twitch profiles for slow and fast motor units (Lee et al., 2011).

Experimental data processing

• 5To extract information about motor unit recruitment that could be used to drive the muscle models, the major components of the EMG signal corresponding to signals from slow and fast motor units were identified using wavelet analysis (von Tscharner, 2000; Lee et al., 2011). Optimized wavelets were derived to identify recruitment patterns of slow and fast motor units (Lee et al., 2011; Wakeling, 2005; Hodson-Tole and Wakeling, 2008). The EMG signal was characterized by its total intensity and by the intensities at the low- and high- frequency bands, corresponding to signals from the whole muscle and from slower and faster motor units, respectively (Fig. 1). The final step in the intensity calculation was applying a Gauss filter to the intensity envelope. The filter width was set to have the same time resolution (75 ms) for all measures of intensity so that temporal-based comparisons could be made between the different models (see Supplementary Material for more details).
• 6
  The EMG intensities were used as excitations for a series of coupled first-order differential equations, constituting transfer functions (Eq. 1), that enabled estimation of the active state of each muscle. Transfer functions were derived for the whole muscle as well as for the slower and faster motor units (Figures 1 and 2; Lee et al., 2011); in particular, constants τ_act1,2,3 and β_1,2,3 were identified for the different motor units (Table 1) and were determined from in situ data pooled from the six goats. Details are described elsewhere (see supplementary materials, Lee et al., 2011).

  $$\begin{array}{l}\frac{d}{\mathit{dt}}(a_1)+\left[\frac{1}{{\tau }_{\mathit{act}1}}\left({\beta }_1+[1-{\beta }_1]\mathit{EMG}(t-t_{\mathit{off}})\right)\right]a_1(t)=\left(\frac{1}{{\tau }_{\mathit{act}1}}\right)\mathit{EMG}(t-t_{\mathit{off}})\\ \frac{d}{\mathit{dt}}(a_2)+\left[\frac{1}{{\tau }_{\mathit{act}2}}({\beta }_2+[1-{\beta }_2]a_1(t))\right]a_2(t)=\left(\frac{1}{{\tau }_{\mathit{act}2}}\right)a_1(t)\\ \frac{d}{\mathit{dt}}(a_3)+\left[\frac{1}{{\tau }_{\mathit{act}3}}({\beta }_3+[1-{\beta }_3]a_2(t))\right]a_3(t)=\left(\frac{1}{{\tau }_{\mathit{act}3}}\right)a_2(t)\end{array}$$ (Eq.1)

Figure 1.

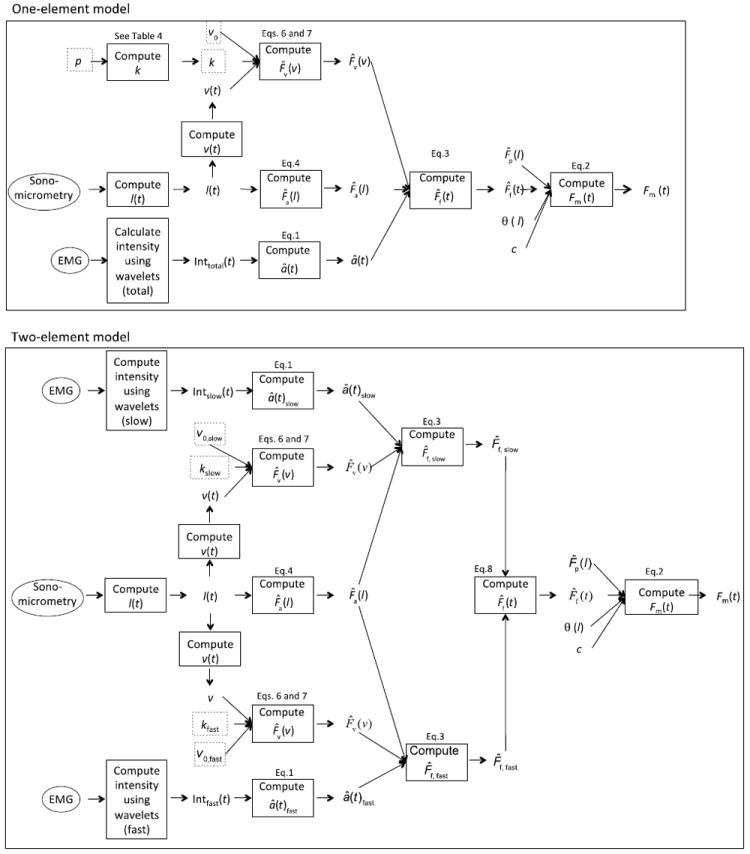
Schematic representations of the one-element and two-element Hill-type models. Parameters outlined in dotted grey were taken from the literature; all other parameters were based on measured data. Contractile elements in the two-element model are formulated like the contractile element in the one-element model except that the activation and key parameters are specific to either slow or fast fibers. The active forces generated by the slow and fast elements are then summed to estimate the total active force. Refer to Table 3 for definitions of all symbols.

Figure 2.

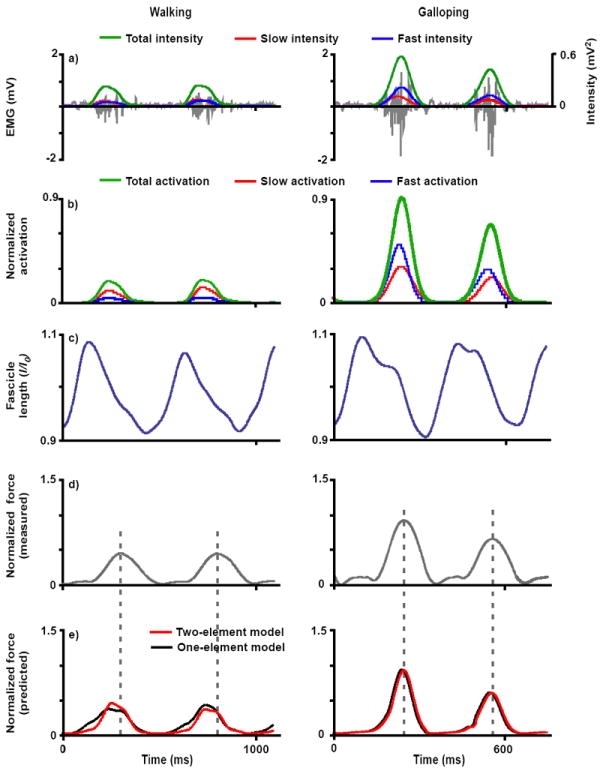
Representative inputs and outputs of the one-element and two-element models for the goat LG muscle during walking and galloping: a) EMG (grey) and total (green), slow (red), and fast (blue) EMG intensity, b) total (green), slow (red), and fast (blue) activation normalized to maximum in vivo activation, c) fascicle length normalized to optimal resting length, d) measured tendon force normalized to maximum in vivo force, and e) muscle forces normalized to maximum in vivo force as predicted by the one-element model (black) and two-element model (red). These are representative trials from one goat. The dotted grey line indicates when the peak force occurs for each step.

Table 1.

Constants for the transfer functions used to determine active state from EMG intensity (Eq. 1; see also Lee et al. 2011).

Constants	Total Intensity	Slow Motor Unit	Fast Motor Unit
τ1	6.37	34.06	18.14
β1	0.59	0.73	0.90
τ2	38.05	36.27	20.91
β2	0.76	0.74	0.99
τ3	15.89	37.82	20.75
β3	0.71	0.92	0.98
toff	2.0	6.5	1.5

Activation levels of the slower and faster motor units were scaled in amplitude such that summation of the two levels equaled the activation level of the whole muscle (i.e., the total activation, Figure 2). This simplified comparison of the one-element and two-element models.

Muscle Models

Three one-element muscle models and a novel two-element model (Wakeling et al. 2012) were used to estimate time-varying forces produced by the MG and LG during the different locomotor conditions (Figure 1). The three one-element models generated similar predictions of muscle force so only one is presented here; the other one-element models are described in the supplementary material. The output of each model, the total muscle force F_m, was estimated by:

$$F_m=c\left[{\widehat{F}}_f+{\widehat{F}}_p(l)\right]\mathit{cos\theta }$$ (Eq. 2)

where F̂_f is the active component of the muscle fiber force and F̂_p is the passive component of the force as a function of fiber length (l). Constant c and the pennation angle, θ, scaled the fiber force to the whole muscle force. In particular, constant c scaled the predicted force from its normalized value to the measured force for each goat. Thus, c reflects the maximum isometric force generated by the muscle. The pennation angle was calculated at each time step as a function of fiber length (l) from the resting pennation angle and the fascicle length, assuming that the thickness of the muscle remained constant (Zajac, 1989; Millard and Delp, 2012; van den Bogert et al., 2011; see Table 2 for mean and standard deviation values of optimal and resting fascicle length and pennation angle). The inputs to each model included the time-varying fascicle lengths, which were also used to calculate fiber contractile velocity and pennation angle, and the activation states (Figures 1 and 2). The activation states were normalized to the maximum activation during incline trotting, consistent with our procedure for normalizing the measured tendon forces. Other parameters used in the models (Figure 1 and Table 3) were either derived from experimental measurements or taken from the literature, and were not optimized to “fit” the in vivo forces.

Table 2.

Mean and standard deviation of muscle architectural parameters

Muscle	Resting fascicle length (mm)	Optimal fascicle length (mm)	Resting pennation angle (degree)
Lateral gastrocnemius	12.6 (1.5)	15.9 (4.2)	21.1 (4.5)
Medial gastrocnemius	13.4 (1.9)	17.0 (3.4)	24.3 (2.2)

Table 3.

Parameters used in the muscle models.

Parameter	Definition	Source
â(t)	Normalized, activation state of fibers	Derived from measured EMG
c	Scalar to calculate actual from normalized force	Measured
Fm	Muscle force	Calculated
Fmax	Maximum in vivo force during incline trotting	Measured
F̄p (l)	Normalized, passive force-length relation	Measured (see Eq. 5)
F̄a (l)	Normalized, active force-length relation	Measured (see Eq. 4)
F̄ν (ν)	Normalized, force-velocity relation	Literature (see Eq. 6 and 7)
k	Curvature of force-velocity relation	Literature (0.29 and 0.18 for fast and slow fibers; Wakeling et al., 2012)
l	Fascicle length	Measured
ν	Fascicle velocity	Derived from l
ν0	Maximum shortening velocity	Estimated (2.74 and 3.59 lopts-1)
		Literature (5 and 10 lopts-1)
θ	Pennation angle	Measured
p	Fractional area of the fast fibers	Literature (0.5 and 0.75)

For the one-element models, the active component of the muscle fiber force was given by:

$${\widehat{F}}_f=\widehat{a}(t){\widehat{F}}_a(l){\widehat{F}}_{\nu }(\nu )$$ (Eq. 3)

where â(t) is the time-varying activation level (Lee et al., 2011) and F̂_a(l) is the active force-length relationship normalized to maximum of 1. The active (Eq. 4) and passive (Eq. 5) force-length curves were based on in situ measurements, taken during supramaximal stimulation, at a range of fascicle lengths. These equations were derived by fitting the in situ data pooled from all goats.

$${\widehat{F}}_a(l)=\frac{((-878.25{(l\ast 1.253)}^2+2200.4(l\ast 1.254)-1192)}{186.24}$$ (Eq.4)

$${\widehat{F}}_p(l)=\frac{e^{-1.3+3.8\ast (l\ast 1.253)}}{186.24}$$ (Eq.5)

The force-velocity relationship, F̂_v(ν), was given by:

$${\widehat{F}}_{\nu }(\nu )=\frac{\left(1-\frac{\nu }{{\nu }_o}\right)}{\left(1+\frac{\nu }{{\nu }_{o}k}\right)}\mathit{for\; \nu }\le 0$$ (Eq. 6)

$${\widehat{F}}_{\nu }(\nu )=1.5-0.5\frac{\left(1+\frac{\nu }{{\nu }_0}\right)}{\left(1-\frac{7.56\nu }{{\nu }_{o}k}\right)}\mathit{for\; \nu }>0$$ (Eq. 7)

where ν is the fiber contractile velocity, ν₀ is the maximum intrinsic speed, and constant k characterizes the curvature of the force-velocity curve. Note that shortening velocity is defined as negative in these equations, while lengthening is defined as positive. ν₀ is presented as a positive value, but it is implemented as a negative value in Eqs. 6 and 7. Different values of ν₀ and k were assigned for the different models, based on assumptions about motor unit recruitment, as described in the following sections.

The one-element model presented here presumed that active muscles display intrinsic properties of progressively faster fiber types as activation levels increase. Thus, at initial low activation levels, the active fibers were assigned a maximum unloaded shortening velocity corresponding to slow fibers (Table 4). As activation levels increased, the maximum shortening velocity also increased. This model is based on classical studies of orderly recruitment during steady stretch reflexes (Hennemen, 1974) and is consistent with previous muscle modeling approaches (e.g. Umberger et al., 2003; Van Soest et al., 1993). Two sets of values representing the maximum unloaded shortening velocities of the slower and faster fibers were tested; this is because previous studies have shown that muscle models are generally sensitive to this parameter (Wakeling et al., 2012). The values we used were (a) 2.74 and 3.59 l_opt s^-1 for the slower and faster motor units, respectively, estimated from in situ measures of activation rates scaled by literature values across a range of species, and (b) 5 and 10 l_opts^-1 for the slow and fast fibers, respectively, based on previous models of larger species (Wakeling et al., 2012). Constant k, which characterizes the curvature of the force-velocity curve, was assigned an intermediate value within the ranges of the slow and fast fibers; we used values of 0.18 and 0.29 for slow and fast fibers, respectively (Wakeling et al., 2012). For the one-element model, curvature k was assumed to be the same for all the fibers within the muscle (Table 4). Since p, the fractional area of the fast fibers, remains unknown for goats, two different values were tested. We used values of 0.75 and 0.5 since our initial immunohistochemical testing of the LG and MG in goats has shown that the LG contains a proportion of fast fibers within this range (unpublished observations, Carr, Miara, Lee, Wakeling, and Biewener).

Table 4.

Force-velocity properties and activation state for the one- and two-element models.

Model	Force-velocity curvature, k	Maximum unloaded shortening velocity, ν0	Activation state
One-element	kslow + (kfast - kslow)p	νo,slow + (νo,fast - νo,slow) â(t)	â(t)
Two-element	kslow	νo,slow	âslow (t)
	kfast	νo,fast	âfast (t)

The two-element differential recruitment model (Figure 1) incorporated independently-activated slow and fast contractile elements in parallel (Wakeling et al., 2012). The EMG intensities at the low- and high- frequency bands were used with the transfer functions (Eq. 1 and Table 1) to estimate the activation levels for the slow and fast elements, â_slow (t) and â_fast (t) respectively. The total active force from the fibers, F̂_f, was given by:

$${\widehat{F}}_f={\widehat{F}}_{f,\mathit{slow}}+{\widehat{F}}_{f,\mathit{fast}}$$ (Eq.8)

where F̂_f,slow and F̂_{f, fast} are the normalized forces for slow and fast fibers, respectively, as determined from Equation 3 using fiber-specific values of â(t), ν₀, and k (Tables 3 and 4).

Comparisons of predicted and measured forces

Simulations were run for the different models, goats, muscles, and gait conditions, varying the values of p and ν₀. Differences between the predicted force and the measured force were characterized by the coefficient of determination, r², and by the root mean square error, RMSE. These measures were useful for quantitatively comparing the accuracy of the time-varying forces predicted by each model. A general linear model ANOVA was conducted to determine if differences in the r² and RMSE values existed between the different models, muscles, gait conditions, fiber-type proportions, and ν₀ values. Differences were considered significant at the α = 0.05 level. Tukey post-hoc analyses were conducted to identify significant differences between levels within a factor when indicated.

Results

The two-element model and all of the one-element models that we tested generally captured the detailed changes in the measured gastrocnemius forces during walking, trotting, and galloping. However, all models exhibited some errors that included inaccurate estimates of the peak force and insufficient rates of force rise and decline (e.g., Figure 3). Across all models, the coefficient of determination values ranged from 0.32 to 0.51 for the LG and from 0.26 to 0.48 for the MG (Figure 4). The RMSE, as a percentage of the maximum in vivo force measured during incline trotting, ranged from 17.0 % to 32.2 % for the LG and from 9.63 % to 15.5 % for the MG (Figure 4). Importantly, the different gait conditions tested the models over a physiological range of force amplitudes and contraction speeds.

Figure 3.

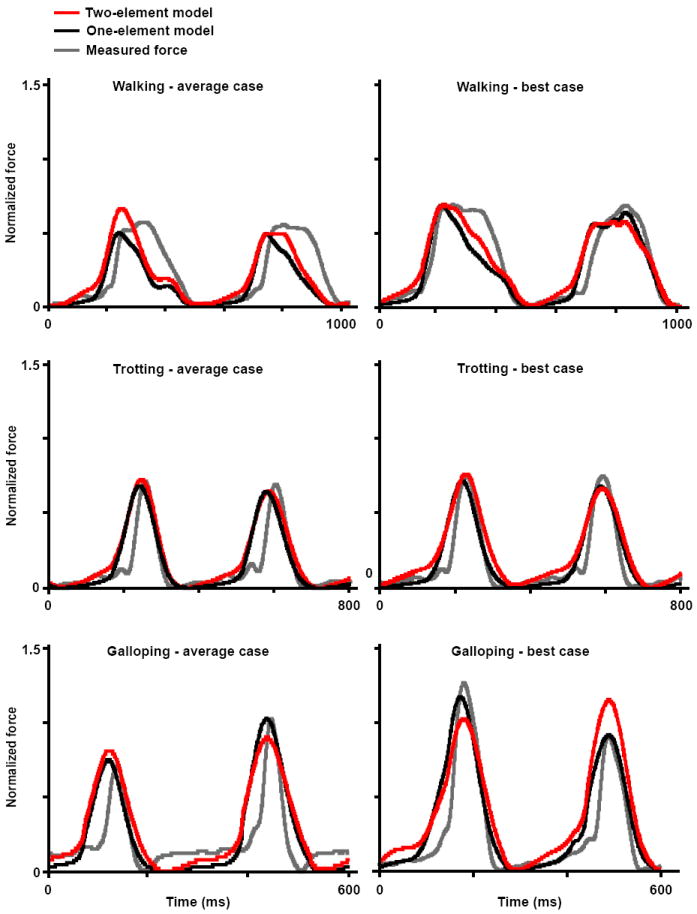
Force profiles of the LG muscle during walking, trotting, and galloping. Measured forces (grey) and predicted forces from the one-element model (black) and two-element model (red) are shown for an average case (i.e., average r² and RMSE values) and for a “best” case. Models were assigned ν_o values of 5 and 10 l_opts^-1 for the slow and fast fibers, respectively, with a fiber-type proportion of 75% fast fibers. These are representative trials.

Figure 4.

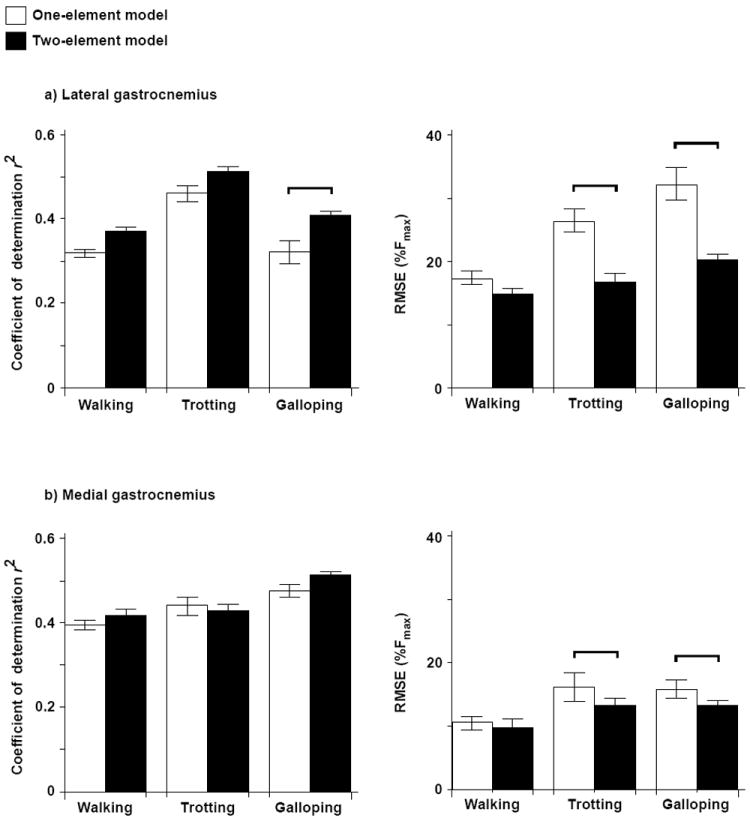
Comparison of r² and RSME values for the one- and two-element models as determined for the different gait conditions and for the a) LG and b) MG muscles. Bars show the mean ± SEM pooled from all the goats. The two-element model was assigned ν_o values of 5 and 10 l_opts^-1 for the slow and fast fibers, respectively, with a fiber-type proportion of 75% fast fibers. Post hoc Tukey tests were conducted to identify significant differences between the models for each gait, and these differences are denoted by the horizontal bars.

The two-element muscle model generally performed better than the one-element models. In particular, the differential model predicted time-varying LG forces with significantly statistically higher r² (better correlation) and lower RMSE (less error) than the one-element model described here, both during galloping (r², p = 0.03; RMSE, p = 0.001; Figures 2-4) and during trotting (RMSE, p < 0.001). The differential model also predicted time-varying MG forces with significantly lower RMSE than the one-element model during trotting and galloping (p = 0.001 and p = 0.01, Figure 4).

Results of the ANOVA revealed that the accuracy of the predicted in vivo force was dependent on muscle, gait, and the choice of ν₀ (Figs. 2 to 5). The models generally predicted force more accurately for the MG than for the LG, with higher r² and lower RMSE for walking and galloping (p < 0.001). Adjusting the fiber-type proportion (50 % fast versus 75% fast) did not appreciably alter forces predicted by the one-element model. However, adjusting ν₀ significantly influenced the accuracy of the predicted LG forces (r², p < 0.001, Fig. 5). When ν₀ was assigned the faster values of 5 and 10 l_opt s^-1, the models predicted in vivo force better (higher r²) than when ν₀ was assigned the slower values of 2.74 l_opt s^-1 and 3.59 l_opt s^-1. The performance of the models also differed significantly across the gait conditions (r², p < 0.001; RMSE, p < 0.001; Figures 3 to 4).

Figure 5.

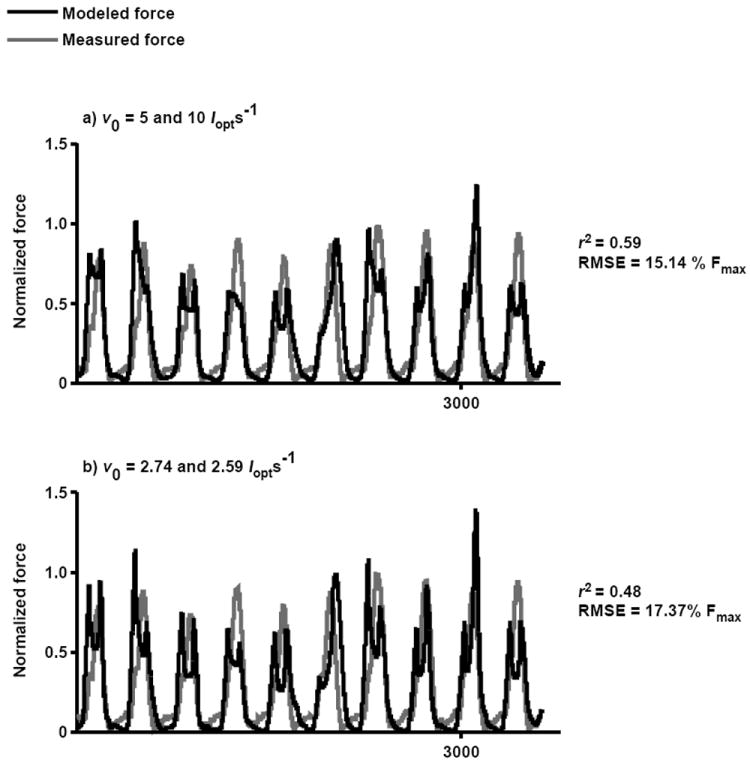
Sensitivity of predicted forces to maximum shortening velocity. The measured force is compared to the LG force predicted using the differential model assuming maximum shortening velocities of the slow and fast fibers to be: a) 5 and 10 l_opts^-1 based on values from the literature and b) 2.74 and 3.59 l_opts^-1 based on in situ measurements. The model was assigned a fiber-type proportion of 75% fast fibers. This is a representative trial with average r² and RMSE values from one goat during trotting.

Discussion

This study examined the accuracy with which a novel, two-element Hill-type model and several commonly-used one-element models predict time-varying forces generated by goat gastrocnemius muscles during locomotion (see supplementary materials for detailed assessments of the other one-element models). Our comparisons of the predicted and measured forces – based on a comprehensive and unique data set from in vivo and in situ experiments – provide evidence that Hill-type models can reproduce key features of whole muscle force. However, across locomotor conditions, the models generated errors ranging from 9.63 % to 32.2 % (RMSE as a percentage of the maximum in vivo force) when averaged across goats and trials. These errors included inaccuracies in magnitude and timing. Our two-element differential model, in which slow and fast contractile elements are activated independently, generally predicted muscle forces more accurately than the one-element models tested, particularly at the faster gaits (Figures 3 and 4). The r² increased from 0.37 to 0.43 (mean across gaits) for the LG, and the RMSE decreased from 25.3 % to 17.2 % (percent of maximum measured force) for the LG and from 13.2 % to 11.5 % for the MG.

Activation dynamics

The main difference, and perhaps the most informative difference, between the two-element differential model and the three one-element models tested was our calculation of the active state used to drive the contractile element(s). Specifically, the differential model was driven by the active states of independent slow and fast fibers acting in parallel (Figures 1 and 2). While differences in the muscle forces predicted by the one- and two-element models during goat locomotion were not dramatic, we believe they are large enough to be relevant. Experimental data from rats (Hodson-Tole and Wakeling, 2009), humans (Wakeling 2004), and goats (Lee et al., 2013) have shown that the different motor unit types can be recruited in a task-specific fashion varying, for example, with changes in fascicle strain rates that accompany changes in locomotor speed. Thus, the two-element model may be particularly relevant when estimating muscle forces during rapid or explosive movements, when accounting for the recruitment patterns and properties of fast motor units is likely to yield substantial improvements. The two-element model is also likely to be helpful when evaluating muscle force generation in individuals with neuromuscular disorders, who frequently exhibit altered or impaired motor unit recruitment. Our two-element model characterizes the sequence in which these motor unit populations are activated (Coggshall and Bekey, 1970) and, as a result, offers the potential to better predict force development across different motor tasks.

Intrinsic properties

Previous in situ studies of Hill-type models have demonstrated that errors in predicted forces are often related to the force-velocity properties assumed (Perreault et al., 2003; Shue et al., 1995). In this in vivo study, we also observed that force-velocity properties influenced the accuracy of the muscle forces predicted (Table 4). Values chosen for the maximum shortening velocity, ν₀, and the proportion of fast fibers, p, dictated the force-velocity properties of the different models (Eqs. 6-7). Assigning p different values between 50% and 75% did not substantially influence the performance of the models, however, assigning ν₀ to have slower (2.74 and 3.59 l_opt s^-1) or faster (5 and 10 l_opt s^-1) values did significantly affect force prediction. This suggests that efforts to more accurately characterize a muscle’s force-velocity properties, by experimentation or optimization, could significantly improve the accuracy of Hill-type models.

The MG and LG muscles are known to vary in architecture, fiber composition, and intrinsic motor unit properties (Wakeling et al., 2011, Maganaris et al., 1998), and these differences between the muscles may explain why the models predicted force more accurately for the MG than for the LG. In both man and goats, it is thought that the MG and LG have different activation-deactivation dynamics due to different motor unit twitch profiles (Lee et al., 2011; Vandervoot and McComas, 1983).

Pennation angle is sometimes assumed to be constant in muscle models. However, pennation angle has been shown to change up to 28° from rest to maximum voluntary contraction within human gastrocnemius muscles (Maganaris et al., 1998). By allowing pennation angle to vary as a function of fascicle length in our models, we observed that the timing of the predicted forces was notably improved.

Limitations

One of the aims of this study was to examine the ability of current and commonly used Hill-type models to accurately reproduce muscle forces measured in vivo. Despite the improvements achieved by incorporating slow and fast contractile elements into Hill-type models, all of models evaluated in this study have limitations that may have contributed to the errors in magnitude and timing. These limitations include, for example, the assumption that activation, force-length, and force-velocity properties are independent and the failure of these models to account for history-dependent effects (see supplementary materials for detailed discussion). In many of the simulations, we observed errors in relative phasing between the predicted and measured forces in which the predicted force developed earlier than the in vivo force. Factors contributing to these errors include the time resolution of the Gauss filter applied in the wavelet analysis and the exclusion of a tendon in the models (see supplementary materials for detailed discussion).

Validation

We previously evaluated the accuracy of MG and LG forces predicted by our two-element model during in situ experiments (Wakeling et al., 2012). The comparisons with in situ forces yielded higher r² values (0.8-0.95) than the comparisons with in vivo forces reported here. However, comparisons of the differences in r² and RMSE values between the one-element and two element models reveal that the two-element model predicted force more accurately than the one-element model under in situ and in vivo conditions (Figures 3-4). Under in situ and in vivo conditions, the r² value was up to 9.7% and 37.4% higher, respectively, for the two-element model than for the one-element models tested (RMSE was 32.2% lower; see supplementary materials for more details).

Very few studies have validated Hill-type models under functionally relevant conditions. Many studies have evaluated models based on in situ data, but these tests have generally been performed under laboratory conditions where fascicle lengths and activations are not typical of those observed in vivo (Perreault et al., 2003; van Ingen Schenau et al., 1998; Sandercock and Heckman, 1997; see supplementary materials for more detailed discussion). A strength of the current study is that inputs driving the models, along with most parameters, were based on experimental measures from the same set of muscles from which force was measured in vivo. Thus, the errors reported here for in vivo locomotor tasks are especially informative – revealing the strengths and weaknesses of Hill-type models under physiologically relevant conditions.