Shared Neural Markers of Decision Confidence and Error Detection

Abstract

Empirical evidence indicates that people can provide accurate evaluations of their own thoughts and actions by means of both error detection and confidence judgments. This study investigates the foundations of these metacognitive abilities, specifically focusing on the relationship between confidence and error judgments in human perceptual decision making. Electroencephalography studies have identified the error positivity (Pe)—an event-related component observed following incorrect choices—as a robust neural index of participants' awareness of their errors in simple decision tasks. Here we assessed whether the Pe also varies in a graded way with participants' subjective ratings of decision confidence, as expressed on a 6-point scale after each trial of a dot count perceptual decision task. We observed clear, graded modulation of the Pe by confidence, with monotonic reduction in Pe amplitude associated with increasing confidence in the preceding choice. This effect was independent of objective accuracy. Multivariate decoding analyses indicated that neural markers of error detection were predictive of varying levels of confidence in correct decisions, including subtle shifts in high-confidence trials. These results suggest that shared mechanisms underlie two forms of metacognitive evaluation that are often treated separately, with consequent implications for current theories of their neurocognitive basis.

Introduction

Human observers are capable of finely calibrated evaluations of their performance. In perceptual decision tasks, for example, participants reliably detect their errors (Rabbitt et al., 1978) and report graded judgments of confidence that correlate closely with objective performance (Fleming et al., 2012). There is growing interest in the neurocomputational basis of these metacognitive evaluations (Fleming and Frith, 2014), fueled by recognition that they are crucial to the effective regulation of behavior (Fernandez-Duque et al., 2000), that they support optimal group decision making (Bahrami et al., 2010), and that their nature may place crucial constraints on models of underlying decision processes (Zylberberg et al., 2012). Here we investigate the relationship between two key metacognitive evaluations—error detection and confidence judgments—that have separately been studied in detail but that are rarely compared directly.

Similar methodological approaches have been used in prior work on errors and confidence: the participant makes a first-order perceptual decision and is then asked to evaluate this just-made choice (either “how confident are you that you were correct?” or “did you make an error?”). Despite this similarity in approach, there is little compatibility between current theories of confidence and error detection (Yeung and Summerfield, 2012). For example, popular models of confidence, such as the balance-of-evidence hypothesis (Vickers and Packer, 1982), explain graded confidence judgments but not why participants sometimes state with certainty that an earlier response was incorrect. Conversely, many theories propose error detection to be all or nothing (Falkenstein et al., 1991; Gehring et al., 1993) and therefore struggle to explain graded judgments of confidence.

Empirical findings are similarly discrepant. For example, Scheffers and Coles (2000) found that error-related electroencephalography (EEG) activity varies in a graded way with subjective confidence, implying that confidence and error detection are two sides of the same coin. However, Charles et al. (2013) recently observed dissociations between graded confidence and binary error judgments. Whereas subjective confidence ratings were predictive of objective performance even when stimuli remained subliminal due to visual masking, error-related EEG activity was evident only on conscious trials.

The present study tested the hypothesis that error detection and confidence are fundamentally related, using multivariate EEG classification to assess whether they share a neural basis. In contrast to prior work focusing on the error-related negativity (ERN), a frontocentral component observed immediately following errors, we focus on the subsequent parietal focused error positivity (Pe) because of its established link to subjective error awareness (Overbeek et al., 2005; Steinhauser and Yeung, 2010). Our core rationale is that if error detection and confidence judgments share underlying mechanisms, then well characterized neural correlates of error awareness should be predictive of participants' decision confidence on a trial-by-trial basis. Specifically, we assessed whether a multivariate classifier trained to distinguish correct versus error trials generalizes to predict subtle variations in correct-trial confidence.

Materials and Methods

Participants.

Sixteen right-handed participants (8 female), 21–30 years old, all with normal or corrected-to-normal vision, gave informed consent and were paid for participation. All procedures were approved by the local ethics committee.

Task and procedure.

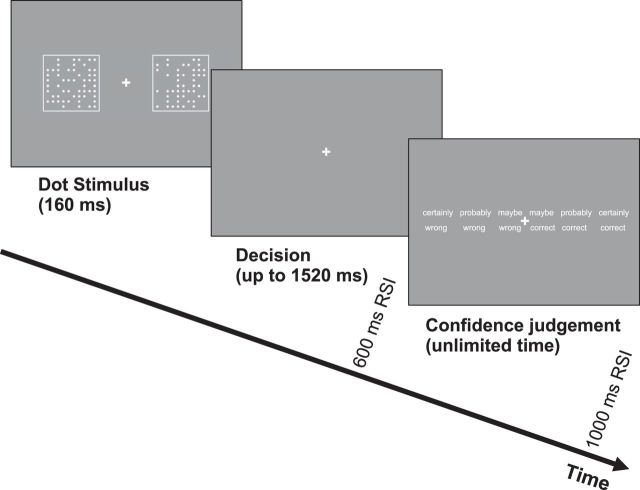
The experiment comprised a series of trials on which participants first performed a perceptual decision task under time pressure, then rated their subjective confidence in this decision (Fig. 1). The perceptual task required participants to judge which of two briefly flashed (160 ms) fields contained more dots by pressing a left-hand or right-hand button. One field contained 45 dots arrayed in a 10-by-10 matrix; the other one contained 55 dots. Within this constraint of a 10-dot difference between the two fields, the displays were randomly generated anew for each trial and each subject. The difficulty level was set through the piloting of the task, aiming for ∼15% errors. There was a 1520 ms deadline for this decision, and participants were encouraged verbally and through written feedback to respond quickly, with no explicit incentives. Speed was stressed so that participants made sufficient numbers of errors to permit planned contrasts of neural activity on correct versus error trials. After participants' responses, the screen cleared for 600 ms, then a 6-point confidence scale appeared with values of “certainly wrong,” “probably wrong,” “maybe wrong,” “maybe correct,” “probably correct,” and “certainly correct.” Our hypothesis is that this scale maps onto a continuum of metacognitive evaluation that encompasses both error detection and correct-trial confidence, rather than a two-dimensional space in which error and confidence judgments are at least partly independent (akin to separate coding of valence and salience in reinforcement learning; Matsumoto and Hikosaka, 2009). Participants had unlimited time to indicate their confidence by pressing one of six keys. The screen then cleared for a 1 s intertrial interval.

Figure 1.

Summary of the task procedure. Participants first pressed a key according to the field containing more dots, then rated their confidence in their decision on a 6-point scale. RSI, Response–stimulus interval.

Participants completed 18 experimental blocks of 48 trials in the main experiment. After each block, participants received feedback indicating their mean correct reaction time and error rate in the block. Before experimental blocks, participants first completed two blocks, also 48 trials long, to practice the perceptual task and confidence rating scale, respectively. Participants were encouraged to use the entire 6-point confidence scale.

Stimuli were presented on a 20 inch CRT (Trinitron, Dell) monitor with a 75 Hz refresh rate using the MATLAB toolbox Psychtoolbox3. Stimuli were 4.7 × 12.3 cm large, resulting in a visual angle of 10.0° × 3.8° when viewed from ∼70 cm. Responses were made on a Cedrus RB-830 response pad. Eight participants saw the confidence scale ranging from “certainly wrong” on the left to “certainly correct” on the right; eight saw the reverse orientation.

EEG recording.

Participants sat in a dimly lit, electrically shielded room. EEG data were recorded using the following Ag-AgCl electrodes in a fabric cap (QuikCap, Neuroscan) with 32 channels: FP1, FPz, FP2, F7, F3, Fz, F4, F8, FT7, FC3, FCz, FC4, FT8, T7, C3, Cz, C4, T8, TP7, CP3, CPz, CP4, TP8, P7, P3, Pz, P4, P8, POz, O1, Oz, O2, as well as the left mastoid, all referenced to the right mastoid on-line and re-referenced to linked mastoids off-line. We measured vertical and horizontal electro-oculogram from above and below the left eye and the outer canthi of the two eyes. Electrode impedances were kept at <50 kΩ. The data were continuously recorded using SynAmps2 amplifiers (Neuroscan), sampled at 1000 Hz and bandpass filtered at 0.1–200 Hz, with gain of 2816 and 29.8 nV resolution.

Data analysis.

Behavioral data analysis focused on the degree to which subjective confidence ratings were predictive of objective accuracy (i.e., calibration). These ratings were treated as varying continuously on a 6-point scale, with 1 reflecting the least confident response (“certainly wrong”) and 6 reflecting the most confident response (“certainly correct”).

EEG data were preprocessed using SCAN software (version 4.4, Neuroscan). Ocular artifacts were corrected using a regression-based approach. Response-locked epochs were extracted from the continuous data, baseline corrected to −100 to 0 ms preresponse. Trials were rejected for artifacts if the signal exceeded −100 to 100 μV in the electrodes Fz, FCz, Cz, CPz, and Pz. The data were then low-pass filtered offline at 12 Hz (with essentially identical results using higher filter cutoffs).

EEG analysis focused on the 600 ms interval between participants' perceptual decisions and subsequent appearance of the confidence scale. Errors in speeded decision tasks are associated with characteristic event-related brain potentials, as follows: a frontocentral negativity (i.e., ERN) peaking within 100 ms of incorrect responses, followed by a more extended centroparietal positivity (i.e., Pe; Falkenstein et al., 1991). Our analyses focused on the Pe, which has previously been shown to vary robustly with participants' self-reported awareness of their errors (Nieuwenhuis et al., 2001; Overbeek et al., 2005). There is no standard method for calculating Pe amplitude. We adopted parameters from our prior work (Steinhauser and Yeung, 2010), which proved appropriate to the morphology of the waveforms observed. Specifically, Pe amplitude was calculated as the difference between error and correct-trial waveforms in an interval of 250 to 350 ms postresponse. We also contrasted the response-locked Pe with the stimulus-locked P3 component, which has previously been reported to vary with subjective confidence (Hillyard et al., 1971). We quantified the P3 as the average voltage in a window from 350 to 500 ms poststimulus.

Of critical interest was the relationship between the Pe and participants' confidence judgments. We predicted that variation in the error-related Pe, as measured in the period after participants' responses but before their confidence ratings, would be predictive of fine-grained changes in confidence—consistent with the hypothesis that error detection and confidence lie on a single continuum. To quantify Pe amplitude robustly on single trials, we trained a classifier based on spatial linear integration to distinguish between objectively correct and incorrect responses, using a subset of the data from each participant (a matched-size sample of correct and incorrect responses). This method has been described in detail previously (Parra et al., 2002), including in its application to quantifying error-related EEG activity (Steinhauser and Yeung, 2010). In brief, the method identifies the spatial event-related potential (ERP) component (i.e., topography) that maximally discriminates between two conditions of interest (e.g., correct and error trials). Often, as here, the method effectively isolates the topography of the dominant ERP component at a given latency. The identified classifying topography can then be used to provide a robust estimate of component amplitude on single trials: improvement in signal-to-noise ratio is achieved in single trials by (weighted) combination of data across electrodes, much as signal-to-noise ratio is improved in conventional ERP analyses by averaging across trials.

Previous research has shown that this approach can robustly index single-trial Pe amplitude to distinguish objectively correct and incorrect responses (Steinhauser and Yeung, 2010). The novel question addressed here was whether a classifier trained in this way would similarly predict variations in confidence on a single-trial level. Specifically, we assessed whether a classifier trained to discriminate errors versus a matched subset of correct trials would be predictive of varying levels of confidence on the remaining set of untrained correct responses. If the classifier generalizes in this way—in particular, to predict subtle variation in correct-trial confidence—this would provide evidence for shared neural correlates of error detection (as studied extensively in past research on the Pe) and subjective confidence (as assessed here). Such evidence would run counter to the suggestion that error detection and confidence judgments are separate dimensions of metacognitive evaluation. For completeness, we ran analyses in which a subset of untrained error trials was also included in the test set. The results were essentially identical to those reported below; however, variation in Pe amplitude here could reflect changing proportions of correct versus error trials across conditions of interest in the test set, whereas our critical question is whether Pe amplitude distinguishes effectively among trials that are objectively correct and judged as such by participants.

Results

Behavioral data

Participants made perceptual decisions with a mean reaction time of 427 ms (SE = 19 ms) and a mean error rate of 17.5% (SE = 1.7%). They were more confident (on the 6-point scale) for trials with correct responses (5.0) than for error trials (2.7; t₍₁₅₎ = 14.4, p < 0.01). Accuracy varied monotonically as a function of subjectively rated confidence with high calibration (Fig. 2). Participants made errors on 97.1% of trials judged “certainly wrong”, compared with an error rate of 1.4% on trials judged “certainly correct”. Error rates differed significantly over levels of confidence (F_(5,75) = 208.8, p < 0.01), with a reliable linear within-subject contrast (F_(1,15) = 1351.9, p < 0.01).

Figure 2.

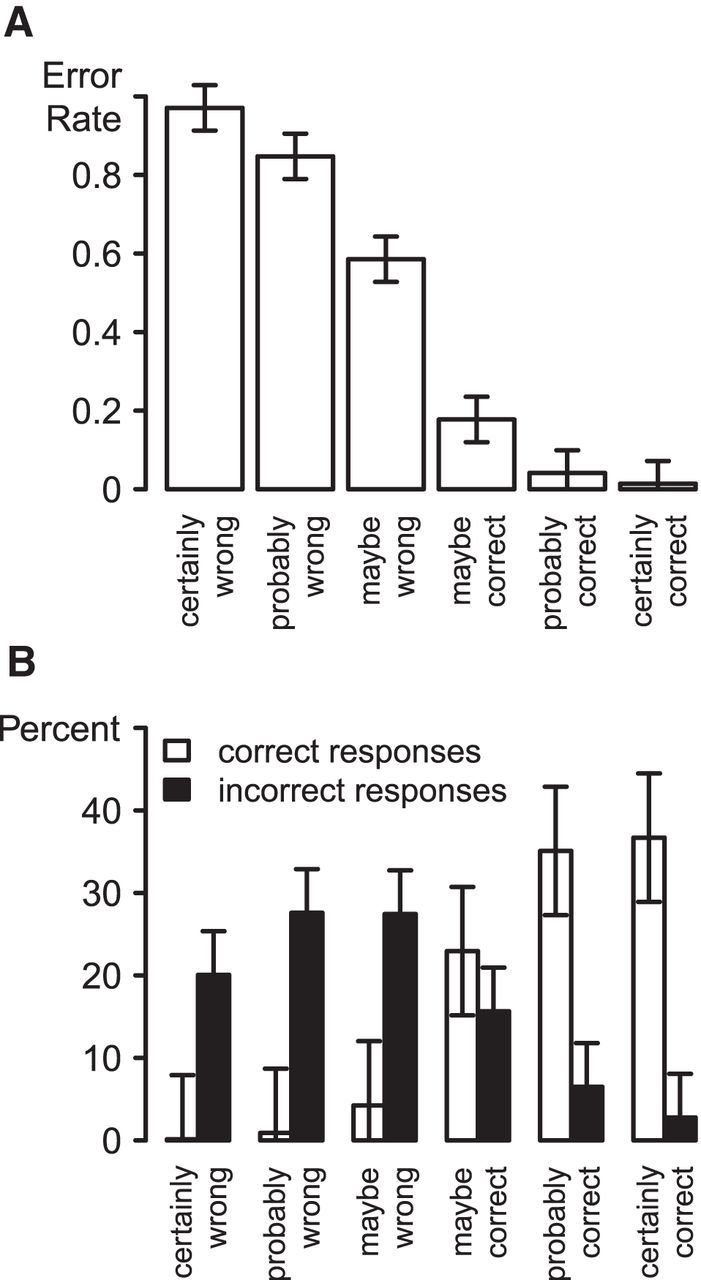
A, Objective accuracy as a function of subjective confidence. B, Distribution of confidence levels as a function of objective accuracy. Error bars indicate within-subject confidence intervals.

ERP data

In the grand-averaged ERP data (Fig. 3A), collapsed across all trials and participants, amplitudes of both ERN (−40 to 60 ms) and Pe (250–350 ms) were modulated as a function of decision confidence (for the ERN: F_(5,75) = 5.3, p < 0.01; with a significant linear within-subject contrast, F_(1,15) = 14.3, p < 0.01; for the Pe: F_(5,75) = 16.7, p < 0.01; with a significant linear within-subject contrast, F_(1,15) = 32.3, p < 0.01). Pairwise comparisons of trials classified as correct revealed significant differences in Pe amplitude between the categories “maybe correct” and “probably correct”, as well as “maybe correct” and “certainly correct” (t values ≥3.9, p values ≤0.01). Thus, the amplitude of both components was largest (i.e., most negative for the ERN and most positive for the Pe) on trials rated “certainly wrong”, and was gradually reduced as subjective confidence increased. In contrast, the stimulus-locked P3 exhibited precisely the opposite relationship (Fig. 3B), increasing in amplitude as confidence increased (F_(2.7,40.1) = 5.1, p < 0.01), with a reliable linear within-subject contrast (F_(1,15) = 11.2, p < 0.01). These results demonstrate a clear functional dissociation between the P3 and Pe. In additional analyses, we confirmed that the inverse relationship between Pe amplitude and confidence was replicated using prestimulus rather than preresponse baseline, thus ruling out any potential baseline contamination artifact from the stimulus-locked P3 effect.

Figure 3.

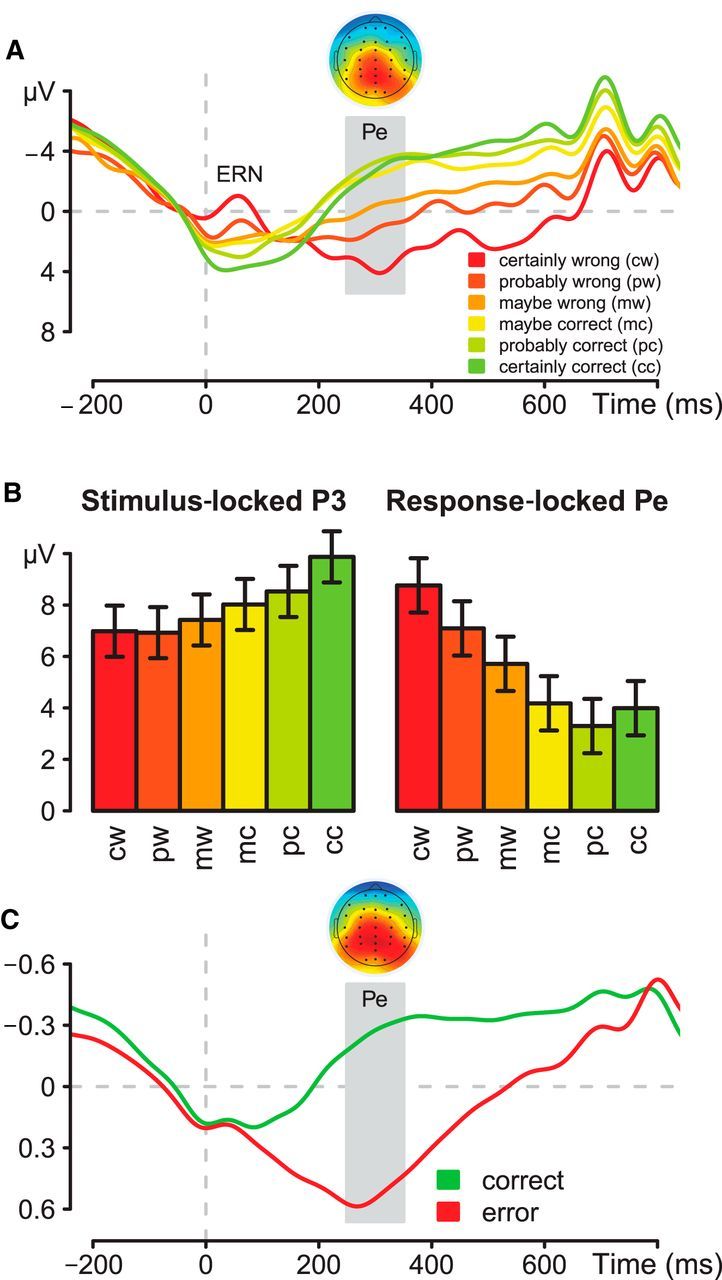
A, Pe at electrode Pz, conditioned on level of confidence for errors and correct trials; response-locked ERP and topography for the difference between “certainly wrong” and “certainly correct” conditions from 250 to 350 ms; the topographic plot indicates voltages as colors from blue (−8 μV) to red (+8 μV). B, Stimulus-locked P3 and response-locked Pe at electrode Pz, conditioned on level of confidence for errors and correct trials with a prestimulus baseline for both potentials. C, Time course and spatial projection of the discriminating component identified by the classification analysis of errors versus correct responses, coded in arbitrary units.

These results extend previous ERN analyses (Scheffers and Coles, 2000) to demonstrate a clear association between Pe amplitude and confidence. However, averaged ERPs are inherently ambiguous about the precise relationship between error-related neural activity and confidence. It could be that amplitude reflects graded variation in confidence, as we hypothesize, but it could also be that error-related neural activity is all or none (Charles et al., 2013), with amplitude changes across confidence bins reflecting variation in proportions of trials on which this activity is triggered (i.e., from rarely, when participants feel “certainly correct”, to almost always, when they feel “certainly wrong”).

Single-trial EEG data

To distinguish between these alternative interpretations—which suggest fundamentally different models of the relationship between error detection and confidence—we next used multivariate classification to robustly index Pe amplitude on individual trials. In analyses not reported here, we found that classification based on the ERN failed to demonstrate consistent association with single-trial decision confidence (see Discussion).

To quantify the Pe on single trials, we used linear integration to derive a discriminating component that maximally distinguishes correct-trial and error-trial waveforms. The classifier was trained on all error trials and a matched-sized set of correct response trials (mean = 296 of error and correct responses combined; range 102–514). Replicating previous findings (Steinhauser and Yeung, 2010), we found optimal classification performance using a training window of 250–350 ms postresponse. For this window, the mean single-trial discrimination performance for the 16 participants was robust: A_z = 0.83 (range 0.74–0.91), where A_z is the area under the ROC curve. The time course and spatial topography of this discriminating component indicated that the extracted component corresponded closely to the Pe (Fig. 3C).

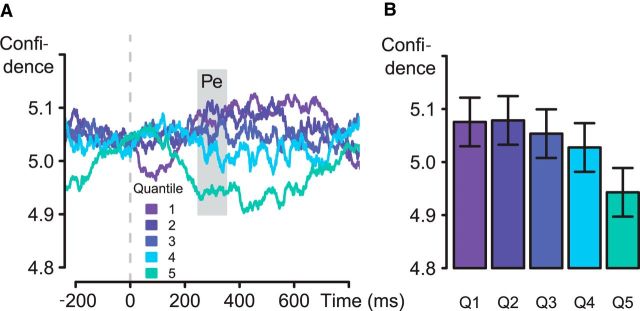
Our primary question was whether this classifier, trained to predict objective accuracy, would also predict variation in correct-trial confidence. We therefore applied the classifying component to the response-locked EEG data from the subset of correct trials not used in classifier training (mean = 553 trials across participants; range 344–757), yielding an estimate of Pe amplitude for each time point on each of these trials. The resulting values were averaged across a moving window of 51 ms, and for each time point were then split into quintiles (smallest to largest Pe amplitude). We then calculated the mean confidence within each quintile. The results (Fig. 4) indicated that correct-trial confidence indeed covaried with the amplitude of the discriminating component (F_(4,60) = 6.1, p < 0.01), with a significant linear within-subject contrast for confidence (F_(1,15) = 7.0, p = 0.02). Confidence varied inversely, and monotonically, as a function of Pe amplitude. Pairwise comparisons of adjacent quintile bins with Bonferroni correction revealed a reliable difference only between quintiles four and five (t₍₁₅₎ = 3.5, p < 0.01).

Figure 4.

A, Moving average confidence (window width, 51 ms) for quintiles of discriminating components; correct trials only (response locked); classifier trained on objective accuracy. B, Averaged over a time window ranging from 250 to 350 ms poststimulus. Error bars indicate within-subject confidence intervals.

Thus, even on trials matched for objective accuracy, Pe amplitude varied in a manner predictive of confidence. Moreover, the resulting gradations in confidence were observed around a high mean value (5 = “probably correct”), with most of the data points lying on the upper half of the confidence scale and therefore reflecting high confidence. This result suggests that the information reflected in the Pe not only reflects graded certainty about having made an error (Steinhauser and Yeung, 2010) but also reflects the graded certainty of having made a correct response—evidence that these judgments lie on a common continuum. Moreover, inspection of the distribution of single-trial Pe amplitudes for each participant individually revealed unimodal rather than bimodal histograms, providing further support for the hypothesis that differences in Pe amplitude reflect graded changes (in confidence) rather than changes in the underlying proportions of qualitatively different neural patterns (reflecting binary error/correct judgments).

Our final analysis of the Pe–confidence association specifically aimed to rule out the possibility that this association is driven by changes in the proportion of false error detections—rather than true gradations in correct-trial confidence—across Pe-classifier amplitude quintiles. The analysis paralleled the previous one, but now mean confidence was calculated only for trials that were both objectively correct and subjectively rated as such. Yet, we predicted that variation in the level of confidence on these trials would follow Pe amplitude. Consistent with this prediction, mean confidence varied significantly over Pe-classifier quintiles for these trials (F_(4,60) = 3.1, p = 0.02), with a marginally significant linear within-subject contrast (F_(1,15) = 3.1, p = 0.10). Thus, changes in Pe amplitude are associated with subtle shifts in confidence, with increased amplitude associated with a change in the balance from “certainly correct” judgments to evaluations that responses are only “probably correct” or “maybe correct”.

Discussion

The present study provides new insight into the neural mechanisms of metacognition and the relationship between error monitoring and confidence. We find that the Pe, an EEG index of error processing, also varies with decision confidence on correct trials. Thus, a Pe-classifier trained to discriminate between objectively correct and incorrect trials was predictive of fine-grained differences in correct-trial confidence. Crucially, this association did not reflect changing proportions of trials classified as errors across confidence ratings, but rather reflected truly graded changes in correct-trial confidence: Pe amplitude was predictive of subtle shifts in confidence (e.g., from “certainly” to “maybe”) on trials that were objectively correct and accurately judged so by participants.

The observed association of Pe amplitude with both error detection and decision confidence indicates that these two metacognitive evaluations reflect similar underlying mechanisms (Yeung and Summerfield, 2012). In prior work on error detection, binary error judgments have been studied, often with concurrent EEG recording; in the memory and perceptual decision-making literatures, the focus has typically been on graded judgments of correctness or certainty. These lines of research address similar questions with similar methods, but have rarely been linked. Our findings suggest a strong link between error awareness and decision confidence, with substantive implications for current theories in the respective fields. First, linking decision confidence to well characterized EEG correlates of error processing should place useful constraints on emerging theories of the neural basis of metacognitive monitoring (Fleming and Frith, 2014). Moreover, associations between confidence and errors present a significant challenge to many current models of decision confidence, which propose that confidence judgments are formed at the time of the primary decision—yet error judgments are known to depend on continued processing of stimulus and response information after the initial decision (Yeung and Summerfield, 2012).

Meanwhile, in error monitoring research there has been debate over whether error detection is all-or-none (Falkenstein et al., 1991; Wessel, 2012) or graded (Scheffers and Coles, 2000; Steinhauser and Yeung, 2010). Our findings strongly support the latter hypothesis, and extend it to show that the continuum of error certainty is continuous with fine-grained judgments of certainty that a response is correct: on the 6-point confidence scale used in our study, confidence on correct trials varied around a high mean value (5.0) with low SD (0.8). Correspondingly, we observed very fine-grained variations in correct-trial confidence as a function of Pe amplitude, spanning a relatively narrow range of values clustered around high confidence judgments (quintile range, 4.9–5.1).

As such, the present findings bear on the question of whether neural correlates of error processing vary discretely or continuously, and help to resolve ambiguities in prior research on this question. Thus, whereas Wessel (2012) suggests that the late Pe reflects all-or-none error awareness, and Charles et al. (2013) have made a corresponding argument for the ERN, Scheffers and Coles (2000) reported systematic variation in ERN amplitude with confidence. In this context, it is noteworthy that we found both the ERN and Pe to vary in amplitude with subjective confidence, but only the Pe was predictive of a graded change in confidence across trials in our multivariate analysis. This difference between ERN and Pe might simply reflect greater signal-to-noise ratio for the latter component (although we note that the ERN is robustly measurable on individual trials; Parra et al., 2002). However, a more intriguing possibility is that ERN amplitude fails to predict the variation in confidence on single trials because it is an all-or-none signal (Charles et al., 2013), and that the observed association with confidence seen in averaged ERPs (Fig. 3A; Scheffers and Coles, 2000) reflects variation in the probability of this all-or-none signal being triggered across trials with differing levels of confidence. If correct, this interpretation suggests a reconciliation of previously contradictory findings. Regardless, our findings indicate that the Pe is a stronger correlate of error awareness and can simultaneously index associated variation in decision confidence.

Our findings also have practical implications in showing that Pe amplitude provides a robust “noninvasive” index of confidence. Metacognitive evaluations are an important component of decision making; they vary with objective performance and usefully support adaptation to an ever-changing environment—for example, participants slow down after detecting errors to prevent further mistakes (Laming, 1979). Measures of confidence therefore provide an important index of how participants exert cognitive control. But assessing them can be difficult. In particular, requiring participants to make repeated confidence judgments is time consuming, imposes a cognitive burden that alters underlying decision processes (Baranski and Petrusic, 1998), and may even change the nature of metacognitive evaluations (Grützmann et al., 2014). EEG provides a robust, nondisruptive index of confidence that circumvents these problems, enabling researchers to assess subjective confidence without requiring participants to make explicit judgments.

In conclusion, the present study examined neural correlates of metacognition in perceptual decision making. Our findings indicate that well characterized neural correlates of error awareness are predictive of graded changes in decision confidence. We propose that the Pe provides a generic index of decision confidence and is not limited to binary error detection, suggesting that shared mechanisms underlie error monitoring and confidence judgments. As such, EEG measures of the Pe promise to provide a useful noninvasive and robust index of metacognitive evaluation that might be leveraged in future research to assess levels of confidence whenever direct measurement is impossible or inconvenient, and hence used to shed further light on the underlying mechanisms of metacognition in decision making.