Molecular dynamics and Monte Carlo simulations for protein–ligand binding and inhibitor design

Abstract

Background

Non-nucleoside inhibitors of HIV reverse transcriptase are an important component of treatment against HIV infection. Novel inhibitors are sought that increase potency against variants that contain the Tyr181Cys mutation.

Methods

Molecular dynamics based free energy perturbation simulations have been run to study factors that contribute to protein–ligand binding, and the results are compared with those from previous Monte Carlo based simulations and activity data.

Results

Predictions of protein–ligand binding modes are very consistent for the two simulation methods, which are attributed to the use of an enhanced sampling protocol. The Tyr181Cys binding pocket supports large, hydrophobic substituents, which is in good agreement with experiment.

Conclusions

Although some discrepancies exist between the results of the two simulation methods and experiment, free energy perturbation simulations can be used to rapidly test small molecules for gains in binding affinity.

General significance

Free energy perturbation methods show promise in providing fast, reliable and accurate data that can be used to complement experiment in lead optimization projects. This article is part of a Special Issue entitled “Recent developments of molecular dynamics”.

1. Introduction

Optimization of protein–ligand binding affinity is a central goal of small molecule drug discovery. A wide range of computational methods has been developed for this purpose, but free energy perturbation (FEP), in combination with molecular dynamics (MD) or Monte Carlo (MC) sampling, is a particularly attractive option, because it provides a rigorous theoretical means to compute changes in the free energy of binding. There is a growing list of examples of drug discovery programs that have benefited from insights obtained from FEP predictions [1,2]. Indeed, to borrow an example from our own lab, FEP was used, in conjunction with biological assays and X-ray crystallography, to aid the optimization of a 5-μM docking hit to an extremely potent (55 pM) anti-HIV agent [3,4]. Yet, the broad use of FEP has yet to be realized [5], mainly due to perceived difficulties in obtaining accurate predictions on a timescale that can impact live projects.

In recent years, there have been signs that these limitations in the accuracy, reliability and speed of FEP simulations are being overcome. The predictive power of FEP relies on the assumption of ergodicity, that is, that in effect all relevant geometries of the protein–ligand complex are being sampled with the correct Boltzmann weight. Numerous examples of quasi-ergodic sampling have been reported in both the MD and MC literature, whereby the protein and/or the ligand are trapped for long times in local free-energy minima [6-8]. There are, however, a wide range of enhanced sampling methods available, usually based on tempering the system or modifying the underlying potential energy surface, which can circumvent this problem without significantly affecting the computational cost [9]. Even in the limit of complete sampling, the accuracy of FEP is dependent on the quality of the employed force field. Although the functional form of most force fields has remained largely unchanged, parameter determination and benchmarking are being performed on increasingly large quantum mechanical and experimental data sets [10-13], thus improving the transferability of the parameters and confidence in the results. In addition, adding extra physical terms such as polarization promises to further improve the description of ligand binding. Finally, an important consideration is the time taken to obtain the results, both in terms of computational cost and human effort. The move to exploit the computing power of graphics processing units (GPUs) by entirely re-writing molecular dynamics algorithms has resulted in order-of-magnitude speedups [14,15], while automated workflows significantly reduce the set-up time for the calculations [16].

In this paper, we compare FEP results using two sets of software, MCPRO and Desmond, for the retrospective design of inhibitors of a well-studied drug target. MCPRO has been used extensively for lead optimization through FEP calculations with MC sampling of protein–ligand complexes [1,17]. An attractive MD/FEP alternative has recently emerged. Namely, Desmond, which is distributed as part of the Schrödinger package and is fully integrated with Maestro [18,19], which allows the efficient set-up of FEP calculations with MD sampling. Both MCPRO and Desmond optionally include replica exchange with solute tempering (REST) for enhanced sampling [7,20,21]. This allows the heating of local regions of the system, thus substantially improving traversal of the free energy surface while sampling rigorously from the Boltzmann ensemble. The REST algorithm has been shown to improve agreement with experiment in typical medicinal chemistry projects [8,22]. Both codes use OPLS force fields [23,24], though there are differences in the parameters and the assignment of partial charges [11,12,25,26].

The application of MCPRO with REST to the optimization of non-nucleoside inhibitors of HIV-1 reverse transcriptase (NNRTIs) has previously been described [8]. This class of molecules is an important component of anti-HIV treatment; however, patients who begin NNRTI treatment often develop the Tyr181Cys (Y181C) mutation, which renders many agents inactive. For example, the benzyloxazole molecule with R = H, shown in Fig. 1, has an EC₅₀ of 6 nM towards the wild-type protein, but 420 nM towards the variant strain bearing the Y181C mutation [27]. It was hypothesized that substituents at the 4-R position might fill the cavity vacated by Y181, thus restoring activity against the mutant form [27]. Indeed, FEP calculations predicted that bulkier alkyl groups, such as ethyl and isopropyl, should give gains in binding free energy, and assays using infected T-cells showed that both analogues have sub-10 nM potency against both viral strains [8,27]. The nature of the bulky alkyl groups at the 4-R position necessitates enhanced sampling methods to cross torsional energy barriers, and the assay data spans two orders of magnitude. Thus, the current data set provides an excellent test of the ability of the FEP methodology to distinguish between weak and strong inhibitors in a typical medicinal chemistry setting. In what follows, the extent to which MD-based FEP is likely to be useful in a lead design effort is evaluated by testing the reliability, accuracy and speed of the simulations, and the results are compared with our previous MC-based study and assay data.

Fig. 1.

The benzyloxazole molecule.

2. Computational details

2.1. Desmond

Structural preparation of the benzyloxazole ligands in complex with the HIV-RT receptor followed identical protocols as described elsewhere [8,27-30]. Briefly, the model system was built from the PDB ID: 1S9E file [31], using the MCPRO [17] and BOMB [1] software packages. The system was truncated to include only the 178 amino acids closest to the ligand. The Y181C variant was generated manually from the wild-type structure. All complexes were relaxed using conjugate gradients’ minimization in MCPRO prior to the simulations. It should be noted that the system preparation could also have been performed using the Protein Preparation Wizard in Maestro [19]. However, using an identical initial system affords a direct comparison between the Desmond FEP scheme and previously published MCPRO results [8].

In Desmond [18], the systems were solvated in orthorhombic, periodic boxes, with a 5 Å (10 Å) buffer between the system and the edge of the simulation box for bound (unbound) simulations. No counter ions were used and the systems were overall charged to be neutral. The protein and ligands were treated using the OPLS2.1 force field [12], and water with the SPC model. Ligand charges were assigned using a combination of the Cramer and Truhlar CM1A charge model [25], and a set of bond charge correction terms (BCC) [26]. The Maestro force field builder [19] identified two torsional angles in the benzyloxazole molecule with missing OPLS2.1 parameters. A torsional scan was automatically run at the LMP2/cc-pVTZ(-f)//B3LYP/6-31G** level, and the parameters were obtained by fitting to the resulting quantum mechanical energy profile. The ligand R-group FEP transformations were set up using the Maestro software [19]. The systems were equilibrated using standard Desmond set-up protocols, which comprise short minimization and MD runs. The final averaging stage of each FEP window was run at 300 K in the NPT ensemble for 5 ns unless otherwise stated.

The ligand R-group mutation is controlled by an alchemical parameter λ, which varies between 0 and 1 over the course of the FEP simulation. Sampling is enhanced to some extent in Desmond by allowing periodic replica exchange moves along the alchemical λ-coordinate, which is a protocol known as λ-hopping. It has been shown that sampling in FEP simulations may be enhanced still further by scaling the potential energy of a selected subsystem by a factor less than one at intermediate λ-windows using the replica exchange with solute tempering (REST) procedure [7,20-22]. In REST, since the overall effect of the scaling is to increase the rate of transitions across free energy barriers, the selected subsystem is often referred to as the “hot” region. The scaling factor is related to the effective temperature of the hot region; a higher effective temperature corresponds to a smaller potential energy scaling factor. It should be emphasized that the hot region does not have a higher kinetic energy than the rest of the system. By allowing replica exchanges with acceptance probabilities determined by the Metropolis criterion between neighboring λ-windows, the conformations that are sampled in the high temperature, intermediate λ-windows are able to propagate to the end-points of the FEP alchemical transformation, thus enhancing sampling at all values of λ. In what follows, Desmond simulations with high temperature, enhanced sampling at intermediate alchemical λ-windows are referred to as FEP/REST simulations.

Following the standard Desmond FEP protocol, the simulation was split into 12 λ-windows, with replica exchange attempted every 1.2 ps. The hot region is determined automatically as the group of the ligand that is being mutated. Although it is possible to extend the hot region to include more of the ligand and the receptor [22], by limiting the hot region to a single group, very high effective temperatures can be employed while maintaining good exchange rates between replicas. Effective temperatures were selected automatically with the aim of achieving 30% exchange rates between λ-windows. The highest effective temperature, reached at the central λ-window, was in excess of 1400 K for all of the transformations studied here. The free energy differences between the initial and final states are calculated using the Bennett acceptance ratio (BAR) method [32], and the errors estimated using bootstrapping [33].

2.2. MCPRO

The corresponding MC/FEP simulations have been described in detail elsewhere [8], but it is worth explicitly highlighting the main differences between the approaches of MCPRO and Desmond. The biggest difference is in the method of sampling the degrees of the freedom of the protein–ligand complex and the ligand in water. The MCPRO calculations used MC sampling with REST for the ligand and a fixed protein backbone. Backbone sampling is possible via concerted rotations, but this is often not used [34]. Furthermore, a ‘flip’ algorithm allowed selected dihedral angles to undergo attempted jumps, which are much larger than typical MC moves [35], and this has been shown to work well with the REST method [8]. Although both codes use OPLS force fields [23,24], there are differences in their parameterization, particularly for the torsional energetics, which has been trained on different quantum mechanical data sets [10,12]. In addition, assignment of ligand partial atomic charges in both cases follows the CM1A scheme, but in MCPRO environmental polarization is included via a charge scaling factor [36]. Finally, the free energy changes reported here were computed using 11 λ-windows of simple overlap sampling, which has been shown to be well-converged for the types of small mutations investigated [37]. In practice, to incorporate the REST scheme, at each λ-window, four replicas are run in parallel on the same node, each representing a different effective temperature.

3. Results

3.1. Isopropyl to ethyl

To investigate the benefits of using FEP/REST in a typical medicinal chemistry setting, the energetics of the R = isopropyl to ethyl transformation were studied first. The chosen transformation is interesting, because it involves two common hydrophobic groups, and the symmetry of the isopropyl group means that the user has a choice of two methyl groups which may be mutated to hydrogen to give ethyl. The free energy of the transformation should, of course, be independent of which of these two mutation paths is chosen. It has previously been shown [8] that this mutation demonstrates the problems of non-ergodic sampling when enhanced sampling methods are not used — simulations with slightly different starting conditions gave free energies that differed by up to 0.5 kcal/mol and, more worryingly, the two different methyl to hydrogen mutation pathways showed differences in excess of 1.5 kcal/mol. By incorporating the REST enhanced sampling protocol, alongside the ‘flip’ algorithm for attempting large jumps in select dihedral angles [35], it was shown in that study that much more consistent results, which are independent of both starting conditions and mutation pathway, could be obtained.

Table 1 shows a comparison of the free energies of the R = i-Pr to Et transformation in the wild-type HIV-RT protein, using a range of simulation protocols within Desmond. Paths 1 and 2 denote the two branches of the i-Pr group, which may be mutated from methyl to hydrogen to give ethyl. Using standard FEP, with no enhanced sampling, there is a difference of nearly 1 kcal/mol in the computed ΔG between the two mutation pathways, which should give identical results. This is very similar to previous observations that used MCPRO with no enhanced sampling procedure [8], and clearly reflects incomplete sampling. The discrepancy is somewhat improved by using the λ -hopping scheme in Desmond, and the difference in computed free energies falls to close to 0.2 kcal/mol. The λ-hopping scheme [38] allows periodic replica-exchange moves along the alchemical λ-coordinate. In theory, conformational sampling is enhanced in this scheme via mixing of the coordinates sampled along the FEP trajectory. However, as discussed in more detail elsewhere [39,40], sampling will be incomplete if there are no values of λ that reduce a particular free energy barrier. Our results are consistent with this picture and previous observations in the literature [7], in that λ-hopping improves sampling over standard FEP, but some dependence on the mutation pathway remains. In contrast, using the FEP/REST scheme, in which intermediate λ-windows are run at higher effective temperatures, the free energy of the i-Pr to Et transformation is effectively independent of the mutation pathway (differences less than 0.1 kcal/mol).

Table 1.

Comparison of Desmond FEP protocols for the transformation of R = i-Pr to Et in wild-type HIV-RT.

		Averaging time (ns)	ΔG (kcal/mol)a	Computational time (min)b
Path 1	FEP	5	−1.18	511
	λ-Hopping	5	−0.45	583
	FEP/REST	1	−0.46	154
	FEP/REST	5	−0.43	584
Path 2	FEP	5	−0.19	508
	λ-Hopping	5	−0.22	593
	FEP/REST	1	−0.48	152
	FEP/REST	5	−0.48	584

^aΔG is the computed free energy change for the bound leg of the FEP calculation.

^bRun on three Nvidia K20 GPUs.

The conformational sampling during the FEP/REST simulations may be compared with previous results using MCPRO. In this respect, the key degree of freedom is the dihedral angle labeled φ in Fig. 2. Given the differences between the two computational methods that were outlined in Section 2.2, the agreement between the sampled conformations in the two simulations is remarkably good. In particular, when R = Et, the dihedral angle distribution shows one main peak close to 240°. However, when R = i-Pr, the dihedral angle distribution has two peaks, close to 180° and 330°. These two configurations are shown in Fig. 3, and are the source of poor convergence in this system for FEP simulations without enhanced sampling methods. The large free energy barrier that hinders inter-conversion between the two conformers arises from contacts between the methyl groups and Trp229.

Fig. 2.

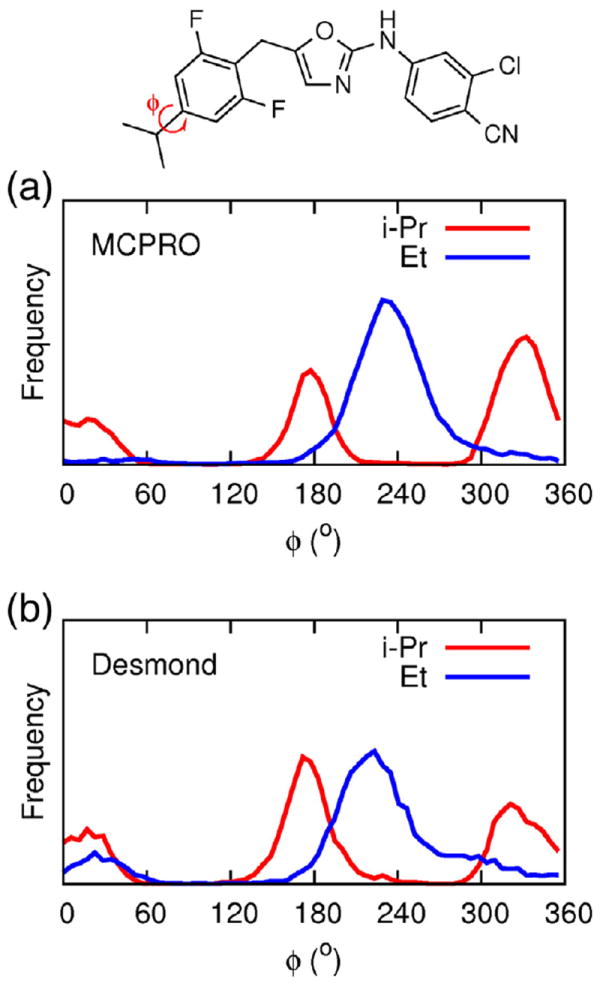
Dihedral angle distributions along the R = i-Pr to Et transformation inWT HIV-RT from (a) MCPRO [8] and (b) Desmond FEP/REST simulations.

Fig. 3.

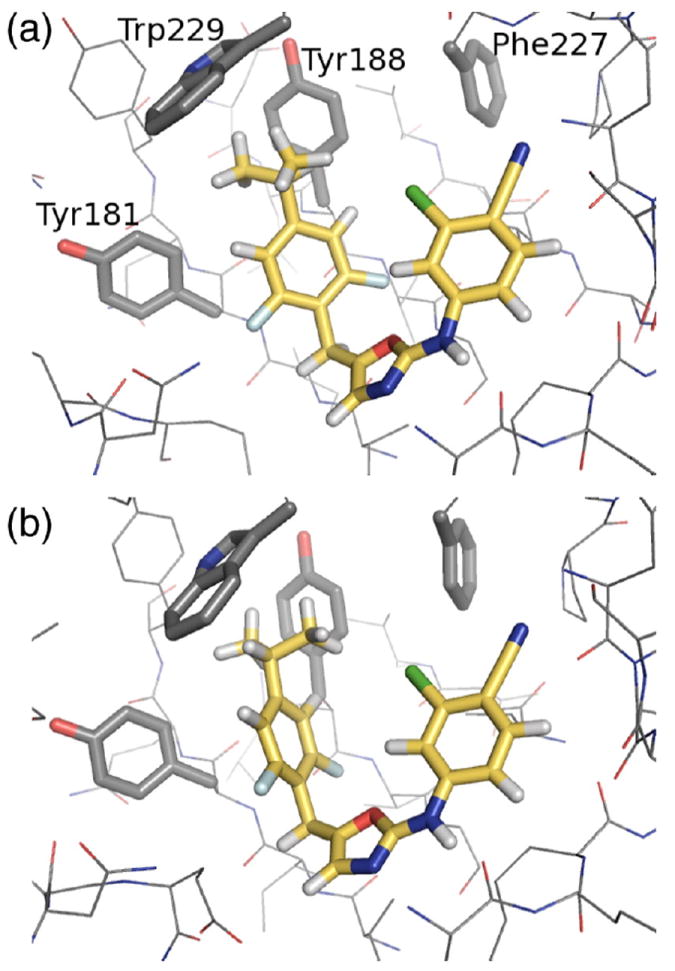
Snapshots from the Desmond FEP/REST simulation showing R = i-Pr at (a) φ = 180° and (b) φ = 330°.

Table 1 also compares the computational expense of the three schemes used in Desmond. While standard FEP is slightly less demanding than the enhanced sampling methods used here, the lack of consistency in the results makes it unsuitable for this system. FEP/REST runs in essentially the same time as the λ-hopping scheme. Furthermore, the efficiency by which the method crosses free energy barriers means that a substantially reduced simulation time can be used. Reducing the length of the averaging section of each λ-window from the default of 5 ns to 1 ns gives a maximum discrepancy (ΔΔG) of just 0.03 kcal/mol for this transformation. However, it should be emphasized that FEP transformations involving larger changes, or higher free energy barriers, may take longer to converge. The total run time of just 2.5 h on three GPUs substantially increases the number of FEP simulations that can be performed as part of a lead optimization effort. As a comparison, the MCPRO/REST calculations required around 800 CPU-hrs for each FEP simulation. The main difference is, of course, the speedup that the GPU implementation of Desmond brings, though this study also highlights the performance gain that the λ-hopping scheme would bring to MCPRO; the number of replicas could be reduced by a factor of 4, and the computation time would be reduced to approximately 200 CPU-hrs.

3.2. NNRTI design

It has been shown in the previous section that FEP calculations with Desmond for the present system are consistent under different simulation conditions, due to the FEP/REST enhanced sampling algorithm, and may also be run in short times with reasonable computational resources. However, to make an impact in lead optimization projects, it is necessary that the data can be used to test hypotheses, guide experiments, and/or rationalize experimental results. In this case, our hypothesis was that bulky substituents R in Fig. 1 might differentially improve potency against the Y181C-bearing variants of HIV-RT. Of course, the quantitative outcome is unclear owing to the subtleties of steric interactions, solvation, and entropic considerations.

Table 2 collects the relative free energies of binding of seven benzyloxazole analogues, for both the wild-type and Y181C mutant, and compares them with previously reported MCPRO (using REST enhanced sampling [8]) and experimental EC₅₀ results [27]. It is emphasized that the experimental data are from cell-based assays so at best qualitative agreement with the FEP results is expected. In agreement with the MCPRO results and the assays, replacing R = Me by the larger ethyl group is favorable in the WT protein. From the Desmond simulations, propyl, isopropyl and t-butyl are also expected to show similar activity. However, these substitutions are disfavored by MCPRO, but the differences are all within 1.5 kcal/mol. Interestingly, R = OEt should be more potent than CH₂OMe according to the results from Desmond, in contrast to MCPRO and the experimental results. However, the ΔΔG between methyl and ethoxy from MCPRO (3.15 kcal/mol) seems too much large, while the Desmond result is consistent with the small experimental difference in activity. To investigate the sampling in these cases, the two-dimensional distributions of dihedral angles of the R-group sampled during the MC and MD simulations are plotted in Fig. 4. Using REST enhanced sampling, large areas of conformational space are covered by both MCPRO and Desmond. The identities of the deepest free energy wells are similar, though there are some differences, in particular the MD-based algorithm appears to sample more widely. This may be due to differences in the implementation of the enhanced sampling schemes since Desmond is able to reach higher effective temperatures by incorporating REST into the λ-hopping FEP scheme. It may also stem from differences in the force fields or further technical issues that are discussed in more detail in Section 4. The conformations sampled in the R = OEt simulation are very similar in the two sets of simulations, and so the large difference in the relative free energy computed using Desmond and MCPRO is unlikely to be due to insufficient sampling of the R-group.

Table 2.

Computed relative free energies of binding using FEP/REST in MCPRO and Desmond.

R	MCPRO (kcal/mol)a		Desmond (kcal/mol)b		EC50 (μM)c
	WT	Y181C	WT	Y181C	WT	Y181C
Me	0.00	0.00	0.00	0.00	0.011	0.210
Et	−0.74	−2.28	−0.58	−0.65	0.0013	0.0069
Pr	0.69	−1.60	−0.75	−1.11	–	–
i-Pr	0.14	−4.40	−0.78	−1.75	0.0052	0.0072
OEt	3.15	0.01	0.37	0.10	0.028	0.048
CH2OMe	1.72	1.02	1.50	0.97	0.0036	0.690
t-Bu	0.73	−3.39	−0.43	−1.90	–	–

^aFrom Ref. [8]. The estimated statistical uncertainties range from 0.08 (Et) to 0.22 kcal/mol (OEt).

^bStatistical uncertainties range from 0.06 (Et) to 0.11 kcal/mol (OEt).

^cFrom Ref. [27].

Fig. 4.

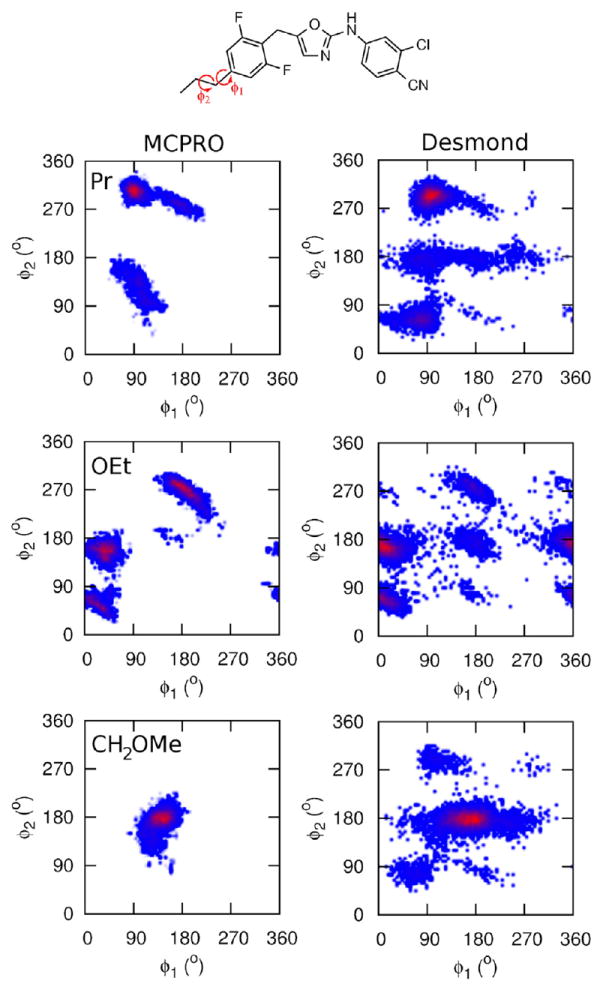
Sampling of dihedral angle distributions from MCPRO and Desmond FEP/REST simulations of the inhibitor bound to the wild-type HIV-RT protein for R = Pr, OEt and CH₂OMe.

Turning to the Y181C mutant, the results from Desmond do indicate that larger alkyl groups are beneficial for activity. In agreement with MCPRO, R = i-Pr and t-Bu are expected to be the most potent inhibitors. Experimentally, the R = Et and i-Pr analogues are equally potent and are both sub-10 nM inhibitors of replication of the Y181C viral strain. The propyl analogue was not pursued, while attempts to prepare the t-butyl one were unsuccessful [27]. As was demonstrated in MCPRO simulations of the benzyoxazole inhibitors [8], the Y181C mutation increases the available space for accommodation of a bulkier R-group. Fig. 5 shows example snapshots from the simulations with R = i-Pr and CH₂OMe. For R = i-Pr, Cys181 is in close contact with a methyl group of the ligand. However, for R = CH₂OMe, the substituent is preferentially oriented away from Cys181 to avoid a steric clash with Trp229, which may help to explain why the CH₂OMe analogue is the least potent towards the variant strain, both computationally and experimentally.

Fig. 5.

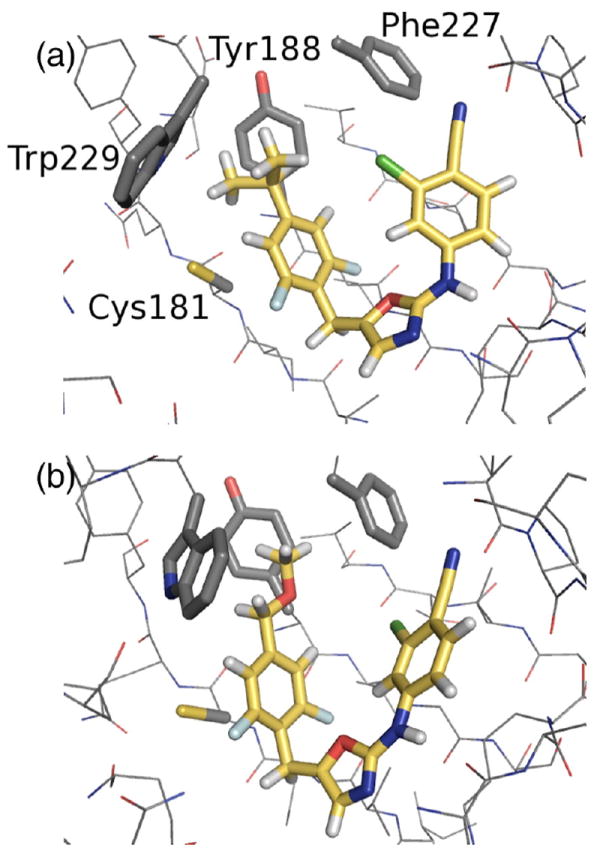
Snapshots from the Desmond FEP/REST simulations showing (a) R = i-Pr and (b) R = CH₂OMe with the Y181C variant of HIV-RT.

4. Discussion and conclusions

FEP simulations using the Desmond MD code have been evaluated in a retrospective study of the binding of benzyloxazole inhibitors to both wild-type and the Y181C variant of the well-studied drug target HIV-RT. The project is representative of a lead optimization effort whereby a hypothesis has been made, which may improve a molecule’s potency, and rapid, accurate computational analyses are desired to determine whether the proposed change is worth further pursuit. In this case, the hypothesis is that bulkier R groups for the benzyloxazole shown in Fig. 1 could better fill the hydrophobic cavity created by Tyr181 to Cys181 change, thus improving potency against the mutant strain. Presented with the computed results in Table 2, one would be motivated to pursue experimentally the ethyl, propyl, isopropyl and t-butyl analogues and to skip the ethoxy and methoxymethyl ones. This decision would have been productive.

The FEP simulations studied here are relatively challenging from a sampling perspective, because the hydrophobic substituents have been shown to adopt a number of different conformations that are separated by substantial free energy barriers [8]. Here, it has been shown that, despite the use of different sampling approaches and force fields, there is good agreement between the sampled conformations of the ligands using MCPRO and Desmond (Figs. 2 and 4). It has also been shown that, as with MCPRO, the computed free energies for the R = i-Pr to Et transformation are robust with respect to the chosen mutation pathway when the REST enhanced sampling is included. Furthermore, computational times as low as 2.5 h on three GPUs have been noted for obtaining an FEP result. Thus, with reasonable resources, FEP predictions can be obtained in a same-day mode on a large scale.

Despite the agreement between the two approaches concerning the ligand binding modes, there are discrepancies in the description of the free energetics of binding. However, most differences are of the order of 1 kcal/mol or less, and where larger differences exist, the direction of the change is in agreement. For example, relative free energies of −4.40 and −1.75 kcal/mol are reported for i-Pr binding to the Y181C mutant, using MCPRO and Desmond, respectively. While the magnitudes of the free energy disagree, the conclusions that i-Pr is a promising substituent to pursue do not and, indeed, the i-Pr analogue shows sub-10 nM potency against both viral strains [27]. The remaining discrepancies between the results may arise from: i) while REST enhanced sampling has been applied to the ligand, enhanced sampling for protein side chains in the binding site may be beneficial; ii) the protein back-bone was not sampled in the MC calculations; and iii) again the force fields were not identical. The pattern that the range of the present free-energy results seems overly large with MCPRO in comparison to experiment and Desmond likely reflects better sampling in the MD simulations as indicated in Fig. 4. Overall, both approaches appear to be fully viable and when used together they provide the opportunity of obtaining a consensus view. MC- and MD-based FEP calculations can be expected to become an increasingly valuable tool for complementing, rationalizing and suggesting experiments in the field of protein–ligand binding and inhibitor design.