Convergence and reproducibility in molecular dynamics simulations of the DNA duplex d(GCACGAACGAACGAACGC)

Abstract

Background

The structure and dynamics of DNA are critically related to its function. Molecular dynamics (MD) simulations augment experiment by providing detailed information about the atomic motions. However, to date the simulations have not been long enough for convergence of the dynamics and structural properties of DNA.

Methods

MD simulations performed with AMBER using the ff99SB force field with the parmbsc0 modifications, including ensembles of independent simulations, were compared to long timescale MD performed with the specialized Anton MD engine on the B-DNA structure d(GCACGAACGAACGAACGC). To assess convergence, the decay of the average RMSD values over longer and longer time intervals was evaluated in addition to assessing convergence of the dynamics via the Kullback-Leibler divergence of principal component projection histograms.

Results

These MD simulations —including one of the longest simulations of DNA published to date at ~44 μs—surprisingly suggest that the structure and dynamics of the DNA helix, neglecting the terminal base pairs, are essentially fully converged on the ~1–5 μs timescale.

Conclusions

We can now reproducibly converge the structure and dynamics of B-DNA helices, omitting the terminal base pairs, on the μs time scale with both the AMBER and CHARMM C36 nucleic acid force fields. Results from independent ensembles of simulations starting from different initial conditions, when aggregated, match the results from long timescale simulations on the specialized Anton MD engine.

General Significance

With access to large-scale GPU resources or the specialized MD engine “Anton” it is possibly for a variety of molecular systems to reproducibly and reliably converge the conformational ensemble of sampled structures.

INTRODUCTION

To fully understand the biological relevance, regulation and function of DNA in processes ranging from replication to transcription and repair, it is important to gain atomic level insight into the sequence specific structure, deformability and dynamics of DNA [1–3]. This includes understanding the subtle influences of the surrounding solvent, ligands, ions and proteins on the structure and dynamics of DNA. Towards this end, many experimental, theoretical, and simulation approaches have been applied to provide this atomistic insight into DNA structure and dynamics on timescales ranging from very fast femto- and pico-second processes to longer millisecond timescale events such as base pair opening.

On the experimental side, the bulk of our structural understanding has come from high-resolution crystallography and NMR studies. Through the published structures of small to moderately sized DNA duplexes in the PDB [4] and Nucleic Acid Database [5,6], we have a fair-to-excellent understanding of the variations in sequence dependent DNA structure at the di- to tetra- nucleotide level. Although most structures in the databases tend to hide dynamics due to ensemble and time averaging, some extremely high resolution DNA crystal structures [7] have been able to trap multiple DNA backbone conformational substates. Relaxation dispersion NMR experiments have been able to identify transient and low populated Hoogsteen base pairs [8] in DNA duplexes, and solid state NMR experiments have been able to identify large amplitude dynamics in the sugar puckers at CpG steps in crystals [9] of the Dickerson dodecamer. Although these structure-based experiments show a population of conformations, they do not provide ready insight into the timescales of the dynamics. A wide variety of additional experimental approaches have been applied in order to assess dynamics on nanosecond or faster timescales. These approaches range from varied NMR experiments [10–14] and Fourier transform IR difference spectroscopy [15] to triplet anisotropy decay [16], electron paramagnetic resonance, and pulsed electron-electron double resonance to active nitroxide or other spin labels [17–19]. Common to each experiment is identification of motions on the sub-microsecond timescale, typically from picoseconds up to the low-nanosecond timescale. Jumping to longer timescales, NMR has been able to characterize internal base pair opening events on the 5 to 100 and greater millisecond timescales [20–24]. Insight has also come from early theoretical approaches that helped interpret experimental persistence length estimations, nanosecond scale fluorescence depolarization, fluorescence anisotropy, and other experiments through the development of analytic chain [25], elastic rod [26], worm like chain [27], and also coarse-grained bead models [28] to characterize DNA flexibility. Torsional flexibility could also be analyzed with early atomistic potentials and conformational/energetic analyses [29]. Again, characteristic in each was probing motion effectively, on the picosecond to low nanosecond timescale regime. In fact, motion within this timescale appears to be rich as probed by the time-resolved dynamic Stokes shift in the fluorescence of base pair analogues which suggest a power-law behavior in these fast dynamics due to not only conformational changes of the DNA, but interactions with solvent and ions [30,31]. In other words, rather than seeing specific decay times corresponding to a particular observable, as seen by NMR or interpreted in other analyses that are investigating a particular process or structural feature of the DNA, the time-resolved Stokes-shift experiments suggest that motion is occurring all across the ps-ns timescale range and that there is no unique multi-exponential fit that can explain the data [32]. A better fit is a logarithmic fit over the range of 40 ps to 40 ns [33]. As will become apparent later, this is actually consistent with the current MD simulation results that suggest fairly diffuse motion across the many degrees of freedom including the DNA, water and ions, with motion that rapidly decays as we average over longer and longer timescales and effectively disappears on the 1–5 μs timescale [34].

As pointed out by others and reaffirmed here, explorations of DNA dynamics to date show rich behavior in the picosecond to low microsecond regime and also dynamics on the 5–100+ millisecond timescale. However there is a distinct lack of evidence for motion at the microsecond to millisecond timescale. Are dynamics flat on this timescale, or do DNA motions continue the power-law behavior seen on the 40 ps – 40 ns timescale across the 1 μs – 1 ms timescale? This question is difficult to answer since few experimental techniques can resolve DNA duplex dynamics over this time range. MD simulations tens of microseconds in length were performed to attempt to address this question. The extreme length of these simulations (currently the longest simulations of DNA to date) was facilitated by access to resources like the specialized MD engine Anton from D. E. SHAW Research (DESRES). Our simulation results, coupled with the detailed experimental knowledge of base pair opening rates, suggest that motion is flat in the microsecond to millisecond regime for Watson-Crick DNA helices. This is supported by selective off-resonance carbon R_1ρ NMR relaxation dispersion spectroscopy by Al-Hashimi—one of the few experimental techniques able to see into dynamics in the microsecond timescale—investigating a 1,N6-ethenoadenine (eA) lesion/mismatch in a DNA duplex [35]. Compared to Watson-Crick DNA helices that do not show exchange processes or internal dynamics on this timescale, the NMR results of the mismatch clearly resolve exchange processes on the 26 ± 8 μs timescale, which is consistent with the higher expected opening rates. However, before jumping into the simulation results and a more elaborate discussion of the implications of a 1 μs – 1 ms gap in DNA helix dynamics [34], it is worthwhile to review progress to date and note that previously, due to limits in computational power, MD simulations were effectively limited to the sub-microsecond range.

To provide further historical context, simulation methods have also been applied to complement experiment and the theoretical/analytic interpretations of the data. The most widely applied methods have been molecular dynamics (MD) simulations which have been enabled by significant advances in the simulation methodologies and force fields. Although lagging behind protein systems, a number of large-scale simulations of nucleic acids (NA) over the past ~25–30 years have been published [36] with considerable acceleration in application projects starting in the mid-90’s when fast and parallelized particle mesh Ewald methods [37,38] and better force fields became available [41–44]. Such simulations have provided a detailed atomic-level picture of nucleic acid structure and motion [43]; moreover, due to their highly charged nature and sensitivity to their surroundings, MD simulations of nucleic acids have also been a rather sensitive probe of the (un)reliability of the simulation methods and force fields. To push to longer timescales in MD simulation, the community has long benefited greatly from the availability of and easy access to state-of-the-art high performance and/or specialized computer systems [44–46]. As computer power has grown over the past decade and the community has routinely been able to reach longer and longer MD simulation time scales, repeatedly such simulations have sampled hitherto unknown conformational states and exposed artifacts in the force fields [47–51].

The longer MD simulation timescales sampled have allowed not only a more thorough study of nucleic acids and provided a more rigorous test of force field parameters for nucleic acids, but also exposed serious deficiencies in the force fields that when fixed have significantly improved their accuracy [37,54–58]. In ~2002–2004, a large-scale assessment of DNA sequence-dependent structure and dynamics was performed via a divide and conquer approach by the ABC consortium, resulting in a set of 39 MD simulations of DNA 18-mer sequences with all possible tetrameric repeats (136) on the 300 ns time frame [58,59]. Analysis of these MD simulations allowed characterization of tetrameric DNA sequence specific structure and dynamics, showed results consistent with interpretations of the crystal data, and exposed the potential for long-lived conformational substates [58–61]. A similar approach on embedded tetra-nucleotide sequences was performed not long after by Sarai, whose MD simulations enabled the development of harmonic potentials of mean force for dinucleotide flexibility which provided further insight into differential DNA tetramer sequence structure and dynamics and mechanisms of DNA sequence recognition and specificity [62,63]. During these systematic investigations of the sequence dependence of tetrameric repeats in DNA, we learned about artifacts from anomalous α,γ transitions bringing γ to trans (fixed by parmbsc0) [64] and salt crystal formation at abnormally low concentrations [49,65]. Further improvements to the force fields in Amber removed “ladder-like” structures in RNA helices [66–69] and may improve ε/ζ backbone states in DNA [70]. Similar improvements in the CHARMM force fields for RNA and DNA have been published [71,72].

The acknowledged lack of convergence of the structure and dynamics in these MD simulations pushed groups to perform MD simulations on increasingly longer timescales. The first published microsecond length DNA simulations were reported by Orozco and his group [73], with the results clearly showing that even 1 μs of MD was insufficient to fully converge the structure and dynamics of a small DNA duplex. These observations led the ABC consortium to extend their simulations of the 36 tetrameric repeat sequences over the last few years to at least the 1–3 microsecond timescale (unpublished results). More recently, the Orozco work has been extended to bring simulations of the Dickerson dodecamer to the 4 μs time scale [74,75]. Although the authors claim convergence of the internal properties of the helix on the 250–300 ns time scale, longer timescales are likely required to fully relax the B_I/B_II populations, bimodal twist distributions at CpG steps, and ion distributions. Moreover, “end-effects” from terminal base pair opening and fraying are clearly not converged [76]. This begs the question: How long does an MD simulation of a B-DNA helix have to be to sample the dominant structural and dynamic features? Even with access to high performance computing facilities with thousands of CPUs and efficient ports of MD codes to very fast graphics processing units (GPU), this is still a challenging question. However, with access to the very fast Anton special purpose MD engine [77] developed by D. E. Shaw Research—available at the Pittsburgh Supercomputing Center (PSC) through competitive allocation to resources—answering this question becomes tractable. Using such resources, currently MD simulations can provide detailed structural and dynamical information about the atomic structure of biomolecules on timescales up to milliseconds.

In 2011, and then again in 2012–13, we were awarded an allocation of 50,000 and 100,000 —processor hours, respectively, on the Anton machine at PSC to study MD on DNA duplexes. This was sufficient time to perform MD on one of the ABC DNA duplexes for a total of about 56 μs. In deciding which sequence to simulate, it was noted that an interesting feature had emerged in the simulations of one particular sequence of the DNA tetrameric repeats by the ABC consortium [58,59,61]: a bimodal distribution in the twist at particular CpG steps (see Figure 6 in reference [74]). This is the GAAC sequence which flanks the CpG steps with the A-rich sequence AACGAA. In addition to displaying a bimodal twist distribution, the GAAC sequence has bio-relevance, similar to the TATA sequence, since it has been shown to participate as a transcriptional control and initiator for DNA replication [78,79]. Also, like DNA TpA steps, DNA CpG steps show multiple modes of motion and enhanced flexibility [62,75,80]. To better understand the structure and dynamics of this GAAC sequence and to see if we could obtain some form of convergence in the distributions of structural parameters in simulations beyond 1 μs, longer timescale simulations were performed on Anton. The GAAC 18-mer sequence of d(CGACGAACGAACGAACGC) was simulated with conditions matching the original ABC calculations [58,59,61] except in a larger orthorhombic box as required for Anton simulations at that time. The initial MD simulation was started from a canonical B-DNA structure and MD was performed for ~12 μs. The initial analysis showed significant and reversible terminal group fraying, as well as unexpected convergence in the structure and dynamics on the ~1–5 μs time scale for the internal base pairs. Although terminal base pair fraying is expected on the microsecond time scale [81–83], the effective rigidity of the internal DNA duplex when averaged over the ~1–5 μs time scale was confusing as we had never seen such convergence before in MD simulations. Essentially, if average structures are created over intervals of ~3 μs or longer at different time points in the trajectory and overlaid, the RMSD fits show overlap of all atoms, neglecting the terminal 3–4 base pairs, to better than 0.2 Å. Such strong agreement in the structures from different time intervals was unexpected, especially as we assumed that the DNA duplex should display longer time scale breathing, twisting and bending events and to potentially display internal base pair opening events. However, as internal base pair opening occurs on the ~5–100+ ms time scale (or somewhat faster for AT base pairs not in A-tracts and/or GC base pairs in GpC sequence repeats on ~1ms time scale, both of which are mostly absent in our GAAC sequence, [21,23]) clearly these MD simulations are not long enough to see internal base pair opening events with high probability.

However, healthy skepticism and lack of understanding of these initial results prompted us to repeat the simulations not only on Anton, but also using the standard Amber MD engines. Given the underlying differences in hardware between CPU, GPU, and Anton, and differences in the underlying approximations and models of numerical precision, not only between Anton and Amber simulations, but also between the Amber CPU and GPU implementations [45], it was prudent to determine whether these differences can affect the outcome of MD simulations. So after running simulations on the ~12 μs time scale on Anton which only required 1–2 days of Anton computer time, we started the relatively slow process of Amber simulations on CPUs (2 simulations of ~ 2 μs each) and on GPUs (2 simulations of ~4 μs each) to study and detect any possible differences due to hardware and methods. Additionally, in order to reach aggregate simulation times approaching those sampled on Anton, we also explored multiple molecular dynamics simulations [84–86] where an ensemble of 100 independent simulations (ENS) were performed using Amber MD engines and the AMBER ff99SB force field with the parmbsc0 modifications starting from the same DNA structure but with the ion positions independently randomized by swapping with waters for each simulation as described in the methods. These simulations were performed over a six month period starting on a local CPU cluster, continued during friendly user access on the Keeneland Initial Delivery NVIDIA Tesla M2090 GPU system at XSEDE/Georgia Tech, and finally extended to ~900 ns for each independent simulation using the GPU resources on the University of Illinois Blue Waters Petascale resource, for a total aggregate time of ~84 μs. To demonstrate that the effective DNA rigidity on the μs-scale was not only a property (or artifact) of the AMBER force field, we also included another ensemble of 100 independent simulations on Blue Waters using the CHARMM all36 (C36) force field [71] with a total aggregate time of ~91 μs.

Overall, the results suggest that we are able to converge the internal DNA helical structure on the ~1–5 μs time scale as determined by two independent measures of convergence: an assessment of the convergence of internal motions by comparing overlap of principal component projection histograms as a function of time, and a novel measure of overall structural convergence which we term RMS average correlation (RAC) [87]. These observations suggest that there is little significant motion of the internal DNA helices on the timescale of 1 μs – 1 ms. The results also show that reversible base pair opening of the termini occurs frequently, is associated with ion binding events in the groove, can be long-lived, and can go beyond the first base pair. Comparisons of the Anton, Amber CPU and Amber GPU runs show that between them there is little apparent difference in the structure and dynamics of the internal B-DNA helix, with the exceptions that 1) convergence of the terminal base pair opening events occurs on time scales significantly longer than 10 μs and cannot be captured completely via ensembles of shorter and independent MD simulations, and 2) transient base pair opening events to the fourth base pair are only observed when the data is written at frequencies greater than 50 ps. Convergence of the structure and dynamics is also seen with the CHARMM C36 force field, although on a slightly longer time scale due to larger and more frequent terminal base pair opening events.

METHODS

A canonical B-DNA structure with the sequence d(GCACGAACGAACGAACGC) was generated as specified in the original ABC simulations to allow for a consistent comparison. [58–61] The structure was parameterized using the Amber ff99SB force field [88] with the parmbsc0 corrections for α/γ torsions [64], explicit solvent was added using the SPC/E [89] water model for a total of 19012 solvent molecules in an orthorhombic periodic box. Potassium ions were added to neutralize the charge (34 K⁺), and additional 60 K⁺ and Cl⁻ ions were added for a total excess ion concentration of ~150 mM using the Smith and Dang ion parameters [90]. All of the Amber MD simulations were run using PMEMD from Amber 12 and Amber 14 [91,92]. After the models were built, the ion positions were randomized using PTRAJ [87] by swapping random water and ion positions such that no ion was closer than 4 Å to another and all ions were greater than 6 Å away from the DNA to avoid any biasing created by the initial placement of the ions. The simulation protocol is equivalent to the earlier ABC simulations with the exception that the box was made to be nearly cubic since the Anton specialized MD engine did not support general triclinic unit cells at the time the simulations were performed.

The large series of simulations were run (see Table 1) using the same minimization, heating, and equilibration procedures: The solvated structures were minimized using 1000 steps of steepest descent followed by 1000 steps of the conjugate gradient minimization, applying a restraint force constant of 25 kcal/mol-Ų to the entire solute molecule. With the same restraints, heating was done over 5000 steps of MD from 100 to 300 K with a time step of 2 fs, using a weak coupling thermostat [93] at constant pressure and constraining bonds involving hydrogen using SHAKE with the tolerance set to 0.00001[94]. A non-bonded cutoff of 9 Å was used. Long range electrostatics were handled using particle mesh Ewald (PME) using the default PME parameters for Amber with automated pair list updating. After heating, the restraints applied to the DNA were slowly decreased from 5 to 0.5 kcal/mol-A² in 5 intervals, each step first minimizing using 1000 steps of steepest descent followed by 500 steps of conjugated gradient minimization and time step of 2 fs, followed by 50 ps of MD at 300 K, constant pressure and temperature, both with Berendsen coupling constants of 0.2 ps.

Table 1.

The molecular dynamics simulations performed and total time. The ENS and the CHARMM C36 trajectories consist of an ensemble of 100 independent MD simulations aggregated together omitting the first 100 ns of data, see text.

Simulation set	Duration (μs)	Force Field
Anton1	12.27	ff99SB + parmbsc0†
Anton2	44.06	ff99SB + parmbsc0†
CPU1	2.18	ff99SB + parmbsc0
CPU2	2.16	ff99SB + parmbsc0
GPU1	4.33	ff99SB + parmbsc0
GPU2	4.33	ff99SB + parmbsc0
Ensemble (ENS)	83.51	ff99SB + parmbsc0
CHARMM	90.89	CHARMM C36

^†Converted to *.cms format using “amber_topNrst2cms.py”

Anton1 and Anton2 simulations were run using the special purpose supercomputer for molecular dynamics, Anton, built by DE Shaw Research, Inc. using multiple different versions of the Anton software and microcode (initially 2.4.1 and then 2.4.5). To convert the Amber parameter and topology files into formats appropriate for Anton, the available “amber_topNrst2cms.py” script on the computer anton.psc.edu was used with Desmond [95] to create the needed *.cms file. Note that there is a bug in the “amber_topNrst2cms.py” script that will erroneously assign zero mass to C5′ atoms when converting from Amber topologies, so the generated files were hand-edited to fix the mass and further checked to make sure the resulting *.cms file contained the correct Amber ff99 + parmbsc0 force field parameters. The Anton “guess_chem”, “refinesigma”, and “subboxer” programs were then run to set up inputs appropriate for Anton and a series of “anton_run” commands performed to do the simulations. For the Anton runs, constant 300 K temperature and 1 bar pressure with weak coupling using a coupling time “tau” of 10.0, a maximum and minimum velocity scaling of 1.2 and 0.85, and a maximum and minimum expansion per step of 1.05 and 0.97 and kappa of 4.5×10⁻⁵ were imposed. The integration time step used was set to 2 fs and “max_strain” was set to 0.08 performing RESPA [96] on the long-range non-bonded interactions every third step. The AMBER CPU simulations were run using the PMEMD code on Intel-based cluster either in one of the XSEDE systems or at the Center for High Performance Computing (CHPC) at the University of Utah. The GPU simulations were run using the PMEMD.cuda implementation of SANDER from Amber 12 and Amber 14 on NVIDIA Tesla M2090 cards [97]. Production simulations in Amber were performed at constant pressure and 300 K using the weak coupling algorithm for temperature and pressure control with a relaxation time of 5 ps [94]. For the equilibration and production a 2 fs integration time step was used. Long range interactions were calculated using PME with default parameters and a ~1 Å grid spacing [38]. The coordinates were recorded every 50 ps for the Anton simulations (due to IO considerations), and every 1 ps for the CPU and GPU simulations. The CPU and GPU simulation trajectories were written more frequently to determine if the frame rate influenced the analysis. Trajectory data was processed with PTRAJ, CPPTRAJ and Curves+ [87,98], with Anton trajectory data first transformed to the DCD format using VMD [99].

The ENS (ensemble) simulation consists of 100 independent simulations using the same starting structure but randomized ion positions (by random exchanges with water for each of the ensemble instances, as described previously) and different initial velocity distributions. The simulations was run initially using the CPU version of PMEMD on a local parallel Infiniband CPU cluster, followed by runs using the GPU (CUDA) version of PMEMD on the XSEDE Keeneland Initial Delivery system (kids) on NVIDIA Tesla M2090 GPUs, which were then continued on the NVIDIA K20X XK nodes on Blue Waters, for an average of 800+ ns total for each individual simulation. After the run, the first 100 ns of each trajectory from each replica were discarded as “equilibration”. The remaining frames were concatenated together, resulting in effectively one large 83+ μs trajectory. The CHARMM simulations were generated following the same methodology, except for the use of a different nucleic acid force field, water model and ion parameters. The CHARMM TIP3P water model and ion parameters for counter ions were used. The CHARMM C36 force field was modified so that the atom names match the PDB (and AMBER) standard and the c37b2 version of CHARMM was used to generate the initial PSF and coordinate files. These were then converted into AMBER compatible parameter/topology/coordinate formats using the CHAMBER [100] utility of AmberTools. Each of the 100 replicas for CHARMM was run in the NCSA Blue Waters Petascale Resource for a total aggregated trajectory of 91+ μs, with the MD trajectory written at 10 ps intervals. The reference structure used for RMSD calculations in the case of CHARMM was built using the first 10 μs of data from the aggregated ensemble.

Global and local DNA parameters were obtained with Curves+ [98] for the first 2 μs of the all the trajectories to facilitate comparison with AMBER CPU simulations. Additionally, the analysis was also performed for Anton1, Anton2, ENS and CHARMM for the first 10 μs of the simulation (included in the supporting information). The rest of the analysis was performed using both PTRAJ and the AmberTools 13 and Amber 14 versions of CPPTRAJ [87]. Average structures used for comparison between the different simulations were obtained doing an RMS mass-weighted fit to the initial structure followed by a straight coordinate average over all frames or the specified time interval. Analysis of the water and ion distribution was obtained using the “grid” command of CPPTRAJ with a grid size of 100 Å and 0.5 Å spacing. The straight coordinate averaged structure (RMS fit to the first frame) used as a reference for the grid analysis was obtained using the first 10 μs of the Anton 2 simulation. See Supporting Information Table S2 for the input scripts to perform similar analysis. All of the molecular graphics were generated using the UCSF Chimera visualization tool [101].

Two relatively new analysis features of CPPTRAJ were further developed and utilized to assess convergence. This first is the “RMS average correlation” (RAC) or “rmscorr” functionality which loosely can be thought of as a pseudo-autocorrelation function for RMSD values; this essentially measures the convergence of the overall average structure at different time intervals within a single trajectory. For a given time interval or lag (τ) a straight coordinate running average over that time interval is performed over the entire trajectory; each sliding averaged structure over the time interval τ is then either fit to the first averaged structure (time 0−τ) or a reference structure specified by the user, and finally the average RMSD value of all averaged structures of length τ is calculated according to:

$$\mathit{RAC}(\tau )=\frac{{\sum }_{t=0}^N\mathit{RMSD}(\mathit{AvgCrd}(t,t+\tau ))}{N-\tau +1}$$

where N is the total number of frames. At time τ=1, this is the standard average RMSD over the whole trajectory. When τ approaches the end of the trajectory length, the value approaches zero and loses meaning. For μs length trajectories, calculating these values at every time point becomes incredibly computationally demanding despite the OpenMP parallelization of the command. Therefore an “offset” option was added such that the values are calculated at τ=1, τ=1*offset, τ=2*offset, …, τ=n*offset and normally a “stop” time is chosen to truncate the calculation before the final time sampled in the trajectory. To our knowledge, this type of analysis has not been previously done by others, so significant experimentation with the “rmscorr” command was performed in order to better understand the results; we show and explain the utility of this analysis through several examples. Input scripts for CPPTRAJ that we used are supplied in the Supporting Information.

In order to assess the convergence of the internal motions (i.e. the dynamics) between independent trajectories, we looked at the overlap of histograms of principal component (PC) projections obtained from each simulation trajectory as a function of time [102,103]. First, to ensure that the eigenvectors obtained from each simulation being compared match, the coordinate covariance matrix (using only heavy atoms) is calculated using a combined trajectory from both simulations [104]. Each frame of the trajectory is RMS-fit to the overall average coordinates in order to remove global rotational and translational motions. Next, the projection along these eigenvectors of each coordinate frame from the first simulation trajectory is calculated; this is then repeated for the second simulation trajectory. Finally, at each frame t a histogram for each simulation of the PC projection values for a given PC is constructed, and the overlap of these histograms was calculated using Kullback-Leibler divergence, KLD [105]:

$$\mathit{KLD}(t)=\sum _{i=0}^{M}ln\left(\frac{\mathit{hPC}{1}_N(t,i)}{\mathit{hPC}{2}_N(t,i)}\right)\mathit{hPC}{1}_N(t,i)$$

where hPCX_N(t, i) denotes bin i of the histogram from trajectory X for the projection of PC N using data from frames 0 to t, and M is the total number of histogram bins (400 in this case). In order to better avoid cases where one histogram bin is zero and the other is not (where KLD is not defined), histograms were constructed using a Gaussian kernel density estimator with a bandwidth obtained via the normal distribution approximation of the PC data. This analysis was performed with CPPTRAJ which was released with AMBER 14 in April, 2014. In addition to the scripts in the Supporting Information, the topologies, the raw trajectories, and all of the analysis files are available for download at http://www.amber.utah.edu/DNA-dynamics/GAAC.

To simplify notation, for the remainder of the article we refer to the three different GAAC motif repeats of the 18-mer DNA sequence as GAAC1 which corresponds to base pairs (bps) 5–8 and 29–32, GAAC2 which corresponds to bps 9–12 to 25–28, and GAAC3 which corresponds to bps 13–16 to 21–24.

RESULTS

Convergence of the structure and dynamics: How long does an MD simulation have to be until the average properties of a DNA duplex do not change with the AMBER force field in SPC/E water?

The previous work by Dršata and co-workers [75] make the qualitative claim that the basic structural parameters for the internal parts of the helix converge within 300 ns. This work generally agrees with this assessment depending on how one defines convergence and for what properties, although it would be safer to state that simulations on the order of ~1–5 μs in length or longer are likely necessary to fully converge the structural properties of a free DNA duplex in solution, minus the two (or more) terminal base pairs on each end. In the sections that follow, we highlight what differences in structural properties to expect for simulations on different time scales. With access now to longer MD simulation from independent simulations, we can attempt to push this assessment a step further to understand and quantitatively define how well independent trajectories self-consistently converge and/or agree with each other.

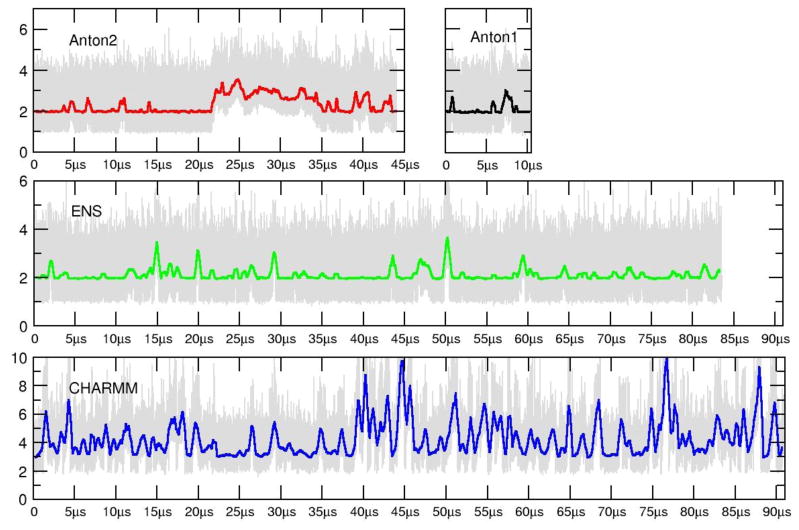
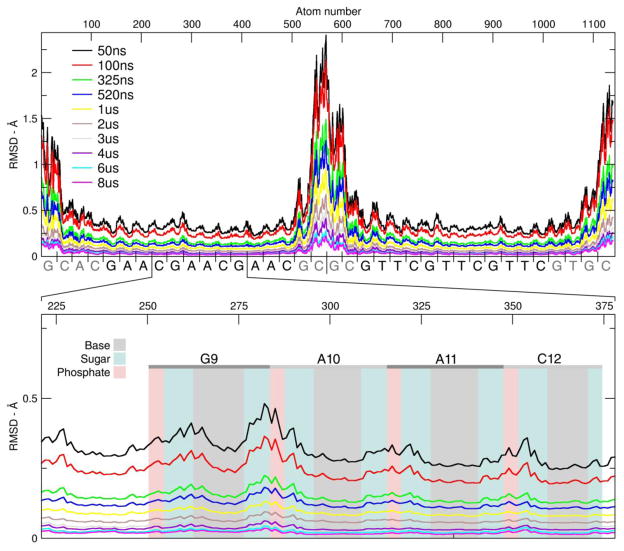
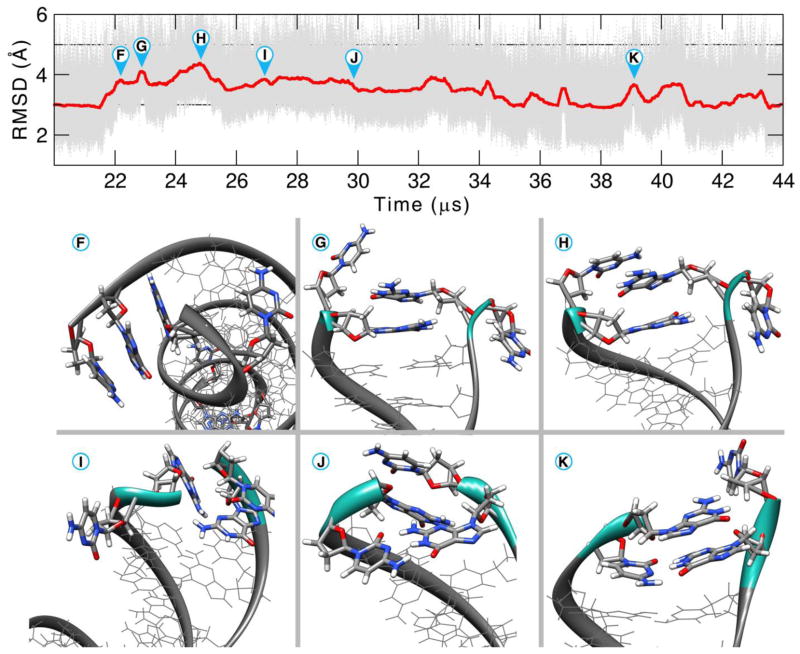
RMSD plots as a function of time are shown for the Anton1, Anton2, ensemble AMBER (ENS) and ensemble CHARMM (CHARMM C36 force field) simulations in Figure 1. The reference structure used for the AMBER force field runs (Anton1, Anton2, and ENS) is the average structure over the first 10 μs of the Anton1 simulation. So as not to bias the CHARMM results, the reference structure used for the CHARMM run is the average structure over the first 10 μs of the CHARMM simulation. In the runs with the AMBER force field, the RMSD values of all atoms are in the range of 1–6 Å. The spikes in the running average of the RMSDs (discussed in more molecular detail later) correspond to terminal base pair opening events, on either one or both ends of the helix. These opening events tend to occur on the μs time scale with open state lifetimes on the ns-μs time scale. As is evident from the plots, too few events have been observed to show complete convergence. Also, in the ensembles of aggregated independent simulations the bumps in RMSD values are not as high and either abruptly end or show shorter duration. This is an artifact of the aggregation of independent MD trajectories, each with insufficient time to fully explore terminal fraying events. However, we note that in the ENS simulations where trajectory information was saved every 1 ps, very transient base pair opening events to the fourth base pair were observed which are not seen in the Anton simulations where the data is saved at 50 ps intervals. The Anton2 run shows fairly consistent behavior to the other two simulations with the exception of a larger deviation from the average structure at ~21.5 μs to higher RMSD values. This event corresponds to the terminal base pairs of both ends opening simultaneously, with one end of the helix actually fraying two base pairs. Just prior to the end of the simulation run (at ~44 μs), the base pairs had completely reformed; the run was not extended any further since our Anton allocation was exhausted. The RMSD plot for the ensemble CHARMM runs is on a different scale with larger transient deviations from the reference; like with the Anton and ENS simulations, the deviations correspond to fraying events on each side of the chain. Multiple base pair openings and backbone deformations are detected for the CHARMM dataset going as far as 3 base pairs, causing pairing mismatches. The observed RMSD plots are consistent with previous simulation work on DNA with the exception of the repeated base pair opening events, which have not been observed at this level of detail previously since prior simulations were significantly shorter. Before going into further details analyzing the structure and dynamics, various measures of convergence were calculated to better assess how long MD simulations of a DNA duplex should be in order to fully converge the structure and dynamics.

Figure 1.

RMSD values (Å) as a function of time for the Anton1 (black), Anton2 (red), ENS (green) and CHARMM (blue) simulations. The plots show the RMSD values of all atoms to the 10 μs average structure at 50 ps intervals from the Anton1 simulations (in gray) and also a running average over 5000 frames. Note that the CHARMM RMSD (Å) values are on a different scale to accommodate the larger fluctuations caused by increased base pair opening observed with the CHARMM C36 force field.

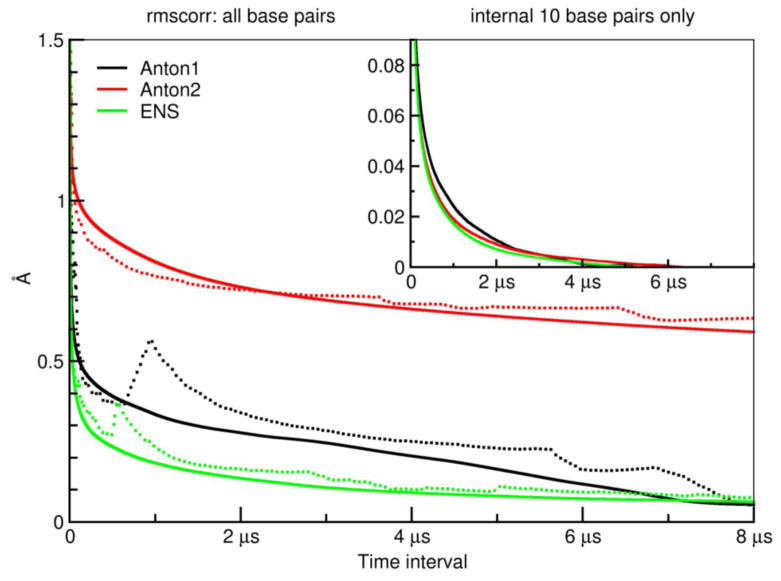
Figure 2 shows the decay in the “RMS average correlation” (RAC) as a function of increasing time interval for the Anton1, Anton2, and ENS simulations. The RAC for a given time interval is the average RMSD of all running averaged structures over that time interval—see the Methods for a more complete description. The solid and dotted lines in each case represent RMS-fits to different reference structures; the solid lines are from fitting to the overall average structure, and the dotted lines are from fitting to the first averaged structure for each time interval (i.e. for time interval τ the first structure is the average from 0 to τ).

Figure 2.

RMS average correlation (RAC) computed at different time intervals using the “rmscorr” command in CPPTRAJ for the Anton1, Anton2, and ENS simulations. In the main plot, the fit is over all DNA heavy atoms of running average structures over the full trajectories (with frames spaced at 50 ps intervals) calculated at each time interval from 50 ps to 8 μs (with an offset of 50 frames) referenced in the RMS fit to either the average structure over the entire trajectory (solid) or the first calculated running average structure from 50 ps to N where N is the time (dotted) for the Anton1 (black), Anton2 (red), and ENS (green) simulations. The initial values at 50 ps are in the 3–4 Å range. The inset plot provides the same information except that the RMS fit is to a common average structure (the 0–10 μs average structure from the Anton1 simulation) and only includes the 10 internal base pair heavy atoms; moreover, to better highlight the decay the small final RMSD value is subtracted from all values (this value was 0.009 Å for Anton1, 0.026 Å for Anton2, and 0.026 Å for ENS).

Since the RAC is a relatively novel analysis, we will first describe some of its features that are dependent on the reference used to RMS-fit (overall average versus first average). Specifically, by definition, as you average over longer periods of time you will necessarily get closer to the average structure. However, if you consider a fit to the first structure (averaged over different time intervals), deviations like base pair opening at different times may produce structures that are effectively further away from the first structure average. For example, consider cyclohexane and its conversion between the two chair conformations. If you compare running averages in time to the flat average structure, the deviations will tend to get smaller. However, if you do the calculation to the first running average structure as you progress will have cases where in the lifetime of a particular chair conformation you may compare left-chair conformations of the reference to right-chair conformations in the time average leading to an effective increase in the RMSD. In other words, the bumps in the dotted line plots expose structural changes on different time scales.

In the case of the 12.27 μs Anton1 simulation (black lines), the decay when fit to the overall average is smooth until 3–4 μs, after which decay occurs more rapidly as the RAC values begin to approach zero at the end of the trajectory (which must happen by definition). In contrast, when fit to the first averaged structure the decay is less smooth, with a particularly pronounced spike at ~1 μs, which corresponds to base pair opening events seen in the Anton1 simulation. The RAC values from the Anton2 (red lines) trajectory show fewer features in the dotted plots since we had periods during the MD trajectory with very few opening events and also a long period of a large opening event. Effectively, there is less correlation in the time scales of events that would lead to significant feature shifts from the solid and dotted plots. It is also evident that the RAC values do not decay as quickly to zero; this is because of the different structural features on the 8 μs timescale in the parts where little opening is occurring to where significant opening is occurring. Finally, the ensemble of independent MD trajectories (green lines) shows the smoothest behavior and decay to zero more rapidly. This is an artifact of the shorter time scales of the simulations (~1 μs per ensemble instance) which means the opening events are less frequent and effectively of shorter duration (due to truncation of the opening event as the simulation was terminated at finite scales, i.e. we get more partial opening events in the termini) and less complete. Despite this, the dotted green shows features of the opening as seen in the Anton1 trajectory on the ~1 μs time scale.

To assess the time scale of convergence within a given simulation one can choose a cutoff point where the slope of the RAC values approaches zero, indicating no further changes in the average structure as sampling time increases. Inset in Figure 2 are the RAC values to the full simulation average structures for the internal ten (GAACGAACGA) base pair heavy atoms. What is remarkable is how fast the decay to the average structure is, such that across all three trajectories, the RMSD to average structures over time scales from ~80–130 ns lead to RMSD values of less than 0.1 Å. By 3 μs, the deviation is less than 0.01 Å with essentially complete convergence in the structures of the heavy atoms of the internal ten base pairs on the 4–6 μs time scale. Although surprising to us, this rapid decay is consistent with the previously discussed fast timescale NMR, fluorescence anisotropy, and electron paramagnetic resonance decays and also with the timescales of DNA, water and ion motion probed by dynamic Stokes shifts with most decays complete by the hundreds of nanoseconds. To better understand what deviations these small changes in structure correspond to, shown in Supporting Information Figure S1 is an overlay of the three average structures from the long trajectories omitting the terminal four base pairs. The small deviation corresponds to small alterations in the backbone geometries at the ends, differences likely due to the proximal opening events and lack of complete convergence. Interestingly, although opening events are minimal beyond the first or second base pair with the AMBER force field, these transient events lead to an observed lack of complete convergence in the DNA structure at the fifth base pair. The RAC profile calculated from the CHARMM simulations shows a similar fast decay to less than 0.5 Å in the first 120–150 ns of simulation time going to less than 0.1 Å by ~ 2.3 μs [34]. Due to more significant base pair opening events and disruption of the structure of the internal helix, the converge of the dynamics occurs on a longer timescale than was observed in the AMBER simulations, and also with a higher final RMS value of ~0.6 Å [34].

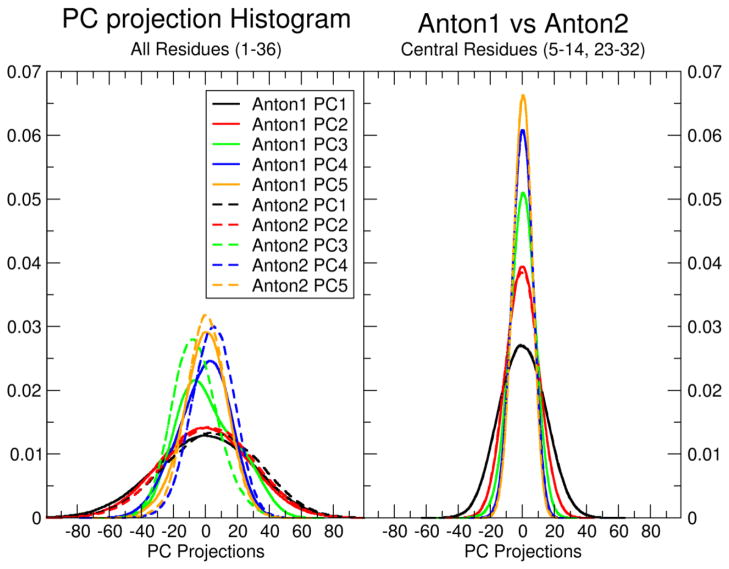
While the RAC is a measure of structural convergence within a single simulation, it is also of interest to measure how well two independent MD simulations converge with respect to each other. Principle component analysis (PCA) in Cartesian space can be used to assess the dynamic properties (i.e. the motions) of a given system. Figure 3 shows the overlap of histograms of the first five principle component (PC) projections from the Anton1 and Anton2 simulations (see Methods for complete details). When the PCA is performed on all atoms (Figure 3, left), there is reasonable overlap between the first and second PCs, but much poorer overlap for the remaining 3 PCs, particularly the third PC. Visual examination of pseudo-trajectories created by projecting the averaged coordinates along each PC shows that the first two PCs correspond to global bending and twisting motions, while the remaining 3 PCs correspond mostly to motions at the termini. A video file showing the described motions is available for download in the Supporting Information. The min/max values using the pseudo-trajectories for total bend are 40.1° and 6.9° respectively, the values for twist range from 29.6° to 32.2°, for tilt −1.7° to −0.5°, roll 7.3° to 4.3° and total length measured from the center of the termini base pairs is 51.8 Å to 56.3 Å to respectively. This also agrees with the experimental observation of a negative twist/stretch coupling measured by Prisner and co-workers [19]. When the PCA is performed on only the 10 internal base pairs (Figure 3, right), there is almost perfect overlap of all 5 PC histograms. These results are consistent with the RAC results, which showed that the decay of RAC values was much faster when fit on only the 10 internal base pairs. Consistent with the comparisons of Anton1 and Anton2, in Figure S2 we show the overlap of the principle component histograms from the Anton2 and the ENS simulations where we notice a closer similarity between both simulations on all the components.

Figure 3.

Overlap of principle component (PC) histograms from PC analysis in Cartesian space calculated from the combined Anton1 and Anton2 simulation trajectories with independent projection of the PCs on the separate trajectories.

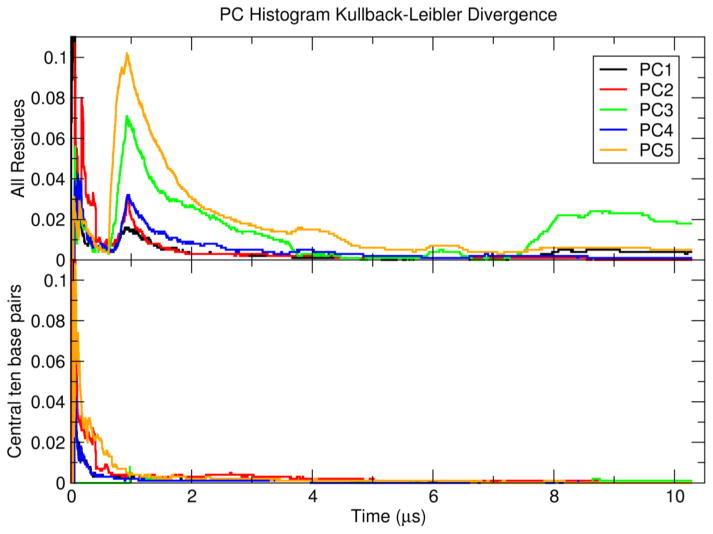
The convergence of the dynamic properties of the Anton1 and Anton2 simulations was quantified by measuring the overlap of the PC histograms via Kullback-Leibler divergence as a function of simulation time, shown in Figure 4. When the PCA is performed on all residues (Figure 4, top), the first two PCs are relatively well-converged within 2 μs. The remaining PCs take longer to converge, particularly the third PC which actually shows an increase in divergence around 8 μs. This is consistent with the observation that PCs 3–5 correspond mostly to terminal motions, and confirms that base pair fraying events are why the simulations are not fully converged on the multiple-μs time scale. As further evidence for this, when the PCA is performed on the 10 internal base pairs only (Figure 4, bottom), the first five PCs are all relatively well converged within 1 μs.

Figure 4.

Kullback-Leibler divergence of PC projection histogram overlap calculated from the Anton1 and Anton2 simulations as a function of time.

Opening events contribute to the majority of structural deviations as is shown in Figure 5. To highlight what these structural deviations refer to, straight coordinate running averages over the trajectories were performed independently on the ENS trajectory at 50 ps intervals with time windows for averaging of 50 ns, 100 ns, 1 μs, 3 μs and 6 μs time scales. The resulting running-averaged trajectories were then independently clustered using CPPTRAJ with the average-linkage clustering algorithm, a sieve of 250 frames, and RMSD omitting the terminal base pairs on each end as the distance metric; this resulted in 15 clusters. Molecular graphics of overlays of the 15 representative structures from each of the clusters is shown in Figure 5. For the shorter time interval structures (i.e. a running average over 50 ns), we notice the wide fluctuations produced by the base opening events at both ends of the DNA molecule while the central base-pairs display only minor structural differences between the 15 representative structures from the clusters used to build the overlay. For the longer time scale conformational averaging, terminal base pair openings are still present at both sides of the structure although the central base-pairs show a tighter comparison with less fluctuation. This shows that as more sampling space is explored, reaching a converged state becomes more accessible.

Figure 5.

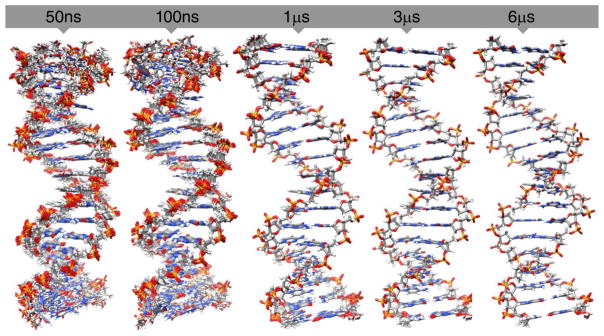
Molecular graphics of representative structures from 15 clustering of straight coordinate running averaged trajectories over different time intervals for all atoms in the DNA 18-mer helix. Running averages over the ENS trajectory were performed over different time intervals (50 ns, 100 ns, 1 μs, 3 μs and 6 μs, side and top view) and the derived trajectory was clustered using CPPTRAJ with the average-linkage algorithm into 15 clusters omitting the terminal base pairs using a sieve of 250 frames. The structures of the representative member of the 15 clusters over each time interval are shown colored by atom.

The atomic fluctuations over different “running average” time windows for the ENS simulation are shown in Figure 6. The values show how much each particular atom fluctuates with respect to the reference used to compute the calculation. Each line is a running average of the atomic fluctuation using increasing window size. When the time window for the running average is 50 ns, the base pairs at the start and at the end of the DNA chain show fluctuations about the average structure in the range of 1.0–2.5 Å. In contrast, base pairs close to the center of the DNA show movement only in the 0.2–0.5 Å range. As we have previously discussed, high fluctuations on both terminal edges of the DNA are produced mainly by base pair opening events. For this sequence, the fluctuations of the first two base pairs on each side suggest frequent fraying events. As the window of the running average is increased and more sampling space become available, the fluctuations start to converge to the average structure, hence lowering the difference. On the bottom plot of Figure 6 we zoom in on the GAAC1 section (residues 8 to 13, atoms 251 through 377). The shaded sections in the figure group the atoms that form the nucleotide (base, deoxyribose and phosphate group). For the 4 bases (gray area) in GAAC1, the bases display low fluctuations of less than 0.2 Å in all of the windows until the fluctuation is less than 0.001 Å at a running average of 8 μs. For the sugar (teal) and phosphate group (light red), the fluctuations are slightly larger and between 0.2 and 0.3 Å. The change of fluctuation range as increasing the windows of the averaging suggest that the main variations detected in the simulations are present in the backbone of the chain. Also, analysis including the base pairs present at the edges will show high variability due to the increased fluctuations caused by fraying.

Figure 6.

Atomic fluctuations of the ENS simulation. Each line represent the fluctuation using increasing running average intervals. Top plot, atoms from 1 to 1139. Bottom plot, detail of GAAC2, from atoms 221 to 378. The shaded area represents the segment of the plot were the atoms of the base, the sugar (atoms C1′ to C5′, including hydrogens) or the phosphate (P, O1P, O2P, O5′ and O3′) moiety can be found. The trajectory was RMS fit to the average structure of the entire simulation with a time step of 50 frames.

Implications for the time-dependent flexibility of DNA?

To summarize the convergence, for the internal ten base pairs the Kullback-Leibler divergence of the first five principal components from the Anton1 and Anton2 trajectories fall below 0.005 by 1 μs and below 0.001 by 5 μs. Similarly, considering the RAC analysis for the ten internal base pairs, the slope is essentially flat by 5 μs with deviations below 0.03 Å by ~1 μs. The convergence times in the 1–5 μs time frame suggest that minimal changes in structure are observed when time-averaged beyond 5 μs despite MD sampling out to over 44 μs. This perhaps should be expected since if the internal dynamics are effectively converged, the only way to see additional modes of motion is via internal base pair opening. As discussed, internal base pair opening is well known from experiment to occur on significantly longer time scales, that is ~5–100+ milliseconds. Although internal base pair opening is slightly faster (> ~1 ms) for AT base pairs not in A-tracts and in GpC repeats [23,106], both of which are mostly absent in the “GAAC” sequence, the time scales for internal base pair opening, likely an activated process, are still three orders of magnitude slower than the fast convergence in the structure and dynamics observed here. If the models and force fields are correct, neglecting internal base pair opening in the millisecond time scale, all of the structural fluctuations are effectively converged very rapidly and on the range of 1–5 μs. This has considerable significance since the conformation of the helix, its flexibility, and interactions with water, salt and other ligands have critical impacts on biological function, including gene expression and regulation.[34] It is well appreciated that DNA deformability, bending and twisting, and dynamics, along with sequence dependent structure are crucial for protein recognition, so it is somewhat surprising that the internal dynamics of the helix converge so rapidly.

Groove width profiles for GAAC1, GAAC2 and GAAC3 for the seven simulations are shown in Figure S3. The characteristic minor-groove narrowing with A-tract sequences is present in A6, A7, A10, A11, A14 and A15. In contrast, the major-groove shows a narrowing in both C8pG9 and C12pG13 steps. Between the seven simulations, the average deviation is 0.05 Å except with A15 and C16 which have an average deviation of 0.12 and 0.24 for the major and minor groove respectively. The top plots in S7, which is an average of the averages from the entire simulations, shows that a direct comparison between our dataset suggests similar and small fluctuations which show a good agreement between the results.

How different are results on the 1 μs time scale between Anton and AMBER on CPUs and GPUs?

To detect and quantify any significant difference or biasing between simulations calculated by each computer methodology we performed extensive measurements of global and local parameters of the seven sets of simulations. Visualization of an overlay of average structures between Anton1, Anton2, CPU1, CPU2, GPU1 GPU2 and ENS simulations extracted from 1 to 2 μs is presented in Figure S4 and shows that the structural differences are actually fairly minor. The structures show all-atom RMS deviations in the range of 0.5 to 1.2 Å except for some more significant distortions on the termini base-pairs where the difference is over 1.2 Å. Excluding the starting base pair (bp, residues 1 and 36) and ending bp (residues 18 and 19), the RMSD average difference between all the structures is less than 1 Å. In we show two different measures of RMSD between all the simulations. The data was obtained comparing an average structure between 1 and 2 μs of the total simulation time. The bottom diagonal shows the comparison values using all atoms and all residues and the top diagonal shows the comparison values using all atoms without the first base pair at each end of the DNA chain. Except for the CHARMM values, the distances are less than 0.4 Å away from each other, which suggest a high similarity between the simulations, independent of the platform on which they were run. The CHARMM values using all residues have a mean value of 4.52 Å difference between the rest of the simulation, which goes to 4.15 Å if we do not include the termini base pairs for the RMSD measurement. This deviation between the AMBER and CHARMM results will be discussed in detail later on. Additional comparisons of the RMSD values among the simulations can be seen in Figure S5.

Comparison of DNA structural parameters on μs time scale

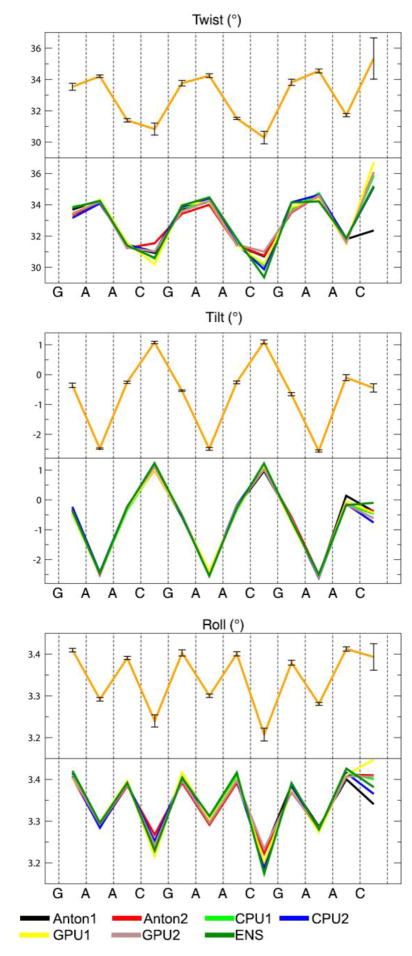
Information about the intra-base pair helicoidal parameters for twist, roll and tilt are shown in Figure 7. The complete set of intra and inter-base pair helicoidal data are included in Figures S6 and S7 of the supporting information. The terminal base pairs show higher variability due to the incompletely converged base pair opening events. This can be seen in the structural parameters used to evaluate the simulations, where the GAAC1 and GAAC2 sequences mostly show very similar values and small deviations due to their distance from the termini. The GAAC3 sequence however, being only two base pairs in from the termini, displays more significant differences and larger deviations, most notably in twist, tilt, roll, buckle, opening, propeller and stretch. Also notable are larger than expected deviations at the CpG steps for roll, twist, buckle and stretch, which is indicative of the greater difficulty in converging the bimodal distributions for this step as seen previously [74,75]. Despite these small differences on the 1 μs time scale, the helicoidal parameters are mostly converged and show the expected sequence dependent trends.

Figure 7.

Selected intra-base-pair values using the first 2 μs for each simulation. Values for twist roll and tilt of the 3 GAAC motifs. Bottom plots show the seven simulations of this work, top orange plot shows the average values.

The structural parameters twist, roll and tilt were also computed independently for the first and second halves of the trajectories to further measure convergence (Figure S8). The plots show normalized distributions for the twist, roll and tilt structure parameters of the C4pG5 step for all simulations. The overlay of the distribution shows a high level of similarity between the simulations with less than 0.01° of difference.

The DNA dynamics of the backbone show a characteristic bimodal distribution between two distinct conformations belonging to the B family, known as B_I and B_II that can be characterized in terms of the ε and ζ torsion values in the DNA backbone [74,107,108]. The complete simulation trajectory was analyzed and the average time spent in each substate for each simulation is shown in Table 3. Given the large standard deviations, the sampled distributions are essentially indistinguishable. The complete B_I/B_II values for each step are available in Table S1 in the Supporting Information. The distribution between B_I/B_II conformations for GpA steps (G5pA6, G6pA10 and G13pA14) in the GAAC sequence shows a distribution of ~70–30% which matches experimental quantification performed by Hartmann using NMR analysis of 63–37% [108]. For the adenine steps A6pA7 and A10pA11 the distribution remains close to 90–10% in the seven systems tested and close to the observed value of 88–12%. For the steps G13pA14 and A14pA15, even as they close to the end of the sequence, the distribution remains close to the experimental values. In Figure S9 of the supplemental information we show the groove widths and helical information using the average value from the first 10 μs of simulation. The major groove is 1–2 Å lower in comparison to the AMBER simulations (Anton1, Anton2 and ENS simulations are included as reference, using the same average window). This causes increased values in the minor groove. Toward the GAAC3 section of the DNA, the values show a higher fluctuation due to base pair opening. This is also present in the opening, propeller, shear, stagger and stretch parameters, which show increased deviations toward GAAC3. In Table S3 we show the CHARMM and Anton2 averaged helicoidal parameters obtained from the first 10 μs average structures from the full trajectory using residues 3–16, 21–34 and the same parameters from an experimental DNA NMR structure (PDB id: 1NAJ). Although the experimental and simulation numbers are not directly comparable due to the different sequence, overall, as seen in Figure S1, the rise, base pair tipping and roll in the CHARMM simulations are slightly too high whereas propeller is likely too low.

Table 3.

Average distribution percentages between the B_I-B_II backbone conformational substates using the first 2 μs for each simulation.

	BI (Std. dev.)	BII (Std. dev.)
Anton1	86.9 (11.3)	13.3 (11.1)
Anton2	87.2 (10.5)	12.8 (10.5)
CPU1	86.6 (11.6)	13.4 (11.6)
CPU2	86.8 (10.8)	13.1 (10.9)
GPU1	86.8 (11.8)	13.2 (11.8)
GPU2	86.9 (10.7)	13.1 (10.7)
ENS	86.5 (12.1)	13.5 (12.1)

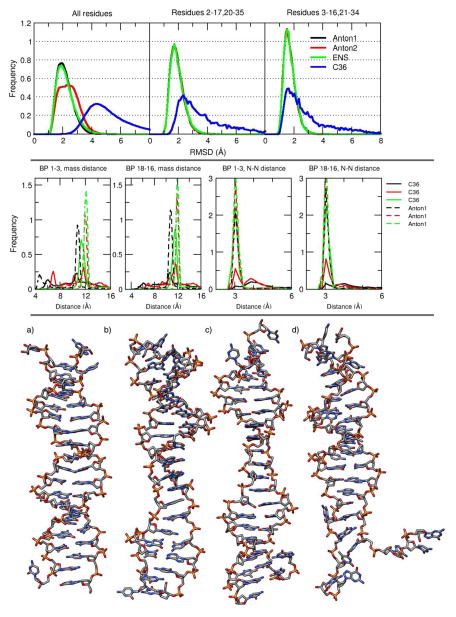
The RMSD values from the CHARMM simulation in Figure 1 show higher deviations from the reference structure caused by multiple structural fluctuations during the entire simulation. The RMSD distributions for the Anton1, Anton2, ENS, and CHARMM (C36) simulations are shown in the top panel of Figure 8. When all residues are included in the analysis, the Anton2 and the CHARMM simulations wider distributions compared to the ENS and Anton1 simulations. This is caused by multiple base pair opening events in the Anton2 and CHARMM simulations. If the base pairs at both edges of the DNA are taken out of the analysis, the histogram of the Anton2 simulation now matches with the Anton1 and ENS simulations. However, the distribution from the CHARMM simulation is still relatively wide, ranging from 2 to 10 Å RMSD. If only base pairs 3 through 16 are considered, although the CHARMM distribution remains wide, the peak of the distribution now matches relatively well with the other three simulations.

Figure 8.

Top: histogram of RMSD values for the Anton1 (black), Anton2 (red), ENS (green) and CHARMM C36 (blue). The reference for the AMBER simulation was a 10 μs average structure from Anton1. For the CHARMM simulation, the reference used was also a 10 μs average structure obtained from the full CHARMM simulation. Middle: normalized histograms of the distance vs. time of end base pairs for CHARMM and Anton1. Each of the plots represents a histogram of the distance vs time analysis for the 3 base pairs at the end of the DNA chain, using the full CHARMM trajectory. The two plots on the middle-left were calculated using the distance between the center of mass for residues 1, 36 (black), 2, 35 (red) and 3, 34 (green) and the base pairs on the other end of the DNA chain (pairs 18,19, 17,20 and 16,21). The solid lines are from the CHARMM simulation, dashed lines are from the Anton1 simulation. The two plots on the middle-right were obtained measuring the distance between the N1 atom of guanine and N3 of cytosine which gives a good measure to determine base pair opening. Bottom: the 4 representative structures of the most populated clusters from the clustering analysis using the full C36 trajectory (no hydrogens are shown). The clustering was obtained using the average-linkage algorithm (see Table S2 for exact CPPTRAJ input).

To compare the dynamics at each end of the DNA chain between the CHARMM and Anton1 simulations, the distribution of distances between the center of mass of residues comprising the base pairs at each end of the DNA (i.e. base pairs 1–3 and base pairs 16–18) is shown in the two left-most plots of the middle panel in Figure 8. The left-most plot shows distance distributions for base pairs 1–3, which are comprised of residues 1 and 36, 2 and 35, and 3 and 34 respectively. The experimental value between the center of mass of a GC base pair is ~12 Å which we can see is highly populated for the 2^nd and 3^rd base pairs in the Anton1 simulation (dashed red and green lines). The distance distribution of the first base pair (dashed black line) in the Anton1 simulation shows peaks at 11 Å and ~4.5 Å due to base pair opening events. In the CHARMM simulation, the distance distribution for the first base pair (solid black line) ranges from 4 Å to 15.5 Å, with slightly higher populations around 5 Å which corresponds to mismatched stacking structures, explaining the decreased distance value between the bases (see below). Base pair 2 (solid red line) shows a population peak at ~11.8 Å corresponding to a correct Watson-Crick (WC) pairing between the two bases and another peak at ~7 Å which corresponds to a stacking mismatch, reducing the distance between both residues. Although the 3^rd base pair (solid green line) has a peak that is close to the correct pairing distance, the fluctuations of the simulation are too high to allow for a stable WC pairing. The second-to-leftmost plot shows distance distributions for base pairs 16–18, which are comprised of residues 16 and 21, 17 and 20, and 18 and 19 respectively. In the Anton1 simulations, the distance distributions for base pairs 16 and 17 (green and red dashed lines) show the majority of the population at the expected value of ~12 Å, while base pair 18 (black dashed line) shows a more broad distribution due to the fraying effects studied in this article. For the CHARMM simulation, the fraying effects are somewhat reduced since the population is increased to the expected value as we move from the 18^th to the 16^th base pairs. The two right-most plots of the middle panel of Figure 8 show the distribution of distances between the N1 atom of guanine and the N3 atom of cysteine. Using these atoms as anchors to measure the distance between two base pairs helps in the detection of opening between DNA base pairs and complements the analysis done using the center of mass of the nucleotide. In a similar manner as with the previous observations, the Anton1 simulation have a maximum population at the experimental value of ~3 Å increasing from the 1^st to the 3^rd and from the 18^th to 16^th base pairs. For the CHARMM simulation, the distribution of distance values looks similar for base pairs 1–3 and for base pairs 18–16. The outer-most base pairs (1 and 18) of the CHARMM simulation have peaks around 4 Å, the next base pairs in (2, 3,17, and 16) show peaks closer to the experimental value, but still having significant population in the 4 Å area.

The bottom panel of Figure 8 shows the representative structures of the 4 most populated clusters from a clustering analysis performed using the full CHARMM trajectory (the CPPTRAJ input used to perform this analysis is shown in Table S2). The structure a represents a cluster populated in >81% of the trajectory for CHARMM, and structures b, c, and d represents 6.5 %, 3.7 %, and 1.3% respectively. The analysis produced over 20 clusters with less than 0.01% of population present in the trajectory, which suggests a constantly changing structure in the simulation which is consistent with the wide RMSD population distribution shown in the top panel of Figure 8. Despite the large structural fluctuations of DNA in the CHARMM simulations shown in Figure 8, the high population of a single cluster compared to all other clusters indicate that by ~2 μs the structure has converged for at least the internal portion of the helix.

Events requiring longer simulation times

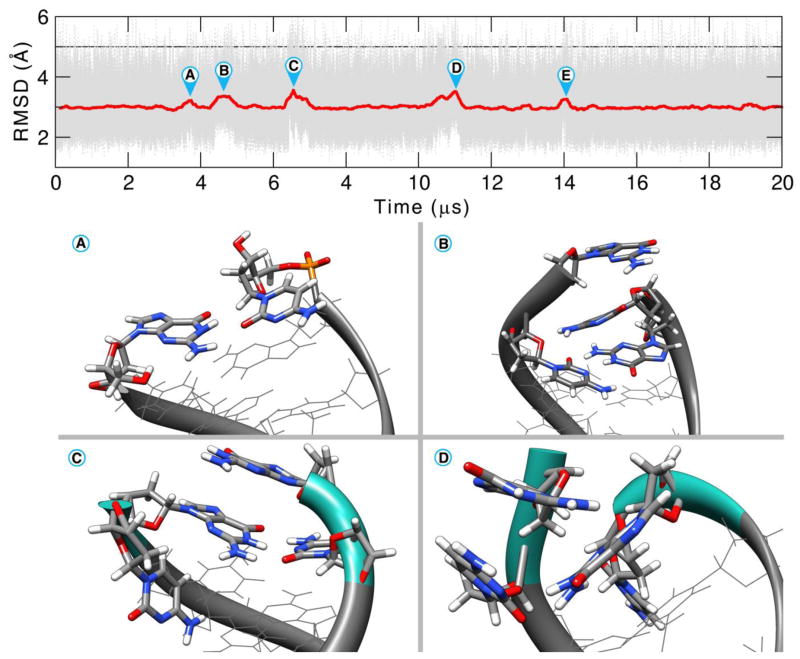
Extending the simulation time allows exploration of different aspects of the base pair opening. The opening events explore different conformational space (e.g. minor or major groove binding, base pair flipping), show differential interactions with ions and solvent, and can be observed to go beyond the second or third base pair. The Anton2 MD simulation of 44+ μs is one of the longest continuous simulations of DNA performed to date and shows a rich dynamic behavior of opening events on both ends of the helix. Although fraying of DNA has commonly been observed at the termini in MD simulations on the microsecond scale [83,109–111], few examples have explored the diversity of structure and dynamics sampled here with openings beyond the first base pair, and, in spite of seeing multiple events, the MD simulations are not yet long enough to fully characterize the opening events. Referring back to Figure 1, multiple fraying events are present during the first 20 μs. The detail of the first half of the simulation is shown in Figure 9. In conformation A and E we see a base mis-pairing between residues G1 and C36 with a RMSD difference of 0.9 Å. In conformation B a stacking interaction was formed between the end base pairs C18 and G19 after fraying and a higher difference of 1.1 Å is observed. The bases remained stacked for almost 500 ns before returning to the canonical base pairing. In conformation C, residue C36 breaks the pairing and twists toward the minor groove (difference of 1.3 Å). Conformation D has 2 step base-pair openings (base pairs 1–36 and 2–35). C36 twists toward the minor groove. This results in a backbone distortion and a flip of 19° on the χ angle of G35. The resulting orientation allows for a NH-π type of interaction between the diazine ring of the cytosine and the amino hydrogen of G1.

Figure 9.

RMSD for the Anton2 simulation of the residues 1 to 36 showing the first 20 μs of simulation. For clarity, the RMSD values are presented with a 5000 frame running average. See text for discussion.

During the second half of the simulation, a long distortion caused by multiple opening events and interaction of the opening base with the minor groove is seen. The dynamics from 20 to 44 μs of Anton2 are shown in Figure 10. Multiple fraying events occur at the same time on both sides of the DNA chain, raising the RMSD values. Although the long-lived opening event hints at instability of the DNA duplex, by the end of the simulation both termini have reformed the native Watson-Crick base pairing. Investigating the time course, at 21.5 μs, the first and second base pairs open and G1 forms a stacking interaction with G35 (conformation F). From the RMSD values, this stacking formation is formed with the first base pair opening (RMSD 1.1 Å) and the approach of the guanines to form the stacking interaction. The process takes ~350 ns. In a similar manner, the same stacking configuration occurs on the other side of the chain with first and second base pair openings and stacking of C19 with G17 (difference of 3.7 Å RMSD from the starting structure). Rearrangement of the stacking in G1 and G35 and the flipping of both the free C2 and C36 causes widening of the minor groove and splitting of the double helix, increasing the RMSD to 3.2 Å (conformation G). Residues C18 and G19 remain in the stacking configuration. Conformation H has the highest RMSD difference from the starting structure with 3.5 Å. Residue 2 flips back on top of G35 which was forming the stacking with G1 and C36 goes into the major groove. The distances between the C1′ atoms from the 3^rd base pair increases from 8.6 to 9.0 Å in this conformation. At the other side of the DNA chain, base pairing between residues 17 and 20 reforms, although residue 18 flips toward the minor groove. This conformation remains for ~100ns and the residue 1–35 stacking is lost. Simultaneously, between configurations H and I, the base pairing reforms at residues 17–20 and 18–19, lowering the overall RMSD values. The configuration I where the residues 1, 2, 35, and 36 are not forming Watson-Crick pairing, and not interacting with each other in any other form, remains for ~10 μs. Multiple short-lived single base pair openings occur between residues 18 and 19, reforming each time. In configuration J the base paring between residues 2 and 35 reforms and residues 1 and 36 flip back inward from the DNA grooves. The reference RMSD value of ~3 Å is once again obtained until 35.1 μs. The rest of the simulation time we observe fraying similar on both ends to the one in conformation K, with a single base flipping toward either groove.

Figure 10.

RMSD for the Anton2 simulation of the residues 1 to 36 showing the second half of the simulation, from 20 to 45 μs. For clarity, the RMSD is presented with a 5000 frame running average. See text for discussion.

A preference for base pair opening and fraying events is shown in the 1–36 base pair, which may be caused by the closer presence of an AT base-pair as opposed of the 18–19 end, which has 3 consecutive GC base pairs. It is important to notice that multiple opening events occur at the same time and in a short time scale. The opening events occurring when reaching 21.5 μs shift the structure to a distorted DNA chain in ~2 μs. This distortion is eventually lost and the original structure is once again obtained only after ~12μs of simulation. This is important because routine applications of MD to nucleic acids include aggregate sampling times on the 1–2 μs timescale, which leaves out important sampling conformations and folding-refolding events that only can be achieved with longer simulations.

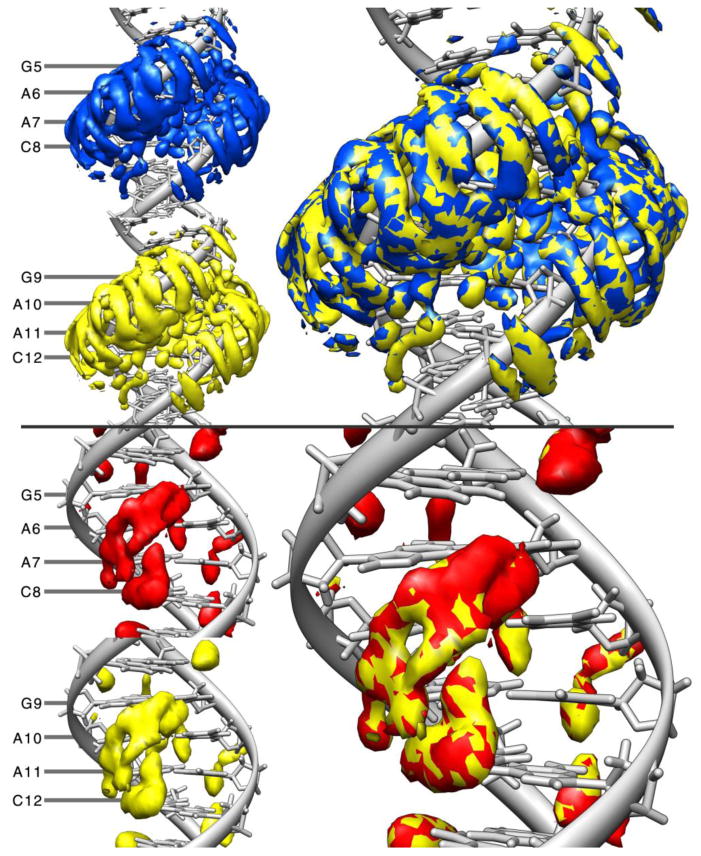
Further estimates of convergence are shown by characterizing the average water and ion density around the various GAAC repeats in the Anton2 simulation as shown in Figure 11. The top part of the figure shows a rendering of the binned water density on top of molecular graphics of average structures for the GAAC1 and GAAC2 regions using equivalent contouring levels and on the top-right side an overlay of both the densities. We observe that qualitatively, both densities are similar, suggesting the same solvation density for both GAAC1 and GAAC2 sites.

Figure 11.

Water (top) and K⁺ (bottom) densities for Anton2. On the top figure, blue represents the water density grid around residues 5 to 8 and the density around residues 9 to 12 is in yellow. The bottom plot represents the K⁺ density grid for residues 5 to 8 in red and residues 9 to 12 in yellow. The different colors aid to distinguish each grid when they are combined on the right side. Both grids were calculated using the first 10 μs of the simulation. The resulting grid from GAAC2 was then translated to match GAAC1 using cpptraj and the overlay of both densities is shown in the right. Reference for both computations was an average 10 μs structure obtained from the Anton2 simulation.

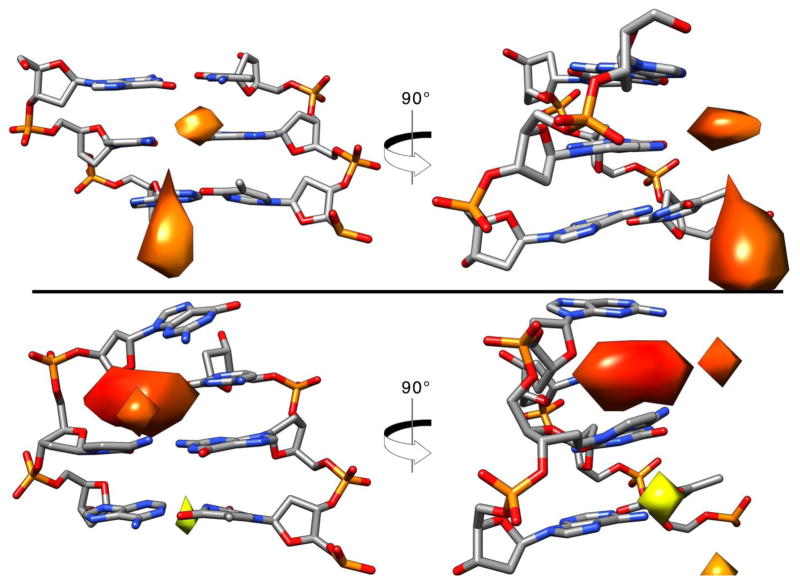
The ion distribution match in a similar manner presented as an overlay in Figure 11, bottom right. Ion distribution at the end base pair of the DNA is presented in Figure 12. The top image shows a structure of the most populated cluster of the Anton2 simulation with the Watson-Crick pairing formed. The distribution of the K⁺ ions is present toward the mayor groove, similar to what is shown in the previous image. Bottom image shows the second most populated cluster with an opening event where G1 has shifted, breaking the pairing with C36. Analysis of this structure revealed inclusion of K⁺ density inside the cavity left where the G1 was. It is possible that a direct influence of the ions present in the simulations contribute to the frequency of the base pair opening events [23,81,111,112], although further studies will have to be done.

Figure 12.

Base opening events in relation to ion binding. Top: most populated structure from clustering analysis of Anton2 using average-linkage algorithm into 10 clusters. The 5x bulk K⁺ ion density is shown, only base-pair steps 1 through 3. Bottom: second most populated representative structure with an opening event and the K⁺ grid using the same ion density. Coloring of the grids are based on closeness to the center of the grid: red is closer, yellow is farther.

CONCLUSION

In this work we present extensive analysis of multiple μs-length MD simulations of DNA using Amber12 and Amber 14 on multiple computer architectures. The results show that despite the underlying differences in hardware, the simulations run on different architectures overall show very little structural variation with respect to one another. The main difference between the simulations is in the dynamics of terminal base pair fraying, which is not completely converged even on the μs time scale. Using the Anton supercomputer, we were able to perform one of the longest MD simulations of DNA to date (~45 μs). It is important to note that even though multiple terminal base pair fraying events occurred during this simulation, including one event that involved multiple base pairs over many μs; these base pairs were able to reform, indicating the current force field is reasonably robust. Additionally, we show that for the latest AMBER and CHARMM force field for nucleic acids, there is a fast decay in the dynamics of the internal section of the DNA chain. The amount of sampling and simulation time obtained with the current computer power is enormous and can provide a wealth of data, but this is a double-edge sword. We are now reaching the point where the data becomes available faster than we can actually perform the analysis. Although we observe very transient base pair opening events up to 4 base pairs when data is recorded every 1 ps that are not observed when data is recorded every 50 ps, considering the data explosion and I/O-efficiency considerations from frequent data writes on high performance computing systems such as Blue Waters, we now only save the data at 10 ps intervals (which appears to be a good compromise). Extensive simulation time is only useful with modern and detailed analysis methods to properly gain insight into phenomena of interest. Furthermore, more elaborate sampling technologies, such as temperature replica exchange, Hamiltonian and multi-dimensional replica exchange, meta-dynamics and umbrella sampling, enabled by access to national large-scale computational resources, such as the Blue Waters Petascale Resource, require efficient and complete methods to study convergence [101, 102]. Analysis of the internal modes of vibration with PCA and RMSD average correlation provides a further measure of comparison between the different simulations and their convergence.

Table 2.

RMSD values in Å between the average structures from 1 to 2 μs of MD simulation. The bottom diagonal values represent the RMSD using all the atoms, the top diagonal is using all atoms of residues 2–17 and 20–35.

	Anton1	Anton2	CPU1	CPU2	GPU1	GPU2	ENS	CHARMM
Anton1		0.14	0.08	0.06	0.11	0.12	0.07	4.03
Anton2	0.15		0.14	0.12	0.13	0.17	0.11	4.14
CPU1	0.18	0.23		0.054	0.064	0.10	0.089	4.19
CPU2	0.093	0.17	0.11		0.056	0.096	0.069	4.19
GPU1	0.32	0.38	0.23	0.27		0.065	0.090	4.18
GPU2	0.37	0.39	0.24	0.29	0.23		0.093	4.19
ENS	0.095	0.14	0.17	0.11	0.29	0.27		4.17
CHARMM	4.57	4.50	4.53	4.53	4.52	4.52	4.53

HIGHLIGHTS.

• The structure of the internal DNA helix converges on the 1–5 μs time scale.

• Terminal base pair openings on the μs time scale are structurally diverse.

• Ensembles of molecular dynamics simulations match long time scale simulations.

• AMBER CPU and GPU simulations match those performed on Anton.

• MD with multiple force fields suggest absence of dynamics from 1 μs – 1 ms.