Conflicts of Interest, Selective Inertia, and Research Malpractice in Randomized Clinical Trials: An Unholy Trinity

Abstract

Recently a great deal of attention has been paid to conflicts of interest in medical research, and the Institute of Medicine has called for more research into this important area. One research question that has not received sufficient attention concerns the mechanisms of action by which conflicts of interest can result in biased and/or flawed research. What discretion do conflicted researchers have to sway the results one way or the other? We address this issue from the perspective of selective inertia, or an unnatural selection of research methods based on which are most likely to establish the preferred conclusions, rather than on which are most valid. In many cases it is abundantly clear that a method that is not being used in practice is superior to the one that is being used in practice, at least from the perspective of validity, and that it is only inertia, as opposed to any serious suggestion that the incumbent method is superior (or even comparable), that keeps the inferior procedure in use, to the exclusion of the superior one. By focusing on these flawed research methods we can go beyond statements of potential harm from real conflicts of interest, and can more directly assess actual (not potential) harm.

1. Introduction

One might have hoped that Altman’s (1994) scathing criticism of “the scandal of poor medical research”, among other calls for reform, would have served as a wake-up call to ensure that a discipline as important as clinical trials would be met with a commensurate level of professionalism, so that pretty much only the best research methods would be used. Not only is this not the case, but in fact one might even question if the situation has improved at all since then. Not that this even matters; even if there is demonstrable improvement, which is questionable, the situation as it is at this point in time is still intolerable; there is no consolation in arguing that it was even worse earlier. One scathing report declared that the majority of published research findings are false, and added that the situation is especially acute when there is “greater flexibility in designs, definitions, outcomes, and analytical modes; when there is greater financial and other interest and prejudice; and when more teams are involved in a … chase of statistical significance” (Ioannidis, 2005). Another review found that this problem is especially likely when the studies are sponsored by the manufacturers (Lundh et al., 2012).

The Institute of Medicine (2009) recently issued a report concerning conflicts of interest in medical research, and calling for more research into this important field. Lexchin (2012) addressed some mechanisms by which bias can be introduced into medical studies so as to produce the favored outcomes that bring profits to the sponsors. Though this list is already quite illuminating and alarming, it is also somewhat incomplete, in that it does not include flawed statistical methods that can also create biases to swing the results in the favored direction. We aim to bridge this gap, and hope that our paper will be complementary to Lexchin (2012).

Of course, conflicts of interest cannot explain all of the problems with medical research. Sometimes improper methods are used even when there is no hidden incentive to use these methods. And once improper methods become established as the norm, they become quite difficult to dislodge. So inertia is a problem as well. We could leave it at that, and declare that conflicts of interest and inertia are two distinct problems that conspire to compromise the quality of randomized trials, and call it a day. But, alas, the two apparently distinct problems seem to be related, in that the tension between inertia and progress is governed, at least to some extent, by expediency. Which serves the interests of the research team more, the newer and better method (not that new methods always are better) or the status quo? This consideration seems to figure into the calculus that determines which methods stay and which go, so there is selective inertia. So while any new method will need a certain “escape velocity” to ascend to the point of actually being used, some may need a greater escape velocity than others.

The history of medicine is replete with examples of useless and even harmful (in some cases fatal) treatments that became the norm. See, for example, Chapter 1 of Harrington (1997) and Chapter 11 of Panati (1989). We can look back now and laugh about leeches and bloodletting, without ever realizing that future generations may take an equally dim view of our research practices. “You mean to tell me”, they may ask, “that the researchers of the early 21^st Century actually preferred approximate analyses to the very analyses they were trying to approximate? I forgot now, was this the same time that they used leeches?”. And these future generations would not be so far off the mark.

Bloodletting actually killed patients in the here and now, right there where and when it was applied. When a researcher uses a flawed method, there is no corpse in his or her office. The computer does not blow up. The adverse effects are all way downstream, displaced in both space and time, and unlikely to ever get traced back to the source, which was the poor decision to use a flawed method, which then resulted in exaggerated treatment effects, which in turn led to overly optimistic usage guidelines, which in turn led to more patients taking the treatment than should have, with predictable morbidity and possibly mortality. We will take a critical look at some of these flawed methods, and hope that the day will come soon when they too are behind us forever.

In fact there are many, many improper methods in common usage; it might take an encyclopedia to list all of them. So there is no effort to be comprehensive. Rather, we aim for what might be considered to be the lowest hanging fruit (not necessarily in terms of frequency of use, but rather in terms of how transparent the flaw is). We do not address methods that are merely suboptimal. Nor do we address flawed methods if these flaws are difficult to understand. Though we discuss statistical methods, we restrict attention to those that are so blatantly wrong that just about anybody can appreciate the egregious nature of the flaws, so no statistical background is required to understand the main themes of this article. We shall focus on 1) the perverse preference of approximations over the very quantities they are trying to approximate; 2) a common randomization method that introduced more problems than it solved; 3) a method for evaluating trial quality that is akin to simply declaring by fiat that all trials are of the highest quality; 4) a method that allows sponsors to treat patients with their treatments and then simply exclude from the analyses any outcomes they find inconvenient (including deaths); 5) outright lying about using the appropriate analysis population; and 6) wasting information by combining fundamentally different outcomes for the purpose of analysis (and, often, for the purpose of presentation, too).

Through a combination of freezing, boiling, centrifuge, filtering, and possibly other methods it is possible, in some cases, to separate pure water from its contaminants. It is quite alluring to believe that the same can be said for separating valid inference from its contaminants. Surely, given the plethora of statistical adjustment techniques, it must be not only possible but also easy to filter out biases and arrive at the truth even when the study had biases? For that matter, surely if the results are impressive enough, then who cares how they were arrived at? Let the technicians worry about the minutia of the methodological details, and let the movers and shakers concern themselves with the important issues. Few would actually say this explicitly, but this kind of thinking is almost always operating in the background, driving decisions to overrule the researchers who raise objections based on concerns over flawed methodologies.

So it is worth noting that these flaws we discuss are not appendages that can be cut off. Rather, they are woven into the fabric of the trial, and will rear their ugly heads in just about any analysis. Ignoring the biases is a strategy, in fact a rather popular one. Unfortunately, it is not a very good strategy if our concern is with arriving at the truth. There is no place in serious research for any of the flawed methods we shall discuss, because any one of them can invalidate a trial all by itself. Yet they persist and thrive. Were all of these methods eradicated, there would still be other flawed methods in common use, but at least this would be a great start. It is our hope that exposing these flawed methods for what they are is the first step along this path to better research.

2. Parametric Analyses

When we think about what it means for a food to be organic, we may wonder why such food would even need to carry a special label. After all, shouldn’t organic food be just plain old food, and anything that is not organic would need a special label, such as polluted food? And yet a burger and fries, with soda and dessert, have become standard fare to a large enough portion of our population that this, and similar food items, are what have come to be known as just plain old food, and so it is the organic, healthy, all natural, and non-GMO foods that need to distinguish themselves with special labels. This is a shame, because at a casual glance one might consider organic food to be new, untested, possibly unsafe. Without the facts, one may interpret prudent avoidance as advocating conventional food and avoiding organic food. The situation is not so different when it comes to non-parametric (exact) analyses. Instead of labeling these as standard analyses, as they should be, and labeling everything else as inexact approximations, we instead label the inexact analyses as standard, and hence the exact ones need to justify themselves. In a conservative culture, in which sponsors do not want to bring something new before regulators, and regulators likewise do not wish to propose something new to the sponsors they regulate, the status quo remains in effect past its usefulness. This does not require any intricate theory to understand. It comes down to a very simple issue. Do we prefer an approximation, or do we prefer the very quantity it is trying to approximate?

Red herrings pack the water like sardines, but if we keep our eye on the ball, then we will see right through these feeble attempts to justify and defend the indefensible. There may be cases in which there actually is a reason to present a parametric analysis in addition to the exact one, but there can never be a reason to present the parametric analysis exclusively, to the exclusion of the exact analysis that it is trying to approximate. Why, then, do we see exact p-values about as often as we see the tooth fairy? Certainly inertia is part of the problem. Precedent tends to be followed even when misguided.

There is also a more sinister reason. Deep inside, we all know that no data are really normally distributed (Geary, 1947). Perlman et al. (2013) recently made this point in a rather amusing way, by pointing out that if heights, e.g., were normally distributed (as often claimed), then with probability one we would at some point encounter someone with a negative height. And we thought Eddie Gaedel was an invincible designated hitter! It is nothing short of astonishing that anybody in this day and age, let alone researchers whose job it is to know better, still claim that data can have a normal distribution, or, even worse, that without a strong reason to suspect otherwise, must necessarily be normally distributed. This violates both logic and the public trust placed in the researchers, and suggests the possibility of negative IQ scores too.

OK. So no data have a normal distribution, technically speaking. But surely the central limit theorem ensures that this does not matter, since parametric analyses are robust to violations of the assumptions? In fact no, they are not. At least not in the way they are understood to be. Nobody can meaningfully bound the difference between the exact p-value and the parametric one for any given set of data, at least not without actually computing both (Berger, 2000). We want to be able to argue that the approximate p-value was 0.001, and that parametric analyses are robust, so therefore even without computing the exact p-value we can still infer that it cannot exceed, say, 0.01. But this inference is simply not supported by the central limit theorem, which actually has very little to say about an actual study with a finite sample size.

Using parametric analyses can also serve as part of a manipulation that results in doubly jeopardy. One cannot state in the protocol that an exact analysis will be used and then argue later that the data were so normally distributed that the parametric approximation was better than the exact p-value. This would be recognized as nonsense (just how normally distributed would the data need to be to render the approximation preferable to the very quantity it is trying to approximate?). However, one can always move forward, towards more valid and justifiable analyses. So one can state in the protocol that a parametric analysis will be used. Doing so leaves open discretion to change that later to an exact analysis on any basis. This means that the level of scrutiny for normality can depend upon the results of the parametric analyses. If the results of the parametric analyses are to our liking, then we never stop to ask if they were justified (as if they even could be justified). But if these parametric analyses fail to show a treatment effect, then we start to question why. Maybe the data were not normally distributed? Maybe we should use an exact analysis instead? This line of reasoning results in the opportunity to effectively take two (or more) bites of the apple.

The focus of this section has been on a rather obvious fact, as opposed to one that requires in depth knowledge to appreciate. Anyone can understand that there is no way for an approximation to be better than the very quantity it is trying to approximate. This is a maxim that cannot be disputed. Nor can it be disputed that no real clinical trial data can have a normal distribution. To argue otherwise is to argue (correctly) that you do not really understand what the normal distribution is. For a distribution to be normal, it would need to satisfy an infinite number of probability statements, including having a positive probability of taking on both positive and negative values exceeding the number of microns between the earth and Deneb, over 1000 light years away, coincidentally roughly the same distance, depending on the metric, that normality is from reality.

As an example, we note that Chaudhry et al. (2002) used the approximate t-test for five measures of readers’ perceptions of papers with and without declarations of competing interests. These measures were interest, importance, relevance, validity, and believability, and the corresponding p-values for the five measures were 0.004, 0.016, 0.006, 0.001, and <0.001. Jacobs (2003) re-analyzed the data with exact methods, after pointing out the flaws in using approximate methods for the data at hand. Three of the five p-values lost significance, specifically interest (p=0.054), importance (p=0.21), and relevance (p=0.054). Of course, 0.054 is close to 0.05, so one might be tempted to declare it close enough. This is bad policy, and bad statistics, and not to be confused with selecting an alpha level other than 0.05. While it is perfectly reasonable to select an alpha level other than 0.05 (Berger, 2004), maybe even 0.055, this selection needs to be made prior to viewing the data (and the p-value). Otherwise, one is left wondering just how broad this fuzzy inclusion region actually is. Would 0.06 have been OK? What about 0.07? Where is the line drawn? In other words, what is alpha? And it is not what we said it was up front, then we have a serious problem, and are guilty of drawing the bull’s eye around where the dart happened to hit.

Moreover, notice that the p-value for importance went from 0.016 (approximate) to 0.21 (exact). This may surprise those who consider the choice of an exact or an approximate test to be a “fourth decimal problem” that hardly warrants the attention of today’s modern statistician. In fact, the StatXact manual (1995, page 21) states that “It is wise to never report an asymptotical p-value without first checking its accuracy against the corresponding exact or Monte Carlo p-value. One cannot easily predict a priori when the asymptotic p-value will be sufficiently accurate”. This is excellent advice, but we can go a step further and ask why one would then discard the gold standard, in the form of the exact permutation p-value, once it is in hand, to use instead an approximation to it?

Given the indisputable nature of the line of reasoning, from a lack of normality to a lack of robustness of parametric analyses in any meaningful sense to the need to present exact analyses, either alone or in conjunction with parametric analyses, it is rather alarming that even so obvious a measure meets with resistance. If we cannot get even the easy ones right, then one is left to wonder about any hope of solving the more challenging problems that face clinical trials researchers. When researchers argue that a variable is normally distributed, or that parametric analyses are sufficiently robust despite deviations from normality, this is not just a disagreement between experts, because advancing these arguments is clearly incompatible with being an expert. Experts are the ones who get it right, not the ones who offer credentials as excuses for getting it wrong.

3. Permuted Block Randomization

Similar to the parametric analyses considered in Section 2, permuted blocks also permeate clinical research as, in some sense, the standard method of randomization. It is not the frequency of use that causes permuted blocks to be problematic; if they were used just once, then that would be once too often, though they did at one time serve an important function. Parametric analyses are not inherently flawed; they were developed as approximations to the exact analyses that, given the computing capabilities at the time, could not be computed for any but the smallest data sets. So parametric analyses represented a good idea, and remained a good idea until the time that computing caught up and exact analyses could be conducted, thereby rendering parametric approximations obsolete. Likewise, permuted blocks came about at a time when the randomization methods in use did not force the treatment groups to remain comparable in size over the duration of the trial. This is an important consideration, because otherwise time trends can result in the confounding of patient characteristics and treatment assignments through a common association with time, or chronological bias (Matts and McHugh, 1983).

The permuted blocks procedure was the first randomization procedure to address chronological bias, which it did (and still does) successfully by forcing returns to perfect balance (in group sizes) at the end of each block. But these forced returns to perfect balance allow for prediction of future allocations, and selection bias. Uniformly better methods have since come along to supplant the permuted blocks procedure as the best randomization procedure. Specifically, the big stick (Soares and Wu, 1982) and maximal (Berger, Ivanova, and Deloria-Knoll, 2003) procedures are based on specifying a maximally tolerated imbalance (MTI) between group sizes over the course of the trial, so they match the ability of permuted blocks to control chronological bias. However, they are both much less predictable than permuted blocks, so they therefore do a better job of ensuring allocation concealment and preventing selection bias (Berger, 2005).

True, this is an issue only in unmasked or imperfectly masked trials, so in theory permuted blocks should be acceptable in perfectly masked trials. But the reality is that no trial can ever be known to be perfectly masked, so this is a moot point. Moreover, there is no tradeoff. There is no benefit in using permuted blocks in perfectly masked trials relative to using the big stick or maximal procedures. At best, the permuted blocks procedure is merely as good; at worst, it is much worse. From a game theoretic perspective, then, using the big stick or maximal procedure is not only the minimax solution but it is also the Bayes solution for any prior distribution that places any mass on the possibility of the trial being less than perfectly masked. Using the terminology of decision theory, the permuted blocks procedure is not admissible, since at least two dominating procedures have been identified, and can be used just as easily.

But there is even more. This article, as whole, deals with situations in which a better method is not used very much in practice and an inferior one is. Hopefully it will be clear to any reader why this form of inertia represents a major problem, but one would at least accept inertia in the case of two equally good procedures. So generally a new procedure needs a clear win to supplant the current standard of care. Alas, this paradigm, though useful in other contexts, is not useful in this particular context. Selection bias arises because an intelligent adversary acts on his or her ability to predict future allocations. Our job, then, is to keep this intelligent adversary in the dark, and this means switching just for the sake of switching (Berger, Grant, and Vazquez, 2010).

So inertia is a problem even if a new method comes along that is only equally good as (not necessarily better than) the incumbent; it is doubly problematic if the new method is actually better than the existing one. Hence, permuted blocks should not be used at all (Berger, 2006A), even if (or, in light of our need to keep investigators in the dark, especially if) they represent the industry standard (Berger, 2006B), and even with varying block sizes (Berger, 2006C). Nor is this a hypothetical concern; Berger (2005) lists 30 actual trials that are suspect for selection bias, and Fayers and King (2008) discussed a 31st. Not all 31 of these trials used permuted blocks, but the permuted blocks procedure is arguably the worst of all true randomization procedures (alternation does not qualify) in terms of susceptibility to prediction and selection bias.

4. The Jadad Score

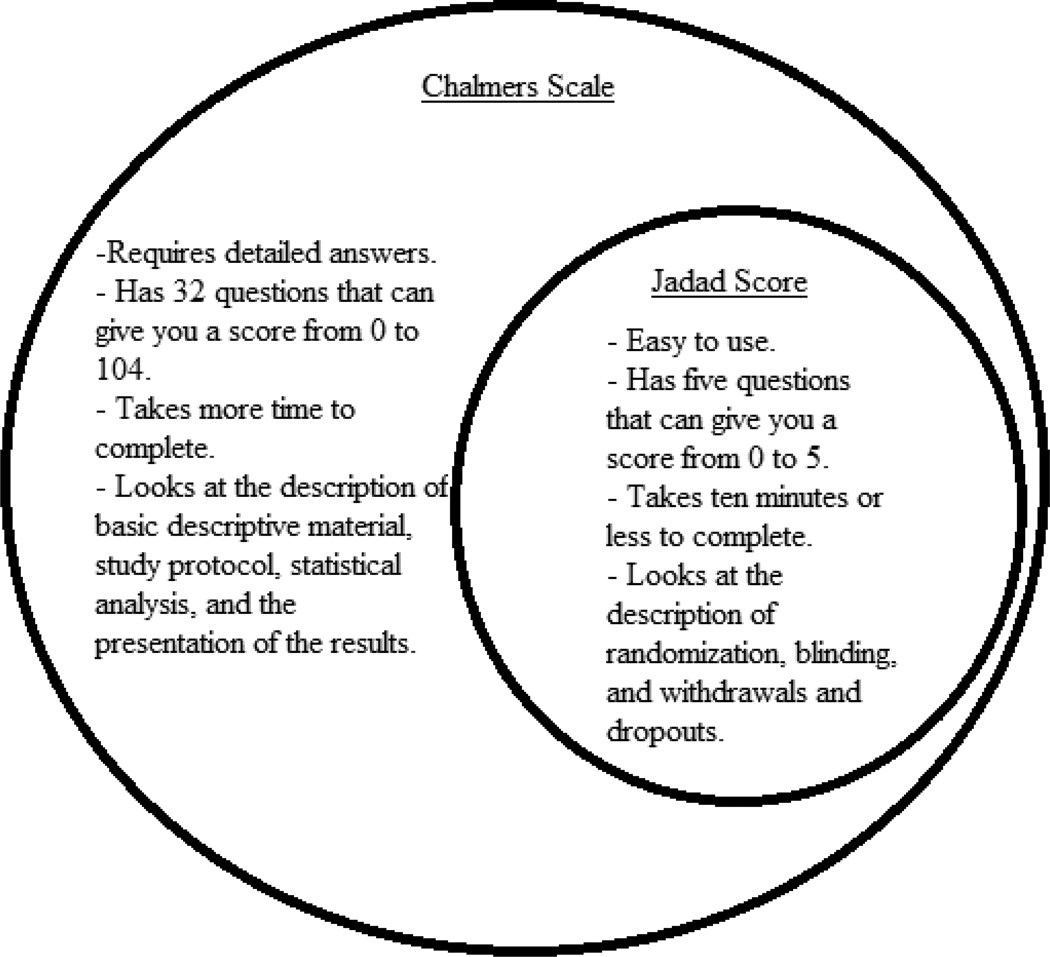
The knock on parametric analyses and permuted blocks is that they are obsolete, and have run their course, since uniformly better methods now exist. However, at least each did serve a useful purpose at one time. Sadly, the same cannot be said for the Jadad score (Jadad et al., 1996), which represented a huge step backwards even when it was first proposed in 1996, 15 years after the far superior Chalmers scale was proposed (Chalmers, 1981). See the Venn diagram in the figure below. The danger inherent in using the Jadad scale is not hypothetical. When a trial is perceived as valid and rigorous, it goes on to inform policy and future medical decisions. If such a trial is flawed, and misrepresents the truth, then a distorted version of the truth exerts its influence, and, therefore, denies truly informed decision making. This being the case, it should be absolutely clear that fatally flawed trials masquerading as rigorous trials represent a tremendous public health problem. But does this actually happen?

In fact, it does. As one example, Berger (2006D) evaluated a trial (Bookman et al., 2004) examining the safety and efficacy of a topical solution, relative to an oral treatment, to relieve the symptoms of osteoarthritis of the knee, that Towheed et al. (2006) subsequently rated as a perfect Jadad score of 5/5. How rigorous was this trial? We shall argue that the trial was in fact not rigorous at all, but instead was fatally flawed, and should never have been allowed to inform any future medical decisions. Berger (2006D) listed no fewer than ten flaws, some of which could unilaterally invalidate the trial, that were missed by the Jadad Score. These include: 1) unmasking; 2) prediction of future allocations; 3) selection bias; 4) performing arithmetical operations on numbers assigned fairly arbitrarily to non-numeric categories; 5) failure to present the most meaningful data structures; 6) using post-randomization data as baseline data; 7) failing to apply a penalty for an unplanned interim analysis; 8) carrying forward the last observation without mentioning any sensitivity analyses; 9) using an analysis requiring so many unverifiable assumptions that it cannot be taken seriously in the context of an actual clinical trial; and 10) excluding from the analysis some post-randomized data.

Palys and Berger (2012) provide another example, this one with Bridoux et al. (2012) using the Jadad Score instead of a more appropriate evaluation. The Jadad score is based on only the most cursory examination of the trial, asking only five questions:

1. Was the study described as random?

2. Was the randomization scheme described and appropriate?

3. Was the study described as double–blind?

4. Was the method of double blinding appropriate?

5. Was there a description of dropouts and withdrawals?

Whereas a perfect 5/5 may be necessary for a valid trial, it certainly is not even close to sufficient. A useful assessment of trial quality will need to be much more inclusive. The Chalmers scale is one such assessment, as the figure below illustrates.

The Chalmers scale has four parts (La Torre, 2004), and gets at the important issues in trial quality that are missed by the Jadad score. This is not to say that no further improvements are possible. Berger and Alperson (2009) provided a general framework that an appropriate assessment of trial quality would need, and Alperson and Berger (2013) followed this up with more detailed information, including not only the need for the assessment tool to be comprehensive but also the need for scores to be multiplied, not added. With the innovations in the past several decades since the Chalmers score was introduced, some used prudently and others not, it would seem that a more modern assessment tool would be best, but still one that preserves the best elements from the Chalmers score, and maybe even uses it as a template. But under no conditions can the practically empty Jadad score ever be justified as an evaluation tool.

5. Run-In Enrichment

A run-in period occurs before randomization, and consists of a period during which all prospective patients are treated the same way, typically with the active treatment, although there are also placebo run-in periods. We will consider only active run-in periods, as they arguably lead to the more egregious error, although many of the criticisms raised will apply to placebo run-in periods as well. Though there are issues arising directly from the use of this design itself, the bigger issue is the resulting patient selection that grows out of it; generally only those patients showing some sort of positive response, or possibly not showing a contraindication, will then go on to get randomized.

Even putting aside the issue of patient selection, there is still the issue of creating a drug dependency, which may be more or less pronounced depending on the drug class. Treating all patients with the active treatment, and then suddenly withdrawing half of them to receive the control (possibly placebo) during the randomized phase, confounds the treatment effect with the dependency effect. One can imagine an ineffective treatment that creates a dependency spuriously being found to be effective because those patients continuing to be treated with it fared better than those patients whose treatment abruptly stopped, but this result is entirely dependent on the addiction created by offering all patients this same treatment prior to randomization. This design tests the effect of withdrawing from the treatment, rather than the effect of initiating treatment in a naïve population, and yet typically we will see a claim that the treatment has been demonstrated to be effective.

Moreover, when this design is coupled with patient selection, we face even bigger problems. As Berger, Rezvani, and Makarewicz (2003) pointed out, the resulting bias is sufficient to create the illusion that a useless treatment is effective. Given the nature of most pharmacological treatments, it is not a great leap of faith to posit that more patients would find their side effects intolerable as compared to placebo. Nevertheless, let us suppose equality anyway. That is, suppose that among a cohort of patients, 20% cannot tolerate placebo, another 20% would respond to it, and 60% tolerate it but do not respond to it. Let us use these same proportions with the active treatment. All that remains to specify now is the overlap, as in which patients respond to both, and so on.

Clearly, the devil is in the details, and we can specify the overlap so as to bring about any results we want to obtain. For example, the most extreme bias would result if we were to specify that the early responders to the active treatment were the same patients who would continue to respond to the active treatment in the randomized phase and who would not respond to the control in the randomized phase. Conversely, no bias would result if the same patients who respond to one treatment also respond to the other treatment (the so called strong null hypothesis, see, for example, Berger, 2000). But we will avoid the extremes and instead consider a more intermediate (and, hopefully, realistic) scenario to illustrate the bias that results from this design. So consider a null situation, in which there is a 25% response rate to each treatment, with 50 responders to each treatment among a cohort of 200 patients, and 20 respond to both, as in Table 5.1.

Table 5.1.

Overall Response Patterns (Principle Strata)

	Control Non-Response	Control Response	Total
Active Non-Response	120	30	150
Active Response	30	20	50
Total	150	50	200

With no special enrichment, we would expect to see roughly 25% response rates in each treatment group, depending on how the randomization splits the patients. The numbers in Table 5.1 are unobserved counterfactual responses that tell us how each patient would respond to each treatment; let us not confuse this with actual data. But now suppose that we add in a pre-randomization run-in phase, with patient selection based on some preliminary test that is predictive of subsequent response to the active treatment in the active phase. In other words, this design over-selects (for randomization) those patients most likely to respond to the active treatment. We will specify that among the selected patients, 35% respond to the active treatment, whereas the control response rate is still 25%, and among the patients not selected, 15% respond to the active treatment and, again, the overall response rate of 25% still applies for the control group. Even without examining the tables, this should already raise red flags, and the bias should already be evident. But we will make it formal, and quantify this bias, in the next two tables.

Table 5.2 clearly shows that using the active run-in to screen patients has changed a null situation into one in which we expect to find a (spurious) treatment effect, since, among the randomized patients, 35% respond to the active treatment and only 25% respond to the control treatment. Of course the opposite treatment effect would be in play if we were to instead conduct the randomized trial on the excluded patients, as in Table 5.3.

Table 5.2.

Response Patterns (Principle Strata) Among Selected Patients

	Control Non-Response	Control Response	Total
Active Non-Response	50	15	65
Active Response	25	10	35
Total	75	25	100

Table 5.3.

Response Patterns (Principle Strata) Among Non-Selected Patients

	Control Non-Response	Control Response	Total
Active Non-Response	70	15	85
Active Response	5	10	15
Total	75	25	100

The key point, however, is not to be found in the tables, but, rather, only upon stepping back and reflecting on the situation. One may argue that it is ethically imperative to make use of any information that distinguishes patients in the way that the tables reflect. If we can identify two groups of patients, one of which is more likely to show a treatment effect, then how could we not exploit this information? Alas, the key is in how we glean this information. If it were based on observable patient characteristics, such as age or gender or disease severity, then this would be a very good idea. So, for example, if we know from prior studies that a certain segment of the population is unlikely to tolerate the treatment under investigation, then ethically this subgroup should be excluded from the study. This is self-evident, and not at all controversial. But this is not the issue.

The issue is rather that we do not know which patients do not show a tendency towards bad outcomes or side effects, so we need to find this out from treating them. And once we do treat them, and find out that some did in fact suffer serious adverse events, we do not try to find the salient similarities of these patients in an effort to identify other patients (not in this study) who may also be advised to avoid this treatment. Rather, we leave it as a black box, these patients, and only these patients, did not do well on our treatment, so we exclude them and proceed as if they were never treated at all.

It should be clear how this creates a distortion of the results so that they no longer provide meaningful information for future patients contemplating taking this treatment. As a rather extreme example, to make the point, suppose that 1000 patients are screened with this active run-in phase. Of these, 900 (90%) die, so only 100 get randomized, 50 to the same treatment, and 50 to the control. Among these 100, the active treatment produces measurably better outcomes. We publish the results on only these 100 highly select patients and declare our treatment safe and effective. This is nothing short of research malpractice, and it denies future patients the right to an informed decision. The other 900 patients are certainly relevant to the decision any future patient makes regarding this treatment. Excluding them from the most relevant analyses, even if including them in secondary analyses, is a clear and deliberate attempt to manipulate results so as to obtain a preferred result. It is certainly not science.

6. Misrepresenting the Use of ITT

Many competitors to the intent-to-treat (ITT) analysis population have been proposed. It has been argued that the “as treated” population, for example, better addresses the biological plausibility of the treatment effect. This may be true, but in a pivotal Phase III trial we are evaluating a policy decision. If a beneficial treatment requires a work-up that few can tolerate, then this has to count against the entire treatment strategy (this is somewhat in keeping with the theme of Section 5). Hence the need for the ITT population. Alas, this is not even the issue we address in this section.

We would have much more respect for researchers who do not use the ITT population and come right out and say that they are not using it, and provide reasons for not using it. We would find these reasons unconvincing; we would still want to see the ITT analyses anyway, but we might at least be convinced of the value of other complementary analyses that can be presented in addition to the ITT analyses. What we find dishonest and unjustifiable is misrepresenting the use of the ITT population.

The ITT population is defined unambiguously as the set of patients who were randomized, with no exclusions for any reason whatsoever. If a patient was randomized, then we can infer the intention to treat this patient, and this intention remains intact even if that patient was ultimately not treated for any reason, or even if that patient received the wrong treatment, or even if that patient dropped out and contributed no data at all. This much is clear and irrefutable. What may be somewhat less clear is the situation in which a patient was randomized and was subsequently found to have been ineligible in the first place. For example, perhaps patients with certain lipid profiles are ineligible, but it takes time to get these lipid profiles back from the lab, and treatment needs to commence at once, and cannot wait for the lab results. So, optimistically, patients get randomized, and then later some are found to have been ineligible.

Here one can argue that there was a blanket intention to disqualify such ineligible patients, but that this specific patient was randomized (and intended to be treated, and also actually treated) only because we did not realize that this patient was ineligible. So was the intention to randomize this patient or not? Compelling arguments can be made both ways, so here one might argue that the actual definition of ITT is ambiguous, and that is fair enough, but certainly the key analyses should be provided both ways with a clear explanation of why this was necessary. Either way, this is not at all the same as excluding patients because they received the wrong treatment, did not receive any treatment, or did not produce usable data. These exclusions are much more questionable, and are certainly not consistent with ITT analysis by any stretch of the imagination. Labeling such analyses ITT is simply dishonest, and using the phrase “modified ITT” is only marginally less so. There is no excuse for either.

7. Dichotomizing Ordered Categorical Data

Early in my career I was an isolated statistician working at a CRO specializing in oncology trials. In this capacity, I was called upon to handle the analysis of all types of cancer endpoints, including objective tumor response, which in its most common form assumes the ordered categories complete response, partial response, stable disease, and progression. It was not at all clear to me how such an endpoint should be analyzed, but from attending conferences I had amassed a fairly extensive network of seasoned statisticians whom I respected and looked up to, so I contacted many of these statisticians and conducted an informal survey to find out how they would handle such data. Certainly I was not the only one facing this situation. I was eager to learn from the best. And I did learn, but not the lessons they intended to teach me.

With remarkably few exceptions, these “seasoned” statisticians steered me to one of two analyses, either dichotomizing the endpoint to render it binary or assigning numerical scores to facilitate the use of a t-test. Naturally, I was stunned. I did not even have my doctoral degree yet, and even I could see the flaws in both approaches. Equating fundamentally different outcomes to ease the burden the researcher faces in analyzing the data is hardly innocuous; this wastes information and loses discriminatory ability. The loss of power should be patently obvious, but a less obvious effect may be to cover up a “loss” and leave only a “win” for the active treatment. For example, imagine three ordered categories, improved, no change, and worsened, with data as in Table 7.1.

Table 7.1.

Hypothetical Ordered Categorical Data

	Worse	No Change	Improved	Total
Control	15	70	15	100
Active	30	50	20	100

Compared to the control group, the active treatment produces more improvements (20% vs. 15%), and also more deterioration (30% vs. 15%). So what are we to make of these data? Clearly, the sponsor would have an incentive to highlight the improvement rate and suppress the deterioration rate, and this can be accomplished by combining the first two categories into a single “no improvement” category as in Table 7.2

Table 7.2.

Hypothetical Ordered Categorical Data Dichotomized

	No Improvement	Improved	Total
Control	85	15	100
Active	80	20	100

Table 7.2 gives the impression that the active treatment is superior to the control, even though the manufacturers of the control could make the exact same argument by instead combining the last two columns of Table 7.1 into a single “no worsening” column. This is why Berger (2002) argued against dichotomizing ordered categorical data for analysis, and especially for presentation. The arbitrary nature of which columns to combine (as in, where to draw the line of demarcation) is matched by the arbitrary nature of our other type of analysis, namely assigning numerical scores. Of course, the former is a special case of the latter, as dichotomizing is the same as assigning numerical scores of 0 to some columns and 1 to the rest. The ubiquitous temptation to instead assign consecutive integers to the columns provides something we can all agree on, and this near universal agreement translates into something apparently objective.

Alas, this “natural” assignment of consecutive integer scores is not nearly as objective as it may at first seem. First of all, imagine empty columns, so that whereas we had pre-specified five categories with scores of 1, 2, 3, 4, and 5, respectively, it turned out that only the first, second, and fifth columns had any patients. Do we go with 1, 2, and 5, or do we instead drop the two empty columns and go with 1, 2, and 3? This seemingly insignificant decision can mean the difference between statistical significance and the lack thereof. Second of all, even with no empty cells, the choice of scores can still determine whether a given set of data does or does not reach statistical significance, or, in extreme cases with offsetting or compensating effects (as in Table 7.1), even the direction of the effect. Why, one may ask, don’t we just use the right set of scores?

The answer to this seemingly simple question is that no set of scores is right in any meaningful sense of the word. Implicit in this analysis is the presumption that the data are measured on an ordered categorical scale. That is to say that they lack any interval meaning, so whereas we know the relative ordering among the categories, we most certainly do not know anything about the relative spacings between them. Nor can we ever know this. How could we? How could we possibly declare on behalf of all patients that a complete response beats a partial response more than a partial response beats no response? At the heart of the issue we have a value judgment, and each patient will have his or her own set of preferences. That is to say, there is no correct set of scores. The scores are neither data nor parameters. Rather, they are artificially imposed as a stand in for patient preferences. They have no place in serious science.

If numerical scores cannot be used, then how are we to analyze ordered categorical data? In fact, there are better ways. The class of non-linear rank tests contain the best analyses, in terms of objectivity and global power profiles, though in general there is no uniformly best test. Suitable choices would include the Smirnov test, the convex hull test, and various adaptive tests (Berger et al., 1998; Berger and Ivanova, 2002), and though standard software packages do not support the convex hull test or the adaptive tests, their improved power may still make them ideal choices even if customized programming is required to conduct them. Even without the ability to program these superior tests, a researcher can still use the Smirnov test to great advantage relative to the linear rank tests based on numerical scores, as it is a standard feature of StatXact. Hence, the better methods are not only out there, but in fact at least one of them is also readily available for use. There is no reason to use a linear rank test.

8. Conclusions

One may liken the task of those of us who would reform the practice of clinical trials to the unenviable task of having to sell unbiased scales to those grocers who benefit directly from the biases of the scales they currently use. These grocers have no incentive to repair the broken scales, or to start using better ones. The issue, of course, is not just the cost of the new (unbiased) scales, but also the fact that these new scales would be far too revealing of past abuses and would not permit comparable future abuses (a.k.a., profits and lucrative bonuses). From a societal perspective, then, we see that the grocers cannot be allowed to police themselves, because waiting for them to change a situation beneficial to themselves is akin to waiting for Godot. They are not the ones hurt by the status quo, so the appeal needs to go directly to those who are, meaning the public.

There is a rather obvious conflict of interest in having the party with the greatest vested interest in obtaining particular outcomes be the very party conducting the testing, and enjoying the discretion that is afforded to the experimenter. We would like to believe that this conflict is of academic interest only, that the harm is only potential, that it never actually materializes, that no sponsor would actually exploit the situation. But is this reality? In fact, it is not. The abuses are well documented, and would fill an encyclopedia, so it is not possible to be comprehensive here, but one recent example is the overwhelming propensity of researchers to modify the primary outcomes between the protocol stage and the final report stage (Dwan et al., 2013). This is not supposed to happen at all, and when it does, it represents dishonesty on the part of the investigators.

Are there also other ways that investigators try to gain an unfair advantage (whether or not they recognize this advantage as being unfair)? In fact there are, and we have discussed several of these, focusing on the ones falling within the realm of statistical methodology (certainly there are others as well). In particular, we have discussed 1) using approximations over the very quantities they are trying to approximate; 2) permuted block randomization; 3) the Jadad score; 4) run-in selection; 5) misrepresentation of the ITT analysis population; and 6) combining fundamentally different outcomes for the purpose of analysis (and, often, for the purpose of presentation, too). There is no place in serious research for any of these flawed methods. Their use may or may not represent an intent to cheat, but certainly they can be done in such a way that the treatment effect is grossly exaggerated, even if this was not the intention.

But this is just the tip of the iceberg. There are many other flawed methods that are used frequently in practice, and these flawed methods conspire to produce the favored outcome whether or not it reflects reality. Hence this paper is not about parametric analyses, permuted blocks, the Jadad score, run-in enrichment, improper ITT analysis populations, or unjustifiable analyses of ordered categorical data. These are but examples, manifestations of the larger problem, which is, as noted, the fact that the same party that produces and sells the treatments also produces the scales that measure these treatments. This clear conflict of interest is what needs to be fixed first.

We see, then, two distinct levels of problems. At one level, we have fatally flawed trials being accepted as rigorous and convincing proof of the safety and efficacy of novel treatments, and helping to shape medical policy. This alone is enough of a problem to warrant serious attention that, to this point, has been conspicuously absent. At the second, deeper level, we see that the “machine” that produces these fatally flawed trials itself is broken. This machine is the influence that sponsors enjoy in the trials that will go on to test their own treatments. The discretion to place a heavy finger on the scale so as to tip it towards heavier readings is not abstract or hypothetical; there are very tangible ways that sponsors can design trials to distort the findings towards better outcomes. We have discussed some of these but, as noted, there are many, many others as well. The problem goes way deeper than these specific flawed methods. Without impartial investigators, trial results can simply not be accepted at face value.