Neural Activity Reveals Preferences Without Choices

Abstract

We investigate the feasibility of inferring the choices people would make (if given the opportunity) based on their neural responses to the pertinent prospects when they are not engaged in actual decision making. The ability to make such inferences is of potential value when choice data are unavailable, or limited in ways that render standard methods of estimating choice mappings problematic. We formulate prediction models relating choices to “non-choice” neural responses and use them to predict out-of-sample choices for new items and for new groups of individuals. The predictions are sufficiently accurate to establish the feasibility of our approach.

I. Introduction

A central problem in microeconomics is to predict the distribution of households' choices in not-yet-observed situations (e.g., after some policy intervention). The dominant tradition is to draw inferences from actual choices within some closely related domain. Unfortunately, that traditional approach often proves problematic due to various practical limitations of choice data: in some settings, data for closely related choices are either unavailable or extremely limited; the opportunity sets for naturally occurring choice problems are often impossible to characterize absent strong assumptions about expectations and other important considerations; and concerns about uncontrolled factors, selection, and the endogeneity of opportunity sets are endemic.

A sizable literature on stated preference (SP) techniques explores the feasibility of drawing reliable inferences from hypothetical choice data in contexts where actual choice data are either absent or deficient (for overviews, see Shogren, 2005, 2006). It is well established that answers to standard hypothetical questions are systematically biased, typically in the direction of overstating willingness-to-pay (WTP) and toward alternatives that are viewed as more virtuous.¹ Two classes of solutions have been examined: one attempts to “fix” the hypothetical question;² the other seeks to correct for the bias through ex post statistical calibration.³ Because the limitations of those approaches are widely acknowledged, their use is largely confined to contexts where choice data pertaining to closely related decisions are entirely unavailable (e.g., in the environmental context, to value pristine coastlines, biodiversity, and the like),⁴ rather than merely deficient.

Despite the limitations of stated preference techniques, measures of elicited preferences remain potentially useful as long as it is possible to uncover stable predictive relationships between them and real choices. Furthermore, since there may also be stable relationships between real choices and a much broader class of non-choice variables, there is no a priori reason to limit a prediction exercise to elicited preferences. Potential predictors include any reaction to elements of a contemplated opportunity set that occur when an individual is not engaged in actual decision-making (e.g., a subjective report or neural measurement assessed while imagining a consumption experience).

These observations suggest a more general strategy for predicting choices in situations where standard revealed preference methods are problematic: uncover the statistical relationships between real choices and combinations of non-choice variables, and use them (along with assessed values of the non-choice variables) to predict behavior out of sample in domains of interest. Because accurate forecasts of real choices “reveal preferences” in the classic sense of identifying what an individual would choose, we refer to this general class of procedures as non-choice revealed preference (NCRP).⁵ Viewed from this perspective of this broader strategy, the historical success of the stated preferences approach may have been limited by its narrow focus on answers to hypothetical questions.

Potentially predictive non-choice measures fall into two broad categories: subjective reports (including but not limited to hypothetical choices), and physiological and neurobiological responses. An obvious virtue of relying on subjective reports is that the data are comparatively cheaper to collect. However, a rapidly growing body of work in psychology and neuroscience suggests that the biological measures might have predictive value-added over the subjective reports, probably because choices are systematically influenced by automatic processes that are not accessible to conscious awareness, but that can be measured with neurobiological techniques (see Dijksterhuis et al., 2006, Berns et al., 2010, Chua et al., 2011, and Falk et al., 2011). It is important to emphasize that the actual predictive power of non-choice responses is by no means evident without empirical confirmation, and hard to judge a priori without the type of systematic exercise carried out here.

This paper takes a first step in the development of NCRP methods that exploit non-choice physiological responses: it evaluates the promise of those methods by investigating whether (and to what extent) non-choice neural responses measured using whole brain functional magnetic resonance imaging (fMRI) predict real choices.⁶ We recognize that the use of neural data raises issues of practicality, as its collection is likely to remain costly and inconvenient in the near term. In comparison, other physiological responses such as pupil dilation and skin conductance are easier to measure (and subjective responses are easier still). We nevertheless focus on whole brain fMRI measures because they provide a fairly comprehensive (albeit not perfect) picture of all the responses to a given stimulus, and thus are more likely to capture predictive information. By establishing the predictive power of such measures, we lay the foundation for subsequent efforts to identify the physiological manifestations of the predictive neural responses that are most easily and practically measured.

Because this first step is a substantial undertaking, the current paper does not fully execute the agenda articulated above. In particular, we make no attempt here to evaluate the incremental predictive power of neural data (over and above non-choice subjective reports), identify the most cost-effective physiological predictors, develop prediction models exploiting multiple varieties of non-choice variables, or bring the methods to practical applications. Nor have we exhausted all the possibilities for fine-tuning our methods to achieve the greatest possible predictive power from neural data (either at the image acquisition stage or the statistical analyses stage). These are tasks for ongoing and subsequent work.

Consistent with our objective of providing proof of concept, we confine attention to a narrow choice domain, consisting of choices among food items. Subjects “passively” view pictures of 100 snacks while undergoing an fMRI brain scan. After the passive scan is complete, they are unexpectedly asked to make choices among 50 pairs of snacks (one of which is implemented), with each snack appearing in one and only one pair. After completing the choices, they are asked to rate the extent to which they liked each item. Section III describes our experimental procedures in greater detail.

Our first objective is to construct, for each subject, a statistical model that predicts that subject's choices accurately out of sample (Section IV.A). Leaving out two pairs of items at a time, we estimate a prediction model based on the other 48 pairs, and use it to predict the individual's choice for the excluded pairs. Were we studying continuous choices, we would examine prediction bias, both overall and conditional on the values of the predictors. Because we are instead predicting dichotomous choices, we examine calibration, which is analogous to bias. A probability model is well-calibrated if predicted probabilities closely match actual choice frequencies. For example, events that are predicted to occur with 70% probability should actually occur 70% of the time. We evaluate calibration both overall and conditional on the values of the predictors.

A high degree of calibration would not, by itself, imply that non-choice neural responses are powerful predictors of choices. For example, a model that employs no predictors and assigns a 50% probability to the first of any two randomly ordered alternatives is perfectly calibrated. However, that model performs poorly with respect to resolution. Resolution is high when the predicted probability is close to 0% or to 100%. A perfectly calibrated model with perfect resolution is ideal in the sense that it always predicts the outcome correctly.

Our focus on evaluating the calibration and resolution of probabilistic predictions is one of several important factors that distinguish this paper from the rest of the literature on the neural correlates of choice (see Section II for additional detail). A common practice in that literature is to report rates of successful classification (“success rates” for short). While we also report success rates (using probability > 50% as the classifier), we are of the view that the calibration and resolution of probabilistic forecasts are of greater interest to economists. A success rate reflects a particular blend of a model's calibration and resolution, one that provides a sufficient statistic for predictive performance under circumstances not commonly encountered in economics (e.g., where the object is to decide whether or not to treat a medical condition in a setting with a symmetric loss function). Knowing whether a success rate is high or low does not reveal whether one can use a model to construct accurate probability distributions for predicted choices, which is a paramount concern in economic applications.

For just over half of our subjects, we find that non-choice neural responses contain information that is useful in predicting choices, in the sense that our models significantly improve upon uninformed out-of-sample predictions (a 50% success rate), usually with p < 0.01. Moreover, even though there is no necessary relationship between success rates and calibration, we find that these models are on the whole well-calibrated out of sample. The difference between overall success rate (68.2%) and the expected success rate (72.9%) is modest. More significantly, across choice problems (within subject), there is a striking relationship between predicted probabilities and realized frequencies: a 10-percentage point increase in the former translates into roughly an 8-percentage point increase in the latter. Notably, that relationship is not driven by extreme cases (i.e., choice problems for which one item is universally and strongly preferred). While by no means perfect, this performance is, in our view, reasonably impressive in light of the task.

In contrast, for just under half of our subjects, success rates are low (below 60%), and our models do not significantly improve upon uninformed predictions (50% success rate), even at p < 0.10. Though low success rates do not necessarily imply poor calibration, these models also yield inaccurate out-of-sample probability statements. Thus, our procedure works well for just over half of our subjects, but not at all for the others.

Predicting choices on the level of a single individual is a demanding objective, one that goes beyond the requirements of most economic analyses, which are more typically concerned with aspects of group behavior – averages, aggregates, and possibly distributions. Group averages may be easier to predict, for example because various types of noise average out over multiple individuals. Accordingly, we next ask whether it is possible, for any particular group of individuals, to fit a model relating a measure of average subjective value to average non-choice neural responses for one set of items, and use that model successfully to predict the average subjective values of items not contained in the original set, based on the non-choice neural responses they induce (see Section IV.B). Compared with the successful half of our individual-level prediction exercises, our group-level prediction exercise achieves higher resolution and success rates, and the quality of calibration is comparable. We achieve this result despite including all subjects in the group-level analysis, regardless of whether their individual-level prediction exercises were successful.

If non-choice neural activity exhibits a sufficiently similar relation to choice across subjects, then it should be possible to construct a single prediction model and use it without recalibration to predict choices based on neural measurements taken from new individuals or groups. Such a model would have considerable practical value in that, once estimated, it would vastly simplify the steps required to formulate additional predictions. To predict behavior in new situations, one could collect data on non-choice neural responses to the relevant prospects for a new group of individuals and apply an existing predictive model. It would not be necessary to gather the requisite data to estimate new predictive models for those subjects. Accordingly, we also investigate whether predictive models are portable across groups of individuals. We achieve a moderate degree of success when predicting a group's average valuation for new objects from a relationship estimated with data pertaining to other objects, gathered from another group.

Taken together, our results demonstrate that non-choice neural reactions to images of potentially desirable objects contain a great deal of information that can be used to predict decisions made by a particular individual, or average decisions made by a group of individuals, in new choice situations. Future improvements in methods and measurement technologies are likely to enhance the success of this approach.

II. Related literature on the neurobiology of choice

There is a substantial literature in neuroscience concerning the neural correlates of choice. With very few exceptions (discussed below), that literature is concerned with identifying neural activity that reliably encodes value signals during the act of choice; see, for example, Hsu et al., (2005), Kable & Glimcher (2007), Knutson et al. (2007), Plassmann et al. (2007, 2010), Hare et al. (2008), and Levy et al. (2010). Consequently, the issues those studies address differ fundamentally from the ones that motivate our inquiry. Certainly, as Knutson et al. (2007) emphasize, it is possible to predict choices from neural activity measured during the act of decision-making. However, some economists take the view that there is little value in predicting choices in a setting where choices are themselves observable. If one's objective is to extrapolate choices based on neural activity in settings where choices are not observed, correlations between choice and choice-related neural reactions are not helpful (at least not directly).

Two recent studies suggest, however, that the brain's valuation circuitry may be active even when people are not actively engaged in choice. Lebreton et al. (2009) show that activity in the ventromedial prefrontal cortex (vmPFC) and the ventral striatum (vStr) while subjects were asked to judge the age of paintings, faces, and houses correlates with their subjective ratings for the same items (elicited in a separate task). Kang et al. (2011) show that activity in the vmPFC and the vStr correlates with the value of the stimuli during both real and hypothetical choices, which suggests that neural responses to real and hypothetical choices may share many common features. Thus, there is reason to hope that one can also reliably predict choices based on non-choice neural responses.

The current study is most closely related to recent neuroscience papers by Tusche et al. (2010) and Levy et al. (2011), both of which have elements of predicting choice (or tasks related to choice) from non-choice neural responses.⁷ To understand the key differences from our work, it is helpful to summarize several features of our analysis that are critical for the economic applications we envision. First, we are concerned with predicting real choices from neural responses during non-choice activity. Second, our interest is in out-of-sample prediction, rather than within-sample fit. We are concerned with predicting choices over one set of alternatives using a relationship estimated with data for a disjoint set of alternatives.⁸ Third, our objective is not merely to predict the more likely choice, but in addition to derive reliable probability statements concerning the alternatives. We seek a procedure that reliably indicates whether a particular alternative will be chosen with, say, 60% probability rather than 90% probability. Fourth, we are concerned with several distinct types of prediction exercises: within subject, within group, across subjects, and across groups. Predicting average behavior within and across groups likely has the greatest potential value for economics.

These four features distinguish our paper from the two studies listed above. None of them attempts to predict choices among one set of alternatives from a relationship estimated with a disjoint set of alternatives, nor do they attempt to derive and validate probability statements concerning alternatives. Both studies focus exclusively on within-subject classification or prediction, and they do not attempt to predict average behavior for groups, or choices across subjects. Tusche et al. (2010) study the neural correlates of hypothetical choices rather than real choices. Levy et al. (2011) predict real choices, but their subjects also made real decisions concerning the same objects during scanning, and hence their procedure does not truly involve non-choice neural responses in the sense defined here.

To be precise, the exercise in Levy et al. (2011) involves two phases: a localizer task and a neurometric prediction task. In the localizer task, subjects make decisions about whether or not to play lotteries. The goal of the task is to localize areas of the brain involved in valuation computations for each individual subject. In the prediction task, subjects are passively shown pictures of various types of goods (DVDs, CDs, stationary, monetary lotteries) and neural responses in the value areas identified in the localizer task are taken for each subject and good. After scanning, subjects make choices for every possible two-element subset of the items, repeated twice. Several differences between their design and ours deserve emphasis. First, we predict choices on entirely new choice sets: in our task the choice pair consists of two new items, neither of which was used in fitting our model. Second, in Levy et al. subjects are also asked, every few trials, to make a purchase decision regarding the same stimuli used in the prediction task. Although these trials are not used in their neurometric prediction exercise, there is a concern that the mere presence of interspersed choice trials alters a subject's outlook on the items in question, so that they treat the passive trials more like actual purchase decisions. These differences between our task and that of Levy et al. are likely to make our exercise relatively more difficult than theirs. Finally, we employ a different prediction methodology that makes use of all the voxels in the brain rather than a specific region. In practice we are able to improve modestly upon the overall success rates achieved by Levy et al., despite the greater difficulty of the task.

The current paper also bears on the debate over the role of neuroeconomics within the broader field of economics. Various possibilities, such as the potential to develop useful neural tests of economic theories, remain controversial (see, for example, the contrasting views of Camerer, Loewenstein, and Prelec, 2004, Gul and Pesendorfer, 2008, and Bernheim, 2009). In contrast, it is hard to imagine even a traditionalist objecting to our agenda on the grounds that it is orthogonal to the goals of the field (in that our goals coincide with those of the stated preference method), or that it pursues those goals in a manner that is conceptually illegitimate (in that the task at hand is simply one of predicting an outcome using statistical models along with information that one could in principle collect). A skeptic might well question whether the method will prove useful in practice, but that is an empirical question, and hence one that should be resolved on the basis of evidence rather than prior belief.

III. Experimental Design

A. Procedures

Thirty-five right-handed subjects participated in the experiment (age range: 19 to 36 years old, 11 female).⁹ Subjects were pre-screened to ensure that they regularly ate the types of foods used in the experiment, and that they met the standard criteria required for the safe and reliable acquisition of fMRI data. Subjects were paid $100 for participating, and were offered a $10 bonus for limiting their head motion during the fMRI task (which, if excessive, invalidates the procedure). Despite these incentives, in-scanner head motion for eight subjects exceeded a pre-specified limit of 2mm in any direction during a scanner run. After excluding those eight subjects, 27 usable subjects remained.

Subjects were instructed to refrain from eating or drinking anything other than water for four hours prior to the experiment. At the outset of a session, they were advised that the experiment would consist of three stages, and that they would receive the instructions for each stage only after completing the previous stage.¹⁰ Thus, as described below, when viewing images of snack foods in stage 1, subjects were not aware that they would subsequently face choices among pairs of those items in stage 2.

Stage 1. Passive viewing of foods during fMRI scan

In the first stage, subjects viewed images of 100 different snack foods while we measured their neural responses (see Figure A1 of Appendix A for sample images, and Table A1 of Appendix A for a list of all foods used in the experiment). Foods were shown in randomized order with each item appearing three times. Each image was visible for 2.75 seconds. Between images, a small white fixation cross centered on a black screen was shown for 8.25 seconds. For technical reasons related to the acquisition of the neural data, each session was divided into 6 identical blocks each consisting of 50 image presentations, separated by breaks of roughly one minute.

To enhance the psychological salience of the images, we told subjects that they would be required to eat at least three spoonfuls of one of the food items at the end of the session. With 50% probability, the item would be selected at random, and with 50% probability it would be determined in a subsequent stage of the experiment. However, subjects were not told that that they would be asked to make choices among the alternatives.

Given the tedious nature of the task, we inserted five additional “catch” trials at random intervals within every block. During each such trial, the subject was instructed to press a button indicating whether the displayed item was sweet or salty. Subjects were given a maximum of 2.75 seconds to respond, after which a fixation cross screen appeared for 8.25 seconds. The foods shown in the catch trials were different from those used in the passive viewing trials, and we did not use the neural responses from the catch trials in the prediction exercises described below. In 93.1% of the catch trials, subjects responded within the time allowed, which suggests that they attended to the images.¹¹

We collected measures of neural activity using BOLD-fMRI (blood-oxygenated level dependent functional magnetic resonance imaging).¹² Instead of making assumptions as to which brain regions were likely to generate predictive non-choice responses, we measured activity throughout the entire brain, and used all of the data in our prediction exercises. It is natural to conjecture that brain regions previously shown to be involved in valuation, such as the medial prefrontal cortex or the ventral striatum,¹³ will play critical roles in predicting choices. However, we decided to carry out our prediction exercise using the entire set of brain responses for three reasons. First, we wanted to demonstrate that the NCRP methodology proposed here does not depend on knowledge of which brain circuits are involved in the choice process, or how to measure their activity. Second, the usefulness of a brain region for our predictive task depends on: 1) how cleanly we can measure neural activity in the region; 2) how well that activity correlates with automatic valuations; and 3) how much predictive information the activity in that region adds over and above other activity used to construct the predictions. We use data from the whole brain to allow for the possibility that neural activity in some brain regions will prove informative after accounting for neural activity in other regions. This is particularly important, because the signal-to-noise of BOLD-fMRI in areas typically associated with valuation (like ventral striatum and ventromedial prefrontal cortex) is relatively low. In fact, the accuracy of our method declines when we restrict attention solely to the ventral striatum and ventromedial prefrontal cortex, indicating the value of our whole-brain approach. Third, many psychological processes exhibit some correlation with value, such as attention and arousal. This implies that many voxels, besides those in areas known to be involved in valuation, will also degrees relative to the anterior commissure-posterior commissure line (Deichmann et al., 2003) and an 8-channel phased array head coil to maximize functional contrast-to-noise in areas of the ventromedial prefrontal cortex which, as described in Section II, have been shown to play a critical role in valuation. Each volume consisted of 44 axial slices covering the entire brain. The imaging parameters were: echo time, 30ms; field of view, 192mm; in-plane resolution and slice thickness, 3mm; repetition time (TR), 2.75s. correlate with values, and would have independent noise (Litt et al., 2011). These independent measurements are useful in prediction.

BOLD-fMRI operates by measuring changes in local magnetic fields resulting from local inflows of oxygenated hemoglobin and outflows of de-oxygenated hemoglobin that occur when neurons fire. The BOLD signal is correlated with aggregate neural activity within relatively small “neighborhoods” (tiny cubes, known as voxels). One complication is that BOLD responses are slower than the associated neuronal responses: although the bulk of the neuronal response takes place in 4 to 6 seconds, subsequent BOLD measurements are affected for as much as 24 seconds. Even so, as long as trials are spaced sufficiently far apart, one can attribute most of the BOLD signal to trial-specific neural responses. In our experiment, each trial spanned a total of 11 seconds (2.75 seconds for an image, and 8.25 seconds for a fixation cross on a black screen), and BOLD measurements were obtained in 3-mm³ voxels every 2.75 seconds. With this design, the BOLD signal provides a good measure of local neural responses to each image. This is an approximation, but it suffices for our purposes. Presumably, a sharper measure of neural activity would yield even greater predictive power than that of the somewhat noisy measure used here.

Stage 2: Pairwise choices

In the second stage of the experiment, subjects were shown pairs of food items outside the scanner, and were asked to choose their preferred item from each pair. They were told that, with 50% probability, one of the pairs would be selected at random, and they would receive their choice from that pair.

The first ten subjects were shown 200 pairs of items drawn randomly with replacement from the 100 foods viewed in stage 1. The remaining 17 subjects were shown 50 randomly selected pairs, with each item appearing in a single pair. As discussed below, the first procedure is not appropriate for some portions of our analysis (a fact which we did not realize until we examined some preliminary results). Accordingly, some of the results reported below are based on all 27 subjects, while others are based on the last 17.

Foods were randomly assigned to left and right positions on the screen. As is common in such tasks, there was a small spatial bias: subjects chose the left item 53% of the time (p<0.05, binomial test). When estimating our forecasting models, it is important to ensure that our predictions do not benefit artificially from this bias (as they would if we used models describing the probability of choosing the object displayed on the left). Accordingly, for every subject, we randomly divided the choice pairs into two equal sets: in one, the chosen item was designated as the “target,” while in the other the item not chosen was so designated. The choice for any trial was then coded as a 1 if the target item was chosen, and as a 0 otherwise. With this assignment, the unconditional probability that our discrete choice variable equals 1 in any given trial is exactly 50 percent, and the predictive success of more elaborate models must be judged against that neutral benchmark (rather than 53 percent).¹⁴

Stage 3: Preference ratings

In the final stage of the experiment, subjects were asked to indicate the extent to which they liked each food item, using a discrete scale from -3 (strongly dislike) to 3 (strongly like). They viewed pictures of all 100 items sequentially and entered liking ratings through button presses, proceeding at their own pace. They were told that their ratings would not affect the item they received at the end of stage 3, but they were also strongly encouraged to provide ratings that reflected their true preferences.

After each subject finished rating the items, we tossed a coin to determine whether he or she would receive an item chosen at random, or the item chosen in a randomly selected choice trial from stage 2 (where the item or choice trial was selected by drawing a number from an envelope). Subjects were required to eat at least three spoonfuls of the selected item, and were allowed to eat more if desired. Subjects were instructed to remain in the lab for 30 minutes, during which time they were not permitted to eat anything else.

B. Initial data processing

Before analyzing the predictive power of non-choice BOLD responses, the raw data must be converted into a usable form. First, we corrected for head motion to ensure that the time series of BOLD measurements recorded at a specific spatial location within the scanner is always associated with the same brain location throughout the experiment.¹⁵ Second, we removed low-frequency signals that are unlikely to be associated with neuronal responses to individual trials.¹⁶ Third, we realigned the BOLD responses for each individual into a common neuroanatomical frame (the standard Montreal Neurological Institute EPI template). This step, called spatial normalization, is necessary because brains come in different shapes and sizes, and as a result a given spatial location maps to different brain regions in different subjects. Spatial normalization involves a nonlinear re-shaping of the brain to maximize the match with a target template. Although the transformed data are not perfectly aligned across subjects due to remaining neuroanatomical heterogeneity, the process suffices for the purposes of this study. Any imperfections in the re-alignment process introduce noise that reduces our ability to predict choices.

For the analyses described in Sections V (which involve comparisons across subjects), we also spatially smoothed the BOLD data for each subject, by making BOLD responses for each voxel a weighted sum of the responses in neighboring voxels, with the weights decreasing with distance.¹⁷ This transformation addresses residual problems arising from neuroanatomical heterogeneity across subjects. In effect, smoothing assumes that any particular voxel in one subject's brain can play the same predictive role as neighboring voxels in another subject's brain; without smoothing, we would be assuming that only the same voxel can play the same predictive role.

The final step was to compute, for each subject and each voxel, the average non-choice neural response to each food item. We began by removing predicted neural responses that were related to the task (e.g., seeing the image of a food item) but common to all items.¹⁸ The object of this step is to restrict attention to BOLD responses that are specific to individual food items, and therefore likely to be helpful in predicting choices. Second, we averaged the residual response over the three presentations of each food item, collected 2.75 and 5.5 seconds after the onset of stimulus. In constructing this average, we omitted measurements from full brain scans (known as volumes) that exhibited excessive within-volume variation across voxels.¹⁹ This exclusion criterion reduces noise (and thereby improves predictive accuracy) by eliminating signals that are outliers with respect to the typical range of BOLD responses for food items.

IV. Predicting choices involving new items, within subjects and groups

The canonical task motivating our investigation is to determine how people will behave when confronted with some new or difficult-to-observe choice situations. Imagine assembling a group of individuals, measuring their non-choice neural responses to prospects that we can actually implement, as well as to the new choice situations, and then presenting them with unanticipated choices among the implementable prospects. We can then estimate the relationship between their choices and non-choice responses for the implementable prospects, and use that relationship along with non-choice neural responses for the new situations to predict behavior in those situations. Do the non-choice neural responses contain enough information to make reasonably accurate predictions?

In this section, we implement the procedure outlined in the previous paragraph and use it to make and evaluate predictions both within subjects and within groups.

A. Within-subject predictions

In this subsection, we focus on the accuracy of within-subject predictions. For reasons detailed below, we restrict attention to subjects 11 through 27, each of whom made decisions for 50 pairs of food items, with no item appearing twice.

Statistical methods

We adopt a logit probability model for choices. For every subject i and choice pair t, let y_it = 1 if the target food was chosen, and y_it = 0 otherwise.²⁰ For every subject i, choice pair t, and brain voxel v, let d_itv denote the difference between the measured neural responses in voxel v to the target and non-target food items offered in choice pair t (i.e., the response for the target food minus the response for the non-target food). Also let D_it denote the vector of differential neural responses for all voxels. The following probability statement describes our model:

$$\text{Pr}[y_{\mathrm{i}\mathrm{t}}=1|{\mathbf{D}}_{\mathrm{i}\mathrm{t}}]=\frac{exp({\gamma }_0+{\mathbf{\gamma }}^{\mathbf{\prime }}{\mathbf{D}}_{\mathbf{i}\mathbf{t}})}{1+exp({\gamma }_0+{\mathbf{\gamma }}^{\mathbf{\prime }}{\mathbf{D}}_{\mathbf{i}\mathbf{t}})}.$$ (1)

Because our object is accurate out-of-sample prediction, we employ standard methods for estimating and evaluating predictive models. A central tenet of the prediction literature is that within-sample fit is a poor gauge of out-of-sample fit (cf. Efron, 1986). Therefore, we employ cross-validation (Stone, 1974) for both model assessment and model selection. Typically, one proceeds by dividing the sample into a “training sample” which is used for estimation, and a “hold-out” sample that is used to evaluate predictions. By removing two choice pairs at a time from the set of 50, we create 25 training samples (each consisting of 48 observations) and 25 associated hold-out samples (each consisting of 2 observations). For each training sample, we estimate the model and use it to predict choices for the associated hold-out observations. We then assess the model's out-of-sample predictive performance over all 25 hold-out samples (50 predictions in all).

To ensure the representativeness of both the training and hold-out samples, we randomly partitioned the 50 choices into 25 pairs, with each pair containing one choice from which the target item was chosen, and another from which it was not chosen. Each such pair served as a hold-out sample, and the complement served as a training sample. This procedure, known as stratified cross-validation, yields training and hold-out samples in which the target item is chosen exactly 50 percent of the time, just as in the full sample (by construction). Leave-one-out cross-validation is an approximately unbiased method for estimating the true (expected) prediction error (Hastie et. al, 2009, page 242). However, leave-one-out cross validation estimators may have high variance, and simulation studies have concluded that stratified cross-validation has better performance in terms of both bias and variance than regular cross-validation (Kohavi, 1995). Because our samples are unbalanced with leave-one-out cross validation, we compromise and employ stratified leave-two-out cross validation.

As the literature recognizes, evaluating the predictive performance of a categorical probability model involves some inherent ambiguities. Alternative standards for defining a “predicted outcome” have been proposed. In the context of binary models, Cramer (1999) proposes identifying an alternative as the predicted outcome if its predicted probability exceeds its baseline frequency in the population.²¹ By construction, in our experiment, the baseline frequency for selecting the target item is exactly 50% for each subject. Consequently, we classify the target item as the predicted choice if its predicted probability exceeds 50%; otherwise, the non-target item is the predicted choice. We classify a particular prediction as a “success” if the predicted item was in fact chosen.

Notice that our task involves prediction from small samples (48 observations). It therefore raises two important and closely related issues: model selection and overfitting.

The model selection problem is obvious: because we estimate each model using only 48 observations, we cannot use all 45,000 potential predictors (voxel-specific BOLD signals).²² Instead we must focus on a small handful of predictors, in effect leaving out large numbers of presumably relevant variables. If we intended to interpret estimated parameters as reflecting causal effects, the left-out variable problem would be fatal. Accordingly, it is essential to emphasize that our objective here is purely prediction. When predicting from a small sample, it is worthwhile to include a variable only if the incremental predictive information it carries is sufficient to justify sacrificing a scarce degree of freedom. Thus, for example, when two important causal factors are highly correlated, it is often appropriate to include only one, because each reflects most of the predictive information contained in the other. Naturally, with either factor omitted, the coefficient of the included factor will not measure its causal effect; on the contrary, that coefficient will also reflect the causal effect of the omitted factor. Even so, the omission of a causal factor does not impart a bias to predictions (conditional on the included predictors), and may well reduce variance. Statistical tools for model selection include the Akaike Information Criterion (AIC), the Bayesian Information Criterion (BIC), cross-validated predictive performance, LASSO (which we describe and implement below), and others.

The overfitting problem arises because, with small samples (and especially with many predictors), there is a substantial likelihood that some predictor will be highly correlated (within sample) with the outcome variable purely by chance. While OLS estimates will still yield statistically unbiased predictions, the variance of the prediction error can be extremely high, and hence predictions can prove inaccurate. The most obvious case occurs when the number of predictors equals the number of observations. In our analysis, any combination of 48 linearly independent predictors will yield a perfect fit within sample, but the resulting model will generally perform very poorly out of sample.

Various techniques have been developed to address the overfitting problem. Shrinkage estimators (of which ridge regression is the best known example) compensate for overfitting by shrinking the overall size of the estimated coefficient vector. Such estimators can attenuate the sensitivity of predictions to changes in the predictors, and hence reduce variance, thereby improving the overall accuracy of out-of-sample predictive performance according to measures such as mean-squared prediction error (a commonly used statistic that encompasses both the bias and the precision of a prediction). We address the model selection and overfitting issues using LASSO (the Least Absolute Shrinkage and Selection Operator; see Tibshirani, 1996) combined with cross-validation. As the name implies, LASSO, like ridge regression, is a shrinkage procedure.²³ For both procedures, one optimizes a standard criterion for within-sample fit (for example, minimizing the sum of squared residuals in the case of a regression, or maximizing likelihood) subject to a penalty that increases monotonically in the size of the coefficient vector. For ridge regression, one measures the size of the coefficient vector using the L2-norm (i.e., the square root of the sum of squared coefficients). For LASSO, one uses the L1-norm (i.e., the sum of the absolute values of the coefficients). While both methods of penalization lead to shrinkage, only LASSO also accomplishes variable selection.²⁴

In our context, the LASSO procedure involves maximizing the following penalized log-likelihood function over the parameters γ₀ and γ = (γ₁,…,γ_νi), where ν_i is the number of voxels for subject i:

$$\frac{1}{T}{\sum }_{t=1}^T\{y_{it}log{p}_{it}+(1-y_{it})log(1-p_{it})\}-\lambda {\Vert \mathbf{\gamma }\Vert }_1.$$ (2)

Here, T denotes the number of trials in the training set, p_it = Pr [y_it = l[D_it] and ║γ║₁ denotes the L₁ norm on γ.²⁵ In the LASSO objective function the L₁ penalty receives a weight of λ.²⁶ Larger values of λ lead to greater shrinkage and to more aggressive variable selection. The value of λ is determined through cross-validation, which is a procedure for simulating out-of-sample predictive performance entirely within a training sample. For our analysis, we randomly divided each training sample into five sets of approximately equal size, indexed k = 1,…,5 (called folds in the statistical prediction and machine learning literatures). For each k, we estimated the penalized regression model for each possible value of λ in a pre-specified grid using only the data from the k − 1 other folds. We then used the estimated models to predict choices for the left-out fold, and computed the accuracy of the predictions by comparing them to the actual choices. The value of λ with the highest successful prediction rate across all of the folds, λ*, was then used to estimate the model with all of the observations in the training sample.²⁷ Importantly, note that the selection of λ* is blind with respect to outcomes in the actual hold-out sample; thus, accuracy within the hold-out samples remains a valid gauge of the procedure's out-of-sample performance.

The LASSO procedure not only achieves beneficial shrinkage, but also in effect ensures that a variable remains in the model with a non-zero coefficient only if its incremental predictive value is sufficient to justify the sacrifice of a degree of freedom. Thus, in our setting the procedure selects the brain voxels with the neural responses that provide the most valuable predictive informative concerning subsequent choices.

Prior to implementing the LASSO procedure, we reduced the vast set of candidate voxels by excluding those that failed to meet a simple statistical criterion. Ryali et al. (2010) have shown that this initial screening step can improve predictive accuracy in studies employing fMRI data, even when the subsequent estimation procedure selects voxels automatically (as is the case here). For every voxel, we computed a simple two-sided t-test for the hypothesis of no difference between neural responses (within the training sample) to foods that were chosen and those that were not. We then ranked voxels by the absolute values of their t-statistics, and retained only those exceeding some threshold percentile.²⁸ Intuitively, the purpose of this initial screening step is to focus attention on voxels that are likely to contain highly predictive information. For each prediction task, we examine the robustness of prediction success rates with respect to a range of screening criteria, and then present more detailed results based on analyses for which the top 1% of voxels were retained. Note that the voxel selection procedure, like the selection of λ*, is completely blind with respect to outcomes in the actual hold-out sample; thus, accuracy within the hold-out samples remains a valid gauge of the procedure's out-of-sample performance.

As we mentioned at the outset of this section, data gathered from our first 10 subjects were not used for within-subject predictions. Recall that those subjects made choices from 200 pairs of items, drawn randomly with replacement from our set of 100 items. Thus, when the full sample is divided into a training sample and a hold-out sample, the items that belong to pairs in the hold-out sample also typically belong to pairs in the training sample. The resulting overlap between the sets of items represented in the training and hold-out samples can lead to spurious predictive accuracy. ²⁹

Results

Figure 1 plots the mean success rates, defined as the fraction of holdout observations for which the predicted item was chosen, as a function of the percent of voxels retained after initial screening, with the retained percentiles ranging from 0.01% to 100%. When 1% of voxels are retained, the mean success rate is 61.3%, which represents an economically and statistically significant improvement over the uninformed 50% benchmark (p < 0.0001, one-sided t-test). Performance falls sharply when fewer than 1% of voxels are retained, but declines only slightly when fewer are eliminated. Indeed, when we abandon the initial screening step (i.e., retain all voxels), our overall success rate, 59.3%, remains significantly better than the uninformed benchmark (p < 0.001), and is not significantly different from the rate obtained when retaining 1% of voxels (p=0.23, paired t-test). Thus we find, in contrast to Ryali et al. (2010), that the initial voxel-screening step yields only a small and statistically insignificant improvement in this measure of predictive accuracy. For the rest of this section, we will focus on the results obtained using the 1% screening criterion; our conclusions are not substantially affected by applying less restrictive screens.

Figure 1.

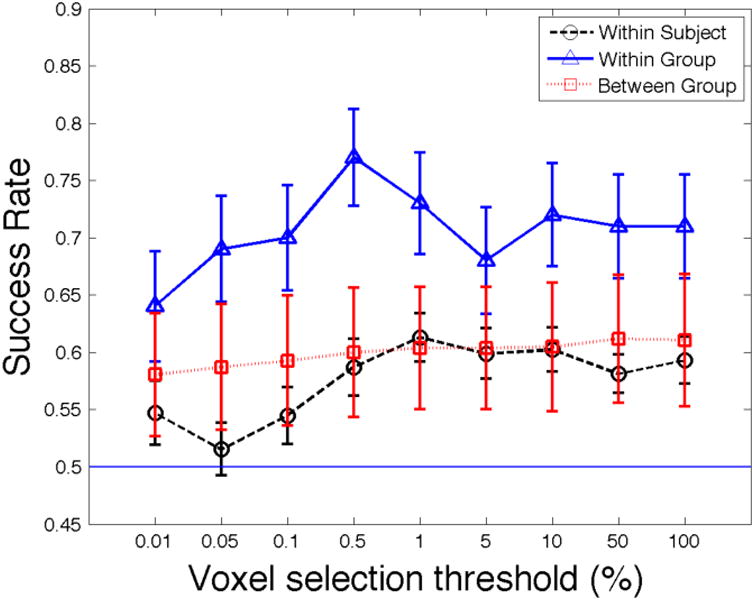
Overall success rate as a function of the percent of voxels retained after initial screening when predicting choices for new items.

Notes: The between group standard errors are bootstrapped using the 200 population draws.

The first data column in Table 1 provides results on success rates for each subject (numbered 11 through 27 because this analysis excludes the first ten subjects). There was considerable cross-subject variation in success rates, which ranged from a low of 44% to a high of 76%, with all but one exceeding 50% and four exceeding 70%. These rates exceeded the uninformed benchmark by a statistically significant margin for 9 out of 17 subjects at the 5% level (amongst whom the overall success rate was 68%), and for 8 out of 17 subjects at the 1% level. Plainly, non-choice neural responses contain a substantial amount of predictive information for those subjects. For subsequent reference, we have shaded all of the rows in the table associated with high-success-rate subjects (i.e., those whose success rates exceeded the uninformed benchmark by statistically significant margins), so that their results are easily distinguished from those of low-success-rate subjects (i.e., the complementary set).

Table 1.

Predictive accuracy for choices involving new items, within subject.

		Predicted probability of the more likely item			LPM
Subject	Success rate	Mean	Std dev	p-value for bias	Slope	Std err. of slope
11	0.66***	0.663	0.138	0.966	0.966	0.485
12	0.52	0.702	0.156	0.013**	0.550	0.459
13	0.62**	0.728	0.143	0.090*	1.579	0.434
14	0.66***	0.768	0.133	0.126	0.133	0.517
15	0.58	0.711	0.128	0.074*	0.230	0.559
16	0.52	0.742	0.147	0.005***	-0.075	0.494
17	0.58	0.730	0.136	0.050*	-0.325	0.527
18	0.76***	0.738	0.141	0.726	0.393	0.437
19	0.54	0.733	0.142	0.014**	-0.332	0.508
20	0.58	0.692	0.148	0.114	0.698	0.476
21	0.62**	0.748	0.140	0.070*	0.517	0.499
22	0.72***	0.697	0.130	0.727	0.381	0.501
23	0.68***	0.717	0.144	0.567	0.955	0.454
24	0.70***	0.763	0.118	0.320	1.328	0.544
25	0.44	0.760	0.145	0.000***	-0.420	0.494
26	0.52	0.733	0.141	0.007***	-0.312	0.515
27	0.72***	0.738	0.155	0.761	1.114	0.392
Group Mean	0.613***	0.727	0.140	< 0.001***	0.434	0.488
Std. Dev.	0.089	0.028	0.010		0.615	0.043

Notes: Based on an initial voxel selection threshold of 0.01. Asterisks are used to denote statistical significance only in the columns for “success rate” (difference from uninformed benchmark of 0.50, binomial test for individual rates, 1-sided t-test for group mean rate) and “p-value for bias” (difference between success rate and mean predicted probability, two-sided t-test), as follows:

^*denotes p<0.1;

^**denotes p<0.05;

^***denotes p<0.01. “Success rate” is the frequency with which the item with highest predicted choice probability in each pair was actually chosen; “p-value for bias” refers to the test statistic for the hypothesis that the success rate equals the mean predicted probability, and “LPM” refers to a simple linear probability model relating a success indicator to the predicted probability. “Group Mean” is the mean of within-subject means, and “Std. Dev.” is the standard deviation of within-subject means.

As we mentioned in the introduction, a success rate is a particular blend of the resolution and calibration of a probabilistic prediction.³⁰ Resolution refers to the degree of certainty. The statement that an individual will choose the target item with either 1% or 99% probability involves high resolution, while the statement that he will choose that item with either 49% or 51% probability involves low resolution. Calibration refers to the degree to which the probabilistic prediction matches actual frequencies. To illustrate, suppose that for some group of pairwise choices, a model predicts that the target will be chosen with an average probability of 75%. The model's predictions are well-calibrated if the realized frequency that the target is chosen, for any reasonably large group of observations, is close to the average predicted probability. If it is not close, the model's predictions are poorly calibrated. In the preceding example, if the realized frequency is 55% rather than 75%, the model's probabilistic predictions are poorly calibrated. The same is true if the frequency is 95%.

According to these definitions, the predictions of the uninformed benchmark (50-50) have zero resolution but are perfectly calibrated (because the overall success rate, 50%, matches the predicted probability of the most likely item in every pair). In contrast, the typical deterministic model will be highly resolved, but in all likelihood poorly calibrated (because it is rarely possible to forecast outcomes with certainty).

Knowing only that the average success rate for our procedure is 61.3%, one cannot say anything about the resolution or calibration of the underlying predictions. Yet such distinctions are plainly crucial. If our procedure typically yielded predicted probabilities of the more likely item on the order of 90% but achieved an overall success rate near 60%, its success would be only directional, and one would not be able to take its probabilistic predictions seriously. On the other hand, if on average our procedure yielded predicted probabilities of the more likely item near 60% (i.e., in line with the observed success rate), then although one could complain that its predictions had somewhat low resolution, at least they would be well-calibrated.³¹

With respect to potential complaints concerning low resolution, it bears emphasizing that the value of an accurate predictive model should not be discounted merely because its predictions are not as highly resolved as one might like. On the individual level, certain determinants of choice may be fundamentally unpredictable (see, e.g., Krajbich, Armel, and Rangel, 2010), in which case the resolution of any well-calibrated probabilistic prediction is necessarily limited. Fortunately, such idiosyncratic randomness likely averages out over multiple decisions, so it should still be possible to predict the average behavior of groups with reasonably high resolution (see Sections IV.B and V).

The second data column in Table 1 sheds light on the resolution of our procedure's predictions. Focusing for the moment on the second-to-last row, we see that the mean predicted probability of the more likely item is 72.7%. For a perfectly calibrated model, this number equals the expected success rate. Yet we see that there is a sizable and highly statistically significant gap (or bias) of 11.4 percentage points between the mean predicted probability and the overall success rate of 61.3% (p <0.001). At this level of aggregation, one cannot describe the models' probabilistic predictions as well-calibrated.

A careful examination of the results for individual subjects tells a more interesting and nuanced story. Based on our initial analysis of success rates for individual subjects, it is entirely possible that our procedure works well for some subjects, and poorly (or not at all) for others. For example, some subjects may not meaningfully attend to the images of food items during stage 1.³²

To evaluate the calibration of the predictive model for each subject, we first test the hypothesis that the success rate equals the mean predicted probability of the more likely item. The fourth column of Table 1 contains the p-values for those subject-specific tests. Comparing the shaded and unshaded lines, we see a striking pattern. We cannot reject equality of the success rate and the expected success rate with 95% confidence for any of the high-success-rate subjects, and we reject equality with 90% confidence for only two of these subjects (and would have expected roughly one rejection by chance). In contrast, we reject equality at the 90% confidence level for seven of the eight low-success rate subjects (and with 88% confidence for the eighth), at the 95% confidence level for five, and at the 99% confidence level for three. Visually, asterisks (indicating levels of statistical significance) tend to appear in the first data column when no asterisks appear in the fourth, and vice versa.

Overall, for high-success-rate subjects, the mean success rate is 68.2%, while the expected success rate is 72.9%; the difference (or bias) is modest but statistically significant (p = 0.042). Though the predictions are not right on the mark, they are remarkably close given the nature of our out-of-sample prediction exercise. Interestingly, our predictions are equally resolved for the low-success-rate subjects: the expected success rate is 72.6%. However, the mean success rate for those subjects is only 53.5%, and the difference (or bias) is large and highly statistically significant (p < 0.001).

One might be tempted to discount the preceding results as a possible coincidence: if the overall success rate is below the overall mean predicted probability, and if the latter does not vary between low- and high-success-rate subjects, then it is not surprising that the success rate for high-success-rate subjects is closer to that group's mean predicted probability of the more likely item. Thus, we view this first test as providing only a relatively weak preliminary indication concerning the model's performance among high-success-rate subjects.

Fortunately, a more demanding test is available. So far, we have made no use of variation in the strength of predictions across hold-out observations (e.g., whether the predicted probability of choosing the target item is 51% or 98%). According to Table 1, the mean within-subject standard deviation of the predicted probability is substantial (0.140). Moreover, the predicted probability of the more likely item is distributed fairly evenly between 50% and 100% (see Figure A2 in Appendix A). Using this variation allows us to determine whether our predictive procedure is functioning properly. If, for example, the predicted probability averages 60% within one large group of hold-out observations and 80% within a second group, and if the model is generating valid out-of-sample probabilities, the frequency with which the more likely item is chosen should be approximately 60% in the first group and approximately 80% in the second. Even if the model is just capturing tendencies, that frequency should be noticeably higher in the second group than in the first.

We implement this idea as follows. First, we rank the hold-out observations (pooled across all subjects) according to the predicted probability of the more likely choice (i.e., the probability of choosing the target item if the model indicates that the target is more likely, and the probability of choosing the non-target item if the model indicates that the non-target item is more likely). Second, we divide the observations into deciles based on that probability. Third, for each decile, we compute the frequency with which the item identified as more likely was in fact chosen (i.e., the success frequency). Finally, we examine the relationship across deciles between the average predicted probability of choosing the more likely item and the actual frequency with which that item was actually chosen.³³

Figure 2A plots the results, pooled over all subjects. The horizontal axis shows the predicted probability of choosing the more likely item, while the vertical axis shows the frequency with which that item was actually chosen. For an ideal predictive model, the data points would line up along the 45-degree line (i.e., the predicted probabilities and the success frequencies would always coincide). Though our procedure does not achieve this ideal, there is nevertheless an obvious and reasonably strong positive relationship between the predicted probabilities and success frequencies. Between the first and eighth deciles, the actual success rate increases roughly half a percentage point for every one percentage point increase in the predicted probability; beyond the eighth decile, it declines modestly. Overall, the predictive performance of the model is encouraging, at least directionally.

Figure 2.

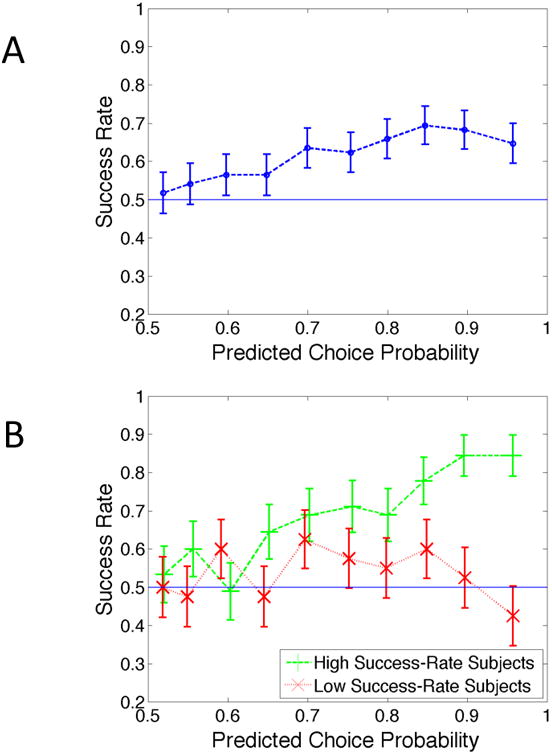
Success rate for within-subject predictions of choices involving new items as a function of predictive choice probability of the more likely item.

Notes: (A) the entire group, and (B) separately for high-success-rate and low-success-rate subjects.

Figure 2B performs the same analysis separately for low- and high-success-rate subjects. The results are striking. For the eight low-success-rate subjects, there is no relationship between success frequencies and predicted probabilities: the line moves up and down a bit, but overall is fairly flat. With these problematic subjects removed, the procedure's performance is much improved. For the nine high-success-rate subjects, the relationship between success frequencies and predicted probabilities increases more sharply than the one in Figure 2A, and is much closer to the ideal (i.e., the 45 degree line). For the lowest two deciles, within which the average predicted probability is 53.8%, the overall success frequency is 56.7%, while for the highest two deciles, within which the average predicted probability is 92.7%, the overall success frequency is 84.4%.

To sharpen these impressions, we conduct additional statistical analyses. For each subject i and choice trial t, we define a binary success indicator, S_it, which equals unity when the subject chooses the item predicted as more likely (with this trial treated as a hold-out observation), and zero otherwise. Let P_it denote the predicted probability that the subject i will choose the item identified as more likely in choice trial t (again, when this choice trial is treated as a hold-out observation). Assuming that P_it is in fact a correct probability, it follows trivially that E[S_it|P_it] = P_it. Thus, S_it = P_it + ε_it, where E[ε_it|P_it] = 0 (in particular, ε_it equals 1-P_it with probability P_it, and -P_it with probability 1- P_it). Accordingly, our strategy is to estimate simple linear probability models (LPMs) of the following form:

$$S_{it}=\alpha +\beta P_{it}+{\varepsilon }_{it}.$$ (3)

If the predicted probability statements are in fact correct, we should obtain α=0 and β=1.

We estimate two versions of the preceding linear probability models, one for the nine high-success-rate subjects, and one for the eight low-success-rate subjects. We use weighted least squares to account for the inherent heteroskedasticity in the linear probability models, following the procedure in Wooldridge (2003, page 455). In these regressions, each observation consists of a single hold-out choice pair; thus, the regression for high-success-rate subjects uses 50 × 9 = 450 observations, while the regression for low-success-rate subjects uses 50 × 8 = 400 observations. For the eight low-success-rate subjects, we obtain an intercept of 0.551 (s.e. = 0.129) and a slope of −0.023 (s.e. = 0.174). The combination of low success rates and the absence of any detectable relationship between the two variables indicates that our forecasting procedure fails for those subjects. In contrast, for the nine high-success-rate subjects, we obtain an intercept to 0.118 (s.e. = 0.113) and a slope 0.775 (s.e. = 0.152). Here, the relationship between the two variables is strong, positive, highly statistically significant, and within the general vicinity of the ideal. However, we reject the hypothesis that the intercept is in fact zero and the slope unity (p = 0.012). With that qualification, our prediction model performs well out of sample for the nine high-success-rate subjects.

Conceivably, the strong results obtained for the LPM estimated with high-success-rate subjects could be attributable to compositional effects: success rates might be unrelated to predicted probabilities within subject, but subjects with higher success rates might also have higher predicted probabilities. In practice, Table 1 provides little reason to anticipate significant compositional effects, because the means and standard deviations of the predicted probabilities (the second and third data columns) are quite similar across subjects (the cross-subject standard-deviations of these statistics are only 0.028 in the case of the within-subject mean, and 0.010 in the case of the within-subject standard deviation).

To rule out the possibility that our LPM results for high-success-rate subjects reflect compositional effects, we estimate another LPM with subject-fixed effects. Our estimate of β increases to 0.808 (s.e. = 0.157). We also estimate an LPM separately for every subject. The slope coefficients and associated standard errors are reported in the last two data columns of Table 1. Because each regression employs only 50 observations, the standard errors are large. Still, the overall pattern is striking. For the high-success-rate subjects, the slopes are all positive and range from a low of 0.133 to a high of 1.579. The mean slope is 0.818 and the median is 0.955, with three of the nine slopes exceeding unity. In contrast, for the low-success-rate subjects, five of the eight slopes are negative. They range from a low of −0.420 to a high of 0.698, with a mean of −0.002 and a median of −0.194.

We conclude that our within-subject procedure for predicting choices involving new items performs successfully for roughly half (nine of seventeen) of our subjects. The overall success rate is 68% for that group, and subject-specific success rates are close to subject-specific mean predicted probabilities of the more likely item, our expected success rates. Moreover, success frequencies mirror predicted probabilities across hold-out observations, both overall and within subjects. The predicted probabilities are not always spot-on for this group, but they are close.

We acknowledge that the procedure works poorly for the rest of our subjects: the overall success rate is only 54%, subject-specific success rates differ considerably from subject-specific mean predicted probabilities, and success frequencies bear no discernable relation to predicted probabilities across hold-out observations.³⁴

B. Within-group predictions

Our investigation in this subsection parallels that of Section 4.A, except that we study average behavior among groups, rather than the choices of specific individuals. Our objective is determine whether the average neural responses among a group of individuals contain enough information to make reasonably accurate predictions concerning the group's average behavior in new situations, using a model estimated with data concerning the same group.

Here we predict measures of subjective valuation, averaged across group members. A natural alternative strategy would have been to predict the fraction of subjects choosing the target item from a given pair. Unfortunately, that alternative is inconsistent with our experimental design, which employed different random pairings of the items for different subjects.

As explained in Section III, stage 3 of our experiment elicits preference ratings (on a scale of −3 to +3) for each item from every subject. We acknowledge that that our elicitation protocol is not incentive-compatible and that these ratings may not provide cardinally meaningful measures of willingness-to-pay (WTP), but we study them nevertheless for two reasons. First, preference ratings were elicited after the subjects made incentivized choices, from which it follows that (i) subjects had already thought about their preferences for each item in an incentive-compatible context, and (ii) subjects were likely to provide ratings that rationalized their choices. Second, these ratings were in fact highly correlated with choices: subjects choose the item with the highest rating 85.1% of the time in the 50-choice condition (subjects 1-10; p<10^-12, one-sided t-test vs. chance) and 90.1% of the time in the 200-choice condition (subjects 11-27: p<10^-8, one-sided t-test vs. chance). Third, and more importantly, to the extent preference ratings are noisy measures of subjective valuation, our results likely understate the true predictive power of non-choice neural responses.

Statistical methods

Before aggregating subjective ratings across our 27 subjects, we normalized each subject's ratings using a z-score transformation. We then computed the mean normalized ratings for the group, denoted Z_j for item j, as well as the group's mean non-choice neural responses, denoted M_j for item j, where M_j is a vector containing the average (across the group) neural response for each voxel v, denoted M_vj.³⁵

As a first step, we simply ask whether the average non-choice neural responses to an item predict whether its average subjective rating is above or below the median rating (denoted Z^med). This is an interesting comparison because it stands in for a binary choice between the item in question and the median-rated alternative. We assume that the probability of an above-median rating for any item j is given by the logistic function:³⁶

$$\text{Pr}(Z_j>Z^{\mathit{\text{med}}}|{\mathbf{M}}_j)=\frac{exp({\gamma }_0+{\mathbf{\gamma }}^{\mathbf{\prime }}{\mathbf{M}}_j)}{1+exp({\gamma }_0+{\mathbf{\gamma }}^{\mathbf{\prime }}{\mathbf{M}}_j)}.$$ (4)

Plainly, realizations of this process cannot be independent across items (because half of the items must be above the median). However, with a sufficient number of items, correlations across observations are presumably small, so we ignore them and treat the model as a simple approximation of the true process.

By removing two items at a time from the set of 100, we create 50 training samples (each consisting of 98 observations) and 50 associated hold-out samples (each consisting of two observations). For each training sample, we then estimate the model and use it to predict whether the average valuations for the hold-out observations will fall above or below the median valuation of items within the training sample. We then assess the model's out-of-sample predictive performance over all 100 predictions. We classify a prediction as a success if the item's average subjective rating falls into the half of the training sample rating distribution that the model identifies as more likely.

As in the previous section, we applied a screening criterion to reduce the number of candidate voxels prior to estimating the model for any given training sample. Using only the training data, for each voxel v we regressed M_vj on a binary variable indicating whether Z_j was above Z^med. We then ranked the voxels according to the absolute values of the t-statistics of the slope coefficients and retained those falling within some specified quantile. Then we estimated the probability model using the LASSO procedure, selecting the penalty parameter through 5-fold cross-validation, where the folds were assigned at random.

The second step in our analysis of group behavior was to predict the actual value of Z_j, an item's average subjective rating across all subjects, rather than a binary indicator of its position relative to the median. For this analysis, we employed a LASSO-penalized linear regression of Z_j on M_j. In the initial screening step, for each voxel v we regressed M_vj on Z_j, then ranked all voxels by the t-statistics of the slope coefficients, and retained the highest 1%. All other procedures were identical, except that the LASSO penalty parameter, λ*, was chosen to maximize cross-validated mean-squared-error (which is appropriate here given that the objective is to predict a continuous variable).

As mentioned previously, the data gathered from our first 10 subjects are suitable for this analysis. Only the stage 2 choice data for those subjects have the feature that a single item plays a role in more than one observation (which produces violations of the assumed separation between training and hold-out samples), and we do not use those data here. Thus, throughout this section we present results based on all 27 subjects.

Results

We begin with an analysis of predictions concerning the probability that the average subjective rating for a given hold-out item will fall above the median rating for items in the training sample. Figure 1 plots the overall success rate as a function of the percent of voxels retained after initial screening, with the retained percent ranging from 0.01% to 100%. Our procedure maximizes the success rate when 0.5% of voxels are retained. The overall success rate is then 77%, which represents an economically and statistically significant improvement over the uninformed 50% benchmark (p < 0.001, one-sided t-test). Performance falls sharply when fewer than 0.5% of voxels are retained in the initial screening step, but is fairly robust when fewer are eliminated, with success rates generally exceeding 70%. Recalling that classifications of ratings relative to the median stand in for binary choices between any given item and an alternative of median value, we note that we achieve a significantly higher overall success rate for within-group predictions than for the within-subject predictions discussed in Sections IV.A (compare the pertinent lines in Figure 1). To avoid cherry-picking results section-by-section, we adopt the same screening criterion here as in the previous section (1%), which yields a success rate of 73%, rather than the success-rate-maximizing 0.5% criterion. Our conclusions are not substantially affected by applying less restrictive screens.

Figure 3A illustrates the relationship between the predicted probability of an above-median rating and an item's average rating. Each data point corresponds to a food item; circles and crosses represent, respectively, correctly and incorrectly classified items. A strong positive relationship is easily discerned: our model plainly tends to predict higher probabilities of above-median ratings for more highly rated items.

Figure 3.

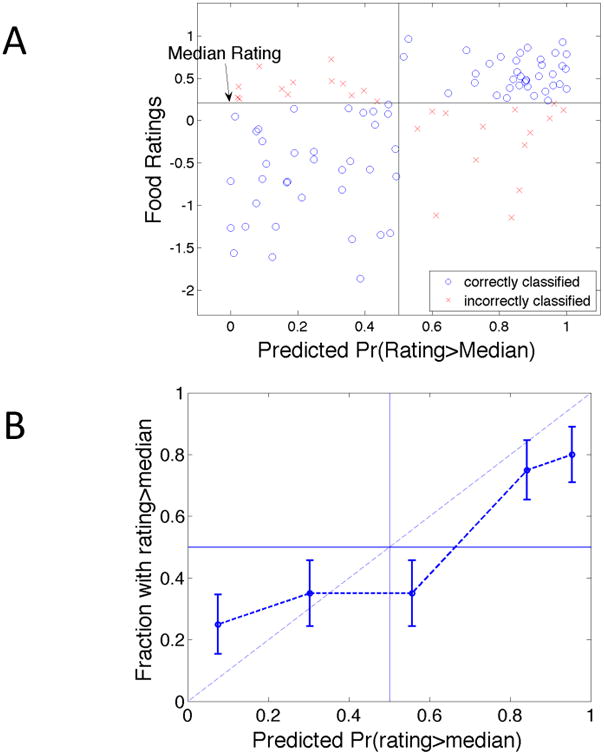
Predicting above-and-below-median ratings for new items within groups.

Notes: (A) Scatter plot of mean ratings versus predicted probability that item is in the upper half of the group's valuation distribution. Circles denote correct predictions. Crosses denote incorrect predictions. (B) Fraction of items with ratings exceeding the median versus average predicted probability of rating exceeding the median, grouped by quintiles of the latter.

As in Section IV.A, we perform an initial test of the validity of the model's predictive probability statements by comparing the average predicted probability with the overall success rate. On average, the model predicts that items will fall into the more likely half of the rating distribution with 79% probability. This figure is close to the actual success rate (73%), and the gap is statistically insignificant (p = 0.388, two-sided t-test).

For a more discerning assessment of the model's predictive validity, we grouped items into quintiles (20 items in each) based on the predicted probability that the item's average rating exceeded the median, and then, for each quintile, computed the frequency with which the group's ratings of those items actually fell above the median. Results appear in Figure 3B. A strong positive relationship between predicted probabilities and realized frequencies is readily apparent. While the five data points do not line up along the 45 degree line, the empirical relation bears some resemblance to that ideal.

To sharpen this impression, we estimated a linear probability model (again using weighted least squares, to account for heteroskedasticity of the error term) relating a binary variable indicating whether an item's average rating was above the median to the predicted probability of that event. The estimated intercept is 0.173 (s.e. = 0.080), and the slope is 0.624 (s.e. = 0.127). We reject the joint hypothesis that the intercept is zero and the slope is unity with 95% confidence (p = 0.013). Although the point estimates may not support a literal interpretation of the model's predictive probability statements, on the whole its quantitative out-of-sample performance is promising.

Next we turn to predictions of the average rating itself, rather than its relation to the median. Figure 4 plots average normalized ratings against predicted ratings. The predictions are by no means exact, but there is once again a strong positive relationship. To summarize that relation, we regress the actual rating on the predicted rating using ordinary least squares and plot the regression line. With unbiased predictions, our regression would yield an intercept of zero and a slope of unity. We obtain an intercept of -0.012 (s.e. = 0.060) and a slope of 0.712 (s.e. = 0.144), and fail to reject the joint hypothesis of interest with 90% confidence (p = 0.136). The predicted ratings account for 20% of the variation in the actual ratings.

Figure 4.

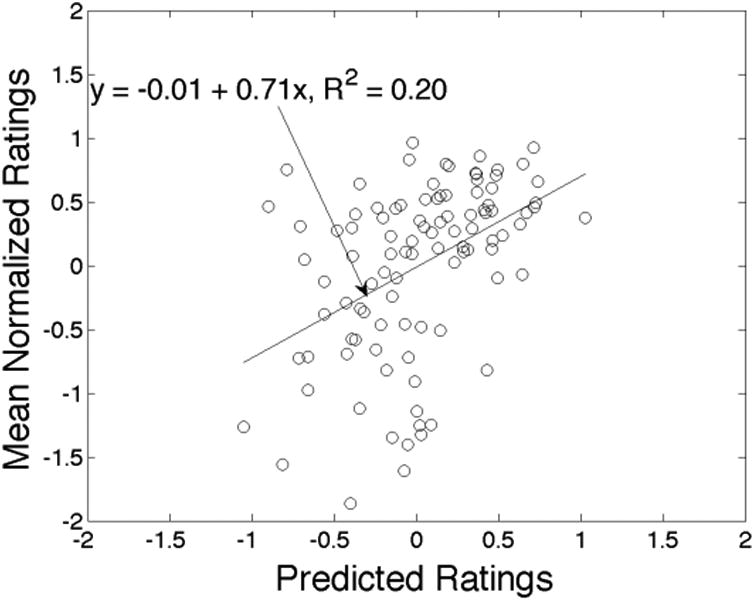
Predicting average ratings for new items within groups.

Notes: Scatter plot of actual vs. predicted mean normalized ratings for each item. Each point represents a different food item. Least-squares regression line included.

We conclude that our within-group procedure for predicting the average ratings of new items performs with considerable success. For the binary prediction task, the overall success rate is well over 70%, considerably higher than for within-subject predictions, and predicted probabilities match up reasonably well with realized frequencies. Predicted ratings also track average ratings and plainly contain usefully predictive information.

Conceivably, one might achieve greater predictive accuracy by conditioning on higher moments of the distribution of predicted ratings. Likewise, it may be possible to predict additional parameters of the distribution of actual ratings, such as variance. These are important questions, but we leave them for future research.

V. Predicting choices across groups

The method of prediction developed and implemented in the previous section requires the use of separate forecasting models calibrated to each individual or group. If non-choice neural activity exhibits a sufficiently similar relation to choice across subjects, then it should be possible to construct a single prediction model and use it without recalibration to predict choices based on neural measurements taken from new individuals or groups. Such a model would have considerable practical value in that, once estimated, it would vastly simplify the steps required to formulate additional predictions. In particular, to predict behavior in new situations, one could collect data on non-choice neural responses to the relevant prospects for a new group of individuals, and apply the existing model. It would not be necessary to collect new measurements from the same set of individuals used to estimate the original model, or to re-estimate the model with additional data elicited from the new group. Indeed, with sufficient research, it might be possible to converge upon a single, stable formula for predicting new choices based on non-choice neural responses.

In this section we explore the feasibility of developing a single model for predicting choices from non-choice neural responses that is portable from one group to another. Specifically, we investigate whether it is possible to estimate the model with data on one group's choice distributions over various sets of items and, with reasonable accuracy, use it to predict another group's choice distributions over sets of new items.

Statistical methods

The methods used here are identical to those of Section VI.B, with some exceptions involving the nature of the training and hold-out samples. As in Section IV.B, all twenty-seven subjects were included in this analysis. Here, we randomly divide the subjects into a training group of 14 subjects and a hold-out group of 13 subjects. By removing two items at a time from the set of 100, we create 50 training sets (each consisting of 98 items) and 50 associated hold-out sets (each consisting of two items).

For each set of training items, we then estimate the same two models as in Section IV.B using data on the training subjects. We use one model to predict whether the average ratings of the hold-out subjects for the hold-out items will fall above or below the average rating of the median item for the hold-out subjects, and the other to predict the average ratings themselves.

To ensure that our results cannot be attributed to a potentially idiosyncratic division of the subjects, we repeat this exercise 200 times, selecting the training and hold-out groups randomly each time. We thereby generate a total of 20,000 predictions.

Results and discussion

We begin with an analysis of predictions concerning the probability that the hold-out group's average subjective rating for a given hold-out item will fall above the median rating for items in the training data. Figure 1 plots the overall success rate (averaged over the 200 population draws) as a function of the percent of voxels retained after initial screening, with the retained percent ranging from 0.01% to 100% of voxels. Our procedure maximizes this rate when 50% of voxels are retained. The average overall success rate is then 61.2%,³⁷ which represents an economically and statistically significant improvement over the uninformed 50% benchmark (p < 0.001, one-sided t-test). Here, the initial voxel selection criterion has a fairly small effect on the success rate. To avoid cherry-picking results section-by-section, we will adopt the same screening criterion here as in Section IV (1%), which yields an average overall success rate of 60.3%, rather than the success-rate-maximizing 50% criterion. Our conclusions are not substantially affected by applying less restrictive screens.

As in Section IV, we perform an initial check on the validity of the model's predictive probability statements by comparing the typical probabilistic prediction with the average overall success rate. On average, the procedure predicts that items will fall into the more likely half of the rating distribution with 79.7% probability. That figure is not close to the average overall success rate of 60.3%, and the gap is statistically significant (p < 0.001, two-sided t-test). Consequently, the procedure does not generate quantitatively accurate probability statements for the hold-out data.

For a more revealing assessment of the model's predictive validity, we grouped individual predictions into deciles (2000 predictions in each) based on the predicted probability that the hold-out item's average rating among the hold-out group would exceed the median, and then, for each decile, computed the frequency with which the hold-out group's average ratings of those items actually fell above the median. Results appear in Figure 5, which shows a strong positive relationship between predicted probabilities and realized frequencies. The relationship does not, however, lie close to the 45 degree line.

Figure 5.

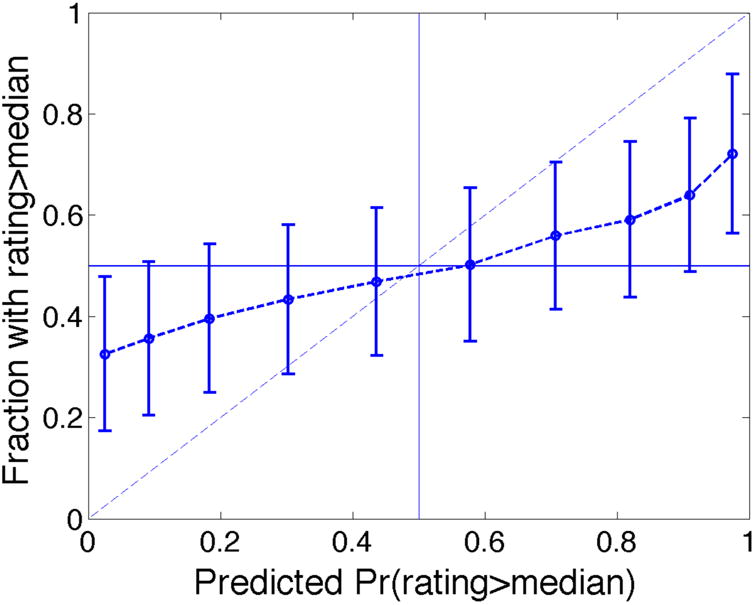
Predicting above-and-below-median average ratings for new items and new groups.

Notes: Fraction of items with ratings exceeding the median versus average predicted probability of rating exceeding the median, grouped by deciles of the latter. Standard errors computed via bootstrap over the 200 population draws.

To sharpen these impressions, we estimated linear probability models (via weighted least squares) relating a binary variable indicating whether the hold-out group's average rating of a hold-out item was above the median, to the predicted probability of that event. Pooling all 20,000 predictions, the estimated intercept is 0.317 (s = 0.006), and the slope is 0.364 (s.e. = 0.010). Adding fixed effects for each of the 200 population draws, the coefficient estimates and standard errors are the same to three decimal places. We also estimated a separate LPM for each population draw. The mean slope is 0.360 (s.e. = 0.158), and the median is 0.354.³⁸ Although these estimates do not support a literal interpretation of the model's predictive probability statements, they are directionally accurate. Thus, they provide evidence that the predicted probabilities contain a good deal of information that is useful for predicting across subjects.

As in our within-group exercise, we also directly predict the average rating using a linear regression with LASSO penalty. We then estimate an ordinary least squares regression of mean normalized rating (for the hold-out food in the holdout group) on predicted rating for all 20,000 predictions, with fixed effects for each of the 200 population draws. The constant is -0.002 (s.e. 0.066) and the slope is 0.528 (se 0.012). The R² from this regression is 0.091.³⁹ While the results from this exercise are not as strong as for the within-group analysis, the predicted ratings are clearly related to the actual ratings of the group.

VI. Some extensions

In this section, we briefly summarize two extensions of our analysis. The first investigates whether it is possible to improve upon predictions derived with LASSO estimates through the use of alternative statistical tools. The second examines the anatomical location of predictive brain activity.

Zou and Hastie (2005) propose a procedure known as the Elastic Net, which they argue improves upon LASSO in many settings. The Elastic Net penalty is a convex combination of the LASSO (L₁) and Ridge (L₂) penalties. Like LASSO, it accomplishes variable selection, but has a greater tendency to retain correlated predictors (e.g., in the current context, activity in neighboring voxels). The procedure yields modest improvements. For example, with respect to the first prediction task examined in Section IV.B (predicting whether the average food rating for a group is above or below the median rating), the overall success rate is unchanged at 73%. Notably, however, when we estimate a linear probability model relating an above-median indicator variable to the predicted probability that the item falls above the median, we obtain a slope coefficient that is close to unity (0.870, s.e. 0.171); moreover, we fail to reject the joint hypothesis that the slope is one and the intercept (0.064, s.e. = 0.100) is zero (p = 0.692).

It is natural to wonder whether the predictive voxels are concentrated in regions that are known to play important roles in valuation (Rangel and Hare, 2010). Because LASSO retains only a small handful of predictors (21.1 on average in our analysis) and typically discards all but one of any highly correlated set, there is a tendency for the predictive voxels to be widely dispersed. That tendency is not necessarily bad from a predictive perspective. LASSO may benefit by selecting anatomically distant voxels with activity that is associated with the underlying value signal but that does not mirror localized noise, and indeed the Elastic Net, which in contrast tends to retain predictive clusters, performs only marginally better. However, the Elastic Net proves more useful in generating images of the anatomical locations of predictive voxels. For the Elastic Net estimates, we find that the predictive voxels are to a large extent concentrated in brain regions that are broadly associated with choice and value, including the ventral striatum, subgenual cingulate cortex, orbitofrontal cortex, insula, and inferior parietal lobe.

VII. Concluding remarks

The preceding analysis points to the feasibility of inferring the choices people would make (if given the opportunity) at least in part based on their neural responses to prospects when they are not making actual decision making. It represents an important and challenging milestone in the process of developing methods for estimating choice mappings that could be used in settings where pertinent choice data are nonexistent, limited, or contaminated by spurious factors, so that more conventional methods of estimation are inapplicable or problematic. Possible examples include inferring willingness-to-pay for new products or for the avoidance of environmental damage, controlling for unobserved product characteristics in supply-and-demand estimation, and the estimation of the behavioral impact of interventions where naturally occurring events are insufficiently clean to permit reliable inferences.

It is important to acknowledge the limitations of our analysis. Our procedure is entirely unsuccessful for nearly half of our subjects. Moreover, even for subjects to whom it is applied successfully, in many instances it yields relatively weak predictions (e.g., predicted probabilities near 50 percent rather than 100%), and consequently achieves only a moderate overall success rate (68.2%).

We note, however, that our procedure also yields strong predictions in many instances. For the individual-level models, the degree of resolution is reasonably high overall, and the models are well-calibrated for just over half of our subjects. Compared with the successful half of our individual-level prediction exercises, our group-level prediction exercise achieves higher resolution, and the quality of calibration is comparable (though somewhat lower), despite the fact that we include all subjects, regardless of whether their individual-level prediction exercises were successful.

In addition, there is every reason to believe that refinements of the procedure will ultimately yield substantial improvements in predictive accuracy. Better methods can be developed to enhance attentiveness in the scanner and to weed out inattentive subjects. Advancements in knowledge of the brain and improved statistical methods may provide better guides to voxel selection. Technological advances will undoubtedly enhance our ability to detect and measure stimulus-specific neural responses.

Perhaps the greatest potential for improving predictive accuracy lies in exploring combinations of non-choice responses to potential prospects. One promising avenue is to supplement fMRI information with subjective non-choice responses, such as hypothetical choices, response times, and visual fixations, as well as other neurometric data, such as pupil dilation,⁴⁰ facial temperature and muscle movement, SCRs, and the like. The latter types of measurements are easier and less costly to obtain than fMRI data, and may ultimately turn out to be highly predictive. Physiological responses may prove particularly valuable in detecting discrepancies between hypothetical statements and true tendencies.