The Direct Incorporation of Perfusion Defect Information to Define Ischemia and Infarction in a Finite Element Model of the Left Ventricle

Short abstract

This paper describes the process in which complex lesion geometries (specified by computer generated perfusion defects) are incorporated in the description of nonlinear finite element (FE) mechanical models used for specifying the motion of the left ventricle (LV) in the 4D extended cardiac torso (XCAT) phantom to simulate gated cardiac image data. An image interrogation process was developed to define the elements in the LV mesh as ischemic or infarcted based upon the values of sampled intensity levels of the perfusion maps. The intensity values were determined for each of the interior integration points of every element of the FE mesh. The average element intensity levels were then determined. The elements with average intensity values below a user-controlled threshold were defined as ischemic or infarcted depending upon the model being defined. For the infarction model cases, the thresholding and interrogation process were repeated in order to define a border zone (BZ) surrounding the infarction. This methodology was evaluated using perfusion maps created by the perfusion cardiac-torso (PCAT) phantom an extension of the 4D XCAT phantom. The PCAT was used to create 3D perfusion maps representing 90% occlusions at four locations (left anterior descending (LAD) segments 6 and 9, left circumflex (LCX) segment 11, right coronary artery (RCA) segment 1) in the coronary tree. The volumes and shapes of the defects defined in the FE mechanical models were compared with perfusion maps produced by the PCAT. The models were incorporated into the XCAT phantom. The ischemia models had reduced stroke volume (SV) by 18–59 ml. and ejection fraction (EF) values by 14–50% points compared to the normal models. The infarction models, had less reductions in SV and EF, 17–54 ml. and 14–45% points, respectively. The volumes of the ischemic/infarcted regions of the models were nearly identical to those volumes obtained from the perfusion images and were highly correlated (R²= 0.99).

Introduction

The 4D XCAT phantom is commonly used in the simulation of medical image data, particularly single photon emission tomography (SPECT), positron emission tomography (PET), x-ray computed tomography (CT) and magnetic resonance imaging (MRI). These phantoms provide realistic models of the anatomical structures. The XCAT incorporates realistic respiratory and cardiac motions, based upon tagged MRI data, into the simulations which include the physics of the instrumentation involved in the imaging process. When combined with an accurate imaging process simulator, the XCAT can produce accurate and realistic simulated image data that closely mimics those acquired from patients. However, one of the limitations of the 4D XCAT phantom was that the cardiac motion incorporated in the XCAT was based upon a single set of gated tagged MRI data of a single normal male subject so that the definitions of pathologies such as ischemia and infarction in the phantoms had no physiological basis. Our previous work sought to overcome this limitation through the incorporation of a physiologically based FE mechanical model for the LV into the 4D XCAT phantom. These models were found to accurately simulate both the normal motion of the LV as well as abnormal aneurysmal motions due to ischemia [1] and infarction [2]. This work demonstrated that the incorporation of the FE data was possible; however, the lesions used for this work were overly simplistic in terms of the geometries being depicted (both ischemic and infarcted see Fig. 1).

Fig. 1.

Infarct model with simplified infarct region (black) surrounded by a one element thick BZ (white). This type of model was demonstrated in our previous work [2].

The cessation of blood flow to a region of the heart initiates a dynamic process, where the material properties radically change over time [3]. Myocaridal tissue is considered acutely ischemic in the first 6 h following the cessation of blood flow and the passive material properties of the tissue are essentially the same as nonischemic tissue [3] with the primary effect of the loss of blood flow being the lack of contraction. Beyond 6 h, cell death (necrotic phase) begins and at this point the tissue is considered infarcted. In the days that follow, inflammatory processes govern the mechanical behavior of the tissue with tissue stiffening being the primary manifestation [3–6]. This phase is highly dynamic making it extremely difficult to model as the material properties of the tissue are in a state of change. This phase lasts until the amount of new collagen substantially increases (fibrotic phase) signaling the beginning of scar formation after approximately 7 days in humans [7]. The material properties stabilize (>7 weeks), with the gradual decrease in the amount of collagen being introduced into the lesion area [3–6]; however, the infarcted region does continue to change with remodeling in the form of lesion extension, expansion, and thinning. For the purposes of the following work, the remodeling aspects of the process have not been included in the analysis and the infarct material properties having been stabilized [3–6]. The underlying assumption being that the application of the technology described below will be applied to images that document the remodeled LV.

In order to produce realistic XCAT based images that accurately incorporate the altered mechanics of these conditions, the ischemic/infarcted regions had to be more realistic in size and shape so that the images that were produced by the XCAT represented the type of lesions found in the clinical setting. The traditional method for defining infarcted regions for use in a FE model of the LV has been manual segmentation of lesions within image data sets. The typical modalities used to define an ischemic or infarcted region were perfusion based PET or SPECT imaging as well as delayed enhanced MRI. The manual segmentation process tends to be time intensive, particularly when a number of infarcted regions are to be defined in single or multiple models.

The following work describes a process that has been designed to address these problems. A semi-automatic methodology has been developed that uses direct interrogation of perfusion images in order to define the lesions in the mechanical models. The efficacy of the methodology was evaluated using a set of perfusion maps that were produced by the 4D PCAT phantom [8]. The PCAT phantom allows for the definition of ischemic/infarcted regions based upon the user defined stenoses in a computational cardiac circulatory system. The extent and location of the stenosis in the coronary tree can be varied allowing the PCAT to produce a wide variety of ischemic/infarcted regions in the LV. The PCAT can produce bull's eye images representing the relative perfusion in the LV as well as full 3D volumetric perfusion maps. It is these 3D perfusion maps that were used to define the ischemic and infarcted regions demonstrated in the current study. The methodology is image based so it can be readily applied to perfusion CT and MRI images though this application is beyond the scope of the current work.

Materials and Methods

Perfusion Map Generation and Image Thresholding.

The 4D XCAT phantom has a beating heart model and the proximal large branches of the coronary arterial tree, which were segmented from patient CT data. To model a realistic perfusion map, a 4D PCAT phantom was developed by extending the XCAT proximal large coronary arterial branches to construct a model of the detailed coronary arterial tree using a computer generation method [10]. The iterative rule-based coronary arterial tree generation method was based on morphometric, anatomic, and bifurcation properties of normal coronary arterial trees. The generation method has vessel and boundary avoidance algorithms which guided the growth directions of the daughter segments at each bifurcation. Two daughter segments at each bifurcation point were generated and the results were iterated upon until segments of the largest six orders were constructed. Anatomic details were enhanced through the modeling of the atrioventricular openings of the left and right ventricles, and through the use of properly scaled morphometric data for the human coronary arterial tree. Given the specific location of a stenotic artery segment, the affected downstream vascular segments suffered from the reduction of blood flow due to the stenosis in the proximal segment were determined by iteratively tracing down the arterial tree [9]. The distance from each branch in the arterial tree for each myocardial region was determined. Neighboring branches were identified as affected if their distances were within a predefined effective perfusion range. The activity of each myocardial voxel was computed as a function of inverse-distance-weighted average of the flow of these neighboring vascular segments. In addition, parameters of the computer generation method was fine-tuned with input from experienced physicians such that the generated myocardial perfusion maps with known defects matched those found in clinical studies. A coronary arterial tree model with perfusion defects, including the LAD, LCX, and RCA, was generated using this scheme. The model of the coronary arterial tree with the six largest branches had vessel diameters down to 120 μm, consisted of 3940, 1232, and 3902 segments for the LAD, LCX, and RCA, respectively.

In the top row of Fig. 2, the computed generated coronary arterial tree with severe stenoses (90%) at two locations in LAD, at proximal LCX, and at proximal RCA are shown. In the bottom row of Fig. 2, the bull's-eye plots of the corresponding myocardial perfusion maps generated by incorporating the coronary arterial tree with the different stenoses in the PCAT phantom are depicted. They were qualitatively well matched to those found in typical clinical cases from patients with known 90% stenosis by our experienced physicians. The perfusion defect regions in the image space were segmented from the simulated myocardial perfusion maps using IMAGEJ [11] thresholding function (Fig. 3). The binary images on the right-hand side of Fig. 3 were created using a lower and upper threshold intensity levels of 6% and 90% of the maximum intensity value, respectively, with the defect regions having zero intensity.

Fig. 2.

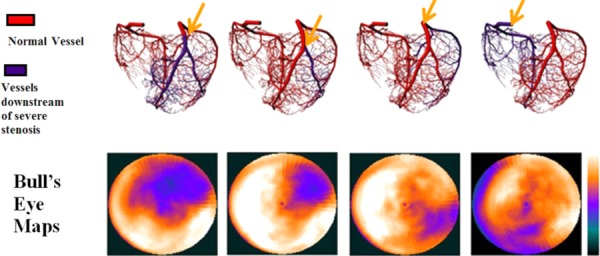
The location of the occlusions (top) used to define the perfusion maps in the PCAT. Arrows indicate the location of the vessel occlusions. The resulting bull's eye maps (bottom) showing the extent of the perfusion defects.

Fig. 3.

Thresholding was used to isolate the ischemic/infarcted regions of the myocardium. A midventricular, short axis slice of the 3D perfusion map for the proximal LAD with a 90% occlusion is shown on the left. The ischemic/infarcted region is shown on the right with threshold values of 6% (lower cutoff) and 90% (upper cutoff) of the maximum intesity.

FE Model Generation.

The geometry of the FE model of the LV was based upon gated high resolution CT images of a normal male subject acquired on a Siemens X-ray multislice CT scanner (Siemens AG, Erlangen, Germany). The image dataset corresponding to the beginning of diastole, approximately 1/3 of the way into diastole [1,2,12,13] was used to define the undeformed, reference configuration of the FE model. The boundaries of the epi- and endocardial surfaces of the LV were segmented using the software program ITK-Snap [14]. These surfaces were then used to define a FE mesh using TrueGrid [15], a preprocessing program for the generation of hexahedral based FE models. The models were given transversely isotropic passive material properties [1,2,16] and a time varying elastance model [1,2,17,18] was used to define the active contractile function of the models.

Interrogation of Image Data Sets.

The custom interrogation program was run on the binary images (0 = black and 255 = white) to define the ischemic or infarcted zones within the FE models of the LV. The program can determine the average intensity values for locations in the images that correspond to the interior of each element of the FE model. The program was applied to the thresholded binary images described above, initially to define the ischemic/infarct regions. The process was repeated for the infarction models in order to define a BZ surrounding the infarction.

Defining the normal perfusion and ischemic/infarcted regions for the FE models required the definition of material points in space for three separate coordinate systems. The first coordinate system was the real world coordinates of the heart upon which the LV geometry was based upon. The second coordinate system was the image (voxel based) coordinates of the images depicting the heart in the XCAT produced perfusion maps. It was these images that were used to determine the extent of the ischemic and infarcted regions in the LV models. Finally, there are the natural coordinates of the FE elements themselves [19] which were used to define the location of the element integration points in the image space. The following text describes in detail the process of going between these coordinate systems in order to assign a set of voxel intensity values to each element of the FE model.

The first step in the process was to determine nodal coordinates (real world coordinates) values in the image space (I_x, I_y, I_z). This was done by determining the relative location of a nodal point in image space as follows:

$$\begin{array}{c}\multicolumn{1}{c}{I_x=\frac{(x_i-x_0)}{(x_1-x_0)}{I}_y=\frac{(y_i-y_0)}{(y_1-y_0)}{I}_z=\frac{(z_i-z_0)}{(z_1-z_0)}}\end{array}$$ (1)

where x_i, y_i, and z_i were the real world coordinates of the nodal point and x ₀ and x ₁ are the boundary values of the geometric range in the x direction of the images in terms of the real world coordinates. Similarly, y ₀ to y ₁ and z ₀ to z ₁ are the geometric range portrayed in the images. For example, a 2D image with image dimensions of 256 × 256 would have real world range of 1–10.7 cm for each dimension of the image. In this case, x ₀ would be 0 and x_l would be 10.7 and the y ₀ would be 0 and y_l would be 10.7. Equation (1) gives the relative voxel location for a given point of the ith node in terms of the geometric ranges. The voxel locations for each node were then determined as follows:

$$\begin{array}{c}\multicolumn{1}{c}{{\xi }_i=I_x({\mathrm{size}}_x-1){\eta }_i=I_y({\mathrm{size}}_y-1){\mu }_i=I_z({\mathrm{size}}_z-1)}\end{array}$$ (2)

where size_x, size_y, and size_z are the image dimensions in the x, y, and z directions. For the 2D example above, size_x and size_y would be 256. Therefore, ξ_i, η_i, and μ_i are the coordinates within the image for a given node of an element. Equations (1) and (2) were used to determine the nodal locations in image space for every element of the FE LV model. Each node of the FE model now has the original set of x_i, y_i, and z_i nodal coordinates as well as image based nodal coordinates (ξ_i, η_i, and μ_i).

The integration points (Fig. 4) of the hexahedral elements were used to determine voxel intensity values associated with the interior of each element of the FE model through the use of the FE shape functions. The image coordinates for the eight integration points were determined from the eight shape functions that are defined by

Fig. 4.

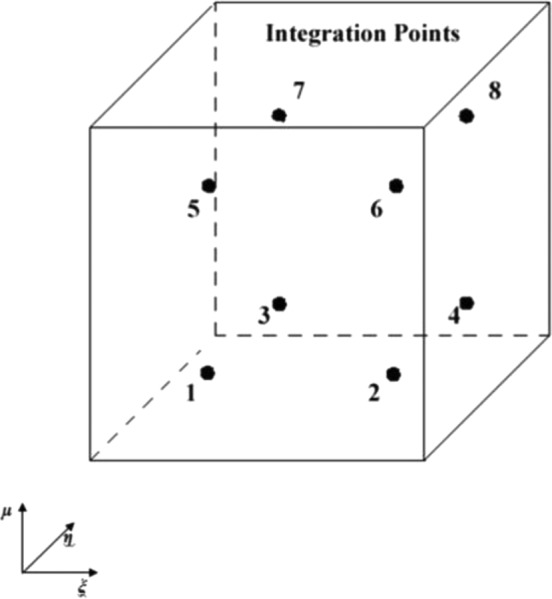
The locations of the integration points within a hexahedral element

$$N_i=\frac{1}{8}(1+\xi {\xi }_i)(1-\eta {\eta }_i)(1-\mu {\mu }_i)$$ (3)

where ξ_i, η_i, and μ_i are the image coordinates of the ith node which are multiplied by the values of ξ, η, and μ (Table 1). The voxel coordinates for each integration point within each element [19] is given below for the image coordinate system

Table 1.

Shape function values

	ξ	η	μ
1	−1	−1	−1
2	+1	−1	−1
3	+1	+1	−1
4	−1	+1	−1
5	−1	−1	+1
6	+1	−1	+1
7	+1	+1	+1
8	−1	+1	+1

$$\begin{array}{c}\multicolumn{1}{c}{{\mathrm{voxel}}_x=\sum _{i=1}^8{N}_i{X}_i{\mathrm{voxel}}_y=\sum _{i=1}^8{N}_i{Y}_i{\mathrm{voxel}}_z=\sum _{i=1}^8{N}_i{Z}_i}\end{array}$$ (4)

where X_i, Y_i, and Z are the natural FE coordinates of the integration point (±0.577, ±0.577, ±0.577 for an eight node hexahedral element). The natural FE coordinate system has a range of (−1 to 1) in the x direction, (−1 to 1) in the y direction, and (−1 to 1) in the z direction The resulting coordinates (voxel_x, voxel_y, and voxel_z) are the coordinates of the integration points in the image space (voxel coordinate system described above) where the image intensities of the 3D perfusion maps were sampled. The intensity values for each integration point were averaged to define an average intensity value for each element of the FE LV model.

Identifying Ischemic and Infarcted Regions.

The program was applied to the binary images described above such that the elements with an average intensity below an initial user defined threshold (250) within the program were given ischemic or infarcted material properties depending upon the model being defined. It was the results of the initial analysis that was used to define the ischemic and infarcted regions. The ischemic and infarcted regions for these models were identical since the same analysis produced both regions. The ischemic region was defined as having normal passive properties. The infarction models had the passive material properties altered compared with normal and had an additional BZ surrounding the lesion area defined. The BZ tissue exhibits hypocontractile behavior while still having normal perfusion [20–25]. Mechanical factors such as tethering have been suggested to explain the underlying depressed function in the BZ myocardium [21,26–30]. In order to define the BZ surrounding the infarcted regions, the thresholded image data sets were altered by applying a 5 voxel Gaussian blur to increase the size of the perfusion uptake deficient region (Fig. 5). The perfusion definition program was run on the blurred images such that regions below the user defined threshold setting were defined as BZ, provided the element had not been previously defined as infarcted.

Fig. 5.

A 5 voxel Gaussian blur was applied to the thresholded image (left) to increase the size of the lesions (middle). This image was processed in order to define the BZ (right) which is the region with normal perfusion that borders the infarcted region.

Thresholding alone was not sufficient to define the BZ as it did not provide a continuous BZ around the infarcted region. Additionally, there were isolated BZ elements defined near but not immediately bordering the infarcted regions. In order to create a contiguous BZ without spurious elements, the FE connectivity was utilized to create a continuous BZ definition. The neighbors of each element were determined using the connectivity information. If a BZ element was found to not have at least 1 infarct element neighbor (sharing at least 1 node with an infarcted defined element), it was then redefined as the element type it was before BZ thresholding (normal perfusion material properties). If an element was found to have an infarct neighbor but was not previously defined as BZ, it was then redefined as a BZ element.

Ischemia/Infarction Material Definitions.

The passive myocardium was defined as a transversely isotropic material that has been described previously [1,2,31] and the active contraction portion of the material model was a time varying elastance material model [1,2,17,18]. In the acute ischemia (<6 h from onset) models, the passive material properties of the elements representing the affected regions were the same as the normal myocardium. In contrast, in the infarction models, the elements that were defined as scar were defined to be stiffer in the fiber direction by approximately 20 times that of the normal LV [1,2,31]. The active contraction within both the ischemic and infarcted regions was eliminated by altering the calcium sensitivity in the time varying elasticity definition of contraction [1,2,28]. The fiber distributions within these regions were not altered [32,33] for either type of pathology.

BZ.

The mechanics of the BZ was reproduced by altering the active contraction within the BZ. This was done by reducing the active contraction in the BZ through the reduction of T _max in the time varying elastance material model by 50% [34–36].

Extent of Ischemic/Infarcted Regions.

The extent of the infarcted mesh in each of the FE models was compared with perfusion defects of the PCAT generated perfusion maps by comparing the material definitions in the LV model with renderings of the perfusion maps. The volumes of the ischemic/infarcted zones were determined by conducting a voxel count on the thresholded images. These volumes were then compared with the element volumes of the ischemic/infarcted definitions in the FE models. The volumes were compared and a regression analysis was made from the results.

FE Models.

The FE models were run over the entire cardiac cycle. The effects of the presence of the ischemic and infarcted regions were evaluated by comparing the SVs and EFs of the ischemia and infarction LV models with the normal FE model from which they were derived. The fiber strain distributions for midventricular short axis slices for each type of vessel occlusion were compared in order to assess the type (dyskinetic, akinetic, or hypokinetic) and relative magnitude of the deformations within the lesions.

Cardiac Gated SPECT Simulations.

The XCAT phantom with the new deformation models defined by various perfusion defects was used to simulate gated cardiac SPECT images. The 4D XCAT phantom [37] was used to create realistic heart models of 16 frames per cardiac cycle. The beating heart model of the 4D XCAT phantom with the new deformation models was used in the 4D simulation. Projection data were simulated for a typical ^99mTc-sestamibi myocardial perfusion gated SPECT (16 gates) study. The projections were generated by using an analytical projector. The projections were simulated including the effects of nonuniform attenuation, detector response, and scatter. The projection data were reconstructed into 128 × 128 image matrices with 0.3125 cm pixel size using filtered back projections (FBPs) and ordered subsets expectation–maximization (OS–EM) reconstruction algorithms. The OS–EM algorithm was implemented with correction for attenuation, detector response, and scatter using eight subsets, 64 updates. The gated transaxial reconstructions were reoriented and stacked to generate cine-images of gated short axis slices.

Results

Extent of Ischemic/Infarcted Regions.

There was excellent agreement between the renderings of the PCAT-produced 3D image (Fig. 6, left) showing the perfusion deficient regions and the corresponding ischemia/infarction mesh defined in the FE models (Fig. 6, right). The comparison with the rendered perfusion images indicated that the relative size and shape were captured using this methodology in both the ischemia models (Fig. 6, right column—blue alone is ischemia) as well as the infarct models which had the additional BZ region defined (Fig. 6, right column—green BZ and blue infarct). The volumes of the ischemic/infarcted regions of the models were nearly identical to those volumes obtained from the images (Table 2). The volumes were also highly correlated (R ²= 0.99) (Fig. 7). The BZ definitions produced by the interrogation program were continuous, one element in width around the scar definitions and did not have any spurious BZ element definitions.

Fig. 6.

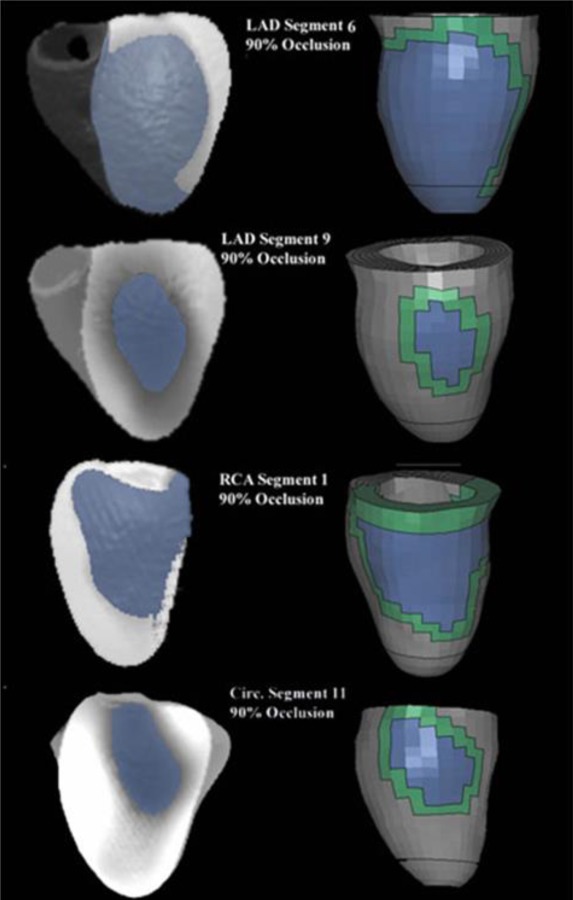
The ischemic/infarcted regions of the FE models show similar size and shape compared with the renderings of the perfusion maps. The ischemic/infarcted regions are defined as the blue interior regions for the models. The BZ is the continuous region surrounding the infarct. RCA segment 1 has had the RV removed from the rendered images.

Table 2.

Comparison of the ischemia and infarction volumes from the images with the FE element volumes

Model	Image volume (mm3)	Element volume (mm3)
LAD 6	54,591	52,613
LAD 9	8100	7100
RCA 1	16,505	15,165
LCX 11	42,878	40,184

Fig. 7.

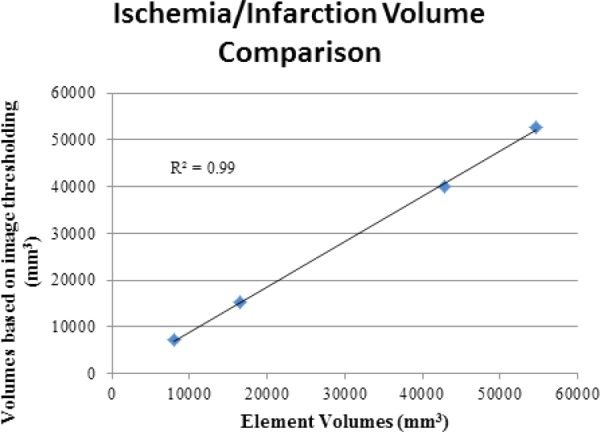
The comparison of the ischemic and infarcted volumes given in Table 2 shows a slight tendency toward underestimation

FE Model.

The presence of ischemic and infarcted regions had a direct effect upon the function of the LV as determined by the end-systolic and end-diastolic volumes. The ischemic models showed no change in the diastolic function (Table 3) but showed altered systolic function with increased end-systolic volumes compared with the normal case. The result was a reduction in SV and EF with the increase in end-systolic volume was due to the aneurysmic bulging of the LV wall. The ischemia models had reduced SV by 18–59 ml as well as lower EF values by 14–50% points compared to the normal models. The infarction models, in general, showed slightly less reduction in SV and EF, 17–54 ml and 14–45% points, respectively (Table 3). The increased aneurysmic bulging (dyskinetic motion) at end-systole resulted in fiber strains that were approximately 15% higher in the ischemia models than the corresponding infarction models. The strain distributions of the ischemia and infarction models display dyskinetic behavior compared with the normal wall thickening seen in the normal model. The lesions in these models showed positive end-systolic fiber strains (elongation) and wall thinning in both the ischemia and infarction models with both of these attributes being greater in the ischemia models than the corresponding infarction models (Fig. 8). All of the regions of the normal model showed negative end-systolic strains in the fiber direction (contraction) and wall thickening consistent with normal cardiac function.

Table 3.

Comparison of the cardiac hemodynamic parameters due to the addition to the LV of either an ischemic or infracted region

Model	End-diastolic volume (ml)	End-systolic volume (ml)	SV (ml)	EF (%)
Normal	118	50	68	57.63
Ischemia
LAD 6	118	109	9	7.63
LAD 9	118	68	50	42.37
RCA 1	118	102	16	13.56
LCX 11	118	99	19	16.10
Infarction
LAD 6	113	99	14	12.39
LAD 9	116	64	52	44.83
RCA 1	115	96	19	16.52
LCX 11	116	84	32	27.59

Fig. 8.

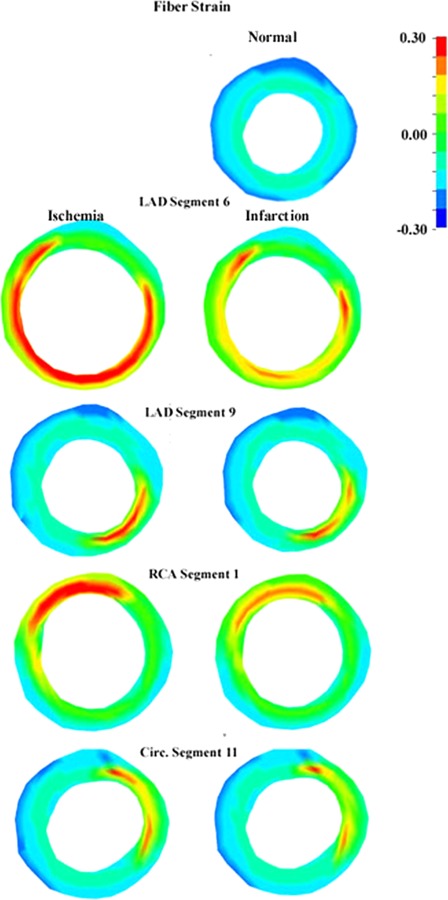
Positive fiber strain result from the aneurysmic deformations associated with the ischemic (left column) and infarcted (right column) regions (positive fiber strains—elongation) as demonstrated in these midventricular short axis slices. This is in contrast to the deformations of the normal model (right column—top) which shows fiber contraction (negative fiber strains).

Gated Cardiac SPECT Results.

The reconstructed images provided by the 4D XCAT phantom (Fig. 9) using the FE models demonstrate the quality of the images that can be produced (Fig. 10), both noise free and those with noise. These cine images show the aneurysmic motion of the perfusion defects over the entire cardiac cycle with the largest amount of aneurysmic motion occurring at end-systole when the walls within the defect thin and circumferentially elongate. This is in contrast to the remote myocardium which shows the normal wall thickening and circumferential shortening of normal cardiac function.

Fig. 9.

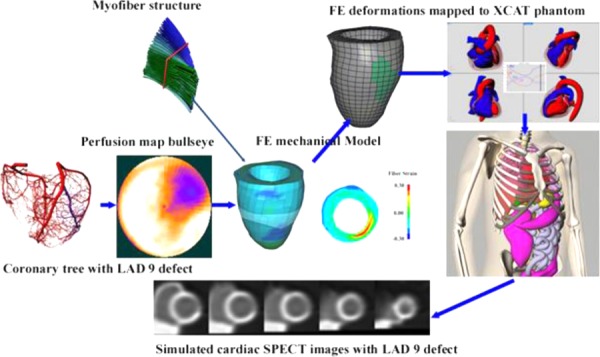
This demonstrates how the ischemia mechanical model was defined from the PCAT perfusion data. The deformations predicted by this mechanical model were then used to define the LV within the XCAT phantom. This was used to create simulated SPECT images, in this case noise-free, which can reproduce the dyskinetic (aneurysmic) deformations of acute ischemia.

Fig. 10.

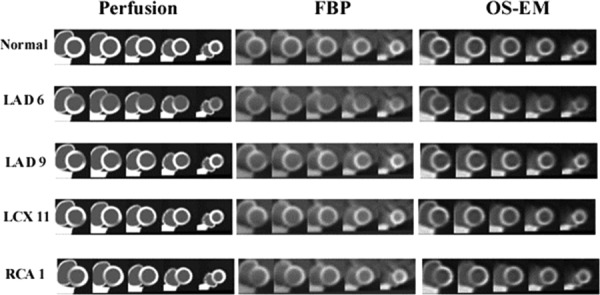
Short axis cine reconstructed images corresponding to each perfusion defect. PCAT derived perfusion images (left), 4D XCAT reconstructed using FBP (center) and OS–EM reconstruction.

Discussion

The current study demonstrates the successful incorporation of the PCAT perfusion defect information directly into a FE based mechanical model. This methodology is predicated upon the fact that the origin and coordinates determined in the original geometry definition have not been lost or altered in the process of mesh creation. There must be a one to one correspondence for each node with the corresponding location in the original image space. Furthermore, the images used to create the geometry must be coregistered with the perfusion images. Without this correspondence, the methodology will completely fail. This being the case, this process is especially well suited to multimodality imaging such as SPECT/CT, PET/CT, and PET/MRI. In these cases, the simultaneous acquisitions of the perfusion and anatomical information result in coregistered images that can be used to define model geometry as well as the ischemic/infarcted regions as described above.

This methodology allows for the definition of complex regions of ischemia or infarction based upon the PCAT perfusion information. The relative coarseness of the FE mesh does, however, limit the accuracy of the regions defined as ischemic or infarcted and was the primary reason for the differences in the volumes found in Table 2. The elements that straddle the boundary of the perfusion defect become defined as either normal elements or BZ elements though the selection of the threshold value within the interrogation program. The user can compensate for this effect by altering the threshold used by the element definition program. This would allow for the expansion of the BZ to several elements rather than a single layer of elements. A finer mesh would result in a superior reproduction of the lesion regions in the FE models but at the expense of some additional computational time.

An evaluation of the relative accuracy of the PCAT to reproduce the results of an occlusion of a specific vessel was beyond the scope of the present work and will be the subject of another separate study. The utility of the PCAT was that it could produce more realistic perfusion defects than were not available for our previous work [1,2]. The lesions could be defined with a high degree of control and reproducibility by controlling the location and size of the occlusion within the coronary tree.

The methodology described above was based upon using hexahedral elements for the FE models but can be readily applied to other element types such as tetrahedral elements. The shape function definitions for other elements would be substituted for those defined in Eq. (3). The interior integration points of the different element types could then be used in the same fashion as the eight interior points were used for the present study.

The pathological FE models showed distinctly altered behavior compared with the normal model. The strain results indicate that the regions showed dyskinetic motion during systole (aneurysmic bulging) which resulted in positive fiber strains (tension) compared with the normal model as well as the remote myocardium both of which undergo wall thickening (fiber shortening—negative strains). The stiff wall of the infarction models resulted in less aneurysmic bulging of the LV wall both in diastole and systole. The volume results of the infarction models (Table 4) demonstrate that the stiffened wall improves cardiac output, namely, by allowing for far less aneurysmic bulging during systole compared with the ischemic models. This decreased bulging more than compensated for the decreased diastolic volumes due to the passive filling phase of the cardiac cycle. This resulted in increased SV as well as increased EF compared with the ischemic models, thus the wall stiffening helped maintain cardiac output. However, it should be noted that there is often an increase in filling pressures following acute MI [38,39]. Thus, in cases where there is no pulmonary congestion, this increase in pulmonary pressure would likely negate the effects of a decrease in end-diastolic volumes and would benefit the patient in the short-term.

Our results indicate that acute ischemia can result in a large, sudden decrease in cardiac function which is commonly seen in the clinical setting [40]. In particular, the results show that ischemia and infarction at the RCA-1, LCX-11, and LAD-6 locations result in severely compromised function (Table 3) due to the relatively large size of the lesions (Table 3) with function reduced to fatal or near fatal levels. This decrease in function can prove to be fatal if not for the compensatory increase in contractility demonstrated by the remote myocardium (hypercontractility) [40]. This hypercontractility helps maintain cardiac output following the onset of ischemia. The length of time the remote myocardium can maintain hypercontractility depends upon the relative health of this tissue [41]. The current study confirms the value of this compensatory mechanism as an increase in the contraction of the remote myocardium would help maintain cardiac output increasing EF and SV thus improving the chances of survival of the subject. It should also be noted that a common cause of death in post-MI patients is the development of arrhythmias due to the conduction abnormalities introduced by the scar tissue. This facet of the disease process is beyond the scope of the current model and would require a conduction/mechanical model in order to evaluate such as those developed by Kerckhoffs et al. [12,13,42,43].

The target size of the BZ was 1.7 ± 3.0 mm as documented by Lee et al. [44]. This resulted in BZs that were one element across, from infarct to normal tissue. So the exact size of the BZ varied by the size of the elements within these regions. The definition of the code in its current incarnation stipulates that the BZ be only 1 element across due to the use of the connectivity relations to ensure a complete BZ without gaps or spurious BZ elements defined. BZ definitions that are more than one element wide would require that one side of the element must be normal and the other side must be infarct or previously defined BZ. Multiple BZ analyses (two or more) would be required to accomplish this.

The models used in the present study represent snapshots of the LV at two specific time points, in this case with identical perfusion maps, rather than representing a time history of the heart. In other words, the models do not represent the geometry and material changes due to the progression from ischemia to infarction as this follows a relatively complex path. The fibrous phase lasts another 21 days [7]. The fiber stiffening used in our model was designed to mimic the stiffening which resulted from the initial scar formation. This fibrous phase is followed by a remodeling phase. This phase is marked by the thinning of the scar and an expansion of the surface area of the infarction LV wall. The incorporation of wall thinning complete with a realistic expansion of the surface area based upon PCAT perfusion defects will be addressed in future work.

In addition to the thinning and expansion of the infarcted region, the compensatory hypercontractility of the remote myocardium can lead to wall thickening of the remote myocardium in order to normalize the increased wall stress [45,46]. However, unless the workload of the remote myocardium is reduced this hypertrophy often leads to adverse changes in the remote myocardium resulting in decreased contractility and heart failure [46]. This hypertrophy is generally considered a target for treatment [45–47].

The methodology described above can be readily applied to first pass enhanced MRI (ischemia/infarction) as well as delayed contrast enhanced MRI (infarction) could be used to define the perfusion defects. The thresholding values would need to be altered in these cases but in general the work flow would be the same (Fig. 11). Additionally, one could apply the methodology to both types of MRI imaging in order to define subendocardial infarction surrounded by an ischemic region [48–51]. Additionally, it could be applied to perfusion CT images (Fig. 12).

Fig. 11.

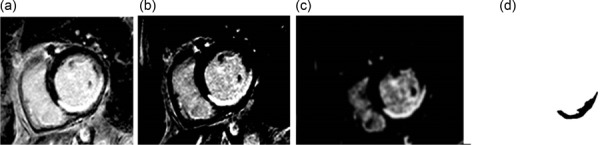
Thresholding was used to isolate the enhanced region of the myocardium. (a) The delayed enhanced MRI image with an anterior defect. (b) A thresholding value of 185 (lower threshold) was used to isolate the enhanced perfusion region. (c) A 3 voxel Gaussian blur was applied to the thresholded image to smooth the boundary of the enhanced region. (d) The image theresholded to isolate the enhanced region.

Fig. 12.

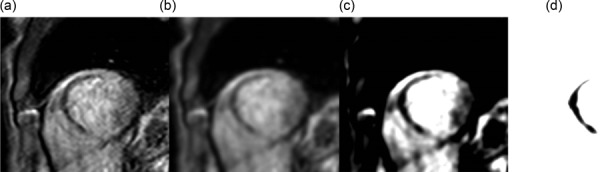
Thresholding was used to isolate the no-reflow zone of the myocardium in this (a) perfusion MRI image. (b) A 5 voxel Gaussian blur was applied to the image. (c) The contrast was enhanced and (d) a thresholding value of 190 was used to isolate the no reflow region. The underlying cause of no reflow is microvascular obstruction, which is confined to the irreversibly damaged necrotic zone of the infarct [54].

One of the limitations of the current methodology is that we did not test it on an LV/RV model. Figure 3 and the perfusion images used to create Fig. 6 indicate that the ischemic regions extend into the RV. Infarctions that include both ventricles would affect the function and physical interaction of the ventricles. However, for the purposes of development of this technology the use of an LV model was sufficient to show that the methodology works well. Nothing in the results would indicate that it could not be applied to a biventricular model.

One of the future improvements that will be made to this series of mechanical models will be the incorporation of fiber distributions based upon diffusion tensor MRI (DTMRI) imaging data. The definition of the fiber vectors associated with the DTMRI images will be similar to the methodology described above. However, rather than sample a single image data set to associate a single voxel intensity level with each element, the images that represent the first eigenvector of the diffusion tensor will be sampled to determine the x, y, and z components of the fiber vector. This will be repeated for each element within the model representing the myocardial wall. The steps involved in this process will be identical to that described above.

Future improvements to these models will include electrical modeling for stimulation of myocardiac tissue contraction in order to be able to model the conduction abnormalities associated with regions of myocardial infarction. Additionally, these models can have an existing systemic circulatory model coupled to them [52,53]. In this manner, hypertension models can be input into the 4D XCAT. These improvements will greatly expand the types of pathologies that can be modeled using the combined FE/XCAT system. Eventually, the user of the XCAT will be able to modify FE models and reanalyze the mechanical models from within the XCAT interface in order to define new types of models in a seamless fashion.