Short abstract
The objective of this study was to measure the collagen fiber structure and estimate the material properties of 7 human donor scleras, from age 53 to 91. The specimens were subjected to inflation testing, and the full-field displacement maps were measured by digital image correlation. After testing, the collagen fiber structure was mapped using wide-angle X-ray scattering. A specimen-specific inverse finite element method was applied to calculate the material properties of the collagen fibers and interfiber matrix by minimizing the difference between the experimental displacements and model predictions. Age effects on the fiber structure and material properties were estimated using multivariate models accounting for spatial autocorrelation. Older age was associated with a larger matrix stiffness (p = 0.001), a lower degree of fiber alignment in the peripapillary sclera (p = 0.01), and a lower mechanical anisotropy in the peripapillary sclera (p = 0.03).
Keywords: sclera, glaucoma, collagen fiber, finite element model, digital image correlation, inverse finite element analysis, wide angle X-ray scattering
1. Introduction
The sclera, which constitutes more than 80% of the eye-wall, is the white outer shell and principal load-bearing tissue of the eye. The stiffness of the sclera stems from its dense collagenous structure. The collagen fibers, mainly type I (90%) and type III (≤5%) [1,2], are embedded in a hydrated matrix of proteoglycans. They aggregate parallel to each other to form 50 μm thick lamellae superimposed in the scleral plane [3]. The microstructural characterization of the human sclera was first studied by Kokott [4], who used histological scleral sections to measure the preferred orientations of collagen lamellae. Since then, different microscopy methods have been applied to scleral tissue to obtain qualitative insight into collagen structure at various length scales [5]. Electron microscopy and atomic force microscopy have been used to characterize single collagen fibril and measure fibril D-period (∼67 nm) and inclination angle (∼5 deg) [6]. Collection of fibrils within lamellae have been imaged by transmission electron microscopy [3,7]. These studies showed that scleral lamellae are made of collagen fibrils of various diameters, and that spacing between collagen fibrils is irregular. Winkler et al. [8] measured collagen lamellar orientations within and around the optic nerve head (ONH) using second harmonic generation multiphoton microscopy. More recently, techniques have been developed to gain quantitative measures of bulk scleral fiber orientation and distribution, including small-angle light scattering (SALS) [9–11] and wide-angle X-ray scattering (WAXS) [12,13].
The mechanical behavior of scleral tissue at a given point is determined by the mechanical behavior of the lamellae and their orientation distribution [14]. The mechanical behavior of a single lamella is strongly anisotropic and is characterized by the high tensile stiffness of the fibers and the comparatively low stiffness of the interfiber matrix. The term matrix in this study refers to the components of the scleral stroma other than the fibrillar collagens; those are mainly proteoglycans, elastin fibers, cells, and nonfibrillar collagens. It is thought that the collagen fibers (lamellae) are wavy in the matrix at low load [3]. They progressively straighten under external load, which causes the stress–strain response of the lamella to exhibit a nonlinear, strain-stiffening behavior. The stiffness of a collagen fiber is controlled by several factors, including the fiber diameter and the density of intrafibrillar cross-links. The matrix proteoglycans bind to the collagen fibers via their core proteins, predominantly decorin (74%) and biglycan (20%) [15]. Their glycosaminoglycan (GAGs) side chains have been shown to form bridges between adjacent collagen fibers [16]. The GAGs, which are highly negatively charged, retain water and contribute to the incompressibility of scleral tissue. Changes to the extracellular composition or to the lamella distribution are potential causes for change in scleral mechanical properties.
There is substantial evidence that the structure and composition of the sclera are altered with aging. Scleral thickness was found to decrease with age [17,18]. In the matrix, the content of decorin and biglycan decreases in all regions after age 40 [15] and the number of elastin fibers decreases after the second decade [1]. The geometry of the collagen fibers changes with advanced age. Malik et al. [19] showed an increase in cross-sectional area of the scleral collagen molecule with aging, which was associated with an increase in glycation of scleral tissue [2,19]. Age-related accumulation of nonenzymatic cross-links has been reported in various tissues [20] and has commonly been associated with a stiffening of the tissue. Increased mechanical stiffness was measured in the aging human [18,21,22], monkey [17], and mouse [23] sclera. More recently, Fazio et al. [24,25] showed that the strains in the peripapillary sclera were significantly lower in older human specimens. Few studies have measured the effect of age on the anisotropy and degree of fiber alignment of the scleral collagen structure. A study by Yan et al. [9] used light scattering to compare the percentage occurrence of equatorially and meridionally aligned scleral collagen fibril bundles across three age groups (≤30, 30–60, ≥60 yr) in human cadaveric eyes. They did not find significant age-related variations. Using similar methods, Danford et al. [10] confirmed that age was not a significant factor in governing posterior scleral microstructure. Inverse finite element analysis (IFEA) of the inflation behavior of the posterior monkey sclera also did not report significant differences in preferential scleral collagen orientations between young (∼1.5 yr) and old (∼23 yr) animals [17].
Age-related variations in mechanical properties of the sclera have important clinical implications in glaucoma, the second leading cause of blindness worldwide [26]. Glaucoma is an ocular disease that causes damage to the ONH, region of the posterior sclera through which the retinal ganglion cell axons exit the eye and converge to form the optic nerve. It has been hypothesized that, in glaucoma, excessive deformation of the connective tissue of the ONH impairs the normal function of the axons, eventually leading to vision loss [27–30]. Population-based studies have demonstrated that both the incidence and prevalence of glaucoma increase with age [31–33] and older glaucoma patients are more likely to have had the disease for a longer period than younger ones [34]. Recent modeling efforts have shown that scleral stiffness [35,36], thickness [37], and collagen structure [14] significantly influence the response of the ONH tissues to change in intraocular pressure (IOP). Age-related changes in the material properties and/or fiber anisotropy of the sclera may contribute to the increased susceptibility of the older eye to glaucomatous damage [38].
Alterations to the collagen microstructure and mechanical properties of the sclera may also influence the development of myopia. It is unknown whether scleral collagen fiber orientation is affected in myopia. However, there is evidence from both human and animal myopia studies that the scleral extracellular matrix remodels during myopic eye growth [39,40]. Myopic eyes have also been associated with abnormal mechanical behavior such as increased compliance and increased creep rates [39]. To investigate the role of scleral mechanics in the development of myopia, it is important to determine the mechanical behavior and microstructure of the sclera at different ages.
In this study, we estimate the effects of age on the collagen fiber structure and material properties of the matrix and the collagen fibers of the human sclera. Seven intact donor scleras of age ranging between 53 and 91 were subjected to inflation testing [18]. Full-field displacements of the scleral surface calculated with digital image correlation (DIC) were recorded during pressure elevation. After testing, WAXS was used to map the preferred orientations and degree of alignment of the collagen fibers of each sclera [12]. We developed an eye-specific inverse finite element method to calculate the material properties of the sclera [14]. Given the displacement maps from the inflation test and the collagen fiber structure maps from the WAXS experiments, this method determines the material properties of the matrix and collagen fibers. The constitutive model for the sclera was formulated to incorporate the WAXS-measured orientation and distribution of collagen fibers. We evaluated the effects of age on the degree of fiber alignment in the peripapillary sclera and material properties of the sclera, i.e., matrix and fiber stiffness. The mechanical properties of the sclera at one point in time reflect the original properties and the cumulative remodeling effects of age. Remodeling of scleral tissue may have important implications for the susceptibility and progression of glaucoma and myopia.
2. Methods
2.1. Scleral Tissue and Mechanical Test.
Seven human scleras were obtained from the National Disease Research Interchange from six Caucasian donors aged 53 to 91 (Table 1). Donors with a clinical diagnosis of glaucoma and diabetes were excluded. Information about the degree of refractive error was not available for the scleras used in this study. Our experimental protocol to measure the inflation response of the posterior sclera has been described in previous reports [18,41]. In brief, the posterior scleras were excised 3 mm posterior to the equator, firmly glued on a plastic ring fixture using cyanoacrylate, speckled with graphite powder for DIC, and inflated through a series of pressure-controlled load–unload tests within 72 hr postmortem. Each eye was pressurized three times from 1.5 mm Hg to 30 mm Hg at a rate of 1 mm Hg/s, with a 15 min resting period between each cycle. The pressure in the chamber was adjusted through active feedback control of an automated injection system. During inflation, the deforming scleral surface was imaged by two cameras every 2 s. A stereoscopic DIC system (Vic3D, Correlated Solutions, Inc., Columbia, SC) with a 10 μm uncertainty in the out-of-plane displacement [18,42] was used to measured the 3D displacement field of the scleral surface. This estimation of the uncertainty was comparable to the measurements by Ke et al. [43] (between 10 and 20 μm at 20 deg stereo angle) and Fazzini et al. [44] (root-mean-square error between 5 and 20 μm at 20 deg stereo angle). Scleral thickness was measured at 16 locations with an ultrasonic pachymeter at 15 mm Hg prior to the inflation measurements. Axial length was measured with a digital caliper in repeats of three (Table 1). In a previous publication [18], we calculated the strain field directly from the DIC-measured displacements. In this study, we fit the experimentally measured displacement fields to a constitutive model to calculate the material properties of the 7 specimens.
Table 1.
Human scleras subjected to inflation testing and WAXS measurements of the collagen fiber structure
| Sclera | Age | Right/Left | Sex | Axial length (mm) |
|---|---|---|---|---|
| FC53r | 53 | Right | Female | 23.4 |
| MC58l | 58 | Left | Male | 25.8 |
| FC71r | 71 | Right | Female | 23.5 |
| FC77r a | 77 | Right | Female | 23.9 |
| FC77l a | 77 | Left | Female | 23.9 |
| MC77r | 77 | Right | Male | 24.4 |
| FC91r | 91 | Right | Female | 22.8 |
For FC77, both eyes were included in the study.
2.2. Quantitative Mapping of Collagen Fiber Orientation.
After mechanical testing, the specimens were preserved in a 4% paraformaldehyde (PFA) solution until the time of X-ray measurements. Studies have showed that fixation of the tissue in PFA does not lead to significant alterations to the corneo-scleral collagen fiber architecture, as measured by WAXS [45,46]. A 15 mm circular specimen, centered on the ONH, was excised from each intact posterior sclera. WAXS was used to measure the distribution of fiber orientations at 0.5 mm intervals across the entire specimen following the methods fully described in Pijanka et al. [12]. The focused X-ray beam had a wavelength of 0.09795 nm and horizontal/vertical dimensions of 0.2 mm. The WAXS pattern from scleral tissue is dominated by a well-resolved equatorial (i.e., perpendicular to the fiber axis) reflection from the regular 1.6 nm spacing of the constituent collagen molecules aligned near axially within the scleral fibers (Fig. 1). Analyses of the WAXS patterns provide quantitative measurements of the averaged through-thickness collagen fiber orientation of the intact sclera. The collagen structure at one point of the sclera is described by the statistical distribution of collagen fibers D, which is defined as the normalized scatter intensity:
Fig. 1.
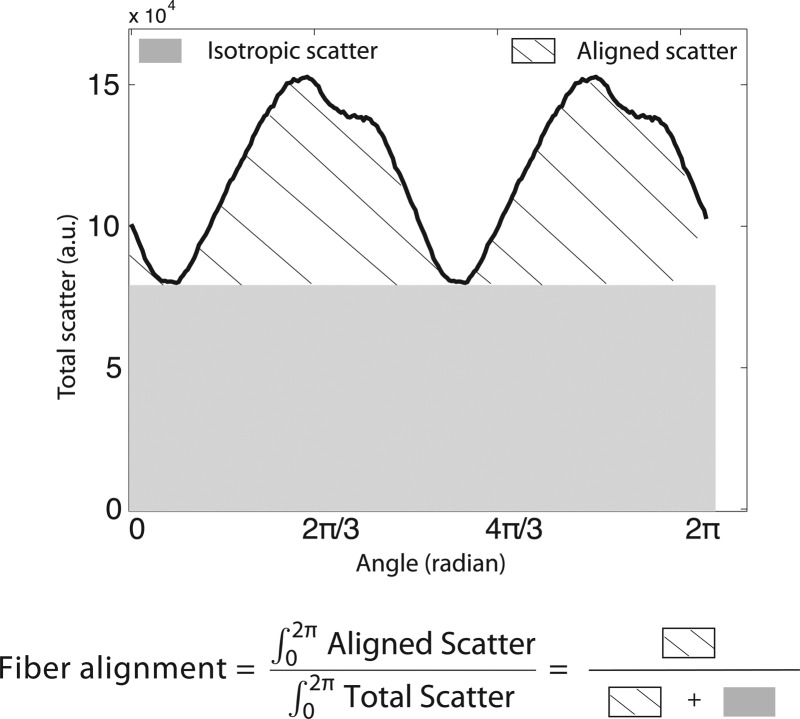
Angular X-ray scatter intensity profile for a WAXS measurement. The total scatter may be separated into that arising from isotropically arranged collagen fibers (shaded region) and that arising from preferentially oriented fibers (hatched region). The degree of fiber alignment was computed as the ratio of the aligned scatter to the total scatter.
| (1) |
where I is the total WAXS scatter, measured by increments of 1.4 deg in Φ. As defined, D(Φ)dΦ represents the number fraction of collagen fibers oriented between the angle Φ and Φ + dΦ. The degree of fiber alignment was calculated for every sampled point in the sclera by dividing the integral of the aligned scatter distribution by the corresponding integral of the total scatter, yielding a single value representing the proportion of fibers preferentially aligned at that point in the tissue (Fig. 1).
2.3. Finite Element Model.
The 3D positions of the scleral surface points were reconstructed using stereoscopic DIC at the baseline pressure of 1.5 mm Hg. This information was combined with the thickness data to create a specimen-specific mesh of the posterior sclera as described in Coudrillier et al. [14] (Fig. 2). In the present study, the geometry included the scleral regions where WAXS patterns were collected, i.e., the entire peripapillary sclera and parts of the midposterior sclera. The ONH was not included in the model; the DIC-measured surface information in this region was not sufficient to reconstruct the accurate geometry of the different tissues of the ONH. The creation of the thickness profile in the peripapillary sclera was detailed in Coudrillier et al. [14], and was based on the observations gathered from different imaging techniques [47–49]. These studies evidenced a rapid thinning of the sclera from the outer peripapillary sclera to the scleral canal. In our model, the thickness at the scleral canal was 0.4 mm [50]. These assumptions were used to create a generic model of the peripapillary sclera that was identical for every specimen [14] (Fig. 2(b)). We used the 16 pachymeter measurements to generate the map of the thickness profile of the region extending from the outer peripapillary sclera to the midposterior sclera. Girard et al. [51] and Grytz et al. [52] used a slightly larger number of thickness measurements (20) but constructed a finite element mesh of the entire posterior sclera. Our model only included scleral regions located within a radial distance of 7.5 mm from the ONH center. We applied the DIC-measured displacements as kinematic boundary conditions to the nodes of the edges of the mesh, i.e., the nodes of the scleral canal, and of the outer midposterior sclera (Fig. 2(b)). By doing so, we did not have to approximate or fit the stiffness of the LC or assume boundary conditions and geometry of the sclera at the holder, which was not in the field of view of the DIC measurements. The idea of restricting the domain of the finite element model in inverse methods was originally presented by Seshaiyer and Humphrey [53] and recently revisited by Raghupathy and Barocas [54]. This method can be applied to calculate material properties of biological tissues with complex geometry or boundary conditions such as the posterior segment of the eye.
Fig. 2.
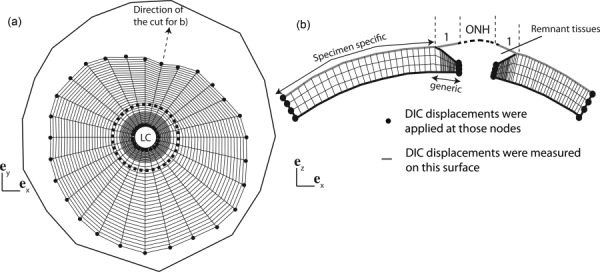
(a) Top view of the surface layer of the finite element (FE) mesh used for the IFEA, showing the nodes at which DIC-measured displacements were applied as kinematic boundary conditions. The outer line represents the location of the most peripheral pixels of the sclera detected by the DIC software. The dashed circle is the border between the generic and specimen-specific mesh. (b) Schematic of the transverse view of the finite element mesh showing the thickness profile in the generic model of the peripapillary sclera. The LC and the remant tissues were not included in the FE model but are represented for clarity. In the inverse analysis, we assumed that the displacements on the surface of the generic peripapillary model were identical to the DIC-measured displacements on the surface of the remnant tissues. The geometry was discretized using mixed Q1P0 trilinear hexahedral elements, with three elements spanning the thickness. The mesh had 40 nodes in the meridional direction and 28 nodes in the circumferential direction. The node density was larger toward the LC to capture the stress concentration due to the compliant tissue of the ONH.
The collagen fiber anisotropy was described at each element of the mesh from the colocalized WAXS measurements [14]. The fiber structure was represented by a vector indicating the preferred collagen fiber orientation in the scleral plane and the normalized WAXS intensity D (Eq. (1)), describing the orientation distribution of collagen fibers along the preferred orientation.
2.4. Inverse Finite Element Method for Parameter Determination.
An inverse finite element method was developed to answer the following question: Given the DIC-measured displacement fields of the scleral surface, u E(X), and the WAXS-measured fiber structure, D(Φ, X), what are the values of the matrix stiffness and collagen fiber stiffness? This question was formulated as a minimization problem of a cost function , which was defined as the difference between the finite element predictions and experimental measurements
| (2) |
where n steps is the number of pressure steps during the loading phase, n nodes is the number of nodes of the outer surface of the mesh, wn are nodal weights is the experimental displacement vector at the pressure step p interpolated to node n, and is the corresponding finite element displacement vector, solution of the forward elasticity problem. In the experiment, we left some remnant tissues around the ONH to prevent leakage during inflation. Consequently, the surface of the generic model of the peripapillary sclera (Fig. 2(b)) and the surface where the DIC displacements were measured were not coincident. However, the remnant tissues were significantly more compliant than the sclera, and we assumed that the displacements of the generic peripapillary model were identical to the DIC-measured displacements of the exposed surface of the remnant tissues. We verified that this was a reasonable assumption in Coudrillier et al. [14], where we showed that the surface displacements of the generic peripapillary sclera differed from those of the remnant tissues by 3% on average. The maximum difference at any particular node was less than 10%. Therefore, we used the vertically projections of the DIC-measured displacements to describe the motion of the peripapillary sclera in the cost function.
2.5. Distributed Fiber Model.
To calculate u FE in Eq. (2), an accurate mathematical description of the mechanical behavior of the sclera is needed. We developed a constitutive model that idealizes the sclera as a planar network of collagen fibers, which are embedded in an isotropic matrix representing components such as elastin, proteoglycans, nonfibrillar collagens, and water. At a given point of the sclera, the mechanical properties are governed by the properties of the matrix and collagen fibers and the planar orientation distribution of the collagen fibers. In this model, we assumed that the properties of the collagen fibers and matrix are uniform across the sclera. Variations in mechanical properties across the sclera solely arise from variations in the collagen fiber structure, represented by D(Φ, X).
In continuum mechanics, the kinematics of the tissue is described by the deformation gradient, F, defined from the displacement vector u as: . F maps a vector of the undeformed configuration to the corresponding vector in the deformed configuration. In the theory of hyperelasticity, the mechanical properties of the sclera are fully characterized by defining an appropriate strain energy function. Both the fiber and the matrix contribute to the mechanical properties of the sclera. We assumed that the collagen fibers and the matrix deform according to the macroscopic deformation gradient F (assumption of affine deformation). Therefore, the strain energy W can be additively decomposed into an isotropic matrix strain energy density that depends on the invariants of the Cauchy–Green tensor C = F ⊤ F, and an anisotropic fiber strain energy density that depends on the distribution of collagen orientations [14,17,55]
| (3) |
where , and are the invariants of C.
Specifically, we described the mechanical behavior of the matrix phase using a nearly incompressible neo-Hookean model [14,17,55]
| (4) |
where μ is the shear modulus of the matrix and κ is the bulk modulus. A large bulk modulus κ = 100 MPa was used for all specimen-specific models. This value was more than two orders of magnitude larger than the matrix shear modulus for all specimens, ensuring that volumetric deformation I 3 ∼ 1. The modified invariant is the distortional part of I 1.
The anisotropic part of the strain energy density, W aniso, was modeled using a distributed fiber model and was formulated as the orientation average of the fiber strain energy density, weighted by the probability density function D(Φ, X) for the fiber orientation
| (5) |
where λf(Φ) represents the stretch of a fiber oriented in the e Φ-direction, which was calculated as: . The normalized X-ray scatter intensity from the WAXS measurements defined in Eq. (1) was used to locally define the probability density function D(Φ, X) and varied with location across the sclera.
To reproduce the nonlinear stress–strain response due to the uncrimping of the collagen fibers with stretch, the mechanical response of the collagen fiber was described by a two parameter exponential model:
| (6) |
where 4αβ denotes the stiffness of the collagen fiber and β is a strain stiffening parameter. This model was implemented in the finite element code Tahoe,1 where the integral formulation for the stress response was numerically evaluated using a 128-point trapezoidal rule. Following the theory of hyperelasticity, the Cauchy stress tensor was given as
| (7) |
where is the preferred fiber orientation, e p is perpendicular to e f in the scleral plane, 1 is the identity matrix, and .
In summary, the material parameters of the distributed fiber model were
-
–
the matrix stiffness μ, uniform across the sclera
-
–
the fiber parameters α and β, where 4αβ represents the axial stiffness of the fiber, uniform across the sclera
-
–
the experimentally measured local distribution of fiber D(Φ, X).
The optimization of (Eq. (2)) was therefore reduced to a minimization problem in a three-dimensional space (μ, α, β).
2.6. IFEA Algorithm
2.6.1. Sequential Algorithm.
An IFEA was developed to calculate the values of the three material parameters from the inflation experiment. Inverse methods are usually computationally expensive and time-consuming, especially when the forward elastostatic is nonlinear. To reduce the number of calculations of the cost function, a multistep iterative search algorithm was developed to determine the values of the matrix shear modulus μ, and the fiber parameters (α, β). A flow diagram representing the search algorithm is presented in Fig. 3. The iterative search algorithm was implemented as a matlab script and the forward finite element problems were solved using Tahoe.
Fig. 3.
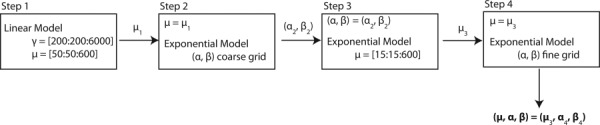
Flow diagram describing the search algorithm for the value of the matrix stiffness μ and fiber parameters (α, β)
-
–In the first step, we made the assumption that the deformation response of the posterior sclera was nearly linear over the range of physiological strains (≤1.5%, Coudrillier et al. [18]). In a first approximation, we replaced the nonlinear model of the anisotropic part of the strain energy density function (Eq. (6)) by a single parameter linear strain energy density function to model the stress–strain response of the collagen fibers
where γ is a measure of the stiffness provided by the fibers. The isotropic matrix response was left unchanged, described as a neo-Hookean material. A grid was created to discretize the (μ, γ)-space, with points every 25 kPa for μ and every 200 kPa for γ. The cost function in Eq. (2) was evaluated for every grid point to search for a mininum. This step provided a first estimate for the matrix modulus μ 1, which was used to narrow down the search interval in the following steps. This step was only used to speed up the convergence of the search algorithm, and μ 1 was usually close but not equal to the final value of the matrix modulus.(8) -
–
In the second step, we fit the parameters of the exponential model of Eq. (6) to the experimental displacements. We fixed the value of the matrix modulus to the result of the first step, μ 1, and evaluated the cost function for a coarse grid for the (α, β)-space, varying α by steps of 10 kPa and β by steps of 10. This yielded an initial estimate (α 2, β 2) for the properties of the collagen fibers.
-
–
In the third step, we refined our initial estimate for the matrix shear modulus μ by fixing (α, β) to (α 2, β 2), and then searched for an optimum μ 3 for μ between the range of 15 and 600 kPa by steps of 15 kPa.
-
–
In the fourth step, the value of μ was fixed to the optimum obtained in the previous step μ 3. We created a fine and specimen-specific discretization of the (α, β)-space. The grid was finer around the region of the minimum of the cost function. This step provided the final estimate for the fiber parameters (α 3, β 3).
Finally, we checked that the parameters of the sequential algorithm provided a minimum by searching the full three-dimensional parameter space centered about (μ 3, α 3, β 3). We used the fine discretization of α and β from step 4 and discretized μ between μ 3 – 75 kPa and μ 3 + 75 kPa by steps of 25 kPa. We found that the minimum of the cost function in the (μ, α, β) space occurred for μ = μ 3; i.e., step 3 provided an accurate estimate of the matrix modulus.
2.6.2. Validation of the Sequential Algorithm.
To validate that the 4-step sequential algorithm converged toward the global minimum and not a local minimum, we also mapped the cost function for a large, dense, full 3D parameter grid. Because this study was computationally expensive, we only used two specimens for validation. The parameter space examined was 0 ≤ α ≤ 200 kPa, 0 ≤ β ≤ 200, and 30 ≤ μ ≤ 1000 kPa. The grid spacing was 25 kPa in μ, 5 kPa in α, and 5 in β.
We next validated that the applied kinematic boundary conditions (Fig. 2) did not overconstrain the solution of the inverse method. We designed a finite element model that included a simplified description of the LC, which was described as nearly incompressible Neo-Hookean material, with shear modulus equal to a tenth of the matrix modulus of the sclera. The material properties of the sclera were (μ, α, β) = (225 kPa, 10 kPa, 100). The sclera and LC were pressurized from the inside, while DIC-measured displacements were applied to the nodes of the base as kinematic boundary conditions (Fig. 4(a)). Nodal displacements of the scleral surface computed in the forward problem were registered as a synthetic experimental displacement field, and used as the target field in the inverse method. The inverse finite element model used the exact same mesh for the sclera, but did not include the LC. Instead, we applied the computed displacement fields of the forward problem as displacement boundary conditions to the nodes of the scleral canal (Fig. 4(b)).
Fig. 4.
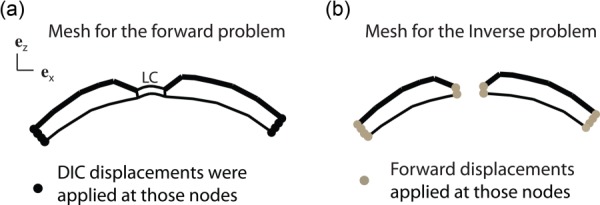
(a) Finite element model used to validate that the applied kinematic boundary conditions did not overconstrain the solution of the IFEA. In this model, the LC was modeled as a neo-Hookean material, with shear modulus equal to a tenth of that of the sclera. (b) We used the same mesh for the sclera in the inverse method. Forward displacements were applied to the edges of the mesh (base and scleral canal).
2.7. Effects of Age on the Mechanical Anisotropy (MA) of the Sclera.
The parameters μ and (α, β) are intrinsic material properties that describe the mechanical behavior of the isotropic matrix and the collagen fibers. The mechanical response of the scleral stroma is determined by the parameters of the constituent materials and the collagen fiber structure. The fiber alignment causes the mechanical properties of the tissue to be anisotropic, the stiffness along the preferred fiber direction is larger than that in the perpendicular direction because the tensile stiffness of a collagen fiber is much larger than the tensile stiffness of the matrix. We evaluated the MA at various locations of the sclera by comparing the stiffness in the preferred fiber direction to the stiffness in the perpendicular direction. We simulated biaxial deformation of a scleral patch containing a single WAXS measurement (Fig. 5(a)). The MA of a nonlinear material depends on the loading conditions and the strain levels at which it is calculated. We reported in a previous experimental study [18] that, on average in the peripapillary sclera, the Green–Lagrange strains were Ep = 1.9% in the meridional direction (perpendicular to the scleral canal) and Ef = 1.1% in the circumferential direction (parallel to the scleral canal). We applied those strains as boundary conditions (Fig. 5) and calculated the mechanical anisotropy as
Fig. 5.
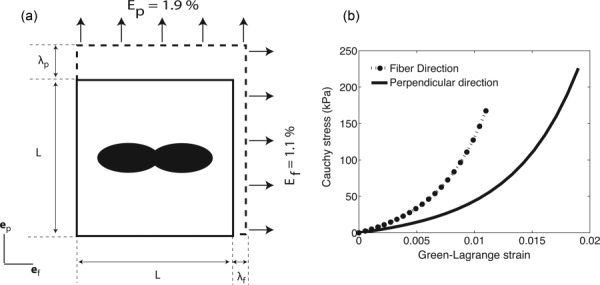
(a) Representation of the single element used to calculate the MA. The fiber structure was described using a single WAXS measurement. A biaxial stretch corresponding to the average strain measured in Coudrillier et al. [18] was applied on the ef and ep faces. (b) Representation of the Green–Lagrange strain/Cauchy stress response. The MA was calculated using Eq. (9).
| (9) |
where is the fourth order stiffness tensor, and are the moduli along the fiber and perpendicular directions. Fazio et al. [24] recently calculated the inflation strain response of the peripapillary sclera and showed significant local shear deformation in this region. Therefore, the applied biaxial stretch in our micromechanical model may not represent the physiological loading of the peripapillary sclera. However, it is a useful measure to compare the effect of variation in collagen structure within a specimen. The average value of the MA was calculated in each quadrant (nasal/inferior, inferior/temporal, temporal/superior, superior/nasal) of the peripapillary sclera, region defined as the annulus of outer radius 2.5 mm centered on the ONH.
2.8. Statistical Analysis.
Linear regression models were used to evaluate the effects of age on matrix and fiber stiffness (μ, α, β). For the degree of fiber alignment and MA, we collected 72 data point per specimen. Mixed linear models with spatial autocorrelation were used to evaluate the effects of age and peripapillary scleral region. For the degree of fiber alignment, a 2D exponential geometrically anisotropic autocorrelation structure was assumed for measurements from each specimen after examining the variogram and Akaike's information criteria. MA did not exhibit spatial correlation, and a compound symmetry correlation structure was assumed. The Tukey–Kramer method was used to adjust pairwise significance levels when comparing the effects of different scleral regions on fiber alignment and MA. Note that correlations between the right and left eye of FC77 were ignored.
In addition, we calculated the power of the models to find a statistically significant effect of age for each outcome using the correlation coefficient (or partial correlation coefficient) for the outcome and age to estimate the true effect. For models with repeat measurements, the observed intracluster correlation coefficient (ICC) assuming compound symmetry was used to obtain the effective sample size prior to calculating the power. All analyses were performed using SAS 9.2 (SAS Institute, Cary, NC).
3. Results
3.1. Effects of Age on the Collagen Fiber Structure.
Figure 6 presents the results of the WAXS measurements for the fiber structure and the contour map of the degree of fiber alignment, locally defined as the ratio of the aligned scatter to the total scatter for FC53r. The polar plots for the other specimens are shown in the supplemental material (found on the Digital Collection under the “Supplemental Data” tab). Some dominant features of the collagen structure were present in all specimens. Those were (1) a ring of aligned circumferential fibers in the peripapillary sclera and (2) two symmetrical oblique features emerging from the temporal pole of the peripheral peripapillary sclera, and oriented toward the superior/nasal and nasal/inferior poles of the midposterior sclera (Fig. 6(a), arrow).
Fig. 6.
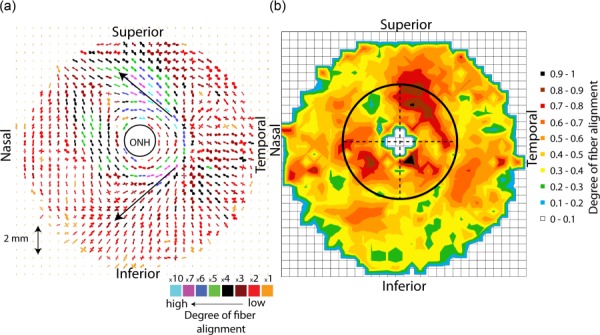
(a) A composite polar plot showing the preferred orientations of aligned collagen fibers for the specimen FC53r. The color scale conveys the degree of fiber alignment. FC53r was representative of the other specimens, showing a strong circumferential fiber alignment in the peripapillary sclera, a much more isotropic midposterior sclera, and two symmetrical oblique features emerging from the temporal pole of the peripheral peripapillary sclera, indicated with arrows. (b) Contour map of calculated degree of fiber alignment, defined as the ratio of the aligned scatter to the total scatter as shown in Fig. 1. The degree of fiber alignment was largest in the temporal/superior quadrant and lowest in the superior/nasal quadrant of the peripapillary sclera.
The average value of the degree of fiber alignment was calculated in each quadrant of the peripapillary sclera (Fig. 6(b)). For all specimens, mean degree of fiber alignment was lowest in the superior/nasal quadrant and largest in the temporal/superior quadrant. Older age was associated with a lower degree of fiber alignment (p = 0.01, Table 2). Figure 7 illustrates the relation between age and average degree of fiber alignment in the different quadrants of the peripapillary sclera.
Table 2.
Results of the multivariate model with spatial autocorrelation for the degree of fiber alignment in the peripapillary sclera with age and peripapillary scleral quadrant as explanatory variables. The variogram for the degree of fiber alignment increases and then levels off as distance between 2 measurements of a same specimen increases, indicating spatial autocorrelation. S stands for superior, N for nasal, I for inferior, and T for temporal. Observed mean degree of fiber alignment was 0.512 ± 0.06 in the NI, 0.509 ± 0.06 in the IT, 0.577 ± 0.07 in the TS, and 0.404 ± 0.05 in the SN.
| Degree of fiber alignment | ||
|---|---|---|
| Variable | Estimate (95% CI) | p-value |
| Age (per 10-yr increase) | −0.043 (−0.073, −0.013) | 0.01 |
| Region: | 0.003 | |
| NI | −0.054 (−0.118, 0.009) | |
| IT | −0.050 (−0.108, 0.008) | |
| SN | −0.123 (−0.181, −0.065) | |
| TS (reference) | 0 | |
Fig. 7.
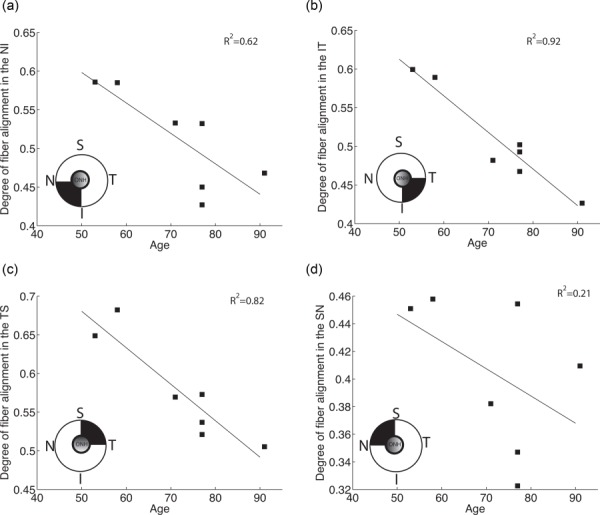
Degree of fiber alignment averaged over each quadrant. Age was associated with a significant decrease in mean degree of fiber alignment (p = 0.01).
3.2. Convergence of the Inverse Analysis
3.2.1. Effects of Nodal Weights in the Cost Function.
Nodal weights were added to the cost function defined in Eq. (2) to improve the sensitivity of the cost function to the fiber parameters (α, β). The nodal weights were proportional to the local degree of fiber alignment, and therefore the displacements of the peripapillary sclera were weighted more. The strains in this region were sufficiently high to exhibit the nonlinear stiffening response of the fibers. Figure 8 illustrates the effects of the nodal weights on the contour of the cost function. This method sharpened the global minimum of the cost function but did not change the location of the minimum.
Fig. 8.
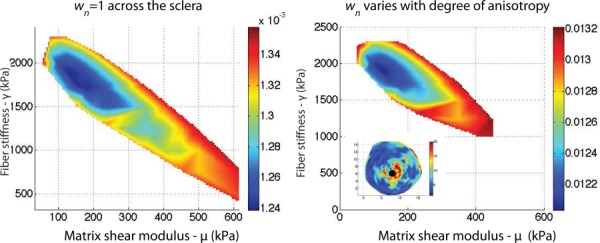
(a) Contour of the cost function in the (μ, γ)-space with wn = 1 for each node (Eq. (2)). (b) Contour of the cost function in the (μ, γ)-space with wn chosen to reflect the degree of anisotropy of the closest WAXS measurement. The weights are represented in the figure on the bottom left. The contribution of the nodes of the peripapillary sclera to the cost function was larger than those of the midposterior sclera. The cost function is represented between its minimum value m and 1.1 m.
3.2.2. Validation of the Algorithm.
Figures 9(a)–9(c) show the steps of the sequential algorithm from Fig. 3 for FC71r. Figure 9(d) maps the cost function for the full parameter grid, 0.1 < α < 200 kPa, 0.1 < β < 150, and 30 < μ < 1000 kPa. The grid spacing was 25 kPa for μ, 5 kPa for α, and 5 for β. The results for the full parameter search returned the same results as for the sequential parameter search. With the sequential algorithm, we were able to obtain an accurate estimate of the global minimum after a few thousand cost function evaluations. In contrast, a minimum of 20,000 cost function evaluations were necessary to map the entire space using the global search algorithm. The sequential algorithm was used to find the global minimum for all specimens. The different steps of the search algorithm are reported in the supplemental material.
Fig. 9.
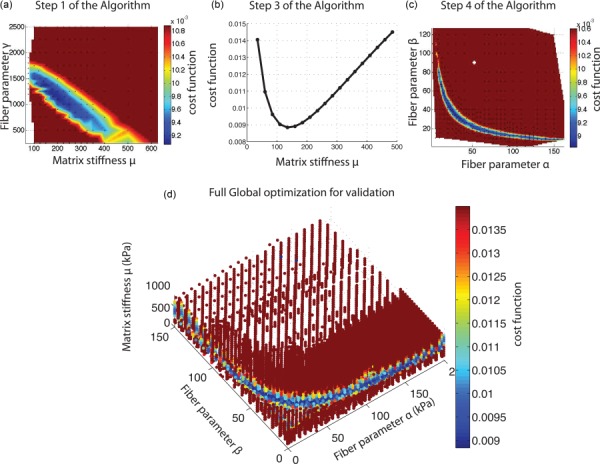
(a) Step 1, (b) step 3, and (c) step 4 of the sequential algorithm as shown in Fig. 3 and explained in Sec. 2.6. (d) Map of cost function for a dense 3D grid. We evaluated 21,519 combinations of material parameters (α, β, μ), with 0 < α < 200 kPa, 0 < β < 150, and 30 < μ < 1000 kPa. Although hard to see in this figure, the global search algorithm confirmed that the restriction for μ obtained in our sequential algorithm was accurate.
We then validated that the applied kinematic boundary conditions did not overconstrain the solution of the IFEA. We used the forward surface displacement fields as a mock experimental displacement field, i.e., we replaced u E(X) in Eq. (2) with the surface nodal displacement field of the forward problem. The target scleral properties were (μ, α, β) = (225 kPa, 10 kPa, 100). The sequential algorithm returned the lowest cost function for (μ, α, β) = (222.5 kPa, 10.5 kPa, 99). The discrepancy between the target and converged parameters, 1% for μ and 4% for αβ, were likely caused by inaccuracies associated with applying surface displacements to all the nodes through the thickness of the scleral canal boundary. The difference between the converged and target parameters decreased with increased mesh density in the peripapillary sclera.
3.3. Effects of Age on the Material Properties of the Matrix and Collagen Fibers.
The converged material parameters for the matrix and collagen fibers returned by the IFEA algorithm are presented in Table 3. The contours of the model-predicted and DIC-measured displacement fields are illustrated in the supplemental material. The error of the fit, defined as the average nodal error between experimental and model predicted surface displacements, was low at every pressure step, less than 20%, because we prescribed the DIC displacements at the scleral canal and base of the mesh, which eliminated uncertainties associated with LC properties and constraints imposed by the holder.
Table 3.
Matrix modulus μ, parameters of the exponential fiber model (α, β), and fiber stiffness (4αβ) obtained by global optimization
| μ | α | β | Fiber stiffness: 4αβ | |
|---|---|---|---|---|
| kPa | kPa | — | MPa | |
| FC53r | 100 | 204 | 11 | 8.976 |
| MC58l | 130 | 6 | 47 | 1.128 |
| FC71r | 150 | 26.5 | 38 | 4.028 |
| FC77l | 220 | 13.5 | 136 | 7.344 |
| FC77r | 225 | 15 | 145 | 8.700 |
| MC77r | 190 | 135 | 14 | 7.560 |
| FC91r | 250 | 2 | 137 | 1.096 |
The stress–strain responses in the fiber and perpendicular directions were evaluated by simulating an equibiaxial stress loading to 60 kPa (Fig. 10). The calculations used the specimen-specific converged parameters for the matrix and fiber stiffness and a specimen-specific description of the orientation distribution D(Φ). To generate Fig. 10, we fit a von Mises distribution function to the average normalized X-ray scatter intensity in the peripapillary sclera for D(Φ).
Fig. 10.
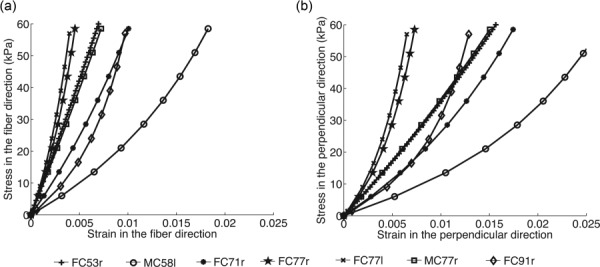
Stress–strain curves in the fiber (a) and perpendicular (b) directions obtained from an equibiaxial stress to 60 kPa, corresponding to the hoop stress in a thin-walled sphere of radius 12 mm and thickness 1.2 mm at a pressure of 90 mm Hg. The fiber structure was represented by a von Mises function, which was fit to the specimen-specific averaged fiber distribution in the peripapillary sclera.
The results of the univariate models for the material properties of the matrix and collagen fibers with age as the explanatory variable are presented in Table 4. Older age was predictive of a larger matrix stiffness μ (p = 0.001, Fig. 11(a)). Older age was not associated with significant change in fiber stiffness 4αβ for normals (p = 0.68, Fig. 11(b)).
Table 4.
Results of the univariate model for the matrix and fiber stiffness accounting for the effects of age
| Outcome | Variable | Estimate (95% CI) | p-value |
|---|---|---|---|
| Matrix stiffness μ in kPa | Age (per 10-yr increase) | 40.8 (25.0, 56.6) | 0.001 |
| Fiber stiffness 4αβ in MPa | Age (per 10-yr increase) | −0.52 (−3.52, 2.49) | 0.68 |
Fig. 11.
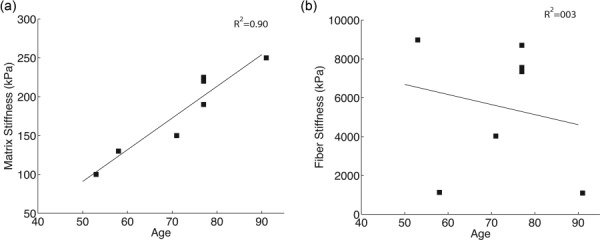
(a) Matrix shear modulus μ and (b) fiber stiffness 4αβ plotted versus age
3.4. Effects of Age on the MA of the Sclera.
In this section, we evaluate how the age-related changes in the degree of fiber alignment and material properties combine to affect the MA of scleral tissue defined in Eq. (9). Figure 12 maps the MA for each WAXS measurement of FC77r. The maps of MA for the other specimens are available under “Supplemental Data” tab for this paper on the ASME Digital Collection. As expected, the MA was highly correlated with the degree of fiber alignment (p < 0.0001). MA in the peripapillary sclera followed the regional pattern of the degree of fiber alignment, being largest in the temporal/superior quadrant and lowest in superior/nasal quadrant. Older age was associated with a lower MA (p = 0.03, Table 5 and Fig. 13).
Fig. 12.
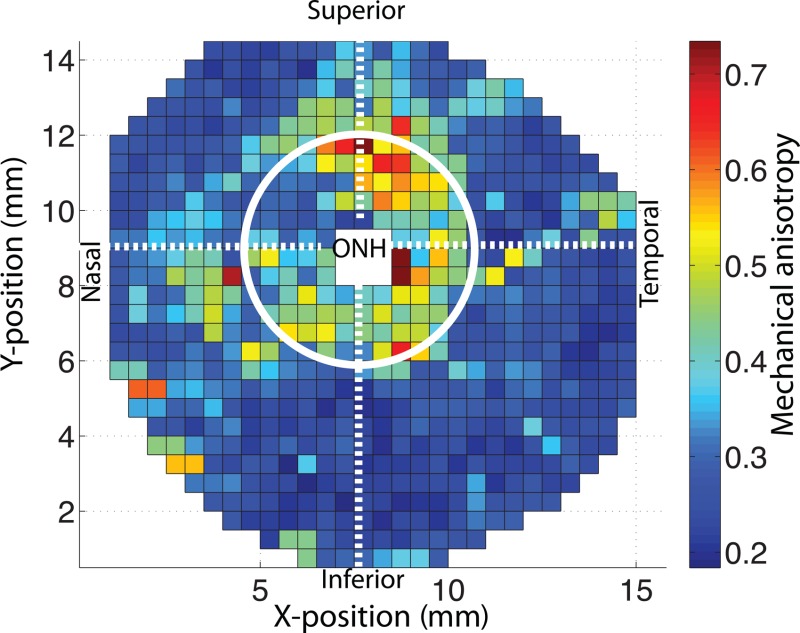
Map of the MA defined in Eq. (9) for FC77r. The MA was largest in the temporal/superior quadrant of the peripapillary sclera and lowest in the superior/nasal quadrant of the peripapillary sclera.
Table 5.
Results of the multivariate model with spatial autocorrelation for the MA in the peripapillary sclera with age and peripapillary scleral quadrant as explanatory variables. Since MA did not exhibit spatial correlation, a compound symmetry correlation structure was assumed. S stands for superior, N for nasal, I for inferior, and T for temporal. Observed mean degree of fiber alignment was 1.220 ± 0.77 in the NI, 1.187 ± 0.80 in the IT, 1.408 ± 0.89 in the TS, and 1.050 ± 0.64 in the SN.
|
Mechanical anisotropy | ||
|---|---|---|
| Variable | Estimate (95% CI) | p-value |
| Age (per 10-yr increase) | −0.487 (−0.910, −0.065) | 0.03 |
| Region: | 0.001 | |
| NI | −0.184 (−0.336, −0.033) | |
| IT | −0.222 (−0.374, −0.071) | |
| SN | −0.359 (−0.511, −0.207) | |
| TS (reference) | 0 | |
Fig. 13.
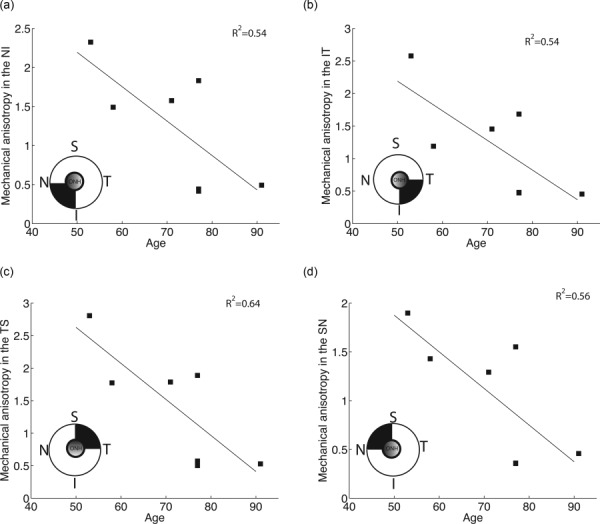
Average MA in each quadrant of the peripapillary sclera plotted versus age
3.5. Power Analyses.
We calculated the statistical power of the models to detect significant age effects for the fiber alignment, matrix and fiber stiffness, and MA. As shown in Table 6, the sample size of this study was sufficiently large to detect significant age-related effects for matrix stiffness, degree of fiber alignment, and MA (power > 0.80). However, we would need considerably more specimens to confidently estimate the effects of age on the fiber stiffness.
Table 6.
Statistical power of the models to find statistically significant age effects for the different outcomes of this study.
| Outcome | AdjustmentVariables | Observed correlation between outcome & age | Observed intraclusterCorrelation a | Power | Minimum # of specimensfor at least 80% power b |
|---|---|---|---|---|---|
| Matrix stiffness | None | 0.9476 | — | 1.00 | 4 |
| Fiber stiffness | None | −0.1964 | — | 0.07 | 203 |
| Fiber alignment | Ppscl quadrant | −0.4371 | 0.0247 | 1.00 | 2 |
| MA | Ppscl quadrant | −0.6536 | 0.3828 | 0.9 | 6 |
For compound symmetry correlation structure.
To find significant association given the observed partial correlation.
4. Discussion
In this study, we determined the age-dependent material properties of seven human scleras from the IFEA of inflation tested specimens. The finite element models used specimen-specific descriptions of the collagen fiber structure provided by WAXS measurements to model the anisotropic stress response of the tissue. The model assumed that spatial variations in the material properties were caused by changes in the collagen structure, specifically in the preferred fiber orientation and degree of alignment. The remaining three parameters described the material properties of the collagen fibers and matrix material. We were able to accurately fit the experimental displacement fields of the inflation tested specimens with only three material parameters and the WAXS-measured spatially varying collagen fiber structure. The principal findings of this work were that older age was associated with a significant decrease in the degree of collagen fiber alignment in the peripapillary sclera (p = 0.01), a significant increase in the matrix stiffness (p = 0.001), and a significant decrease in MA (p = 0.03).
The degree of fiber alignment represents the relative number of collagen fibers oriented in the preferred fiber direction compared to the fibers randomly oriented. In the peripapillary sclera, the collagen fibers are preferentially aligned in the circumferential direction. The age-related decrease in degree of fiber alignment indicates that the collagen fiber structure becomes more random in the aging sclera; i.e., the relative number of circumferentially aligned fibers is lower in older scleras.
The observed age-related stiffening of scleral tissue is consistent with our recent experimental work including 35 normal specimens [18]. In this study, we calculated the strain fields from the DIC-measured displacements and stresses modeling the midposterior sclera as a thin ellipsoid shell subjected to an internal pressure. We showed that the meridional and circumferential strains at 22 mm Hg were significantly lower in older specimens. In addition, the stresses and strains were related through a constitutive model, which assumed the presence of two unidirectional fiber families oriented in the circumferential and meridional directions. We showed that the stiffness of the circumferential fiber family was larger in older eyes. In the present study, we propose a more detailed constitutive model and consider the contribution of the matrix and dispersed collagen fibers to the tissue stress response. Because of the lower number of specimens included in this study (7 out of the 35), the age-related variations in fiber stiffness were not significant. Interestingly, the matrix stiffness demonstrated a significant age-related increase, with a 2.2-fold increase in shear modulus between age 53 and 91. Age-related stiffening in collagen-rich tissue is commonly attributed to the accumulation of nonenzymatic glycation type cross-links of collagen fibrils with age [2]. Therefore, we expected to observe greater age-related effects in the fiber stiffness rather than in the matrix stiffness. Our findings suggest that age-related remodeling may also occur in the matrix. The stiffening of the matrix may be attributed to an age-related decrease in the proteoglycan composition [15] that was found to be coincident with a decrease in tissue hydration [56]. Other matrix proteins such as elastin or glycoprotein may also be degraded or synthesized with age. Further experimental studies quantifying changes in the composition of scleral extracellular matrix with age, and numerical studies evaluating the contribution of the different proteins to the matrix stiffness are needed.
We found that the mechanical anisotropy, similarly to the degree of fiber alignment, was significantly lower in older scleras. The mechanical anisotropy depends on both the collagen fiber structure and the material properties of the collagen fibers and matrix. The dependence of the mechanical anisotropy on the matrix and fiber stiffness is complex because of the nonlinear material behavior. However, our finding suggests that the decreased fiber alignment is the principal factor determining mechanical anisotropy. This age-related decrease in mechanical anisotropy would decrease the ability of the sclera to shield the ONH against excessive tensile deformation and may explain the increased susceptibility of the older eye to glaucoma. The mechanical anisotropy was defined as the ratio of the material tangent modulus in the fiber direction to that in the perpendicular direction under biaxial stretch state. The applied stretch corresponded to the average circumferential and meridional strains measured in the peripapillary sclera at 22.5 mm Hg in 35 specimens [18]. The mechanical anisotropy depends on the deformation state and pressure loading conditions. To verify that our conclusions held under different loading conditions, we also calculated the MA in an equibiaxial stress simulation to 21 kPa, which corresponds to the hoop stress in a thin-walled sphere of radius 12.5 mm and thickness 1.2 mm at a pressure of 30 mm Hg (). We found that it also significantly decreased with age (results not shown). Our calculation did not consider the presence of shear strains, which may be significant as shown by Fazio et al. [24].
Several limitations should be considered when interpreting the results of this study. First, our conclusions were drawn from a relatively low sample size (7 specimens). Our access to the Diamond Light Source, where we performed the WAXS measurements was limited to a few days, which limited the number of specimens that we could analyze. However, the power analyses revealed that the sample size was large enough to detect significant age-related effects in matrix stiffness, degree of fiber alignment, and mechanical anisotropy. We observed significant variability in the measure of the fiber stiffness. However, this type of variability has commonly been observed in human scleral tissue and the stiffness values reported in the present study are consistent with those from recent mechanical characterizations of the human sclera. Using biaxial experiments on human scleral strip specimens, Eilaghi et al. [57] reported measures of stiffness between 0.5 MPa and 7.5 MPa. A recent uniaxial mechanical characterization of the sclera using uniaxial strip tests reported values of toe moduli varying between 1 kPa and 95 kPa, and heel moduli varying between 0.5 MPa and 13 MPa [58]. One could argue that the variability observed in those experiments cannot be compared to that observed in the present study because of the differences in experimental protocol. However, Grytz et al. [52] subjected scleral specimens to inflation testing and calculated matrix and fiber stiffness using an inverse method. This comparable study reported matrix stiffness between 110 kPa and 820 kPa. The authors applied a different constitutive model to represent the collagen fiber response. However, they observed a similar variability in the material parameters related to the fiber response, which varied by more than an order of magnitude between the most compliant and the stiffest specimens.
Second, we assumed that the only cause of spatial variations in scleral mechanical properties was the variations in the collagen fiber structure. The mechanical behavior of the matrix and the fibers were identical in the peripapillary sclera and midposterior sclera. In this model, the matrix included the elastin fibers, which were assumed to be randomly oriented. Although this is probably a valid description in the midposterior sclera, Hernandez et al. [59] showed that the elastin fibers of the LC insertion zone of the peripapillary sclera are circumferentially oriented, providing further mechanical reinforcement. In addition, elastin content is larger around the ONH than in the midposterior sclera. Separating the contribution of the elastin fibers from the matrix would require to add a term to the strain energy density (Eq. (3)) dependent on a structure tensor describing the orientation of the elastin fibers. This would increase the number of parameters to be estimated and therefore the computational cost of the inverse method. Quigley et al. [60] showed that the average collagen fiber diameter is smaller in the peripapillary sclera than in the midposterior sclera. Different fiber material properties could have been assigned to different regions of the midposterior sclera. But this would also have increased the number of parameters to optimize. With only 3 material parameters and the experimentally determined fiber structure, the model was able to accurately reproduce the experimental displacements.
Third, it should be remembered that our WAXS method yields thickness-averaged data. This method is very robust in regions where the fiber alignment is unidirectional, which includes the peripapillary region. However, the method becomes less robust in regions where there is a mixture of uni- and biaxial dominant orientations [61]. In addition, Pijanka et al. [12] carried out multiphoton microscopy to show that the circumferential alignment of the fibers in the peripapillary sclera is limited to the mid-to-outer 2/3 of the sclera and does not extend through the full thickness of the tissue. WAXS cannot reveal depth-dependent information, nor can it detect collagen fibers that do not lie in the plane of the sclera. In these respects, WAXS presents a highly quantitative yet simplified view of the full tissue architecture. Recently, Petsche and Pinsky [62] modeled the 3D organization of the corneal stroma fiber structure by introducing a 3D distribution function. The spatial distribution of fibers was calibrated to out-of-plane shear measurements that are not available for scleral tissue. However, the effects of out-of-plane fibers on the inflation response of the cornea were minimal. The effects of out-of-plane fibers on the inflation response of the midposterior sclera are likely to be minimal as well. However, the physiological loading conditions in the ONH region are complex, with significant shear deformation. It would be interesting to evaluate the effects of out-of-plane fibers in the peripapillary sclera on scleral and ONH mechanics. We did not flatten the scleras to perform the WAXS experiment. Therefore, there is a mismatch between the X-ray beam direction and the normal to the scleral tissue, increasing with radial distance to the ONH. The effective tissue thickness presented to the X-ray beam is increasingly elevated by the curvature, with a proportional increase in total (i.e., isotropic and aligned) X-ray scatter, which increases the size of the polar vector plots. The estimated increase in the total scatter caused by scleral curvature was calculated to be < 2% in the peripapillary region, increasing to ∼ 17% at the specimen periphery (based on a posterior scleral radius of curvature of 12 mm). For the small 0.2 mm beam size and dominant planar orientation of the collagen fibers, the specimen curvature would have little effect on the angular distribution of the collagen fibers and the degree of fiber alignment, which is averaged through the thickness. Moreover, the statistical analyses for age were performed for the MA and degree of fiber alignment in the peripapillary region, where the effect of curvature was small. The dominant fiber direction may not be accurate far from the peripapillary region, but the degree of fiber alignment in this region was low and has little effect on deformation response [14].
Fourth, we used an idealized model geometry for the peripapillary sclera that was similar for the seven specimens. This differed from the approach presented in our recent work [14], where the IFEA model did not include the peripapillary sclera. With the previous method, the sensitivity of the cost function to the collagen fiber parameters was low due to the linearity of the experimental stress–strain curve in the midposterior sclera. Since the peripapillary sclera is a region of relatively large strains and fiber alignment, we added this region to improve the convergence of the inverse method. In addition, we weighted the nodal displacements of the peripapillary sclera according to the degree of fiber alignment to increase the contribution of the most nonlinear regions to the cost function. This method helped sharpen the global minimum of the cost function, but did not significantly alter the results of the inverse analysis. The idealized geometry of the peripapillary sclera was based on the averaged measurements of Ren et al. [47], Norman et al. [48], and Vurgese et al. [49]. This most likely did not represent the specific geometry of each specimen and may have influenced the obtained material parameters and the magnitude of the ONH deformation. Furthermore, the positions of the DIC displacement measurements did not coincide with the positions of the idealized finite element model of the peripapillary sclera. We assumed that the stiffness of the remnant tissues was much lower than that of the sclera and therefore the remnant tissues followed the displacements of the underlying sclera. We verified that this was a reasonable assumption in Coudrillier et al. [14].
Fifth, we used DIC to measure the surface displacements of the scleral. We have extensively discussed the limitations of the DIC method in our previous experimental studies [18,42]. We and others have showed that the out-of-plane uncertainty in displacement calculation was around 10–15 μm [18,44,43]. We expect the experimental uncertainty in displacements to have little effects on the values of the material parameters, because our global optimizer minimized the averaged error between DIC-measured and model-predicted displacements over the entire surface and not the local nodal error. Other recent scleral mechanics studies have utilized laser speckle interferometer (ESPI) to measure surface displacement [17,24,25,51]. ESPI was shown to have an unmatched 16 nm accuracy in displacement calculation [63]. Using ESPI, Girard et al. [17] in monkeys and Fazio et al. [24] in humans detected an age-related stiffening of scleral tissue, which is consistent with what we observed using DIC [18]. A similar inverse finite element optimization method was applied to match ESPI-measured displacement fields obtained in an inflation test to model-predicted displacement fields and calculate the anisotropic hyperelastic material properties of the monkey [17,51] and human [22,52] sclera. Although ESPI has a noticeably better displacement resolution than DIC, the quality of the fit in our study is comparable to if not improved over those studies. In addition, the resolution in displacement calculation in our method may be lower because we did not use the inverse method to infer the collagen fiber structure of the sclera from the inflation test. Instead, we directly measured it using WAXS and incorporated this information into our finite element model. Tang and Liu [64] and Morris et al. [65] recently proposed an alternative method to DIC and ESPI to measure the strain response of scleral tissue using ultrasound imaging. In contrast to ESPI and DIC, which can only measure surface deformation, ultrasound imaging can measure the full 3D strain tensor. However, this method has not yet been combined with an IFEA to determine material properties of scleral tissue.
In summary, the mechanical behavior and collagen fiber structure of seven human scleras of age 53–91 were characterized. Older age was predictive of a significantly lower degree of fiber alignment and lower mechanical anisotropy in the peripapillary sclera, as well as a significantly larger matrix stiffness. Age-related variations in scleral mechanical behavior may also be associated with susceptibility to glaucomatous damage. In future work, the methods presented in this study will be applied to evaluate how glaucoma-induced variations in the collagen and matrix properties and anisotropic collagen structure may affect the mechanical response of the ONH.
Acknowledgment
This work was supported in part by the Public Health Service Research Grant Nos. EY021500 (T.D.N.), EY02120 and EY01765 (H.A.Q., Wilmer Institute), the Fight For Sight Grant No. 1360 (C.B.), the Leonard Wagner Charitable Trust, William T. Forrester, and Saranne and Livingston Kosberg (H.A.Q.).
Footnotes
Contributor Information
Baptiste Coudrillier, Wallace H. Coulter Department of Biomedical, Engineering, Georgia Institute of Technology and Emory University, Atlanta, GA 30332, e-mail: baptiste.coudrillier@bme.gatech.edu.
Jacek Pijanka, Structural Biophysics Group, School of Optometry and Vision Sciences, Cardiff University, Cardiff CF24 4HQ, Wales, UK.
Joan Jefferys, Glaucoma Center of Excellence, Wilmer Ophthalmological Institute, Johns Hopkins University School of Medicine, Baltimore, MD 21287.
Thomas Sorensen, Diamond Light Source, Didcot, Oxfordshire, UK.
Harry A. Quigley, Glaucoma Center of Excellence, Wilmer Ophthalmological Institute, Johns Hopkins University School of Medicine, Baltimore, MD 21287
Craig Boote, Structural Biophysics Group, School of Optometry and Vision Sciences, Cardiff University, Cardiff CF24 4HQ, Wales, UK.
Thao D. Nguyen, Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, e-mail: vicky.nguyen@jhu.edu
References
- [1]. Watson, P. G. , and Young, R. D. , 2004, “Scleral Structure, Organisation and Disease. A Review,” Exp. Eye Res., 78(3), pp. 609–623. 10.1016/S0014-4835(03)00212-4 [DOI] [PubMed] [Google Scholar]
- [2]. Keeley, F. , Morin, J. , and Vesely, S. , 1984, “Characterization of Collagen From Normal Human Sclera,” Exp. Eye Res., 39(5), pp. 533–542. 10.1016/0014-4835(84)90053-8 [DOI] [PubMed] [Google Scholar]
- [3]. Komai, Y. , and Ushiki, T. , 1991, “The Three-Dimensional Organization of Collagen Fibrils in the Human Cornea and Sclera,” Invest. Ophthalmol. Visual Sci., 32(8), pp. 2244–2258. [PubMed] [Google Scholar]
- [4]. Kokott, W. , 1934, “Das spaltlinienbild der sklera. (ein beitrag zum funktionellen bau der sklera),” Klin. Monatsbl. Augenheilkd, 92, pp. 177–185. [Google Scholar]
- [5]. Meek, K. , and Fullwood, N. J. , 2001, “Corneal and Scleral Collagens-A Microscopist's Perspective,” Micron, 32(3), pp. 261–272. 10.1016/S0968-4328(00)00041-X [DOI] [PubMed] [Google Scholar]
- [6]. Yamamoto, S. , Hashizume, H. , Hitomi, J. , Shigeno, M. , Sawaguchi, S. , Abe, H. , and Ushiki, T. , 2000, “The Subfibrillar Arrangement of Corneal and Scleral Collagen Fibrils as Revealed by Scanning Electron and Atomic Force Microscopy,” Arch. Histol. Cytol., 63(2), pp. 127–135. 10.1679/aohc.63.127 [DOI] [PubMed] [Google Scholar]
- [7]. Marshall, G. , Konstas, A. , and Lee, W. , 1993, “Collagens in Ocular Tissues,” Br. J. Ophthalmol., 77(8), pp. 515–524. 10.1136/bjo.77.8.515 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8]. Winkler, M. , Jester, B. , Nien-Shy, C. , Massei, S. , Minckler, D. S. , Jester, J. V. , and Brown, D. J. , 2010, “High Resolution Three-Dimensional Reconstruction of the Collagenous Matrix of the Human Optic Nerve Head,” Brain Res. Bull., 81(2), pp. 339–348. 10.1016/j.brainresbull.2009.06.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9]. Yan, D. , McPheeters, S. , Johnson, G. , Utzinger, U. , and Geest, J. P. V. , 2011, “Microstructural Differences in the Human Posterior Sclera as a Function of Age and Race,” Invest. Ophthalmol. Visual Sci., 52(2), pp. 821–829. 10.1167/iovs.09-4651 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. Danford, F. L. , Yan, D. , Dreier, R. A. , Cahir, T. M. , Girkin, C. A. , and Geest, J. P. V. , 2013, “Differences in the Region-and Depth-Dependent Microstructural Organization in Normal Versus Glaucomatous Human Posterior Sclerae,” Invest. Ophthalmol. Visual Sci., 54(13), pp. 7922–7932. 10.1167/iovs.13-12262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11]. Girard, M. J. , Dahlmann-Noor, A. , Rayapureddi, S. , Bechara, J. A. , Bertin, B. M. , Jones, H. , Albon, J. , Khaw, P. T. , and Ethier, C. R. , 2011, “Quantitative Mapping of Scleral Fiber Orientation in Normal Rat Eyes,” Invest. Ophthalmol. Visual Sci., 52(13), pp. 9684–9693. 10.1167/iovs.11-7894 [DOI] [PubMed] [Google Scholar]
- [12]. Pijanka, J. K. , Coudrillier, B. , Ziegler, K. , Sorensen, T. , Meek, K. M. , Nguyen, T. D. , Quigley, H. A. , and Boote, C. , 2012, “Quantitative Mapping of Collagen Fiber Orientation in Non-Glaucoma and Glaucoma Posterior Human Sclerae,” Invest. Ophthalmol. Visual Sci., 53(9), pp. 5258–5270. 10.1167/iovs.12-9705 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13]. Pijanka, J. K. , Abass, A. , Sorensen, T. , Elsheikh, A. , and Boote, C. , 2013, “A Wide-Angle X-Ray Fibre Diffraction Method for Quantifying Collagen Orientation Across Large Tissue Areas: Application to the Human Eyeball Coat,” J. Appl. Crystallogr., 46(5), pp. 1481–1489. 10.1107/S0021889813022358 [DOI] [Google Scholar]
- [14]. Coudrillier, B. , Boote, C. , Quigley, H. A. , and Nguyen, T. D. , 2013, “Scleral Anisotropy and its Effects on the Mechanical Response of the Optic Nerve Head,” Biomech. Model. Mechanobiol., 12(5), pp. 941–963. 10.1007/s10237-012-0455-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Rada, J. A. , Achen, V. R. , Penugonda, S. , Schmidt, R. W. , and Mount, B. A. , 2000, “Proteoglycan Composition in the Human Sclera During Growth and Aging,” Invest. Ophthalmol. Visual Sci., 41(7), pp. 1639–1648. [PubMed] [Google Scholar]
- [16]. Lewis, P. N. , Pinali, C. , Young, R. D. , Meek, K. M. , Quantock, A. J. , and Knupp, C. , 2010, “Structural Interactions Between Collagen and Proteoglycans are Elucidated by Three-Dimensional Electron Tomography of Bovine Cornea,” Structure, 18(2), pp. 239–245. 10.1016/j.str.2009.11.013 [DOI] [PubMed] [Google Scholar]
- [17]. Girard, M. J. , Suh, J.-K. F. , Bottlang, M. , Burgoyne, C. F. , and Downs, J. C. , 2009, “Scleral Biomechanics in the Aging Monkey Eye,” Invest. Ophthalmol. Visual Sci., 50(11), pp. 5226–5237. 10.1167/iovs.08-3363 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Coudrillier, B. , Tian, J. , Alexander, S. , Myers, K. M. , Quigley, H. A. , and Nguyen, T. D. , 2012, “Biomechanics of the Human Posterior Sclera: Age-and Glaucoma-Related Changes Measured Using Inflation Testing,” Invest. Ophthalmol. Visual Sci., 53(4), pp. 1714–1728. 10.1167/iovs.11-8009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Malik, N. S. , Moss, S. J. , Ahmed, N. , Furth, A. J. , Wall, R. S. , and Meek, K. M. , 1992, “Ageing of the Human Corneal Stroma: Structural and Biochemical Changes,” Biochim. Biophys. Acta, Mol. Basis Dis., 1138(3), pp. 222–228. 10.1016/0925-4439(92)90041-K [DOI] [PubMed] [Google Scholar]
- [20]. Bailey, A. J. , Paul, R. G. , and Knott, L. , 1998, “Mechanisms of Maturation and Ageing of Collagen,” Mech. Ageing Dev., 106(1), pp. 1–56. 10.1016/S0047-6374(98)00119-5 [DOI] [PubMed] [Google Scholar]
- [21]. Geraghty, B. , Jones, S. W. , Rama, P. , Akhtar, R. , and Elsheikh, A. , 2012, “Age-Related Variations in the Biomechanical Properties of Human Sclera,” J. Mech. Behav. Biomed. Mater., 16, pp. 181–191. 10.1016/j.jmbbm.2012.10.011 [DOI] [PubMed] [Google Scholar]
- [22]. Grytz, R. , Fazio, M. A. , Libertiaux, V. , Bruno, L. , Gardiner, S. K. , Girkin, C. A. , and Downs, J. C. , 2014, “Age-and Race-Related Differences in Human Scleral Material Properties,” Invest. Ophthalmol. Visual Sci., 55(12), pp. 8163–8172. 10.1167/iovs.14-14029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23]. Myers, K. M. , Cone, F. E. , Quigley, H. A. , Gelman, S. , Pease, M. E. , and Nguyen, T. D. , 2010, “The in Vitro Inflation Response of Mouse Sclera,” Exp. Eye Res., 91(6), pp. 866–875. 10.1016/j.exer.2010.09.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24]. Fazio, M. A. , Grytz, R. , Morris, J. S. , Bruno, L. , Gardiner, S. K. , Girkin, C. A. , and Downs, J. C. , 2014, “Age-Related Changes in Human Peripapillary Scleral Strain,” Biomech. Model. Mechanobiol., 13(3), pp. 551–563. 10.1007/s10237-013-0517-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25]. Fazio, M. A. , Grytz, R. , Morris, J. S. , Bruno, L. , Girkin, C. A. , and Downs, J. C. , 2014, “Human Scleral Structural Stiffness Increases More Rapidly With Age in Donors of African Descent Compared to Donors of European Descent,” Invest. Ophthalmol. Visual Sci., 55(11), pp. 7189–7198. 10.1167/iovs.14-14894 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26]. Foster, A. , and Resnikoff, S. , 2005, “The Impact of Vision 2020 on Global Blindness,” Eye, 19(10), pp. 1133–1135. 10.1038/sj.eye.6701973 [DOI] [PubMed] [Google Scholar]
- [27]. Quigley, H. , Hohman, R. , Addicks, E. , Massof, R. , and Green, W. R. , 1983, “Morphologic Changes in the Lamina Cribrosa Correlated With Neural Loss in Open-Angle Glaucoma,” Am. J. Ophthalmol., 95(5), pp. 673–691. 10.1016/0002-9394(83)90389-6 [DOI] [PubMed] [Google Scholar]
- [28]. Fechtner, R. D. , and Weinreb, R. N. , 1994, “Mechanisms of Optic Nerve Damage in Primary Open Angle Glaucoma,” Surv. Ophthalmol., 39(1), pp. 23–42. 10.1016/S0039-6257(05)80042-6 [DOI] [PubMed] [Google Scholar]
- [29]. Burgoyne, C. F. , Crawford Downs, J. , Bellezza, A. J. , Francis Suh, J.-K. , and Hart, R. T. , 2005, “The Optic Nerve Head as a Biomechanical Structure: A New Paradigm for Understanding the Role of IOP-Related Stress and Strain in the Pathophysiology of Glaucomatous Optic Nerve Head Damage,” Prog. Retinal Eye Res., 24(1), pp. 39–73. 10.1016/j.preteyeres.2004.06.001 [DOI] [PubMed] [Google Scholar]
- [30]. Campbell, I. C. , Coudrillier, B. , and Ethier, C. R. , 2014, “Biomechanics of the Posterior Eye: A Critical Role in Health and Disease,” ASME J. Biomech. Eng., 136(2), p. 021005. 10.1115/1.4026286 [DOI] [PubMed] [Google Scholar]
- [31]. Quigley, H. A. , and Vitale, S. , 1997, “Models of Open-Angle Glaucoma Prevalence and Incidence in the United States,” Invest. Ophthalmol. Visual Sci., 38(1), pp. 83–91. [PubMed] [Google Scholar]
- [32]. Boland, M. V. , and Quigley, H. A. , 2007, “Risk Factors and Open-Angle Glaucoma: Classification and Application,” J. Glaucoma, 16(4), pp. 406–418. 10.1097/IJG.0b013e31806540a1 [DOI] [PubMed] [Google Scholar]
- [33]. Leske, M. C. , Wu, S.-Y. , Hennis, A. , Honkanen, R. , and Nemesure, B. , 2008, “Risk Factors for Incident Open-Angle Glaucoma: The Barbados Eye Studies,” Ophthalmology, 115(1), pp. 85–93. 10.1016/j.ophtha.2007.03.017 [DOI] [PubMed] [Google Scholar]
- [34]. Broman, A. T. , Quigley, H. A. , West, S. K. , Katz, J. , Munoz, B. , Bandeen-Roche, K. , Tielsch, J. M. , Friedman, D. S. , Crowston, J. , Taylor, H. R. , Varma, R. , Leske, M. C. , Bengtsson, B. , Heijl, A. , He, M. , and Foster, P. J. , 2008, “Estimating the Rate of Progressive Visual Field Damage in Those With Open-Angle Glaucoma, From Cross-Sectional Data,” Invest. Ophthalmol. Visual Sci., 49(1), pp. 66–76. 10.1167/iovs.07-0866 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35]. Sigal, I. A. , Flanagan, J. G. , and Ethier, C. R. , 2005, “Factors Influencing Optic Nerve Head Biomechanics,” Invest. Ophthalmol. Visual Sci., 46(11), pp. 4189–4199. 10.1167/iovs.05-0541 [DOI] [PubMed] [Google Scholar]
- [36]. Sigal, I. A. , Yang, H. , Roberts, M. D. , Grimm, J. L. , Burgoyne, C. F. , Demirel, S. , and Downs, J. C. , 2011, “IOP-Induced Lamina Cribrosa Deformation and Scleral Canal Expansion: Independent or Related?,” Invest. Ophthalmol. Visual Sci., 52(12), pp. 9023–9032. 10.1167/iovs.11-8183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37]. Norman, R. E. , Flanagan, J. G. , Sigal, I. A. , Rausch, S. M. , Tertinegg, I. , and Ethier, C. R. , 2011, “Finite Element Modeling of the Human Sclera: Influence on Optic Nerve Head Biomechanics and Connections With Glaucoma,” Exp. Eye Res., 93(1), pp. 4–12. 10.1016/j.exer.2010.09.014 [DOI] [PubMed] [Google Scholar]
- [38]. Burgoyne, C. F. , and Downs, J. C. , 2008, “Premise and Prediction–How Optic Nerve Head Biomechanics Underlies the Susceptibility and Clinical Behavior of the Aged Optic Nerve Head,” J. Glaucoma, 17(4), pp. 318–328. 10.1097/IJG.0b013e31815a343b [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. McBrien, N. A. , Jobling, A. I. , and Gentle, A. , 2009, “Biomechanics of the Sclera in Myopia: Extracellular and Cellular Factors,” Optom. Vision Sci., 86(1), pp. E23–E30. 10.1097/OPX.0b013e3181940669 [DOI] [PubMed] [Google Scholar]
- [40]. Summers Rada, J. A. , Shelton, S. , and Norton, T. T. , 2006, “The Sclera and Myopia,” Exp. Eye Res., 82(2), pp. 185–200. 10.1016/j.exer.2005.08.009 [DOI] [PubMed] [Google Scholar]
- [41]. Myers, K. M. , Coudrillier, B. , Boyce, B. L. , and Nguyen, T. D. , 2010, “The Inflation Response of the Posterior Bovine Sclera,” Acta Biomater., 6(11), pp. 4327–4335. 10.1016/j.actbio.2010.06.007 [DOI] [PubMed] [Google Scholar]
- [42]. Tonge, T. , Murienne, B. , Coudrillier, B. , Alexander, S. , Rothkopf, W. , and Nguyen, D. , 2013, “Minimal Preconditioning Effects Observed for Inflation Tests of Planar Tissues,” ASME J. Biomech. Eng., 135(11), p. 114502. 10.1115/1.4025105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43]. Ke, X.-D. , Schreier, H. , Sutton, M. , and Wang, Y. , 2011, “Error Assessment in Stereo-Based Deformation Measurements,” Exp. Mech., 51(4), pp. 423–441. 10.1007/s11340-010-9450-3 [DOI] [Google Scholar]
- [44]. Fazzini, M. , Mistou, S. , and Dalverny, O. , 2010, “Error Assessment in Image Stereo-Correlation,” EPJ Web of Conferences, Vol. 6, EDP Sciences, p. 31009. 10.1051/epjconf/20100631009 [DOI] [Google Scholar]
- [45]. Boote, C. , Dennis, S. , Huang, Y. , Quantock, A. J. , and Meek, K. M. , 2005, “Lamellar Orientation in Human Cornea in Relation to Mechanical Properties,” J. Struct. Biol., 149(1), pp. 1–6. 10.1016/j.jsb.2004.08.009 [DOI] [PubMed] [Google Scholar]
- [46]. Boote, C. , Hayes, S. , Abahussin, M. , and Meek, K. M. , 2006, “Mapping Collagen Organization in the Human Cornea: Left and Right Eyes Are Structurally Distinct,” Invest. Ophthalmol. Visual Sci., 47(3), pp. 901–908. 10.1167/iovs.05-0893 [DOI] [PubMed] [Google Scholar]
- [47]. Ren, R. , Wang, N. , Li, B. , Li, L. , Gao, F. , Xu, X. , and Jonas, J. B. , 2009, “Lamina Cribrosa and Peripapillary Sclera Histomorphometry in Normal and Advanced Glaucomatous Chinese Eyes With Various Axial Length,” Invest. Ophthalmol. Visual Sci., 50(5), pp. 2175–2184. 10.1167/iovs.07-1429 [DOI] [PubMed] [Google Scholar]
- [48]. Norman, R. E. , Flanagan, J. G. , Rausch, S. M. , Sigal, I. A. , Tertinegg, I. , Eilaghi, A. , Portnoy, S. , Sled, J. G. , and Ethier, C. R. , 2010, “Dimensions of the Human Sclera: Thickness Measurement and Regional Changes With Axial Length,” Exp. Eye Res., 90(2), pp. 277–284. 10.1016/j.exer.2009.11.001 [DOI] [PubMed] [Google Scholar]
- [49]. Vurgese, S. , Panda-Jonas, S. , and Jonas, J. B. , 2012, “Scleral Thickness in Human Eyes,” PloS One, 7(1), p. e29692. 10.1371/journal.pone.0029692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50]. Jonas, J. B. , and Holbach, L. , 2005, “Central Corneal Thickness and Thickness of the Lamina Cribrosa in Human Eyes,” Invest. Ophthalmol. Visual Sci., 46(4), pp. 1275–1279. 10.1167/iovs.04-0851 [DOI] [PubMed] [Google Scholar]
- [51]. Girard, M. J. , Suh, J.-K. F. , Bottlang, M. , Burgoyne, C. F. , and Downs, J. C. , 2011, “Biomechanical Changes in the Sclera of Monkey Eyes Exposed to Chronic IOP Elevations,” Invest. Ophthalmol. Visual Sci., 52(8), pp. 5656–5669. 10.1167/iovs.10-6927 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52]. Grytz, R. , Fazio, M. A. , Girard, M. J. , Libertiaux, V. , Bruno, L. , Gardiner, S. , Girkin, C. A. , and Crawford Downs, J. , 2014, “Material Properties of the Posterior Human Sclera,” J. Mech. Behav. Biomed. Mater. 29, pp. 602–617. 10.1016/j.jmbbm.2013.03.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53]. Seshaiyer, P. , and Humphrey, J. D. , 2003, “A Sub-Domain Inverse Finite Element Characterization of Hyperelastic Membranes Including Soft Tissues,” ASME J. Biomech. Eng., 125(3), pp. 363–371. 10.1115/1.1574333 [DOI] [PubMed] [Google Scholar]
- [54]. Raghupathy, R. , and Barocas, V. H. , 2010, “Generalized Anisotropic Inverse Mechanics for Soft Tissues,” ASME J. Biomech. Eng., 132(8), p. 081006. 10.1115/1.4001257 [DOI] [PubMed] [Google Scholar]
- [55]. Pinsky, P. M. , van der Heide, D. , and Chernyak, D. , 2005, “Computational Modeling of Mechanical Anisotropy in the Cornea and Sclera,” J. Cataract Refractive Surg., 31(1), pp. 136–145. 10.1016/j.jcrs.2004.10.048 [DOI] [PubMed] [Google Scholar]
- [56]. Brown, C. , Vural, M. , Johnson, M. , and Trinkaus-Randall, V. , 1994, “Age-Related Changes of Scleral Hydration and Sulfated Glycosaminoglycans,” Mech. Ageing Dev., 77(2), pp. 97–107. 10.1016/0047-6374(94)90018-3 [DOI] [PubMed] [Google Scholar]
- [57]. Eilaghi, A. , Flanagan, J. G. , Tertinegg, I. , Simmons, C. A. , Wayne Brodland, G. , and Ross Ethier, C. , 2010, “Biaxial Mechanical Testing of Human Sclera,” J. Biomech., 43(9), pp. 1696–1701. 10.1016/j.jbiomech.2010.02.031 [DOI] [PubMed] [Google Scholar]
- [58]. Chen, K. , Rowley, A. P. , Weiland, J. D. , and Humayun, M. S. , 2013, “Elastic Properties of Human Posterior Eye,” J. Biomed. Mater. Res. Part A, 102(6), pp. 2001–2007. 10.1002/jbm.a.34858 [DOI] [PubMed] [Google Scholar]
- [59]. Hernandez, M. R. , Luo, X. X. , Igoe, F. , and Neufeld, A. , 1987, “Extracellular Matrix of the Human Lamina Cribrosa,” Am. J. Ophthalmol., 104(6), pp. 567–576. 10.1016/0002-9394(87)90165-6 [DOI] [PubMed] [Google Scholar]
- [60]. Quigley, H. A. , Brown, A. , and Dorman-Pease, M. E. , 1991, “Alterations in Elastin of the Optic Nerve Head in Human and Experimental Glaucoma,” Br. J. Ophthalmol., 75(9), pp. 552–557. 10.1136/bjo.75.9.552 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61]. Meek, K. M. , and Boote, C. , 2009, “The Use of X-Ray Scattering Techniques to Quantify the Orientation and Distribution of Collagen in the Corneal Stroma,” Prog. Retinal Eye Res., 28(5), pp. 369–392. 10.1016/j.preteyeres.2009.06.005 [DOI] [PubMed] [Google Scholar]
- [62]. Petsche, S. J. , and Pinsky, P. M. , 2013, “The Role of 3-D Collagen Organization in Stromal Elasticity: A Model Based on X-Ray Diffraction Data and Second Harmonic-Generated Images,” Biomech. Model. Mechanobiol., 12(6), pp. 1101–1113. 10.1007/s10237-012-0466-8 [DOI] [PubMed] [Google Scholar]
- [63]. Fazio, M. A. , Grytz, R. , Bruno, L. , Girard, M. J. , Gardiner, S. , Girkin, C. A. , and Downs, J. C. , 2012, “Regional Variations in Mechanical Strain in the Posterior Human Sclera,” Invest. Ophthalmol. Visual Sci., 53(9), pp. 5326–5333. 10.1167/iovs.12-9668 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64]. Tang, J. , and Liu, J. , 2012, “Ultrasonic Measurement of Scleral Cross-Sectional Strains During Elevations of Intraocular Pressure: Method Validation and Initial Results in Posterior Porcine Sclera,” ASME J. Biomech. Eng., 134(9), p. 091007. 10.1115/1.4007365 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65]. Morris, H. J. , Tang, J. , Cruz-Perez, B. , Pan, X. , Hart, R. T. , Weber, P. A. , and Liu, J. , 2013, “Correlation Between Biomechanical Responses of Posterior Sclera and Iop Elevations During Micro-Volumetric Change in the Eye,” Invest. Ophthalmol. Visual Sci., 54(12), pp. 7215–7222. 10.1167/iovs.13-12441 [DOI] [PMC free article] [PubMed] [Google Scholar]


