Re-examining the upper limit of temporal pitch

Abstract

Five normally-hearing listeners pitch-ranked harmonic complexes of different fundamental frequencies (F0s) filtered in three different frequency regions. Harmonics were summed either in sine, alternating sine-cosine (ALT), or pulse-spreading (PSHC) phase. The envelopes of ALT and PSHC complexes repeated at rates of 2F0 and 4F0. Pitch corresponded to those rates at low F0s, but, as F0 increased, there was a range of F0s over which pitch remained constant or dropped. Gammatone-filterbank simulations showed that, as F0 increased and the number of harmonics interacting in a filter dropped, the output of that filter switched from repeating at 2F0 or 4F0 to repeating at F0. A model incorporating this phenomenon accounted well for the data, except for complexes filtered into the highest frequency region (7800-10800 Hz). To account for the data in that region it was necessary to assume either that auditory filters at very high frequencies are sharper than traditionally believed, and/or that the auditory system applies smaller weights to filters whose outputs repeat at high rates. The results also provide new evidence on the highest pitch that can be derived from purely temporal cues, and corroborate recent reports that a complex pitch can be derived from very-high-frequency resolved harmonics.

I. INTRODUCTION

The information available to the central auditory system when estimating the pitch of a sound depends strongly on the extent to which individual components are resolved in the auditory periphery (see Moore and Gockel, 2011 for a review). When complexes are filtered so that only low harmonics (below about the eighth) are present, individual components fall in different auditory filters and are said to be spectrally resolved. The pitch may be derived by extracting information from these individual components, via place-of-excitation and/or temporal (phase locking) cues. When only very high harmonics are present (above the 14^th), several components interact within each auditory filter and the harmonics are said to be unresolved. There is no spectral cue available to the listener and the only information that can be used to estimate the pitch is the temporal pattern of auditory nerve discharges locked to the stimulus envelope. In that case, the pitch matches the rate of the waveform’s envelope and seems to be independent of its temporal fine structure. This is illustrated by the fact that a harmonic complex tone produces the same pitch as an inharmonic complex tone with the same frequency spacing in Hz between components (Moore and Moore, 2003). In addition, when the components of an unresolved complex having a fundamental frequency of F0 are summed in alternating phase (i.e. odd harmonics in sine phase, even harmonics in cosine phase), the pitch of the complex corresponds to the envelope repetition rate and matches the pitch of a complex with all its components summed in sine phase and a fundamental of 2F0 (Shackleton and Carlyon, 1994). In the remainder of this article, we will refer to this mechanism as the “purely temporal” pitch mechanism (Carlyon et al., 2008). When intermediate harmonics are present (between the 8^th and 14^th), there is still some debate as to how the pitch may be coded (place-of-excitation or temporal cues; c.f. Santurette et al., 2012).

Studies of purely temporal pitch perception in normal-hearing listeners are relevant for the coding of pitch in cochlear implant (CI) users, who have access only to temporal codes to F0. It has been shown that CI listeners can make musical intervals’ judgments or identify simple melodies when a single electrode is stimulated with constant-amplitude electrical pulse trains of different rates (Pijl and Schwarz, 1995a, b; McDermott and McKay, 1997). The upper limit of this mechanism was found to be around 300 pulses per second (pps) although several studies have shown that some CI listeners can perceive increases in pitch up to about 700-800 pps (e.g. Townshend et al., 1987; Kong and Carlyon, 2010; Carlyon et al., 2010). In a recent study, we showed that selectively stimulating the apical channel of a CI using bipolar asymmetric pulses consistently led to higher upper limits than stimulating other channels (Macherey et al., 2011). This result was consistent with animal data showing that inferior colliculus neurons are better at following high stimulation rates when they receive information from the cochlear apex (Middlebrooks and Snyder, 2010). Nevertheless, we also found that the upper limit value correlated negatively, within subjects, with the current level needed to evoke a comfortably loud percept. In other words, electrode channels for which a small amount of current was needed to produce a comfortably loud percept also conveyed temporal pitch cues up to high rates. This observation suggests that other factors (such as neural survival) may play a role in the ability of CI subjects to extract temporal pitch cues at high rates.

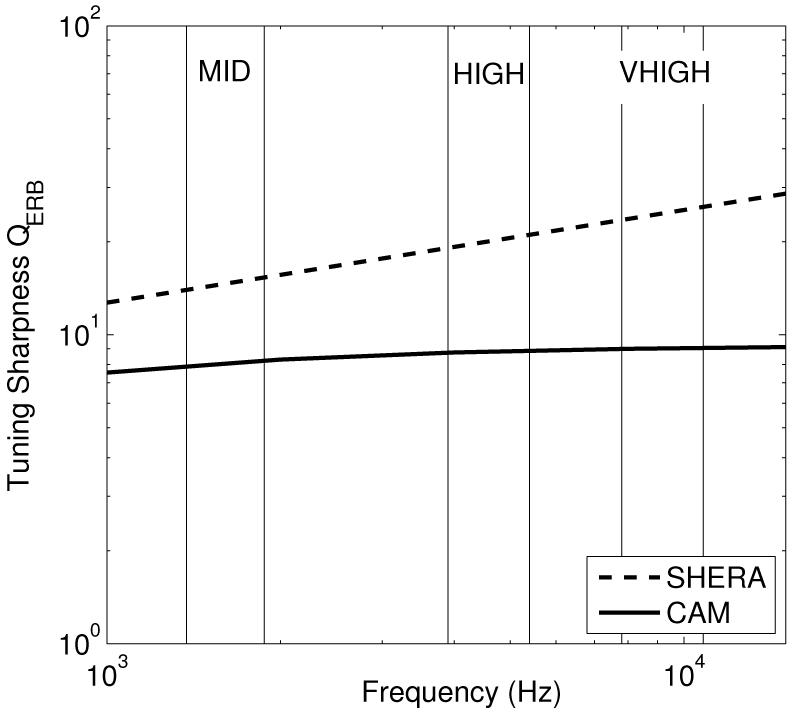
Finding the upper limit of the purely temporal pitch mechanism in normal-hearing (NH) listeners is challenging because, above a certain fundamental frequency that covaries with frequency region, harmonics fall in different auditory filters and spectral cues start to become available to the listener. To partially overcome this limitation, Carlyon and Deeks (2002) used harmonics summed in alternating phase. As previously mentioned, this produces a doubling of the envelope repetition rate compared to when all harmonics are summed in sine phase, but keeps the long-term spectrum unchanged. Carlyon and Deeks measured F0 discrimination for harmonic complexes filtered in three frequency regions (MID, HIGH and VHIGH) illustrated in Figure 1. They found that performance remained good up to higher F0s when the alternating-phase complexes were filtered in higher frequency regions. With further increases in F0, performance improved again, likely due to the presence of resolved harmonics.

Figure 1.

Tuning sharpness of auditory filters expressed as Q_ERB=CF/ERB derived from Glasberg and Moore (“CAM”, 1990) and from Shera et al. (2002). The thin vertical lines indicate the three frequency regions in which the complexes were filtered: MID (1375-1875 Hz), HIGH (3900-5400 Hz) and VHIGH (7800-10800 Hz).

There were two possible explanations for why pitch discrimination broke down at different F0s depending on frequency region. The first explanation had a peripheral basis and relates to the ringing of auditory filters. Due to their broader linear bandwidth, high-frequency filters show a shorter impulse response than lower-frequency filters. Therefore, the temporal representation of individual pulses at the output of high-frequency filters remains accurate up to higher F0s than for lower-frequency filters. Nevertheless, Carlyon and Deeks suggested that filter ringing could not be the sole explanation because the breakdown point, when expressed in terms of the ratio of the F0 over the equivalent rectangular bandwidth (ERB) of the auditory filter centered on the pass-band, was smaller for the highest-frequency region tested compared to lower regions. That calculation was based on the widely-adopted measures of auditory filter bandwidths presented by Glasberg and Moore (1990), also known as the “CAM” auditory filter bank (Hartmann, 1998). The second explanation had a more central basis. Carlyon and Deeks proposed that their results reflected an additional limitation on the temporal pitch extraction mechanism itself, namely that high repetition rates may not be effectively processed by more central parts of the auditory system. However, since the publication of Carlyon and Deeks’ article, Shera et al (2002) have presented evidence that the Q factor of auditory filters increases at high center frequencies, unlike the “traditional” bandwidths derived by Glasberg and Moore (1990; c.f. Figure 1).

Here, we re-examine the upper limit of temporal pitch in NH listeners, and consider both whether the results can be explained using Shera et al’s revised auditory filter measurements, and the nature of any more central processing needed to account for the data. We measure pitch perception using an “optimally efficient” pitch-ranking procedure described by Long et al. (2005). This procedure has the advantage of not requiring a priori assumptions on how the pitch should vary as a function of pulse rate. In Experiment 1, we show that the function relating the pitch to the F0 can sometimes be non-monotonic for alternating-phase complexes and that there is a range of F0s for which an increase in F0 can produce a decrease in pitch. Experiment 2 shows that this pitch reversal corresponds to the transition region between so-called unresolved and resolved complexes, and, importantly, allows us to obtain a value for the highest pitch that can be derived from purely temporal cues. This value can be obtained by measuring the F0 of an alternating-phase complex that is judged to have a pitch equal to a sine-phase complex of 2F0. It differs from the measure usually used to describe the upper limit of temporal pitch, namely the highest pulse rate at which listeners can detect further increase in rate because, for example, a 10% increase in the F0 of an alternating-phase complex might be detectable even if it produces a pitch change smaller than 10% (i.e. if the sine-phase complex to which it is matched needs an increase in F0 smaller than 10% to remain pitch-matched to it). Finally, in Experiment 3, we use a novel way of summing harmonics that can produce a waveform with an envelope repetition rate of four times the F0 and measure the upper limit of temporal pitch for these harmonic complexes.

II. EXPERIMENT 1

A. STIMULI AND METHODS

Four subjects with audiometric thresholds less than 15 dB HL in the 250-8000 Hz frequency range took part in Experiment 1a. They were asked to pitch rank six sets of 400-ms bandpass-filtered harmonic complexes. The complexes in a given set differed only in F0, and the sets differed in both (1) the phase relationships between harmonics and (2) the frequency region of filtering. Two phase relationships were tested. In one condition, harmonics were summed in sine phase (SINE); in the other condition, they were summed in alternating sine-cosine phase (ALT). Three frequency regions were investigated by filtering the complexes using 8^th order Butterworth bandpass filters differing in their pass-bands: 1375-1875 Hz for the “MID” region, 3900-5400 Hz for the “HIGH” region and 7800-10800 Hz for the “VHIGH” region. For each condition, twelve harmonic complexes with F0s ranging from 50 to 582 Hz (log-spaced) were pitch-ranked separately. The complexes were presented at an overall level of 60 dB SPL. To mask distortion products, a background pink noise was presented continuously at a spectrum level of 15 dB SPL at 4 kHz. The signal-to-noise ratio was identical to that used by Carlyon and Deeks (2002) who also measured detection thresholds for the same complexes. This implies that our complexes were presented at the same sensation level of approximately 18 dB. The level of the background noise was therefore presumably sufficient to limit the influence of both quadratic and cubic difference tones (Pressnitzer and Patterson, 2001; Oxenham et al., 2009). Stimuli were generated digitally and presented to the left earpiece of a pair of Sennheiser HD650 headphones. Subjects were seated in a double-walled sound-proofed booth and had to indicate which of two sounds was higher in pitch by clicking on virtual buttons displayed on a computer screen.

We used the optimally-efficient mid-point comparison procedure which provides a way to rank a set of stimuli in a minimum number of comparisons (Long et al., 2005). The procedure was a two alternative forced choice task (2AFC) and started by selecting two stimuli at random and presenting them to the subject who was asked to indicate which one had the higher pitch. After this first trial, the provisional list contained two elements ordered in pitch. In each subsequent trial, a new target stimulus was selected at random from the remaining stimuli of the original set and was first compared to a member of the provisional list; this was always the middle-ranked stimulus, or, if the provisional list had an even number of members, the stimulus with the next-lowest rank. If the target was higher in pitch than this middle-ranked stimulus, it was then compared to the middle-ranked stimulus of the higher-pitched half of the provisional list. The provisional list was further bisected to find the pitch rank of the target stimulus. Once found, the provisional list was updated and another target stimulus was ranked. This procedure continued until all stimuli were ranked. For each condition, this procedure was repeated at least 12 times, leading to a mean rank and a standard error of the mean for each stimulus.

Because the range of F0s did not extend sufficiently to cover completely resolved harmonics in the VHIGH region, Experiment 1b repeated the experiment in the VHIGH region using 9 harmonic complexes with F0s ranging from 191 to 1137 Hz in logarithmic steps. This additional condition was only performed for the ALT phase relationship. Three normal-hearing subjects (S1-S3) took part.

B. RESULTS AND DISCUSSION

The left, center and right panels of Figure 2 show, for the four subjects, the mean pitch rank as a function of F0 for the MID, HIGH and VHIGH regions, respectively. For the SINE complexes (filled squares), all functions monotonically increase as a function of F0. For the ALT complexes (open circles), the pitch increases up to a certain F0, above which it shows a plateau or decreases. At higher F0s, the pitch increases again. The arrows in Figure 2 point to the frequency above which there is a numerical decrease of the mean pitch rank for the ALT complex. This pitch reversal was significant (p<0.05) for subjects S1, S3 and S4 in the HIGH region, and only for subject S3 in the VHIGH region, as shown by paired-sample t-tests performed on the ranks obtained at the start- and end-frequencies of the decreasing part of the function. The pitch reversal was not significant in the MID region. Although only the reversals for S1 and S3 in the HIGH region remained significant after correcting for multiple comparisons (Bonferroni), the effects observed will be corroborated by experiments 2 and 3. Averaging the pitch ranks across all subjects, there was a numerical decrease in mean pitch rank between F0s of 98 and 122 Hz for the MID region, 238 and 373 Hz for the HIGH region and 373 and 466 Hz for the VHIGH region.

Figure 2.

Results of Experiment 1a for four subjects (S1-S4) and three frequency regions (MID, HIGH and VHIGH). Each panel shows the mean pitch rank (+/− 1 standard error) as a function of F0 for both SINE and ALT complexes. Each arrow points to the F0 above which there was a numerical decrease in pitch rank.

These data can be compared to those obtained by Carlyon and Deeks (2002) who tested F0 discrimination in the same frequency regions as used here. They reported that the F0s at which pitch discrimination broke down (i.e. the F0s at which discrimination thresholds were larger than 20%) for ALT complexes were 150, 300 and 424 Hz, respectively, for the MID, HIGH and VHIGH regions. These F0s seem to match the decreasing arm of the pitch functions for the HIGH [238-373 Hz] and VHIGH [373-466 Hz] regions, which are the two regions for which the reversals were significant for some of the subjects (Table 1). This suggests that, at least for these two high-frequency regions, the break-down in performance observed by Carlyon and Deeks may have sometimes been due to a pitch reversal.

Table 1.

Summary of results for experiments 1-3. Values of F0s are expressed in Hz. Corresponding envelope repetition rate values (F0 times 2 [×2] for ALT or times 4 [×4] for PSHC) are shown between brackets in pulses per second (pps). Except otherwise stated, the the reversal/plateau regions correspond to a reversal for all subjects.

	MID	HIGH	VHIGH
Carlyon & Deeks breakdown	150 Hz	300 Hz	424 Hz
Expt 1 start of ALT plateau/drop	78-98 Hz (mean S1-S3=98 Hz)	238-298 Hz (mean S1-S3=278 Hz)	373 Hz
[X 2]	[156-196 pps]	[476-596 pps]	[746 pps]
Expt 1 end of ALT plateau/drop	98-153 Hz (mean S1-S3=132 Hz)	373-466 Hz (mean S1-S3=402 Hz)	582 Hz
Expt 2a 50% point (mean S1-S3)	121 Hz	322 Hz	422 Hz
Expt 2b start of ALT plateau/drop		252-317 Hz (mean S1-S3=274 Hz)	31 5-397 Hz (mean S1-S3=342 Hz)
[X 2]		[504-634 pps]	[630-794 pps]
			Plateau for all, breakpoint not very well defined.
Expt 2b Highest F0 where ALT(F0) = SINE(2F0)		252 Hz	315 Hz
[X 2]		[504 pps]	[630 pps]
Expt 2b Lowest F0 where ALT(F0) = SINE(F0)		400-504 Hz (mean S1-S3=467 Hz)	630-794 Hz (mean S1-S3=735 Hz)
Expt 3a start of PSHC drop		122-153 Hz (mean=143 Hz)	191-238 Hz (mean=207 Hz)
[X 4]		[488-712 pps]	[764-952 pps]
Expt 3a end of PSHC drop		238 Hz	298-373 Hz (mean=346 Hz)
Expt 3b start of PSHC drop		159 Hz	198 Hz
[X 4]		[636 pps]	[792 pps]
			Plateau for S2
Expt 3b start of ALT plateau/drop		252-317 Hz (mean=274 Hz)	3 15-397 Hz (mean=342 Hz)
[X 2]		[504-634 pps]	[630-794 pps]
		Plateau for S1,S2	Plateau for all
Expt 3b Highest F0 where PSHC(F0) =ALT(2F0)		126-159 Hz (mean=147 Hz)	1 57-250 Hz (mean=198 Hz)
[X 2]		[252-318 pps]	[314-500 pps]
[X 4]		[504-636 pps]	[628-1000 pps]
			Plateau for S2

To gain insight into the causes of these pitch reversals, simulations were performed using an implementation of the gammatone filterbank (Slaney, 1994) whose bandwidths are similar to those described by the CAM formula (Glasberg and Moore, 1990). Figure 2A shows the outputs of two simulated auditory filters centered on the edges of the passband of the MID region for two stimuli having different F0s. The two F0s (98 and 122 Hz) were chosen to be at the start and end of the decreasing arm/plateau of the pitch function, respectively. Figures 3B and 3C show the simulation results for the HIGH and VHIGH regions, respectively, for corresponding F0s. The top rows of each part of the figure show that, at the lower F0, the envelope rate of the ALT complex is equal to twice the F0 for all frequency regions and for both auditory filters. The bottom rows show that, at the higher F0, for both the MID and HIGH regions, an auditory filter centered on the upper edge of the passband (right-hand panels) still beats at 2F0. However, an auditory filter centered on the lower edge (left panels) beats at F0. This can be explained by the presence of only two harmonics interacting within the lower-frequency auditory filter; when only two harmonics are combined, they will beat at a rate equal to F0, regardless of their phase relationship. It is only when three or more harmonics are present that the envelope of an ALT complex repeats at 2F0. This observation also provides a possible explanation for why the pitch sometimes went down with increases in F0 for ALT complexes. As the F0 increases from x to y, the repetition rate at the output of a given auditory filter will change from 2x to y, and so if y<2x the repetition rate will drop. Depending on how the subjects combine the outputs of different filters to make their pitch judgments, this could cause the pitch to decrease. This possibility will further be investigated in Section V.

Figure 3.

A, Outputs of two auditory filters centered on the lower-edge (1375 Hz) and upper-edge (1875 Hz) frequencies of the MID region for two different F0s (98 and 122 Hz). The dashed horizontal line shows the duration corresponding to a period of F0 while the solid horizontal line shows the duration corresponding to a period of 2F0; B, Same as (A) but for the HIGH region and for different F0s (238 and 373 Hz); C, Same as (A) but for the VHIGH region and for different F0s (373 and 466 Hz).

While the simulations may explain the psychophysical results obtained in the MID and HIGH regions, they cannot account for the results obtained in the VHIGH region. In this case, even for F0s within the decreasing arm of the pitch function, both auditory filters still beat at 2F0 (c.f. F0=466 Hz in Figure 2C). Consistent with the bandwidths given by the CAM formula, the F0 at which the auditory filter centered on the lower edge of the pass-band of the VHIGH region (7800 Hz) beats at F0 for ALT is approximately 600 Hz (i.e. about twice the F0 at which it occurs in the HIGH region). Simulations using different auditory filterbanks will also be presented in Section V.

Figure 4 shows the results of Experiment 1b using the extended range of F0s in the VHIGH region for ALT complexes (including F0s higher than 600 Hz). Interestingly, the functions all show a plateau between 373 and 466 Hz, even for S3 who previously showed a reversal. For higher frequencies, the pitch monotonically increases. This strongly suggests that there is some ambiguity associated with the pitch in this transition region (sometimes showing a pitch reversal as in Experiment 1a for S3, sometimes a plateau). The fact that this plateau/ambiguity region starts at a relatively lower frequency in the VHIGH region than predicted by the simulations may have two different reasons: (1) First, there is some evidence that auditory filters may be narrower than predicted by the CAM formula at these high frequencies (Shera et al., 2002). If this was the case, this would lower the F0 above which fewer than three harmonics are interacting in auditory filters at the lower edge of the pass-band. Therefore, it would lower the F0 above which some filters repeat at F0 and not at 2F0 in response to an ALT complex, thereby potentially inducing a pitch decrease or plateau; (2) Second, as suggested by Carlyon and Deeks (2002), there may be a limitation in the way temporal pitch cues are encoded at these relatively high rates. If so, even if all filters still beat at 2F0 in response to an ALT complex, these relatively fast temporal cues may not be effectively conveyed to more central parts of the auditory system, thereby leading to a pitch plateau. These possible explanations are further investigated and discussed in Experiments 2 and 3.

Figure 4.

Results of Experiment 1b for three subjects (S1-S3) showing the mean pitch rank (+/− 1 standard error) as a function of F0 for ALT complexes filtered in the VHIGH region.

III. EXPERIMENT 2

A. RATIONALE AND METHODS

Experiments 2a and 2b were designed to check whether the pitch reversal and/or plateau corresponded to the transition region between unresolved and resolved harmonics as defined in previous publications, and to estimate the highest pitch that can be derived from purely temporal cues.

First, as in Shackleton and Carlyon (1994), Experiment 2a used a 2AFC task. In each interval, the ALT complex was followed by a SINE complex at either the same F0 or at 2F0. The subject was asked to indicate in which of the two pairs the pitches of the sounds were most similar. Subjects S1-S3 took part. Five log-spaced F0s were selected for each frequency region (78 to 191 Hz for the MID, 191 to 466 Hz for the HIGH, and 238 to 582 Hz for the VHIGH region) and the five trials were mixed in blocks of 100 comparisons. Four blocks per frequency region were performed, leading to a total of 80 trials per point. When the complex only contains unresolved harmonics, an ALT stimulus at F0 has the same pitch as a SINE complex at 2F0. Conversely, when the complex only contains resolved harmonics, ALT and SINE elicit the same pitch when compared at the same F0.

Second, in Experiment 2b, 4 subjects (S1-S3 and S5) participated in a similar pitch ranking experiment as in Experiment 1a except that both SINE and ALT complexes were mixed in the same block of trials. This allowed us directly to compare the pitches of SINE and ALT complexes, and to estimate the highest pitch that can be derived from purely temporal cues; this was defined as the F0 of a SINE complex having a pitch equal to that of an ALT complex having half that F0 – and, therefore, the same envelope repetition rate. Only the HIGH and VHIGH regions were investigated. For the HIGH region, nine SINE complexes with F0s ranging from 200 to 1252 Hz and six ALT complexes with F0s from 200 to 635 Hz were mixed in the same block of trials. For the VHIGH region, the F0s of the SINE complexes ranged from 250 to 1587 Hz and that of the ALT complexes ranged from 250 Hz to 794 Hz. The ratio between consecutive F0s was 2^1/3 so that it was possible to compare each ALT complex to a SINE complex at the same F0 and to a SINE complex at 2F0. All subjects performed at least 15 blocks per frequency region.

B. RESULTS AND DISCUSSION

Figure 5 shows the results of Experiment 2a. Logistic functions were fitted to the data to obtain an estimate of the transition F0, defined as the F0 at which listeners judged the ALT complex to have the same F0 as the SINE complex on 50% of trials. Averaged across subjects, this transition F0 was 121, 322 and 424 Hz for the MID, HIGH and VHIGH region, respectively. As shown in Table 1, these values are consistent both with the pitch reversals/plateaus observed in experiment 1, and with the F0s at which discrimination performance broke down in the study by Carlyon and Deeks (2002). The transition F0 is also consistent with the results of experiment 2b, which are plotted in Figure 6. These show reversals for the ALT stimuli in the HIGH region starting at 252-317 Hz, and plateaus in the VHIGH region starting at between 315-397 Hz (Table 1). The fact that the transition F0 in the VHIGH region is less than twice that in the HIGH region replicates those findings, but does not distinguish between the two possible explanations – sharper filters in the VHIGH region or a central pitch limitation.

Figure 5.

Results of Experiment 2a for three subjects (S1-S3) showing the proportion of trials where an ALT complex presented at F0 was judged more similar to a SINE complex presented at 2F0 than to a SINE complex presented at F0. The symbols show the data points for each frequency region. The dash-dotted, solid and dotted lines show the logistic functions fitting the data points for the MID, HIGH and VHIGH regions, respectively. The points of subjective equality were 128, 305, and 405 Hz for S1, 109, 281, and 391 Hz for S2, 128, 389, and 482 Hz for S3, respectively for the MID, HIGH, and VHIGH regions.

Figure 6.

Results of Experiment 2b for four subjects (S1-S3 and S5) and two frequency regions (HIGH and VHIGH). Each panel shows the mean pitch rank (+/− 1 standard error) as a function of F0 for SINE and ALT complexes when presented in the same block of trials. The dashed line shows the rank of the ALT complexes translated horizontally so that they are plotted as a function of their pulse rate (i.e., 2F0).

Evidence on the highest pitch that can be perceived using purely temporal cues comes from a comparison of the pitch-ranking functions for the SINE and ALT stimuli. Specifically, when an ALT complex has a pitch equal to that of a SINE complex with an F0 one octave lower, we can conclude that the pitch of the ALT complex is determined by the repetition rate of the envelope. Although the pitch-ranking functions for the ALT and SINE complexes are plotted separately, the pitch-ranking procedure was performed using the combination of all ALT and SINE stimuli for a given frequency region. To facilitate comparisons, therefore, the rankings for the ALT stimuli (circles), shifted horizontally by a factor of 2, have been re-plotted as dashed lines with no symbols. In the VHIGH region, it can be seen that an ALT stimulus with an F0 of 315 Hz is ranked equal in pitch to a SINE complex of 630 Hz. This places a lower limit on the maximum pitch that can be perceived using purely temporal cues; that limit is 630 Hz, equal to the pulse rate of the ALT complex. Above this value the pitch-ranking function for the ALT stimuli is at a plateau; if this is due to the effects of auditory filtering then the highest limit for purely temporal pitch may be somewhat higher.

IV. EXPERIMENT 3

A. RATIONALE AND METHODS

As previously stated, one difficulty in assessing the upper limit of temporal pitch arises from the presence of resolved components above a certain F0 that co-varies with frequency region. Experiment 3 employed a novel method that generates harmonic complexes with arbitrary pulse rates and a fixed F0, with the aim of increasing the range of rates where pitch judgments are based on purely temporal cues. This method extends the principle of ALT complexes to produce higher pulse rates whilst keeping the long-term spectrum of the stimulus unchanged. We have called this stimulus a pulse-spreading harmonic complex (PSHC), as it provides a way to evenly spread pulses across the period of the complex (Hilkhuysen and Macherey, 2014). It is obtained by summing harmonically-related components so that the envelope rate of the stimulus is a multiple of the F0. To illustrate how these stimuli are generated, let us assume a harmonic complex with an F0 of 50 Hz. If we sum the odd harmonics with the same phase (e.g. sine), the resulting stimulus is an inharmonic tone with a pseudo-period of 10 ms (Figure 7A): the true fundamental frequency is 50 Hz but it exhibits 1 “pulse” every 10 ms. In this case, two consecutive pulses (O and O’) have different fine structures. If we sum separately the even harmonics also with the same phase (e.g. cosine), the resulting stimulus is a harmonic complex of 100 Hz, with one pulse (E) every 10 ms (Figure 7B). These two resulting stimuli can then be summed by imposing a relative delay between them so that the final stimulus (O-E-O’-E) has one pulse every 5 ms but still an F0 of 50 Hz (Figure 7C). Consequently, the envelope repetition rate is four times the F0. Consistent with Hilkhuysen and Macherey (2014), this results in what we call a 2^nd-order PSHC stimulus whose mathematical formulation is given in Equation (1) for a complex made of harmonics 1 to N (N is even)¹.

$$PSHC\left(t\right)=\sum _{j=1}^{N∕2}\cos \left(2\pi \left(2j\right)f_{0}t+2\pi \frac{2j}{4}\right)+\sum _{j=1}^{N∕2}\sin \left(2\pi \right(2j-1\left)f_{0}t\right)$$ (Eq.1)

Figure 7.

Illustration of the generation of a PSHC complex. A, waveform obtained by summing the odd harmonic components of a 50-Hz complex tone (in sine phase); B, waveform obtained by summing the even harmonic components of the same complex tone (in cosine phase); C, waveform obtained by summing the odd and even harmonic components of the same complex tone so that the waveform shown in B is translated by a quarter of a period (i.e., 5 ms). The waveform appears as having a repetition rate of 200 pulses per second.

Subjects S1 to S3 took part in two experiments using PSHC stimuli. In Experiment 3a, they compared the pitch of twelve PSHC stimuli having different F0s separately for the HIGH and the VHIGH regions. The F0s were the same as in Experiment 1a. The task was also identical. In Experiment 3b, they compared the pitch of PSHC and ALT stimuli in the same blocks of trials. Once more, the mid-point comparison procedure was used to pitch rank 15 different stimuli separately for the HIGH and VHIGH regions. As in Experiment 2b, the ratio between consecutive F0s was 2^1/3 so that it was possible to compare each PSHC complex to an ALT complex at the same F0 and to an ALT complex at 2F0. For the HIGH region, 9 ALT complexes with F0s ranging from 100 to 625 Hz and 6 PSHCs with F0s from 100 to 317 Hz were mixed in the same block of trials. For the VHIGH region, the F0s of the ALT complexes ranged from 125 to 794 Hz and that of the PSHC ranged from 125 Hz to 397 Hz. At least 15 blocks were performed per frequency region.

B. RESULTS AND DISCUSSION

The results of experiment 3a are plotted in Figure 8, which shows the pitch rank for PSHC stimuli as a function of F0 for subjects S1-S3. All functions show a clear non-monotonic pattern. The starting F0 of the decreasing part of the function was 153 Hz for the HIGH region and 191 Hz for the VHIGH region. Note that the non-monotonicity was significant even in the VHIGH region, where, in experiments 1 and 2, the ALT stimuli showed a plateau. This is important because, unlike a plateau, a non-monotonicity cannot be explained solely by a central limitation, and points strongly to an influence of auditory filtering. Moreover, the F0 at which pitch starts to decrease in the VHIGH region, 198 Hz, is considerably less than twice the corresponding value in the HIGH region – as would be predicted by the “traditional” function relating auditory filter bandwidth to center frequency (CF; Glasberg and Moore, 1990). Hence, unlike the data obtained with ALT stimuli in Experiments 1 and 2, the PSHC data clearly reveal the effects of a limitation that must be strongly influenced by the filtering performed, presumably, by the peripheral auditory system. Section V considers the extent to which any additional, more central, limitations are necessary to account for the data.

Figure 8.

Results of Experiment 3a showing for three subjects (S1-S3) and two frequency regions (HIGH and VHIGH) the mean pitch rank (+/− 1 standard error) as a function of F0 for PSHC complexes.

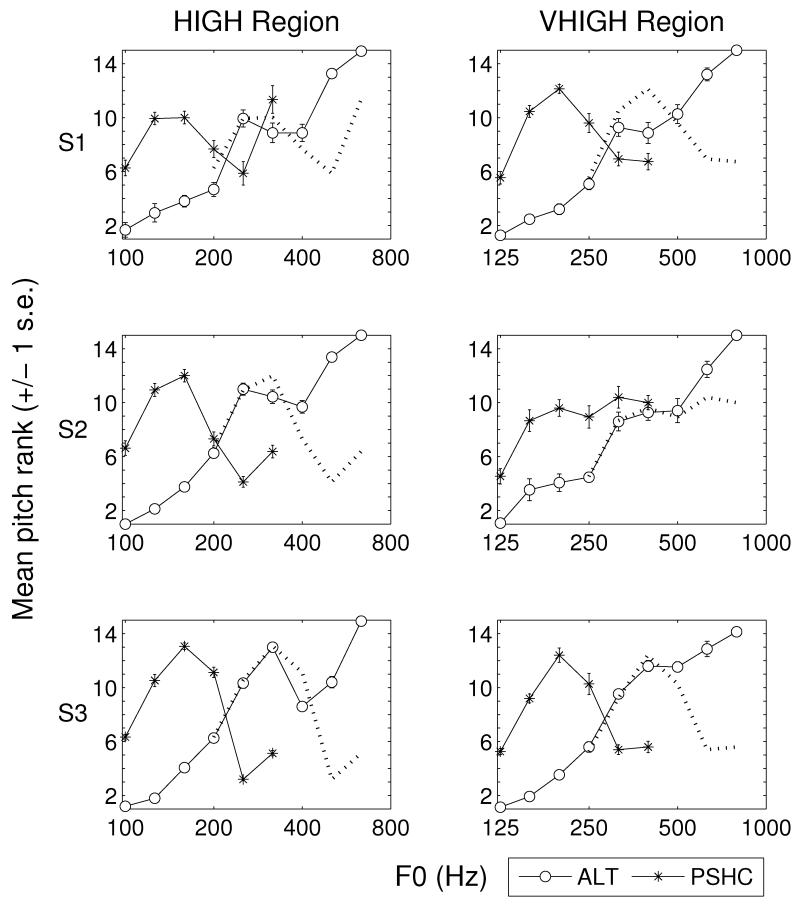
Figure 9 shows the results of Experiment 3b, in which the PSHC and ALT stimuli were pitch-ranked together. The F0s at which the non-monotonicities and plateaus occur are summarized in Table 1 and are generally consistent with the results of experiments 1, 2, and 3a. An interesting finding, which we discuss below, is that there is a range of F0s, in both frequency regions, where the pitch of a PSHC complex is lower than that of an ALT complex having the same F0; that is, the functions cross.

Figure 9.

Results of Experiment 3b for three subjects (S1-S3) and two frequency regions (HIGH and VHIGH). Each panel shows the mean pitch rank (+/− 1 standard error) as a function of F0 for ALT and PSHC complexes when presented in the same block of trials. The dashed line shows the rank of the PSHC complexes translated horizontally so that they are plotted as a function of 4F0.

Figure 10 shows the output of an auditory filter, with a bandwidth derived from the CAM formula, centered on 4589 Hz (the geometric center of the HIGH band) in response to ALT and PSHC stimuli of a range of F0s. At the lowest F0s (top and second rows), the auditory filter output beats at a rate of 2F0 for the ALT complex, and at 4F0 for the PSHC stimulus. At the highest F0 (bottom row), the auditory filter output beats at F0 for both complexes. Note that, for the PSHC stimulus, there is no F0 at which the auditory filter output beats at 2F0; the envelope repetition rate is always either F0 or 4F0. Note also that the F0 at which the envelope repetition rate drops to F0 is higher for the ALT stimulus than for the PSHC stimulus. For example, at an F0 of 317 Hz (third row), the repetition rate has already dropped to F0 for the PSHC complex, but is still equal to 2F0 for the ALT complex. Hence, there is a range of F0s where the auditory filter output beats at a rate of 2F0 for ALT, but at F0 for PSHC. Furthermore, the envelope repetition rate at an F0 of 317 Hz is lower for the PSHC stimulus than for the ALT stimulus, whereas the opposite is true at lower F0s, consistent with the data in Figure 9. Section V provides a more detailed investigation of this finding.

Figure 10.

Outputs of an auditory filter centered in the middle (4589 Hz) of the HIGH region for ALT (left panels) and PSHC (right panels) stimuli for four different F0s (ranging from 100 Hz to 400 Hz) and. The dashed horizontal line shows the duration corresponding to a period of F0 while the solid horizontal line shows the duration corresponding to a period of 2F0 in the left panels and 4F0 in the right panels.

V. SIMULATIONS USING AN AUTOCORRELATION MODEL

A. RATIONALE AND METHODS

To provide further insights into the mechanisms responsible for the pattern of results observed in Experiment 3, we implemented a simple autocorrelation model of pitch. Each signal passed through the model was 200-ms long and was first filtered by three different auditory filterbanks. The filterbanks included (1) the gammatone implementation of Slaney (1994) with CAM bandwidths, (2) the same gammatone implementation with a CF-dependent Q factor as given by Shera et al’s formula Q = β x^a with β=12.7, α=0.3 and x the CF (in kHz), and (3) an implementation of the human dual-resonance non-linear filterbank (DRNL filterbank; Lopez-Poveda and Meddis, 2001). For the DRNL case, the waveforms were first scaled at the appropriate level and passed through the outer and middle ear transfer functions used by Lopez-Poveda and Meddis (2001).

For each filterbank, 30 filters evenly spaced on an ERB scale were simulated. Their CFs ranged from 1/3^rd of octave below the lower cut-off frequency of the input stimulus to 1/3^rd octave above the higher cut-off frequency. Components outside this range are attenuated by more than 19 dB by the bandpass filter. Given the complexes were presented at approximately 18 dB SL, it is very unlikely that these remote components would contribute to the pitch.

The Hilbert envelope of each filter’s output was extracted and the unbiased autocorrelation function of a middle 100-ms segment of each envelope was calculated. This was to avoid the contamination of the autocorrelation computation by the onset of the Hilbert transform. The amplitudes of the peaks of each autocorrelation function were weighted following the approach of Pressnitzer et al. (2001). The weighting decreased linearly from 1 for a peak at a lag of 0 to 0 for a peak at a lag of 33 ms, meant to represent the lower limit of pitch. This weighting function had the effect of increasing the amplitude of the peaks at multiples of F0 relative to the amplitude of the peak at F0. The frequency of the highest peak in each autocorrelation function was assumed to correspond to the “pitch” conveyed by this auditory filter. This procedure was repeated for each simulated filter and the geometric mean of the “pitches” conveyed by all filters was taken as the predicted pitch for the signal. Note that a limitation of this model is that it would not be able to predict the pitch of complexes only containing completely resolved harmonics for which the outputs of all filters will consist of sinusoids having a constant envelope. The model was applied to the ALT and PSHC stimuli used in experiment 3, as these included the most striking pitch reversals. Simulations were obtained for the HIGH and VHIGH regions and for F0s ranging from 50 to 900 Hz.

B. RESULTS AND DISCUSSION

The predicted pitch for the gammatone filter bank with CAM bandwidths is plotted as a function of F0 for both ALT and PSHC stimuli in figure 11A for the HIGH and 11B for the VHIGH region. The vertical solid and dashed lines represent the F0s at which the pitch reversal started and ended for the PSHCs of Experiment 3a (averaged across subjects, c.f. Table 1).

Figure 11.

Predictions of pitch percepts based on the geometric or weighted mean of the envelope repetition rates extracted from each filter outputs. A-B, Predictions obtained using a gammatone filterbank with bandwidths consistent with the CAM formula in the HIGH and VHIGH regions. C-D, Same as A-B using the DRNL filterbank. E-F, Same as A-B using a gammatone filterbank with bandwidths consistent with the formula given by Shera et al. (2002). G-H, Same as C-D including an upper limit of temporal pitch. In this case, the pitch prediction corresponds to the weighted mean of the frequencies of the first peak detected in the autocorrelation functions. For repetition rates below 630 Hz, the weight is 1. For repetition rates above 1000 Hz, the weight is 0. For intermediate rates, the weight follows a linear function as a function of log(rate).

Qualitatively, this simple model captures several aspects of the data. First, it provides an explanation for why we always observed a pitch reversal for the PSHC stimuli but sometimes a plateau for the ALT stimuli. As discussed in section IV.B, as the F0 of a PSHC complex is increased, the envelope rate at the output of an auditory filter changes abruptly from 4F0 to F0, whereas for an ALT complex there is a smaller change from 2F0 to F0. These transitions will occur at different F0s over the range of auditory filters with different CFs that respond to each stimulus. Hence, for a given change in F0 the envelope rate will change for some filters and not others. If, as assumed here, subjects’ pitch judgments are based on some average of the outputs of different auditory filters, then this average should show a larger drop when, for those filters whose envelope rates do change, that change is by a factor of four (PSHC stimuli) than a factor of two (ALT stimuli). Second, in line with the filter outputs shown in figure 10, there is a range of F0s for which the PSHC beats at a lower rate than ALT.

Quantitatively, the model can account for most observations made in the HIGH region. The F0 at which the pitches of ALT and PSHC cross is close to 200 Hz, similar to the crossover obtained in the data (figure 9). Furthermore, the simulations show a clear reversal for PSHC at similar F0s as in the pitch ranking data. However, the model only predicts a plateau for ALT and not a reversal as mainly observed in Experiments 1, 2 and 3.

The predictions for the VHIGH region (Figure 11B) are much less satisfactory. The two functions cross at an F0 of 400 Hz whereas the crossover is about 280 Hz in the data. In addition, the F0 at which the PSHC reversal starts is 1.86 times higher than that at which it starts in the HIGH region (close to the 1.95 factor we would expect based on the ratio of ERBs taken in the center of each band). In contrast, the psychophysical data of Experiment 3 showed that the F0 at which pitch started to drop was only 1.25 times higher in the VHIGH than in the HIGH region; a very similar ratio of 1.24 was observed in experiments 2 and 3b for the ALT stimuli (although note that these showed a plateau rather than a reversal in the VHIGH region).

Figures 11C and 11D show the pitch predictions using the DRNL filterbank. When calibrated at the level at which the experiments were performed (i.e. 60 dB SPL), the model also provides a good account for the data. In particular, the F0 at which the pitch for PSHC starts to decrease is lower than for the gammatone, particularly in the VHIGH region and, consequently, brings the predictions closer to the observations. This may be due to the fact that the DRNL filters (“average filterbank” parameters, c.f. Table III in Lopez-Poveda and Meddis, 2001) are slightly narrower at high frequencies (around 8 kHz) than the CAM filters. Additional simulations (not shown) showed very similar results at lower levels. Above 80 dB SPL, however, the bandwidth of the DRNL filters becomes broader and the pitch reversals are, therefore, shifted towards higher F0s.

Figures 11E and 11F show the results of simulations performed using the gammatone filterbank with a CF-dependent Q factor as given by Shera et al’s formula. The filters appear to be much too narrow overall to qualitatively account for the data. In both frequency regions, the predicted reversal/plateau starts and ends at lower F0s than observed in experiment 3. According to the formula that Shera et al. fitted to their data, the ERB of an auditory filter centered on 9178 Hz (the geometric center of the VHIGH band) is between 1.49 and 1.64 times wider than that centered on 4589 Hz (center of the HIGH band). Not surpisingly, the ratio between the F0s at which the reversal starts in the VHIGH and HIGH regions in the model results is consistent with this formula and is equal to 1.51. Even though this ratio is more similar to the 1.25 found in the psychophysical data than the ratio predicted by the filterbank with CAM bandwidths, it is still significantly lower than it.

We have so far assumed that listeners base their judgments on auditory filters having a wide range of CFs and that they weight these filters equally. However, another possibility is that they apply small weights to filters with very high CFs, so that, in the VHIGH region, judgments are primarily based on the outputs of filters closer to the lower limit of the stimulus frequency region than for the HIGH region. We do not think that this explanation, combined with the CAM filterbank, can account for our data. If we assume that, for the HIGH region, the point at which pitch drops with increasing F0 can be estimated from the output of an auditory filter centered on 4589 Hz (the middle of that band), then, the corresponding auditory filter for the VHIGH region should have an ERB 1.25 times higher. From Glasberg and Moore’s formula this would correspond to a CF of about 5375 Hz. This seems highly unlikely, given that the level of the stimulus at that frequency would have been approximately 29 dB down for that in the passband, and probably masked by the background pink noise. Furthermore, if listeners based their judgments on a very narrow range of auditory filters, then we would expect there to be a narrow range of F0s over which pitch is ambiguous. To take an extreme example, if judgments were based on the output of a single auditory filter, the pitch of an ALT complex should switch abruptly from F0 to 2F0 as the F0 is increased. Inspection of Figure 6 reveals that this transition region – the range of F0s over which the ALT complex had a pitch higher than that of a SINE complex at F0, yet lower than that of a sine complex at 2F0 – was if anything slightly wider in the VHIGH than in the HIGH region. It would, however, be just possible to account for our data by assuming both that auditory filter bandwidths vary with CF in the way proposed by Shera et al., and that listeners’ judgments were based on the lower edge of the passband of the VHIGH stimuli. For example, if one assumes that in the VHIGH region judgments are based on a range of CFs of which the average is 7800 Hz (the lower cutoff of the VHIGH band), the predicted filter bandwidth is only between 1.36 and 1.46 times that in the center of the HIGH region.

An alternative possibility is that, although there is a central limit, this applies to the encoding of modulation rates in individual auditory filters, rather than to the maximum value of a temporal pitch that can be heard. As argued above, it is likely that listeners weight a combination of auditory filters’ outputs when making a pitch judgment. For a PSHC stimulus, for example, this will include some filters that beat at 4F0 and some that beat at F0. The point at which pitch starts to decrease with increasing F0 will correspond roughly to the transition region where most filters beat at 4F0 (low F0s) to where most beat at F0 (high F0s). However, over the range of F0s where resolvability in the VHIGH region starts to change, these envelope repetition rates will be high in those filters that beat at 4F0. For example, in the VHIGH region, pitch starts to drop once F0 reaches 198 Hz, and so some auditory filters will be beating at four times that value, namely 792 Hz. If those high rates are not accurately conveyed by more central structures, then they may receive lower weights than those filters that beat at F0 when estimating the pitch of the stimulus. As a result, judgments would be based on the 4F0 envelope rate only when it occurs in the outputs of nearly all auditory filters. This would cause pitch to drop at a lower F0 than would have been the case without this central limitation. To illustrate this idea, we modified the model by assuming that the calculation of the aggregate rate is a weighted sum of the envelope rates of all filter outputs. The weight was assumed to be 1 for all filters beating at a rate less than 630 Hz which, as shown in experiment 2, is the highest pitch that we know can be derived by purely temporal cues. The weight was assumed to gradually decrease with increases in rate up to 1000 Hz where it is equal to zero (assuming a linear function relating the weight and log(F0)). Figures 11G-H show the results of simulations obtained with this modified model using the DRNL filterbank as it initially provided the best fit to our data. The predictions in the HIGH region (Figure 11E) are hardly affected by this change because for most F0s, the envelope rate in any filter is lower than 630 Hz. The two main changes concern the PSHC and ALT predictions in the VHIGH region (Figure 11H). In particular, the F0 at which pitch starts to drop for PSHC is lower than for the regular model (c.f. Figure 11B) and the reversal is more abrupt. Furthermore, the two functions cross at 250 Hz, close to the crossover of 280 Hz shown by the data. These three features bring the model predictions closer to the psychophysical data.

Although it is beyond the scope of this study to find the model parameters that would provide the best fit to the data, it is worth pointing out that changing (1) the shape of the weighting window applied to the peaks of each autocorrelation function and/or (2) the weighting function that combines the “pitches” of different auditory filters would both have an effect on the exact values of F0 at which the predicted reversals start and end. It may, therefore, be possible to further improve the fit by using other window shapes already proposed in the literature (e.g. Bernstein and Oxenham, 2005) and/or different weighting functions.

VI. GENERAL DISCUSSION

A. PERIPHERAL AND CENTRAL LIMITATIONS ON TEMPORAL PITCH

Carlyon and Deeks (2002) argued that, because the upper discrimination limit of purely temporal pitch did not vary proportionally with the bandpass filter frequencies, the limit was likely to be due to a central limitation. This argument was based on the estimates of auditory filter bandwidth that were widely accepted at that time. The present study allowed us to contrast this explanation with one based on an auditory-filter limitation, in which the Q factor of the filters increases with CF, as has more recently been argued by Shera et al (2002). The finding from experiment 3 that PSHC stimuli show a pitch reversal in the VHIGH region, that occurs at an F0 much less than twice that in the HIGH region, imposes substantial constraints on the possible explanations for our results and for those of Carlyon and Deeks. Specifically, it strongly implies a limitation based on auditory filtering, rather than on more central processes. Indeed, we would not expect a central limitation to produce such pitch reversals. Instead, the pitch should become less salient with increases in rate and possibly show a plateau. In contrast, we have shown that, due to the finite bandwidth of auditory filters, an increase in the F0 of an ALT or PSHC stimulus can produce a decrease in the repetition rate at the filter’s output.

The results and simulations presented here argue against two simple explanations for the observed upper limit of temporal pitch. An explanation based simply on the bandwidth of CAM auditory filters would not, as shown in Figure 2, account for the plateau observed in the pitch-ranking function for ALT stimuli filtered into the VHIGH region. It could also not account for the fact that the ratio between the F0s at which pitch ceases to increase monotonically in the VHIGH vs. HIGH regions is much less than the predicted value of 1.95; this is true both for ALT and PSHC stimuli. That ratio is equal to 1.25, and is also less than the values of 1.49-1.64 predicted by Shera et al’s fit to their data. To account for our results using a limitation based solely on peripheral factors would require a combination of auditory filters overall broader than Shera’s but with a Q increasing at the same rate and for listeners to base their judgments in the VHIGH region on the lower edge of the stimulus passband. On the other hand, the finding of a pitch reversal in the VHIGH region for the PSHC stimuli cannot be accounted for by a central limitation that operates on the maximum pitch that can be derived. Our simulations show, however, that listeners may apply reduced weights to those auditory filters whose outputs repeat at fast rates. That is, any central “upper limit” is likely to apply to the repetition rates at the outputs of auditory filters, and to thereby affect how the different filters’ outputs are combined, rather than to apply after the stage at which this combination has taken place.

B. AUDITORY FILTER BANDWIDTHS AT HIGH FREQUENCIES

There have been relatively few studies investigating the shape of auditory filters above 8 kHz. To our knowledge, only Shailer et al. (1990) and Zhou (1995) derived filter shapes from notched-noise masking data for CFs ranging from 8 kHz to 14 kHz. In both studies, the ERBs of the filters were consistent with the CAM formula. Subsequently, Shera et al. (2002) and Oxenham and Shera (2003) reported overall sharper filters than CAM and also that the Q factor of the filters increased with CF. As previously noted, the data presented here are consistent with Shera et al.’s findings that the Q factor increases with center frequency. However, Shera et al.’s filters are too narrow overall to account for the F0s at which we observed the pitch reversals and plateaus (c.f. Figure 11E and 11F). One reason for this discrepancy may be the higher level used in our experiment. There is evidence that auditory filters broaden with sound level, especially at high frequencies (e.g. Oxenham and Simonson, 2006). Alternatively, Eustaqio-Martin and Lopez-Poveda (2011) have recently argued that the sharp tuning reported by Oxenham and Shera may only be apparent and due to the fact that the filter shapes were derived from measures of psychophysical tuning curves.

Auditory filter bandwidths may also be inferred indirectly by using measures of phase sensitivity. Goldstein (1967) investigated how subjects could differentiate between a sinusoidally-amplitude modulated tone (AM) and the same tone with a phase shift of 90 degrees applied to the carrier frequency. This manipulation yields a stimulus known as a quasi-frequency modulated (QFM) tone whose envelope rate is twice the modulation frequency of the AM tone and whose instantaneous frequency changes periodically. If the carrier and modulator frequencies are close to each other, AM and QFM tones are very easy to discriminate. However, if their spacing exceeds half the filter bandwidth, the three components of each tone are spectrally resolved and AM and QFM sound identical. Goldstein measured the lowest frequency of the modulator above which AM and QFM sounded the same. He performed this experiment for carrier frequencies ranging from 250 Hz to 16 kHz. The function relating this lowest modulator frequency to the carrier frequency increased monotonically for carrier frequencies ranging from 250 Hz to 12 kHz. However, this increase was less than we would expect from the CAM formula. For example, the modulator frequency needed to be increased by a factor of 3 when increasing the carrier frequency from 1 to 4 kHz whereas the CAM formula would predict an increase by a factor of 3.4. For carriers between 4 and 12 kHz, the factor derived from the data was 1.9 whereas the CAM formula would predict a factor of 2.9. Therefore, similarly to our finding, Goldstein’s data are consistent with an increase in Q as a function of center frequency.

C. COMPARISON WITH COCHLEAR-IMPLANT LISTENERS

The data from these three experiments confirm the finding by Carlyon and Deeks (2002) that normal-hearing subjects can perceive differences in envelope repetition rate between unresolved complexes filtered in a VHIGH frequency region up to about 700-800 pps. As argued in the Introduction, this discrimination limit does not necessarily imply that listeners can derive a pitch as high as 800 Hz from unresolved complexes. By measuring the F0 at which an ALT complex is judged to have a pitch equal to a SINE complex of twice the F0, experiment 2 showed that listeners could derive a pitch of at least 630 Hz from purely temporal cues.

The upper “discrimination limit” of 700-800 pps agrees well with that observed for the best-performing CI listeners (Townshend et al., 1987; Kong et al., 2010), and for all listeners tested in a previous study in which we selectively stimulated the apex of the cochlea (Macherey et al., 2011). However, most CI subjects cannot discriminate between pulse trains at such high rates. So it is likely that they experience additional limitations. One of them could be poor neural survival and the failure of auditory nerve fibers to follow high stimulation rates. For CI listeners, the pitch limit (as opposed to the discrimination limit) may be obtained by asking subjects to adjust the pulse rate on a single electrode to produce a given musical interval. Pijl and Schwarz (1995b) tested three such CI users and found that, at low rates (reference at 93 pps), they correctly adjusted the rate of a target stimulus to produce a minor third, a fourth or a fifth. One subject was also able to adjust a fourth with reference to a base-line rate of 396 pps, i.e. he adjusted the rate to 547 pps. Given that his/her matches corresponded to the true intervals at lower rates, we may conclude that he could hear a pitch of 541 Hz based on purely temporal cues, which is close to the 630 pps measured here for normal-hearing listeners.

D. COMPLEX PITCH WITH VERY HIGH FREQUENCY RESOLVED COMPONENTS

Although we have mostly focused on the pitch ranks obtained with ALT and PSHC complexes, it is interesting to note that the pitch monotonically increased for SINE phase complexes over the whole range of F0s tested, including F0s for which individual harmonics were resolved by the periphery. For these relatively high F0s, envelope modulations at F0 at the filter outputs should be minimal. Experiment 2b shows that ALT and SINE complexes elicit the same pitches for F0s higher than 794 Hz in the VHIGH region. This suggests that individual harmonics are resolved above this F0. Therefore, the pitch comparisons between stimuli having F0s higher than 794 Hz could have been based either on the comparison of the pitch of individual components or on the comparison of the “complex” pitch derived from these components (also sometimes called residue pitch, virtual pitch or periodicity pitch).

Two observations argue for the latter. First, the rank assigned to the SINE complex at 1587 Hz was for all subjects higher than the rank assigned to the SINE complex at 794 Hz. Given that all the components present in the 794-Hz complex are also present in the 1587-Hz complex, it is unclear how the subjects could have compared the pitches of these two sounds by comparing the pitches elicited by individual harmonics. Furthermore, unlike the case where difference limens are measured by adaptive procedures, our paradigm leads to quite different stimuli being compared from trial to trial. This makes the strategy of listening to individual components to make pitch judgments quite inefficient. Instead, the present data suggest that our subjects were able to extract a complex pitch from a group of resolved harmonics having frequencies higher than 7800 Hz. This observation is consistent with the findings of Oxenham et al (2011) who showed that a harmonic complex tone with all components resolved and above 6 kHz elicited a pitch equivalent to the pitch of a pure tone having the same F0 and could also convey melody information. Based on these data, Oxenham et al (2011) proposed that either phase locking was not necessary to elicit a complex pitch or alternatively that phase locking information was still useable at these high frequencies. Our method has the potential advantage of not requiring musical judgments. The use of a simple series of forced-choice discriminations may make it more suitable for musically untrained listeners.

E. PULSE-SPREADING HARMONIC COMPLEXES AS A TOOL FOR STUDYING TEMPORAL PITCH

Finally, we have used a novel stimulus (PSHC) that allowed us to manipulate the envelope rate of a harmonic complex by manipulating the phase relationship between the frequency components. This stimulus is perceived at low F0 as having the same pitch as an alternating-phase complex at 2F0 and, therefore, as having the same pitch as a sine-phase complex at 4F0. As recently shown by Hilkhuysen and Macherey (2014), phase relationships of PSHCs can be derived to produce pulse rates even higher than 4F0. These phase relationships may serve useful in studies of neural correlates of pitch perception because they can produce stimuli which have the same spectral content but elicit very different pitch percepts.