L-Measure: a Web-accessible tool for the analysis, comparison, and search of digital reconstructions of neuronal morphologies

Abstract

L-Measure (LM) is a freely available software tool for the quantitative characterization of neuronal morphology. LM computes a large number of neuroanatomical parameters from 3D digital reconstruction files starting from and combining a set of core metrics. After more than six years of development and use in the neuroscience community, LM enables the execution of commonly adopted analyses as well as of more advanced functions. This report illustrates several LM protocols: (a) extraction of basic morphological parameters, (b) computation of frequency distributions, (c) measurements from user-specified sub regions of the neuronal arbors, (d) statistical comparison between two groups of cells, and (e) filtered selections and searches from collections of neurons based on any boolean combination of the available morphometric measures. These functionalities are easily accessed and deployed through a user-friendly graphical interface, and typically execute within few minutes on a set of ~20 neurons. The tool is available at http://krasnow.gmu.edu/cn3 for either online use on any Java-enabled browser and platform, or download for local execution under Windows and Linux.

INTRODUCTION

The quantitative characterization of neuronal morphology is essential to correlate structure, activity, and function in the nervous system at the cellular level. In many studies, dendrites and axons imaged from a variety of histological preparations are digitally traced into 3D reconstructions representing the arborization as a series of interconnected tubules¹. These data files allow comprehensive morphometric investigations, powerful comparative analyses, and the implementation of anatomically detailed computational models^2–6. Digital reconstruction of neuronal morphologies requires specialized software, such as the popular Microbrightfield Neurolucida. Despite ongoing progress in automation attempts, the tracing process remains extremely time-consuming and technically challenging⁷. At the same time, digital morphologies are extremely versatile, and retain considerable scientific utility beyond the original purpose they are collected for. They can often be re-used in follow-up or even completely unrelated research projects⁸. An increasing number of laboratories are freely sharing their 3D reconstructions with the neuroscience community to maximize the impact of their research efforts^9–14. Thousands of neurons are available at NeuroMorpho.Org, and hundreds are downloaded daily. Examples of these neuronal morphologies are illustrated in Figure 1.

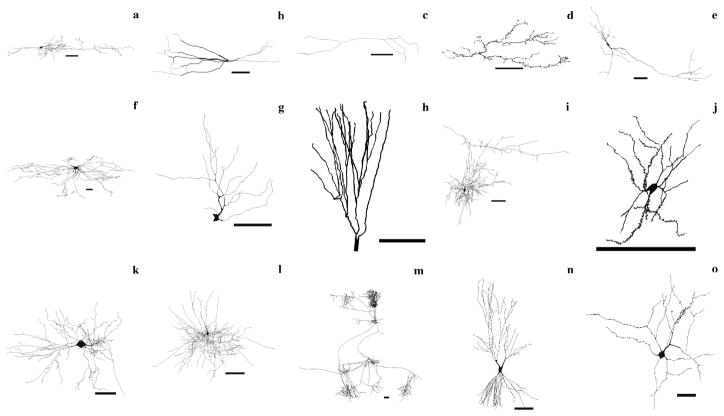
Figure 1.

Representative collection of 15 neurons selected from NeuroMorpho.Org (all scale bars are 100 μm). Ordered by row, from top left: (a) bipolar cell from rat neocortex (C130200-19), (b) parvalbumin cell from rat hippocampus (pv22c), (c) calretinin cell from rat hippocampus (cr10f), (d) climbing fiber from rat cerebellum (NMA), (e) dopaminergic cell from rat basal ganglia (Nigra11h941-1), (f) dorsal spinocerebellar tract cell from cat spinal cord (DSCT4), (g) ganglion cell from salamander retina (mp_ma_40984_gc2), (h) granule cell from rat hippocampus (411884b), (i) Martinotti cell from rat cerebral cortex (cellC150897B-I1), (j) medium spiny neuron from mouse basal forebrain (ACC1), (k) motoneuron from mouse spinal cord (ok_m215), (l) basket cell from rat neocortex (C040600B1), (m) pyramidal cell from cat neocortex (980804axden), (n) CA3 pyramidal cell from rat hippocampus (cell6zr), (o) Renshaw cell from cat spinal cord (renshawcell1).

In order to capitalize on the value of these digital data, we developed and freely distributed L-Measure (LM), a software program to extract morphometric measurements¹⁵. With more than six years of public usage, LM remains the only documented, supported, and freeware tool available online for the neuroscience community to routinely analyze dendritic and axonal morphologies from digital reconstruction files in any of the known file formats. LM measures a battery of over 40 core metric functions (e.g. diameter, length, angles) and can return simple statistics (average, standard deviation, minimum, maximum, and total sum), histogram distributions, or the dependency of one metric on another (e.g. Sholl analysis of number of branches vs. distance from soma). The same functions can also be used to select a specific portion of the arborization for analysis (e.g. at least 5 bifurcations away from the soma). The underlying C++ computational engine, dedicated to file processing and number crunching, can be operated through a “point and click” Java graphical user interface (or via command line for batch execution). LM outputs are visualized on the display and/or saved to files compatible with analysis and graphic programs such as Microsoft Excel. The core LM functionality is depicted in Box 1.

Box 1. Quantitative morphometry by L-Measure.

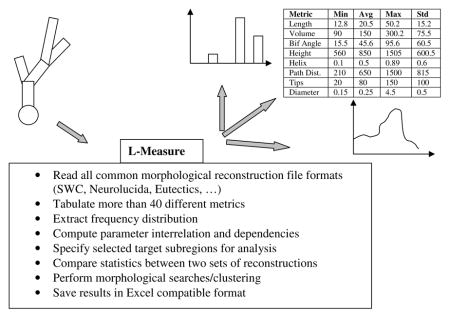
Since its first introduction in 2001, LM has been proven useful in several applications.

1. LM is regularly used for large-scale extraction of morphometrics employed by the online electronic repository NeuroMorpho.Org¹⁶ to characterize the structural content of thousands of 3D digital reconstructions from a variety of cell classes, anatomical locations, experimental procedures, animal species, and reconstruction methods. In particular, LM is utilized whenever the underlying database is updated and at every version release of NeuroMorpho.Org.

2. LM is routinely used by several research groups worldwide to perform detailed comparative analysis on groups of neurons. Classic examples of such applications from the authors’ own studies and collaborations include the quantification of characteristic morphological features across various cell classes and conditions¹⁷, detection of differences induced by specific growth factor¹⁸, analysis of developmental changes¹⁹, and comparison between neurons expressing various neuropeptides²⁰.

3. Thanks to its capability of processing assorted file formats from diverse reconstruction techniques, LM is also used to match morphologies obtained from multiple digital tracing methods both at the detailed branch-by-branch level and with overall statistics²¹. By the same token, LM has served validation purposes in processing the results of automated reconstruction algorithms applied to projection axons in the rat hippocampus neurons (i.e. comparing number of bifurcations, total length, path distance, branch order, and asymmetry with the same metrics extracted from other available morphologies of the same classes²²).

4. LM is also employed for the extraction of parameter distributions from experimental data required for resampling by stochastic computational simulations to generate virtual neurons²³. Similarly, LM is often used to investigate the quality and limitations of these models by comparing their emergent morphological properties with the original experimental data²⁴.

LM is well recognized as a standard tool for morphometric analysis as cited by independent laboratories in a variety of settings, such as the description of computational protocols²⁵, database and information frameworks²⁶, classification of disease-induced dendritic damage²⁷, assessing morphological simulations in spinal injury models²⁸, and analysis of experimental manipulations²⁹. Moreover, it is important to stress that LM provides the ability to extract all morphological measurements underlying the emerging community standards for classification of cellular phenotypes³⁰.

As a “quick start” practical guide of LM functionality, this protocol presents several common procedures illustrating the tool in action. These user case examples are chosen to cover a variety of key operations and the reader is encouraged to try them as an opportunity to explore both basic and new features.

User Operation of L-Measure

We first provide a brief overview of the LM “look and feel” from a user perspective. Although for the sake of precision we refer specifically to the online version accessed with Internet Explorer under Windows XP (the most popular configuration to date), other platforms and the local executables only differ subtly from this description (to set up LM on a local computer, refer to Box 2).

Box 2. Setting up L-Measure in seven easy steps.

1. Go to http://krasnow.gmu.edu/cn3

2. Click on Data/Tools++ tab

3. Select the L-Measure link

4. Of the two downloadable archives for installing LM, choose the appropriate one corresponding to your operating system (Linux or Windows)

5. Download the Lm.zip file, which contains:

   • LM.exe – a C++ executable engine

   • Lm.jar – a Java based graphical user interface that send point and click commands to the executable engine

6. Extract the Lm.zip content on your local machine, ensuring that both LM.exe and Lm.jar reside inside the same directory

7. Double click on Lm.jar to start the GUI interface

   Total time estimate (steps 1–7): 1–2 minutes

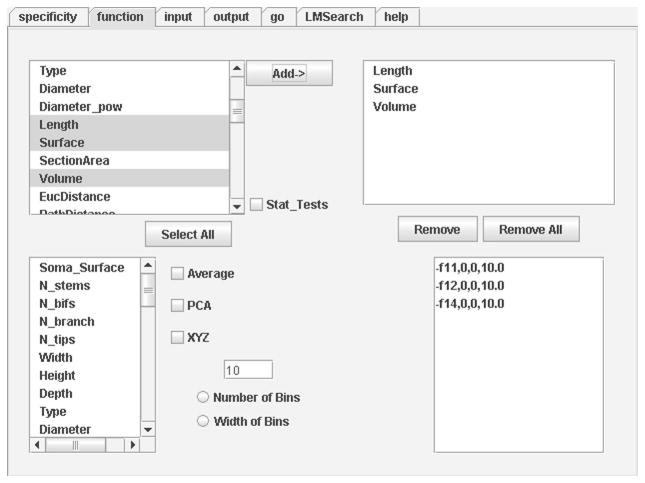
From (http://krasnow.gmu.edu/cn3), LM loads upon selecting “L-Measure” from the “Data/Tools++” page, and clicking on “Online version”. LM appears as a user-friendly graphical interface with seven tabs that can be inter-toggled by a single mouse click (Figure 2). In particular, the help page (rightmost tab) contains an introductory manual and the reference list of available measurements, each with a brief explanation. Several of the remaining tabs are normally accessed in rapid sequence, as described in more details in the “Use Case Examples” below. The typical user delimits the morphological region to which the measurements should be restricted (specificity), selects the parameters to be extracted (function), loads one or more neurons (input), defines how to display or save the results (output), and finally launches the analysis (go).

Figure 2.

In the Function tab users define the metrics to extract. Detailed definition of each metric is available in the Help panel (which also provides general usage information).

All morphological measurements in LM are derived from a core set of metric functions, the majority of which are listed in Table 1. These functions generally extract a measure from each tracing point. In a physical interpretation, these individual points define the ending of each of the interconnected tubular primitives constituting the digital morphology. A subset of these points corresponds to the topological nodes of the trees, i.e. stems (tubules attached to the soma), bifurcations (tubules with two daughters), and terminal tips (tubules without daughters). After parsing the whole neuronal arborization (or the portion delimited by the specificity settings), LM can derive three types of relations from the raw values of the measures. The first is a simple statistical summary consisting of mean, standard deviation, minimum, maximum, and the total sum (for examples, see Table 2 for tabulated values and Figure 3a for a scatter plot obtained from these kinds of data). The second is the frequency distribution histogram, with user-defined bins (illustrated e.g. in the inset of Figure 3a). The third is the interrelation between two measures, also binned by the user, as in the examples of Figure 3b–d.

Table 1.

Partial list of LM metrics (the unit for all dimensional values is μm). All metrics return real values unless otherwise noted. Metrics in the left column return values at each tracing point except the gray shaded ones, which are defined at the whole neuron level. Metrics in the right column return one value for every branch, except the gray shaded ones, which are defined at bifurcation points only.

Somatic Surface	Branch Length
Neuronal Height	Contraction
Neuronal Width	Fragmentation(2)
Neuronal Depth	Fractal dimension
Diameter	Branch Taper
Distance from previous point	Daughter Diameter Ratio
Unit Taper	Parent/Daughter Ratio
Euclidian Distance from Soma	Rall Power
Path Distance from Soma	Rall Ratio
Branch Origin(1)	Power Ratio
Branch Ending(1)	Partition Asymmetry
Branch Order(2)	Local Amplitude Angle
Type(2)	Remote Amplitude Angle
Terminal Degree(2)	Local Tilt Angle
Helix	Remote Tilt Angle
	Local Torque Angle
	Remote Torque Angle

⁽¹⁾Returns binary values (1 or 0, i.e. “Yes” or “No”).

⁽²⁾Returns integer values.

Table 2.

Output of case B. Each line can be read from right to left as: neuron name, metric function, total sum of the function over all tracing points, number of points included in the analysis, number of points excluded (in this case, around 400 points define the cell body, fiduciary axis, axons, etc), minimum value, average, maximum, and standard deviation of the metric function.

Neuron Name	Metric	Tot Sum	P.In	P.Ex	Min	Avg	Max	Std
c11563.CNG.swc	Length	13257.7	933	−410	1.12	14.21	42.51	6.42
c11563.CNG.swc	Surface	13275.9	933	−410	1.05	14.23	117.62	8.48
c11563.CNG.swc	Volume	1187.16	933	−410	0.08	1.27	73.13	3
c10261.CNG.swc	Length	13044.9	1305	−404	1.12	10	33.67	5.43
c10261.CNG.swc	Surface	14951.9	1305	−404	1.4	11.46	294.79	11.27
c10261.CNG.swc	Volume	2153.41	1305	−404	0.11	1.65	316.9	9.43

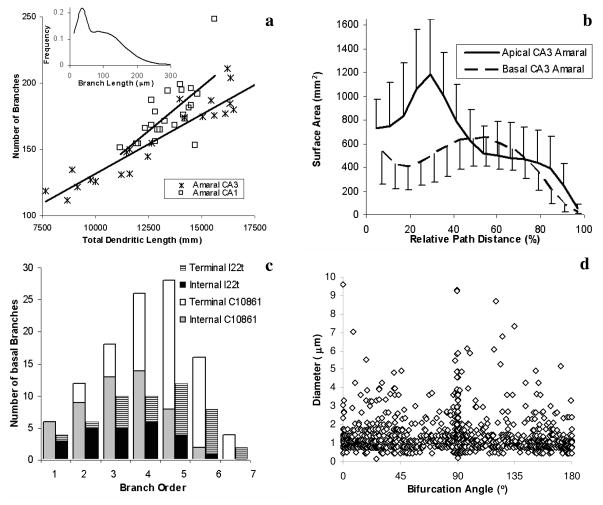
Figure 3.

Examples of graphs from typical morphometric studies performed with LM on reconstructed neurons available at NeuroMorpho.Org. (a) Scatter plot of the overall number of branches in each cell vs. its total dendritic length. Straight lines represent linear fits. Inset shows frequency distribution of Branch Length for all Amaral CA3 group. (b) Distributions of surface area over relative path distance for apical and basal dendrites from CA3 pyramidal cell from Amaral archive. Each point is the average over 24 cells, error bars represent standard deviations. (c) Histograms of the number of basal branches (divided in internal, i.e. ending into a bifurcation, and terminal, i.e. ending into a tip) as a function of branch order (the number of bifurcations from the soma) for CA3 pyramidal cells l22t and c10861. (d) Scatter plot of diameter vs. bifurcation angle for each branch point within all 18 CA3 pyramidal neurons from young rats in Turner’s archive. Artificial noise uniformly distributed between −0.05 and 0.05 was added to all coordinate values for better visualization.

Individual elements of the statistical summary, applied to appropriate functions, yield useful scalar metrics to characterize overall neuronal structure. For example, the maximum Euclidian distance from soma provides a measure of the neuronal size corresponding to the radius of the smallest sphere containing the neuron. The total sum of the distance from previous point is another metric for the extent of the neuron, its overall cable length. A few functions are direct features of the whole cell, such as somatic surface, or the height, width, and depth of the neuron (comprising all of its trees). Several other functions are not defined for every tracing point, but only at the level of branches (right column in Table 1), i.e. the portions of the arbor between two nodes (e.g. the contraction, or ratio between Euclidian and path distance, reflecting neuritic meander), or more specifically at bifurcations (gray shaded background in the right column of Table 1), such as daughter diameter ratio and local amplitude angle. A review of every morphometric function is beyond the scope of the present report. The definitions of all core metrics are available in the LM help tab (and this topic is well represented in the scientific literature²⁹).

Not all elements of the statistical summary are appropriate for every core function (e.g., the sum of all diameters is of questionable significance), and several measures can be obtained in a redundant fashion (e.g. both the sums over all branch lengths and over distances from previous points return total cable length). Moreover, important metrics can be also obtained by combining other core functions (e.g. surface and volume from length and diameter, etc.). Overall, LM can measure more than one hundred independent and meaningful morphological parameters. Additional measures can be extracted by specificity, by usage of histogram distributions, and by interrelating variables. Analyses can be carried out on entire populations of cells, on individual neurons, and on portions thereof. The resulting outputs can be further manipulated for more extensive post-processing or graphical rendering (as displayed in Figure 3).

New Available Functionalities

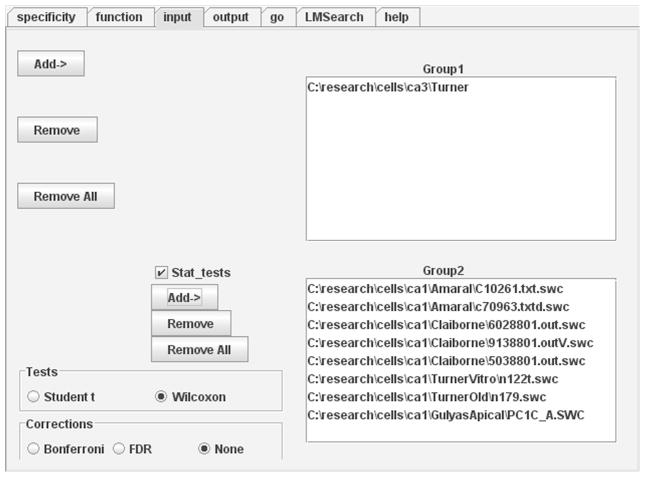
We have recently upgraded LM to include three new features. The first one allows users to test for statistical differences between two groups of neurons, as often performed in neuroanatomical comparisons of an experimental and a control condition (e.g. knock-out vs. wildtype, treated vs. saline, lesioned vs. sham, aged vs. young). The user can load cells in each of the two groups individually and/or selecting entire directories (Figure 4). The parameters to use in the statistics are then chosen from the core functions by selecting the appropriate elements of the statistical summary (Figure 5). The second provides the ability to search large directories of digital reconstructions (e.g. from a series of experiments, or downloaded from an archive) for cells matching specific morphometric criteria (e.g. with less than 20 terminal tips) as shown in Figure 6. The third enables morphological analyses at the individual tree level, i.e. grouping measurements tree-by-tree (each separate part of the arborization that stems directly from the soma) as opposed to an entire cell or set of neurons.

Figure 4.

Input panel with statistical feature enabled (note “Stat_tests” checkbox). All cells from directory \ca3\Turner are loaded as Group1, while eight neurons from five different directories are pooled into Group2. The Input panel identifies the cells to be analyzed, while the Output tab determines if and where the results should be saved to disk.

Figure 5.

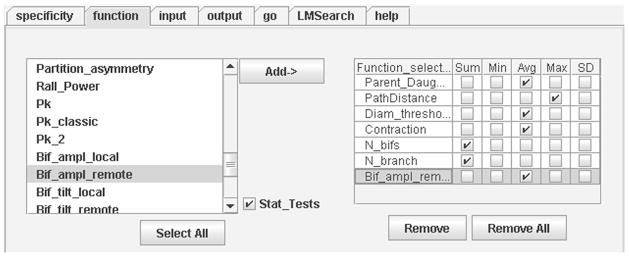
Function panel with statistical features enabled (note “Stat_tests” checkbox). After the morphometric analysis conditions are set, extraction of measurements is initiated in the Go panel.

Figure 6.

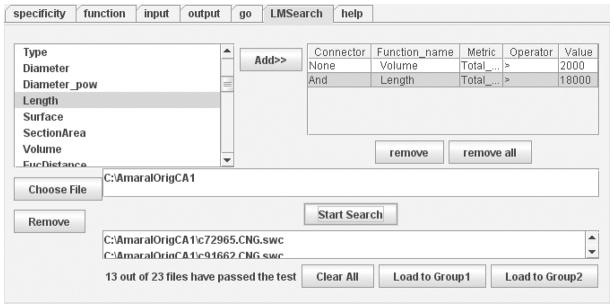
The LMSearch panel allows users to find neuronal reconstructions with particular morphometric characteristics among arbitrarily large sets. In this example, the search criteria indicate a Total Length greater than 18000 μm and a Total Volume greater than 2000 μm³. The resulting output consists of 13 neurons that satisfy these conditions over a total of 23 contained in AmaralOrigCA1 folder.

Potential Applications of L-Measure

Several of the functionalities implemented in LM were inspired by published scientific studies in which important morphometric analyses were performed by hand, or with custom made (and not publicly available) routines. These and many other such reports serve as convincing demonstrations of the research applications for which LM can provide a fast and reliable solution. A recurring theme is the comparative morphological analysis of sets of cells identified or separated by (in principle) independent means. This is a particularly active area of research with respect to GABAergic cells in the cerebral cortex, which are known for their rich diversity. Examples from the adult rat hippocampus alone include the comparison of total dendritic length and soma surface area among three groups of CA1 interneurons identified on the basis of specific chemical markers³², and the extraction of similar metrics from dentate gyrus cells characterized by their electrophysiological properties³³. The issue of cellular classification represents a fundamental scientific question in its own merit, and the extensive battery of measures that are available in LM lends itself to quantitative clustering methods. This kind of strategy was recently used e.g. on the axonal arborizations of interneurons from the monkey prefrontal cortex³⁴, and from the mouse visual cortex³⁵. Alternative classification approaches, also involving large-scale morphometric extraction, were successfully applied to retinal cells in both mammals³⁶ and inframammals³⁷. In some cases, clustering was adopted in later refinements³⁸. More generally, morphometric analysis is prominently used in neuronal classification, as recently exemplified by the distinction of von Economo and pyramidal neurons from human postmortem brains based on branching and symmetry³⁹, or the characterization of speech-specific dendritic features from interhemispheric comparison of magnopyramidal cells⁴⁰. Even when interneuron populations display a continuum of morphological properties, and are thus not amenable to classification clustering, principal component analysis over an extensive battery of morphometric measures may reveal functionally relevant anatomical features such as laminar gradients, as in the cerebellar moleculare layer⁴¹.

Another important line of studies investigates how electrophysiological activity, action potential propagation, and neuronal firing dynamics can be modulated by specific morphological parameters, such as the dendritic surface⁴² and dendritic branching patterns both among different cell types⁴³ and within a single class⁴⁴. Other typical examples include the relation between morphometric distributions that can be easily extracted from LM output and the electrotonic structure of the dendrites (e.g. comparing multiple classes of principal and inhibitory cells in the cat spinal cord⁴⁵). In some cases, the morphometric changes may be linked to the expression of growth factors activated during development. For example, it was shown that the number of dendritic terminal tips and total dendritic length were both regulated by the β-catenin complex during morphogenesis⁴⁶. Interestingly, later deployment of LM on this same experimental preparation enabled more comprehensive studies of absolute and relative effects of β-catenin as well as its effect on simulated spiking patterns¹⁸. Changes in plasticity and neuronal morphology are often observed during development and aging, as well as in disease (Alzheimer’s, Parkinson’s, etc.), and in a variety of experimental conditions. Illustrations of typical potential uses of LM in these cases are offered by reports on the contrasting stress-induced alterations of the distributions of the number of branch points against Euclidean distance in apical vs. basal dendrites⁴⁷. The changes that occur in spatial distribution of branch points and terminal tips with normal animal experience have been similarly compared⁴⁸. LM enables these analysis as well as variations that may be more straightforward to interpret biologically, such as the pattern of dendritic surface (instead of branch counts), which relates to synapse numbers, as a function of the more “physiological” path (as opposed to Euclidean) distance. Last but not least, morphometric parameters are routinely analyzed in the course of computational simulations of dendritic structure, as recently applied to the analysis of the relationship between path and Euclidean distance in spinal motoneurons⁴⁹. All the above examples and results could be suitably replicated with LM.

L-Measure Limitations

Neuronal morphology can be represented and quantified at several levels. The “vector-based” representation of branching structures adopted by most 3D digital reconstruction systems constrains the type of processing enabled by LM. In particular, surface shape analysis and spine or ultra structural metrics are excluded from this type of analysis. Other tools, such as 3DMA⁵⁰ offer a complementary solution from this point of view, allowing automated segmentation and 3D voxel analyses from a stack of images. More generally, although LM provides an extensive (and continuously growing) set of metric, the number of measurable geometric characteristics is practically infinite, so it is unavoidable that some users may be interested in specific analyses that are not (yet) implemented. An alternative commercial product, MicroBrightField’s NeuroExplorer (www.mbfbioscience.com) can be chosen to perform analyses based on terminal distance, convex-hull, or polar histograms. Moreover, LM is restricted to a purely morphometric domain, and does not allow the direct estimation or modeling of functional characteristics, such as eletrotonic structure or electrical impedence. Thus, the additional use of external simulation environment such as NEURON (www.neuron.yale.edu) to investigate the relationship between morphological and electrophysiological properties^6,17,33 is required. However, none of these software applications (3DMA, NeuroExplorer, or NEURON) enables any of the key LM advantages, such as the extensive and unique list of available metrics, the flexibility to access the tool both online and as standalone application, the direct statistical comparison between and/or search within cell groups, and the morphological specification of subparts of neuronal structures.

Step-by-Step Use Case Examples

The procedure detailed below describes a set of representative morphometric analyses. In particular, after a preliminary step of data preparation (A), the protocol illustrates the extraction of total length, surface, and volume data (B). These are standard scalar parameters that quantify various aspects of the neuronal arbor size. Next (C) is the derivation of the histogram distribution of branch length, i.e. the frequency of distances between consecutive bifurcations or between a bifurcation and a termination along the neural path. This metric provides an assessment of the local variability at the branch level within the neuronal population. The following two cases (D and E) characterize the interrelations between surface area and relative path distance, and between number of internal basal branches and branch order, respectively. These are powerful variations of the classic “Sholl analysis”, which was originally introduced to capture the branching patterns as a function of the cell spatial surroundings⁵¹. Sholl plots were defined before the digital era based on the available pencil tracings on paper, as the number of branches intersecting a series of concentric circles versus the radii of the circles. The use of path (instead of radial) distance provides a more natural and “cell-centric” perspective, and also captures the full three-dimensional spatial extent as opposed to a planar projection. The choice of a “relative” coordinate system (essentially normalizing the path to the maximum distance from soma to tips) enables the comparison of trees with very different sizes. Moreover, switching the dependent variable to surface area (from number of branches) enhances the functional relevance of the analysis by reporting a measure related to the neuronal electrotonic structure and the number of synapses. The selection of “internal” branches seamlessly instantiates a further important distinction by including in the analysis bifurcating branches and excluding terminating ones. Finally, the remaining set of user cases exemplifies other aspects of the functionality available in LM. One case (F) consists of the statistical comparison of two sets of neurons based on their total length, total surface, and mean branch order. Another (G) searches and finds within a large data set all the neurons with volume greater than 2000 μm³ and length greater than 18,000 μm. These search results are then pipelined and subjected to statistical analysis (H). The last case (I) tabulates surface area in basal dendrites farther than two bifurcations away from the soma as a function of relative path distance in individual subtrees. These instances are offered as typical usage examples from our practical experience with LM. A large number of additional useful combinations of this functionality provides ample opportunity for other possible morphometric analyses.

MATERIALS

EQUIPMENT

• All protocols have been tested on:

  • Intel Pentium IV processor 2.8GHz with 1.5GB of RAM running Windows XP OS for both online and standalone versions;

  • Intel dual quad core processor 2.0GHz with 4GB of RAM running Linux Fedora 7 OS for both online and standalone versions;

  • Intel core duo 2.16GHz processor with 1GB of RAM running Mac OS X for online version only.

• The LM tool can be downloaded and run locally as a standalone application on Windows or Linux machines (for standalone set up on the local hard drive, follow steps in Box 2).

• LM can also be accessed directly on-line with any (Java enabled) Internet browser and operating system. On the server side the requests are served by an Intel dual quad core processor with 4GB of RAM running on Fedora 7 OS. On the client side, protocols were tested on:

  • Internet Explorer and Netscape on Windows XP machines;

  • Mozilla Firefox on Windows and Linux machines; and

  • Safari on Mac machines.

! CRITICAL: For on-line usage, a security prompt asks for reading and writing privileges. Granting this permission by accepting the signed certificate allows LM to read locally stored cells and write the output results on the user’s local hard disk.

PROCEDURE

(A) Data Preparation

• 1|To run these demonstrations, sets of neurons need to be downloaded from NeuroMorpho.Org. In particular all hippocampal CA1 and CA3 neurons from Amaral’s archive are needed. Go to http://www.NeuroMorpho.Org, and select “Metadata” under the left side “Search by” menu.
• 2|Click on “Brain Region”. Select “Hippocampus” and “CA1” from the dropdown lists.
• 3|Click on “Archive” and choose “Amaral” from the dropdown list.
• 4| Hit the “Show Summary” button and at the bottom of the page click “Select All” and “get SWC files of selected neurons”.
• 5|Download the ZIP file and extract its content to “AmaralOrigCA1” folder on the local hard drive.
• 6|Repeat these steps by choosing “Hippocampus” and “CA3” in the Brain Region menu and submenu respectively, and select “Amaral” under Archive. Finally, download the ZIP file and extract its content to “AmaralOrigCA3” folder.
• 7|Continue with all other cases below (B-I).

(B) Extraction of total dendritic length, surface, and volume data

! CAUTION: Make sure all the windows and checkboxes are reset before switching from one example to another. Use the “Remove All” buttons in the respective panels and uncheck the previously checked options.

1. In the Specificity panel, select Type from left list. Press the Add button.

2. Set = for Operator. Input 4 for Value. A type equal to 4 in NeuroMorpho.Org corresponds to apical dendrites.

3. Select Type from the left list. Press the Add button.

4. For the second row in the left table set OR for Connector. Set = for Operator. Input 3 for Value. A type equal to 3 corresponds to basal dendrites.

5. In the Function panel, select Volume, Length and Surface from the top left list. Multiple functions can be selected by keeping the Ctrl key pressed. Press the Add button. All three metrics should now appear in the top right white window (Figure 2).

6. In the Input panel, click Add (top left) and select the c10261.CNG.swc and c11563.CNG.swc neurons from AmaralOrigCA1 folder.

7. In the Go panel, hitting the Go button will result in a display similar to Table 2.

(C) Histogram distribution of branch length

1. In the Specificity panel, select Type from the left most list. Press the Add Button.

2. Select Operator and set it to =. Input 4 in the Value cell.

3. Select Type from the left list and press the Add Button.

4. For the second row in the left table set OR for Connector. Set = for Operator. Input 3 for Value cell.

5. In the Function panel, select branch_pathlength from both top and bottom left panels. Select Width of Bins and set its value to 25. Press the Add button.

   ! CAUTION: Do not click the Add button before entering the value 25 for Width of Bins. Otherwise, the default value (of 10) will be assumed by the LM executable.

6. In the Input panel, click Add (top left) and select the AmaralOrigCA1 folder. Repeat for the AmaralOrigCA3 folder.

7. In the Output panel, select the Global checkmark.

8. In the Go panel, hitting the Go button will produce the data plotted in the inset of Figure 3a.

(D) Interrelation between surface area and relative path distance

1. In the Specificity panel, select Type from left list. Press the Add button.

2. Select Operator and set it to =. Input 4 for Value cell.

3. Select Type from left list. Press the Add button.

4. In the Function panel, select Surface from top left list and PathDistance from the bottom left list.

5. In the Input panel, click Add (top left) and select the c10861.CNG.swc neuron from AmaralOrigCA3 folder.

6. In the Go panel, hit the Go button to start the measurement process. Figure 3b is generated by executing case D on all Amaral CA3 neurons, first by selecting only apical dendrites and then by selecting only basal dendrites.

(E) Interrelation between number of internal basal branches and branch order

1. In the Specificity panel, select Type from left list. Press the Add button.

2. Select Operator and set it to =. Input 3 for Value cell.

3. Select TerminalSegment from left list. Press the Add button.

4. Set AND as Connector and > as Operator. Input 1 for Value cell. Values greater than 1 return only internal segments.

5. In the Function panel, select N_Branch from top left list and Branch_Order from bottom left list.

6. Select Width of Bins checkmark and set its value to 1. Press the Add button.

7. In the Input panel, click Add (top left) and select c10861.CNG.swc neuron from AmaralOrigCA3 folder.

8. In the Go panel, hit the Go button to start the measurement process. The results are displayed in Figure 3c as “Internal C10861”.

(F) Comparison of two neuron sets based on total length, total surface, and mean branch order

1. In the Specificity panel, select Type from left list and press Add.

2. Set = as Operator. Input 4 for Value cell.

3. Select Type from left list. Press the Add button.

4. Set OR for the second row Connector. Set = as Operator. Input 3 for Value cell.

5. In Function, Add Length, Surface, and Branch_Order, following the steps outlined in Case B above.

6. Mark the Stat_tests box. Of the checkboxes appearing in the top right display (one for each element of the statistical summary), select Sum for Length and Surface, and Avg for Branch_Order.

7. In the Input panel, Add all neurons of the CA1 group by selecting the AmaralOrigCA1 directory as Group1.

8. Check the Stat_tests box and Add all neurons of the CA3 group by selecting the AmaralOrigCA3 folder as Group2.

9. In the Tests options at the bottom of the panel, choose Wilcoxon test and among the Corrections choose Bonferroni.

10. Executing the analysis in the Go panel by clicking on the Go button will yield the (self-explanatory) results in Table 3.

Table 3.

Output of case F. Each line can be read from right to left as metric function, Statistic, sample size for Group1, mean value for Group1, standard deviation for Group1, sample size for Group2, mean value for Group2, standard deviation for Group2, p-value for Wilcoxon test, p-value corrected with Bonferroni.

Function_name	Statistic	N1	Mean1	SD1	N2	Mean2	SD2	Wilcoxon P_Values	Bonferroni correction
Length	Sum	23	13475.14	1095.79	24	13196.08	3149.861	0.45	>=1
Surface	Sum	23	14811.28	1566.22	24	18587.15	6153.017	0.02	0.062
Branch_Order	Avg	23	9.65	1.87	24	13196.08	3149.861	2.14E-09	6.41E-09

(G) Finding neurons with volume greater than 2000 μm³ and length greater than 18,000 μm

1. In the LMSearch panel, Add Volume and Length from the top left metric list. In the top right window, where both functions appear, select Total_Sum as Metric, the symbol > as Operator, and the respective numerical values as in the heading of this use case.

2. To load all the CA1 neurons of Amaral’s archive, click Choose File and select the “AmaralOrigCA1” directory. Upon hitting Start Search, the results appear as in Figure 6.

(H) Statistical analysis of search results

1. Perform the steps described in Case G, and then within the LMSearch panel, click Load to Group1.

2. Repeat the search of Case G, with the following alternative criteria: Volume less than 2000 μm³ OR Length less than 18000 μm³. To do so, the only steps to change are the selection of the Connector as OR for the second function in the right list of the LMSearch panel, and the use of the < symbol under Operator for both functions. After executing the search, select Load to Group2 (if the button cannot be found, enlarge the window).

3. In the Specificity panel, select Type from left list. Press the Add button.

4. Set = as Operator. Input 4 in the Value cell.

5. Select Type from left list. Press the Add button.

6. Set OR for the second row Connector and = as Operator. Input 3 for Value.

7. Go to Input tab, check Stat_tests to enable the statistical comparison analysis. Also, select Wilcoxon from Tests and Bonferroni from Corrections.

8. Switch to the Function tab, check Stat_tests, and select Terminal_degree, Branch_Order, Bif_tilt_local (local bifurcation tilt angle), and Rall_Power metrics. Click the Add button, making sure that all 4 metrics appear in the top left window. Select Max for Terminal_degree and Branch_Order, and Avg for Bif_tilt_local and Rall_Power.

9. In the Go tab, click the Go button. The results will appear as in Table 4.

Table 4.

Output of case H. Each line can be read from right to left as metric function, Statistic, sample size in Group1, mean value for Group1, standard deviation for Group1, sample size in Group2, mean value for Group2, standard deviation for Group2, p-value for Wilcoxon test, p-value corrected with Bonferroni.

Function_name	Statistic	N1	Mean1	SD1	N2	Mean2	SD2	Wilcoxon P_Values	Bonferroni correction
Bif_tilt_local	Avg	13	131.42	3.8	10	132.17	4.34	0.38	>=1
Rall_Power	Avg	13	1.18	0.2	10	1.44	0.14	0.002	0.01
Terminal_degree	Max	13	55.15	13.06	10	57.3	8.86	0.39	>=1
Branch_Order	Max	13	24.23	5.61	10	25.9	4.28	0.18	0.74

(I) Tabulating surface area in basal dendrites farther than two bifurcations away from the soma as a function of relative path distance in individual subtrees

1. In the Specificity panel, select Type from left list. Press the Add button.

2. Set = as Operator. Input 3 for Value cell.

3. Select Branch Order from left panel and press Add. Set AND as Connector and > as Operator. Input 2 in Value.

4. In the Function panel select Surface from the top left metric list, and PathDistance from the bottom left list. Click on Number of bins (determining in how many equal values path distance gets subdivided) and set its value to 5 in the text box. Then, press the Add button.

5. In the Input panel add the single cell c10261.CNG.swc from the AmaralOrigCA1 folder.

6. In the Output panel, mark the Subtrees Group box, and check the Analyze Subtrees option.

7. Finally, hit the Go button in the Go panel. In this case, only 3 subtrees satisfy the Specificity criteria, as presented in Table 5.

Table 5.

Output of case I. Tabulating Surface Area versus Path Distance for the 3 basal sub trees of neuron c10261. Each line can be read from right to left as neuronal tree name, followed by the two tabulated metrics. The V values represent the extracted measures for the 5 bins (e.g. V1: first value for bin 1).

Tree Name	Metric	V1	V2	V3	V4	V5	V6
c10261.CNGtree4.swc	PathDistance	112.7	142.09	171.48	200.87	230.26	259.65
	Surface	26.87	58.51	68.67	90.5	67.42	16.03
c10261.CNGtree2.swc	PathDistance	60.07	108.22	156.36	204.51	252.65	300.8
	Surface	71.4	305.64	403.86	459.72	264.7	93.57
c10261.CNGtree6.swc	PathDistance	84.02	126.05	168.09	210.13	252.16	294.2
	Surface	51.37	162.17	254.11	339.39	211.77	25.36

TIMING

All the examples explained in previous sections can be executed on both local and on-line version of LM. The on-line LM tool response time varies between few seconds to few minutes. For small number of input files (1–3), the output is given almost immediately. If the files are more than 10, then a response time between 1–2 minutes is normal. A statistical test between two groups, each with 10–25 neurons, would take 2 minutes of time. It is preferable to use the standalone version of LM for all computationally heavy tasks such as statistical tests, subtree analysis, and morphological searches. The online LM loading time is between 1–2 minutes depending upon the underlying RAM capacity of the machine and its Internet connection speed.

?TROUBLESHOOTING

• When running the standalone version, if the graphical user interface fails to show up by double clicking the Lm.jar icon, use the command line java –jar Lm.jar instead.

• An official LM support list server provides assistance to LM users in terms of technical and scientific questions (e-mail: l-measure-software-support-list@googlegroups.com).

ANTICIPATED RESULTS

At this stable and mature stage of development, LM strives to balance an intuitive and user-friendly design with a flexible execution of the measurement operations. With moderate practice, users can exploit the most sophisticated options of single-cell morphometry in just a few clicks. The dual availability of LM online and as a downloadable executable allows both an agile use through a standard web browser and the incorporation of the morphometric functionality in scripted batch processes and arbitrary manipulations of the results. In addition to the user documentation, a web-accessible and email-based support group is also active. Future additions and upgrades will be prioritized on the basis of the community requests.

The 8 protocols presented do not exhaustively cover all LM functionality, but show a range of potential applications. For example, Tables 2–5 report the results of morphological analysis carried out on multiple neurons, lending themselves to a direct interpretation. In Table 2, the two cells present total cable lengths of 13257.7 μm and 13044.9 μm, respectively. For the first neuron (c11563.CNG.swc), the distance between two consecutive tracing points averages 14.21 μm (±6.42), ranging from 1.12 to 42.51 μm over 933 data points. In Table 3 two groups of neurons, one with 23 cells and the other with 24, are statistically compared with respect to length, surface, and branch order. Only the difference in the average value of branch order is statistically significant between the two groups. Similarly, Table 4 presents the comparative analysis of two other groups of neurons selected based on a morphometric search. Results show statistical difference only for the average value of Rall’s power. Finally, Table 5 shows results relating surface area to path distance for the 3 basal dendrites of an individual neuron.

With minimal practice, simple variations of the above options will enable the reader to reproduce, alter, and enhance the data displayed in the four panels of Figure 3, which were plotted with MS-Excel after saving the results on the local hard drive as .xls file via the Output File button in the Output panel.