Edge Density Imaging: Mapping the Anatomic Embedding of the Structural Connectome Within the White Matter of the Human Brain

Abstract

The structural connectome has emerged as a powerful tool to characterize the network architecture of the human brain and shows great potential for generating important new biomarkers for neurologic and psychiatric disorders. The edges of the cerebral graph traverse white matter to interconnect cortical and subcortical nodes, although the anatomic embedding of these edges is generally overlooked in the literature. Mapping the paths of the connectome edges could elucidate the relative importance of individual white matter tracts to the overall network topology of the brain and also lead to a better understanding of the effect of regionally-specific white matter pathology on cognition and behavior. In this work, we introduce edge density imaging (EDI), which maps the number of network edges that pass through every white matter voxel. Test-retest analysis shows good to excellent reliability for edge density (ED) measurements, with consistent results using different cortical and subcortical parcellation schemes and different diffusion MR imaging acquisition parameters. We also demonstrate that ED yields complementary information to both traditional and emerging voxel-wise metrics of white matter microstructure and connectivity, including fractional anisotropy, track density, fiber orientation dispersion and neurite density. Our results demonstrate spatially ordered variations of ED throughout the white matter, notably including greater ED in posterior than anterior cerebral white matter. The EDI framework is employed to map the white matter regions that are enriched with pathways connecting rich club nodes and also those with high densities of intra-modular and inter-modular edges. We show that periventricular white matter has particularly high ED and high densities of rich club edges, which is significant for diseases in which these areas are selectively affected, ranging from white matter injury of prematurity in infants to leukoaraiosis in the elderly. Using edge betweenness centrality, we identify specific white matter regions involved in a large number of shortest paths, some containing highly connected rich club edges while others are relatively isolated within individual modules. Overall, these findings reveal an intricate relationship between white matter anatomy and the structural connectome, motivating further exploration of EDI for biomarkers of cognition and behavior.

Introduction

Brain connectomics is a burgeoning field; its network-centric view of the brain has the potential to uncover how information is rapidly communicated and integrated across multiple brain areas. Structural connectomics, based on graph theoretical analysis of networks constructed using white matter fiber tractography, has revealed the presence of highly connected regions, called hubs (Sporns et al., 2011, Hagmann et al., 2007, Hagmann et al., 2008), which are preferentially connected to one another, forming “rich club” networks (van den Heuvel & Sporns, 2011). Additionally, discovery of the modular organization of the brain (Hagmann et al., 2008) has deepened our understanding of which brain areas are densely interconnected, working in concert to solve complex problems.

Traditionally, the emphasis in connectomics has been placed on the cortical and subcortical gray matter regions that form the nodes of the network; however, there has recently been increasing interest in the white matter pathways that constitute the edges of the network (van den Heuvel & Sporns, 2013). However, even in the latest connectome studies, these edges are represented as abstractions within a “connectogram” without realistic three-dimensional spatial embodiment. While this simple representation of the wiring of the human brain is useful for conventional graph theoretical analysis, we posit that that there is valuable information that can be derived from the geometric trajectories of these edges through white matter. We know from numerous diffusion tensor imaging (DTI) studies of white matter microstructure that parameters such as fractional anisotropy (FA) vary across white matter tracts (Pierpaoli et al., 1996). This variation indicates that some tracts are more organized and/or myelinated, which is maintained by increased metabolic output, and are therefore likely to be particularly essential for communication within the brain network. The regional variation of white matter microstructure has been validated using more complex biophysical models based on diffusion MR imaging, such as neurite orientation dispersion and density imaging (Zhang et al., 2011). Track density (TD) imaging (Calamante et al., 2010), which uses streamlines from diffusion tractography to achieve super-resolution images, also shows tract-by-tract variation in streamline packing. It remains to be determined how these regional differences in white matter tract organization are related to the structural connectome.

“Importance maps” have been generated by simulated lesioning of the white matter in healthy controls and then quantifying the effect on network parameters (Kuceyeski et al., 2011). In Kuceyeski et al (2013), a tool is presented that maps changes in white matter integrity to resulting deficits in cortical and subcortical gray matter connectivity using normative data from healthy controls. There has also been an effort to identify those connectome edges most important to the overall network by simulated removal of individual edges to examine the change in graph metrics (Irimia & Van Horn, 2014). These artificial lesion-based methods do uncover variations in “importance” across white matter tracts (Kuceyeski et al., 2011) or connectome edges (Irimia & Van Horn, 2014) not replicated by traditional DTI or tractographic measures; however, they place an emphasis on global network measures to calculate the importance of each voxel or edge. In another new approach to an “edge-centric” perspective on the connectome, de Reus et al., (2014b) decompose the edges of the connectome into link communities, as opposed to segregating nodes into modules, as is commonly done. They uncover communities of edges not detected with node-based methods. They also investigate the relevance of individual edges with respect to network characteristics, such as path length and clustering coefficient, by using an artificial lesioning approach. However, it has recently been shown by the same authors that measuring the effects of artificial lesions on the entire network varies greatly based on the graph metric used (de Reus & van den Heuvel, 2014a), and it remains unclear which metrics are the most appropriate. Furthermore, these simulated lesion-based methods do not directly address the connectomic properties of particular white matter tracts.

In this work, we focus on the anatomic embedding of the structural connectome within the white matter of the human brain. The connectional anatomy of white matter is of great significance, since developmental processes such as myelination progress in an anatomically defined manner, and many common white matter disorders affect specific anatomic regions and/or extend contiguously through the white matter without respecting the boundaries of particular fiber pathways. Therefore, a greater comprehension of the structural connectome's physical instantiation in white matter will shed light on neurodevelopment and many neuropathologies. A crucial advantage of our approach is that connectome edges are not treated as if they were entirely independent of each other. Rather, a region of white matter where different edges converge is recognized, which is important since those edges will share a common vulnerability to lesions at that spatial location.

By tracing the three-dimensional path of each structural connection between cortical and subcortical gray matter regions, we compute the number of edges that pass through each voxel in white matter, a measure we call “edge density” (ED). This concept can be thought of as grouping tractography streamlines into edges that connect cortical and subcortical nodes of the connectome. The network nodes can be defined using a standard atlas parcellation of the gray matter, as is commonly practiced in connectome studies. This approach uses prior anatomic knowledge to maximize the homogeneity of function and connectivity within each node and minimize the overlap of function and connectivity between different nodes. This has the added benefit of improving inter-subject reproducibility since anatomic features (i.e., sulci and gyri) used to perform the atlas parcellation are largely conserved across subjects compared to a random gray matter parcellation, for instance. From whole-brain edge density imaging (EDI), we show that there are large variations amongst white matter tracts in their concentration of connectomic edges. We further map the white matter regions that are enriched with pathways connecting rich club nodes, as well as those with high densities of intra-modular and inter-modular edges. ED is compared to other voxel-wise parameters of FA and TD, as well as fiber orientation dispersion (OD) and neurite density (ND) from neurite orientation dispersion and density imaging (NODDI), to show that edge density yields complementary information to previously described diffusion MR-based measures of white matter for use in better understanding the complex connectional architecture of the human brain during development, healthy aging and in disease states.

Methods

MRI Acquisition

Siemens healthy volunteer data

Ten healthy adult subjects (five male, five female; mean age 26.7 ±5.9 years; nine right-handed) were scanned twice with an average of 30.4±2.7 days between scans. All study procedures were approved by the institutional review board at the University of California at San Francisco (UCSF) and are in accordance with the ethics standards of the Helsinki Declaration of 1975, as revised in 2008.

MRI was performed on a 3T TIM Trio MR scanner (Siemens, Erlangen, Germany) using a 32-channel phased-array radiofrequency head coil. High-resolution structural MRI of the brain was performed with an axial 3D magnetization prepared rapid-acquisition gradient-echo (MPRAGE) T1-weighed sequence (echo time [TE] =1.64ms, repetition time [TR] = 2530 ms, TI = 1200 ms, flip angle of 7°) with a 256-mm field of view (FOV), and 160 1.0-mm contiguous partitions at a 256 × 256 matrix. Whole-brain diffusion-weighted images were collected at b=1000 s/mm² with 30 directions and, for one subject, an additional diffusion series with b=3000 s/mm² with 64 directions was collected. For both diffusion weightings, we used a multislice 2D single-shot twice-refocused spin-echo echo-planar sequence, the iPAT technique for parallel imaging with a reduction factor of 2; NEX=1; interleaved 2 mm axial sections with no gap; in-plane resolution of 2 × 2 mm with a 128x128 matrix; and a field of view of 256 mm. The echo time (TE) and repetition time (TR) were slightly different for the two diffusion weightings: for b=1000 s/mm², TE/TR=80/10000 ms and, for b=3000 s/mm², TE/TR=119/13900ms.

Connectome Construction

Data preprocessing

After the nonbrain tissue was removed using the Brain Extraction Tool (Smith, 2002), the diffusion-weighed images were corrected for motion and eddy currents using the FMRIB linear-image registration tool (FLIRT) with a 12-parameter linear image registration (Jenkinson et al., 2002) using the b=0 s/mm² image as the reference. The FA image was calculated using FSL's DTIFIT. Using FLIRT, the FA map of every subject and session was registered to the T1 in order to obtain a diffusion to structural transform.

Cortical parcellation

The T1-weighed MR images were automatically segmented using the Desikan-Killiany atlas (Desikan et al., 2006) from FreeSurfer 5.1.0 (Fischl et al., 2004) with the default settings of recon-all, resulting in 68 cortical regions and 14 subcortical regions. The 68 cortical regions were transformed to the gray– white matter boundary (GWB) using FreeSurfer. These 82 regions represent the nodes of the connectome.

Fiber Estimation and Tractography

Bedpostx (Behrens, et al. 2007) was run to estimate the fiber orientation at every voxel (with a maximum fiber number of two and other default settings). Then, using FLIRT with the default settings, the affine transform from diffusion to structural space was calculated by registering the FA volume to the T1 volume. Each of the cortical GWB volumes and the subcortical volumes was registered to the diffusion space to be used as seeds for the tractography. Probabilistic tractography was performed with probtrackx2 (Behrens et al., 2007), with 1000 streamlines initiated from each seed voxel; we used the distance weighting option to aid the tracking of long-range connections. To extract only the direct connections between each seed and target region, the target volume was used as a waypoint mask and all 80 other volumes besides the seed and target volumes were included in an exclusion mask. To achieve this objective, 82*81 = 6642 tractography runs were performed using the parallel computing grid infrastructure of the California Institute for Quantitative Biosciences (QB3) at UCSF. The tractography results were then binarized to create a mask of white matter voxels needed to connect each pair of cortical/subcortical regions. In order to compute network properties, we generated a consensus connectome as in Owen et al. (2013a). The consensus connectome had a density of 0.16.

Edge Density Imaging

Edge Density Imaging

We define edge density (ED) as the number of structural connectome edges that pass through a particular voxel in white matter. In this way, the white matter regions that contain many edges have greater weighting, whereas white matter regions that participate in relatively few edges have lesser weighting. ED can be computed as a simple count of the number of edges that pass through each voxel, done by adding together the binarized tractography results, or with several variations that we describe below.

Track Density Imaging

Track Density Imaging (TDI) is defined as the density of streamlines within each voxel, rather than the density of edges (Calamante et al., 2010). We have performed TDI for comparison to EDI. T1 images were segmented using FSL's fast segmentation tool, and resultant white matter masks were registered to each subject's FA map. Probabilistic fiber tractography was performed using probtrackx2 with 1000 streamlines initiated from each white matter voxel, and the resultant streamline probability distribution was considered to be the track density (TD) image.

Comparing ED, FA, and TD

The ED, FA, and TD maps were masked by a white matter mask generated from FreeSurfer to include only white matter voxels for subsequent scatter plots. The mean and standard deviation of Spearman's rank correlation coefficient (ρ) was computed between 1) ED and FA and 2) ED and TD for the first scan of each of the 10 subjects. We also plot histograms of the ED, FA, and TD values for a representative subject and calculate the mean and standard deviation of the skewness (γ₁) and kurtosis (γ₂) for the first scan to quantify differences in the distributions of these voxel-wise measures.

Probability of Crossing Fibers

We computed an approximation of the probability of crossing fibers, p(CF), in every voxel by subtracting the volume fraction of the first fiber (f1) and second fiber (f2) as obtained from bedpostx. We use p(CF)=1-(f1-f2), where p(CF) is bounded between 0 and 1. A p(CF) close to 0 ( f1>>f2), indicates a high likelihood of only one fiber in the voxel, while a p(CF) close to 1 (f1≈f2) indicates the presence of two fibers in the voxel.

Multi-compartment Biophysical Modeling

In order to further compare EDI to other voxel-level parameters of white matter, we applied the NODDI software (http://www.nitrc.org/projects/noddi_toolbox; Zhang et al., 2011; Zhang et al., 2012) to the b=1000 s/mm² and b=3000 s/mm² data from one subject. We computed two parameters: fiber orientation dispersion and intracellular volume fraction, also known as neurite density. OD, first described in Zhang et al. (2011), is a measure of the orientation dispersion or the degree to which the neurites, specifically axonal fibers in white matter, have an incoherent orientation distribution in a particular voxel. ND is the fraction of the tissue compartment that is intracellular, as opposed to extracellular, and is thought to be proportional to the axonal density in white matter. The NODDI code was modified to fit the model to the data normalized by the b=0 s/mm² images per the developers’ recommendation to account for the differing TE/TR times between the b=1000 s/mm² and b=3000 s/mm² acquisitions. The OD and ND maps were masked by a white matter mask generated from FreeSurfer. Then, we calculated ρ for 1) ED and OD and 2) ED and ND for the one subject.

Individual Tract Values and Test-retest Reliability

In order to quantify the ED, FA, and TD of various tracts, we registered each individual subject's T1 MRI to the MNI template and then registered the ED, FA, and TD images to MNI space using the diffusion to structural and structural to MNI transforms computed with FLIRT with the default settings. Using the ICBM-DTI-81 white matter labeled atlas (Mori et al., 2008) and the JHU white matter tractography atlas (Wakana et al., 2004) in FSL, the mean ED, FA, and TD were calculated in 31 supratentorial white matter tracts. We also computed a mean ED and TD image in MNI space by averaging over all scans. To quantify the stability of the tract-wise ED, FA, and TD values, we used the pooled within-group percentage coefficient of variation (CoV) and the intraclass correlation coefficient (ICC). CoV is defined as the ratio of the mean intrasubject standard deviation (SD) to the overall measurement mean (Lachin, 2004; Vaessen et al., 2010). CoV measures the precision of a metric for all subjects. ICC is the ratio of intersubject variance to the sum of intersubject and intrasubject variance. According to the well-established guidelines for clinical research (Fleiss, 1986; Tooth et al., 2005), ICC values below 0.4 are considered poor reproducibility, ICC values between 0.4 and 0.75 are considered fair-to-good reproducibility, and ICC values above 0.75 are considered excellent reproducibility.

EDI with Rich Club Connections

In order to further examine the white matter anatomy of the structural connectome, we segregated the connectome edges based on the connections of the rich club (van den Heuvel & Sporns, 2011). The rich club is comprised of highly connected nodes, known as hubs, which are also densely connected to one another. Following the methods in van den Heuvel & Sporns (2011), we used the maximization of the normalized rich club coefficient to identify the nodes that constitute the rich club for the consensus connectome. The edges between rich club members are termed rich club connections (RC), while edges that connect non-rich club nodes to rich club nodes are termed feeder connections (FC), and the edges that connect non-rich club nodes are referred to as local connections (LC). We computed ED maps of RC, FC, and LC for each scan session, and then generated a mean image for each type of connection in MNI space. In addition, we calculated mean ED for the previously described 31 white matter tracts within the maps of RC, FC, and LC.

EDI with Modular Connections

A module can be defined as a set of nodes that are densely interconnected, and have sparse connections to other nodes not in the module. Communication between members of a module reflects segregation in the network, while communication between modules reflects integration. Module assignments for the consensus connectome were provided by the community detection algorithm proposed in Blondel et al. (2008) as implemented in the Brain Connectivity Toolbox (Rubinov et al., 2010). Due to the stochasticity of the algorithm, we selected the modules that were most stable (appearing most frequently). Then, we calculated ED maps of intra- and inter-modular edges for each scan session. A mean image of the intra- and inter-modular edges was generated in MNI space, and we calculated mean ED of the 31 white matter tracts within the intra- and inter-modular ED maps. The structural core module (Hagmann et al., 2008) is of special importance because it contains many high degree nodes and is the link between the left- and right-lateralized modules. We generated intra- and inter-module ED maps for the structural core module alone and calculated the mean ED for the JHU atlas tracts to determine which tracts facilitate intra- and inter-modular communication for this important module.

Edge Weighted Imaging (Weighted EDI)

To this point, we have only summed the edges traversing each voxel in a binary fashion. Alternatively, it is also possible to assign a weight to every edge and then perform the summation, which we refer to as “edge weighted imaging” (EWI) by analogy to track weighted imaging (TWI) as proposed by Calamante et al., (2012). We have explored two such weightings here: degree-weighted (dwEDI) and edge centrality-weighted (cwEDI). For the degree-weighting, we weight every edge by the mean degree of the two nodes it connects. The motivation for degree weighting follows that of the rich club, where an edge connecting high degree nodes is likely an important edge in the network. The edge centrality-weighting is done by weighting every edge by the edge betweenness centrality (EBC), a graph measure that calculates the fraction of all shortest paths in the network that utilize a certain edge. If an edge has high EBC, it facilitates many shortest paths and must be essential in the quick transfer of information between nodes. Edge betweenness centrality was computed for every edge in the consensus network using the Brain Connectivity Toolbox. We computed ρ between a) ED and dwEDI and b) ED and cwEDI of every white matter voxel for the first scan for all 10 subjects.

Dependence of EDI on Atlas Parcellation and on Diffusion MRI Acquisition Parameters: Since EDI depends on how the network nodes are defined, we examined how EDI results vary with the cortical/subcortical parcellation schemes of the three most commonly used atlases: the Desikan-Killiany atlas from Freesurfer (Desikan et al., 2006), the Automated Anatomic Labeling atlas (Tzourio-Mazoyer et al., 2002), and the Harvard-Oxford atlas (Kennedy et al., 1998). As a complementary analysis using a different form of parcellation and at a higher level of granularity, we employ a newly developed high resolution atlas based on a functional connectivity-based parcellation of the cortex derived from resting state blood oxygenation level dependent (BOLD) functional MRI (Gordon et al, 2014). This functional atlas has 333 cortical parcels, compared to fewer than 110 for each of the three anatomic atlases.

Since the fiber tractography in EDI could depend on the particular diffusion MR imaging acquisition parameters used, we explored how EDI metrics vary with two different diffusion MR imaging protocols: one on a General Electric (GE) scanner and one on a Siemens scanner. The description of the Methods and Results for the comparison of atlas parcellations and of diffusion MRI scan parameters can be found in the Supplementary Materials in Sections S5 and S6 (Figures S2, S3, and S4).

Results

EDI: Variation across tracts and comparison to other white matter parameters

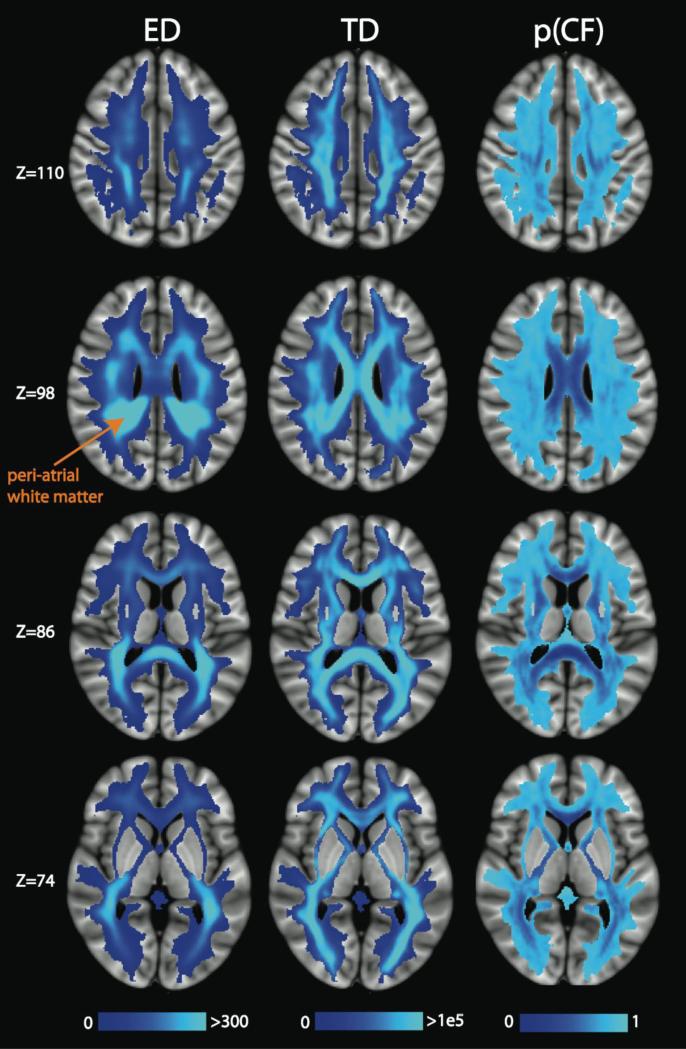
In Figure 1, we display axial slices through the mean ED image (left), mean TD image (center) and the mean p(CF) image (right) in MNI space, derived using the Desikan-Killiany atlas parcellation. ED demonstrates strong regional variation, with the greatest ED values present in deep white matter tracts, especially in the periventricular areas. The ED also tends to be higher in posterior tracts than anterior tracts. This anterior-posterior gradient is particularly evident in the corpus callosum with the splenium being brighter than the genu and body. The periatrial white matter has the highest edge density of all. Since these periatrial regions are close to the corpus callosum, we calculated the percentage of callosal, association, and projection edges passing through these very high ED areas, using the PCR atlas ROI to define the high ED region in each hemisphere, and compared to the edges passing through the ACR. We found that, for the PCR and ACR, the percentage of callosal edges is similar (22-26%) and represent the minority of the edges, while the proportions of association and projection edges differ between ACR and PCR, but together represent the majority of the edges. More details of these results can be found in Section S1 of the Supplementary Materials.

Figure 1.

Axial slices of the mean ED, TD, and p(CF) in MNI space, averaged over all 20 scans (2 per subject). The peri-atrial white matter (orange label) has particularly high ED. These results and those of Figures 2-13 were derived using the Desikan-Killiany atlas parcellation.

Comparing the ED and TD images, we observe the anterior vs posterior differences in the TD maps, too, but to a lesser degree. In the Z=110 slice, the peri-rolandic white matter shows dense streamlines on the TD map, but carries relatively few connectome edges on the ED map. A more even distribution of TD across tracts is evident in the Z=86 and Z=74 slices, whereas voxels of high ED are primarily constrained to the posterior corona radiata (PCR) and splenium of the corpus callosum. The p(CF) maps show that the presence of crossing fibers does not explain the regions of high ED. Rather, there are regions with high ED and high p(CF), such as the PCR, and regions with high ED and low p(CF), such as the corpus callosum.

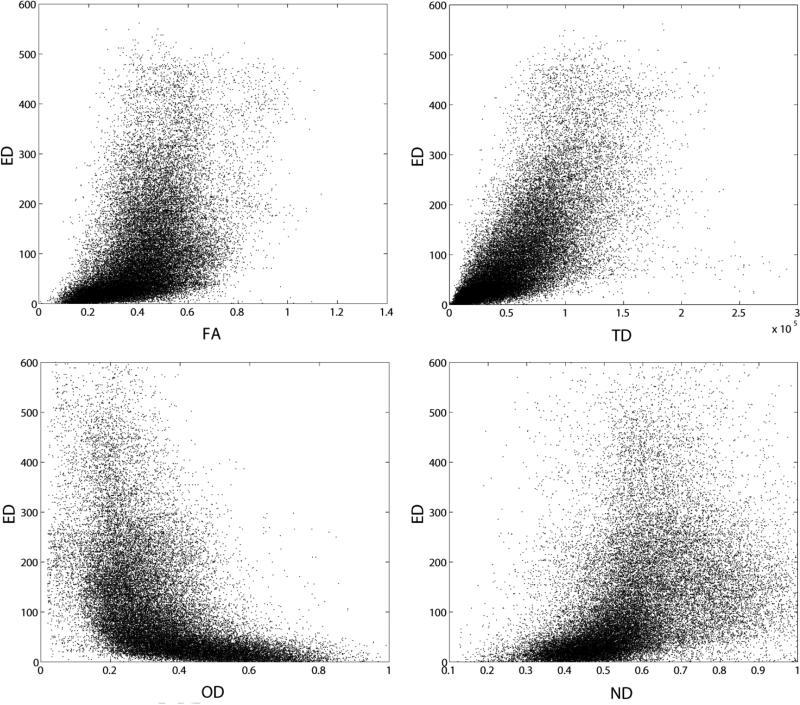
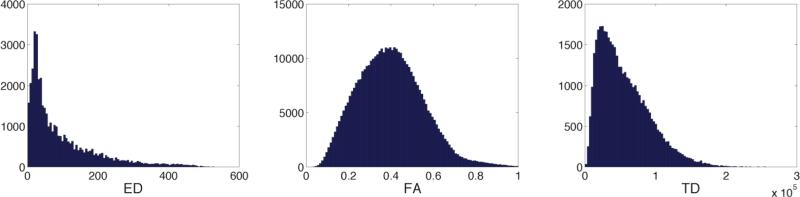
In Figure 2, scatterplots of ED versus FA, TD, OD, and ND are illustrated for one representative subject. We plot one tenth of the voxels for clarity. Most notable is that there is not a straightforward correlation between any of the white matter metrics and ED. The FA vs. ED plot (ρ=0.59±0.04) reveals that there are many voxels with moderate FA (0.3-0.6) that have relatively high ED (ED>100). We demonstrated in Figure 1 that the density of streamlines (TD) and ED do not have the same spatial distribution. While the strongest of these correlations exists between TD and ED, track density accounts for only one-half of the variance in edge density (ρ=0.79±0.02). Interestingly, there is an inverse relationship between ED and OD (ρ=−0.64), i.e., voxels with large orientation dispersion tend to have low ED. The majority of the voxels with high ED (ED>200) have OD of 0.5 or less. The association with ND (ρ=0.57) is to be expected: voxels with higher neurite density also have higher ED, although the voxels with the highest ED are in the middle range for ND, leading to a relatively weak correlation. In Figure 3, the histograms of ED, FA, and TD are presented for one subject. The shape of the distribution is markedly different between parameters; we use the kurtosis and skewness of the distributions to quantify the differences. The histogram of ED has the highest mean skewness (γ₁=1.8±0.2) and kurtosis (γ₂=3.5±1.1), next in order is the histogram of TD with a mean skewness of 1.0±0.1 and mean kurtosis of 0.9±0.5, and the histogram of FA has the lowest mean skewness (γ₁=0.5±0.1) and mean kurtosis (γ₂=0.1±0.1).

Figure 2.

Scatter plots of FA vs. ED, r=0.51 (upper left), TD vs. ED, r=0.71 (upper right), OD vs. ED, r=−0.51 (lower left), and ND vs. ED, r=0.41 (lower right) for one representative subject.

Figure 3.

Histograms of ED, FA, and TD for one representative subject.

Reproducibility of EDI and Region of Interest Analyses

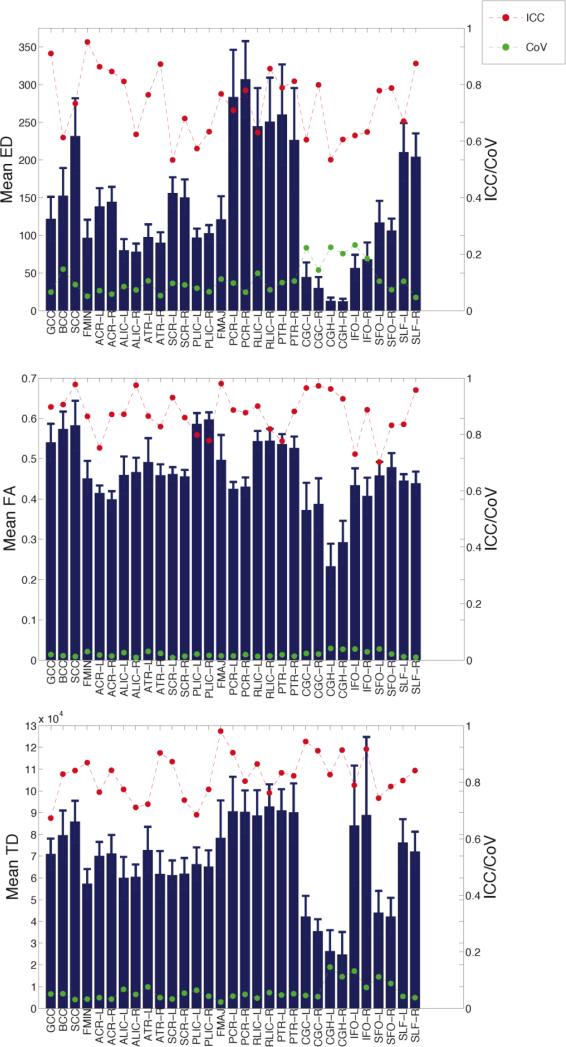
In Figure 4, we display the test-retest reliability of ED, FA, and TD using the two scans acquired from every subject; the reliability metrics are superimposed on the bar graphs for the mean ED, FA, and TD in the 31 white matter tracts (with standard deviation error bars). The increased ED in posterior tracts is evident in these averages: the PCR, posterior thalamic radiations (PTR) and retrolenticular internal capsule (RLIC) have the highest ED. These posterior tracts have average ED that is much greater than their anterior counterparts: anterior corona radiata (ACR), anterior thalamic radiations (ATR), and anterior limb of the internal capsule (ALIC). Likewise, the splenium of the corpus callosum (SCC) has higher ED than both the body (BCC) and the genu (GCC).

Figure 4.

Reliability of mean ED (top), FA (middle), and TD (bottom). The heights of the bars indicate the mean in each white matter tract and the error bars show the standard deviation. The red points/line indicate ICC and the green points/line indicate CoV.

Comparing ED to FA, we find some interesting divergences. First, there is less variation across tracts for FA than for ED; many tracts have average FA in the range of 0.4-0.5. Each segment of the corpus callosum has high FA, yet the GCC and BCC have only moderate ED. The posterior limb of the internal capsule (PLIC) has higher FA than the RLIC or ALIC, but the RLIC has the highest ED. The inferior fronto-occipitial fasciculus (IFO) has relatively low ED given that the FA is in the range of the majority of the tracts.

As expected from the voxel-wise scatterplot of TD versus ED in Figure 2, the tract-specific values of TD and ED are more similar than FA and ED (Figure 4). However, there are several apparent differences. In particular, the bilateral IFOs demonstrate high mean TD but low mean ED. There is also less regional variation in the mean TD values than in mean ED, as also observed with mean FA. The mean TD in many of the posterior tracts is higher than the anterior tracts, although the asymmetry is less dramatic than for ED. To confirm these qualitative findings, in Table S2 of the Supplementary Materials, we provide a statistical analysis comparing the mean ED, FA, and TD in pairs of tracts (anterior versus posterior), as well as the ratio of anterior:posterior for these pairs of tracts (Table S3). We also performed a secondary analysis to determine if the posterior bias in ED is driven by more voxels being seeded in the posterior brain regions. We found no evidence to support this supposition. See Section S3 of the Supplementary Materials for details.

The ICC values in red indicate that the mean ED has excellent reproducibility (ICC>0.75) in 16 tracts and fair-good reproducibility in the remaining tracts, with most ICC values above 0.6 (Figure 4). The CoV values shown in green also point to mean ED being a reliable brain measure with relatively little test-retest variability. We calculated a CoV<10% in 18 tracts, most of which also have high ICC. There are some tracts with high CoV (CoV>20%), which can be attributed to low mean ED. The ICC and CoV for the mean FA indicate better test-retest reliability than for ED; all ICC values are above 0.6 (with 29 tracts at ICC>0.75) and all CoV values are below 5%. The reproducibility of mean TD is also better than mean ED, as all the ICC values for TD are above 0.6 (with 25 tracts at ICC>0.75) and all CoV values are below 15% (with CoV<10% in 27 tracts).

Anatomic embedding of the rich club pathways

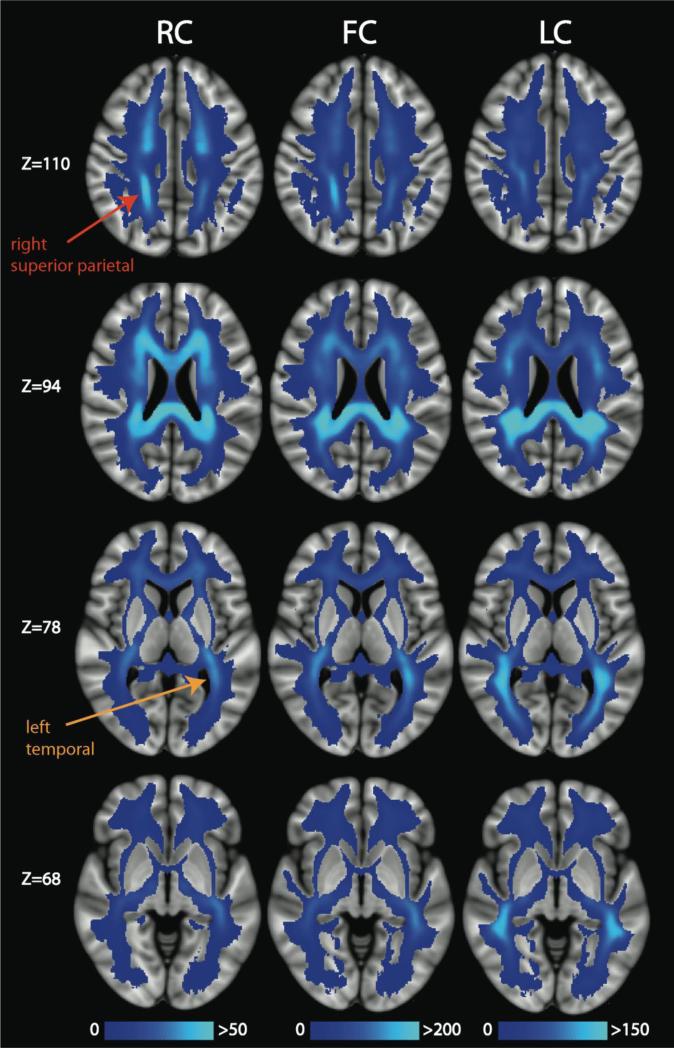
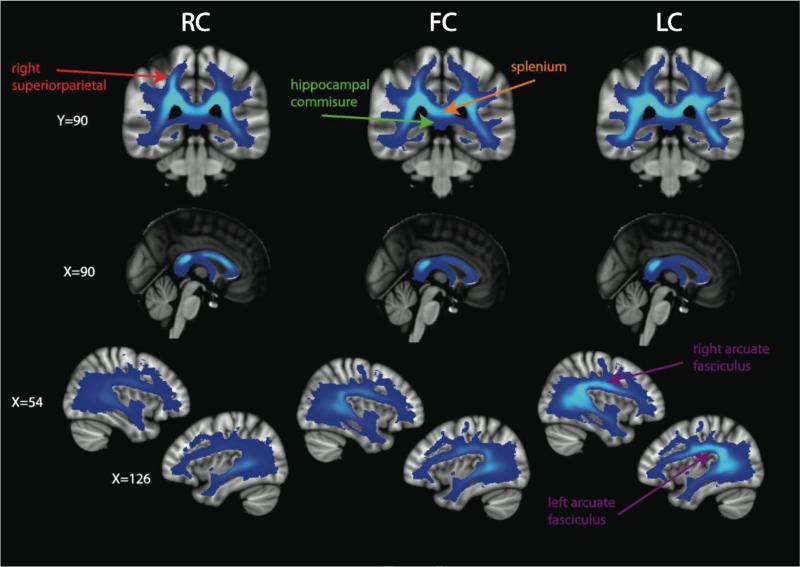
The 12 rich club nodes were identified as: bilateral precuneus, bilateral superior frontal lobes, right superior parietal lobe, left insula, bilateral thalamus, bilateral putamen, and bilateral caudate. These findings are in close agreement with those of van den Heuvel & Sporns (2011). However, they find the bilateral hippocampus to belong to the rich club, whereas we find the bilateral caudate and left insula to be rich club nodes. We display ED broken down into rich club connections (RC), feeder connections (FC), and local connections (LC) in Figures 5 and 6. In the axial slices presented in Figure 5, it is evident that the spatial distributions differ between the RC, FC, and LC. The RC pathways are found primarily in medial white matter tracts and demonstrate a fairly even anterior to posterior distribution. In contradistinction, the FC and LC show a stronger posterior bias than for RC, which accounts for the overall posterior > anterior asymmetry of ED values. FC and LC also extend more laterally than RC, with LC being the most lateral of the three edge subtypes. The RC extend farther superior into the superior corona radiata than the FC and LC, especially in the frontal lobes (Figure 5). In Figure 6, we present alternative views of the RC, FC, and LC. These illustrate that the RC have a right > left asymmetry in the parietal lobes, most evident on the coronal images, that is not as strong for the FC and not present at all for the LC. Conversely, there is a left > right asymmetry in the temporal lobes (z=68) for the RC; this bias is also present in the FC but not in the LC. In the midline sagittal images, we show that the GCC, BCC, and SCC all contain RC pathways, whereas the SCC is more implicated than the GCC and BCC in FC and LC connectivity. In Figure 6, we delineate the SCC and the hippocampal commissure to demonstrate the relatively high RC, FC, and LC in the former and the low RC, FC, and LC in the latter. The parasagittal images at x=54 and x=126 demonstrate that the right and left SLF, including the arcuate fasciculus, are most enriched with LC edges, less so with FC, and only slightly (left more than right) in the RC. To corroborate these qualitative observations on the laterality of edge densities in the parietal and temporal regions, Section S4 of the Supplementary Materials contains a statistical comparison of the left versus right mean ED, RC, FC, and LC values (Figure S1 and Table S4).

Figure 5.

Axial slices of the mean ED for the rich club connections (RC), feeder connections (FC), and local connections (LC). The mean was calculated across 20 scans in MNI space. We point out regions with asymmetrically high mean ED for the RC in right superior parietal (red label) and left temporal (orange label) white matter.

Figure 6.

Alternate views of the mean ED for the RC, FC, and LC. The color bar in Figure 5 applies to these images. A region of high ED for the RC in right superior parietal white matter is indicated with a red label, the splenium (with high RC, FC, and LC) and the hippocampal commissure (with low RC, FC, and LC) are is shown with orange and green labels, respectively, and the arcuate fasciculus, which is particularly high ED for LC, compared to RC or FC, is identified with purple labeling.

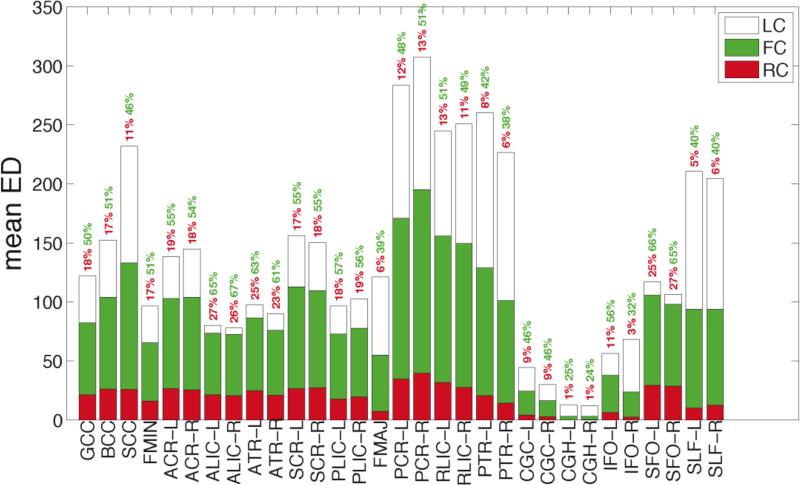
For a more comprehensive analysis of tract-specific measures of RC, FC and LC, we computed their mean values in 31 white matter tracts from the JHU atlas, the results of which are displayed in Figure 7. The RC, FC, and LC are shown in red, green, and white, respectively; the heights of the three bars add up to the mean ED values presented in Figure 7. We also provide the percentage of edges within each tract that are RC (red) and FC (green). There is considerable variability among white matter tracts in their content of rich club connections. The dorsal and ventral cingulum (CGC and CGH, respectively) and the IFO have little contribution from rich club pathways. Percentage-wise, the left and right ALIC (26 and 27%), left and right ATR (25 and 23%), and SFO (25 and 27%) have the largest fraction of RC edges. The feeder connections are less evenly distributed across white matter tracts than even the RC, and their posterior bias is evident when comparing the ACR, ALIC, and ATR with the PCR, RLIC, and PTR, respectively. While the absolute number of FC edges may be higher in the posterior tracts, interestingly, the fraction of edges that are FC is higher in these anterior tracts, with percentages ranging from 54-67% whereas the percentages for the posterior tracts range from 38-51%. Despite their low overall ED, close to 50% of CGC and IFO edges are FC. In contradistinction, the bilateral SLF are enriched with LC, comprising more than 50% of their edges.

Figure 7.

Bar graph for the mean RC (red), FC (green), and LC (white). The percentages reflect the percentage of the tract's edges that are RC (red) and FC (green).

White matter facilitating network segregation and integration

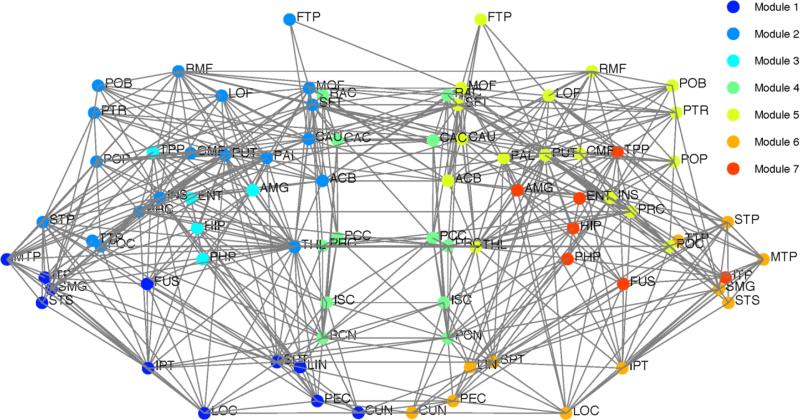
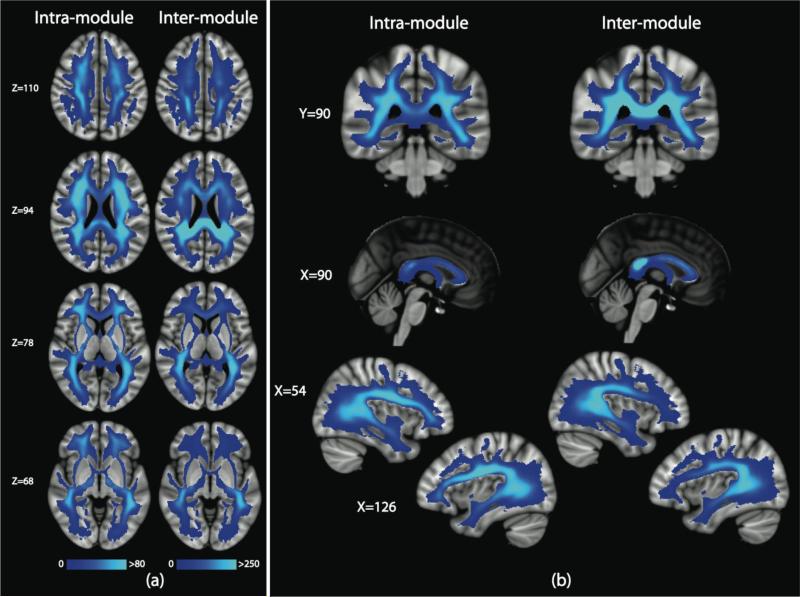
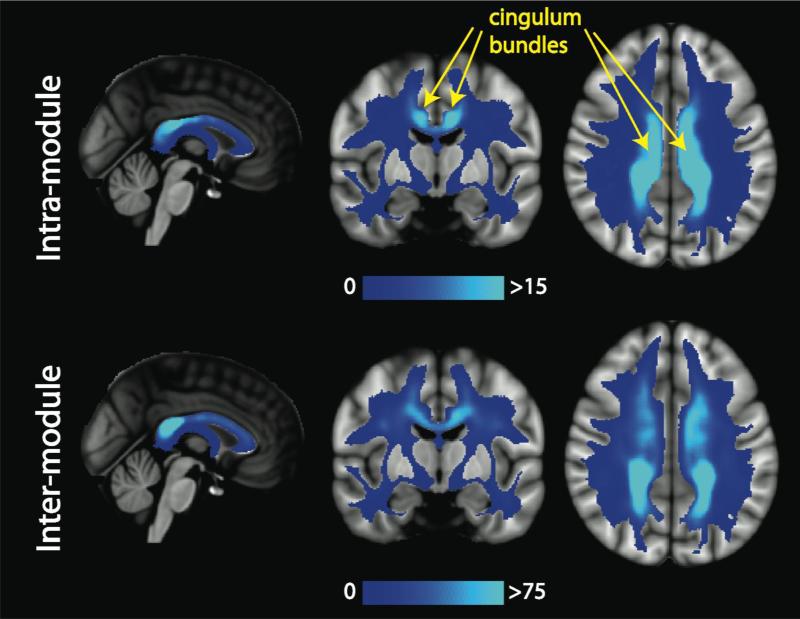
In Figure 8, we provide the modular decomposition of the consensus connectome. There are seven modules detected: a frontal-temporal-subcortical module on the left (Module 2) and right (Module 5), a bilateral structural core module (Module 4), an occipital-temporal-parietal module on the left (Module 1) and the right (Module 6), and a limbic module on the left (Module 3) and the right (Module 7). We subdivide the edges of the connectome into those that are intra-modular versus inter-modular (Figure 9a). We find that the intra-module edges are distributed throughout the brain, without a strong posterior bias. The corpus callosum is not heavily represented in the intra-modular edges, as demonstrated in the midline sagittal view of Figure 9b. The inter-modular edges, however, do exhibit the posterior bias. The corpus callosum carries many inter-module edges and there is a fair amount of symmetry in the parietal and temporal (SLF) regions found to be biased in the statistical analysis of the ED and RC maps. In Figure 10, we explore the intra- and inter-modular connections specifically associated with the structural core module. The cingulum and body and splenium of the corpus callosum carry many of the intra-modular edges for the structural core. The inter-modular edges connecting the structural core nodes with the rest of the brain utilize many white matter tracts, including the PCR, SCC, ACR, SLF and IFO.

Figure 8.

The modular decomposition for the consensus connectome. Seven modules were detected: a frontal-temporal-subcortical module on the left (Module 2) and right (Module 5), a structural core module (Module 4), an occipital-temporal-parietal module on the left (Module 1) and the right (Module 6), and a limbic module on the left (Module 3) and the right (Module 7). Each node is placed at the centroid of the FreeSurfer region. The right side of the brain is displayed on the right of the diagram.

Figure 9.

(a) Mean ED for the intra-module edges and inter-module edges show in axial views and (b) alternative views.

Figure 10.

The mean ED for the intra-module and inter-module edges for the structural core. The cingulum bundles (yellow) are highly utilized by the intra-modular edges of the structural core.

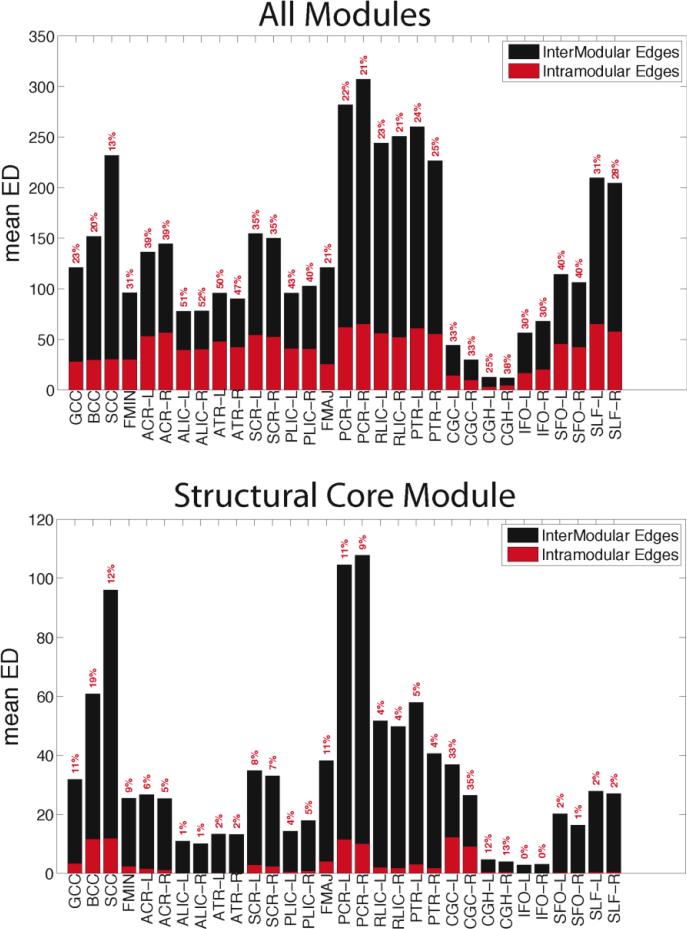
The relative proportions of intra- and inter-modular edges for all modules (top) and only the structural core (bottom) are provided in Figure 11. For all modules, almost half the edges that traverse the ALIC, ATR, and PLIC are used for intra-modular communication, whereas the posterior tracts (SCC, PCR, RLIC, PTR) have relatively low percentages. Most of the large tract-wise variation in ED values is due to its inter-modular component. For the structural core module, the BCC, SCC, PCR, and CGC emerge as the tracts most utilized for intra-modular communication. The CGC has low overall ED, but it emerges as an essential tract in the relaying of information in the structural core, with roughly 35% of its edges communicating within the module.

Figure 11.

Bar graphs for the mean ED for the intra-module (red) and inter-module (black) edges for all 7 modules (top) and just the structural core module (bottom). The percentages in red reflect the percentage of each tract's edges that are intra-modular.

Adding edge weights

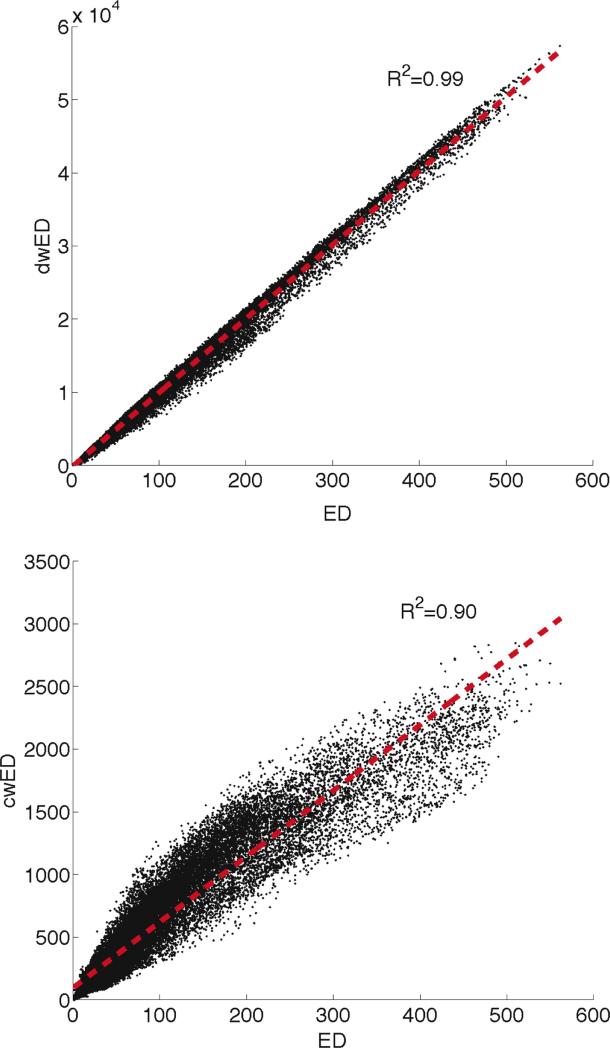
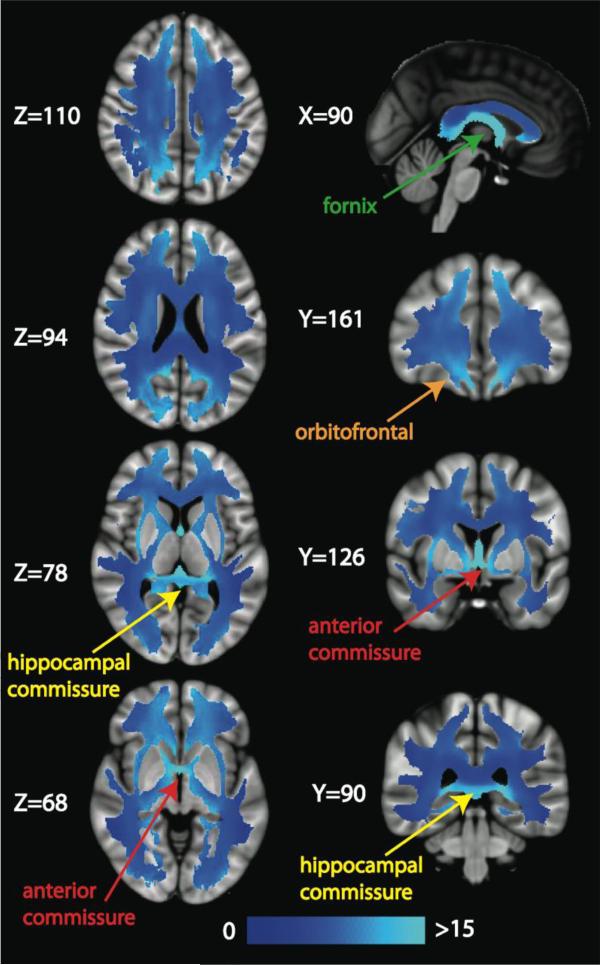
We investigate two weighting schemes for EWI, weighting by nodal degree (dwED) and by edge betweenness centrality (cwED). Plots of the voxel-wise correlation of unweighted ED with dwED (top) and with cwED (bottom) for one representative subject are displayed in Figure 12. The correlation between ED and dwED reveals that weighting by degree does not add much additional information (R²=0.99). This result implies that voxels with high ED do not necessarily carry only high degree edges, rather the degree weightings are evenly spread throughout the white matter. In contradistinction, the scatterplot of ED versus cwED (R²=0.90) shows that the edge centrality weighted values do differ from the ED (and dwED) values. We further investigated this divergence by computing cwED/ED for every voxel in the mean image volume (averaged over 20 scans) in MNI space (Figure 13). The mode of these parametric maps is 7, meaning that more voxels contain 7 shortest paths than any other number of shortest paths. Twenty percent of the voxels have 7 shortest paths and 80% have 5-9 shortest paths. There are regions of white matter that have much greater densities of shortest paths (on average, 20 shortest paths/voxel), such as the fornix (Z=78, X=90, Y=90), hippocampal commissure (Z=78, X=90, Y=90), and anterior commissure (Z=68, Y=126). These tracts connect the hippocampus to the rest of the brain and therefore have high edge betweenness centrality that is not diluted by low betweenness centrality edges. There are also regions in the peripheral white matter in the superior occipital/parietal lobes (Z=110 and Z=94) and in the orbitofrontal cortex (Z=68 and Y=161) that have many shortest paths.

Figure 12.

Scatter plots for the weighted ED: ED vs. dwED (top) and ED vs. cwED (bottom). The red line is a linear fit and we provide the coefficient of determination (R²) for the fit.

Figure 13.

Slices of the average number of shortest paths (or mean edge betweenness centrality) image calculated by dividing the mean cwED image by the mean ED image in MNI space. Several white matter structures with a high average number of shortest paths are illustrated with labels and arrows: the fornix (green label), the orbitofrontal white matter (orange label) and the hippocampal (yellow label) and anterior (red label) commissures.

Discussion

The anatomic embedding of the structural connectome within white matter

Until recently, most connectome research has focused on the gray matter regions that serve as the nodes of the brain graph, including efforts to understand the effect of damage to the network through analysis of the effect of simulated lesions. In Alstott et al. (2009), artificial lesions to nodes along the cortical midline, temporoparietal junction, and frontal cortex were determined to be the most disruptive to the functional connectome. In a subsequent study, targeted attack on the rich club nodes revealed a decrease in network efficiency not replicated by randomly attacking nodes (van den Heuvel & Sporns, 2011). The latest success of this approach has been to show that gray matter lesions in many neuropsychiatric disorders, such as schizophrenia and Alzheimer's disease, tend to occur preferentially in hubs of the connectome (Crossley et al., 2014).

In this study, we explore a new perspective on the structural connectome by characterizing its physical embedding within the white matter of the human brain. Edge density imaging can better elucidate the role of white matter tract anatomy in the complex architecture of the connectome. There has been recent work on identifying fiber pathways linking parts of the connectome (Cammoun et al., 2012) and also on determining the relevance of white matter regions to the entire structural network by examining the effects of simulated lesions to white matter regions (Kuceyeski et al., 2011, 2013) or to graph edges (Irimia & Van Horn, 2014; de Reus & van den Heuvel, 2014a,b) on global network metrics, in analogy to prior work targeting gray matter nodes. In Cammoun et al. (2012), the authors identify pairs of regions in the connectome adjacency matrix that share connectivity through a known fiber bundle. However, this is only performed for a select number of fiber bundles based upon prior knowledge of brain connectivity, instead of in a data-driven manner to link the adjacency matrix back to white matter. The white matter importance maps of Kuceyeski et al. (2011) show that white matter areas of high “importance” are typically focal, frequently peripheral in location and often highly lateralized. Neither the importance maps nor the “connectivity scaffold” of Irimia & Van Horn (2014) have much overlap with the rich club connections from the investigations of van den Heuvel & Sporns (2011) or the regions of highest ED, RC, or FC found in our study. This discrepancy is due to the fact that the simulated lesioning approaches measure the effect on a particular global network metric, such as efficiency (Kuceyeski et al., 2011) or the closely related characteristic path length (Irimia & Van Horn, 2014), rather than by the local density of network edges. It has recently been shown that the results of these artificial lesion-based methods are highly dependent on the specific network metric chosen to judge importance, and that a sufficiently general and robust metric such as communicability, which takes into account other routes beyond just the shortest paths, does demonstrate the importance of rich club edges to global network integration (de Reus & van den Heuvel, 2014a). The lesion-based approach takes a somewhat narrow view of brain networks, however, as it is unlikely that a single edge or single white matter region is the cornerstone of the entire network. It is not possible to directly compare the results from de Reus et al. (2014b) to our results, since the connectome edges are represented as abstractions and not as they are geometrically embedded in the white matter. Nevertheless, the effect of edge deletion when using path length as the measure of edge importance does uncover that many edges in the posterior aspect of the cerebral hemispheres are important to preserving short paths. However, when using other graph metrics, these essential edges are strewn throughout the brain and are not necessarily localized in our high ED regions.

We believe that our approach of measuring the density of network edges provides complementary information for assessing the significance of each white matter voxel in a connectomic framework. Edges are not all treated as if they were independent of each other; rather, their spatial segregation or convergence is mapped within the white matter. Our proposed EDI method also has the flexibility to incorporate the anatomic distribution of edges that connect rich club nodes to each other (RC), those that feed rich club nodes (FC) and those “local connections” (LC) that do not involve the rich club (Figures 5-6). The properties of the rich club have been examined in several publications (van den Heuvel & Sporns, 2011; van den Heuvel et al., 2012; Guusje et al., 2013) and there have been some attempts to link the rich club connections back to the white matter. Rich club and feeder connections tend to have longer projection lengths and rich club connections have higher levels of microstructural organization (Guusje et al., 2013), in agreement with our findings. Our EDI technique can also examine the spatial arrangement of intra-modular and inter-modular axonal pathways (Figures 9-10), which has not been previously investigated, to our knowledge, although very recent work has begun exploring the related concept of link communities (de Reus et al., 2014b).

Edge density imaging: comparison to track density and to metrics of white matter microstructure

We have demonstrated that edge density can be quantified at the single voxel level within white matter or averaged over entire white matter tracts. At both spatial scales, we establish that posterior white matter tracts tend to carry more connectome edges than analogous anterior white matter tracts. Track density imaging corroborates this finding, showing increased density of streamlines in the posterior white matter. This bias is also apparent in the original TD images of Calamante et al. (2010), although not explicitly mentioned in that paper. This result was also anticipated by the very first study of the structural core of the human brain, which showed that many of the most highly connected hubs of the network, such as the precuneus and the posterior cingulate, are located in the posterior aspect of the cerebral hemispheres (Hagmann et al., 2008).

Departing from the traditional definition of edge density as the proportion of all possible edges that are actually present in a simple undirected graph, we named our technique “edge density imaging” by analogy to TDI, since the two are closely related. However, they fundamentally differ in that EDI groups streamlines into the edges of the connectome, based on any given cortical/subcortical gray matter parcellation. A region with dense streamlines could contain one edge or many edges. We further explore the theoretical and practical differences between EDI and TDI in the Appendix. We have demonstrated that, while there is a positive correlation between ED and TD, there are white matter regions where the two strongly diverge. We also show that high ED is not restricted to regions with crossing fibers. This finding is likely affected, in part, by current limitations in tracking through certain areas with crossing fibers, even with a high angular resolution diffusion acquisition as well as fiber reconstruction and tractography methods that explicitly account for more than one fiber population per voxel. In addition to TD, we investigate the relationship between ED and measures of white matter microstructure. We detected a positive correlation of ED with both FA and ND, implying that voxels with more anisotropic diffusion and with greater intracellular volume fraction tend to contain more edges. An interesting divergence between ED and FA is seen in the corpus callosum: the white matter ROIs in the corpus callosum have the highest FA, but the ED is relatively low in most of the corpus callosum. This is explicable, as the corpus callosum has primarily homotopic interhemispheric connections, and therefore might not carry as many edges as tracts that mediate intrahemispheric communication. The periatrial regions of highest ED also showed a great diversity of edge types, including projection, association and callosal pathways (Table S1). There was a negative correlation between OD and ED, indicating that voxels with more edges have lower fiber orientation dispersion. White matter tracts with more highly organized microstructure and greater neurite density presumably have greater metabolic demands. Therefore, it would be predicted that these tracts would also have high edge density and hence greater significance to the overall structural network.

We have established good to excellent test-retest reliability of the mean ED values. The ICC and CoV values are not as high as for FA, as reported in this work or in Vollmar et al. (2010). TDI and EDI have comparable reproducibility, likely due to the fact that both measures are based on tractography. The reliability reported here for TDI is better than reported in Besseling et al. (2012). We have also demonstrated that the mean ED measurements are not highly sensitive to the cortical/subcortical atlas used for the connectome reconstruction, as shown in Section S5 of the Supplementary Materials. Each atlas has a different distribution of nodes across the cortical mantle and the consistency across atlases demonstrates that the ED values are not a heuristic of the atlas used or the exact number of nodes. In Section S6 of the Supplementary Materials, using data from two different types of MR scanners with two different diffusion MR imaging acquisition protocols, we have shown that ED measurements are almost as reproducible as FA and TD.

Regions of high edge density and their potential developmental and clinical significance

A striking characteristic of the ED maps is the generally higher ED in posterior cerebral white matter than in anterior white matter (Figure 1), which is highly statistically significant (Table S2). Although FA and TD also show this posterior > anterior asymmetry, the degree of posterior bias is much greater for ED (Table S3) and is observed across all three commonly used anatomic brain atlases (Figure S2), as well as a functional connectivity-based atlas with a higher level of granularity and a greater proportion of frontal lobe parcels than any of the three anatomic atlases (Figure S3). This feature is also preserved across two different diffusion MR acquisition methodologies (Figure S4). The regions of highest ED, which may constitute a “nexus” for connectome edges in the cerebral hemispheres, are located in the deep white matter of the corpus callosum, internal capsules, and, most conspicuously, the periventricular white matter, especially posteriorly. The periatrial white matter, with the highest edge density of all, has traditionally been referred to as the “terminal zones of myelination” in the radiology literature because of their persistent T2 hyperintensity during childhood brain maturation, although more recent MR imaging studies indicate that this appearance may at least in part be due to prominent perivascular spaces (Welker & Patton, 2012). Additionally, specific periventricular regions of the frontal, parietal, temporal and occipital lobes have been termed the “periventricular crossroads” during fetal white matter development since they contain developing commissural (interhemispheric callosal), association (intrahemispheric corticocortical) and projection (thalamocortical) fiber pathways (Judas et al., 2005). These are areas of both high ED and high probability of crossing fibers, as seen in Figure 1. As shown in Table S1, the fiber pathways that contribute to the very high ED of the periatrial white matter include a mixture of callosal, association and projection tracts, with all three types of edges represented in high proportions.

The posterior > anterior asymmetry and the periventricular distribution of high edge density both have implications for disorders that preferentially affect the posterior and/or periventricular white matter. Perhaps the best-known example is white matter injury of prematurity (Khwaja & Volpe, 2008), also known as “periventricular leukomalacia” because of its spatial distribution. Intellectual disability of varying degrees is common among those born prematurely, and the posterior predilection of preterm white matter injury results in spastic diplegia among severe cases and is a hallmark of “cerebral palsy”. Hence, regions of high ED seem to be particularly vulnerable to white matter injury of prematurity, possibly due to elevated metabolic demand from oligodendrocyte precursors in these areas that may render them uniquely susceptible to ischemia and inflammation. RC edges are even more predominantly periventricular in location than are LC edges, which extend more laterally and peripherally (Figures 5, 6, S4); this may serve to exacerbate the deleterious effects of periventricular white matter injury. A recent connectome study of children with unilateral cerebral palsy due to periventricular white matter lesions reveals abnormally reduced FA of several projection and association pathways, including thalamocortical projection tracts and frontoparietal association tracts (Pannek et al., 2014), confirming that multiple types of connectome edges are involved in white matter injury of prematurity.

Recently, a DTI investigation has shown that children with sensory processing disorders have impaired white matter microstructure in a posterior distribution (Owen et al., 2013b). A follow-up tractography study showed that this disruption of posterior white matter microstructure is also present in autistic children (Chang et al., 2014), who almost universally have sensory processing difficulties, too. Interestingly, the RC edges are not nearly as biased toward posterior white matter as FC or LC edges (Figures 5-6), which might help explain why posterior white matter injury does not have even more devastating consequences for the integrity of the connectome.

In addition to being especially vulnerable to injury during early brain development, the periventricular white matter is also disproportionately affected in senescence through “leukoaraiosis”, an aging-related white matter rarefaction that is thought to be caused by small vessel ischemic disease (SVID) among other factors (Pantoni and Garcia, 1997). Hence, the commonly used Fazekas grading system for leukoaraiosis on MRI specifically evaluates T2-weighted hyperintensity in periventricular and deep white matter (Fazekas et al., 1987). Since periventricular white matter has the highest edge density and the greatest proportion of rich club edges, microstructural damage to these regions would be predicted to disrupt much of the structural connectome, resulting in cognitive decline and deficits in global processing speed. This hypothesis is borne out by a recent connectomic study of SVID that demonstrates strongly reduced structural network efficiency that correlates better with cognitive dysfunction and slowing of processing speed than do conventional MRI measures of white matter lesion load or even microstructural metrics from DTI such as FA (Lawrence et al., 2014). Further supporting evidence comes from their finding that connectivity was most impaired in hub regions overlapping with the rich club nodes of our and prior investigations (van den Heuvel & Sporns, 2011, 2012).

Given that periventricular and callosal white matter is selectively affected in other neurological diseases, including common ones such as multiple sclerosis (Ge, 2006), this is an important avenue for future research. Indeed, a connectome study of multiple sclerosis patients clearly showed the periventricular distribution of white matter lesion load on conventional MRI, which resulted in abnormal global network metrics that correlated with the patients’ clinical and functional status (Shu et al., 2011). As with leukoaraiosis, the worst loss of connectivity in multiple sclerosis was to hub regions of the connectome that correspond well to many of the rich club regions identified in our and prior studies (van den Heuvel & Sporns, 2011, van den Heuvel et al., 2012). An investigation of the structural connectome in subjects with agenesis of the corpus callosum, a congenital malformation that results in partial or complete absence of interhemispheric callosal fibers, demonstrated profound alterations of global network metrics as well as fiber pathways within the structural core (Owen et al., 2013c), in agreement with the cognitive dysfunction found in these individuals (Paul et al., 2007).

Hemispheric asymmetries of edge density and their potential neurobiological significance

In addition to the posterior bias in the ED images, we also found significant lateralization of the mean ED in the parietal and temporal white matter. The right > left asymmetry of ED in the superior parietal regions may reflect the right parietal specialization for visuospatial function in the human brain (Cummings, 1985). Conversely, the leftward bias of ED in the temporal regions may reflect the left temporal specialization for language function in most human brains (Geschwind and Levitsky, 1968). These functionally significant hemispheric asymmetries are not apparent on TD images (Figure 1) and highlight the additional information provided by EDI on the connectomic organization of white matter. Interestingly, in both parietal and temporal regions, the hemispheric laterality exists only for the RC and FC edges and not for LC edges (Figures 5-6 and Table S3). This is because the right superior parietal and left insula nodes belong to the rich club, whereas the left superior parietal and right insula nodes do not. In this way, EDI reveals the structural connectivity underlying functional hemispheric specialization, unlike non-connectomic approaches such as TDI.

Edge weighted imaging

The use of weighted connectome edges is less popular in the literature, where most studies use binarized edges. Those studies that have used weights employ the streamline count or FA integrated along the edge (van den Heuvel & Sporns, 2011). Here we explore degree and betweenness centrality as edge weights. We find that weighting edges by degree does not add much information to the ED measurements when looking across all voxels (Figure 12). ED accounts for 99% and 90%, respectively, of the variance in dwED and cwED. However, examining the average shortest paths images derived from the mean EBC at each voxel (Figure 13), we observe that certain white matter tracts and regions facilitate a great number of shortest paths between nodes. The fornix, hippocampal commissure, anterior commissure and orbitofrontal white matter emerge as tracts that have low ED and do not appear to play a large role in the rich club or intermodular connections, but are utilized by many shortest paths and therefore have high EBC values. In contradistinction, many shortest paths also traverse the white matter in the superior parietal lobes, including the precuneus and postcentral gyrus, and in the cuneus of the occipital lobes, all of which are densely interconnected with the rest of the brain as illustrated by high ED and often high RC, FC and/or intermodular connectivity. Thus, white matter regions with high EBC fall into two categories: (1) tracts in relatively segregated territories such as the hippocampus-fimbria-fornix system or the orbitofrontal regions, and (2) tracts that are more globally integrated into the overall brain network, such as the postcentral gyrus, precuneus and cuneus. These results closely agree with those of Irimia & Van Horn (2014), who find that elimination of either gray matter nodes or white matter edges from the postcentral gyrus, precuneus, and cuneus cause significant changes to the characteristic path length of the entire network, whereas such simulated lesions to the frontopolar regions tend to produce only local effects. It is not surprising that the average shortest paths maps in Figure 13 would match up well with edges important to the characteristic path length, which is highly dependent on the shortest routes. Also, the parietal and occipital locations of these more globally connected network hubs also contribute to the higher ED we detect in posterior white matter compared to anterior regions.

The edge betweenness centrality measure is based on the consensus connectome, and the edges of this connectome are dependent on the threshold used. We calculated the cwED for various densities (0.12-0.32) and found that the high linear correlation between ED and cwED was present for all thresholds. EBC, as a metric, is not rooted in neuroanatomy; rather, it finds the shortest path between all nodes regardless of whether information is actually transmitted that way in the brain and does not consider the geometric distance between nodes. Thus, the results with the EBC weighting must be interpreted with some caution.

Limitations and future directions

Given that this is the first attempt to systematically investigate the trajectory of the connectome edges through the white matter, there are many limitations of the study as well as many productive avenues for future investigation. As with almost all prior connectome studies, the results herein exclude subcortical regions below the diencephalon, specifically the brainstem and cerebellum. We have made an effort to establish that our ED maps are not strongly dependent on node location, given commonly used, low resolution anatomic gray matter parcellations (Figure S2) and a preliminary examination using a functional cortical parcellation at a higher level of granularity (Figure S3). The goal in EDI is to group streamlines into edges that connect nodes that are each internally homogenous, while minimizing the overlap of function and connectivity between different nodes. Therefore, in order to explore larger-scale networks beyond that of the standard anatomic atlases, we chose to use a high resolution atlas generated by connectivity-based parcellation.

Connectivity-based parcellation uses the connectivity profile of every GWB voxel to cluster voxels with similar connectivity into a single region. To date, connectivity-based parcellation based on structural connectivity data has only been successfully applied to individual cortical and subcortical regions, typically using a standard atlas parcellation as a starting point (e.g., Anwander et al., 2007; Beckmann et al., 2009; Klein et al., 2007). In contrast, the entire cortical mantle has been parcellated based on resting-state fMRI, such as the recently developed atlas (Gordon et al., 2014) used to generate the ED results shown in Figure S3. Ideally, we would like to obtain a data-driven partition of the cortical and subcortical GWB voxels into nodes that are by definition relatively internally homogeneous in their structural connectivity, while minimizing overlap of connectivity between distinct nodes.

Since no structural connectivity-based parcellation of the entire cerebral cortex is available to obtain a higher resolution network, we instead use a granular functional connectivity-based cortical parcellation with proven homogenous BOLD connectivity at the node level, referred to as the FXCN atlas. The results obtained with the FXCN atlas confirm the primary findings drawn from the lower resolution anatomic atlases, specifically that posterior cerebral white matter contains generally higher ED than anterior white matter and that periventricular white matter has the highest edge densities, particularly in the posterior periatrial regions.

An extreme approach to obtaining a higher granularity would be to assign each individual voxel at the GWB as a node of the network. These nodes would be small enough to assume that each has reasonably homogenous connectivity. Given that there are 100K-200K voxels at the GWB, this would currently present a prohibitive computational challenge to perform EDI at this scale with n*(n-1) tractography runs and binary masks. We discuss the theory of EDI at the single-voxel per node level in the Appendix.

There are also limitations to the tractographic methods that must be addressed. Most importantly, it is well established that, even with HARDI tractography using multi-fiber models, it is difficult to track through regions of crossing fibers. As such, connections between nodes that are medial in the brain have the advantage of being able to be tracked across the corpus callosum without encountering crossing fibers, compared to lateral cortical nodes. Furthermore, given that areas with the highest ED are in close proximity to the corpus callosum, we wanted to determine if callosal edges were necessary for the relatively elevated ED values in those areas. In Section S7 of the Supplementary Materials, we re-calculate ED without the callosal edges. The posterior>anterior asymmetry and the relatively high ED values in peri-atrial and posterior periventricular white matter are still observed even after excluding callosal edges (Figure S5).

The exact magnitudes of the edge density values should be interpreted with caution; we observe a discrepancy in the maximum ED values for the Siemens and GE data. This is likely due to the GE HARDI acquisition having better angular resolution and better spatial resolution, and, therefore, more accurate tractography. Despite the difference in scaling, we find a high R² value for the correlation between the voxel-wise ED values for the two types of acquisitions, indicating that the spatial distribution of ED values is relatively preserved between them (Figure S4). We use stringent criteria (target, exclusion, and termination masks) for the EDI tractography, but do not use further thresholding of the streamline counts before binarization. It follows that additional thresholding would reduce the maximum ED value, although, in our experience, thresholding truncates long edges. We have chosen to err on the side of including long edges, which are known to be hard to reconstruct, at the risk of including false positives. We predict that EDI performed with a multi-shell HARDI acquisition that has higher angular resolution, with more directional measurements and shells at higher b values, would yield even more precise and accurate tractography, with fewer false positives. This would also cause the exact magnitudes of the ED values to change. However, we do not anticipate that the spatial distribution of high and low ED regions would change dramatically with higher quality data. This is an area for further investigation.

We have shown that the intra- and inter-modular edges have differing distributions in the white matter. It would be interesting to embed the edges of each of the link communities found in de Reus et al. (2014b) to examine the white matter regions that serve these various communities. We hypothesize that the edges of the communities that contain a large number of hubs would traverse white matter regions with high ED. As more illuminating properties of both the structural and functional human connectome emerge in the literature, it will be fascinating to use EDI to uncover the physical instantiation of these connectional topologies within the white matter of the brain.

Like TDI, EDI has super-resolution characteristics since the spatial resolution of streamline density measurements is not limited by the size of the voxels used to acquire the diffusion MR imaging data (Calamante et al., 2010). Therefore, it should be feasible to calculate ED values at submillimeter length scales, which is a promising direction for further research. EWI can also be performed with many more interesting types of edge weighting than those examined herein, such as track distance weighting, weighting by any number of informative graph theoretic metrics, or those used in TWI (Calamante et al, 2012). Similarly, edge densities can be broken down into many potentially useful subsets based on graph theoretic criteria besides the rich club or the modular decomposition demonstrated in this work. Finally, we have validated the test-retest reproducibility of ED measurements and shown relatively equivalent performance on two different scanner platforms and acquisition protocols, paving the way toward the potential use of EDI metrics in clinical research as a quantitative white matter biomarker. Given the prevalence of white matter disorders throughout the lifespan, as well as the early success of connectomic metrics in correlating with cognitive and behavioral impairments in many neurologic and psychiatric conditions, further research using EDI and other novel connectivity-based imaging methods is warranted.

Highlights.

• - edge density imaging (EDI) groups tractography streamlines into network edges

• - EDI maps the anatomic embedding of the structural connectome within white matter (WM)

• - posterior cerebral WM has high edge density, particularly in periventricular regions

• - edge weighted imaging (EWI): EDI map weighted by graph metrics or other WM parameters

Abbreviations

FreeSurfer Regions

AMG

amygdala

STS

bank of superior temporal sulcus

CAC

caudal anterior cingulate

CMF

caudal medial frontal

CAU

caudate

CUN

cuneus

ENT

entorhinal

FTP

frontal temporal pole

FUS

fusiform

HIP

hippocampus

IPT

inferior parietal sulcus

INS

insula

ISC

isthmus cingulate

LOC

lateral occipital

LOF

lateral orbital frontal

LIN

lingual

MOF

medial orbital frontal

MTP

medial temporal

ACB

nucleus accumbens

PRC

paracentral

PHP

pars hippocampus

POP

pars opercularis

POB

pars orbitalis

PTR

pars triangularis

PEC

pericalcarine

POC

postcentral

PCC

posterior cingulate

PRC

precentral

PCN

precuneus

PUT

putamen

RAC

rostral anterior cingulate

RMF

rostral medial frontal

SFT

superior frontal

SPT

superior parietal

STP

superior temporal

SMG

supramarginal gyrus

TPP

temporal pole

THL

thalamus

TTP

transverse temporal

White Matter Tracts

ACR

anterior corona radiata

ALIC

anterior limb of internal capsule

ATR

anterior thalamic radiations

BCC

body of corpus callosum

CGC

dorsal cingulum

CGH

ventral (hippocampal) cingulum

FMAJ

forceps major

FMIN

forceps minor

GCC

genu of corpus callosum

IFO

inferior fronto-occipital fasciculus

PCR

posterior corona radiata

PLIC

posterior limb of internal capsule

PTR

posterior thalamic radiations

RLIC

rentrolenticular part of internal capsule

SCC

splenium of corpus callosum

SCR

superior corona radiata

SFO

superior fronto-occipital fasciculus

SLF

superior longitudinal fasciculus

Appendix

Comparing Edge Density Imaging (EDI) and Track Density Imaging (TDI)

Track Density Imaging (TDI) is defined as the number of tractography streamlines that pass through every voxel. TDI can be seeded from all of the white matter voxels or from only the voxels at the gray-white matter boundary (GWB). Edge density imaging (EDI) groups these streamlines into edges that make direct connections between pairs of cortical/subcortical nodes. The two methods at first glance seem very similar as they both use tractographic measures to define a property of the white matter, but they are in actuality quite distinct for a few key reasons.

The most substantial differences between EDI, as we have defined it in this paper, and TDI are twofold. First, EDI discards the streamline counts by binarizing each edge while TDI is by definition a streamline count. Second, EDI uses a parcellation of the brain to define nodes and then groups streamlines into edges based on these node definitions, while TDI does not group streamlines in any fashion. Hence, EDI puts tailored constraints on the tractography to extract only direct connections between pairs of nodes, while TDI does not use such constraints. In this paper, we have seeded TDI in the white matter as opposed to the gray-white matter boundary, as is done for EDI, as that is how it was originally formulated in Calamante et al. (2010). Seeding TDI at the gray-white matter boundary will change the streamline counts, but it will not cause EDI and TDI to converge for the reasons stated above.

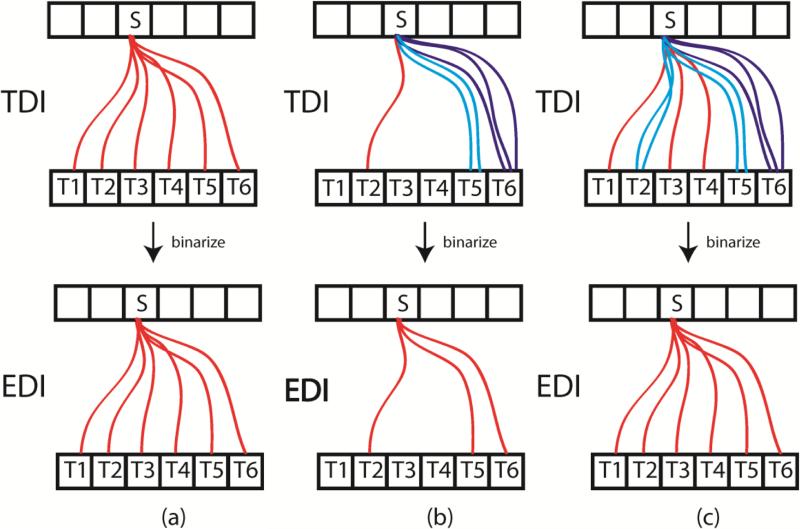
One might wonder if we removed the second difference above, grouping streamlines based on an atlas parcellation, and performed EDI at the single-voxel level at the GWB, would EDI and TDI yield the same result? Doing EDI at this scale means that each voxel at the GWB is considered a distinct node in the connectome and therefore tractography for EDI and TDI would be the same; EDI just requires an additional step of binarization. This binarization performed in EDI, however, would almost certainly cause the resulting ED images to be different from the TDI results. The only way we would achieve the same “binarized effect” for TDI is if each seeded streamline takes a unique path, with each terminating on a different target voxel.

In Figure A1, we illustrate three scenarios for TDI and the resulting EDI images assuming only one GWB voxel per node: all instances have one seed voxel (S) and 6 target voxels (T1-T6). In (a), S is seeded with 6 streamlines and each streamline terminates on a unique target voxel. If we then binarized these edges, assuming each streamline to be above the binarization threshold, we can see that we would get the same result for EDI as for TDI. In (b), S is seeded with 6 suprathreshold streamlines as well, but we see that some streamlines take the same path (for illustration purposes, these duplicate streamlines are not shown to be directly on top of one another). When the edges are then binarized, the resulting EDI image is different from the TDI image. The white matter voxels in the TDI image have different streamline counts (1, 2, or 3) depending on which seed to target pathway they lie on while the same voxels in the EDI image all have only a single edge. In (c), S is seeded with 10 streamlines to demonstrate that a second TDI result, distinct from the one in (a), could yield the same EDI image. Extending this toy example, we can see that it is extremely unlikely that TDI and EDI would yield the same result since probabilistic tractography typically utilizes thousands of streamlines per voxel and hundreds of thousands of voxels are required to cover the entire GWB of the cerebral hemispheres. Both EDI and TDI have weighted versions. We have provided examples of weighted EDI, also known as edge weighted imaging (EWI), in this paper by weighting each binarized edge by the mean degree or edge centrality. Track weighted imaging (TWI) weights every streamline by some track-wise statistic, such as mean FA, mean kurtosis, or standard deviation of the T2 values. We could extend EWI to include these track-wise measures, although we would weight the binarized edges (formed by grouping streamlines with the same seed and target nodes) instead of the individual underlying streamlines as done with TWI. If we performed EWI using every GWB voxel as a node and with the same track-wise measures, EWI would still be different from TWI because of the binarization of the edges before weighting.

Figure A1.

Three example scenarios illustrating the difference between track density imaging (top row) and edge density imaging (bottom row).