Content-specific evidence accumulation in inferior temporal cortex during perceptual decision-making

Abstract

During a perceptual decision, neuronal activity can change as a function of time-integrated evidence. Such neurons may serve as decision variables, signaling a choice when activity reaches a boundary. Because the signals occur on a millisecond timescale, translating to human decision-making using functional neuroimaging has been challenging. Previous neuroimaging work in humans has identified patterns of neural activity consistent with an accumulation account. However, the degree to which the accumulating neuroimaging signals reflect specific sources of perceptual evidence is unknown. Using an extended face/house discrimination task in conjunction with cognitive modeling, we tested whether accumulation signals, as measured using functional magnetic resonance imaging (fMRI), are stimulus-specific. Accumulation signals were defined as a change in the slope of the rising edge of activation corresponding with response time (RT), with higher slopes associated with faster RTs. Consistent with an accumulation account, fMRI activity in face- and house-selective regions in the inferior temporal cortex increased at a rate proportional to decision time in favor of the preferred stimulus. This finding indicates that stimulus-specific regions perform an evidence integrative function during goal-directed behavior and that different sources of evidence accumulate separately. We also assessed the decision-related function of other regions throughout the brain and found that several regions were consistent with classifications from prior work, suggesting a degree of domain generality in decision processing. Taken together, these results provide support for an integration-to-boundary decision mechanism and highlight possible roles of both domain-specific and domain-general regions in decision evidence evaluation.

1. Introduction

Models of perceptual choice characterize decisions as processes in which evidence accumulates in a decision variable toward a boundary, and a choice is made when this boundary is reached. Electrophysiological studies have identified neuronal firing rate patterns resembling an accumulation-to-boundary mechanism in a number of non-human primate brain regions, including the superior colliculus (Ratcliff, 2003; Ratcliff et al., 2007), lateral intraparietal area (Shadlen and Newsome, 2001), dorsolateral prefrontal cortex (Kim and Shadlen, 1999), and frontal eye fields (Hanes and Schall, 1996). These regions show time series of neuronal activity consistent with predictions of sequential sampling models (Ratcliff, 1978; Usher and McClelland, 2001), in which the rate of accumulated neural activity is related to the time to make a decision (Gold and Shadlen, 2001; Hanes and Schall, 1996). Activity in these neurons is influenced by both the quality and availability of sensory evidence and thus may reflect a decision variable (Ditterich et al., 2003). Similar effects have been found in humans. Johnson and Olshausen (2003) used event-related potentials (ERP) and found that the voltage in the mid-frontal (FZ) electrode changed most rapidly for the fastest decisions. In a perceptual discrimination task, Philiastides and Sajda (2006, 2007) identified a late ERP component (~300ms) that tracked aspects of the mean drift-rate in Ratcliff’s drift-diffusion model (DDM). Using whole-brain fMRI, Heekeren and colleagues (2004) found a left superior frontal region whose peak activity reflected the strength of evidence for face-versus-house categorization (see also: Huettel et al., 2005; Kayser et al., 2010; Tosoni et al., 2008).

Due to limitations of EEG and fMRI, it is difficult to localize the source of time-dependent signals. However, by limiting the rate of information, the timescale of a decision can be slowed in order to compensate for the low temporal resolution of fMRI (Bowman et al., 2012; Carlson et al., 2006; Gluth et al., 2012; James et al., 2000). For example, in an object identification task, Ploran and colleagues (2007) gradually revealed objects over 16 seconds and found that activity in thirteen regions accumulated at a rate correlating with decision time. The role of some of these regions as evidence accumulators is supported by other observations. First, the rate of fMRI accumulation is influenced by errors—fMRI activity increases faster prior to the decision when an object is incorrectly identified compared to correct trials (Wheeler et al., 2008). Second, the rate and magnitude of accumulation is significantly less when people fail to commit to a decision (Ploran et al., 2011). Despite this support, it remains unclear whether this activity reflects the integration of information, or instead is due to hemodynamic artifacts or epiphenomenal cognitive events, such as attention, time-on-task, or urgency.

If fMRI accumulation reflects evidence accumulation, it should be directly related to evidence sources, and thus content-specific. To test this prediction, an extended face-house discrimination task was used to examine the evolution of activity within face- and house-selective regions in inferior temporal (IT) cortex (Haxby et al., 1994; Kanwisher et al., 1997). Behavioral and neuroimaging analysis were employed together with drift-diffusion models to directly link model hypotheses to task data. In the task, subjects viewed dynamic movies of noise-degraded faces and houses and made discriminations when reasonably confident. Importantly, the aim of this study differs from previous studies. For example, Heekeren et al. (2004) identified putative regions that appear to compute a decision-rule (“comparators”), but did not directly test whether temporally dynamic changes in IT activity are related to the decision process. Our primary aim was to localize face- and house-selective regions in IT and test whether activity follows an accumulation-like pattern in a content-specific manner. The use of dynamic movies with limited sensory information allowed us to increase the variance of decision times across many seconds, facilitating the investigation of time-sensitive effects using fMRI.

2. Materials and Methods

2.1 Subjects

Twenty-two healthy, right-handed, native English speakers with normal or corrected-to-normal vision participated in a 1.5-hour behavioral and functional magnetic resonance imaging (fMRI) session. Six subjects in total were excluded for excessive movement during scanning (N = 4), incomplete scan data (N = 1), or insufficient behavioral data in all conditions for reliable analysis (N = 1). The remaining 16 subjects (10 female) ranged in age from 21 to 26 years (mean 23.3). Informed consent was obtained from all subjects according to procedures approved by the University of Pittsburgh Institutional Review Board. Subjects were compensated $75 for their time.

2.2 Task

Subjects participated in a functional imaging scan and performed a face/house discrimination task. Subjects viewed short videos of noise-degraded faces and houses and made a forced-choice face/house decision. Stimuli were presented in a 300 × 300 pixel frame centered on a black background and were projected onto a screen at the head of the magnet bore at 1024 × 768 resolution. Subjects viewed the task via a mirror mounted to the radio frequency coil. Subjects were instructed to make a face or house decision when they reached a reasonable level of confidence and indicated their choice with an index-finger button press. Face and house responses were mapped to opposite hands, counterbalanced across subjects. MRI-safe projection equipment and fiber optic response glove system were produced by Psychology Software Tools (PST, Pittsburgh, PA). The PsychoPy software package was used for task presentation and data collection (Peirce, 2007, 2008). Response times (RTs) were recorded and used to approximate decision latency.

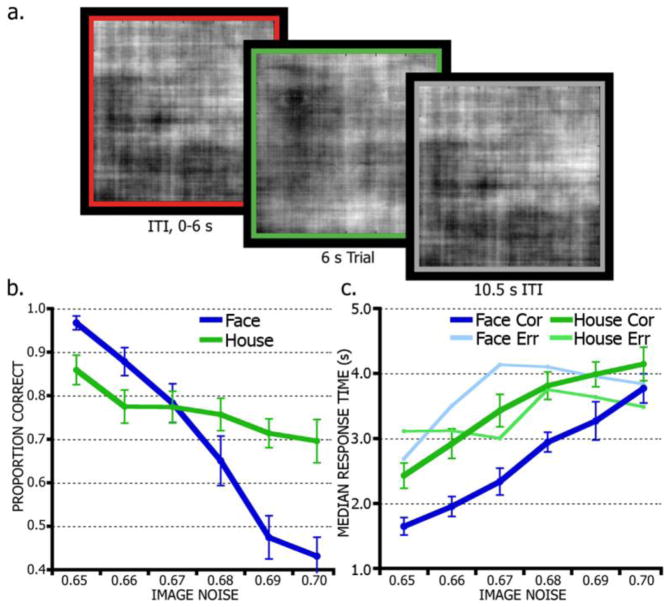
The task implemented a widely spaced event-related design (Figure 1a). Face and house videos were displayed for 6 s, followed by a 10.5 s inter-trial interval (ITI) period to allow the blood-oxygen-level-dependent (BOLD) signal to approach basal levels before the next trial. Trials were further separated with additional ITI jitter of variable length, sampled randomly from an distribution of 0–6 s positively skewed toward the shorter intervals (1.5 s increments, mean 1.64 s) (Dale, 1999). Fully noise-degraded stimuli (~100% noise, completely randomized phase matrix) were displayed during fixation and ITI periods. Each trial period was indicated to the subject with a colored border (4 pixel width) surrounding the stimulus display frame. A green border indicated the trial period; the border turned grey for long ITI periods and red for jitter periods.

Figure 1.

Face/House discrimination task and behavioral performance. (a), Timeline of task trial structure. Subjects first saw a variable-length, fully-degraded stimulus (~100% noise) surrounded by a red border indicating a trial separation period (inter-trial interval, ITI). A green border indicated the 6 s trial period during which the subject made a face or house decision while viewing a movie of a noise-degraded face or house. A grey border indicated an additional 10.5 s ITI period showing a fully-degraded stimulus. (b), Raw accuracy (proportion correct) is shown by noise level and category. Image noise indicates the percentage of noise introduced into the stimuli. (c), Response times for correct and error trials by noise-level and stimulus.

Testing took place over seven runs of 32 trials per run. Each run consisted of 14 face trials, 14 house trials, and four fully noise-degraded trials (two runs featured one extra face and house trial each, and two fewer full-noise trials). Noise levels were balanced across the entire session, featuring 17 trials per face/house at 65–69% noise, 15 at 70% noise, and 24 fully degraded images. Given our limited stimulus set, most stimuli were repeated twice per subject (with 16 stimuli per face/house shown 3 times); repeats of the same stimulus, however, were shown at noise levels differing by at least 2%. Behavioral analysis indicated no performance increase due to repetition (linear trend contrast of stimulus repetition, F_{(1, 15)} = 1.48, p = 0.24). Each subject received a stimulus set with a randomized presentation sequence and unique distribution of noise levels across stimuli.

2.3 Stimuli

The stimulus set consisted of 42 neutral-expression, frontal-view face and 43 house greyscale images, transformed into 6-second movie clips. The source images measured 512 × 512 pixels. Face stimuli were a part of the MacBrain Face Stimulus Set (courtesy of the MacArthur Foundation Research Network on Early Experience and Brain Development, Boston, MA). House images were compiled from searches for public domain photos (Google images) and from photographs around the Pittsburgh area. Backgrounds in the images were erased and cropped, leaving only the face or house on a white background. The stimulus set was entered into the following processing routine to normalize images across the set and introduce graded amounts of noise into each image. Using Matlab (2010a, The Mathworks Inc., Natick, MA), this routine computed the two-dimensional, forward discrete Fourier transform (DFT) of each image using a fast Fourier transform (FFT) algorithm. Each image’s DFT was decomposed into a phase angle matrix and an amplitude matrix. The amplitude matrices of all images in the set were averaged, to help balance differences in image properties across the set, such as contrast, luminance, and brightness. Each individual phase matrix was convolved with a matrix of random noise using an additive white Gaussian noise (AWGN) filter, which combines signal (face or house phase matrix) and noise at a specified signal-to-noise ratio (SNR), producing a single, noise-convolved phase matrix. This allowed us to parametrically vary the amount of discrete evidence available for a given stimulus. To produce the final image, the average amplitude matrix was recombined with an individual noise-convolved phase matrix, and inverted with an inverse FFT algorithm (Heekeren et al., 2004).

Because the AWGN filter produced a random spatial distribution (but constant amount) of noise across an image, this procedure was repeated 90 times for each stimulus, generating 90 still images of the same face or house with identical SNR, but different patterns of noise. These frames were concatenated to produce a 6-second movie clip (at 15 frames per second). Because of the length and low SNR of the movies, the normally sub-second face/house decision process was effectively extended to several seconds, while allowing parametric control over the quality and amount of evidence available on a trial. A range of noise levels was determined via pilot testing to encompass performance at and above threshold, producing a wide range of response times. The resulting stimulus set featured noise levels of 65–70% at 1% increments.

2.4 Image Acquisition

Functional and anatomical images were acquired on a Siemens Allegra 3-Tesla scanner. High-resolution anatomical images were acquired using a T1-weighted MP-RAGE sequence (repetition time [TR] = 1.54 s, echo time [TE] = 3.04 ms, flip angle [FA] = 8 degrees, inversion time [TI] = 800 ms). T2-weighted anatomy images were obtained with a spin-echo sequence (TR = 6.0 s, TE = 73 ms, FA = 150 degrees, 38 slices). Functional images sensitive to the BOLD contrast were acquired with a whole-brain echo-planar T2*-weighted series (TR = 1.5 s, TE = 25 ms, FA = 60 degrees, 3.125 x 3.125 mm in-plane resolution, 3.5 mm slice thickness, 29 slices). The first four images of a run were discarded to allow net magnetization state and RF signal to equilibrate. Subjects were provided with earplugs to minimize scanner noise.

2.5 Functional Imaging Preprocessing

Imaging data were preprocessed to address noise and image artifact. Preprocessing included within-TR slice acquisition time correction, motion correction using rigid-body rotations and translations (Snyder, 1996), within-run voxel intensity normalization to a mode of 1000 to facilitate inter-subject comparisons (Ojemann et al., 1997), and computation of a Talairach atlas space transformation matrix (Talairach and Tournoux, 1988). Following preprocessing, data were resampled to 2 mm isotropic voxels and transformed into stereotaxic atlas space.

2.6 Functional Localization of Stimulus Processing Regions

Subject-level data were analyzed with a voxelwise general linear model (GLM). The GLM treats each data point as the sum of coded effects, produced by modeled events (regressors) and by error (Friston et al., 1994; Miezin et al., 2000; Ollinger et al., 2001). Three levels of stimulus (face, house, noise) and three levels of noise (collapsed into low, medium, and high: low comprised 65–66%, medium 67–68%, and high 69–70%) were entered separately for correct and error trials. Within run, signal drift was modeled as a linear trend and baseline signal was modeled by a constant term. Computationally, a series of 11 delta functions described event-related effects as a time series of the percent of BOLD signal change from baseline, time-locked to trial onset. Importantly for our present aims, this technique makes no assumptions about the shape of the BOLD response, but does assume that the signal sources at each time point sum linearly to yield the observed signal (i.e., recorded BOLD response). Software developed at Washington University in St. Louis was used for image processing and analysis (FIDL).

Face- and house-selective regions within fusiform and parahippocampal gyri were localized for each subject by computing a face minus house t-test contrast for all correct trials. This analysis generated a statistical map showing all voxels sensitive to faces or houses specifically. Statistical maps were smoothed with a 4 mm (2 voxel) full width at half maximum (FWHM) Gaussian kernel. Peak voxels of activity exceeding 95% confidence level (Z < −1.96 or Z > 1.96) were identified, and an 8 mm spherical region of interest (ROI) was grown around each peak. Voxels absent from the initial statistical map were dropped from the ROIs. Subsequent analyses focused on regions located along the ventral surface of the temporal lobe. Each subject contributed at least one face-preferential and one house-preferential region to the analysis.

2.7 Imaging Group-level Analysis

In order to take advantage of trial-by-trial data, the raw time series data were extracted from each subject’s face- and house-preferential ROIs. To do this, a second GLM was created for each subject in which only trend and baseline terms were modeled. The residual error of this model, therefore, contained all trial-level effects plus noise. The residual time series from each run was expressed as percent signal change from the baseline term for that run. Run-wise time series were then segmented into trial-level time series by concatenating 11 time points (16.5 seconds) beginning with the onset of each trial.

We examined the temporal profile of activity in face- and house-preferential ROIs and how these regions process information over time leading up to (and after) a decision. Raw BOLD time series were extracted and sorted by decision (face or house) and binned by response time (RT) into four bins in increments of 1.5 seconds (0.0–1.5 s, 1.5–3.0 s, 3.0–4.5 s, 4.5–6.0 s) for both faces (N = 492, 696, 276, 98) and houses (N = 243, 616, 473, 224). Mean signal change time series from stimulus-preferential regions were computed by averaging all trials within each RT bin separately for face and house decisions.

To quantify the degree of accumulation in these regions, the slope of the leading edge of each time series was defined as the rise in activity between the onset of activity above baseline and the time of peak (Ploran et al., 2011). Time of peak was simply the time point at which the maximum magnitude was reached. Activity onset was computed for each trial by first linearly interpolating each trial’s time series, which generated 1000 time points between each existing time point. To reduce effects of high-frequency noise on the trial-level data without distorting the overall signal shape, each time series was smoothed using a Savitzky-Golay filter before interpolation. Onset was then computed by stepping backward through the interpolated time series, starting at time of peak, until 15% of the peak amplitude was reached. Trials were grouped by RT (4 bins, 1.5 s increments) and by stimulus (face, house). Trial onset and peak times were averaged so that each subject had one onset and time-to-peak measure for each condition. For each subject, slope was then computed as the difference in signal change at peak minus signal change at onset (rise), divided by the time difference between peak time and onset time (run). Statistical differences were assessed in a 2 (stimulus) × 4 (RT) ANOVA using SPSS (Version 21, IBM Corp., Armonk, NY). For all analyses, significance was set to α < 0.05.

2.8 Noise-only trials

Qualitatively, trials during which no overt stimulus was present were examined (i.e., 100% noise stimulus), but subjects still responded and identified it as a face or house. Time series data for no-stimulus (“noise”) trials were grouped by the subjects’ responses (“face” or “house” response) and by RT (“early” and “late”). Because full-noise trials had fewer responses per subject, RT bins were collapsed to two bins corresponding to response windows of 0–3 s (early) and 3–6 s (late). For reference, face and house time series were recomputed using these response windows, as well. Some subjects had too few trials per condition for the group to be tested statistically.

2.9 Linking imaging measures with diffusion model predictions

As a way to better control for effects of difficulty (noise-level) and to establish a direct link between accumulation-like fMRI effects and decision models, the behavioral and imaging data were analyzed using a diffusion model approach. Models were fit to choice and RT data using the HDDM package (Wiecki et al., 2013), which uses hierarchical Bayesian methods to estimate DDM parameters using Markov-chain Monte-Carlo (MCMC). As such, the group- and subject-level parameters were estimated simultaneously. It is important to note that hierarchical DDM fixes some model parameters across conditions, which can limit interpretations. However, our hypothesis focused on a specific relationship between fMRI activity and drift rates, which can be tested directly by allowing drift rate to vary across conditions. This model was then compared relative to an analogous model where boundary separation varied across conditions. Moreover, the hierarchical method tends to require fewer observations for optimal parameter recovery compared to more traditional alternatives and is generally less susceptible to outliers (Wiecki et al., 2013). The DDM treats behavioral RT distributions as the outcome of several parameters describing a decision process, including mean evidence accumulation rate (drift-rate, v), decision threshold (boundary, a, and starting point, z), and non-decision time (t_er) (Ratcliff, 1978; Ratcliff and McKoon, 2008). Under this framework, if the BOLD time series reflected accumulation, the leading edge (i.e., the slope measure described above) should map onto the drift-rate parameter.

In order to directly link the imaging measures to behavior and diffusion model parameters, the trial-level slope metrics were entered as a regressor in the models. This measure, described above, approximates the slope of the leading edge of the BOLD time series, quantifying the degree of neural accumulation for each trial. The slope measure corresponding to the chosen stimulus for each trial was used to estimate model parameters for face and house simultaneously. For instance, if the subject responded “face,” that trial would feature the slope metric from face regions. The drift-rate for the trial should correspond directly to this value. All models included subject-level estimates for boundary, non-decision time, drift-rate, and starting point, parameterized by their group-level means and variances (standard deviation). Drift-rate varied by slope for each of six conditions, separated by stimulus (face, house) and noise-level (low, mid, high). Noise-level was collapsed into three conditions to boost trial counts and improve parameter estimates (low = 65–66%, mid = 67–68%, high = 69–70%). Slope was expected to correlate with drift-rates for face and house and that the slope of the regression (i.e., regression coefficient) should vary by noise-level (for a similar analysis, see Cavanagh et al., 2011). Model parameters were estimated using three MCMC chains each of 10,000 samples, from which the first 3,000 of each were discarded for chain stabilization (burn-in). Proper model convergence was assessed using the Gelman-Rubin statistic, which compares between-chain and within-chain variance. This statistic was near 1.0 (within 0.02) for the parameters, indicating that our sampling was sufficient for proper convergence. The DDM analysis generated estimates of the regression coefficients of the slope/drift-rate regression for each of the six conditions (stimulus × noise-level). If the posterior density of the coefficient was statistically non-zero, then slope and drift-rate exhibited a significant relationship.

To assess the degree to which the models could reproduce the patterns in the observed data (i.e., whether the models fit the data), accuracy and RT data were generated by sampling from the model posterior distributions for each subject. One hundred data sets were simulated from each subject’s model and then compared the mean of these datasets to the empirical data. RT and accuracy conditions were separated by stimulus (face, house) and noise level (low, mid, high) and compared for each stimulus separately with 2 x 3 repeated measures ANOVAs including factors of dataset (empirical, model-predicted) and noise (low, mid, high).

The relationship between slope and RT could be alternatively explained by changes in decision threshold (boundary) and thus unrelated to evidence accumulation. To test this, an alternative model was designed identical to the one above, but instead with slope regressed onto the boundary parameter (a). If the fit of this model is worse than the drift-rate model, then slope most likely reflects accumulation instead of changes in decision threshold. Model performances were compared by evaluating the deviance information criterion (DIC), which measures the lack of fit of the model estimates, taking into account the complexity of the model (i.e., number of parameters used to fit to the data) (Spiegelhalter et al., 2014; Spiegelhalter et al., 2002). A lower DIC indicates a better fit.

2.10 Exploring domain-general versus domain-specific decision regions

In order to explore the relationship of the IT accumulator signals to task-related activity elsewhere in the brain, regions were defined using a whole-brain, repeated-measures ANOVA, similar to the approaches of previous work (Ploran et al., 2007). For each subject’s GLM, events were coded separately for stimulus (face, house) and RT (four bins) across 12 time points, for correct trials only. Factors of stimulus (2 levels), RT (4 levels), and time (12 levels) were entered into a voxelwise ANOVA, which generated an image for each main effect and interaction. Regions were identified using the main effect of time image, so as to not bias toward finding stimulus or RT effects. An algorithm searched the smoothed (4 mm FWHM) main effect of time image for activity peaks exceeding an uncorrected alpha of 0.0001. Spherical ROIs were grown in a 12 mm radius around each peak. Voxels within the spherical ROIs that failed to pass a multiple comparisons and sphericity correction (p < 0.05) were dropped from the ROIs. Regions with fewer than 100 remaining voxels were excluded, to keep consistent with Ploran et al. 2007.

Average BOLD time series were extracted from these ROIs for each stimulus and RT condition. To compare these regions to regions identified and functionally categorized in previous work (Ploran et al., 2007), time of signal onset and time of peak measures were computed for each RT condition, separately for face and house. To facilitate comparisons to the previous study, onset was computed using the Ploran et al. methods, which is similar to the onset measure described above, but instead uses subject-level time series (instead of trial-level) and several threshold levels (10, 15, 20, 25% of peak magnitude). The average of these four onset times was used as the final onset measure. Changes in onset and peak times in each region were assessed for face and house trials separately, using single-factor ANOVAs (3 levels of RT). The first RT bin (RTs < 1.5 s) was excluded due to lower trial counts per subject and low signal magnitudes compared to other conditions. Regions were matched up to previously defined regions by Talairach coordinates and approximate anatomic location. Regions were then classified as either consistent or inconsistent with previous results based on the ANOVA results from tests of activity onset and time of peak, separately for Face and House conditions. Consistent “accumulators” (i.e., regions that were in the accumulator cluster in Ploran et al., 2007) must here show a shift in peak time without changes in onset time. Consistent “moment-of-decision” regions (i.e., regions that were in the “moment-of-decision” cluster) must here show shifts in both onset and peak times. Regions previously categorized as having a “sensory” function should have non-significant effects for peak and onset time to be consistent.

3. Results

3.1 Task Behavior

On average, performance was comparable on face (N = 1960) and house (N = 1908) trials. Subjects accurately identified 79.7% of faces and 81.6% of houses. Trials with no response (N_Face = 6, N_House = 8) and response times (RT) greater than 6 s (N_Face = 143, N_House = 185) were discarded from further analysis. The data were then sorted by noise level and analyzed using a 2 × 6 repeated-measures ANOVA with factors of stimulus (face, house) and noise level (65% to 70% at 1% increments) (Figure 1b). Accuracy was significantly affected by noise level (F_{(3.27, 49.09)} = 50.01, p < 0.001, η_p² = 0.77), but was not significantly affected by stimulus (F_(1,15) = 4.07, p = 0.06, η_p² = 0.21). In addition, noise level had a differential effect on face and house accuracy, indicated by a significant interaction of stimulus and noise level (F_(5,75) = 16.60, p < 0.001, η_p² = 0.52).

Subjects were also faster, on average, at discerning faces from houses, indicated by a significant main effect of stimulus (F_(1,15) = 24.09, p < 0.001, η_p² = 0.63). The main effect of noise level (F_{(2.30, 32.15)} = 32.64, p < 0.001, η_p² = 0.70) also reached significance. Noise level also modulated RT differently for faces than for houses, indicated by a significant stimulus by noise level interaction (F_(5,75) = 2.45, p = 0.04, η_p² = 0.15) in a 2 × 6 ANOVA on RTs (Figure 1c).

3.2 Functional Region Localization

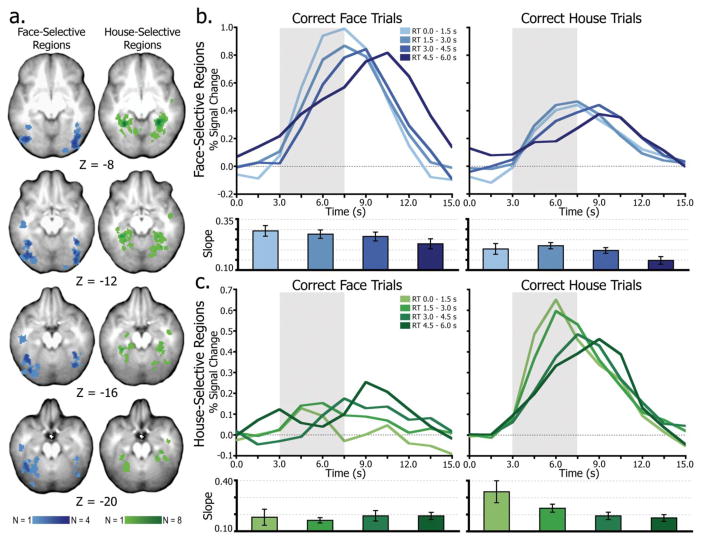
Stimulus-preferential ROIs were identified using individual subject contrasts (all correct face trials minus all correct house trials) at a 95% confidence threshold (Z < −1.96 or Z > 1.96). Using this approach, at least one face-preferential and one house-preferential ROI was identified for each of the 16 subjects. The subject-specific voxelwise data are displayed in an overlap map in Figure 2a, with more overlap across subjects indicated by darker shading. Mean face-preferential region Talairach (Talairach and Tournoux, 1988) coordinates (x, y, z) were in the fusiform gyrus, centered at −35, −59, −16 (mean 75.8 2 mm³ voxels) on the left and 38, −66, −11 (71.9 voxels) on the right. Mean house-preferential region coordinates were in the parahippocampal gyrus, centered at −25, −46, −10 (58 voxels) on the left and 29, −47, −11 (59.4 voxels) on the right.

Figure 2.

Accumulation in IT regions. (a), Composite map of individual subject ROIs indicating face-selective (blue) and house-selective (green) regions. Darker colors indicate more overlap of region loci across subjects. (b), Average time series from all face-selective regions separated by time of subject’s behavioral response. The slope (percent signal change over time) of the leading edge of these time series is plotted below for each condition. The gray box highlights the leading edge of the time series, illustrating the differential rates of accumulation leading up to decision time. (c), results from house-selective regions.

3.3 Time Series Analysis of Accumulation Effects

To determine whether activity in face- and house-selective regions accumulated over time, the temporal profile of activity was examined in stimulus-preferential ROIs (Figure 2a) as a function of response time. Trials were binned in increments of 1.5 s, for correct face and house decisions separately (Figure 2b–c), producing four RT-dependent bins. The time series data were then extracted from the ROIs on a subject-by-subject basis and sorted and averaged by RT. As shown in Figure 2, the rate of change of activity from trial onset (0 s) modulated as a function of RT, primarily for the preferred stimulus (i.e., faces in face-preferential regions and houses in house-preferential regions). In both sets of regions, there was an early onset of activity for the preferred stimulus, regardless of RT. Activity, however, quickly diverged, with earlier decisions associated with a steep leading edge and fast rise to the time of decision, and later decisions associated with a shallow increase to decision time. Importantly, this pattern is similar to data from prior work (Ploran et al., 2007; Ploran et al., 2011; Wheeler et al., 2008) and is consistent with the predictions of an accumulator model. Activity for the non-preferred stimulus (i.e., houses in face-preferential regions and faces in house-preferential regions) appeared to be less dependent on RT, particularly in house-preferential regions.

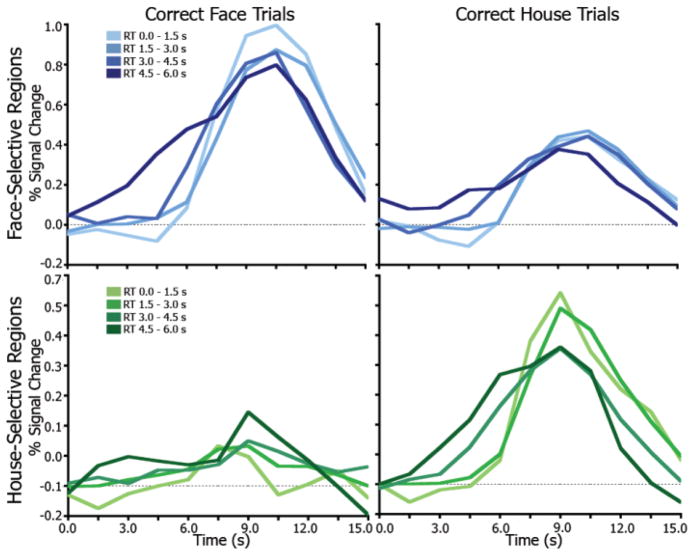
To better visualize accumulation effects, the time series onsets were set to the time of decision (i.e., RT). As shown in Figure 3, activity on trials with later RTs began to rise earlier, with a shallower slope and wider overall response leading up to the common decision time. Shorter RT conditions show a later start and rise quickly with a steeper slope toward the time of decision. This pattern is similar to the single-unit findings of Hanes and Schall (1996; Fig. 3b–c) in which the increase in change in firing rate of frontal eye field neurons was predictive of saccade latency. Similar findings were reported in superior colliculus neurons wherein pre-saccade activity buildup predicted saccade latency in a manner consistent with a drift-diffusion process (Ratcliff et al., 2003).

Figure 3.

Accumulation in IT regions time-locked to time of decision. The time series for all conditions are aligned at the time of decision (RT) in order to better visualize the separation of the accumulation effects. Looking backward from the peak, late RTs (slower accumulation) begin to rise earlier and have a shallower slope and wider overall response. Lighter colors indicate earlier RTs.

The statistical reliability of the accumulation-like activity patterns in face- and house-selective regions was determined by computing the slope of the leading edge of the time series and was then tested with a 2 × 4 ANOVA of stimulus (face, house) and RT (4 bins, 1.5 s increments). For face-selective regions (Figure 2b), there were significant main effects of RT (F_{(1.61, 24.19)} = 6.77, p < 0.01, η_p² = 0.31) and stimulus (F_{(1, 15)} = 26.82, p < 0.001, η_p² = 0.64), but no interaction (F_{(1.88, 28.24)} = 0.16, p = 0.84). There were also significant linear trends across levels of RT (p < 0.05), indicating a decrease in slope as RT increased. These findings suggest that activity patterns in face-selective regions are accumulator-like for both face and house stimuli (main effect of RT). However the main effect of stimulus indicates that there is an overall magnitude difference (face > house) suggesting that in an accumulation-to-boundary framework, the accumulating activity in face-selective regions on house trials may be sub-threshold.

In house-selective regions (Figure 2c) there was a significant main effect of stimulus (F_{(1, 15)} = 11.65, p < 0.01, η_p² = 0.44), but no main effect of RT (F_{(1.20, 18.04)} = 3.10, p = 0.09, η_p² = 0.17). Critically, there was a significant interaction (F_{(1.54, 23.13)} = 4.64, p = 0.03, η_p² = 0.24), wherein the slope on house trials decreased across RT and the slope on face trials did not. Thus, accumulation-like patterns were present on house trials but not on face trials. Because of this interaction, trend differences across RT were tested for face and house trials separately. Face trials did not show changes in slope across RT (F_{(1, 15)} = 0.23, p = 0.64, η_p² = 0.01), whereas house trials exhibited a decrease in slope from early to late RTs (F_{(1, 15)} = 6.54, p < 0.01, η_p² = 0.30).

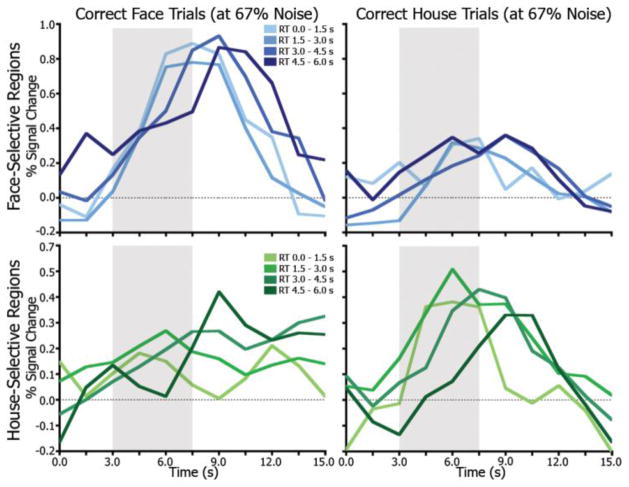
Because RT and noise level were highly correlated (i.e., slower RTs at high noise levels), the accumulation-like patterns observed in stimulus-preferential ROIs may reflect an averaging of signals relating to momentary evidence rather than a time-integrative function. This possibility was evaluated with data from a single noise level. The 67% noise condition was used because trial counts were most evenly distributed across RT conditions. Figure 4 shows the time series data for the 67% noise face and house conditions, separated by RT. Qualitatively, these effects are noisier due to fewer trials, but similar to those of the full dataset shown in Figure 2b–c. The average slope of the leading edge of the time series for these trials decreases as RT increases (area in the grey box in Figure 4), and the time of peak increases with RT. Notably, this pattern is clearest for the preferred-stimulus trials in the respective regions. There were too few trials per subject, however, to perform statistical analyses.

Figure 4.

Accumulation effects at a single noise level. Average time series from all face-selective regions separated by time of RT for trials at 67% noise only. Lighter colors indicate earlier RTs. The grey box highlights the leading edge of the time series, illustrating the differential rates of accumulation leading up to decision time.

3.4 Noise-only trials

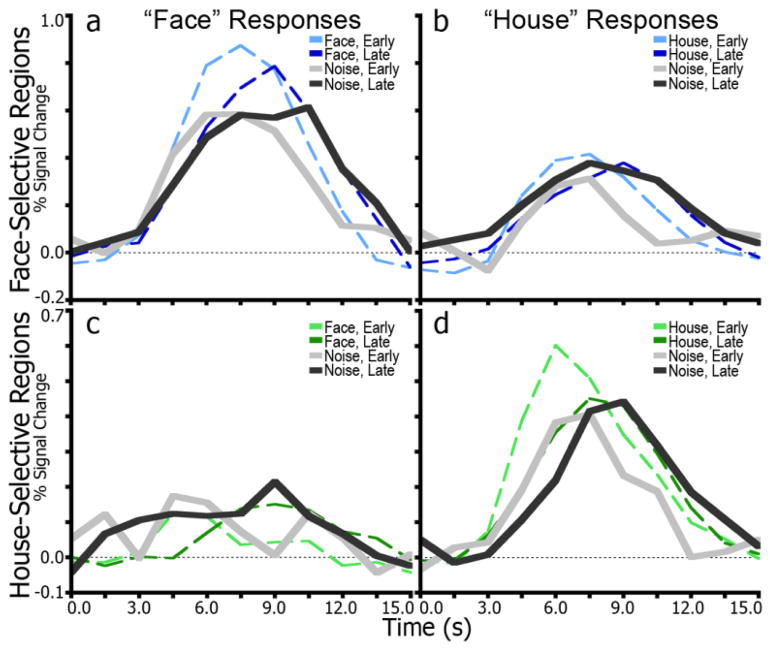
To examine the degree to which activity in the face- and house-selective IT regions represented the subject’s reported perception, time series data were extracted from face- and house-preferential ROIs for trials with no stimulus on which subjects still indicated a response. Figure 5 shows these time series in achromatic hues along with the corresponding time series for correct stimulus trials in chromatic hues. Consistent with the first analysis, there was selectivity in response pattern based on the perception of the subject. For example, activity was greater and more accumulator-like in the face-selective ROIs when subjects reported seeing a face than when they reported seeing a house. Notably, the slopes of the leading edges of the time series for early and late RT trials were similar to the slopes of the preferred stimulus trials in face-preferential ROIs. Together, the data indicate that face- and house- selective regions, whether actual visual features are present or not, play a role in the face vs. house decision, and may not merely aggregate specific visual features. It is worth noting, though, that subjects may have mistakenly perceived features (e.g., eyes, nose, mouth) though they were not present.

Figure 5.

Time series for responses to fully-noise degraded images. (a), time series in face-selective regions for trials on which subjects made a “face” response. Dotted lines indicate face-stimulus trials, and solid lines indicate noise trials. Lighter shades correspond to an early RT window (0–3 s) and darker shades to a later window (3–6 s). (b), results for “house” responses in face-selective regions. Dotted lines indicate house-stimulus trials. (c), time series for house-selective regions for trials with “face” responses. Dotted lines indicate face-stimulus trials. (d), results for “house” responses in house-selective regions. Dotted lines indicate house-stimulus trials.

3.5 Linking imaging measures to diffusion model predictions

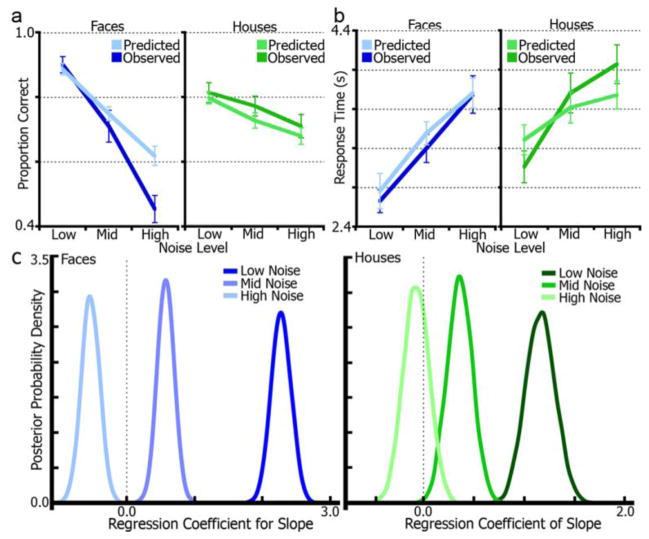
Model fits were assessed using posterior predictive checks of simulated versus empirical data. Figure 6 shows mean model-predicted RT and accuracy data generated from each subject’s posterior distributions plotted against the observed data. For face trials, a repeated-measures ANOVA of dataset (empirical, simulated) by noise level (low, mid, high) found no statistical differences by dataset (main effect) for RT (F_{(1, 15)} = 1.27, p = 0.27, η_p² = 0.08). There was, however, an effect of accuracy (F_{(1, 15)} = 8.68, p = 0.01, η_p² = 0.37). Post-hoc t-tests revealed that only the difference at the high noise-level was significant (t_{(1, 15)} = 4.71, p < 0.01), while the low (t_{(1, 15)} = −0.85, p = 0.41) and mid levels (t_{(1, 15)} = 1.28, p = 0.22) were non-significant. It is important to note that while the accuracy simulations for this condition did not match the empirical data, the RT simulations did. Moreover, as reported below, there was a non-significant correlation between slope and drift-rate in this condition, which is further explained with a secondary model analysis, addressing the effect of high error rates for both high-noise conditions. For house trials, neither RT (F_{(1, 15)} = 0.52, p = 0.48, η_p² = 0.03) nor accuracy (F_{(1, 15)} = 3.04, p = 0.11, η_p² = 0.17) differed by dataset.

Figure 6.

Drift-diffusion model regression of fMRI accumulation measures. (a), Model-predicted (simulated) accuracy data generated from single-subject model posterior distributions plotted with empirical (observed) accuracy data for stimulus and noise-level conditions. (b), model-predicted RT data is plotted with empirical RT data. (c), posterior densities from a diffusion model regression of fMRI accumulation slope and drift-rate by noise-level and stimulus. Distributions that are more than 95% to the left or right of zero signify significant effects. All conditions except high-noise faces displayed a significant effect. Distribution peaks signify the most likely regression coefficient values. Positive regression coefficients correspond to a positive correlation whereas negative coefficients reflect anti-correlations.

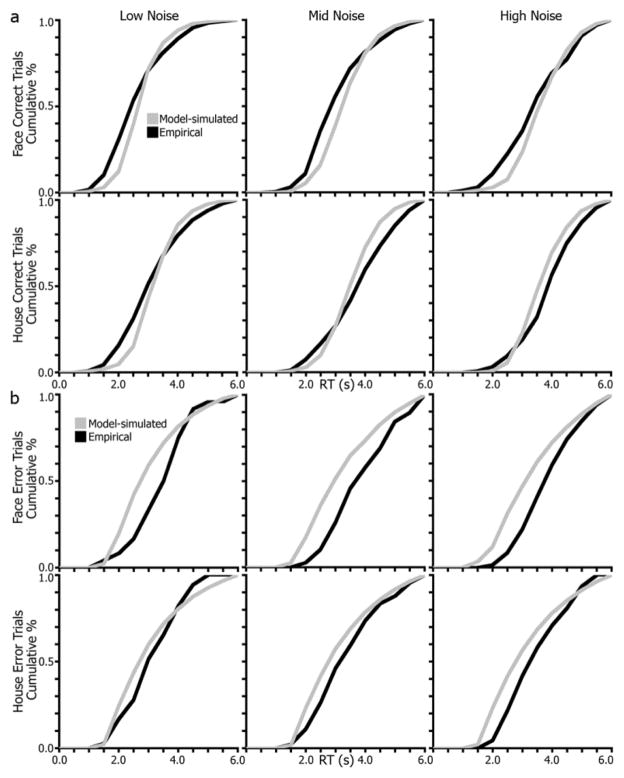
To further inspect model fits, the group-level cumulative RT distributions for model-predicted and empirical RTs are plotted in Figure 7. For correct trials (Figure 7a), the RT distributions generated from the model posteriors are generally close to the observed data. Most deviations between the two curves are under 0.5 s, and importantly, the patterns are similar between model-simulated and empirical curves (e.g., slope and trajectory of the line). Error trials, however, have poorer fits (Figure 7b), specifically for face trials and the lower noise conditions, on which subjects made fewer errors. Though, the models were better at fitting errors on house trials. As discussed below, we address potential concerns about error trials in a secondary model analysis.

Figure 7.

Drift-diffusion model fits comparing simulated and empirical RT distributions. (a), Group-level model-simulated RT distributions (grey lines) are plotted with observed RT distributions (black lines) for correct trials split by stimulus (face, house) and noise level (low, mid, high) conditions. (b), group-level RT distributions for error trials.

Using HDDM, a direct probability measure, P, was derived from the parameter’s probability masses, corresponding to the probability that the regression coefficient is non-zero. P, which will be distinguished from p values using a capital letter, can be interpreted similar to the p values derived from traditional frequentist statistics. An initial model (DIC = 11,610.4) including just face and house conditions (without splitting by noise-level) indicated a significant positive relationship between slope and drift-rate for both face (P < 0.001) and house (P < 0.001), showing that on average, trials with steep slopes (i.e,. fast RTs) are associated with high drift-rates and vice-versa. However, since RT and noise are correlated, the relationship between slope and drift-rate should be affected by noise-level (i.e., difficulty) and thus better fit by a model including it. As displayed in Figure 6c, this model (DIC = 11,086.3) resulted in significant positive slope/drift-rate correlations for face low-noise (P < 0.001), face mid-noise (P < 0.001), house low-noise (P < 0.001), and house mid-noise conditions (P = 0.002). Interestingly, both high-noise conditions fell on the opposite side of zero (suggesting a negative relationship between slope and drift-rate). There was a significant effect for the face high-noise condition (P < 0.001), but not the house high-noise condition (P = 0.325).

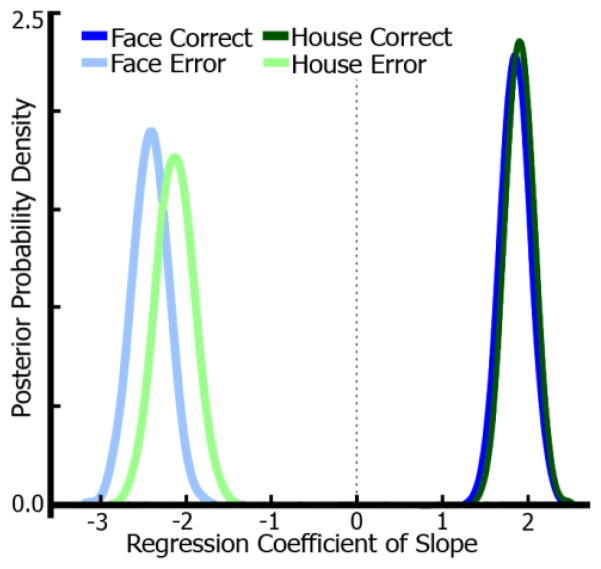
We suspected that the non-effect and negative correlation in the high-noise conditions were due to the high error rates (55% errors for faces, 29% errors for houses), meaning drift-rates would frequently point toward the lower boundary in the model. Because the slope metric did not capture these negative drift-rates due to the fMRI signals being positive and the measure coming from two separate regions (face regions for face responses and vice versa), an exploratory model was fit including only these high-noise trials. Using the same regression approach as above with slope regressed onto drift-rate, regressors for stimulus (face, house) and accuracy (correct, error) were included using high-noise trials only. Figure 8 shows the posterior probability densities for the regression coefficients of this model. Indeed, both correct face (P < 0.001) and house (P < 0.001) trials exhibit a positive relationship between slope and drift-rate. Error trials for face (P < 0.001) and house (P < 0.001) show an anti-correlation between slope and drift-rate. This is primarily due to the way the slope metric is entered into the regression, wherein error trails for face, for example, correspond to the house-selective region’s slope since the subject chose “house” for that particular trial. This means, while the drift-rate in the model is negative, it should still correspond to the “incorrect” slope, as the lower bound in our model always corresponded to the alternative choice (in this example, “house”). This analysis illustrates that even at high noise, the putative measure of neural accumulation was related to drift-rate and was additionally predictive of error trials. Though errors were different, the overall relationship between slope and drift-rate is preserved. Note, accuracy was not entered as a factor in the model with lower-noise levels due to low error rates in some conditions.

Figure 8.

Drift-diffusion model for high-noise trials. Posterior densities from a diffusion model regression of fMRI accumulation slope and drift-rate for high-noise correct and error trials. A separate diffusion model was estimated for high-noise trials only (69–70% noise) and contained a factor of accuracy (correct, error). Results show significant positive correlations between drift-rate and slope for correct trials (both stimuli) and significant anti-correlations for error trials. Due to high error-rates in these conditions, the effects displayed in Figure 6 were unexpectedly non-significant (faces) or anti-correlated (houses).

To confirm that slope better reflects evidence accumulation rather than changes in decision threshold across difficulty conditions, another model was computed in which slope was regressed with the decision threshold parameter (a) instead of drift-rate (v). The DIC of this model (DIC = 11,288.5) was compared to that of the drift-rate model (11,086.3). The lower DIC for the drift-rate model suggests that it is a better fit to the data than the alternative decision threshold model and therefore, that fMRI slope is a better predictor of changes in evidence accumulation rates based on RT than of changes in decision thresholds. A DIC difference of 10 or more between models is typically interpreted as significant (Burnham and Anderson, 2004; Zhang and Rowe, 2014). The difference here of 202.2 exceeds that criterion.

3.6 Assessing domain-general versus domain-specific decision regions

A final analysis sought to identify task-dependent effects in potential decision-related regions outside of IT by comparing the present findings with previous studies that also used a gradual presentation paradigm. Table 2 enumerates the regions identified from the main effect of time activation map. Regions were matched up to those defined in previous work (Ploran et al., 2007) and assessed for whether the underlying activity pattern was consistent or inconsistent with the previously categorized function (i.e., sensory, accumulation, or moment-of-decision). Significant effects for shifts in peak and onset times are also enumerated in tables 2–4. Figures 9 and 10 illustrate region consistency and example single-region time series. Supplementary Figure 1 displays an overlay of the average time series for accumulators and moment-of-decision regions at each time bin in order to qualitatively view differences between categories.

Table 2.

Regions of interest with reliable increases in task-related activity categorized as sensory regions in Ploran et al., 2007. ROI, index of region, ordered by significance of peak activation; Anat location, approximate anatomy encompassed by the ROI; x,y,z, Talairach atlas coordinates of peak activity; BA, approximate Brodmann’s area; Vx, region volume in voxels; F On, p-value from ANOVA of onset time across RT conditions for face trials; F Pk, p-value of peak time across RT conditions for face trials; F ⋂, an x indicates that this region was categorized consistently with comparable region from Ploran et al., 2007; H On, house trial onset time p-values; H Pk, house trial peak time p-values; H ⋂, x marks consistent categorization with region from Ploran et al., 2007; L, left; R, right; Inf, inferior; Occ, occipital; Mid, middle; G, gyrus;

ROI	Anat location	x	y	z	BA	Vx	F On	F Pk	F ⋂	H On	H Pk	H ⋂
7	R Inf Occ G	32	−83	−4	18	366	n.s.	n.s.	X	n.s.	0.02
13	R Lingual G	18	−90	−3	18	231	n.s.	n.s.	X	<0.01	<0.01
18	L Inf Occ G	−17	−89	−4	18	194	n.s.	n.s.	X	n.s.	n.s.	x
22	R Mid Occ G	24	−90	13	18	117	n.s.	<0.01		0.01	n.s.

Table 4.

Regions of interest with reliable increases in task-related activity categorized as moment-of-decision regions in Ploran et al., 2007. ROI, index of region; Anat location, approximate anatomy encompassed by the ROI; x,y,z, Talairach atlas coordinates; BA, approximate Brodmann’s area; Vx, region volume in voxels; F On, face trial onset time p-values; F Pk, face trial peak time p-values; F ⋂, x marks consistent categorization with region from Ploran et al., 2007; H On, house trial onset time p-values; H Pk, house trial peak time p-values; H ⋂, x marks consistent categorization with region from Ploran et al., 2007; L, left; R, right; Med, medial; G, gyrus; Ant, anterior; S, sulcus; Inf, inferior.

ROI	Anat location	x	y	z	BA	Vx	F On	F Pk	F ⋂	H On	H Pk	H ⋂
1	L Med Frontal G	−1	1	26	6	537	n.s.	<0.01		n.s.	<0.01
2	R Ant Insula	32	19	5	13	318	n.s.	<0.01		<0.01	<0.01	x
5	L Ant Insula	−31	20	5	13	212	n.s.	<0.01		0.01	<0.01	x
8	R Thalamus	9	−17	10	--	192	<0.01	<0.01	x	0.01	0.04	x
10	R Intraparietal S	26	−64	48	7	400	n.s.	n.s.		<0.01	<0.01	x
16	L Thalamus	−10	−20	9	--	146	0.02	0.01	x	n.s.	0.05
17	R Med Frontal G	3	14	43	6	330	n.s.	<0.01		n.s.	<0.01
21	R Inf Frontal G	45	15	0	47	148	n.s.	0.01		n.s.	n.s.

Figure 9.

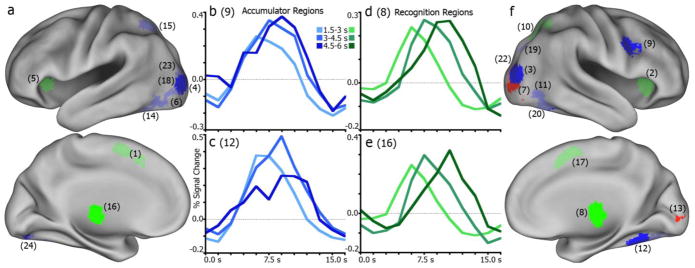
Categorization of regions for correct face trials. (a), left hemisphere regions categorized as accumulator (blue), moment-of-decision (green), or sensory (red) regions. Bright shades indicate consistency in classification with comparable regions in Ploran et al., 2007. Lighter shades indicate inconsistent region function. Numbers in parenthesis designate region index in Tables 2–4. (b), example region (R9, right inferior frontal gyrus) time series for four RT conditions illustrating a consistent accumulator. (c), another consistent accumulator (R12, right fusiform gyrus). (d), example region (R8, right thalamus) time series of a consistent moment-of-decision region. (e), another consistent moment-of-decision region (R16, left thalamus). (f), illustration of right hemisphere regions and functional categorization consistency.

Figure 10.

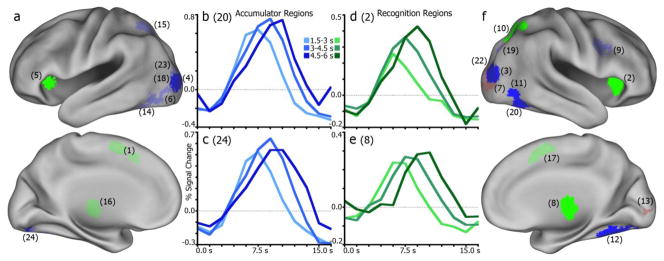
Categorization of regions for correct house trials. (a), left hemisphere regions categorized as accumulator (blue), moment-of-decision (green), or sensory (red) regions. Bright shades indicate consistency in classification with comparable regions in Ploran et al., 2007. Lighter shades indicate inconsistent region function. Numbers in parenthesis designate region index in Tables 2–4. (b), example region (R20, right fusiform gyrus) time series for four RT conditions illustrating a consistent accumulator. (c), another consistent accumulator (R24, left fusiform gyrus). (d), example region (R2, right anterior insula) time series of a consistent moment-of-decision region. (e), another consistent moment-of-decision region (R8, right thalamus). (f), illustration of right hemisphere regions and functional categorization consistency.

Among the sensory regions (Table 2), two were consistent for both face and house conditions, in the lingual and inferior occipital gyri (IOG). Another inferior occipital region was consistent for face trials. A middle occipital gyrus (MOG) region was inconsistent for both faces and houses, but had no discernible pattern to be otherwise classified as an accumulator or moment-of-decision region.

Between face and house conditions, four accumulator regions (Table 3) were also classified as accumulators here, showing a shift in peak time while time of onset of activity remained stable. Two of these regions were in bilateral MOG, and two were in bilateral fusiform gyrus. While these effects were not stimulus-specific, it is worth noting that the accumulation-like activity in the fusiform is consistent with the face- and house-preferential results reported above. For face trials only, a right inferior frontal gyrus (IFG) region was consistent, while for house trials two right fusiform regions were consistent. Inconsistencies were found in two left MOG regions, the left fusiform gyrus, left intraparietal sulcus (IPS), and right superior occipital gyrus (SOG). These regions largely showed patterns more consistent with sensory regions (i.e., no significant peak or onset shifts) for both faces and houses, notably the in the left fusiform, MOG, and IPS. None of the accumulator regions showed the same degree of stimulus specificity as the face- and house-selective IT regions did. While there were discrepancies in categorized function (i.e., consistent or inconsistent) between face and house conditions, there was never an apparent difference in amplitude as seen in the above IT regions.

Table 3.

Regions of interest with reliable increases in task-related activity categorized as accumulator regions in Ploran et al., 2007. ROI, index of region; Anat location, approximate anatomy encompassed by the ROI; x,y,z, Talairach atlas coordinates; BA, approximate Brodmann’s area; Vx, region volume in voxels; F On, face trial onset time p-values; F Pk, face trial peak time p-values; F ⋂, x marks consistent categorization with region from Ploran et al., 2007; H On, house trial onset time p-values; H Pk, house trial peak time p-values; H ⋂, x marks consistent categorization with region from Ploran et al., 2007; L, left; R, right; Mid, middle; Occ, occipital; G, gyrus; Inf, inferior; S Sulcus; Sup, superior.

ROI	Anat location	x	y	z	BA	Vx	F On	F Pk	F ⋂	H On	H Pk	H ⋂
3	R Mid Occ G	33	−84	12	19	321	n.s.	<0.01	x	n.s.	0.01	x
4	L Mid Occ G	−29	−88	0	18	310	n.s.	0.03	x	n.s.	0.01	x
6	L Mid Occ G	−32	−79	−9	18	453	n.s.	n.s.		0.03	0.01
9	R Inf Frontal G	43	3	32	9	314	n.s.	0.02	x	<0.01	<0.01
11	R Fusiform G	39	−62	−11	37	536	n.s.	n.s.		n.s.	<0.01	x
12	R Fusiform G	34	−50	−17	37	374	n.s.	0.01	x	n.s.	0.03	x
14	L Fusiform G	−38	−60	−13	19	549	n.s.	n.s.		n.s.	n.s.
15	L Intraparietal S	−27	−63	46	7	204	n.s.	n.s.		n.s.	n.s.
19	R Sup Occ G	31	−76	26	19	217	n.s.	n.s.		0.01	0.03
20	R Fusiform G	25	−76	−16	19	208	n.s.	n.s.		n.s.	<0.01	x
23	L Mid Occ G	−30	−86	17	19	185	n.s.	n.s.		n.s.	n.s.
24	L Fusiform	−19	−82	−15	19	103	n.s.	0.03	x	n.s.	<0.01	x

Across face and house trials, a region in the right thalamus showed a consistent moment-of-decision pattern (Table 4), with reliable increases in onset and peak times as RT increased. For face trials only, a left thalamus region also was consistent. For houses, the bilateral anterior insula and right superior parietal lobule (SPL) were consistent moment-of-decision regions. Regions categorized as inconsistent for both stimuli included bilateral medial frontal gyrus (meFG) and right inferior frontal gyrus (IFG). Interestingly, these regions (except IFG for house trials) were in one way consistent with an accumulator: a shift in time-to-peak across response time bins without a shifting time-to-onset.

Three regions did not correspond to any region from the previous work. These regions were located in the right thalamus (+1, −29, −2), left inferior parietal lobe (−45, −36, +48), and right precentral gyrus (+37, −24, +55). The thalamus, by these onset and peak metrics, would be categorized as a moment-of-decision region for both face and house, as it illustrates significant changes in onset and peak across RT. There were no significant changes in onset or peak times for either stimulus in the parietal and precentral regions.

4. Discussion

In this study, we tested the content-specificity of accumulation effects in stimulus-preferential regions of IT and furthermore, linked fMRI signatures of accumulation to evidence accumulation parameters in the DDM. A discrimination task was used to target spatially dissociable stimulus-preferential processing areas (Epstein and Kanwisher, 1998; Kanwisher et al., 1997) wherein activity correlates with evidence (Heekeren et al., 2004). fMRI activity was recorded as people made face/house discrimination decisions and found content-specific and time-dependent accumulation patterns in stimulus-selective visual sensory areas of IT. These findings suggest that different sources of evidence are time-integrated separately in category-selective sensory regions. Furthermore, this accumulation-like pattern of activity was present even in the absence of an overt stimulus when perception is still reported.

Many of the accumulator and moment-of-decision regions found in previous work (Ploran et al., 2007; Ploran et al., 2011; Wheeler et al., 2008) were active for this task as well, with some crucial differences between studies and when compared to the IT accumulators. Broadly, accumulators were found in the fusiform, occipital, and inferior frontal gyri, consistent with the prior work. Consistencies among moment-of-decision regions were found in the thalamus and anterior insula. These regions might play a role in domain-general decision processes, such as evidence accumulation and decision rule execution, among other possibilities. The pattern of activity in some parietal lobe and medial frontal regions was inconsistent across tasks, suggesting that their role is task-dependent.

Altogether, these findings offer support for an integration-to-boundary decision mechanism and highlight a critical role of both task-specific and task-general regions in decision evidence integration.

4.1 Characteristics of accumulation

The pattern of an RT-dependent buildup of activity in face- and house-selective regions is consistent with what a sequential-sampling model might predict for an accumulator region’s pattern of activity. These results parallel similar patterns seen at both neuronal and systems levels (for review: Gold and Shadlen, 2007; Heekeren et al., 2008). Heekeren and colleagues (2004) investigated a left superior frontal region in an analysis of stimulus-preferential activity in IT. This region showed fluctuations in peak activity reflecting the amount of evidence in favor of a face/house choice, identifying a key region that might be involved in the computation of a decision rule. However, a strong link between the evidence (face/house) and accumulation processes was missing. In the present study, we evaluated the evolving time series and related specific time windows of activity to behavior and fMRI effects to DDM parameters. In examining the temporal dynamics of the decision process, changes in the rate of activity prior to a decision were related to evidence accumulation, in ways similar to EEG (Philiastides and Sajda, 2006, 2007; Ratcliff et al., 2009; van Vugt et al., 2012) and electrophysiological studies (Hanes and Schall, 1996; Shadlen and Newsome, 2001). Activity in stimulus-preferential regions for the preferred stimulus had a characteristic early onset followed by a gradual increase in activity that corresponded to time of decision. The slope of this increase diverged by RT, with earlier decisions reaching peak faster than later decisions (i.e., faster “accumulation” in an accumulator model). Notably, following a decision, activity began to return to baseline. This is interesting in that the return to baseline was most evident for the earliest RT conditions, while bottom-up sensory information was still being presented. This post-decision decrease (Figure 2) is consistent with a process wherein integration terminates once a decision rule is satisfied, at which point no further assessment of evidence is required despite new incoming sensory information. These patterns and characteristics are similar to those previously found in frontal and parietal regions (Ploran et al., 2007; Ploran et al., 2011).

Critically a quantitative measure of the slope of the leading edge of the time series (i.e., accumulation), depicted in Figures 2 and 3, was predictive of changes in drift-rate in a DDM on a trial-by-trial level. Changes in difficulty (noise-level) and error rates did not abolish this relationship (Figures 6c, 8). Furthermore, the diffusion models indicated that the fMRI accumulation effects reported here correspond better to model-estimated drift-rates than to modulations in decision threshold. This establishes a strong link between human decision-making and neurophysiological studies wherein neural firing rates in putative “accumulator” areas echo predicted diffusion model drift-rates (Ditterich, 2006; Ratcliff et al., 2003; Ratcliff et al., 2007; Roitman and Shadlen, 2002; Rorie et al., 2010).

4.2 Content-specific integration in IT

A clear accumulation-like pattern was present in IT regions for the preferred stimulus, suggesting that evidence is represented and integrated separately by category in spatially distinct locations. Other factors, however, such as urgency or attention, can possibly contribute to these signals. For example, top-down processing relating to the setting of decision rule criteria may introduce subtle changes in magnitude, especially at later RTs (Drugowitsch et al., 2012). Such factors, however, fail to account for RT-dependent shifts in peak, as attention or urgency signals should not follow patterns predicted by accumulation models (i.e., accumulate to a threshold at a differential rate), but rather increase linearly regardless of RT (Cisek et al., 2009; Reddi and Carpenter, 2000; Simen, 2012; Thura et al., 2012). Furthermore, these activity patterns cannot be explained by a time-on-task effect, which characteristically manifests as slower responses associated with greater signal change (Dale and Buckner, 1997). Instead, in these regions, the earliest responses were associated with the largest signal change, and peak signal change decreased as RT increased. The accumulation-like activity pattern is also qualitatively present within a single noise level (Figure 4), suggesting that it is not due solely to the presence of particularly salient momentary evidence. Diffusion model analysis confirms that noise-level has little effect on the relationship between drift-rate and fMRI accumulation, even on error trials (Figures 6c, 8). Additionally, accumulation in IT was percept-dependent; e.g., as long as a subject perceives a face, whether the stimulus is noise or truly a face, activity followed an accumulation-like pattern.

Regions in ventral temporal cortex, encompassing areas with strong selectivity for face and house stimuli (Haxby et al., 1994; Kanwisher et al., 1997), may therefore function to integrate evidence during goal-directed behavior. Interestingly, these regions were also sensitive to the non-preferred stimulus (Figure 2), though the activity amplitude was always less. This further supports predictions of an accumulation-to-boundary account assuming the boundary is a certain magnitude of signal change. There is support for amplitude-defined decision boundaries. Using a countermanding task Hanes and Schall (1996) found that the neuronal spiking rates in the frontal eye fields increased to a common boundary regardless of RT. Shadlen and Newsome (2001) showed comparable results in area LIP during visual motion discrimination. In humans, Ploran and colleagues (2011) demonstrated that activity in accumulator regions was less when subjects failed to reach a decision than when they reached a decision. In the present data, the dampened response to non-preferred stimuli may reflect sub-threshold evidence for that stimulus. It could also, however, represent a degree of non-specificity for the stimulus class, wherein face-selective regions may be sensitive to a wide range of stimuli (Gauthier and Tarr, 1997). In either case, the most critical bit of information for a face/house discrimination appears to be which class of regions is most active at decision time.

Given the behavioral differences between face and house trials, as well as differences among the other analyses, it is possible that subjects are approaching the task with a special strategy for faces (i.e., face/not-face instead of face/house choices), in a manner similar to serial processing models (Townsend and Fific, 2004; Townsend and Wenger, 2004). Several of our results, however, conflict with this account. Given that accumulation was present in house-selective regions, especially for early response times, it is unlikely that subjects were approaching the task with a “face/not-face” approach. The diffusion model analysis of high-noise trials supports this, as there is a similar relationship between fMRI accumulation and drift-rate for correct and error trials when the task is most difficult. These trials would be the most likely for subjects to approach using a serial processing strategy.

There is some concern that the mechanism of these types of decisions, wherein response times are slower than typical sub-second perceptions and stimuli are noisy and degraded, may not generalize to faster perceptual decisions. Typically, as decision processes extend temporally, more systems might become involved to assist the process, for example, to resolve uncertainty, direct attention, adjust criteria, or narrow a search space. These processes could contaminate the behavior, especially RT effects (Ratcliff and McKoon, 2008). However, with a well-designed and controlled task, these concerns can be reduced. In this task, potential contaminant processes would have little benefit to a subject in categorizing a face/house perception. Indeed, RT and accuracy data simulated from the model posterior distributions were markedly consistent with the empirical data (Figure 6), suggesting that these models are capable of explaining relatively slow perceptual decisions in the visual domain. Similar success with the DDM has been seen in characterizing behavior with relatively slow RTs in both visual and non-visual domains (Bowman et al., 2012; Dunovan et al., 2014). The consistency and strong similarities of these data to other studies using fMRI (Bowman et al., 2012; Ploran et al., 2007; Ploran et al., 2011; Wheeler et al., 2008), EEG (Philiastides and Sajda, 2006, 2007), and single-cell recording methods (Gold and Shadlen, 2007; Hanes and Schall, 1996; Shadlen and Newsome, 2001) support the ability to generalize these findings. It is necessary to point out, however, that fMRI accumulation is not necessarily a direct measure of the same effects reported from EEG and neurophysiology studies. The overarching themes of these and other results, though, can be interpreted in a similar manner, albeit cautiously.

Mechanistically, traditional DDM predictions are not wholly in line on a conceptual level with our results, as these models assume that a single unit, or region, with an upper and lower bound is responsible for the accumulation process (e.g., one region accumulating face and house evidence simultaneously). The fMRI data suggest separate accumulators for face and house evidence analogous to an accumulator or counter model (Smith and Ratcliff, 2004). A simple explanation is that a cognitive model does not need to conceptually map onto the neural data directly, but rather produce a testable link between hypothesis and data. However, this conceptual mismatch, in part, implies that a domain-general accumulator must exist to combine content-specific processes in a DDM-like manner. In this study, a number of regions were consistently involved across several visual perceptual decision tasks, and thus could putatively play such a role. Other studies have sought to identify putative domain-general accumulator or monitoring regions (Heekeren et al., 2004). Another possibility to account for the mismatch is that face and house regions, as accumulators, are sufficient to produce decision behavior in conjunction with an external region that determines and applies decision criteria directly (e.g., a “time-of-decision” or comparator region). Regardless of how or where accumulation is monitored or integrated in later decision stages, it is clear that some part of the accumulation process is content specific for categorical perceptual decisions.

4.3 Decision-related regions beyond IT

In comparing the classification of regions in the face/house discrimination task to the classification in an earlier study (Ploran et al., 2007), there were some consistencies and some inconsistencies. Using Ploran et al. ROI classifications as a baseline for comparison, the pattern of activation in seven of twelve accumulators (Table 3) and five of eight moment-of-decision regions (Table 4) was consistent for either face or house stimuli.

Consistent accumulators included fusiform and occipital ROIs, indicating a similar role in the processing of visual features across the two tasks. An inferior frontal ROI was also classified consistently as an accumulator. Some of the occipital/fusiform regions (#6, 14, 19, 23) were inconsistent, which was perhaps due to the greater specificity of visual features in the current study. The left IPS ROI (#15), was also inconsistent, lacking an RT effect in the current study. Thus, accumulation effects in the face/house task were observed almost exclusively in ventral visual processing regions, but not in frontal or parietal regions. The simplest explanation for the lack of frontal and parietal accumulation effects is that this task did not require functions supported those regions. Small changes to a paradigm can fundamentally alter task strategy. To perform the face/house discrimination task, it is only necessary to map two possible percepts (face, house), which can be derived from the sensory stream, onto two possible responses (left, right button press). It is possible, but not necessary, for example, to effortfully generate a verbal or conceptual label to each stimulus. Doing so may in fact be disruptive when the task calls for a simple discrimination. In contrast, in the Ploran et al. study, the task was to identify objects that varied widely in form and function. Thus, the previous task encouraged subjects to consider not only the visual features, but also the conceptual features of each stimulus. A second difference is that there was a verification response required at the end of each trial in the Ploran et al., study, which may require the maintenance of information in working memory. There was no verification response in the current study.

All of the moment-of-decision regions except medial frontal regions near the ACC and pre-SMA, and a right inferior frontal region, were classified consistently across studies. Consistently classified regions included bilateral anterior insula, thalamus, and the right IPS. The function of these late-onset regions remains unknown and may be related to motor planning or execution (Cisek, 2006; Hwang and Andersen, 2009), resolving uncertainty (Grinband et al., 2006), computing and applying decision rules (Simen, 2012), or monitoring of accumulators, among other possibilities.

4.4 Conclusions

This study offers support for the view that stimulus-selective regions in IT perform an integrative function and accumulate decision evidence over time. The fMRI signatures of evidence accumulation appear to be directly tied to sources of sensory evidence and furthermore cannot be adequately explained by an attention or urgency account. Moreover, these signatures are predictive of trial-by-trial changes in a drift-diffusion model parameter that tracks the accumulation of evidence, establishing a critical connection to single-cell neural data in non-human primates (Gold and Shadlen, 2001; Hanes and Schall, 1996; Shadlen and Newsome, 2001) and to the predictions of decision models (Ratcliff and McKoon, 2008; Smith and Ratcliff, 2009; Usher and McClelland, 2001). Altogether, this study provides a link between fMRI measures and model-estimated evidence accumulation parameters, supporting an integration-to-boundary mechanism in human decision-making.

Table 1.

Estimated group-level parameters for two drift diffusion models. All Trials model refers to the model with an fMRI slope metric regressed against drift rate. Drift rates for this model were estimated for three noise conditions (low, mid, high) and two stimulus conditions (face, house). SD indicates standard deviation of the parameter across all subjects. High Noise included the same regression, but for high-noise trials only. Drift rates for this model were estimated for accuracy (correct, error) and stimulus (face, house) conditions.

Model	a	ter	z	ster	sv	sz	VFACE			VHOUSE
							LOW | COR	MID | ERR	HIGH	LOW | COR	MID | ERR	HIGH
All Trials	3.54	0.84	1.80	0.34	0.28	0.08	2.12	0.56	−0.50	1.15	0.37	−0.06
(SD)	0.12	0.08	0.04	0.07	0.04	0.04	0.14	0.12	0.13	0.15	0.13	0.13
High Noise	3.97	1.22	1.93	0.47	0.05	0.07	1.80	−2.37	--	1.86	−2.09	--
(SD)	0.19	0.12	0.06	0.10	0.04	0.07	0.17	0.21	--	0.16	0.22	--

Highlights.

1. Stimulus-selective inferotemporal regions accumulate perceptual evidence

2. Different sources of evidence integrate separately in a content-specific manner

3. Accumulation in stimulus-selective regions reflects diffusion model drift-rate.

4. Time-extended fMRI tasks prove useful to investigate time-sensitive effects.