DANN: a deep learning approach for annotating the pathogenicity of genetic variants

Abstract

Summary: Annotating genetic variants, especially non-coding variants, for the purpose of identifying pathogenic variants remains a challenge. Combined annotation-dependent depletion (CADD) is an algorithm designed to annotate both coding and non-coding variants, and has been shown to outperform other annotation algorithms. CADD trains a linear kernel support vector machine (SVM) to differentiate evolutionarily derived, likely benign, alleles from simulated, likely deleterious, variants. However, SVMs cannot capture non-linear relationships among the features, which can limit performance. To address this issue, we have developed DANN. DANN uses the same feature set and training data as CADD to train a deep neural network (DNN). DNNs can capture non-linear relationships among features and are better suited than SVMs for problems with a large number of samples and features. We exploit Compute Unified Device Architecture-compatible graphics processing units and deep learning techniques such as dropout and momentum training to accelerate the DNN training. DANN achieves about a 19% relative reduction in the error rate and about a 14% relative increase in the area under the curve (AUC) metric over CADD’s SVM methodology.

Availability and implementation: All data and source code are available at https://cbcl.ics.uci.edu/public_data/DANN/.

Contact: xhx@ics.uci.edu

1 Introduction

Identifying the genetic variants responsible for diseases can be very challenging. The majority of candidate variants lie in non-coding sections of the genome, whose role in maintaining normal genome function is not well understood. Most annotation methods can only annotate protein coding variants, excluding >98% of the human genome. Another annotation method, combined annotation–dependent depletion (CADD; Kircher et al., 2014), can annotate both coding and non-coding variants. CADD trains a linear kernel support vector machine (SVM) to separate observed genetic variants from simulated genetic variants. Observed genetic variants are derived from differences between human genomes and the inferred human–chimpanzee ancestral genome. Because of natural selection effects, observed variants are depleted of deleterious variants. Simulated genetic variants are enriched for deleterious variants.

CADD’s SVM can only learn linear representations of the data, which limits its performance. To overcome this, we implemented a deep neural network (DNN) algorithm that we have named deleterious annotation of genetic variants using neural networks (DANN). A DNN is an artificial neural network with several hidden layers of units between the input and output layers. The extra layers give a DNN-added level of abstraction, but can greatly increase the computational time needed for training. Deep learning techniques and graphics processing unit (GPU) hardware can significantly reduce the computational time needed to train DNNs. DNNs outperform simpler linear approaches such as logistic regression (LR) and SVMs for classification problems involving many features and samples.

2 Methods

2.1 Model training

DANN trains a DNN consisting of an input layer, a sigmoid function output layer, and three 1000-node hidden layers with hyperbolic tangent activation function. We use deepnet (https://github.com/nitishsrivastava/deepnet) to exploit fast Compute Unified Device Architecture (CUDA) parallelized GPU programming on an NVIDIA Tesla M2090 card and applied dropout and momentum training to minimize the cross entropy loss function. Dropout reduces over-fitting by randomly dropping nodes from the DNN (Srivastava, 2013). Momentum training adjusts the parameter increment as a function of the gradient and learning rate (Sutskever et al., 2013). DANN uses a hidden node dropout rate of 0.1, a momentum rate that increases from 0.01 to 0.99 linearly for the first 10 epochs and then remains at 0.99, and stochastic gradient descent (SGD) with a minibatch size of 100. As a baseline comparison, we trained a LR model. For LR training, we applied SGD using the scikit-learn library (Pedregosa et al., 2011) with parameter α = 0.01, which we found to maximize the accuracy of the LR model. LR and DNN are sensitive to feature scaling, so we preprocess the features to have unit variance before training either model. We also train an SVM using the LIBOCAS v0.97 library (Franc and Sonnenburg, 2009) with parameter C = 0.0025, closely replicating CADD’s training.

2.2 Features

There are a total of 949 features defined for each variant. The feature set is sparse, and includes a mix of real valued numbers, integers, and binary values. For example, amino acid identities are only defined for coding variants. To account for this, we include Boolean features that indicate whether a given feature is undefined, and missing values are imputed. Moreover, all n-level categorical values, such as reference allele identity, are converted to n individual Boolean flags. See the Supplementary of Kircher et al. (2014) for more details about the features and imputation.

2.3 Training data

CADD’s training data consist of 16 627 775 ‘observed’ variants and 49 407 057 ‘simulated’ variants. We trained all three models on this dataset to differentiate the simulated variants from the observed variants. To account for the imbalance between the two datasets, we randomly sampled 16 627 775 simulated variants for training. These 33 255 550 variants are split into a ‘training set’, a ‘validation set’ and a ‘testing set’ in an ∼ 8:1:1 ratio. The three models are trained on training set. For SGD, each gradient step is not guaranteed to minimize the loss function; at 1/10 epoch intervals throughout the 20 epochs of training the validation set is evaluated to select the ‘best’ model that maximizes classification accuracy on the validation set. The validation set is also used to fine tune hyperparameters such as dropout rate, minibatch size, and so forth. Finally, the models are regularly evaluated on the testing set to monitor for overfitting. In contrast, Kircher et al. (2014) trained CADD using an ‘ensemble’ strategy that involves training SVMs on 10 different subsets of the training data. We found little performance improvement when we applied this strategy.

3 Results and discussion

To compare the performance of the three models, we generated receiver operating characteristic (ROC) curves discriminating the 3 326 573 simulated and observed variants in the testing set and calculated area under the curve (AUC) scores (Fig. 1a). We used the discriminant values of the SVM and the sigmoidal function output of the DNN and LR models as classifiers for the ROC curves. We do not directly compare to CADD because it can only evaluate 100 000 variants at a time and CADD was already trained on testing set variants; however, the SVM, we trained performs very similarly to CADD despite being trained on a smaller dataset (data not shown). The classification accuracies of the SVM, LR and DNN models are 58.2, 59.8 and 66.1%, respectively. A few observations emerge from our analysis. First, LR performs better than SVM, suggesting that the max margin regularization used by SVM plays little role in this particular dataset. Second, DNN performs significantly better than both LR and SVM, leading to a 19% reduction in the error rate and 14% improvement in the AUC relative to SVM. This suggests the importance of accounting for nonlinear relationships among features, likely due to the heterogeneity of features generated in genome annotations. Third, although DNN improves on the linear methods, its accuracy is still unsatisfactory. We suspect a few factors might contribute to this: (i) The training data are inflated with mislabeled samples. Observed variants can be under positive or weak purifying selection, and therefore be functional. Conversely, many simulated variants can be nonfunctional since they are randomly sampled from the genome. (ii) The features currently used in genome annotation are insufficient for functional prediction. (iii) The model training needs further improvement.

Fig. 1.

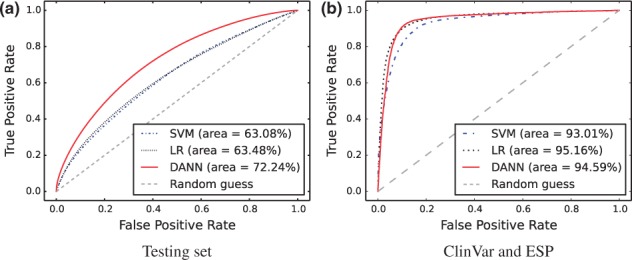
ROC curves comparing performances of the neural network (DANN), support vector machine (SVM), and logistic regression (LR) models in discriminating (a) ‘simulated’ variants from ‘observed’ variants in the testing set and (b) pathogenic ClinVar variants from likely benign ESP alleles (DAF ≥ 5%)

We also generated ROC curves showing the models discriminating pathogenic mutations defined by the ClinVar database (Baker, 2012) from likely benign Exome Sequencing Project (ESP; Fu et al., 2013) alleles with a derived allele frequency (DAF) ≥5% (Fig. 1b, n = 10 000 pathogenic/10 000 likely benign). Coding variants constitute 85.6 and 43.0% of the ClinVar and ESP databases, respectively, reducing the difficulty of annotation since many more informative features are available in coding regions. For variants with multiple gene annotations, we only selected the gene annotation that yielded the highest score from each model. All three models greatly improve on the AUC metric, with the LR and DANN models outperforming SVM; however, the performance gap between the models is much smaller than the gap in the testing set.

In conclusion, we have improved considerably on CADD’s SVM methodology. We can even achieve better performance with LR, suggesting that LR is the preferred linear classifier in this case. DANN achieves the best overall performance, substantially improving on the linear methods in terms of accuracy and separation on the testing set, which contains mostly non-coding variants. This makes DANN the most useful annotation algorithm since the vast majority of human variation is non-coding. When limited to a coding-biased dataset, all three models perform well, but the performance gap is small. Given DANN’s superior performance for annotating non-coding variants, which comprise the overwhelming majority of genetic variation, we expect DANN to play an important role in prioritizing putative causal variants, such as those derived from GWAS, for further downstream analysis.

Funding

National Institute of Biomedical Imaging and Bioengineering, National Research Service Award (EB009418) from the University of California, Irvine, Center for Complex Biological Systems (NIH R01HG006870).

Conflict of interest: none declared.