Large-scale binding ligand prediction by improved patch-based method Patch-Surfer2.0

Abstract

Motivation: Ligand binding is a key aspect of the function of many proteins. Thus, binding ligand prediction provides important insight in understanding the biological function of proteins. Binding ligand prediction is also useful for drug design and examining potential drug side effects.

Results: We present a computational method named Patch-Surfer2.0, which predicts binding ligands for a protein pocket. By representing and comparing pockets at the level of small local surface patches that characterize physicochemical properties of the local regions, the method can identify binding pockets of the same ligand even if they do not share globally similar shapes. Properties of local patches are represented by an efficient mathematical representation, 3D Zernike Descriptor. Patch-Surfer2.0 has significant technical improvements over our previous prototype, which includes a new feature that captures approximate patch position with a geodesic distance histogram. Moreover, we constructed a large comprehensive database of ligand binding pockets that will be searched against by a query. The benchmark shows better performance of Patch-Surfer2.0 over existing methods.

Availability and implementation: http://kiharalab.org/patchsurfer2.0/

Contact: dkihara@purdue.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Small molecules, such as metabolites and drugs, have important interactions with protein receptors, regulating many different processes in biological systems. Therefore, predicting binding ligands can provide important information for elucidating protein functions. Predicting binding ligands for proteins can also provide useful information for computational drug discovery, drug side effects and protein design. By combining computational screening with experiments, protein–ligand interaction networks can be revealed (Liu et al., 2011).

In principle, ligands for a protein can be predicted by identifying a global or local structure similar to known proteins. FINDSITE (Brylinski and Skolnick, 2009) and GalaxySite (Heo et al., 2014) use a modeled structure by threading to predict binding ligands for a target protein. Global structure-based methods capture distant evolutionary relationships that provide powerful information for function prediction; however, such methods have difficulty for cases where proteins of largely different global structures bind the same ligand molecules.

Local structure-based methods aim to identify similarity between a target pocket and known binding sites. Local structure can be compared at different structure levels. Catalytic Site Atlas (Porter et al., 2004) and AFT (Arakaki et al., 2004) compare a few functional residues in binding sites, where similarity is quantified with the root-mean-square deviation (RMSD) of the residues. Pseudocenters of residues (Gold and Jackson, 2006; Shatsky et al., 2006) as well as atom-level representation were also used (Hoffmann et al., 2010). However, cases have been reported where binding site residues for some ligand types are not always well conserved (Denessiouk et al., 2001; Moodie et al., 1996; Nagano et al., 2002).

Alternatively, surface representations have been used for describing binding pockets. Surface representations do not explicitly specify residue/atom positions in pockets and thus are coarser representations. The advantage of a surface representation is that it can attenuate a certain level of differences in pocket shapes, which are commonly observed in pockets of the same ligand type. eF-Seek (Kinoshita and Nakamura, 2005) constructs a triangle mesh to represent protein surface. Das et al. (2009) used a histogram of distances between nodes in a triangle mesh that represents a protein surface. SMAP performs pocket alignment using Delaunay tessellation and amino acid residue comparison (Xie and Bourne, 2008). ILBind (Hu et al., 2012) combines FINDSITE and SMAP for inverse ligand binding protein prediction.

Besides binding ligand prediction methods discussed earlier, there are methods that predict binding pocket location in proteins using various pocket descriptions. Those descriptions include grid representation (Capra et al., 2009; Kawabata, 2010; Li et al., 2008), atom triangles (Xie and Hwang, 2012) and α-shape (Liang et al., 1998). COACH (Yang et al., 2013) takes a consensus of multiple programs.

Mathematical moment-based approaches have been identified to be suitable for molecular surface representation. Moment-based methods can naturally control the resolution of the surface description, and physicochemical properties on the surface can be represented in the same way as surface shape. Thornton and her colleagues used spherical harmonics for describing binding pockets (Kahraman et al., 2007; Morris et al., 2005). In our earlier works, Pocket-Surfer, global pocket shape and the surface electrostatic potential are represented using 3D Zernike descriptors (3DZD; Chikhi et al., 2010). Subsequently, we proposed Patch-Surfer, which represents a pocket as a set of small local surface patches, each of which is described by 3DZD (Sael and Kihara, 2012). The local patch representation of pockets enables the method to identify corresponding regions in pockets even if the global shapes of pockets are different.

Although Patch-Surfer compared favorably against the existing methods in terms of prediction accuracy, it was tested on small datasets with a limited number of ligand types. In this work, we compiled a large dataset of over 6000 non-redundant pockets with 2707 different ligands with which our method was tested. Moreover, the algorithm was significantly improved in four more aspects: First, we introduced a new feature of a patch called the approximate patch position (APPS) that describes the relative position of the patch in a pocket. Second, we use geodesic distance rather than Euclidean distance for computing distance between patches in a pocket. Third, the procedure to identify corresponding patches in two pockets was revised so that the selected patch pairs are guaranteed to yield the minimum (i.e. best) score. Finally, we also consider similarity of ligands when scores for each ligand are computed. On the large dataset, we show that Patch-Surfer2.0 shows overall higher accuracy than the previous version as well as existing methods.

2 Methods

2.1 Non-redundant binding pocket database

A non-redundant database of pockets with bound ligands was constructed based on the protein-small-molecule database (PSMDB; Wallach and Lilien, 2009). Starting from 5438 protein–ligand complexes from PSMDB, we selected a non-redundant set of 2444 different ligand types in the 6547 pockets by careful examination of ligand–protein interactions. One hundred seventeen ligand types have more than five pockets. The selection procedure and the list of the 117 ligands are provided in Supplementary Material (Supplementary Table S1).

2.2 The Patch-Surfer2.0 algorithm

The original Patch-Surfer algorithm was described in our previous papers (Sael and Kihara, 2010, 2012). Here we outline the algorithm with an emphasis on the new implementation.

In Patch-Surfer, a query pocket in a protein is segmented into overlapping local patches, each of which fits within a sphere of 5.0 Å radius. A surface patch is characterized with four features: geometric shape, surface electrostatic potential, hydrophobicity and concavity, each of which is described with 3DZD. A query pocket is compared with pockets of known binding ligands in a database, and binding ligands will be predicted from the list of pockets ranked by the similarity to the query. To compute the similarity of two pockets, corresponding patches in the two pockets are identified, and a similarity score is computed based on geometric and physicochemical similarity of paired patches.

2.2.1 3D Zernike descriptors

3DZD is a series expansion of a 3D function that allows a compact and rotationally invariant representation of a 3D object (Canterakis, 1999). 3DZD has been successfully applied for various biomolecular surface representations (Kihara et al., 2011). To compute 3DZD for a pocket patch, a voxelized shape representation was created by mapping atoms of the patch onto a 3D grid and assigning each voxel a value of 1 if it is overlapped atoms and 0 otherwise. To represent physicochemical values, i.e. electrostatic potential, hydrophobicity or concavity, the values are mapped onto the grid instead of 1. The value-mapped 3D grid was considered as a 3D function, f(x). This f(x) is expanded into a series in terms of Zernike-Canterakis basis defined as follows:

$${\Omega }_{nl}^m=\frac{3}{4\pi }{\displaystyle {\int }_{|x|\le 1}f(x){\overline{Z}}_{nl}^m(x)dx}$$ (1)

where

$$Z_{nl}^m(r,\vartheta ,\varphi )=R_{nl}{Y}_l^m(\vartheta ,\varphi )$$ (2)

We used order n = 15, which corresponded to 72 invariants. $Y_l^m(\vartheta ,\varphi )$ is the spherical harmonics and $R_{nl}(r)$ is the radial function. Then, the 3DZD, $F_{nl}$, is calculated as norms of vectors ${\Omega }_{nl}$. The norm gives rotational invariance to the descriptor:

$$F_{nl}=\sqrt{{\displaystyle \sum _{m=-l}^{m=l}{({\Omega }_{nl}^m)}^2}}$$ (3)

The distance of two 3DZDs is quantified with the Euclidean distance (L2 norm) of the vectors of F_nl. The distance of two patches, pd3DZD, is a weighted average of 3DZDs of four features mentioned earlier. The weights were taken from our previous work (Sael and Kihara, 2012).

2.2.2 Approximate patch position

APPS is a new term introduced in Patch-Surfer2.0. The APPS is a histogram of geodesic distances between the center of a patch and the other patch centers in the pocket. The geodesic distance is the distance measured along the surface. The histogram tells a rough position of a patch in the pocket, e.g. near an edge or around the center. Geodesic distances were binned into 40 with a 1.0 Å interval. APPS for two patches is quantified by the L2 norm of their histograms.

2.2.3 Geodesic relative position difference

GRPD captures relative positions of patches in a pocket. Given two pockets with identified corresponding patches between them, GRPD for a new patch pair is the average difference of geodesic distances between each of the new patches to existing patches in each pocket:

$$\text{GRPD}(A,B,s_i^A,s_j^B,m^{A,B})=\frac{1}{|m^{A,B}|}\times {\displaystyle \sum _{k\in m^{A,B}}|G2(s_i^A,s_k^A)-G2(s_j^B,s_{m^{A,B}(k)}^B)|}$$ (4)

(s^A_i, s^B_j) denotes a pair of patch centers in pocket A and B, respectively, to be examined, m^A,B is a list of corresponding patches between pockets A and B, and | m^A,B | is the number of corresponding patches. | m^A,B | is at most the number of either of the size of pocket A or B (i.e. the number of patches in the pocket), whichever smaller. The corresponding patch in pocket B for patch k in pocket A is denoted as s^B_mA,B(k). G2 is the geodesic distance between two patch centers. In the original Patch-Surfer, we used the Euclidean distance, but we revised it to the geodesic distance in Patch-Surfer2.0.

2.2.4 Combined scores

The three scoring terms mentioned earlier are combined into a composite score. Two terms, the patch physicochemical distance using 3DZD termed pd3DZD and APPS, are combined with a weight factor, w₁:

$$\text{MScore}(A,B,m^{A,B})=w_{1}pd3\text{DZD\hspace{0.17em}}(A,B,m^{A,B})+(1.0-w_1)\text{\hspace{0.17em}APPS\hspace{0.17em}}(A,B,m^{A,B})$$ (5)

The Matching score (MScore) represents similarity of corresponding patches in pockets A and B. Then, we further combined GRPD with MScore to yield the Total score (TScore), with w₂:

$$\text{TScore\hspace{0.17em}}(A,B,m^{A,B})=w_2*\text{MScore\hspace{0.17em}}(A,B,m^{A,B})+(1.0-w_2)*\text{GRPD}(A,B,m^{A,B})$$ (6)

Finally, the average TScore was computed as the final similarity score between the two pockets for m^A,B.

$$\text{avgTScore\hspace{0.17em}}(A,B)=\frac{n_A}{|m^{A,B}|}\left(\frac{1}{|m^{A,B}|}{\displaystyle \sum _{k\in m^{A,B}}\text{TScore\hspace{0.17em}}(A,B,m^{A,B})}\right)$$ (7)

The first term n_A/|m^A,B| is for penalizing when the number of matched pairs |m^A,B| is smaller than the number of patches in the query, n_A. The smaller the score is the more similar the pockets are.

2.2.5 Auction algorithm for identifying corresponding patches

To compute the scores, the correspondence of patches between two pockets A and B, m^A,B, is identified with a modified auction algorithm (Sael and Kihara, 2010), which optimizes a target score by matching patches. In the original Patch-Surfer, only pd3DZD was optimized, and after the correspondence was established, the other terms were added to ‘reevaluate’ the matches. In PatchSurfer2.0, the final score (7) is used as the target function. Thus, the optimality of the matching pairs in terms of the total score is guaranteed.

2.2.6 Ligand-type prediction score

A query pocket will be compared with all the pockets in the database, and the pockets in the database will be ranked by avgTScore. Based on the ranked pocket list, predictions of binding ligands will be made using Pocket_Score_w, which is the score of a query pocket P for a ligand type F:

$${\text{Pocket\_score}}_w(P,F)={\displaystyle \sum _{i=1}^k\left(w_{l(i),F}\log \left(\frac{n}{i}\right)\right)}·\frac{{\displaystyle {\sum }_{i=1}^k{w}_{l(i),F}}}{{\displaystyle {\sum }_{i=1}^n{w}_{l(i),F}}}$$ (8)

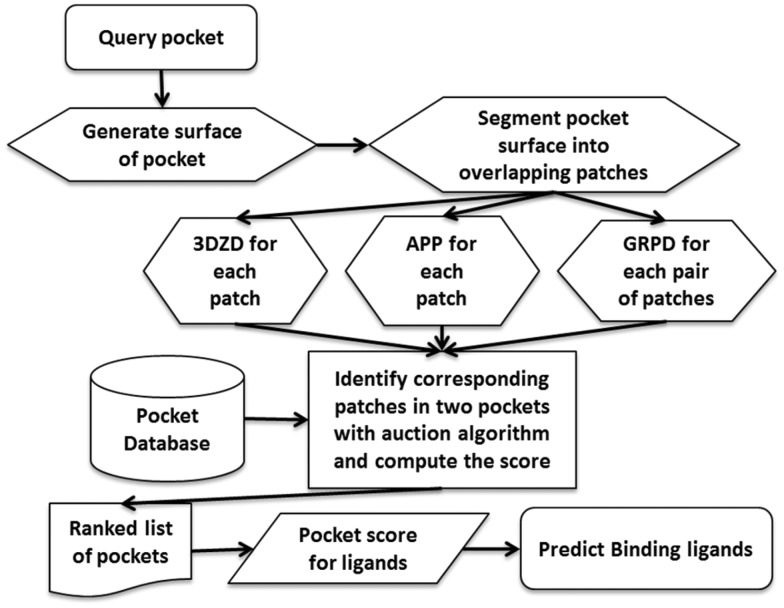
In essence, this is a type of k-nearest neighbor (where k is the number of top matches counted in computing the score), but distinguishes itself by three important enhancements for this particular problem. First, a retrieved pocket at rank i contributes to the overall score with a decreasing score of log(n/i) as the rank decreases, where n is the number of pockets in the database. w_l(i),F is a similarity score of two ligands, the ligand of the retrieved pocket at rank i and the ligand F, computed with SIMCOMP (Hattori et al., 2003). SIMCOMP uses a graph matching algorithm to compare chemical structures of two molecules. Its score ranges from 0.0 to the highest score, 1.0. If the raw SIMCOMP score was less than 0.72, we set w_l(i),F = 0. The second term expresses the enrichment factor of ligand F within the rank k. The ligand similarity score w_l(i),F is newly used in Patch-Surfer2.0. In the original Pocket_Score (Chikhi et al., 2010), we simply considered only the same ligand as the query, i.e. δ_l(i),F, which is 1 when l(i) equals to F and 0 otherwise. The entire procedure of Patch-Surfer2.0 is illustrated in Figure 1.

Fig. 1.

Flowchart of Patch-Surfer2.0

3 Results

3.1 Analysis of score components

In Patch-Surfer2.0, three parameters, w₁, w₂ (5 and 6) and k (8), must be determined. The optimization was performed on a subset of the non-redundant binding pocket database, which contains pockets for seven ligand types: adenosine monophosphate (AMP), adenosine triphosphate (ATP), flavin adenine dinucleotide (FAD), flavin mononucleotide (FMN), glucose (GLC), heme (HEM) and nicotinamide adenine dinucleotide (NAD).

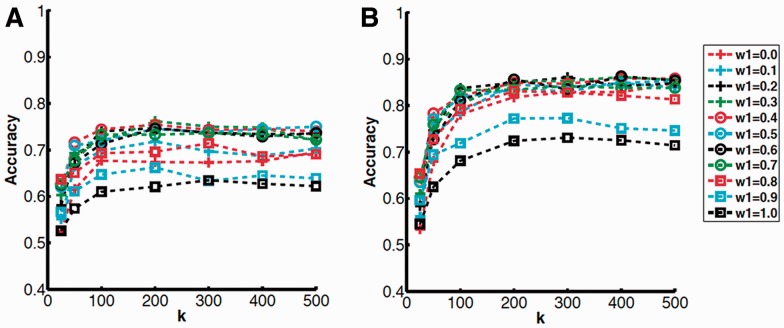
First, we determined the w₁ that optimizes MScore. Values of w₁ were explored from 0.0 to 1.0 with an interval of 0.1 with a combination of different k, which was changed from 25, 50, 100, 200, 300, 400, to 500. Each pocket of the seven ligand types was selected as query and compared with all the remaining pockets in the database. Then, binding ligands were predicted by Pocket_Score_w from the ranked list of pockets.

Figure 2 shows the average Top 10 and Top 15 accuracy of the seven ligand types with different combinations of w₁ and k (more results on Top 5, 20 and 25 accuracy are provided in Supplementary Figure S1). The Top X accuracy indicates the frequency of queries whose correct ligand is predicted within the Top X predicted ligands ranked by score. The accuracy increases as k increases and nearly plateaus at k = 200. We selected 0.4 for w_1, because the accuracy was the highest when averaged over all the values of k for Top 5, 10 and 15 accuracies. We selected 200 for k.

Fig. 2.

Average accuracy relative to k and w₁ values. Each line corresponds to a result with different w₁. A, Top 10; B, Top 15 accuracy

With the w₁ values decided earlier, we used the same process to determine w₂ for TScore (Supplementary Fig. S2). These plots show a similar trend to Figure 2; the curves in general plateaued at k = 200. We chose 0.8 for w₂, because that gives the maximum average accuracy over k for Top 5, 10, 15 and 20. k was set to 200 where the accuracy peaked with w₂ = 0.8.

Table 1 summarizes the accuracy of MScore and TScore using the determined parameter values as well as individual terms, pd3DZD, APPS and GRPD, and the original Patch-Surfer. TScore showed higher accuracy than Mscore and all the individual scores and original Patch-Surfer for all Top 5 to Top 25 accuracy. Among the individual scores, APPS, the newly added term in this work, outperformed the other two individual scores. APPS showed even higher accuracy than the original Patch-Surfer. MScore that combines pd3DZD and APPS was more accurate than using either one of the scores individually.

Table 1.

The average accuracies by different scores

	Top 5	Top 10	Top 15	Top 20	Top 25
TScore	0.562	0.760	0.871	0.914	0.932
MScore	0.552	0.754	0.849	0.898	0.931
pd3DZD	0.484	0.621	0.724	0.891	0.933
APPS	0.538	0.674	0.818	0.894	0.920
GRPD	0.410	0.488	0.616	0.737	0.855
PatchSurfer	0.491	0.658	0.785	0.860	0.895

Figure 3 examines the effect of considering the ligand similarity weight, w_l(i),F, in Pocket_score_w (8). The motivation of using the weight is to give credit when a pocket is retrieved, whose natural ligand is the same as the query but has been crystallized with a different molecule (e.g. a drug). Since a bound molecule to a pocket is usually similar to its natural ligand, the weight can provide a partial score to the query’s natural ligand. Top 5 to Top 25 accuracies obtained by two scores were compared, ones computed with Pocket_score_w with w_l(i),F and those obtained with Pocket_score with δ_l(i),F. Overall, the accuracies improved by using the w_l(i),F weight. An improvement of larger than 0.05 for Pocket_score_w over Pocket_score was observed for 14 cases while a decrease in accuracy by more than 0.05 was observed for four cases.

Fig. 3.

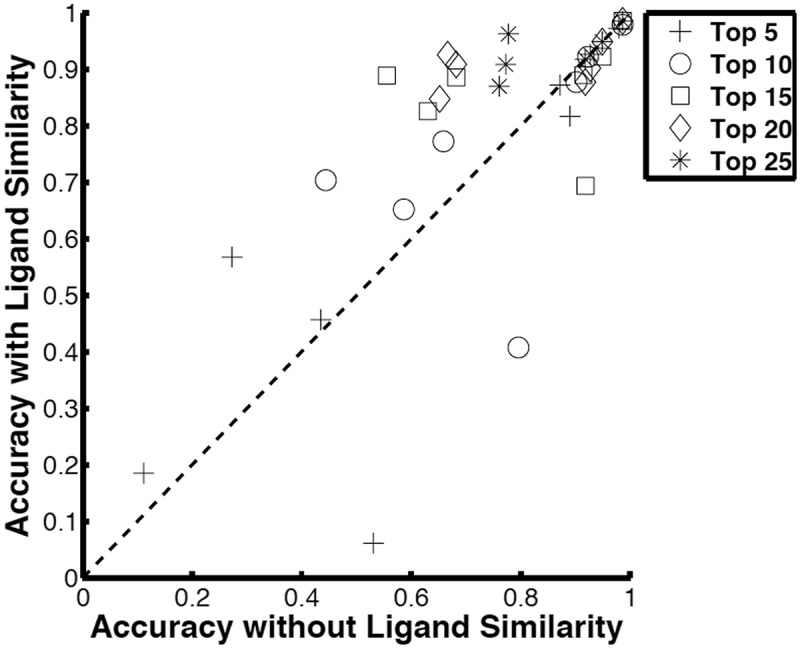
Comparison of accuracy with and without ligand similarity weight in Pocket_Score_w

In the development stage, we have also incorporated a scoring term that evaluates the pocket size difference between a query and a retrieved pocket into MScore as in the original of Patch-Surfer. However, it did not show an improvement in accuracy. This may be because the new APPS term, which is a histogram, already contains the pocket size information (data not shown).

3.2 Prediction on the remaining ligand types

Using the optimized parameters in the previous section, we benchmarked Patch-Surfer2.0 for the rest of the ligand types in the binding pocket database. Table 2 shows the average accuracies for the remaining 110 ligand types.

Table 2.

Average predictive accuracies for the remaining ligand types and the all ligand types

	Top 5	Top 10	Top 15	Top 20	Top 25
110 ligands	0.234	0.417	0.526	0.592	0.642
117 ligandsa	0.254	0.438	0.547	0.611	0.659
Group (72)b	0.325	0.499	0.603	0.675	0.734
Group (65)	0.371	0.538	0.642	0.711	0.772
Group (60)	0.402	0.578	0.678	0.744	0.796
Group (55)	0.431	0.610	0.711	0.771	0.821
Group (50)	0.459	0.628	0.726	0.791	0.835

^aAll 117 ligands were used including the seven ligand types in Table 1. ^bAccuracies were calculated for ligand groups clustered with a SIMCOMP similarity score of 0.72, 0.65, 0.60, 0.55 and 0.50. All 117 ligand types were used.

Top 10 and Top 15 average accuracies are 0.417 (0.438) and 0.526 (0.547). In the parentheses, the average accuracy for all the 117 ligand types are shown, since these are the accuracy that will be experienced in practical prediction situations by users. Although these accuracies are lower than the results on the training set in Table 1, considering that the large number of pockets and ligand types stored in the ligand database these accuracy values are useful in practical applications. Indeed as we see later in more detail, Patch-Surfer2.0 outperformed existing methods. In Table 2, we also show the results when similar ligands are grouped by SIMCOMP. The cutoff values used (0.72–0.50) make modest and reasonable grouping of ligands. Even a SIMCOMP score of 0.50 clusters only ligands with up to a few atom changes: for example, monosaccharides including glucose and mannose are grouped but not combined with sucrose or phosphono-fructopyranose, and NADH is grouped with NADP but not clustered with ATP. Thus, biologically meaningful separation of ligands is still maintained with a lower cutoff value of grouping. When ligand groups are considered, ligands in the same group are considered as ‘identical’ molecule when accuracy is computed. With the ligand grouping with a SIMCOMP score of 0.5, Top 5 and Top 10 accuracy reached 0.46 and 0.63, respectively.

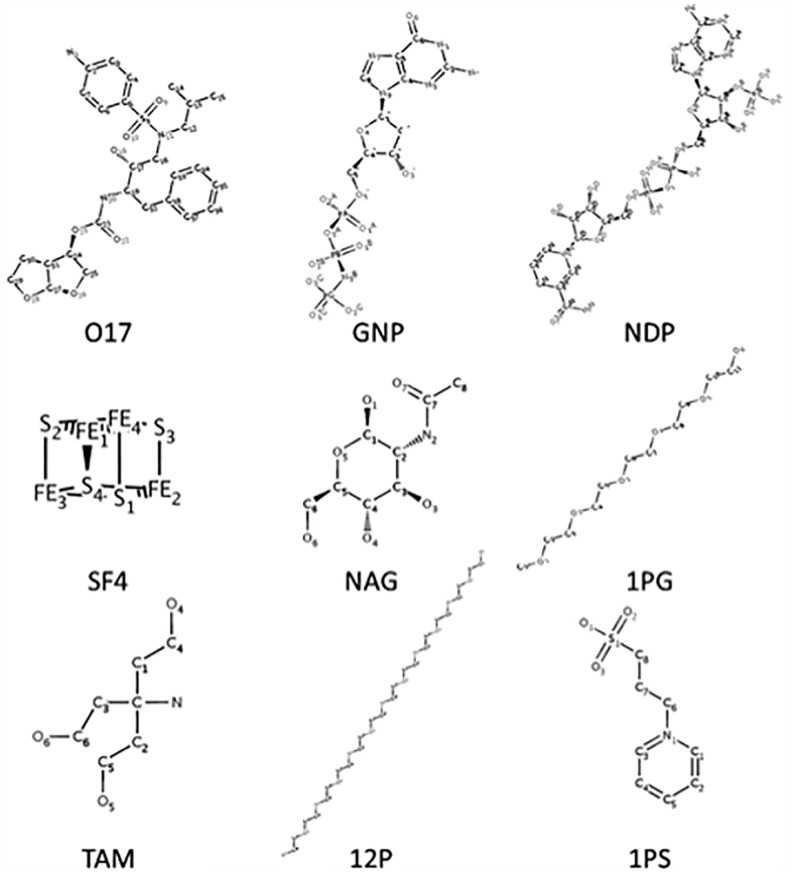
Until now we reported average accuracy over different ligand types. Next we take a closer look at the results for different ligands. Prediction accuracy can vary considerably from ligand to ligand. Among the 117 ligand types, 28 ligands (25.5%) have an accuracy of over 0.7 in Top 10 accuracy, while it was 0.0 for 15 ligands (13.6%). Figure 4 shows five ligands that were predicted well and four that were predicted poorly. The five well-predicted ligands are diverse in structures and functions, including natural ligands and their analogs, and drug molecules. These include not only rigid ligands but also flexible ones with multiple rotatable bonds and are observed to bind different targets in different conformations.

Fig. 4.

Ligand types that were predicted with high or low accuracies. The first five ligands, 017 to NAG, have over 0.9 Top 10 accuracy. The latter four ligands, 1PG to 1PS, have an accuracy of 0.0 at Top 25 or Top 20 accuracy. Ligands are specified with the PDB codes: 017, darunavir; NDP, NADPH Dihydro-Nicotinamide-Adenine-Dinucleotidephosphate; SF4, iron-sulfur cluster; NAG, N-acetyl-d-glucosamine; 1PG, methoxy-polyethylene glycol; TAM, tris-aminomethane; 12P, dodecaethylene glycol; 1PS, 3-pyridin-1-ium-1-ylpropane-1-sulfonate

We examined whether the prediction accuracy deteriorates for binding pockets for flexible ligands. We define the ligand flexibility ratio as the number of rotatable bonds per heavy atom. Overall, we see a weak trend; the correlation coefficient between the ligand flexibility ratio (Supplementary Table S1) is −0.45 and −0.50 for Top 10 and Top15 accuracy, respectively. Ligand binding is difficult to predict if ligands are too flexible as the four failed cases in Figure 4. In particular, 1PG and 12P are extreme: they have 14 and 37 rotatable bonds and ligand flexibility ratio of 0.82 and 0.92, respectively (by comparison, the ligand flexibilities of 017, GNP and NDP, are 0.32, 0.25 and 0.27, respectively). However, 1PG and 12P are polyethylene glycols, which are precipitants in sample preparation for X-ray crystallography and are not relevant to biological functions of the proteins. We found other polyethylene glycols, 2PE, P33, PE4, 1PE, P6G, 15P as well as two similar molecules, C8E and PG6, have a flexibility ratio over 0.8 and have poor prediction accuracy of below 0.125 for Top 10 accuracy (except for C8E whose accuracy was 0.375). The other two poorly predicted ligands, TAM and 1PS, are molecules commonly used as buffers. Thus, the poor prediction results for the four ligand molecules may be reflecting the fact that the molecules in precipitant or buffer bind non-specifically to proteins.

Removing flexible ligands increases the prediction accuracy. In Table 3, we show the accuracy when 10 ligands with a flexibility ratio over 0.8 are excluded from the queries. Compared with the results in Table 2, Top 10 accuracy has improved from 0.438 to 0.472 for the all 107 ligands and 0.628 to 0.663 when ligands were grouped with SIMCOMP score of 0.5. Because the extremely flexible ligands are not relevant to biological functions of target proteins and also grouping with SIMCOMP score of 0.5 only groups similar ligands, the last row of Table 3 is the accuracy that is most relevant to practical use of Patch-Surfer2.0. In Supplementary Table S2, the accuracy was computed after further excluding flexible ligands, which have a flexibility ratio over 0.7, 0.6 and 0.5. The accuracy improved after more ligands were excluded but the largest improvement was observed when the 10 ligands with the flexibility ratio >0.8 were excluded.

Table 3.

Accuracy excluding ten extremely flexible ligands

	Top 5	Top 10	Top 15	Top 20	Top 25
100 ligandsa	0.252	0.452	0.567	0.635	0.683
107 ligands	0.272	0.472	0.587	0.653	0.699
Group (72)	0.345	0.531	0.637	0.706	0.756
Group (60)	0.426	0.613	0.707	0.767	0.807
Group (50)	0.487	0.663	0.754	0.810	0.845

^aTen flexible ligands were removed from queries used in Table 2.

3.3 Prediction for apo proteins

We have further compared Patch-Surfer2.0’s performance on 32 apo proteins with their counterpart of the holo proteins in the binding pocket database (Supplementary Table S3). The results (Table 4; Supplementary Table S3 and Fig. S3) show that the accuracy for apo target proteins was not deteriorated, rather, higher than the results for holo proteins. This is interesting but consistent with our previous work (Sael and Kihara, 2012).

Table 4.

Accuracy of holo and apo proteins.

	Top 5	Top 10	Top 15	Top 20	Top 25
holo	0.250	0.375	0.500	0.625	0.719
apo	0.344	0.594	0.688	0.750	0.844

Ligand binding residues for holo proteins were taken from their apo counterpart.

3.4 Comparison with other existing methods

In our previous papers, we have reported that the accuracy of the original Patch-Surfer is higher than Pocket-Surfer (Chikhi et al., 2010) and four other similar pocket descriptors, 2D and pseudo-Zernike descriptors, Legendre moments and spherical harmonics (Sael and Kihara, 2012). Moreover, Patch-Surfer also showed better prediction performance than the four existing methods eFseek, SiteBase, PROSURFER and XBSite2F (area under the curve, AUC, was 0.86 for Patch_Surfer, and 0.49, 0.60, 0.57 and 0.55 for the four methods, respectively; Kihara et al., 2011). Additionally, in Table 5, Patch-Surfer2.0 was compared with eF-Seek and a recently developed method, APoc (Gao and Skolnick, 2013). Fifteen ligands were used for this comparison.

Table 5.

Comparison with two existing methods

Ligands			AMP	ATP	FMN	GLC	NAD	ACR
Number of pocketsa			43/46	38/44	48/49	15/27	38/39	5/8
Rel.	P-S2.0		2.94	3.93	4.47	2.24	11.15	12.39
pAUC	eFSeekb		0.12	0.18	0.61	2.04	0.24	7.50
AUC	P-S2.0		0.74	0.78	0.80	0.61	0.88	0.88
	APocc		0.64	0.75	0.76	0.45	0.88	0.64
ADN	ANP	BCN	GLO	HEC	MLT	MPO	PLP	PMP
14/15	33	4/6	5/6	12/13	15/18	7	29/30	6/7
2.64	5.10	2.95	26.6	14.1	3.05	2.73	7.10	3.27
0.52	0.31	8.35	9.86	2.02	1.13	0.76	0.64	0.25
0.69	0.81	0.79	0.93	0.85	0.65	0.66	0.80	0.72
0.61	0.77	0.48	0.81	0.68	0.43	0.36	0.66	0.90

^aThe number of query pockets used for the comparison with eF-Seek (left) and Apoc (right). The numbers are different because common entries between the pocket databases by Patch-Surfer2.0 and eF-Seek were used as queries. Only one number is shown when the number were the same for eF-Seek and Apoc. The average AUC of receiver operator characteristic of the number of queries are shown.

^bFor the performance comparison with eF-Seek, we computed partial AUC (pAUC) that is the AUC computed up to the maximum false-positive rate (FPR) against the pAUC of the random retrieval up to the same FPR. Thus, rel_pAUC = pAUC/pAUC_random where pAUC = AUC/(1.0*maxFPR).

^cAPoc was run locally using the same database as Patch-Surfer2.0.

Patch-Surfer2.0 showed higher relative partial AUC (Table 5) than eF-Seek for all but one ligand. In comparison with APoc, Patch-Surfer2.0 showed higher AUC for 13 ligands and a tie for NAD. The average relative partial AUC and AUC by Patch-Surfer2.0 for the latter 10 ligands (ACR to PMP) were not lower than those for the first five (AMP to NAD), which were used for parameter optimization.

3.5 Examples of predictions

Finally, we show several examples of Patch-Surfer2.0 predictions. In Supplementary Table S4, we show a typical example of a search result. The query was a NAD binding pocket (glucose dehydrogenase, 1gco_A). Among the top ten matched pockets, four of them bind NAD, three of them bind nicotinamide-adenine-dinucleotide phosphate (PDB code: NAP) or nicotinic acid adenine dinucleotide (DND), which are similar to NAD with SIMCOMP score of 0.88 and 0.87, respectively. The rest of the three ligands are BEI (Inhibitor Bea322) and two cases where multiple small ligands bind to the pockets. BEI is similar to NAD in size and has two aromatic rings as NAD does. The latter two cases show similarity to NAD in terms of size when the total size of ligands in the pockets is considered and has common local structures.

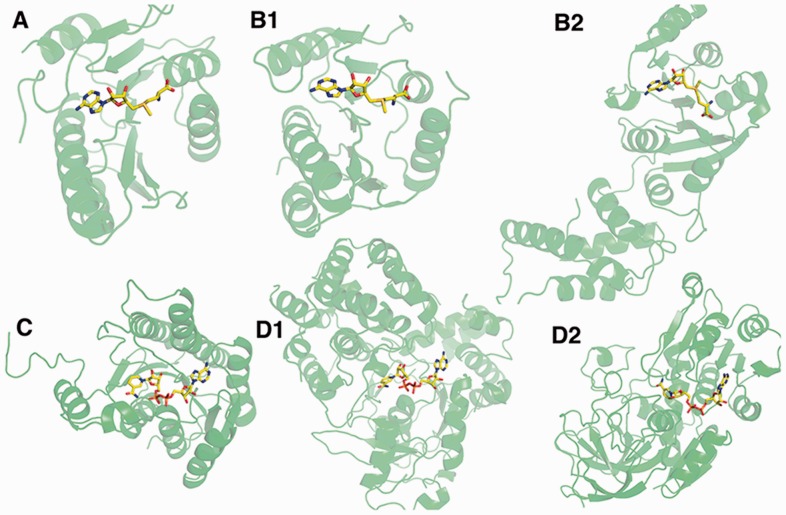
Figure 5 shows examples of ligand binding pockets identified at a high rank for query pockets. Figure 5A and B are binding pockets for S-adenosylmethionine (SAM). B1 is an example of retrieved pocket that has a similar global structure as well as similar pocket shape to the query protein. In contrast, B2 is a case that the retrieved protein is not structurally similar and also the ligand binds in a different conformation from the query, which indicates that the pocket shape is different to the query. In the second example, Figure 5C and D are NAD binding pockets. Both of the two retrieved pockets, D1 and D2 are from different global structures. TM-score (Zhang and Skolnick, 2005) is less than 0.5 for both proteins to the query. The first one (Fig. 5D1) has a similar pocket shape with an RMSD of NAD of 1.0 Å, while the second one (Fig. 5D2) binds NAD in a different conformation. These examples illustrate that Patch-Surfer 2.0 identifies pockets of the same ligand type that have different overall shapes and locate in a protein of globally different structures.

Fig. 5.

Examples of identified pockets. A is the query, 2plw-A that binds SAM. B1 and B2 are retrieved pockets for 2plw-A at the rank 1 and 6, respectively, 3dou_A and 1zq9_A. The TM-Scores between the query and the two proteins are 0.86 and 0.56, and the RMSD values of ligands are 0.65 Å and 1.75 Å, respectively. C, a query, 1gco_A. D1 and D2 are retrieved pockets for 1gco_A at the rank 1 and 8, 1lj8_A and 2jhf_A. TM-scores between the query is 0.40 and 0.38, and RMSD of ligands are 1.00 Å and 2.28 Å, respectively

4 Discussion and conclusion

We have presented Patch-Surfer2.0, which compares a query pocket to known ligand binding pockets and predicts binding ligand molecules for the query. Among the five major technical improvements that have driven the method to achieve substantially higher accuracy than the original Patch-Surfer, APPS had the largest contribution to the highest accuracy among the individual score components. APPS captures not only positions of patches in a pocket but also reflects the size of the pocket. By using a patch representation of pockets, Patch-Surfer2.0 recognizes pockets for the same ligand by identifying common local regions in pockets, even if the global folds of the proteins are different and the pockets do not share a common global shape.

Funding

This work was supported by the National Institutes of Health [R01GM097528]; National Science Foundation [IIS1319551, DBI1262189, IOS1127027 to D.K.]; National Research Foundation of Korea [NRF-2011-220-C00004].

Conflict of interest: none declared.