Multiple associated variants increase the heritability explained for plasma lipids and coronary artery disease

Abstract

Background

Plasma lipid levels as well as coronary artery disease (CAD) have been shown to be highly heritable with estimates ranging from 40%–60%. However, top variants detected by large-scale genome-wide association studies (GWAS) explain only a fraction of the total variance in plasma lipid phenotypes and CAD.

Methods and Results

We performed a conditional and joint association analysis using summary-level statistics from two large GWAS meta-analyses: (1) the Global Lipids Genetics Consortium (GLGC) study, and (2) the Coronary ARtery DIsease Genome-wide Replication and Meta-analysis (CARDIoGRAM) study. There were 100,184 individuals from 46 GLGC studies for plasma lipids, and 22,233 cases and 64,762 controls from 14 studies for CAD. We detected a number of loci where multiple independent SNPs were associated with lipid traits within a locus (12 out of 33 loci for high-density lipoprotein cholesterol [HDL-C], 10 of 35 loci for low-density lipoprotein cholesterol [LDL-C], 13 of 44 loci for total cholesterol [TC], and 8 of 28 loci for triglycerides [TG]), reaching genome-wide significance (P<5×10⁻⁸), nearly doubling the heritability explained by GWAS (3.6% to 7.6% for HDL-C, 5.0% to 8.8% for LDL-C, 5.5% to 8.8% for TC, and 5.7% to 8.5% for TG). Multiple SNPs were also associated with CAD (3 of 15 loci, 9.6% to 11.4% of increased heritability).

Conclusion

These results demonstrate that a portion of the missing heritability for lipid traits and CAD can be explained by multiple variants at each locus.

Introduction

Plasma lipids and lipoproteins are heritable risk factors for coronary artery disease (CAD),¹ with heritability estimates ranging from 40%–60% for total cholesterol (TC), LDL-cholesterol (LDL-C), HDL-cholesterol (HDL-C), and triglycerides (TG) and 30%–60% for CAD.^2-5 Genome-wide association studies (GWAS) for plasma lipids and CAD have successfully identified at least 95 gene regions for plasma lipids and 46 for CAD.^1,6 Despite the success of GWAS, single nucleotide polymorphisms (SNPs) at these loci explain only a modest proportion of the heritability - 20% to 25% of the heritability for plasma lipids, and less than 10% of the heritability of CAD.¹ These observations have led to the general question of how to account for the unexplained heritability.

Typically GWAS uses a single-locus test, in which each variant is tested individually for association with a specific phenotype and the best SNP at each locus is reported. A single SNP may not capture the overall amount of variation at a locus because there may be multiple causal variants at a locus. If individual level genotype data are available, we can detect additional SNPs using conditional analysis; however, conditional analysis is often infeasible when many studies have contributed results to a large-scale meta-analysis.

Recently, Yang et al. developed a conditional and joint association analysis tool that leverages summary-level statistics and estimated linkage disequilibrium (LD) from a reference sample with individual-level genotype data.⁷ In the current study, we applied this approach to lipid traits studied by the Global Lipids Genetics Consortium (GLGC) as well as to the dichotomous trait of CAD studied by the Coronary ARtery DIsease Genome-wide Replication and Meta-analysis (CARDIoGRAM) Consortium.^5,6

Methods

GWAS Summary-level Statistics for Lipids and Coronary Artery Disease

We obtained the summary-level statistics (rsID, effect allele, the other allele, frequency of the effect allele, effect size, standard error, P value and sample size) from the GLGC meta-analysis study for lipids⁶ and from the CARDIoGRAM meta-analysis study for CAD.⁵ These studies included up to 100,184 individuals from 46 studies for lipids, and 22,233 cases and 64,762 controls for CAD, respectively.

Reference Samples for Linkage Disequilibrium

We used the European ancestry individual-level genotype of 9,796 individuals and phenotype data of the Atherosclerosis Risk in Communities Study (ARIC) cohort⁸ as a reference sample. ARIC represents a large population-based cohort and this cohort contributed to the GLGC and CARDIoGRAM meta-analyses. SNP quality control was performed, excluding SNPs with missingness >2%, minor allele frequency (MAF) <0.01 or Hardy-Weinberg equilibrium (HWE) P value <1×10⁻⁶. Among a total of 805,437 genotyped SNPs, 617,428 SNPs were retained in the ARIC data. We discarded samples with missingness >3% and one of each pair of samples with an estimated genetic relatedness >0.25. A total of 8,682 individuals of European ancestry in the ARIC cohort were included for LD calculation. The SNP data for ARIC were phased by MaCH and imputed into the HapMap Phase 2 CEU panel by minimac, the same panel that was used for the initial GWAS.^9,10 We used the best guess genotypes of the imputed SNPs and excluded imputed SNPs with HWE P value <1×10⁻⁶, imputation quality Rsq <0.3 or MAF <0.01 and retained 2,490,789 SNPs in the ARIC cohort.

Conditional and Joint GWAS Analysis

We performed a stepwise model selection procedure to select independently associated SNPs using the GCTA tool available online (http://www.complextraitgenomics.com/software/gcta/massoc.html) for each lipid trait and CAD. Briefly, the procedure begins with the most significant SNP with P<5×10⁻⁸ in the single-SNP meta-analysis and tests all the remaining SNPs conditional on the selected SNP(s) in the model. It then selects the SNP with the minimum conditional P value and fits all the selected SNPs in a model, dropping the SNP with the largest P value >5×10⁻⁸. The algorithm iterates until no SNP is added to or removed from the model. The joint effects of all selected SNPs are estimated after the model has been optimized. We define a locus as a chromosomal region at which adjacent pairs of associated SNPs are less than 1 megabase (Mb) distant. Details about the conditional and joint analysis are fully described in ref. 7.

Estimation of the Variance Explained by the Joint Association

We calculated the variance explained using the following equation where β_M and β_J are effect sizes in standard deviation units obtained from the original meta-analysis and the joint analysis, respectively.¹¹

$$q^2=2\times {\beta }_{\mathrm{M}}\times {\beta }_{\mathrm{J}}\times \text{MAF}\times (1-\text{MAF})\times 100$$

Variance explained was calculated for (1) the top SNPs from original meta-analysis, and (2) the top original SNPs plus the additionally associated SNPs found from the conditional and joint analysis.

Replication Analysis for Lipid Traits

We replicated the variance explained by all jointly associated SNPs detected from the GLGC data using 7,312 individuals from the Malmö Diet and Cancer (MDC) cohort as an independent sample in two models: Method A) A multiple regression of the SNPs selected from the discovery set (GLGC); Method B) A replication analysis using the SNPs with their effect sizes estimated from the discovery sample (GLGC) to predict the phenotype in MDC. In Method A, two predictors were created in the MDC cohort by PLINK¹² for each lipid trait, one based on all additionally associated SNPs or its proxy SNPs (r²>0.8) and the other based on the GWAS top SNPs only, and the observed lipid phenotypes were regressed on the predictors. In Method B, we created two predictors in the MDC cohort but with SNP effects estimated from the GLGC dataset and regressed the observed lipid phenotypes on the predictors. In both methods, adjusted R² values of MDC were compared with the explained variances for lipid traits in GLGC. Also, we checked the independency of multiple associated SNPs within a locus by comparing β from the model using multiple SNPs and β from the model using each SNP within each locus that has the largest number of multiple associated SNPs for each trait.

Informed Consent and Institutional Review Board Approval

Most of the analyses utilized summary statistics from prior publications. For genetic association analyses in the MDC cohort using de-identified genotype and phenotype data, each participant had provided written informed consent, and approval was given by the institutional review board at Partners Healthcare.

Results

Lipid Phenotypes

Using summary statistics of ∼2.5 million SNPs from the GLGC meta-analysis of 100,184 individuals for four lipid fractions along with SNP LD estimated in 8,682 unrelated European-Americans selected from the ARIC cohort study (See Methods), we identified 62, 61, 68, and 41 jointly associated SNPs for each lipid trait (HDL-C, LDL-C, TC, and TG) with P<5×10⁻⁸ (Supplemental Tables 1-4), respectively. When compared with previous results conducted by conventional conditional analysis in the original GLGC study, we could detect more additionally associated SNPs with each trait (11 vs. 29 for HDL-C, 12 vs. 26 for LDL-C, 12 vs. 24 for TC, and 9 vs. 13 for TG, Supplemental Table 5).

For the loci where the increasing alleles of at least two SNPs were negatively correlated, some associated variants were undetected in the original GWAS. For example, rs180349 and rs3741298 at the APOA1-C3-A4-A5 locus on chromosome 11 did not exhibit a significant association with HDL-C in single-SNP meta-analyses (P value from the single-SNP meta-analysis [P_M]=8.67×10⁻³ and 4.12×10⁻⁴, respectively), but both SNPs reached genome-wide significance when fitted jointly (Supplemental Table 1). In addition, the significance and effect size of the leading SNP at the locus also increased (P_M=2.94×10⁻⁴² to P_J=1.84×10⁻⁷³ for rs964184) (Supplemental Table 1). There were 12 of 33 HDL-C, 10 of 35 LDL-C, 13 of 44 TC, and 8 of 28 TG loci harboring more than two associated SNPs, with the maximum number of 9, 9, 6, and 7 SNPs at a locus, respectively. The lead SNPs (33 for HDL-C, 35 for LDL-C, 44 for TC, and 28 for TG) explained 3.6%, 5.0%, 5.5%, and 5.7% of phenotypic variance, respectively. These values were almost doubled (7.6% for HDL-C, 8.8% for LDL-C, 8.8% for TC, and 8.5% for TG) when all jointly associated SNPs (62 for HDL-C, 61 for LDL-C, 68 for TC, and 41 for TG) were taken into account.

Coronary Artery Disease

Using summary statistics of ∼2.5 million SNPs from the CARDIoGRAM meta-analysis of 22,233 cases and 64,762 controls for CAD along with the same reference SNP data from the ARIC cohort described above, we identified 18 jointly associated SNPs for CAD with P<5×10⁻⁸. Of these SNPs associated with CAD, 3 of 15 loci represent multiple associated SNPs within a single locus (Figure 1, Supplemental Table 6).

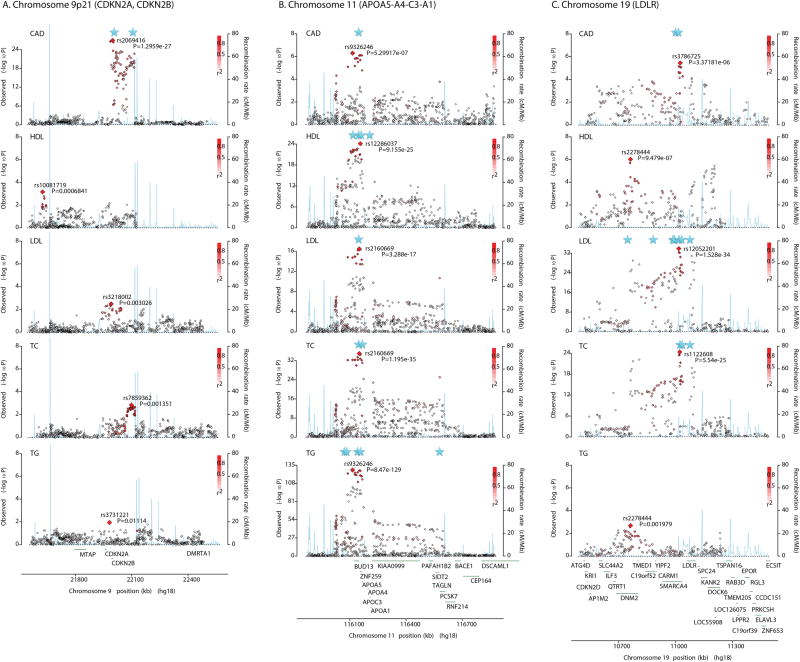
Figure 1.

Regional association plots of three loci with significant joint associations for CAD. A, CDKN2A and CDKN2B on chromosome 9p21. B, APOA5-A4-C3-A1 on chromosome 11. C, LDLR on chromosome 19. SNPs are plotted as red diamonds with –log₁₀ P (y-axis) from the meta-analysis result for each trait. Significant joint association is marked as blue star corresponding to genomic position (x-axis) (See Supplemental Tables 1-6 for details). Color scheme illustrates linkage disequilibrium r² based the 1000 Genomes European Ancestry (CEU) data. Genes are shown at the bottom of each plot. Note that scale of y-axis is different from each figure.

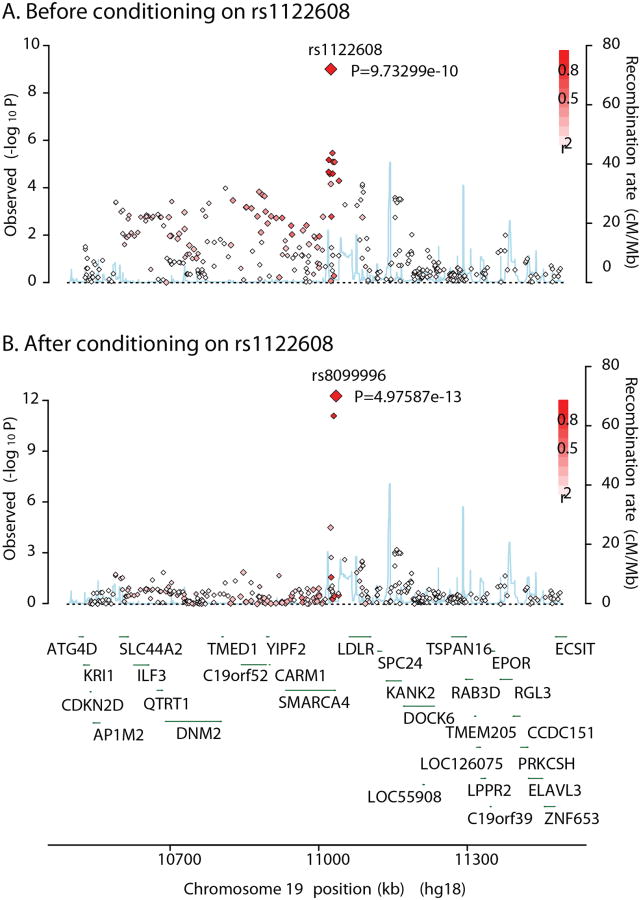
We found a significant joint association with CAD in the LDLR region, where multiple common variants for LDL-C and rare mutations in familial hypercholesterolemia have been previously reported.¹³ Two SNPs, rs8099996 and rs1122608, which are 11,024 bp apart, were retained in the stepwise model selection as jointly associated SNPs with P_J<3.5×10⁻¹¹ (Supplemental Table 6). The secondary SNP (rs8099996; P_M=0.67) was masked by the primary SNP (rs1122608; P_M=9.7×10⁻¹⁰) in single-SNP analyses but it appeared significant (rs8099996; P=5.0×10⁻¹³) in conditional analysis on the primary SNP (Figure 2). This region was also significant for LDL-C and TC (Figure 1C). While the 9p21 CDKN2A and CDKN2B region was only significant for CAD in joint association analysis, the APOA5-A4-C3-A1 gene cluster locus was significant for four lipid traits as well as CAD (Figures 1A-1B). When they were fitted jointly, their effects, as well as statistical significance, were substantially increased compared to those in single-SNP analyses. The 15 leading SNPs explained 9.6% of phenotypic variance. The three additional SNPs detected by the joint analysis accounted for 1.8% of the variance explained.

Figure 2.

Example of a locus with a secondary joint association signal conditioning on a primary signal. A, SNPs are plotted as red diamonds with −log₁₀ P (y-axis) from the meta-analysis result for CAD. The rs1122608 SNP is a primary signal at this LDLR locus. B, P values of the same SNP sets, which were calculated from conditional analysis on rs1122608, are plotted.

For a set of 184 SNPs in the Supplemental Tables 1-4, we evaluated the associations with CAD in CARDIoGRAM meta-analysis. Of these 184 SNPs, 38 SNPs were nominally associated (P_M<0.05) and 20 SNPs showed a significant association after the Bonferroni's correction (P_M<2.2×10⁻⁴) (Supplemental Tables 1-4).

Replication of the Lipid Results in an Independent Sample

We validated the direction of effect in each SNP between GLGC results and MDC results for all the jointly associated variants (Supplemental Figure 1). The multiple regression analysis showed that the prediction R² values of top primary SNPs were 4.6%, 5.8%, 6.7%, and 5.2%, consistent with the estimate of 3.6%, 5.0%, 5.5%, and 5.7% of variance explained in the discovery sample (GLGC), for HDL-C, LDL-C, TC, and TG, respectively (Supplemental Figure 2: Method A). And the R² values of the additionally associated SNPs were 5.2%, 3.1%, 2.7%, and 2.2%, in line with the estimate of 4.0%, 3.8%, 3.3%, and 2.8% of variance explained by these SNPs in the discovery sample (GLGC), respectively (Supplemental Figure 2: Method A).

In addition, when we used the SNP effects estimated from the GLGC dataset (the second method), the R² values of top primary SNPs were 3.4%, 4.6%, 4.6%, and 4.4%, consistent with the estimate in the discovery sample (GLGC), and those of the additionally associated SNPs were 4.1%, 3.1%, 2.6%, and 2.2%, in line with the estimate of those explained by these SNPs in the discovery sample (GLGC), respectively (Supplemental Figure 2: Method B). Therefore, these replication analyses in an independent sample confirmed that additional associated variants could explain approximately 2%–4% of phenotypic variation for each lipid trait.

Supplemental Figure 3 shows that β from the multiple SNP model and β from the single SNP model are consistent for each locus with the largest number of multiple SNPs (A:HDL-C for CETP locus, B:LDL-C for APOE-C1-C2 locus, C:TC for APOE-C1-C2 locus, D:TG for LPL locus), suggesting that the variants from the multiple SNP model are independent.

Discussion

In this study, we detected a number of loci where multiple independent SNPs were associated with lipid traits and accounting for these variants nearly doubled the heritability explained by the previous GWAS results (HDL-C, LDL-C, TC, and TG). In addition, the joint associations of lipid traits were validated in an independent sample.

GWAS results have explained only a fraction of the heritability of complex traits. There has been extensive debate regarding this unexplained heritability, with hypotheses ranging from rare variants to epistasis.^14-16 Here, we explored the possibility of multiple independent signals at a given locus as a contributor to the unexplained heritability.

Conditional analysis has been used as a tool to identify secondary association signals at a locus, starting with the top associated SNP, across the whole genome followed by a stepwise procedure of selecting additional SNPs, one by one, according to their conditional P values. However, nearly always, pooled individual level genotype data are unavailable in large-scale meta-analyses. In that sense, the tool we used is useful in terms of saving computational time and cost because it does not require individual genotype data except for the samples used as a LD reference. As a result, the current study clearly indicates that an increased portion of the missing heritability could be explained by the joint influence of multiple variants within a locus, suggesting the importance of digging into known loci to identify causal variants and understand the genetic architecture of complex diseases.

For plasma lipids, we found that many signals at specific loci can explain a large proportion of the variance. From our estimation, 9 SNPs in the CETP locus could explain as much as 2.6% of variance explained in HDL-C, 9 SNPs in the APOE-C1-C2 locus explained 2.1% of that in LDL-C, 6 SNPs in the APOE-C1-C2 locus explained 1.1% of that in TC, 7 SNPs in the LPL locus explained 1.7% in that of TG, and 2 SNPs in the CDKN2A/CDKN2B locus explained 2.8% of that in CAD trait. This is consistent with a previous report that suggests greater heritability of common variants in known loci.¹⁷

The variance explained by the top SNPs for each lipid trait from the GLGC dataset was relatively small compared with the one from the original article.⁶ This could be due to variability in estimates from different studies as well as the different method employed in this analysis compared to that of original GWAS, where only one study (i.e., the Framingham Heart Study) contributed to the estimation of variance explained. Although we showed evidence of multiple associations at several loci using summary statistics of the CARDIoGRAM meta-analysis, recently published data of the CARDIoGRAMplusC4D meta-analysis with 63,746 CAD cases and 130,681 controls based on the Metabochip array might also be useful to find additional associated signals.¹

In summary, we detected a number of loci where multiple associated SNPs within a single locus were associated with lipid traits or CAD. For lipid traits, these variants nearly doubled the heritability explained.