A comparison of multiple indicator kriging and area-to-point Poisson kriging for mapping patterns of herbivore species abundance in Kruger National Park, South Africa

Abstract

Kruger National Park (KNP), South Africa, provides protected habitats for the unique animals of the African savannah. For the past 40 years, annual aerial surveys of herbivores have been conducted to aid management decisions based on (1) the spatial distribution of species throughout the park and (2) total species populations in a year. The surveys are extremely time consuming and costly. For many years, the whole park was surveyed, but in 1998 a transect survey approach was adopted. This is cheaper and less time consuming but leaves gaps in the data spatially. Also the distance method currently employed by the park only gives estimates of total species populations but not their spatial distribution. We compare the ability of multiple indicator kriging and area-to-point Poisson kriging to accurately map species distribution in the park. A leave-one-out cross-validation approach indicates that multiple indicator kriging makes poor estimates of the number of animals, particularly the few large counts, as the indicator variograms for such high thresholds are pure nugget. Poisson kriging was applied to the prediction of two types of abundance data: spatial density and proportion of a given species. Both Poisson approaches had standardized mean absolute errors (St. MAEs) of animal counts at least an order of magnitude lower than multiple indicator kriging. The spatial density, Poisson approach (1), gave the lowest St. MAEs for the most abundant species and the proportion, Poisson approach (2), did for the least abundant species. Incorporating environmental data into Poisson approach (2) further reduced St. MAEs.

1. Introduction

Kruger National Park (KNP), South Africa, provides 19,485 km² of protected habitats for the unique biodiversity of the African savannah. Accurate estimation of abundance of large herbivores in both space and time is an integral component of conservation and management activities in KNP. Monitoring herbivore spatio-temporal abundance patterns can help detect and mitigate unacceptable levels of population change. Consequently, annual aerial surveys to monitor large herbivore populations have been conducted for the last 40 years. Results from these surveys have, inter alia, been used to understand (1) herbivore distribution patterns in relation to resources (e.g. Smit 2011), (2) how dynamic environmental factors influence herbivore population trends (e.g. Ogutu and Owen-Smith 2003, Owen-Smith and Mills 2006), (3) population declines and possible reasons therefore (Harrington et al. 1999, Kshatriya et al. 2001) and (4) how past management actions and possible future scenarios have or may influence herbivore distribution patterns (e.g. Smit and Grant 2009, Smit and Ferreira 2010).

From 1980 to 1993, the whole park was surveyed annually, but this was costly and time consuming. It involved almost 4 months of near-constant flying with four observers on board. In 1998, the park-wide census approach was replaced by a sampling strategy whereby the number of animals is recorded along 800 m wide East–West transects, spaced at intervals of 2.5–5.6 km (Kruger et al. 2008). However, such strip transects leave ‘gaps’ in the data spatially. The park currently uses a distance sampling method (Buckland et al. 1993) to estimate the total number of various species in the park from the transect data. This method is based on fitting for each species a detection function based on the count data collected in various distance bands perpendicular to the aircraft. This method can also be used for ground surveys (Ogutu et al. 2006). Currently, Kruger Park scientists use the ‘DISTANCE’ software developed by Thomas et al. (2004) for this analysis (Kruger et al. 2008).

While the distance method generates global estimates of a species population in the park which are helpful in identifying increases or declines in population numbers, these estimates cannot be used to fill the gaps between survey transects and produce maps of animal distribution in a given season. Such maps are particularly useful for understanding herbivore distribution patterns in relation to resources, how dynamic environmental factors influence herbivore population trends and how management actions, such as artificial water provision and fire management, influence herbivore distribution patterns. In addition, especially for less abundant species or species that tend to be clustered in space, the following assumptions of the distance method are not met: (1) all animals on the transect line are detected, (2) animals are counted accurately, (3) all animals are observed in their original locations and (4) 60–80 sightings of each species are made per transect. Another potential problem with the distance method is that there seems to be a lot more noise in the total counts for the park when it is used (1998–2005) compared with the counts based on the full survey of the park (1985–1993) (Figure 1b), and the associated confidence intervals are wide. The large uncertainties and the spatial gaps associated with analysing the transect data with the distance method have prohibited using the data from the past 14 years to the same extent as the data from the previous surveys where the entire park was censused. Techniques that can (1) provide reliable interpolation results for the gaps left by the sampling design and (2) increase the accuracy of the population estimates will greatly increase the value of this data set and will allow the answering of ecological and management questions currently not possible. In this article, our primary aim is to determine if multiple indicator kriging or area-to-point Poisson kriging can achieve the first of these goals.

Figure 1.

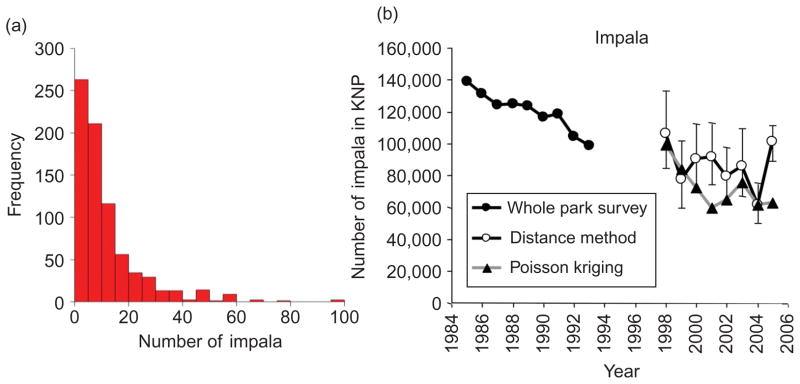
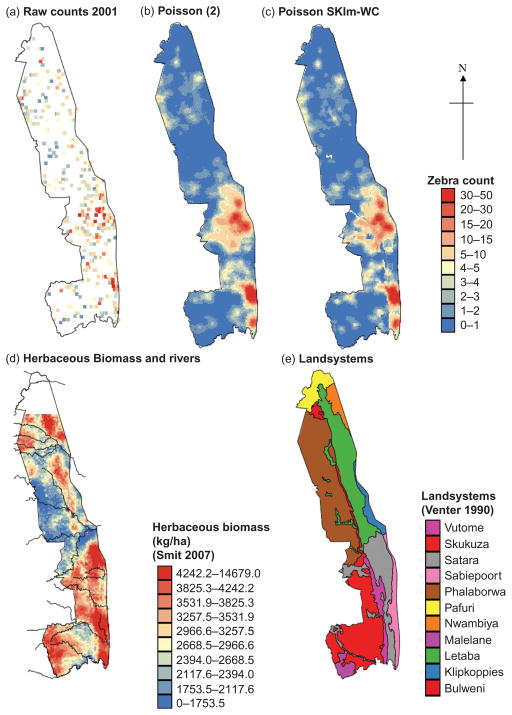
(a) Histogram of impala count observations along transects in Kruger National Park for 2001 and (b) numbers of impala observed in Kruger National Park when the whole park was surveyed (1985–1993) and estimated from transects using the distance method (with 95% confidence intervals) and area-to-point Poisson kriging approach (2), 1998–2005.

There have been several applications of geostatistics to the mapping of wildlife populations. For example, Vandermeer and Leopold (1995) used variants of kriging to assess population size for the European storm petrel while Palma et al. (1999) presented an application to the Iberian lynx. At first glance, geostatistical methods seem ideal for populating data gaps between transects since they do not require some of the assumptions of the distance method, and numerous studies have demonstrated the greater accuracy of kriging relative to other common interpolation methods such as inverse distance, cubic splines and classification (Voltz and Webster 1990, Gotway et al. 1996, Kravchenko and Bullock 1999).

Steffens (1992) completed a geostatistical study of animal count data from KNP and suggested that should the park ever have to reduce the density of survey due to budget constraints, geostatistical methods would be appropriate for populating data gaps. Steffens (1992) recognized that the count data at point locations could not be directly used for ordinary kriging and counts first had to be aggregated to blocks. Yet, he proceeded to use traditional method of moments variograms and cross-variograms when the histograms for the derived animal count data were all highly positively skewed. When data are highly skewed or contain numerous outliers, the method of moments variogram estimator can be extremely unstable (Lark 2000, 2002, 2003, Kerry et al. 2007a, b, Bellier et al. 2010). This is especially the case for the rarer species or those that tend to cluster spatially. Rossi et al. (1992) provided a comprehensive overview of the ways in which geostatistical tools could be used to interpret and map patterns of spatial dependence in organisms and the many environmental variables with which they interact. They noted that the traditional variogram provides an incomplete and misleading summary of these patterns when the local means and variances change spatially or when data contain many outliers. They suggested the use of indicator variograms for presence/absence data and robust variogram estimators when there are many outliers in the data. Indicator variograms have been used to characterize variables with highly skewed histograms in several pollution studies (Goovaerts 1994, Goovaerts et al. 1997, Van Meirvenne and Goovaerts 2001, Lin et al. 2002, Saito and Goovaerts 2002, Liu et al. 2004, Lee et al. 2007) where indicator kriging was used to estimate the probability that various critical pollution thresholds are exceeded in a given location. Indicator kriging has also been used to delineate high-density areas in spatial Poisson fields of unexploded ordnance (Saito and McKenna 2007). Therefore, in conjunction with Rossi et al.’s (1992) recommendation, and the fact that animal count data are usually highly skewed, we first adopted an indicator approach for the animal count data treating each count number as a separate threshold. The number of separate variograms that need to be computed, modelled and used in post-processing can, however, make the approach very time consuming and computationally intensive. To facilitate the implementation of the indicator approach with many thresholds, Goovaerts (2009) devised an auto-indicator kriging (Auto-IK) approach whereby the variograms for each threshold are computed and modelled automatically, followed by multiple indicator kriging. We investigate the use of this approach here with the animal count data.

We also explored a more recent approach to mapping count or density data that were devised after the review paper by Rossi et al. (1992), namely Poisson kriging (Monestiez et al. 2006, Bellier et al. 2010). The positive skew in the histograms of animal count data tends to approach the Poisson distribution (Figure 1a) and thus seems more appropriate for use with Poisson kriging than robust estimators because the latter are designed more specifically to deal with outliers rather than underlying asymmetry. Poisson kriging was developed by Monestiez et al. (2006) to obtain accurate maps of relative abundance of whales in the Mediterranean Sea on the basis of spatially heterogeneous observation efforts and infrequent and sparse animal sightings. The same approach was then applied to rates of phenomena like diseases (Goovaerts 2005) or crime (Kerry et al. 2010) where the denominator is a population size instead of observation time. Data based on larger populations receive more weight in the computation of the variogram and the kriging estimate through the incorporation of an ‘error variance’ term, derived from the Poisson distribution. Here, we applied the Poisson approach using two types of denominator for the KNP animal count data: (1) size of observational areas to map the spatial density of each species and (2) total number of animals from all species within areas of fixed size to map the relative proportion of each species. The predictions from both Poisson kriging methods were converted to counts to allow direct comparison with the estimates from multiple indicator kriging. The change of support associated with the computation of point estimates from block data (blocks of various sizes in Poisson approach (1) and constant size in Poisson approach (2)) was accomplished using area-to-point kriging (Kyriakidis 2004). This is an important issue that previous wildlife studies like that of Steffens (1992) did not take into account. Dealing with the change of support using area-to-point Poisson kriging allows the production of reliable maps of animal distribution patterns while also giving sensible total population estimates of each species for the park that are similar in magnitude to those of the distance method (see Figure 1b for an example). Area-to-point Poisson kriging, although evident in the health geography literature, has not been used in the wildlife context where administrative geographies with known populations are not in place, and this requires the development of new methods for preprocessing data.

As mentioned earlier, the main aim of this article is to compare the performance of multiple indicator kriging and two area-to-point Poisson kriging approaches for mapping the spatial distribution of species abundance. Multiple indicator kriging and Poisson kriging are univariate approaches as animal abundance is estimated using only the spatial autocorrelation among animal counts. Such spatial autocorrelation is, however, an expected function of animal social behaviour and spatial autocorrelation in environmental factors which influence animal distribution. Therefore, the benefit of incorporating environmental data as secondary information into Poisson kriging approach (2) was also briefly explored.

2. Methods

2.1. Animal count observations

Animal counts were made during the dry season when leaves are generally absent from trees from a fixed-winged aircraft flying at approximately 76 m height and a speed of 167–185 km h^–1. A frame fitted to the aircraft (or calibrated strips drawn on the side windows of the aircraft) enabled animals to be located within distance classes (up to 50, 100, 200 and 400 m) from the plane on either side (see Figure 2 in Kruger et al. 2008). This means that observations were made along East–West running transects that were 800 m wide, but also included a 36 m invisible zone under the aircraft. Transects were spaced at various intervals to achieve a specified percent coverage of the park in different years. For example in 1998–2000, 64 transects were spaced at 5.6 km intervals to achieve 15% coverage of the park. The coverage of the park in other years was 22% in 2001–2003 and 22% in the south and 28% in the north in 2005–2006. Each time an animal or group of animals was observed from the plane, the position along the transect was recorded using a GPS, as well as the number of animals observed, the species and the distance class from the plane. No indication, however, was given of which side of the plane the animals were observed, and each species observed was recorded separately. Some potential errors associated with these observation methods include but are not limited to

1. miscounting/mere estimates of the count when large herds of the same species are present or altogether missing individuals or small herds (Redfern et al. 2002);

2. animals under the plane are not counted;

3. counts are likely to be influenced by environmental conditions (e.g. vegetation cover) as well as differences in cryptic colouration of animals (e.g. zebra is more conspicuous than impala) (Redfern et al. 2002);

4. location inaccuracies due to time delay in position recording when multiple species are present in one location; and

5. animals that move from one side of the plane to the other during flight can be double counted.

2.2. Environmental data

Several environmental data sets were available for KNP. The continuous variables included herbaceous biomass (B) estimated by cokriging of ground measurements of herbaceous biomass with Advanced Very High Resolution Radiometer (AVHRR) imagery (Smit 2007), distance to large rivers (DR), artificial water holes (DW) and woody cover (W) (Bucini et al. 2010). The categorical variables included ecozones (E) (Hendry 2004), geology (G) (Venter 1990), landscape (L) (Gertenbach 1983) and land systems (LS) (Venter 1990).

2.3. Preprocessing of animal count data

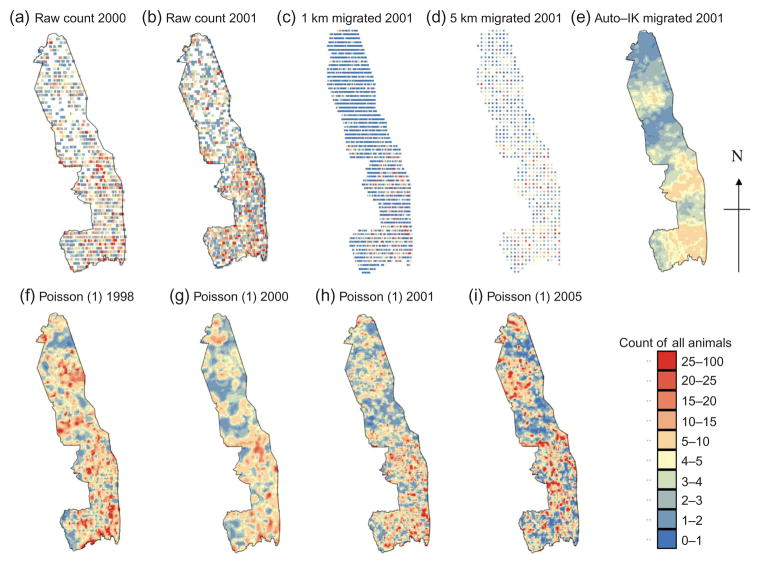
As animal counts were recorded along transects and records made only when an animal or group of animals was observed, the raw count data contain no zero counts. They are a point pattern of presences (Figure 2a and b), but we know that along the transects, the observations are separated by areas with zero counts. To account for this type of sampling, data were preprocessed by migrating the observations to the nearest point on a grid, that is, the centroids of blocks were assigned the number of animals within a particular block. This is akin to the pooling to blocks employed by Steffens (1992). Grids of different spatial densities were explored (results not shown here), and it was found that for East–West transects (800 m wide) 5.6 km apart, within-transect spacing intervals of 1 km (Figure 2c, 5167 data points) and 5 km (Figure 2d, 1082 data points) were most suitable for investigating the rarer and most abundant species, respectively (Table 1). Both the raw count data (Figure 2a and b) and the data migrated to grids were used with the Auto-IK approach.

Figure 2.

Maps of counts of all animals: (a) raw count data for 2000, (b) raw count data for 2001, (c) 2001 counts migrated to a grid with 1 km spacing along transects 5.6 km apart, (d) 2001 counts migrated to a grid with 5 km spacing along transects 5.6 km apart and (e) 2001 counts produced using Auto-IK and migrated data and (f) 1998 counts, (g) 2000 counts, (h) 2001 counts and (i) 2005 counts produced by Poisson approach (1).

Note: For (a) and (b) white areas show zero counts and dark blue is ≥ 1, for (c)–(i) dark blue is 0–1.

Table 1.

Background information on species and environmental variables found significant in Poisson regression of each species.

Species/abbreviation	Feeding guild	Rank of abundance	Index of herding	Significant variables (abbreviations) in Poisson regression
Elephant bulls (Eb)	Mixed feeder	5	5	Woody cover (W)
Giraffe (Gi)	Browser	4	3	Herbaceous biomass (B), geology (G)
Impala (Im)	Mixed feeder	1	1	Herbaceous biomass (B), distance to river (DR), land system (LS)
Kudu (Ku)	Browser	5	3	a
Warthog (WH)	Grazer	5	3	a
Waterbuck (WBk)	Grazer	5	3	Distance to river (DR)
White Rhino (WR)	Grazer	5	4	Herbaceous biomass (B), woody cover (W)
Wildebeest (WiB)	Grazer	3	1	Herbaceous biomass (B)
Zebra (Ze)	Grazer	2	2	Herbaceous biomass (B)

Notes: Rank of abundance shows the relative abundance of the species based on historical data (1 is most abundant and 5 least). Index of herding shows the degree to which the species groups in herds based on the inter-quartile range of herd size (1 is most prone to herding and 5 is least). Species with comparable abundance (or index of herding) were given the same rank.

^aNone of the available environmental variables were significant in Poisson regression.

For Poisson kriging (Monestiez et al. 2006), count data need to be preprocessed to yield a ratio. The following two types of denominator were considered:

1. the observational area (ratio = spatial density, Figure 3a) and

2. the total number of animals in a given area or block (ratio = proportion of a species, Figure 3b).

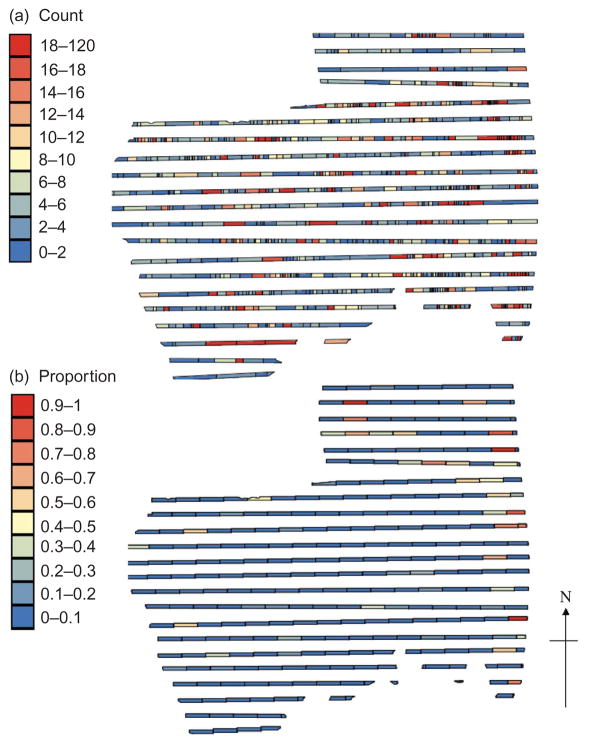
Figure 3.

Calculation of (a) spatial density of all animals from 800 m wide transect data for Poisson approach (1) and (b) proportion of impala from 5 km long blocks of the 800 m wide transect data (i.e. number of impala in 5 km by 800 m block/total number of all animals in 5 km by 800 m block) for Poisson approach (2).

Figure 3a illustrates how spatial density for Poisson approach (1) along the 800 m wide transects was calculated. The midpoints between each observation and its two neighbours were considered as the limits of the area associated with each observation. Therefore, a large distance between successive observations of an animal translates into a large observational area. The observational area for the first and last observations on each transect was calculated to the park boundaries on one side. Figure 5b shows how the proportion of each animal was calculated for Poisson approach (2). Unlike approach (1), the size of each block (i.e. observational area) is constant. Each 800 m wide transect was divided into 5 km long blocks, and the total number of a given species observed in the 5 km by 800 m block was divided by the total number of all animal species in the 5 km by 800 m block giving a proportion of each species per block.

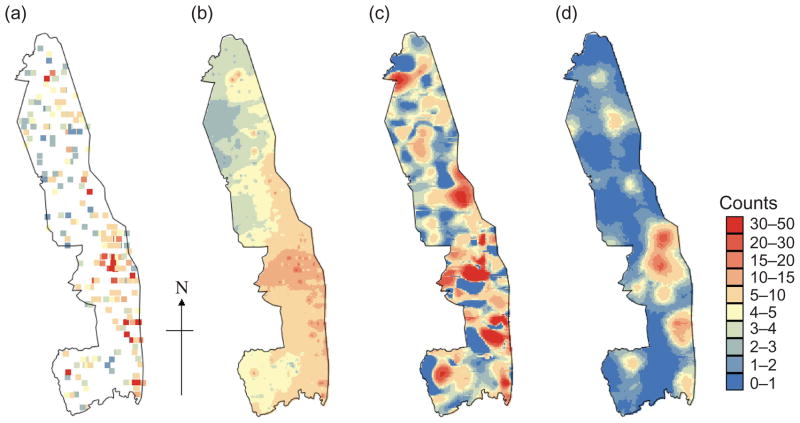
Figure 5.

(a) Observed counts of zebra in 2000 and kriged maps of counts produced by (b) Auto-IK and raw count data, (c) Poisson approach (1) and (d) Poisson approach (2).

Note: For (a) white areas show zero counts and dark blue is ≥1, for (b–d) dark blue is 0–1.

2.4. Geostatistical methods

2.4.1. Multiple indicator kriging

The indicator approach computes the animal count at each location u as the mean of the local probability distribution F(u;z|(n)) = Prob{Z(u) ≤ z|(n)} that is estimated for a series of thresholds z_k using kriging of indicators defined as follows:

$$i({\mathbf{u}}_{\alpha };z_k)=\{\begin{array}{ll}1\hfill & \text{if}z({\mathbf{u}}_{\alpha })\le z_k\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (1)

where the observations z(u_α) are either animal data migrated to a grid (many zero counts) or raw animal count data (lowest count is 1). In its traditional implementation, this non-parametric approach can be rather tedious since it requires the estimation and modelling of the following experimental semivariogram for each threshold z_k:

$${\widehat{\gamma }}_I(\mathbf{h};z_k)=\frac{1}{2N(h)}\sum _{\alpha =1}^{N(h)}{[i({\mathbf{u}}_{\alpha };z_k)-i({\mathbf{u}}_{\alpha }+\mathbf{h};z_k)]}^2$$ (2)

where N(h) is the number of pairs of observations separated by a vector h. The indicator variogram 2γ̂_I (h; z_k) measures how often two z-values a vector h apart are on the opposite side of the threshold value z_k. Therefore, it quantifies the lack of spatial connectivity of the values exceeding z_k. The probability Prob{Z(u) ≤ z|(n)} is then estimated as a linear combination of n(u) neighbouring indicators (Equation (1)) as follows:

$$\text{Prob}(\mathbf{u};z_k\mid (n))=\sum _{\alpha =1}^{n(u)}{\lambda }_{ak}i({\mathbf{u}}_{\alpha };z_k),k=1,\dots ,K$$ (3)

The weights λ_ak are the solution of the following system of (n(u)+1) linear equations:

$$\begin{array}{c}\sum _{\beta =1}^{n(\mathbf{u})}{\lambda }_{\beta k}{\gamma }_I({\mathbf{u}}_{\alpha }-{\mathbf{u}}_{\beta };z_k)-{\mu }_k={\gamma }_I({\mathbf{u}}_{\alpha }-\mathbf{u};z_k),\alpha =1,\dots ,n(\mathbf{u})\\ \sum _{\beta =1}^{n(\mathbf{u})}{\lambda }_{\beta k}=1\end{array}$$ (4)

where μ_k is a Lagrange multiplier accounting for the constraint on the weights.

The application of multiple indicator kriging in this study was greatly facilitated by the use of the public-domain Auto-IK program (Goovaerts 2009), which provides fully integrated indicator kriging with automatic computation and modelling of indicator semivariograms for many thresholds that are either automatically calculated or manually specified by the user. In addition, the program computes the mean and the variance of each probability distribution after increasing its resolution by performing a linear interpolation between tabulated bounds provided by the sample histogram (Deutsch and Journel, 1998). The optimal number of thresholds was determined by comparison of the leave-one-out (LOO) cross-validation statistics (mean absolute error and mean squared deviation ratio; MAE and MSDR) and the variogram structure from multiple runs with different numbers of thresholds and threshold values. The runs with the lowest MAEs, MSDR values closest to 1 and indicator variograms that showed most structure were selected.

2.4.2. Poisson kriging

The Poisson approach is parametric and models the noise attached to each observation using a Poisson distribution. Here the observations are ratios, r(v_α) = z(v_α)/d(v_α), that take the form of spatial density (d(v_α) = size of observational area v_α) or proportion of animals (d(v_α) = total number of animals in a given area v_α); see previous section on data processing. The animal density/proportion for a location u is estimated as the following linear combination of n(u) neighbouring ratios:

$$\widehat{r}(\mathbf{u})=\sum _{\alpha =1}^{n(\mathbf{u})}{\lambda }_{\alpha }r(v_{\alpha })$$ (5)

For Poisson approach (1) where the denominator is the size of observational areas, count estimates are computed by multiplying the ratio estimate r̂(u) by the area d(u).

The kriging weights λ_a are computed by solving the ‘Poisson kriging’ system:

$$\begin{array}{c}\sum _{\beta =1}^{n(\mathbf{u})}{\lambda }_{\beta }\left[{\overline{C}}_R(v_{\alpha },v_{\beta })+{\delta }_{\alpha \beta }\frac{m\ast }{d(v_{\alpha })}\right]+\mu (\mathbf{u})={\overline{C}}_R(v_{\alpha },\mathbf{u}),\alpha =1,\dots ,n(\mathbf{u})\\ \sum _{\beta =1}^{n(\mathbf{u})}{\lambda }_{\beta }=1\end{array}$$ (6)

where δ_αβ = 1 if α = β and 0 otherwise. Interpolator (5) can be interpreted as a form of kriging with non-systematic errors where observations with low denominators d(v_α) receive less weight in the estimation. This is accomplished by adding the ‘error variance’ term, m^*/d(v_α), to the diagonal of the kriging system (6), leading to smaller weights for ratios measured over smaller areas/populations. The influence of these ratios on semivariogram computation is also reduced by using the following weighted estimator:

$${\widehat{\gamma }}_{Rv}(\mathbf{h})=\frac{1}{2{\sum }_{\alpha ,\beta }^{N(\mathbf{h})}\frac{d(v_{\alpha })d(v_{\beta })}{d(v_{\alpha })+d(v_{\beta })}}\sum _{\alpha ,\beta }^{N(\mathbf{h})}\left\{\frac{d(v_{\alpha })d(v_{\beta })}{d(v_{\alpha })+d(v_{\beta })}{[r(v_{\alpha })-r(v_{\beta })]}^2-m^{\ast }\right\}$$ (7)

where N(h) is the number of pairs of areas (v_α, v_β) whose observational area/population-weighted centroids are separated by the vector h and m^* is the observational area/population-weighted mean of the N area ratios. The usual squared differences, [r(v_α) – r(v_β)]², are weighted by a function of their respective observational area/population sizes, d(v_α)d(v_β)/[d(v_α) + d(v_β)], which gives more importance to more reliable data pairs based on large observational areas/large total counts of animals (Monestiez et al. 2006, see also Kerry et al. 2010).

An additional difficulty is the fact that the measurement supports (areas v_α) and prediction supports (point location u) have different spatial extents. Accounting for these different supports in the kriging system requires the use of area-to-area C̄_R(v_i, v_j) and area-to-point C̄_R(v_i, u) covariances and knowledge of the point-support covariance C(h). Inference of the point-support covariance from the areal covariance (Equation (7)) was conducted using the deconvolution procedure developed by Goovaerts (2008) and implemented in BioMedware SpaceStat software (BioMedware 2011). The approach is illustrated for impala in Figure 4. This procedure seeks the point-support variogram (deconvoluted, solid grey line, Figure 4) that once regularized (grey dashed line, Figure 4) is closest to the areal-support variogram (black dashed and solid lines in Figure 4). The point-support variogram (area-to-point kriging) was used for producing maps and total population numbers for the park, but the areal-support variogram was used for LOO cross-validation using the various pre-processed data.

Figure 4.

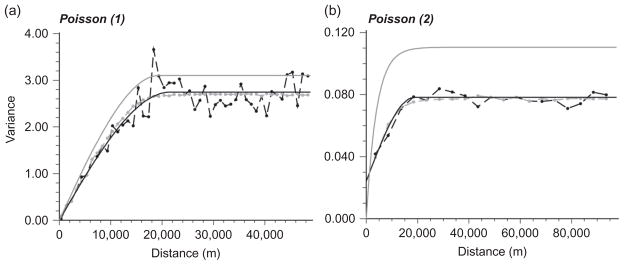
Experimental variogram for areal data (black dashed line), model for areal data (black solid line), deconvoluted variogram (solid grey line) and theoretically regularized variogram (grey dashed line) for 2001 counts of impala using (a) Poisson approach (1) and (b) Poisson approach (2).

2.4.3. Incorporation of environmental data into Poisson kriging

Simple kriging with local means (SKlm) was used to incorporate environmental data into the mapping of animal abundance. The Poisson kriging estimator (Equation (5)) thus became

$$\widehat{r}(\mathbf{u})=\sum _{\alpha =1}^{n(\mathbf{u})}{\lambda }_{\alpha }[r(v_{\alpha })-m(v_{\alpha })]+m(\mathbf{u})$$ (8)

where the local means m(v_α) and m(u) were derived using the arithmetical average of the species count in a given environmental category/class, that is, the local mean is assumed constant and only one categorical variable is used. The kriging weights are estimated using Poisson kriging and the variogram of residuals.

2.4.4. Cross-validation

LOO cross-validation was used to assess the relative performance of Auto-IK and both Poisson methods for estimating counts of animals along transects. Poisson kriged estimates of spatial densities or proportions were converted back to counts to allow direct comparison with the estimated counts produced by indicator kriging. In the LOO cross-validation approach, each observation is deleted one at a time and estimated using the remaining observations within a search radius that was set to slightly larger than the variogram range. The set of observations and their estimates are then usually compared using the following three statistics: mean error (ME), MAE and MSDR. Since the MEs were close to 0 (i.e. no marked bias) and most of the MSDR values were close to 1 (i.e. magnitude of kriging variance reflects the variance of prediction errors), the interpretations here will be based on MAE. The number of observations used for each method, year and species varies since data were preprocessed in various ways to implement the different kriging methods and account for differences in transect spacing and the number of observations of given species between years. To account for these effects, MAEs were divided by the standard deviation of the data to give standardized MAEs (St. MAE) and allow proper comparison between the methods and years.

3. Results and discussion

3.1. Multiple indicator kriging using Auto-IK

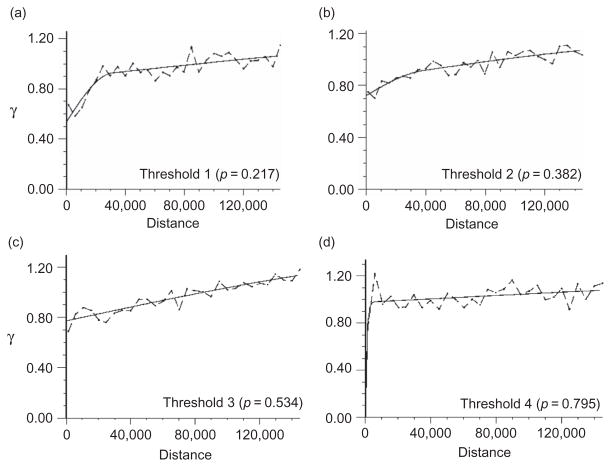
Table 2 shows the St. MAEs of prediction obtained by LOO cross-validation for the Auto-IK approach. Using the raw count data instead of the migrated grid data leads to slightly lower St. MAEs because the lack of zero values in raw counts artificially reduces prediction errors in overestimation situations. The optimal number of thresholds for Auto-IK was determined by multiple runs in which the cross-validation statistics and the form of the variograms were compared. According to Goovaerts (2009), the accuracy of indicator kriging predictions is expected to increase with the number of thresholds. However, in this case, we found the reverse to be true as the variograms for the rare large counts were pure nugget. Consequently, the optimal number of thresholds in each case was between 3 and 10, and this led to a poor prediction at the locations with large counts. Comparison of the raw counts (Figure 5a) and the Auto-IK estimates based on raw counts (Figure 5b) illustrates the overestimation of the low counts and the underestimation of the large counts for zebra in 2000. Indicator variograms for zebra in 2000 (Figure 6) indicate the lack of spatial connectivity of large counts (threshold 4), which explains the poor estimation of these counts in Figure 5b.

Table 2.

Standardized mean absolute errors (St. MAEs) of prediction computed using leave-one-out (LOO) cross-validation for several methods.

St. MAEs
Species	Year	Auto-IK		Poisson kriging		Poisson SKlm
		Raw count data	Migrated data	Poisson (1)	Poisson (2)	SKlm-WC
All	1998	0.4776	0.6669	0.0031	b	b
All	2000	c	c	0.0040	b	b
All	2001	0.5360	0.5590	0.0039	b	b
All	2005	0.4579	0.4248	0.0037	b	b
Eb	2000	a	a	0.3935	0.1071	c
Eb	2001	a	a	0.3657	0.1430	d
Gi	2000	0.5463	0.7347	0.0446	0.0686	c
Gi	2001	0.6300	c	0.0371	0.0814	0.0510
Im	2000	0.6716	0.9253	0.0152	0.0674	c
Im	2001	0.6469	c	0.0204	0.0591	0.0199
Ku	2000	a	a	0.2997	0.0804	c
Ku	2001	a	a	0.1651	0.0659	0.3947
WH	1998	a	a	0.4718	0.0520	c
WH	2000	a	a	0.3944	0.0430	c
WH	2001	a	a	0.1690	0.8767	0.0944
WH	2005	a	a	0.3630	0.0700	c
WBk	1998	a	a	0.0415	0.0305	c
WBk	2000	a	a	0.3050	0.0496	c
WBk	2001	a	a	0.1019	0.0200	0.0019
WBk	2005	a	a	0.0187	0.0317	c
WR	2000	a	a	0.3518	0.0599	c
WR	2001	a	a	0.6237	0.0621	0.1711
WiB	2000	a	a	0.0333	0.0276	c
WiB	2001	a	a	0.0359	0.0159	0.0072
Ze	2000	0.4759	0.6387	0.0219	0.0421	c
Ze	2001	0.4675	c	0.0198	0.0340	0.0113

Notes: (1) Auto-indicator kriging (Auto-IK) with raw count data and data migrated to a grid; (2) Poisson kriging approaches (1) and (2); and (3) simple kriging with local means (SKlm) estimated using a within-class (WC) approach.

^aSpecies counts not possible with this method due to pure nugget variograms.

^bPoisson approach (2) not possible for estimating all animals.

^cData not investigated with this method for this animal in this year.

^dVariogram of regression residuals showed no structure.

Figure 6.

Indicator variograms computed and modelled by the Auto-IK program for 2000 zebra count data and four thresholds: (a) 2, (b) 3, (c) 6 and (d) 10 animals.

Comparison of the observed counts (Figure 2b) with migrated data (Figure 2d) and estimates obtained using migrated data (Figure 2e) shows that for all animals in 2001, the Auto-IK approach based on migrated data reasonably identifies the locations of low counts. However, the indicator variograms for the larger thresholds (i.e. larger counts) were still pure nugget and the number of thresholds had to be restricted, thus areas with large counts were poorly estimated. Note that Table 2 does not report any prediction errors for the lower density species because indicator variograms for all thresholds were pure nugget. This shows that the Auto-IK approach is definitely not suitable for mapping these species.

The total number of impala in KNP estimated by Auto-IK for 2000 was just 2394 which is more than an order of magnitude too low when compared with Figure 1b. This clearly demonstrates the inability of this method to produce sensible total population estimates of a species in the whole park as well as local estimates of species distribution. This result probably stems from the fact that the indicator approach does not take into account the change of support when kriging from blocks to points and most indicator variograms have a large nugget effect (Figure 6).

3.2. Poisson kriging

3.2.1. Poisson kriging approach (1)

Table 2 shows the St. MAEs for Poisson kriging using approach (1). The St. MAEs for all animals in 1998, 2000, 2001 and 2005 are all two orders of magnitude lower than those for the Auto-IK approach. The greater accuracy of these Poisson kriged estimates (Figure 2g and h) is illustrated by comparison with the maps of raw count data (Figure 2a and b) and estimates obtained by multiple indicator kriging (Figure 2e). Figure 2g and h shows that both areas with high and low counts are well estimated in comparison to Figure 2a and b. The greater ability of Poisson approach (1) to distinguish between areas of high and low counts compared with Auto-IK probably relates to the shape of variograms. For Auto-IK (Figure 6) even the most structured indicator variograms include more than 50% nugget variance. In contrast, the areal-support variograms for Poisson approach (1) all have a nugget:sill ratio of 0 (Table 3 and Figure 4a).

Table 3.

Variogram parameters of areal-support variograms for Poisson approaches (1) and (2) for all animals and most abundant examples of key feeding groups in different years.

Species	Year	Poisson approach (1)		Poisson approach (2)
		Nugget:sill ratio	Range (km)	Nugget:sill ratio	Range (km)
All	1998	0	7.6	a	a
All	2000	0	10.4	a	a
All	2001	0	3.2, 22.2	a	a
All	2005	0	3.6, 21.9	a	a
Gi	2000	0	55.2	0.11	12.4, 139.4
Gi	2001	0	12.6	0.67	10.8
Im	1998	0	6.1	0	34.3
Im	1999	0	14.2	b	b
Im	2000	0	15.3	0.15	35.7
Im	2001	0	21.6	0.27	17.5
Im	2002	0	10.9	b	b
Im	2003	0	52.3	b	b
Im	2004	0	11.4	b	b
Im	2005	0	41.2	0.10	21.9
Ze	2000	0	23.6	0.59	73.1
Ze	2001	0	13.2	0.51	25.8

^aPoisson approach (2) not possible for all animals.

^bPoisson approach (2) not investigated for this year.

Table 2 indicates that for the most abundant species (impala, zebra and giraffe; see Table 1 for rank of abundance) Poisson approach (1) has markedly lower St. MAEs than Auto-IK, yet the improvement is not as large as for the ‘all animal cases’.

3.2.2. Poisson kriging approach (2)

Table 2 shows that St. MAEs for the most abundant species are larger for Poisson approach (2) than for Poisson approach (1), whereas the less abundant species (those with a rank of 5 in Table 1) often display the opposite trend. This suggests that Poisson approach (2) is most effective for estimating the less abundant species and Poisson approach (1) for the most abundant species.

For Poisson approach (2), the optimal block size for investigating the proportions of different species is an important parameter to determine. The St. MAEs (not shown) suggested that larger (5 km) blocks were more suitable for the most abundant species and smaller (1 km) blocks for the less abundant species. For example, for a less abundant species, three adjacent 1 km cells could contain some animals and be surrounded by cells with zero counts, leading to a short-range variogram. However, if a 5 km block size were used, there would be only one cell with a larger count surrounded by cells with zero counts and the variogram would appear as pure nugget. This typically does not happen for the more abundant species where specimens are found in many cells. The results also suggested that the optimal block size may be influenced by other factors such as average herd size and the preferred habitat of the species.

3.2.3. Variography

The lack of structure in the indicator variograms for all thresholds and particularly the thresholds for large counts are in part responsible for the poor prediction performance of the Auto-IK approach with the more abundant species. Complete lack of variogram structure was responsible for the failure of Auto-IK to predict the less abundant species. The nugget:sill ratio of the variograms for Poisson approach (2) (Table 3) tends to be smaller for the most abundant species, impala, and greater for the less abundant species.

This means that there is less of a random component when an impala or group of them is spotted compared with the less abundant species such as giraffe and zebra. For Poisson approach (1) all areal-support variograms in Table 3 had a nugget:sill ratio of 0. The difference in the sill values of areal and deconvoluted variograms is the largest for Poisson approach (2) where the variogram has a shorter range and larger nugget:sill ratio (Figure 4b). This is expected since the impact of aggregation (i.e. reduction in the sample variance and symmetrization of the histogram) decreases as the spatial pattern becomes more continuous (Goovaerts 2008).

The range of variograms (Table 3, see impala in particular) for a given species is sometimes consistent between years and sometimes not. We hypothesize that the variogram range for a given species may be similar in years with similar resource conditions; for example, ranges could be smaller for dry years because forage and water resources have a more restricted distribution in low rainfall years. This hypothesis needs to be further investigated.

3.2.4. Differences between years

The different kriging approaches were each implemented for more than 1 year. The St. MAEs in Table 2 give some indication of how the prediction performances vary between years when different sampling densities were used. The sampling density was lower in 1998–2000 than 2001–2006; however, there is no consistent pattern as to whether a greater density of observations lowers St. MAEs for a given kriging method. This suggests that for geostatistical approaches, in contrast with the distance method, spending extra time and money on collecting denser data may not be necessary. If there were an advantage to sampling more densely, one would expect the St. MAEs to be lowest for 2005 and highest for 1998 and 2000 consistently. This result is likely to relate to whether the scale of spatial variation in the data for a given year has been properly resolved by the variogram. Kerry and Oliver (2003) showed for soil properties that an accurate variogram for kriging can be obtained so long as samples are collected at an interval smaller than half the variogram range of appropriate ancillary data. Therefore should a geostatistical approach to populating data gaps be adopted in the park, it would be useful to compute the variogram for various animal food resources in distinct areas of the park to determine what the sampling density should be in a given year. We intend to conduct an in-depth study of these geostatistical sampling issues in the context of KNP by computing variograms for each species for the years when the whole park was surveyed.

Figure 2g–i shows that there are some consistencies in the patterns of abundance of all animals with the north of the park usually having fewer animals. This is likely due to the rainfall gradient, with average annual rainfall being generally higher in the south than in the north of the park. Furthermore, Figure 2 also shows that the spatial distribution of all animals in 2000 (Figure 2g) greatly differs from the other years in that animal distribution patches seem larger and more ‘smoothed out’ (Figure 2f, h and i). This difference is hard to distinguish from the raw count maps (Figure 2a and b), which stresses the need for interpolation between transects to make sensible management decisions as the year 2000 had very distinctive weather.

We hypothesize that the larger patches and smoother appearance of the distribution of all animals in 2000 (Figure 2g) reflect the unusual climatic conditions in this exceptionally wet year which resulted in widespread flooding. The annual recorded rainfall in KNP for 2000 was 1249 mm compared with the long-term average of 557 mm (based on records from nine rainfall stations in the park since 1941). We therefore propose that due to the high rainfall of 2000, forage and water resources were more widely and evenly distributed than in years with lower rainfall. Based on how the sizes of patches in the distribution of all animals vary between years with different climatic conditions, and the fact that we know that animal distributions are influenced by changes in their habitat, we investigated the incorporation of environmental variables into Poisson approach (2) to see if St. MAEs were further reduced.

3.3 Poisson kriging with secondary information

This preliminary analysis was conducted for the 2001 data to illustrate the benefit of incorporating environmental variables into estimation. The types of environmental data used are listed in Section 2.2 and two examples, one continuous, variable (herbaceous biomass (B) (Smit 2007), and one categorical variable (LS) (Venter 1990, a classification of the park into areas of broadly similar geomorphology and vegetation) are shown in Figure 7d and e, respectively. The biomass data could not be incorporated into the SKlm-within-class (WC) approach detailed in Section 2.4.3, but the value of these and other continuous environmental data was briefly investigated through Poisson regression. Table 1 shows for each species the environmental data with significant contributions and regression MAEs smaller than those of Poisson approach (2). Clearly, several of the environmental data sets could be useful in a Poisson kriging approach similar to that of Bellier et al. (2010) where environmental variables are used to determine the trend or local drift in the animal counts. However, for warthog and kudu, none of the available environmental data are useful. Given that herbaceous biomass is the continuous variable most frequently identified as significant in Poisson regression (Table 1) and that the LS classification of Venter (1990) includes consideration of broad vegetation type, we employed a simple WC approach to SKlm where only the categorical data (LS) are used. The approach proceeds in two steps: (1) the average proportion of a species (i.e. local mean) is derived from the secondary information (LS classification) and (2) residuals are interpolated using Poisson kriging and added to the local mean.

Figure 7.

(a) Observed counts of zebra in 2001, kriged maps of counts produced by (b) Poisson approach (2) and (c) Poisson SKlm-WC, (d) Smit (2007)’s herbaceous biomass and (e) Venter’s (1990) land systems.

Note: For (a) white areas show zero counts and dark blue is ≥ 1, for (b–c) dark blue is 0–1.

Table 2 lists the St. MAEs achieved for each species using the SKlm-WC approach. For elephant bulls, the variogram of the class residuals showed no structure and the St. MAEs for warthog and kudu for SKlm-WC exceed those for Poisson approach (2). This latter result is probably caused by the lack of significant contribution of these environmental data in Poisson regression (Table 1). Until appropriate environmental covariates are found for predicting these species, the univariate Poisson approach (2) appears to be one of the most accurate options for mapping species abundance.

The St. MAEs in Table 2 show that SKlm-WC using the LS classification outperforms Poisson approach (2) for giraffe, impala, waterbuck, wildebeest and zebra. For waterbuck and wildebeest, the order of magnitude drop in St. MAEs (Table 2) for SKlm-WC compared with Poisson approach (2) clearly shows the benefit of the simple LS classification for predicting the location of these species. For some species (giraffe, impala and zebra), there is little difference in St. MAEs for Poisson approach (2) and SKlm-WC. In particular, the maps for zebra display only minor differences which occur mainly in some isolated areas of the Letaba landsystem (Figure 7e), where medium counts of zebra are predicted despite predominantly low counts of zebra being observed (Figure 7c). The analysis here suggests that the straightforward SKlm-WC approach to incorporating environmental data into Poisson kriging is useful and, as it only uses one categorical data set, it avoids potential multi-colinearity problems.

4. Conclusions

This study indicated that multiple indicator kriging is less accurate than Poisson kriging for mapping animal abundance. Regardless of whether raw count or migrated data are used, the rare occurrences of large counts cause only a few indicator variograms to show any structure and the number of thresholds had to be reduced. The total population estimates derived from this method were more than an order of magnitude too low, and the pure nugget indicator variograms for all thresholds make this method of no use at all for mapping the lower density species.

Based on St. MAEs, Poisson approach (1) is more suitable for mapping the more abundant species and Poisson approach (2) for less abundant species. Total population estimates for all species derived from area-to-point Poisson kriging approach (2) are similar to those produced by the distance method (results for impala only are shown in Figure 1b), the current method used by KNP to estimate total species populations in the park. The benefit of area-to-point Poisson kriging is its ability to produce accurate maps of species distributions in addition to sensible total population totals. The uncertainty attached to the total population estimates produced by area-to-point Poisson kriging methods needs to be modelled using stochastic simulation for a proper comparison with the distance method in this aspect.

Incorporating environmental data in Poisson approach (2) reduced St. MAEs for most species, particularly for waterbuck and wildebeest. As warthog and kudu abundance was not significantly related to any of the available environmental data, suitable environmental covariates need to be found for these species. Potential covariates are abundance patterns of these species from previous years when the whole park was surveyed. This preliminary study illustrated the utility of a straightforward SKlm-WC approach, however, given the range of variables identified as significant in Poisson regression; more complex methods that incorporate various continuous and categorical environmental data into Poisson kriging are worth investigating.

Poisson approaches that incorporate secondary information are recommended for mapping species abundance wherever suitable environmental data and sufficient knowledge of the environmental factors that are linked to the distribution of a particular species are available. In particular, Bellier et al. (2010) showed that taking account of the heterogeneity of wildlife population habitats (i.e. non-stationarity in spatial trends) in Poisson kriging leads to different estimates in sparsely sampled areas (extrapolation situation). If such information is not available or until more exhaustive research of the best environmental covariates is done, Poisson approach (1) is recommended for mapping relatively abundant species and Poisson approach (2) for less abundant species. Using such approaches that consider only spatial autocorrelation is sensible in such instances because the spatial autocorrelation in animal counts is likely to reflect indirectly the social behaviour of the species or spatial autocorrelation in the environmental characteristics that influence its distribution.