Disaggregation of legacy soil data using area to point kriging for mapping soil organic carbon at the regional scale

Abstract

Legacy data in the form of soil maps, which often have typical property measurements associated with each polygon, can be an important source of information for digital soil mapping (DSM). Methods of disaggregating such information and using it for quantitative estimation of soil properties by methods such as regression kriging (RK) are needed. Several disaggregation processes have been investigated; preferred methods include those which include consideration of scorpan factors and those which are mass preserving (pycnophylactic) making transitions between different scales of investigation more theoretically sound. Area to point kriging (AtoP kriging) is pycnophylactic and here we investigate its merits for disaggregating legacy data from soil polygon maps. Area to point regression kriging (AtoP RK) which incorporates ancillary data into the disaggre-gation process was also applied. The AtoP kriging and AtoP RK approaches do not involve collection of new soil measurements and are compared with disaggregation by simple rasterization. Of the disaggregation methods investigated, AtoP RK gave the most accurate predictions of soil organic carbon (SOC) concentrations (smaller mean absolute errors (MAEs) of cross-validation) for disaggregation of soil polygon data across the whole of Northern Ireland.

Legacy soil polygon data disaggregated by AtoP kriging and simple rasterization were used in a RK framework for estimating soil organic carbon (SOC) concentrations across the whole of Northern Ireland, using soil sample data from the Tellus survey of Northern Ireland and with other covariates (altitude and airborne radiometric potassium). This allowed direct comparison with previous analysis of the Tellus survey data. Incorporating the legacy data, whether from simple rasterization of the polygons or AtoP kriging, substantially reduced the MAEs of RK compared with previous analyses of the Tellus data. However, using legacy data disaggregated by AtoP kriging in RK resulted in a greater reduction in MAEs. A jack-knife procedure was also performed to determine a suitable number of additional soil samples that would need to be collected for RK of SOC for the whole of Northern Ireland depending on the availability of ancillary data. We recommend i) if only legacy soil polygon map data are available, they should be disaggregated using AtoP kriging, ii) if ancillary data are also available legacy data should be disaggregated using AtoP RK and iii) if new soil measurements are available in addition to ancillary and legacy soil map data, the legacy soil map data should be first disaggregated using AtoP kriging and these data used along with ancillary data as the fixed effects for RK of the new soil measurements.

1. Introduction

In traditional soil survey, surveyors use their knowledge of soil forming factors combined with aerial photographs and field-based soil observations to delineate soil classes as polygons on a map. Typical soil profiles of these classes are often described and published as a memoir which may include values of key soil properties at various depths. This traditional approach gives no indication of variability in these soil properties within or between classes and it has no statistical basis which can lead to bias (Carré et al., 2007a). In the last 10–15 years the need for raster based digital soil maps has been emphasized and a digital soil mapping (DSM) approach has been developed (McBratney et al., 2003). Such maps have pixels of different sizes depending on the scale of interest and have values of key soil properties, such as soil organic carbon (SOC) concentration, available at several depths (McBratney et al., 2003). More specifically, DSM has been defined as the creation and population of spatial soil information by the use of field and laboratory observational methods coupled with spatial and non-spatial soil inference systems (Carré et al., 2007b; Lagacherie and McBratney, 2007).

Polygon maps representing soil classes at various levels of national or international classification systems exist in many locations. Effective methods are required for the disaggregation and incorporation of such a wealth of ‘legacy soil data’ into DSM at national and regional scales. Appropriate use of this historical data could ensure that additional sampling effort associated with modern digital soil mapping is minimized. De Bruin et al. (1999) and Eagleson et al. (1999) proposed approaches that use hierarchical spatial reasoning for disaggregation of soil polygons. Bui and Moran (2001) investigated some such methods empirically along with other methods for spatial disaggregation of soil polygon maps in the Murray–Darling basin, Australia.

The theoretical merits of several forms of spatial disaggregation were investigated by McBratney (1998); the author suggested transfer functions and pycnophylactic interpolation should be applied. Mass preservation in pycnophylactic methods (Tobler, 1979) means that the mass or values over all the finer pixels contained within a polygon is preserved; in other words the average of the values in the finer pixels gives the polygon value. McBratney (1998) noted that the mass preservation property of pycnophylactic splines is a useful feature for disaggregating soil data as it could make transitions between scales in DSM more sensible. This could mean that intense sampling at each scale is not essential. Mass preservation is also a feature of the recently developed geostatistical approach of area to point kriging (Kyriakidis, 2004). The typical centroid-based approach to kriging from areas to points assumes that the spatial support of units is constant (Goovaerts, 2006). Hence it is not appropriate for use with polygon data of varying shape and size (Gotway and Young, 2002). The advantage of AtoP kriging is that it incorporates the variable size and shape of polygons in variogram deconvolution and kriging. Recently, Goovaerts (2010, 2011) used AtoP and regression kriging (RK) to incorporate both point field measurements and areal data (calibration of geological map) in the spatial interpolation of heavy metals in the Swiss Jura. Sensitivity analysis indicated that these new kriging procedures improve prediction over ordinary kriging and traditional RK based on the assumption that the local mean is constant within each mapping unit. To our knowledge, the advantages associated with AtoP kriging have not been used for disaggregating legacy soil maps and for optimizing DSM or compared to current state-of-the-art methods in DSM.

Current DSM methods in more data-rich settings include RK (McBratney et al., 2003) to map variation in important soil properties such as organic carbon based on ancillary data. Soil organic carbon is arguably one of the most important soil properties due to the benefits it confers such as enhancing soil structure through aggregation, improved water holding and cation-exchange capacities and also acting as a store of terrestrial carbon. In a recent study, two types of ancillary data (altitude and airborne radiometric measurements of potassium) were shown to be effective for improved mapping of soil organic carbon across all of Northern Ireland within a RK framework (Rawlins et al., 2009). However, the authors did not incorporate disaggregated legacy data into their procedure.

In this study we use area to point (AtoP) kriging to disaggregate soil organic carbon (SOC) data from a polygon map and compare it with disaggregation by simple rasterization of the same data. We also compare these methods with AtoP regression kriging (AtoP RK) which includes some hierarchical spatial reasoning in the disaggregation process (Liu et al., 2008; Yoo and Kyriakidis, 2009). In this approach, ancillary data are used to inform on within-class variation in key scorpan factors (McBratney et al., 2003) such as relief and parent material, i.e. they provide a local mean and the residuals are AtoP kriged. The errors involved with each disaggregation approach are investigated. We then use the same regression models and data as Rawlins et al. (2009), but we add legacy map SOC data disaggregated by simple rasterization (polygon SOC) and AtoP kriging (AtoP SOC) as extra fixed effects in RK. This two-step approach (Liu et al., 2008) to incorporating legacy data into RK was used to allow direct comparison with the results of Rawlins et al. (2009), however, there is no guarantee that the pycnophylactic or mass preserving property of AtoP kriging is preserved with a two-step AtoP RK procedure. Goovaerts (2010, 2011) introduced an approach where point and areal data are incorporated in one-step (i.e. one kriging system solved) instead of the two-step approaches (AtoP kriging followed by RK kriging) used here. Although this methodology, coined area-and-point (AAP) kriging, is theoretically more efficient than a two-step approach, and is pycnophylactic, it is not currently available in commercial software.

The errors associated with incorporating polygon SOC and AtoP SOC into RK using the six models of Rawlins et al. (2009) are investigated and a suitable number of samples for mapping SOC across Northern Ireland based on the available covariates is suggested. We comment on the benefits for DSM of disaggregating data from legacy soil polygon maps using simple rasterization, AtoP kriging and AtoP RK and incorporating the former two types of disaggregated legacy data into RK.

2. Geostatistical theory

2.1. Area to point kriging

Consider the problem of estimating the value of a soil property z at any location u_s within a study area A from a set of B areal data {z(vβ); β=1,…,B}. These areal or legacy soil polygon map data are typically measured on spatial supports (mapping units) v_β of various sizes and shapes. Area to point (AtoP) kriging can be viewed as the counterpart of block kriging in that point estimates $z_{\text{AtoP}}^{*}({\mathbf{u}}_{\mathrm{s}})$ are obtained as the following linear combination of areal (block) measurements:

$$z_{\text{AtoP}}^{*}({\mathbf{u}}_s)=\sum _{k=1}^K{\lambda }_k({\mathbf{u}}_s)z(v_k),$$ (1)

where K is typically smaller than the total number of areal data B; for example (K— 1) is the number of blocks adjacent to the block v_β where the point estimation is conducted. The kriging weights are the solution of the following ordinary kriging system:

$$\begin{array}{cc}\sum _{k\prime =1}^K{\lambda }_{k\prime }({\mathbf{u}}_s)\overline{C}(v_k,v_{k\prime })+\mu ({\mathbf{u}}_s)=\overline{C}(v_k,{\mathbf{u}}_s)\hfill & k=1,\dots ,K\hfill \\ \sum _{k\prime =1}^K{\lambda }_{k\prime }({\mathbf{u}}_s)=1,\hfill \end{array}$$ (2)

where µ(u_s) is the Lagrange multiplier. Like in traditional block kriging, the block-to-point covariances C̅(v_k,u_s) are approximated by the average of the point support covariance C(h) computed between the location u_s and a set of P_k points discretizing the block v_k (Fig. 1a). A similar procedure is used for the block-to-block covariances C̅(v_k,v_k′) = Cov{Z(v_k),Z(v_k′)} and involves averaging C(h) computed between any two points discretizing the blocks v_k and v_k′ (Fig. 1b). A key property of the AtoP kriging estimator is its coherency or pycnophylactic property: the aggregation of the P_β point estimates within any given entity v_β returns the areal datum z(v_β):

$$z\left(v_{\beta }\right)=\frac{1}{P_{\beta }}\sum _{s=1}^{P_{\beta }}{z}_{\text{Atop}}^{*}({\mathbf{u}}_s)$$ (3)

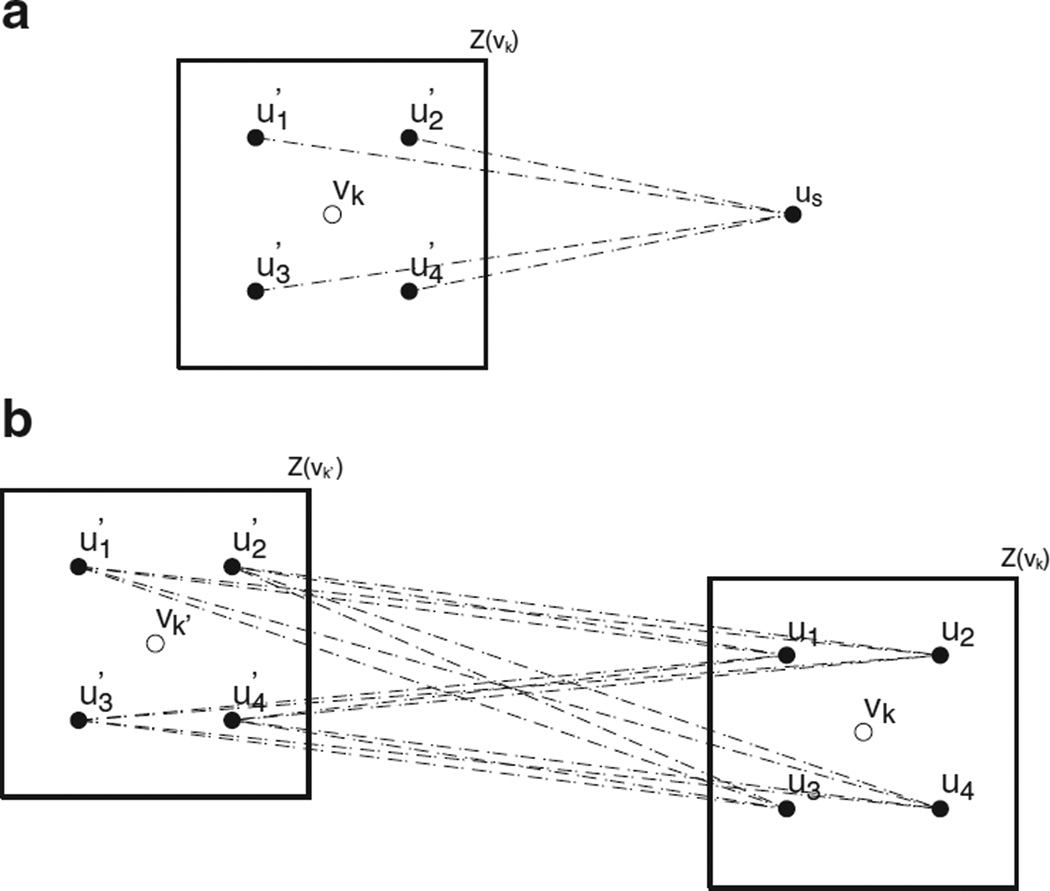
Fig. 1.

(a) Representation of the discretization procedure used to estimate: (a) block-to-point and (b) block-to-block covariances as the average of point-to-point covariances.

To satisfy this constraint, the same K areal data must be used for prediction at each of the P_β discretizing points u_s. Uncertainty about the areal data can be incorporated into the kriging system by adding a noise variance term to the diagonal elements of the kriging matrix (i.e. block-to-block covariances), leading to the filtering of that areal noise during the disaggregation procedure. This is similar to the Poisson or binomial AtoP kriging approaches introduced by Goovaerts (2010) where the areal data are mortality rates that might be unstable and for which the pycnophylactic property is not desirable.

By analogy with ordinary kriging, the AtoP kriging variance associated with estimate (1) is computed as:

$${\sigma }_{\text{AtoP}}^2({\mathbf{u}}_s)=C(0)-\sum _{k=1}^K{\lambda }_k({\mathbf{u}}_s)\overline{C}(v_k,{\mathbf{u}}_s)-\mu ({\mathbf{u}}_s).$$ (4)

where C(0) is the variance of the point process or sill of the point support variogram model (see Section 2.2).

2.2. Variogram deconvolution

The estimation of the block-to-block and block-to-point covari-ance terms in the kriging system (Eq. (2)) requires knowledge of the point support covariance C(h) or point support variogram model γ(h). Since only areal or polygon data are available, one must proceed in two steps: 1) compute and model the variogram of the areal data, and 2) deconvolute the block-support model to derive the point support variogram. In this paper, the point support variogram model was inferred using the iterative deconvolution procedure of Goovaerts (2008) that seeks the point support model that, once regularized, is the closest to the model fitted to the areal data.

This procedure is illustrated graphically in Fig. 2a. The experimental variogram of the legacy soil polygon map (areal) data is computed (black dashed line) and then modeled by a weighted least squares fitting procedure (black solid line). A candidate point support or deconvoluted model is then chosen (solid gray line) and this is regularized using Eq. (21) in Goovaerts (2008). The regularized model (gray dashed line) is then compared to the model fitted to the experimental variogram of the areal or polygon data. Based on the differences between the regularized model and the areal model, the optimal point support model is rescaled and provides a new candidate model for the next iteration. The deconvoluted model which when regularized is closest to the model for the areal data is used for AtoP kriging. This deconvolution procedure is unlike conventional deconvolution methods – developed for regular mining blocks – because it takes into account the irregular shape and size of areal units (Kerry et al., 2010).

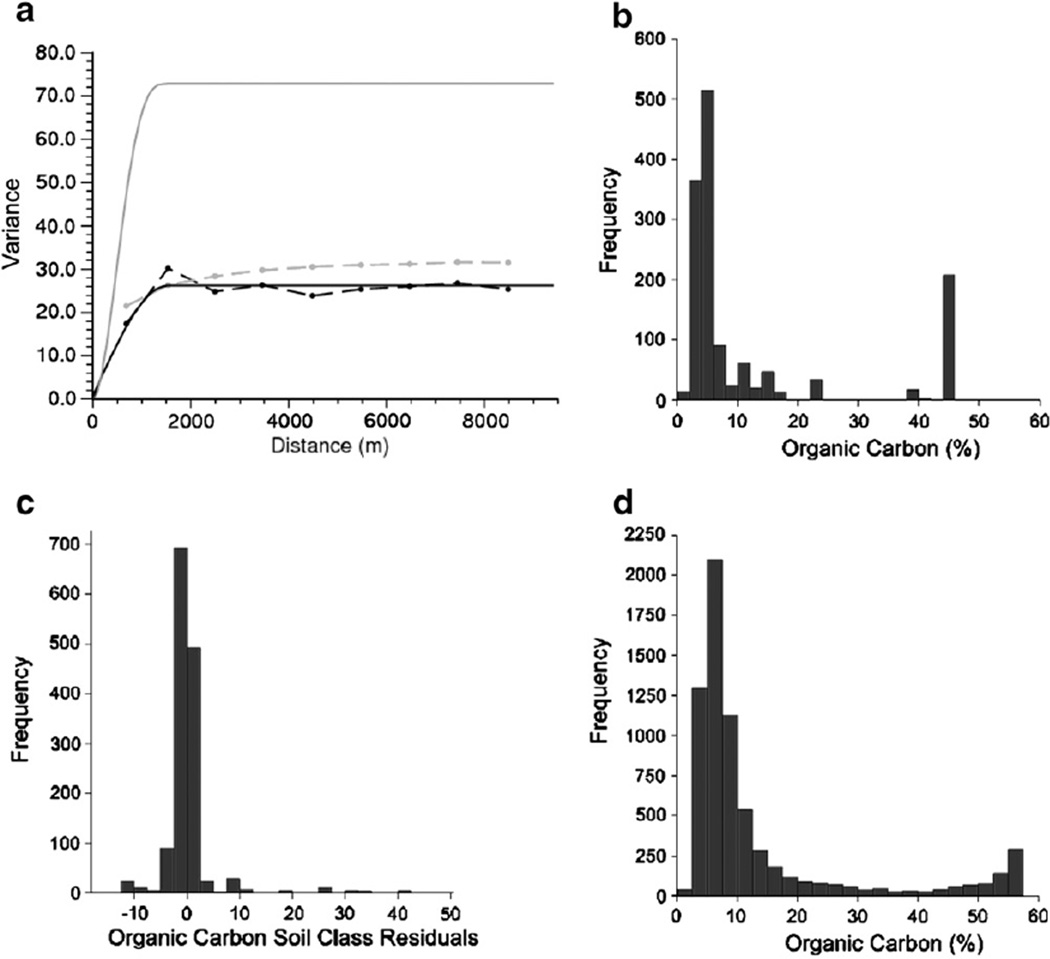
Fig. 2.

(a) Variogram deconvolution procedure shown with experimental variogram (dashed black line) and model for soil polygon map data (solid black line), deconvoluted variogram model (point support, solid gray line) and theoretically regularized variogram model (dashed gray line). Histograms of (b) organic carbon for legacy soil polygon map data, (c) organic carbon soil class residuals for legacy soil polygon map data and (d) organic carbon from samples (n=6862) in the Tellus survey.

2.3. Area to point regression kriging

The disaggregation of legacy data using the AtoP estimator (Eq. (1)) accounts only for the geometric properties of the different blocks v_β. Mapping the variability within each block v_β is likely to improve if ancillary data correlated with the soil property z (e.g. elevation or remotely sensed data) are available at a finer scale. We consider here the situation where these ancillary data are known at all N nodes of the interpolation grid and to simplify equations we present the case of a single secondary variable y. Let {y(u_s); s =1,…,N} denote the grid of ancillary data and {y(v_β); β=1,…,B} be their average value within the B blocks v_β. A straightforward way to incorporate these ancillary data is to use them to derive the local mean m of the soil property z using a regression model: m*(v_β)=f[y(v_β)], then conduct AtoP kriging on the residuals. The RK estimate is written as follows:

$$z_{\mathrm{RK}}^{*}({\mathbf{u}}_s)=m*({\mathbf{u}}_s)+\sum _{k=1}^K{\lambda }_k({\mathbf{u}}_s)+[z(v_k)-m*(v_k)],$$ (5)

where the local mean m*(u_s) is computed as a function of the ancillary data at that location: m*(u_s)= f[y(u_s)]. In this paper we used the same regression model f(.) for both areal and point data, under the implicit assumption that the model is linear. The weights λ_k assigned to the K neighboring areal data are the solution of the following simple kriging system:

$$\sum _{K\prime =1}^K{\lambda }_{k\prime }({\mathbf{u}}_s){\overline{C}}_R(v_k,v_{k\prime })={\overline{C}}_R(v_k,{\mathbf{u}}_s),\alpha =\dots n(\mathbf{u})$$ (6)

where the block-to-block covariances C̅_R(v_k ,v_k′) = Cov{R(v_k), R(v_k′)} are derived from the point support covariance of the residual random function R(u)=Z(u) – m*(u) using the discretization procedure described in Fig. 2a.

2.4. Incorporation of soil map polygon data into regression kriging

Consider the situation where legacy data {z(v_β); β=1,…,B} are supplemented by a set of field measurements of the soil property z of interest {z(u_α); α=1,…,n}. In this paper, the two sets of data were combined using the following regression kriging estimate:

$$z_{\mathit{\text{RK}}}^{*}(\mathbf{u})=m*(\mathbf{u})+\sum _{\alpha =1}^{n(\mathbf{u})}{\lambda }_{\alpha }[z({\mathbf{u}}_{\alpha })-m*({\mathbf{u}}_{\alpha })]=m*(\mathbf{u})+\sum _{\alpha =1}^{n(\mathbf{u})}{\lambda }_{\alpha }r({\mathbf{u}}_{\alpha }).$$ (7)

The local means m*(u) and m*(u_α) are identified either with the AtoP kriging estimates (AtoP SOC), legacy data disaggregated by AtoP kriging, (Eq. (1)) at these locations or with the value of the legacy data at these locations disaggregated by simple rasterization (polygon SOC, i.e. assuming that the local mean is constant within the mapping units). In other words, soil map legacy data (either AtoP SOC or polygon SOC) are used to derive the spatial distribution of the local means of field data, and the variation in field data that is not explained by soil map legacy data (i.e. residuals) is then interpolated using kriging. The weights λ_α assigned to the n(u) neighboring residuals are the solution of the following simple kriging system:

$$\sum _{\beta =1}^{n(\mathbf{u})}{\lambda }_{\beta }{C}_R({\mathbf{u}}_{\alpha }-{\mathbf{u}}_{\beta })=C_R({\mathbf{u}}_{\alpha }-\mathbf{u})\alpha =1,\dots n(\mathbf{u}),$$ (8)

where C_R(h) is the covariance of the residual random function R(u)= Z(u) – m*(u). Assuming the independence between the local mean and the residual random function, the prediction variance for estimate (7) can be computed as the sum of the estimation variance for the local mean and the residual kriging variance:

$${\sigma }_{\mathit{\text{RK}}}^2(\mathbf{u})={\sigma }_m^2(\mathbf{u})+C_R(0)-\sum _{\alpha =1}^{n(\mathbf{u})}{\lambda }_{\alpha }{C}_R({\mathbf{u}}_{\alpha }-\mathbf{u}).$$ (9)

The variance ${\sigma }_m^2(\mathbf{u})$ is the AtoP kriging variance (Eq. (4)) or the prediction variance for that unit’s local mean, depending on whether the local means are identified by disaggregation with AtoP kriging (AtoP SOC) (Eq. (1)) or simple rasterization of the areal legacy data (polygon SOC).

As mentioned in the Introduction, the regression kriging estimate is not optimal in that it is computed in two steps: 1) estimation of the local mean, and 2) kriging of residuals. This allowed direct comparison with the work of Rawlins et al. (2009), but unlike the one-step approach introduced in Goovaerts (2011), there is no guarantee that the regression kriging estimates still fulfill the coherency or pycnophylactic property of the original AtoP estimates. In addition, the regression kriging variance tends to exceed the kriging variance of Goovaerts (2011) AAP kriging estimator.

3. Materials and methods

3.1. Soil sampling

The soil sampling was undertaken between July 2004 and March 2006 comprising the collection of a sample of topsoil from a site in every other square kilometer of the Irish National Grid, by simple random selection within each square, subject to the avoidance of roads, tracks, railways, urban areas and other seriously disturbed ground. This was part of the Tellus survey of Northern Ireland http://www.bgs.ac.uk/gsni/tellus/. There were 6862 sample sites in total. At each site soil was taken with a hand auger from depths of between 5 and 20 cm from five holes at the corners and center of a square with a side of length 20 m and combined to form a bulked sample. All soil samples were air-dried in a dedicated temperature controlled oven at 30°C for between 2 and 3 days, disaggregated and sieved to less than 2 mm. From each a 50 g sub-sample was ground in an agate planetary ball mill. Loss on ignition (450°C) was determined for the air-dried disaggregated fraction. These values were multiplied by 0.58 to give percent SOC equivalents. Replicate analyses were done to ensure accuracy and repeatability of results. The differences between replicate analyses were small. The SOC values from these 6862 soil sample data from the Tellus survey had a positively skewed distribution (Fig. 2d) with a skew of 1.99 which was reduced to 0.94 upon log transformation. When these Tellus soil sample data were used in regression kriging log SOC was used. The SOC values from the Tellus survey points are shown in log form in Fig. 3a to enable visual distinction given the large range of SOC values in Northern Ireland. A prediction set of 3000 samples was selected randomly and the other samples (n=3862) were used for validation.

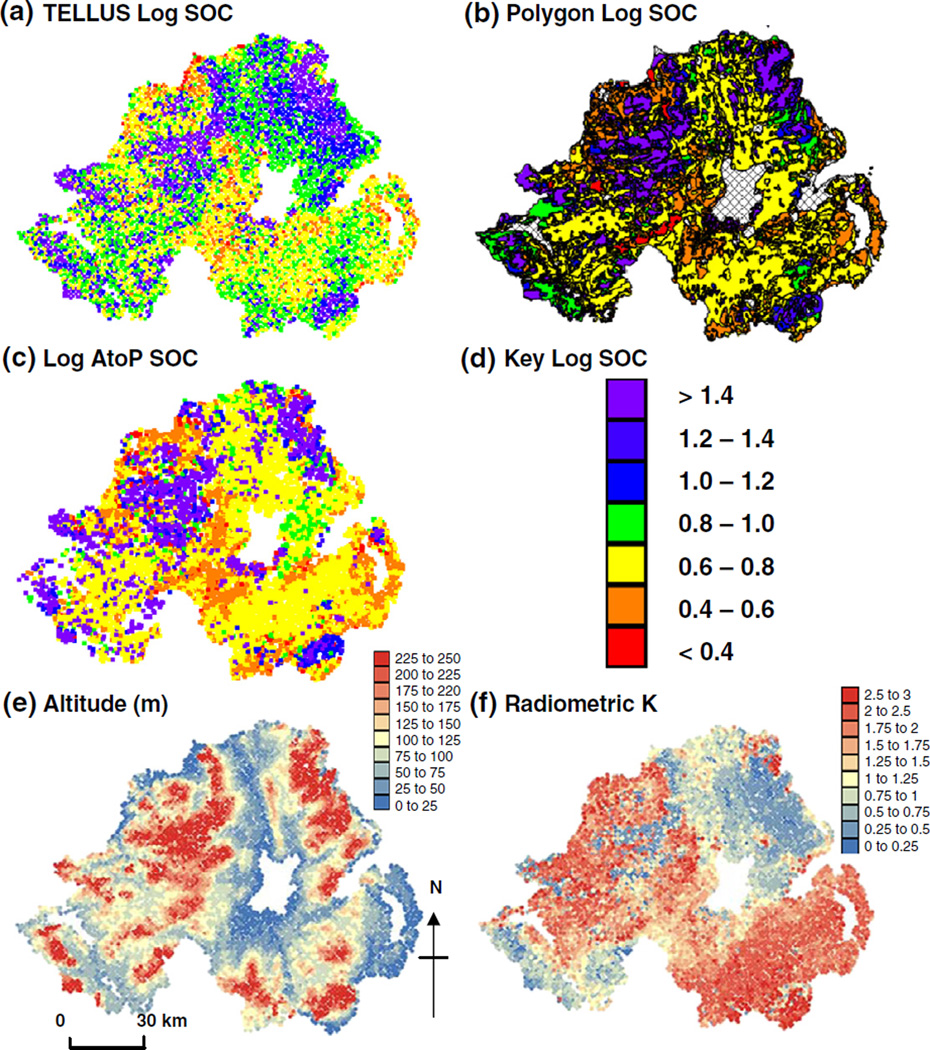
Fig. 3.

The distribution of measured and estimated SOC data and covariates across Northern Ireland: (a) Tellus survey measured log SOC (n=6862), (b) polygon map log SOC, (c) area to point (AtoP) kriged log SOC, (d) the key for Log SOC in a–c, (e) altitude (m) and (f) airborne radiometric K (%).

3.2. Legacy soil map

A 1:250,000 digital map (courtesy of the Agricultural, Food and Bio-sciences Institute of Northern Ireland; AFBINI) of soil associations (polygons) and associated typical percent SOC concentrations was used here as legacy soil data. This soil map and associated memoir (Cruickshank, 1997) resulted from the first full survey of the soils of Northern Ireland completed by the Department of Agriculture and Rural Development (DARD) between 1988 and 1997. In this survey, the soils of Northern Ireland were systematically sampled on a regular 5 km grid. The soils were described, analyzed and classified into soil series. Soil profiles were characterized from each major soil series in the agriculturally-important areas (areas below 200 m) and the physical and chemical properties of these profiles were determined. The survey identified 308 distinct soil series, the locations of which were published as a 1:50,000 scale soil series maps. The 1:250,000 polygon map is a generalization for the 1:50,000 maps. The soil carbon values provided for the soil associations in the 1:250,000 map are from 0 to 30 cm depth and are typical values for the soil association in that polygon rather than actual values recorded within that polygon. The log transformed % SOC concentrations associated with this map are shown in Fig. 3b. The 1:250,000 scale map was used in this analysis over the 1:50,000 scale maps as it was thought a more appropriate scale when considering the whole of northern Ireland, and SOC percentages for peat areas were not included for the 1:50,000 maps.

According to Cruickshank (1997) the proportions of the dominant soil types in Northern Ireland comprise 54% gleys, 24% rankers and peats and 16% freely drained soils, with minor soil types accounting for the other 6%. The dominance of gleyed soils and peats reflect the wet climate of Northern Ireland (mean annual precipitation of around 1 m) which in combination with a varied topography results in a wide range of SOC contents across the study area. The SOC concentrations associated with the 1:250,000 polygon map (Figs. 2b and 3b) were disaggregated first by simple rasterizing (500 m pixels) to give what we subsequently refer to as polygon SOC, where all pixels within a polygon received the same SOC concentration. They were also disaggregated using AtoP kriging and AtoP RK, the theory of which is described earlier and procedures for calculating which are described later. Although the log of polygon map SOC values was not used in analysis, the SOC values from the polygon map are shown in log form in Fig. 3b to allow comparison with the log SOC values from the Tellus survey points (Fig. 3a).

3.3. Ancillary data

Two ancillary datasets were available for use as covariates (Rawlins et al., 2009). The first was airborne radiometric K (%) for the whole of Northern Ireland collected as part of the Tellus airborne geophysical survey in 2005 and 2006 (Fig. 3f). The flight lines were spaced 200 m apart and the spacing between measurements along the flight line was between 60 and 70 m yielding around 1.2 million values; the detector was an Exploranium GR820 256 channel gamma spectrometer. Data were processed to correct for aircraft and cosmic background radiation, aircraft altitude and spectral interactions. The second covariate was altitude from a Digital Elevation Model (Fig. 3e) which was available at 50 m resolution based on airborne, photogrammetric acquisition (Ordnance Survey of Northern Ireland's ® data). We used a GIS spatial join procedure to associate each soil sampling observation with the values of its nearest airborne radiometric K (%) survey observation and its altitude in metres.

In data-rich scenarios such as Northern Ireland, ancillary data, recent soil measurements and disaggregated legacy soil data can be used together to predict soil organic carbon using RK. Only those ancillary data with a strong spatial correlation with SOC values, and for which there were sound theoretical reasons for this correlation, were considered as suitable covariates. Prior to RK, the correlations between SOC and the various ancillary data were calculated and the theoretical basis for them identified.

Gamma-ray attenuation and soil moisture typically show strong spatial correlation and this can be extended to SOC because it accumulates in wet or waterlogged soil. Fig. 3f shows the spatial variation in radiometric K whilst the distribution of log SOC from the Tellus survey is shown in Fig. 3a; their Pearson correlation coefficient (r) is −0.67. There is also typically a spatial correlation between SOC and altitude; precipitation tends to increase and temperature decrease with increasing altitude. Both of these factors aid the accumulation of SOC because mineralization decreases with temperature and soils which are waterlogged for more of the year have slower rates of soil carbon decomposition. Fig. 3e shows the variation in altitude compared to log SOC from the Tellus survey (Fig. 3a); the Pearson correlation coefficient (r) between altitude and log SOC is 0.60. The Pearson correlation (r) between the polygon SOC values (rasterized) and the Tellus SOC concentrations was 0.61. The polygon map SOC values were also disaggregated by AtoP kriging as described in Sections 2.1 and 3.4. Fig. 3c shows the log of the AtoP SOC values to allow comparison to log SOC from the Tellus survey (Fig. 3a) and the Pearson correlation (r) between these values was 0.68 showing that there is some correspondence between the legacy soil map SOC and recent soil survey data and that relationship is strengthened when legacy data are disaggregated using AtoP kriging (AtoP SOC) instead of being assumed constant within each mapping unit (polygon SOC).

3.4. Geostatistical analysis

3.4.1. Disaggregation of soil polygon data using AtoP kriging and AtoP regression kriging

Geostatistical disaggregation of the soil polygon SOC data was done using two methods available in the software SpaceStat (BioMedware Inc, 2011): AtoP Kriging (hereafter called AtoP) and AtoP RK. Both methods use only the soil polygon data and do not require any new soil sample data, however, the latter method uses appropriate ancillary data to inform on the within polygon variation in SOC.

The frequency distribution of untransformed SOC concentrations from the legacy soil polygon map (Fig. 2b) is somewhat different to that of the Tellus soil sample data (Fig. 2d). The legacy soil polygon map SOC values relate to soil types; mineral soils with low SOC (mean SOC, 4.8%), organo-mineral soils (mean SOC, 14.3%) and organic soils (mean SOC, 44.8%). Therefore, we computed the variogram for the legacy soil map areal or polygon data from class residuals of these three broad groups (Fig. 2c). The large outliers in the distribution of class residuals (Fig. 2c) suggest that some soils in the legacy map have been mis-classified. A model was fitted to this variogram of the class residuals and deconvoluted as described earlier. We then applied AtoP kriging to the polygon class residuals to estimate their values at the Tellus soil sample locations. The variogram decon-volution and AtoP kriging of the class residuals were undertaken using the SpaceStat ™ software (BioMedware, Michigan). We then added the class mean from the soil group to these residuals to give area to point kriged SOC which we subsequently refer to as AtoP SOC. The mean absolute errors (MAEs) between AtoP SOC and the measured SOC values at the Tellus soil sample locations were calculated as were the mean errors (MEs), mean squared deviation ratios (MSDRs) and median squared deviation ratios (MeSDRs). The main focus in each cross-validation study mentioned later is on the MAEs, but the latter cross-validation statistics were computed to check that the data were unbiased (ME) and that an appropriate model had been used (i.e. MSDR close to 1 or MeSDR close to 0.455).

A similar procedure was followed for AtoP RK. First, linear regression was performed in which the polygon SOC values were the dependent variable whilst the independent variables were altitude, radiometric K and squared radiometric K that were averaged within each polygon. This combination of independent variables was generally optimum from the analyses published by Rawlins et al. (2009) and these variables are related to the scorpan factors relief and parent material (see explanations of correlations earlier) making them particularly appropriate theoretically for disaggregating soil polygon information. The residuals from regression were then used to compute the areal support variogram which was deconvoluted as before. Area to Point kriging was then applied to the regression residuals to estimate their values at the Tellus soil sampling locations using the deconvoluted variogram. These residuals were then added to the SOC estimates obtained by applying the areal regression model to the same independent variables available at the Tellus soil sampling locations. The MAEs between the AtoP RK SOC estimates and those measured at the Tellus soil sample points were calculated.

3.4.2. Incorporating disaggregated soil polygon map data into regression kriging

Once soil polygon data were disaggregated using either simple rasterization (polygon SOC) or AtoP kriging (AtoP SOC), they could be used as a fixed effect in estimating SOC concentrations by RK of new soil sample data from the Tellus survey. Rawlins et al. (2009) used RK to incorporate altitude and radiometric K in various combinations into the estimation of SOC. The six models (referred to subsequently as models 1–6) used by Rawlins et al. (2009) are summarized in Table 1. Here we added the polygon SOC values and the AtoP SOC values as extra fixed effects in each of the six models used by Rawlins et al. (2009). In each case, the log SOC values for the prediction set of 3000 Tellus soil survey data were used as the dependent variable to compute the regression models. The residuals from these models were kriged to the 3862 validation sites and were added to regressed values at each location then back-transformed. The MAEs associated with each model based on these separate prediction and validation sets were then calculated.

Table 1.

Fixed effects for the six models applied by Rawlins et al. (2009).

Model	Fixed effects
1	Constant (i.e. the mean)
2	Constant plus altitude
3	Constant plus K
4	Constant plus K plus K2
5	Constant plus altitude plus K
6	Constant plus altitude plus K plus K2

3.4.3. Jack-knife procedure

A jack-knife procedure was undertaken to investigate the impact of the interpolation algorithm and sample size on the prediction errors. One hundred repeated random selections of sample subsets of size 100, 200, 300 … 2000 were created from the original 6862 Tellus soil data. The 100 random subsets were used for prediction to the remaining Tellus soil survey locations using RK with models 1–6 (see Table 1), and models 1–6 plus polygon SOC or AtoP SOC. As before, MAEs were calculated to determine the relative magnitudes of estimation error.

4. Results and discussion

4.1. Disaggregation of legacy soil polygon map data

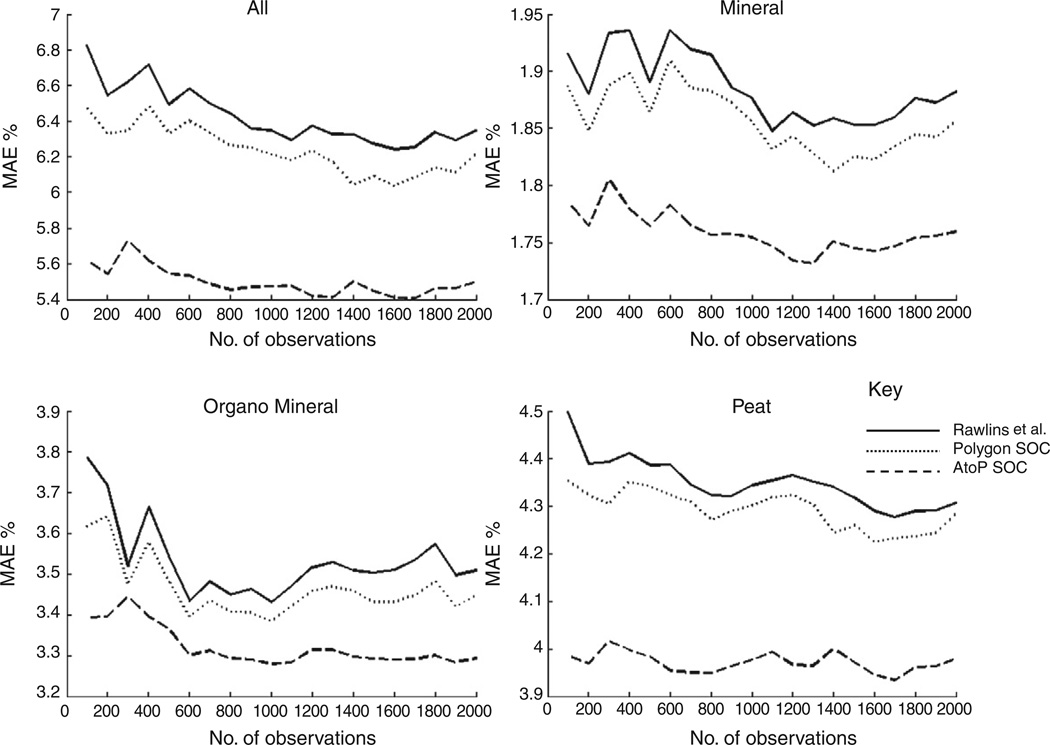
Table 2 shows the MAEs based on disaggregation of the SOC data from the legacy soil polygon map. When all soil types are considered, simple rasterization (polygon SOC) has slightly smaller MAEs than AtoP SOC. However, while the MAEs are similar for mineral and peat soils for AtoP SOC and polygon SOC (around 4 and 18%, respectively), the AtoP disaggregation method has substantially smaller MAEs (13.0%) for organo-mineral soils than the polygon SOC approach (15.2%). The lowest MAEs in each soil class were those for AtoP RK where ancillary data (altitude and radiometric K) account for within polygon variation of soil SOC suggesting that such data related to scorpan factors add value to the disaggregation approach.

Table 2.

Mean absolute errors (MAEs) for different methods of disaggregating SOC polygon data (soil polygon data used for prediction and Tellus validation data n=3862 used for validation).

Disaggregation method	MAE
	All soils	Mineral soils	Organo-mineral soils	Peat soils
Polygon SOC	6.81	4.16	15.20	17.16
AtoP SOC	7.44	4.99	13.03	17.92
AtoP RK SOC	4.72	2.82	7.99	13.31

Simple rasterization of the polygon map produces sharper boundaries in SOC content between soil types and assumes there is no variation in SOC concentration within a given soil class. Although sharp boundaries occur between some soil types in the field, there is always some variation within soil types. Also, it is more common for changes between soil types to be gradual rather than sharp. This is reflected in the AtoP approach which accounts for the spatial configuration of the soil polygons and the underlying trends in the spatial distribution of SOC within and between soil classes. Differences in the MAEs suggest that there are regions, particularly for organo-mineral soils where the AtoP kriging may be more appropriate than simple rasterization as a disaggregation procedure.

Table 2 shows that AtoP RK produces the lowest MAEs of all disag-gregation methods for all soils and all soil types. This shows that if data from a polygon map are to be disaggregated without use of any extra soil sample information, incorporating ancillary data that relate to soil-forming factors can bring significant benefits. Incorporating ancillary data that are related to soil-forming or scorpan factors (McBratney et al., 2003) into the disaggregation of soil legacy data is more theoretically sound than simple rasterization or AtoP kriging alone, however, when the simple two-step AtoP RK procedure is used as here, rather than a one-step approach (Goovaerts, 2011), the pycnophylactic property can be lost.

These results show that where current soil data are scarce and funding is not available for new soil survey, the disaggregation of data from legacy soil maps is a cost-effective alternative strategy for DSM. This disaggregation of legacy soil maps relies on the soil polygons with (AtoP RK) or without (AtoP) quantitative ancillary data which are relatively inexpensive to collect but provide some indication of within polygon variations of soil properties. No new soil measurements need to be collected for such disaggregation approaches.

4.2. Incorporation of disaggregated legacy soil polygon map data into regression kriging

When new soil data are available, it is expected that incorporation of disaggregated legacy data with ancillary data in RK of the new soil data will be more fruitful than merely using a polygon map and ancillary data to disaggregate the polygon data. Using 3000 Tellus soil sample data for prediction and 3862 for validation, Table 3 shows the MAEs for RK with and without AtoP SOC and polygon SOC. Of the other cross-validation statistics (not shown), the MEs were close to zero showing no real bias in the data. Some MSDR values were close to one, however, given that some soils were mis-classified as peat and the MSDR is the ratio of the squared errors to the kriging variance, these large errors dominated the squared errors and produced some large MSDR values. In such cases a MeSDR close to 0.455 provides a better evaluation of whether an appropriate model has been used. The MeSDRs were close to 0.455.

Table 3.

Mean absolute errors (MAEs) from cross-validation of regression kriging for a) Rawlins et al. (2009) models 1–6, b) Rawlins et al. models 1–6 plus polygon SOC, and c) Rawlins et al. models 1–6 plus AtoP SOC (Tellus data n=3000 used for prediction and Tellus data n=3862 used for validation).

		Model 1	Model 2	Model 3	Model 4	Model 5	Model 6
All soils	(a) Rawlins et al.	6.46	6.08	4.43	3.86	4.53	4.02
	(b)+polygon SOC	6.13	5.94	4.32	3.82	4.43	3.96
	(c)+AtoP SOC	5.60	5.37	4.11	3.66	4.18	3.77
Mineral soils	(a) Rawlins et al.	1.93	1.85	1.62	1.57	1.61	1.57
	(b)+polygon SOC	1.88	1.82	1.62	1.56	1.60	1.56
	(c)+AtoP SOC	1.81	1.75	1.62	1.58	1.59	1.57
Organo-mineral soils	(a) Rawlins et al.	3.32	3.40	2.66	2.64	2.86	2.69
	(b)+polygon SOC	3.35	3.35	2.72	2.65	2.82	2.68
	(c)+AtoP SOC	3.43	3.27	2.86	2.81	2.78	2.70
Peat soils	(a) Rawlins et al.	4.35	4.20	3.58	3.15	3.62	3.30
	(b)+polygon SOC	4.21	4.17	3.46	3.11	3.56	3.25
	(c)+AtoP SOC	3.89	3.90	3.19	2.82	3.36	3.04

Table 3 shows that when all soil types are considered, incorporating polygon SOC into each model reduces the MAEs, and inclusion of AtoP SOC reduces the MAEs further. This is also the case for peat soils. The patterns are less consistent for mineral and organo-mineral soils, the reduction in MAE is smaller when polygon SOC and AtoP SOC are included in RK for some models, but not for others. However, even when MAEs do not show a distinct benefit from incorporation of polygon SOC and AtoP SOC in RK, the values are very similar to those when they are not incorporated. When certain combinations of altitude and radiometric K data are used, the advantage of including polygon SOC and AtoP SOC values decreases. The best combinations of ancillary data (lowest MAEs) for each of the three soil types and all soils (Table 3) were those in model 4 (constant plus K plus K²) and model 6 (constant plus altitude plus K plus K²). It should be noted that in Table 3 the MAE for all soils for model 6 is greater than each of the three individual soil types because for all soils it was assumed that the mean is constant whereas for the individual soils the mean was only constant within areas of the same broad soil class.

If the MAEs from cross-validation of RK (Table 3) which were computed using 3000 soil data are compared with those from mere disaggregation of legacy soil data from the polygon map by AtoP RK (Table 2; i.e. no new soil sample data), the MAEs of the latter are similar to the former for all soil types (around 4%), but are about double those of the former for individual soil types (Table 3).

4.3. Jack-knife analysis

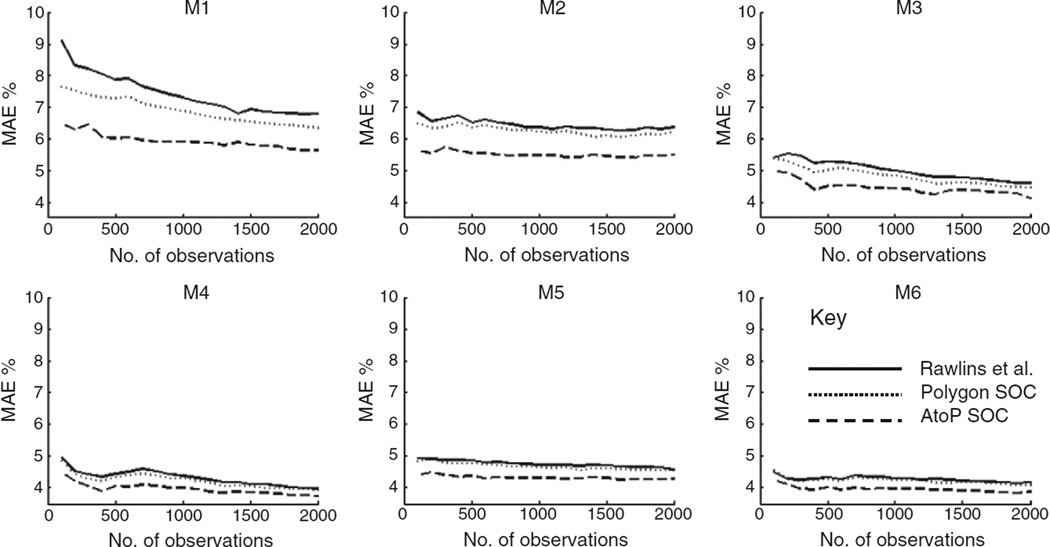
The cross-validation results earlier were based on a single, random prediction subset of Tellus data from 3000 locations. The results demonstrated that it is worthwhile including disaggregated polygon data into RK of SOC. The benefits of a jack-knife procedure, which involves repeatedly selecting random subsets of various size are that it provides a better overall indication of the value of: 1) incorporating disaggregated legacy soil polygon map data into RK and, 2) which models produce more accurate estimates. Fig. 4 shows the MAE jack-knife results for models 1–6 for all soil types plotted on the same scale. The MEs (not shown) were close to zero showing no bias except for very small sample sizes (<30) and MEs were also an order of magnitude lower for sample sizes ≥300. As for the results documented in Section 4.2, depending on the random nature of whether mis-classified samples were included in the jack-knife procedure for a given sample size or not, the MSDRs were sometimes but not always close to one. The MeSDRs were close to 0.455 and gave a better indication of whether a suitable model had been used for RK.

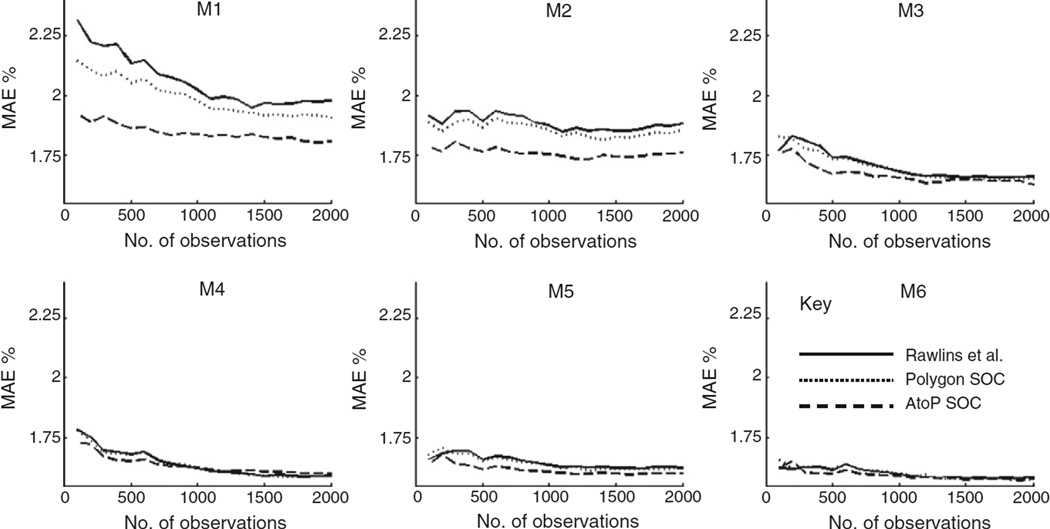
Fig. 4.

Jack-knife results for all soil types for models 1–6 (M1–M6).

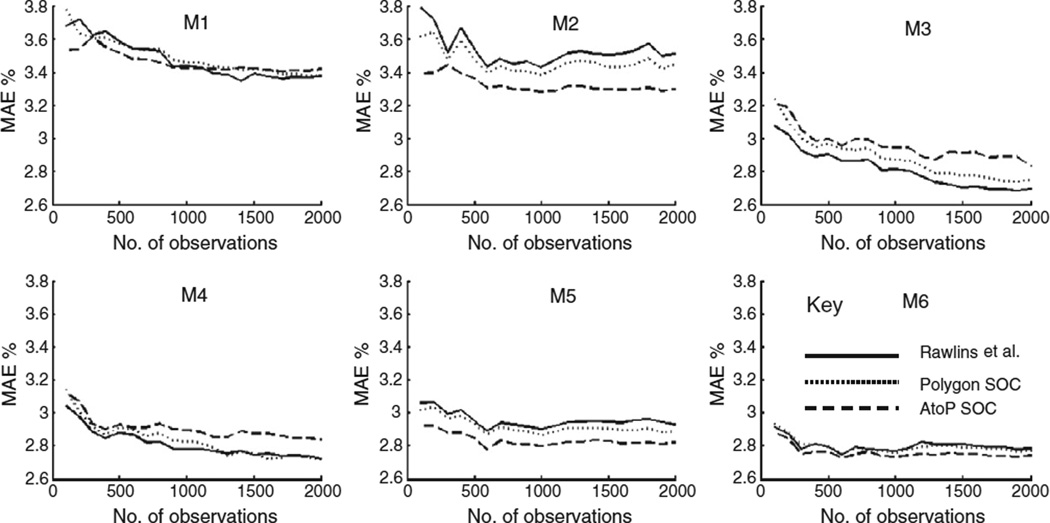
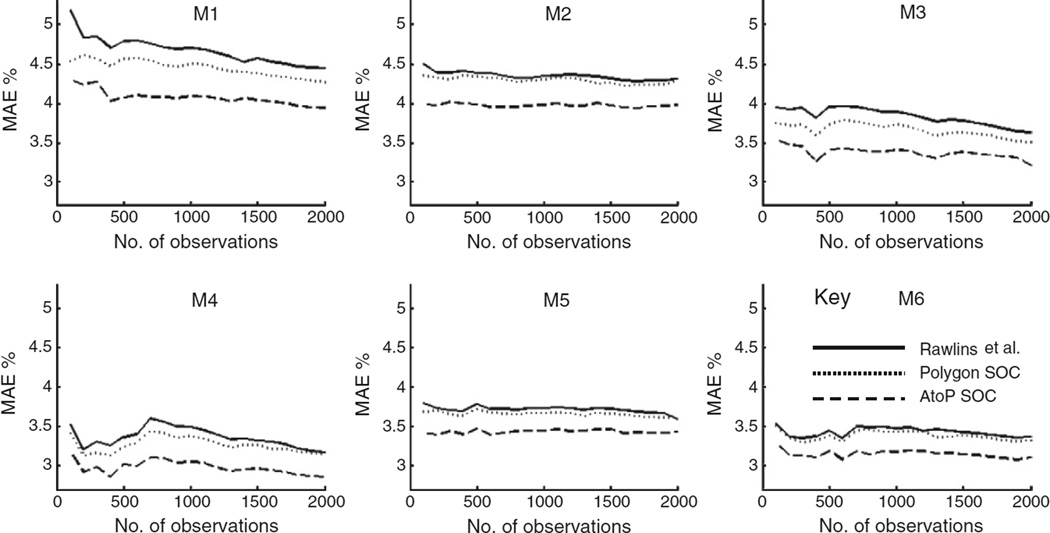
In Fig. 4, the MAEs are somewhat smaller at all sample sizes when polygon SOC is included, but there is a more marked reduction in MAEs when AtoP SOC is incorporated into RK. The MAEs are smallest, generally for models 4 and 6 (around 4%). Fig. 5 also shows, for mineral soil types, that MAEs are smaller at all sample sizes when polygon SOC is included and smaller still when AtoP SOC is included in RK. The only exception to this is for sample sizes greater than about 1000 for models 4 and 6, but MAEs are generally smallest for model 6 (around 1.6%). For organo-mineral soils (Fig. 6), the patterns are reversed for models 3 and 4 with MAEs being largest at all sample sizes when AtoP SOC is included in RK and smallest when compared to the approach adopted by Rawlins et al. However, the MAEs are smallest (around 2.8%), especially for small sample sizes for model 6. For peat soils (Fig. 7) the advantage of incorporating polygon SOC and AtoP SOC into RK is the most marked of any of the soil types; model 4 has the lowest MAEs overall (around 3%). Fig. 7 also shows the largest differences between MAEs when comparing the different approaches (Rawlins et al., polygon SOC and AtoP SOC) when compared with Figs. 4–6. This, and the relatively small MAEs that were obtained for peat soils when AtoP SOC was incorporated into models 4 and 6, clearly indicate that in Northern Ireland where there is a large variation in SOC concentrations one of the major benefits of legacy data is that it identifies the distribution of peat. This is particularly the case when legacy data is disaggregated using AtoP kriging.

Fig. 5.

Jack-knife results for mineral soil types for models 1–6 (M1–M6).

Fig. 6.

Jack-knife results for organo-mineral soil types for models 1–6 (M1–M6).

Fig. 7.

Jack-knife results for peat soils for models 1–6 (M1–M6).

The MAE values for the best performing models (4 and 6) from the jack-knife procedure are similar to those reported from cross-validation in Table 3, but they show that they are more consistent in general than suggested by cross-validation alone, and that beyond a certain point collecting additional soil samples at other locations provides little benefit in terms of reducing MAEs.

Overall, model 6 had the lowest MAEs (Figs. 4–7) so we chose to examine these results in greater detail (Fig. 8). They show that incorporating polygon SOC into RK leads to a small reduction in MAE, about 0.05 and 0.1% reductions for all soil types and peat, respectively. However, for mineral and organo-mineral soils, incorporating polygon SOC has little effect for sample sizes less than 1200. However, including AtoP SOC in RK reduced MAEs by 0.35–0.4% on average for all soils and peat and by about 0.03–0.05% for mineral and organo-mineral soils. Figs. 8 and 4 show that a suitable sample size for RK when incorporating AtoP SOC data is around 300 where the curve levels out and there is not a great advantage in terms of reducing MAE of collecting more samples. This sample size also coincided with a marked reduction in MEs. In many areas, airborne radiometric survey data are unavailable for DSM, whilst altitude data is usually available at some resolution, so we examined in greater detail the results for model 2 in which only altitude is included as a covariate (Fig. 9). The advantage of incorporating AtoP SOC data over polygon SOC in RK is clear and very marked for all soil types and sample sizes. For AtoP SOC, MAEs are reduced by about 1% for all soil types whereas for the polygon SOC, MAEs are only reduced by about 0.2% compared with Rawlins et al.'s models. These reductions in MAEs are at least double the MAE reductions reported earlier for model 6. Fig. 9 also shows that if only altitude data were available as a covariate, around 600 measurements of SOC concentration would be suitable given where the curve levels out; 300 more than was the case for when radiometric K data were included. However, without radiometric K data (model 2), the MAEs are consistently larger compared to when it is included as a covariate (model 6).

Fig. 8.

Jack-knife results for model 6 for all soil types.

Fig. 9.

Jack-knife results for model 2 for all soil types.

The results of the jack-knife procedure show the consistent improvement of MAEs when polygon SOC and AtoP SOC are incorporated into RK and they show that it is better to incorporate legacy soil data as AtoP SOC than polygon SOC. Using more ancillary data can reduce the number of soil samples that need to be collected for RK. Practitioners may need to evaluate the relative costs and benefits of collecting extra soil samples versus including extra ancillary data. Certainly, if the legacy data being used are old or lacking specific information on methodology, the benefits of collecting extra soil samples as opposed to ancillary data are clear.

5. Conclusions

Our analysis shows that for disaggregating legacy SOC data from a polygon map, an AtoP RK approach is more effective than simple rasterization. An AtoP RK approach is theoretically sound because it allows for within class variability, spatial autocorrelation and scorpan factors as represented by ancillary data. In the case of estimating SOC concentrations across Northern Ireland, the AtoP RK approach does not require the collection and use of new soil measurements, but could produce overall MAEs that are similar to those in which 3000 new soil SOC measurements which were distributed throughout the study area are included. The cross-validation and jack-knife results show that incorporating AtoP SOC into RK where some new soil samples are required in addition to legacy data is desirable to reduce errors further, especially for mineral and organo-mineral soil types. Nevertheless, the jack-knife results suggest that between 300 and 600 new soil measurements would be suitable depending on the availability of ancillary data for the study area. Incorporating polygon SOC into RK with various numbers of spatially distributed soil measurements reduces errors at all sample sizes and for most models. Using AtoP SOC reduces MAEs further for Northern Ireland.

These results clearly show that legacy data is useful and should not be disregarded in DSM approaches, and that there are differences in the performance of methods for disaggregating legacy data in DSM. Nevertheless, some important cautionary notes should be made and some additional research conducted before these methods are widely employed with a wide range of soil properties and in vastly different pedological settings.

The legacy soil data used here were collected between 1988 and 1997, and at similar soil depths to new soil data, and are thus likely to be more useful than older legacy data or data that have been collected at markedly different depths. This is especially the case for properties like SOC which can change over time and markedly with depth. The temporal aspect is likely to be less of an issue with more permanent soil properties like soil texture, but differences in the methods of determining soil texture between legacy data and new sample data may also reduce the usefulness of legacy data. The current research has shown the usefulness of the AtoP approach for disaggregating legacy data and then incorporating it into RK, but many locations do not have such a wide range of SOC values within small areas and this approach needs to be tested in areas with far less variability in SOC and in areas with older legacy data. Also the two-step approach used in this study does not ensure that the pycnophylactic property of AtoP kriging is preserved. We did this to allow direct comparison with previous analysis of the Tellus data, but recommend that practitioners use the one-step approach outlined by Goovaerts (2011) when appropriate software becomes available if the pycnophylactic property is very important to their study. The AtoP approach is clearly most useful for DSM in a data-rich scenario where current soil survey data, ancillary data and legacy data are available, but this research highlights the relative magnitude of the errors associated with scenarios when less data is available. Therefore these approaches should be adaptable to situations where less data is available to give a first rough estimate of how SOC varies in the area and perhaps inform future sampling protocols.