An Approach to Evaluating and Comparing Biomarkers for Patient Treatment Selection

Abstract

Despite the heightened interest in developing biomarkers predicting treatment response that are used to optimize patient treatment decisions, there has been relatively little development of statistical methodology to evaluate these markers. There is currently no unified statistical framework for marker evaluation. This paper proposes a suite of descriptive and inferential methods designed to evaluate individual markers and to compare candidate markers. An R software package has been developed which implements these methods. Their utility is illustrated in the breast cancer treatment context, where candidate markers are evaluated for their ability to identify a subset of women who do not benefit from adjuvant chemotherapy and can therefore avoid its toxicity.

1 Introduction

There is an enormous amount of research effort being devoted to discovering and evaluating markers that can predict a patient’s chance of responding to treatment. A December, 2013 PubMed search identified 8,198 papers evaluating such markers over the last 2 years alone. Treatment selection markers, sometimes called “predictive” (Simon (2008)) or “prescriptive” (Gunter, Zhu, and Murphy (2007)) markers, have the potential to improve patient outcomes and reduce medical costs by allowing treatment provision to be restricted to those subjects most likely to benefit, and avoiding treatment in those only likely to suffer its side effects and other costs.

Methods for evaluating treatment selection markers are much less well developed than for markers used to diagnose disease or predict risk under a single treatment. In the medical literature, the most common approach to marker evaluation is to test for a statistical interaction between the marker and treatment in the context of a randomized and controlled trial (see Coates, Miller, O’Toole, Molloy, Viale, Goldhirsch, Regan, Gelber, Sun, Castiglione-Gertsch, Gusterson, Musgrove, and Sutherland (2012), Busch, Ryden, Stal, Jirstrom, and Landberg (2012), Malmstrom, Gronberg, Marosi, Stupp, Frappaz, Schultz, Abacioglu, Tavelin, Lhermitte, Hegi, Rosell, Henriksson, and (NCBTSG) (2012) for some recent examples). However this approach has limitations in that it does not provide a clinically relevant measure of the benefit of using the marker to select treatment and does not facilitate comparing candidate markers (Janes, Pepe, Bossuyt, and Barlow (2011)). Moreover, the scale and magnitude of the interaction coefficient will depend on the form of the regression model used to test for interaction, and on the other covariates included in this model (Huang, Gilbert, and Janes (2012)).

There is a growing literature on statistical methods for evaluating treatment selection markers. A number of papers have focused on descriptive analysis, specifically on modeling the treatment effect as a function of marker (see Bonetti and Gelber (2004), Royston and Sauerbrei (2004), Cai, Tian, Wong, and Wei (2011), Claggett, Zhao, Tian, Castagno, and Wei (2011), Zhao, Tian, Cai, Claggett, and Wei (2011)). In general these approaches are not well-suited to the task of comparing candidate markers. Other papers have proposed individual measures for evaluating markers (see Song and Pepe (2004), Baker and Kramer (2005), Vickers, Kattan, and Sargent (2007), Brinkley, Tsiatis, and Anstrom (2010), Janes et al. (2011), Huang et al. (2012)), some of which we adopt as part of our analytic approach as described below. Still others have focused on the specific problem of optimizing marker combinations for treatment selection (Lu, Zhang, and Zeng (2011), Foster, Taylor, and Ruberg (2011), Gunter, Zhu, and Murphy (2011), Qian and Murphy (2011), McKeague and Qian (2013), Zhang, Tsiatis, Laber, and Davidian (2012)). A complete framework for marker evaluation, on par with those developed for evaluating markers for classification (Pepe (2003), Zhou, McClish, and Obuchowski (2002)) or risk prediction (Pepe and Janes (2012)), is still forthcoming.

In this paper, we lay out a comprehensive approach to evaluating markers for treatment selection. We propose tools for descriptive analysis and summary measures for formal evaluation and comparison of markers. The descriptives are conceptually similar to those of Bonetti and Gelber (2004), Royston and Sauerbrei (2004), Cai et al. (2011), but we scale markers to the percentile scale to facilitate making comparisons. Our preferred global summary measure is the same as or closely related to that advocated by (Song and Pepe (2004), Brinkley et al. (2010), Janes et al. (2011), Gunter et al. (2011), Qian and Murphy (2011), McKeague and Qian (2013), Zhang et al. (2012)), a component of which was described by Zhao et al. (2011), Baker and Kramer (2005). We also propose several novel measures of treatment selection performance, motivated by existing methodology for evaluating markers for predicting outcome under a single treatment, i.e. for risk prediction. We develop methods for estimation and inference that apply to data from a randomized controlled trial comparing two treatment options where the marker is measured at baseline on all or a stratified case-control sample of trial participants. For illustration, we consider the breast cancer treatment context where candidate markers are evaluated for their utility in identifying a subset of women who do not benefit from adjuvant chemotherapy. Appendices include the results of a small-scale simulation study that evaluates the performance of the methods in finite samples and a description of the R package we have written that implements these methods.

2 Setting and Notation

Suppose that the task is to decide between two treatment options, referred to as “treatment” (T = 1) and “no treatment” (T = 0). The clinical outcome of interest, D, is a binary indicator of a bad event within a specific time-frame following treatment provision; we refer to this outcome as an “adverse event” or “event”. The outcome D is thought to capture all potential impacts of treatment, so that any decrease in the rate of events justifies treatment; a generalization is discussed in Section 6.1. To achieve this, D may be chosen to represent a composite outcome such as an indicator of treatment-associated toxicity or death. We assume that the marginal treatment effect ρ₀ − ρ₁ ≡ P(D = 1|T = 0)−P(D = 1|T = 1) is positive, so that the default approach is to treat all subjects. The question is whether a marker, Y, if measured prior to treatment provision, is useful for identifying a subset of subjects who can avoid treatment. Note that the scenario where the marginal treatment effect is negative (or zero) and Y identifies a subset who benefit from treatment can be handled by simply reversing the treatment labels.

We focus on the ideal setting for evaluating treatment efficacy, a randomized and controlled trial (RCT) comparing T = 1 to T = 0. By necessity, this must be a relatively large trial; it is well-known that large sample sizes are generally needed to detect statistical interactions. We assume to begin that Y is continuous and measured at baseline on all trial participants. We generalize our methods to case-control sampling from within an RCT in Section 6.2.

3 Motivating Context

We illustrate our methods in the breast cancer treatment context. Women diagnosed with estrogen-receptor-positive and node-positive breast cancer are typically treated with both hormone therapy (e.g. tamoxifen) and adjuvant chemotherapy following surgery. This is despite the fact that it is generally well-accepted in the clinical community that only a subset of these women actually benefit from the adjuvant chemotherapy, and the remaining women suffer its toxic side effects, not to mention the burden and cost of unnecessary treatment (Early Breast Cancer Trialists Collaborative Group (2005)). A high public health priority is to identify biomarkers that can be used to predict which women are and are not likely to benefit from the adjuvant chemotherapy (Dowsett, Goldhirsch, Hayes, Senn, Wood, and Viale (2007)). The Oncotype DX recurrence score is an example of a biomarker that is currently being used in clinical practice for this purpose. This marker is a proprietary combination of 21 genes whose expression levels are measured in the tumor tissue obtained at surgery (Paik, Shak, Tang, Kim, Baker, Cronin, Baehner, Walker, Watson, Park, Hiller, Fisher, Wickerham, Bryant, and Wolmark (2004), Paik, Tang, Shak, Chungyeul, Baker, Kim, Cronin, Baehner, Watson, Bryant, Constantino, Geyer, Wickerham, and Wolmark (2006), Albain, Barlow, Shak, Hortobagyi, Livingston, and Yeh (2010)). The marker has been shown to have value for identifying a subset of women who are unlikely to benefit from chemotherapy (Paik et al. (2006), Albain et al. (2010)).

To illustrate our methods, we simulated a marker, Y₁, with the same performance as Oncotype DX in the SWOG SS8814 trial which evaluated adjuvant chemotherapy (cyclophosphamide, doxorubicin, and fluorouracil) given before tamoxifen for treating post-menopausal women with estrogen-receptor positive, node-positive breast cancer (Albain, Barlow, Davdin, Farrar, Burton, Ketchel, Cobau, Levine, Ingle, Pritchard, Lichter, Schneider, Abeloff, Henderson, Muss, Green, Lew, Livingston, Martino, Osborne, and the Breast Cancer Intergroup of North America (2009), Albain et al. (2010)). We also simulated another marker, Y₂, which we will demonstrate is a much stronger marker. Both markers Y₁ and Y₂ are measured at baseline for 1,000 participants randomized with equal probability to tamoxifen alone (T = 0) or tamoxifen plus chemotherapy (T = 1). The outcome, D, is breast cancer recurrence or death within 5 years of randomization and the marginal treatment effect is ρ₀ − ρ₁ =0.24 − 0.21=0.03 as seen in SS8814. Marker Y₁ is simulated to mimic the Oncotype DX distribution; ${\sqrt{Y}}_1$ is normally distributed with mean 4.8 and standard deviation 1.8. Marker Y₂ is standard normal. Each marker is related to D via a linear logistic model, logit P(D = 1|T,Y) =β₀ +β₁T +β₂Y +β₃YT, where for Y₁ the model coefficients are chosen to mimic the performance of the Oncotype DX recurrence score (Albain et al. (2010)). Methods for simulating the data are described in the appendix.

4 Methods for Evaluating Individual Markers

4.1 Treatment Rule

Given that the task is to decide between treatment and no treatment for each individual subject, it is sensible and common to define a binary rule for assigning treatment on the basis of marker value. Let Δ(Y) = P(D = 1|T = 0,Y) − P(D = 1|T = 1,Y) denote the absolute treatment effect given marker value Y. The rule

$$\text{do}\text{not}\text{treat}\text{if}\mathrm{\Delta }(Y)<0$$

can be shown to be optimal in the sense that it minimizes the population event rate (Brinkley et al. (2010), Zhang et al. (2012), Janes, Pepe, and Huang (2013)). Some of the marker performance measures we consider evaluate the properties of this rule; other performance measures do not depend on specification of a treatment rule. We refer to subjects with Δ(Y) < 0 as “marker-negatives” and Δ(Y) > 0 as “marker-positives”. More general treatment rules are considered in Section 6.1.

4.2 Descriptives

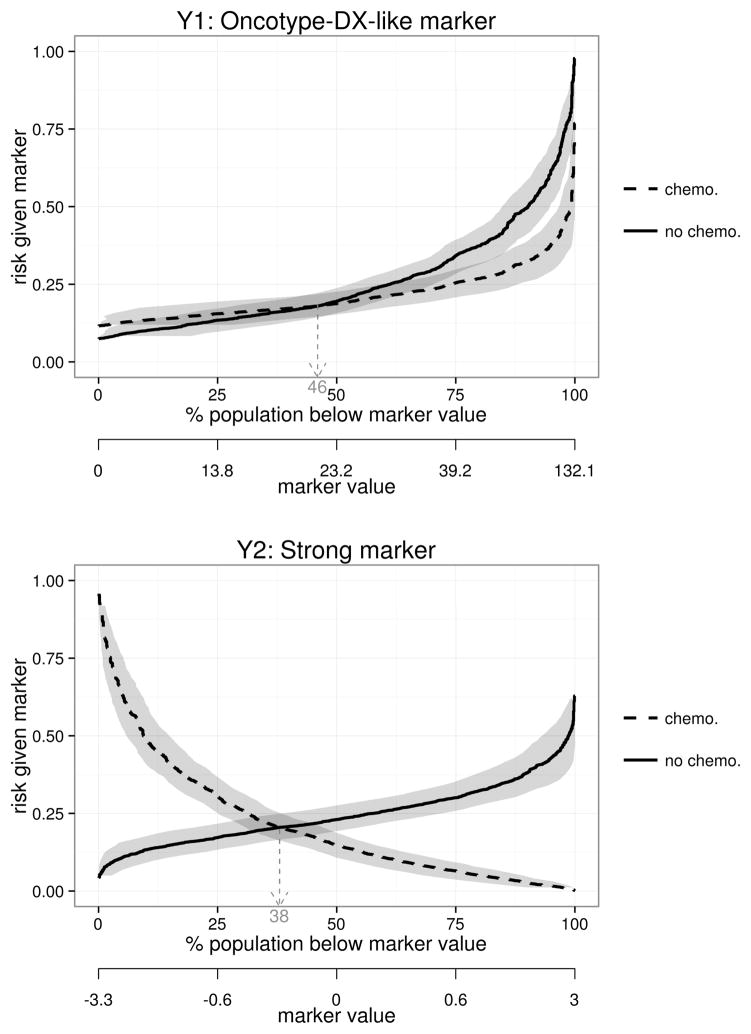
For descriptive analysis, it is useful to display the distribution of risk of the event as a function of the marker under each treatment. We plot “risk curves” P(D = 1|T = 1,Y) and P(D = 1|T = 0,Y) versus marker percentile F(Y), where F is the cumulative distribution function (CDF) of Y (Janes et al. (2011)). Figure 1 shows the risk curves for the Oncotype-DX-like marker, Y₁, and the much better marker, Y₂. From these one can visually assess the variability in response on each treatment as a function of marker value. One can also determine the proportion of subjects with negative treatment effects who can avoid chemotherapy, 46% for Y₁ vs. 38% for Y₂.

Figure 1.

Risk of 5-year breast cancer recurrence or death as a function of treatment assignment and marker percentile, for Y₁, the Oncotype-DX-like marker (top), and the strong marker, Y₂ (bottom). Horizontal pointwise 95% confidence intervals are shown. Fourty-six percent of women have negative treatment effects according to Y₁ vs. 38% with Y₂; these women can avoid adjuvant chemotherapy.

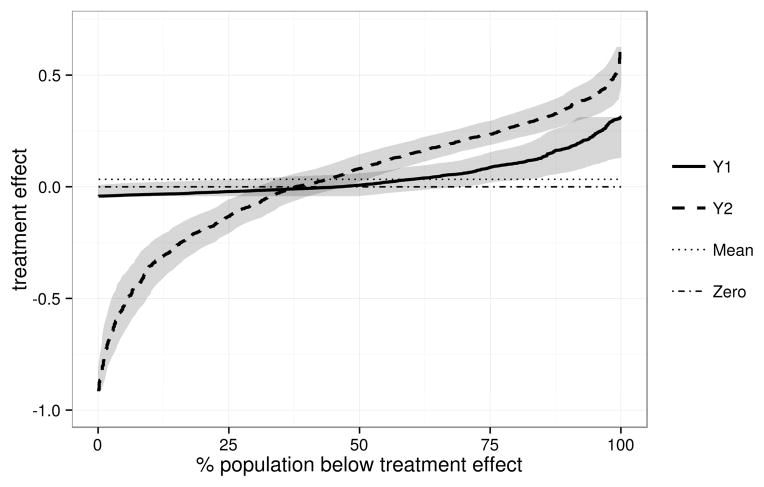
Another informative display is the distribution of treatment effect, as summarized by Δ(Y) vs. F_Δ(Δ(Y)) where F_Δ is the CDF of Δ(Y) (Huang et al. (2012)). The example shown in Figure 2 reveals that Y₂ has much greater variation in marker-specific treatment effect than does Y₁. For Y₂ a greater proportion of marker-specific treatment effects are extreme whereas for Y₁ the range is smaller and most treatment effects are near the average of ρ₀ − ρ₁ = 0.03.

Figure 2.

Distribution of the treatment effect, as measured by the difference in the 5-year breast cancer recurrence or death rate without vs. with treatment, Δ(Y) = P(D = 1|T = 0,Y)−P(D = 1|T = 1,Y), for the Oncotype-DX-like marker (Y₁) and the strong marker (Y₂). Horizontal pointwise 95% confidence intervals are shown.

4.3 Summary Measures

The following are useful measures for summarizing marker performance that depend on specification of the treatment rule:

• Average benefit of no treatment among marker-negatives,

  $$\begin{array}{l}{B}_{\mathit{neg}}=P(D=1\mid T=1,\mathrm{\Delta }(Y)<0)-P(D=1\mid T=0,\mathrm{\Delta }(Y)<0)\\ =E(-\mathrm{\Delta }(Y)\mid \mathrm{\Delta }(Y)<0)\end{array}$$
• Average benefit of treatment among marker-positives,

  $$\begin{array}{l}{B}_{\mathit{pos}}=P(D=1\mid T=0,\mathrm{\Delta }(Y)>0)-P(D=1\mid T=1,\mathrm{\Delta }(Y)>0)\\ =E(\mathrm{\Delta }(Y)\mid \mathrm{\Delta }(Y)>0)\end{array}$$

• Proportion marker-negative, P_neg = P(Δ(Y) < 0)

• Decrease in population event rate under marker-based treatment,

  $$\begin{array}{l}\mathrm{\Theta }=P(D=1\mid T=1)-[P(D=1\mid T=1,\mathrm{\Delta }(Y)>0)P(\mathrm{\Delta }(Y)>0)+P(D=1\mid T=0,\mathrm{\Delta }(Y)<0)P(\mathrm{\Delta }(Y)<0)]\\ =[P(D=1\mid T=1,\mathrm{\Delta }(Y)<0)-P(D=1\mid T=0,\mathrm{\Delta }(Y)<0)]P(\mathrm{\Delta }(Y)<0)\\ =B_{\mathit{neg}}·P_{\mathit{neg}},\end{array}$$

  where we define P(D = 1|T, Δ(Y) < 0) = 0 if P(Δ(Y) < 0) = 0. The measure Θ, or a variation on it, has been advocated by many as a global measure of marker performance (Song and Pepe (2004), Brinkley et al. (2010), Janes et al. (2011), Gunter et al. (2007), Zhang et al. (2012), McKeague and Qian (2013)). Θ varies between 0 and ρ₁. The minimum value of 0 corresponds to an entirely useless marker with constant marker-specific treatment effect, Δ(Y) = ρ₀ − ρ₁ > 0 for all Y. For such a marker, Θ = ρ₁ − [ρ₁ · 1+0 · 0] = 0. The maximum value of Θ is achieved when P(D = 1|T = 1, Δ(Y) > 0) = P(D = 1|T = 0, Δ(Y) < 0) = 0, so that Θ =ρ₁ − [0 · P(Δ(Y) > 0)+0 · P(Δ(Y) < 0)] =ρ₁.

The constituents of Θ, namely B_neg and P_neg, are helpful for dissecting the impact of the marker. The measures B_neg and B_pos inform on the average benefit of the treatment policies recommended to marker-negatives and marker-positives, respectively. B_neg itself has been advocated by some as a measure of marker performance (see Zhao et al. (2011), Baker and Kramer (2005)), but clearly cannot be interpreted in isolation as it can be made arbitrarily large by making the marker-negative subgroup more extreme; i.e. the size of the subgroup (P_neg) is also relevant.

We also consider two marker performance measures that do not depend on specification of a treatment rule:

• Variance in treatment effect, V_Δ =Var(Δ(Y)) = ∫ (Δ(Y)− (ρ₀ − ρ₁))² dF_Δ

• Total gain, the area between the treatment effect curve and the marginal treatment effect, TG = ∫ |Δ(Y) − (ρ₀ − ρ₁)| dF_Δ.

The V_Δ and TG measures suffer because of lack of clinical interpretation, but have the advantage of being independent of treatment rule and potentially form the basis for more efficient comparisons of markers. These measures are extensions of those used to evaluate markers for predicting risk of the event under a single treatment, rather than the treatment effect.

Table 1 contains estimates of V_Δ and TG measures for markers Y₁ and Y₂ in the breast cancer example. Focusing on Y₂, we see that the population impact of Y₂-based-treatment is a 10% reduction in the 5-year recurrence or death rate; this is a consequence of 38% of subjects avoiding adjuvant chemotherapy and a 26% reduction in the event rate due to avoiding chemotherapy in this subgroup. Among marker-positives, chemotherapy decreases the event rate by 21% on average. Less interpretable, but somewhat useful for global marker comparisons, are the values of V_Δ = 0.08 and TG = 0.22.

Table 1.

Estimates of various measures of marker performance for the Oncotype-DX-like marker (Y₁) and the strong marker (Y₂) in the breast cancer example.

		Marker Y1	Marker Y2	Marker Y1 vs. Y2
Measure	Estimator	Estimate (95% CI)	Estimate (95% CI)	Estimated Diff. (95% CI)	P-value for diff.
Θ	Θ̂e	0.013 (−0.010,0.044)	0.090 (0.060,0.122)	−0.076 (−0.111, −0.042)	< 0.002
	Θ̂m	0.010 (0.000,0.037)	0.099 (0.071,0.129)	−0.088 (−0.115, −0.061)	< 0.002
Bneg	${\widehat{B}}_{\mathit{neg}}^e$	0.029 (−0.106,0.082)	0.238 (0.170,0.309)	−0.209 (−0.342, −0.129)	< 0.002
	${\widehat{B}}_{\mathit{neg}}^m$	0.023 (0.000,0.057)	0.262 (0.209,0.310)	−0.239 (−0.294, −0.178)	< 0.002
Bpos	${\widehat{B}}_{\mathit{pos}}^e$	0.089 (0.020,0.157)	0.203 (0.157,0.263)	−0.114 (−0.193, −0.043)	< 0.002
	${\widehat{B}}_{\mathit{pos}}^m$	0.098 (0.035,0.162)	0.211 (0.176,0.258)	−0.113 (−0.184, −0.052)	< 0.002
Pneg	P̂neg	0.461 (0.000,0.700)	0.377 (0.304,0.470)	0.084 (−0.358,0.236)	0.768
VΔ	V̂Δ	0.007 (0.001,0.019)	0.080 (0.057,0.109)	−0.073 (−0.103, −0.046)	< 0.002
TG	$\widehat{TG}$	0.066 (0.024,0.110)	0.224 (0.187,0.263)	−0.158 (−0.221, −0.102)	< 0.002

4.4 Estimation and Inference

Our proposed estimation and inference methods build on methodology developed for risk prediction (see Huang, Sullivan Pepe, and Feng (2007), Huang and Pepe (2010b,a)). This section overviews these approaches which are evaluated in a small-scale simulation study described in the appendix. An R software package that implements these methods is also described in the appendix.

4.4.1 Estimation

Given data consisting of i.i.d copies of (Y_i,T_i,D_i), i = 1, …,N, the first step in estimation is to fit a model for risk as a function of T and Y. We use a general linear regression risk model with an interaction between T and Y,

$$g(P(D=1\mid T,Y))={\beta }_0+{\beta }_{1}T+{\beta }_{2}Y+{\beta }_{3}YT.$$ (1)

Typically we let g be the logit function because of its advantages with case-control data (see Section 6.2) and because we have found logistic regression to be remarkably robust to model mis-specification. We note that the general linear model (1) is flexible in that the marker Y can itself be a transformed marker value. The risk and treatment effect estimates that result from fitting from this model are written $\widehat{P}(D=1\mid T=0,Y)={\widehat{\mathit{Risk}}}_0(Y)=g^{-1}({\widehat{\beta }}_0+{\widehat{\beta }}_{2}Y),\widehat{P}(D=1\mid T=1,Y)={\widehat{\mathit{Risk}}}_1(Y)=g^{-1}({\widehat{\beta }}_0+{\widehat{\beta }}_1+{\widehat{\beta }}_{2}Y+{\widehat{\beta }}_{3}Y)$, and $\widehat{\mathrm{\Delta }}(Y)={\widehat{\mathit{Risk}}}_0(Y)-{\widehat{\mathit{Risk}}}_1(Y)$. We estimate the marker and treatment effect distributions empirically and denote these by F̂ and F̂_Δ. The estimated risk curves are ${\widehat{\mathit{Risk}}}_0(Y)$ and ${\widehat{\mathit{Risk}}}_1(Y)$ versus F̂(Y). Pointwise α-level horizontal confidence intervals inform about the variability in the proportion of participants at or below a given risk level; we obtain these using the percentile boot-strap method. The estimated treatment effect curve is Δ̂(Y) vs. F̂_Δ. Here pointwise horizontal confidence intervals capture the variability in the estimated proportion of individuals with treatment effects below a certain value.

For the summary measures that depend on treatment rule, we consider both “empirical” and “model-based” estimators. An empirical estimator uses the estimated risk model (1) to classify individuals as marker-positive or marker-negative, and the performance of this rule is estimated empirically. For a model-based estimator, the risk model is used both to classify each individual and to estimate the performance of the classification rule. For example, the empirical estimator of B_pos estimates the average treatment effect empirically given Δ̂(Y) > 0, and the model-based estimator averages Δ̂(Y) for this subgroup. The empirical estimators are less efficient but less reliant on risk model assumptions than model-based estimators (see appendix). The estimators are listed below, where e and m superscripts indicate empirical and model-based estimators, P̂ denotes an empirical probability estimate and Ê denotes an empirical mean:

$$\begin{array}{c}{\widehat{B}}_{\mathit{neg}}^e=\widehat{P}(D=1\mid T=1,\widehat{\mathrm{\Delta }}(Y)<0)-\widehat{P}(D=1\mid T=0,\widehat{\mathrm{\Delta }}(Y)<0)\\ {\widehat{B}}_{\mathit{neg}}^m=\widehat{E}(-\widehat{\mathrm{\Delta }}(Y)\mid \widehat{\mathrm{\Delta }}(Y)<0)\\ {\widehat{B}}_{\mathit{pos}}^e=\widehat{P}(D=1\mid T=0,\widehat{\mathrm{\Delta }}(Y)>0)-\widehat{P}(D=1\mid T=1,\widehat{\mathrm{\Delta }}(Y)>0)\\ {\widehat{B}}_{\mathit{pos}}^m=\widehat{E}(\widehat{\mathrm{\Delta }}(Y)\mid \widehat{\mathrm{\Delta }}(Y)>0)\\ {\widehat{P}}_{\mathit{neg}}=\widehat{P}(\widehat{\mathrm{\Delta }}(Y)<0)\\ {\widehat{\mathrm{\Theta }}}^e={\widehat{B}}_{\mathit{neg}}^e·{\widehat{P}}_{\mathit{neg}}\\ {\widehat{\mathrm{\Theta }}}^m={\widehat{B}}_{\mathit{neg}}^m·{\widehat{P}}_{\mathit{neg}}=\int -\widehat{\mathrm{\Delta }}(Y)I[\widehat{\mathrm{\Delta }}(Y)<0]d{\widehat{F}}_{\mathrm{\Delta }}\end{array}$$

The treatment-rule-independent summary measures are estimated using the following model-based estimators:

$$\begin{array}{l}{\widehat{V}}_{\mathrm{\Delta }}=\int {(\widehat{\mathrm{\Delta }}(Y)-({\widehat{\rho }}_0-{\widehat{\rho }}_1))}^{2}d{\widehat{F}}_{\mathrm{\Delta }}\\ \widehat{TG}=\int \mid \widehat{\mathrm{\Delta }}(Y)-({\widehat{\rho }}_0-{\widehat{\rho }}_1)\mid d{\widehat{F}}_{\mathrm{\Delta }},\end{array}$$

where ρ̂₀ and ρ̂₁ are empirical estimates of P(D = 1|T = 0) and P(D = 1|T = 1). Confidence intervals for each summary measure are obtained using the percentile bootstrap.

4.4.2 Hypothesis Testing

Testing whether a marker has any performance for treatment selection is of interest for two reasons. First, this is a logical first step in marker evaluation. Second, the performance measures described above may have poor statistical properties at and near the null of no marker performance. This is similar to problems that have been identified with measures of risk prediction model performance (see Vickers, Cronin, and Begg (2011), Kerr, McClelland, Brown, and Lumley (2011), Pepe, Kerr, Longton, and Wang (2011), Seshan, Gonen, and Begg (2012), Demler, Pencina, and D’Agostino (2012), Kerr, Wang, Janes, McClelland, Psaty, and Pepe (2013)); Section 7 includes further discussion of this point. Therefore, we advocate a simple pre-testing approach, whereby the marker performance measures are only estimated if the null hypothesis H₀ : Θ=0 corresponding to no marker performance is rejected.

For an unbounded marker, under risk model (1), H₀ is equivalent to $H_0^1:{\beta }_3=0$ where β₃ is the coefficient of interaction in the risk model. Therefore H₀ can be tested using a (most-powerful) likelihood ratio (LR) test for β₃. However if Y is bounded, $H_0^1$ implies H₀ but the reverse does not hold; it is possible that β₃ ≠ 0 but Θ = 0. Therefore we perform two hypothesis tests: $H_0^1:{\beta }_3=0$ is tested using a LR test and $H_0^2:-{\beta }_1/{\beta }_3\notin (Y_{\mathit{min}},Y_{\mathit{max}})$ using a Wald or percentile-bootstrap-based test, where −β₁/β₃ is the marker value where Δ(Y) = 0 under model (1) and Y_min and Y_max are the known upper and lower limits for Y. That is, testing $H_0^2$ assesses whether the marker positivity threshold Y such that Δ(Y) = 0 lies within the range of possible marker values. We declare H₀ to be rejected if both $H_0^1$ and $H_0^2$ are rejected. Using two-sided α-level tests for $H_0^1$ and $H_0^2$ controls the overall type-I error rate at α since $P(\text{reject}{H}_0^1\text{and}\text{reject}{H}_0^2\mid \mathrm{\Theta }=0)\le \mathit{min}(P(\text{reject}{H}_0^1\mid \mathrm{\Theta }=0),P(\text{reject}{H}_0^2\mid \mathrm{\Theta }=0))=\alpha$. Other approaches have been proposed for testing the null of no marker performance (e.g. Gail and Simon (1985), Shuster and J. (1983)); optimizing this test is not our focus.

For the unbounded markers Y₁ and Y₂ in our breast cancer example, H₀ is rejected with p = 0.005 and p < 0.0001, respectively.

4.5 Calibration Assessment

Assessing model calibration is a fundamental step in marker evaluation. We rely on standard methods for visualizing and testing goodness of fit for the risk model (1), and extend these methods to assess calibration of the treatment effect model.

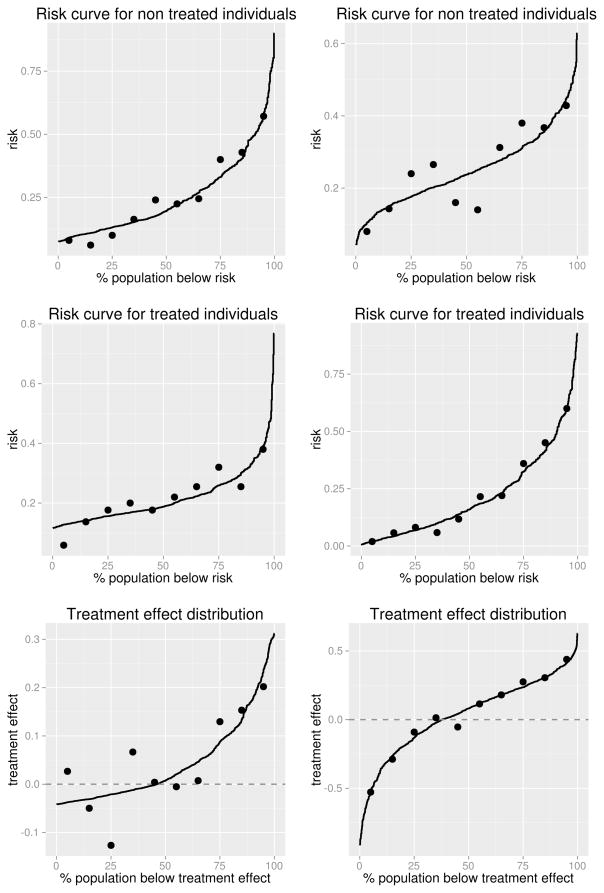
Since patients are provided risk estimates under both treatment options, first we assess the fit of the risk model separately in the two treatment groups. Specifically, we define a well-calibrated model to be one for which P(D = 1|T = 0, Risk₀(Y) = r) ≈ r and P(D = 1|T = 1, Risk₁(Y) = r) ≈ r. To assess this, we split each treatment group t = 0,1 into G equally-sized groups where the observations in each group have similar ${\widehat{\mathit{Risk}}}_t(Y)$. Commonly G = 10 and the groups are based on quantiles of ${\widehat{\mathit{Risk}}}_t(Y)$. In each group, we calculate the average predicted risks, ${\overline{\mathit{Risk}}}_{tg}(Y)$, and the observed risks, P̂(D = 1|T = t, G = g). Following Huang and Pepe (2010a), we plot the distribution of ${\widehat{\mathit{Risk}}}_0(Y)$ and ${\widehat{\mathit{Risk}}}_1(Y)$, overlaying the G observed risk values on the plot, as shown in Figure 3.

Figure 3.

Plots assessing calibration of the risk and treatment effect models, for the Oncotype-DX-like marker (left) and the strong marker (right).

To formally assess model calibration, a traditional Hosmer-Lemeshow goodness of fit test (Lemeshow and Hosmer (1982)) can be applied separately to the two treatment groups. Specifically, for group T = t the test statistic

$$H{L}_t=\sum _{g=1}^G\frac{N_{tg}{(\widehat{P}(D=1\mid T=t,G=g)-{\overline{\mathit{Risk}}}_{tg}(Y))}^2}{{\overline{\mathit{Risk}}}_{tg}(Y)(1-{\overline{\mathit{Risk}}}_{tg}(Y))},$$

where N_tg is the number of participants in the g^th group for T = t, is compared to a χ² distribution with G − 2 degrees of freedom.

Another aspect of calibration is the extent to which the treatment effect model fits well. We want to ensure that P(D = 1|T = 0, Δ(Y) =δ) − P(D = 1|T = 1,Δ(Y) =δ) ≈ δ. Following the approach above, we split the data into G evenly-sized groups based on Δ̂(Y) and calculate the average predicted treatment effect, Δ̄_g(Y), and observed treatment effect, P̂(D=1|T =0,G=g) − P̂(D=1|T =1,G= g), in each group. We plot the treatment effect curve and overlay the G observed treatment effect values as shown in Figure 3. Based on Figure 3 we see that the risk and treatment effect models for Y₁ and Y₂ in the breast cancer example are well-calibrated; the Hosmer-Lemeshow test statistics are 4.5 (p = 0.81) and 8.9 (p = 0.35) given T = 0 and 5.0 (p = 0.76) and 2.9 (p = 0.94) given T = 1. The Risk₀(Y₂) and Δ(Y₁) curves suggest some evidence of poor calibration, which in our simulated data setting is attributable to sampling variability in the observed risks that are calculated using 50 observations each.

5 Comparing Markers

The descriptives and summary measures proposed herein form the basis for comparing candidate markers. We assume that the two markers, Y₁ and Y₂, are measured on the same subjects, i.e. that the data are paired. With unpaired data, the analyses described above can be applied to each individual data set and inferences can be drawn easily given that the estimated summary measures are statistically independent.

For drawing inference about the relative performance of two markers given paired data, confidence intervals for the differences in performance measures and hypothesis tests of whether these differ from zero are informative. We fit separate models for P(D = 1|T,Y₁) and P(D = 1|T,Y₂), use these to estimate performance measures for Y₁ and Y₂, respectively, and bootstrap the differences in estimated performance measures. While global measures of marker performance such as Θ, V_Δ, and TG are appropriate as the basis for formal marker comparisons, differences in the other summary measures inform about the nature of the difference between markers. We advocate Θ as the primary measure on which to base marker comparisons, given its clear clinical relevance and interpretation.

The results of the comparative analysis for the breast cancer example are shown in Table 1. We can see clearly that Y₂ has uniformly better performance than Y₁, with an estimated 10% vs. 1% reduction in the 5-year recurrence or death rate. Despite the fact that there are estimated to be fewer marker-negative subjects based on Y₂ (38% vs. 46%), there is a much greater estimated benefit of no chemotherapy among Y₂-marker-negatives (26% vs. 2% reduction in the 5-year recurrence or death rate). In general the variation in treatment effect is larger for Y₂.

6 Extensions

6.1 General Treatment Rules

In some settings there may be additional consequences of treatment that are not captured in the outcome, for example treatment-associated toxicities. This means that a treatment effect somewhat above zero may still warrant no treatment because it is offset by the other consequences of treatment. In these settings the optimal treatment rule can be shown to be

$$\text{do}\text{not}\text{treat}\text{if}\mathrm{\Delta }(Y)<\delta ,$$

where δ > 0 is equal to the burden of treatment relative to that of the adverse event (Vickers et al. (2007), Janes et al. (2013)). The performance measures described above generalize naturally to this treatment rule:

$$\begin{array}{l}{B}_{\mathit{neg}}(\delta )=P(D=1\mid T=1,\mathrm{\Delta }(Y)<\delta )-P(D=1\mid T=0,\mathrm{\Delta }(Y)<\delta )\\ B_{\mathit{pos}}(\delta )=P(D=1\mid T=0,\mathrm{\Delta }(Y)>\delta )-P(D=1\mid T=1,\mathrm{\Delta }(Y)>\delta )\\ P_{\mathit{neg}}(\delta )=P(\mathrm{\Delta }(Y)<\delta )\\ \mathrm{\Theta }(\delta )=P(D=1\mid T=1)-[P(D=1\mid T=1,\mathrm{\Delta }(Y)>\delta )P(\mathrm{\Delta }(Y)>\delta )+P(D=1\mid T=0,\mathrm{\Delta }(Y)<\delta )P(\mathrm{\Delta }(Y)<\delta )]\\ =B_{\mathit{neg}}(\delta )·P_{\mathit{neg}}(\delta ).\end{array}$$

Note that the V_Δ and TG measures do not require specification of a treatment rule. Further generalization to the setting where the burden of treatment and/or of the adverse event varies between individuals, perhaps as a function of Y, is described by Janes et al. (2013).

6.2 Case-Control Sampling

The methods described above apply to the setting where the marker is measured at baseline on all RCT participants. However when the outcome D is rare, case-control sampling from within the RCT is a well-known efficient alternative that recovers much of the information contained in the entire trial population. This section extends the methods to the setting where the data consist of a case-control sample from the RCT, or a case-control sample stratified on treatment assignment, T. We consider case-control designs that sample all or a fixed proportion of the cases in the RCT, as well as a number of controls (perhaps stratified on T) that is a fixed multiple of the number of cases sampled.

Consider first unstratified case-control sampling. Suppose N_D and N_D̄ cases and controls occur in the trial “cohort” (N = N_D +N_D̄). The case-control sample consists of a sample of n_D = f · N_D cases and n_D̄ = k · n_D controls, where f ∈ (0,1] and the control:case ratio k is an integer. Commonly all the cases are sampled (f = 1) and 1–5 controls are sampled per case. Alternatively f may be set to a value less than 1 for a common event or when budget concerns or sample availability limit the number of cases that can be sampled; in these instances we assume that selection into the case-control sample is completely random conditional on D = 1.

Let S = 1 be an indicator of selection into the case-control sample. Given the case-control data, the task is to correct the estimates of P(D = 1|T,Y,S = 1) and P(Δ(Y) < δ |S = 1) for the case-control sampling. Suppose that an estimate of P(D = 1) is available from the cohort. Using Bayes’ Theorem and the assumption of case-control sampling that P(S=1|T,Y,D)=P(S=1|D) we obtain he following identity which is used to correct the estimates of P(D = 1|T,Y,S = 1) for the case-control sampling:

$$\begin{array}{l}\text{logit}P(D=1\mid T,Y,S=1)=log\frac{P(S=1\mid T,Y,D=1)P(D=1\mid T,Y)}{P(S=1\mid T,Y,D=0)P(D=0\mid T,Y)}\\ =log\frac{P(S=1\mid D=1)}{P(S=1\mid D=0)}+\text{logit}P(D=1\mid T,Y)\\ =log\frac{P(D=1\mid S=1)P(S=1)P(D=0)}{P(D=0\mid S=1)P(S=1)P(D=1)}+\text{logit}P(D=1\mid T,Y)\\ =\text{logit}P(D=1\mid S=1)-\text{logit}P(D=1)+\text{logit}P(D=1\mid T,Y).\end{array}$$

This result was originally cited by Prentice and Pyke (1979) as the rationale for using logistic regression to model risk with case-control data. Note that P(D = 1|T,Y,S = 1) can be estimated using the logistic regression risk model (1) fit to the case-control data, P(D = 1) can be estimated from the trial cohort, and P(D = 1|S = 1) estimated from the case-control data.

The distribution of Δ(Y), or equivalently of Y itself, can be estimated in the cases and controls in the case-control data and corrected to the cohort distribution via

$${\widehat{F}}_{\mathrm{\Delta }}(Y)={\widehat{F}}_{{\mathrm{\Delta }}_{\overline{D}}}^{cc}(Y)\widehat{P}(D=0)+{\widehat{F}}_{{\mathrm{\Delta }}_D}^{cc}(Y)\widehat{P}(D=1),$$

where superscript cc denotes estimation in the case-control sample and D and D̄ subscripts denote case and control subsets.

We use a modified bootstrapping procedure for case-control data. To reproduce the variability in the cohort from which the case-control study is sampled, we first sample $N_D^{\ast }~\mathit{Bin}(N,\widehat{P}(D=1))$ and set $N_{\overline{D}}^{\ast }=N-N_D^{\ast }$. Next we sample $n_D^{\ast }=f·N_D^{\ast }$ cases and $n_{\overline{D}}^{\ast }=k·n_D^{\ast }$ controls from the subjects in the case-control study. The estimation procedure is then performed in each bootstrap sample and quantiles of the bootstrap distribution are used to characterize uncertainty.

Case-control sampling stratified on treatment assignment can also be accommodated. Here we assume a cohort with (N_D0,N_D̄0,N_D1,N_D̄1) subjects in each D×T stratum. The case-control sample consists of n_D0 = f₀ · N_D0 and n_D1 = f₁ · N_D1 cases for fixed proportions f₀ and f₁ in the two treatment groups, and n_D̄0 = k₀ · n_D0 and n_D̄1 = k₁ · n_D1 controls for fixed control:case ratios k₀ and k₁. Assume that estimates of P(D = 1|T = 0), P(D = 1|T = 1), and P(T = 1) are available from the cohort. A similar identity can be exploited for estimation:

$$\text{logit}P(D=1\mid T,Y)=\text{logit}P(D=1\mid T,Y,S=1)+\text{logit}P(D=1\mid T)-\text{logit}P(D=1\mid T,S=1)$$

The distribution of Δ(Y) combines empirical CDFs from the four D×T strata:

$${\widehat{F}}_{\mathrm{\Delta }}(Y)={\widehat{F}}_{{\mathrm{\Delta }}_{\overline{D}0}}^{cc}(Y)\widehat{P}(D=0,T=0)+{\widehat{F}}_{{\mathrm{\Delta }}_{{\overline{D}}_1}}^{cc}(Y)\widehat{P}(D=0,T=1)+{\widehat{F}}_{{\mathrm{\Delta }}_{D0}}^{cc}(Y)\widehat{P}(D=1,T=0)+{\widehat{F}}_{{\mathrm{\Delta }}_{D1}}^{cc}(Y)\widehat{P}(D=1,T=1).$$

Bootstrapping is implemented by first sampling $N_1^{\ast }~\mathit{Bin}(N,P(T=1))(N_0^{\ast }=N-N_1^{\ast }),N_{D0}^{\ast }~\mathit{Bin}(N_0,\widehat{P}(D=1\mid T=0))$, and $N_{D1}^{\ast }~\mathit{Bin}(N_1,\widehat{P}(D=1\mid T=1))$ where $N_t^{\ast }=N_{Dt}^{\ast }+N_{\overline{D}t}^{\ast }$. The stratified case-control sample is then sampled from the case and control subsets.

For calibration assessment, we plot observed and predicted risks and treatment effects as described in Section 4.5, where all are corrected for the biased sampling as described above. We also implement a variation on the Hosmer-Lemeshow test applied to case-control data (expression (7) of Huang and Pepe (2010a)).

7 Discussion

This paper proposes a statistical framework for evaluating a candidate treatment selection marker and for comparing two markers. Estimation and inference techniques are described for the setting where the marker or markers are measured on all or a treatment-stratified case-control sample of participants in a randomized, controlled trial. An R software package was developed which implements these methods. Developing a solid framework for evaluating and comparing markers is fundamental for accomplishing more sophisticated tasks such as combining markers, accounting for covariates, and assessing the improvement in performance associated with adding a new marker to a set of established markers.

Our approach to marker evaluation also applies when the marker is discrete. In addition, it can be applied when there are multiple markers and interest lies in evaluating their combination; Δ(Y)=P(D=1|T =0,Y)− P(D=1|T =1,Y) is the combination of interest and the measures described here can be used to summarize the performance of this combination.

This work extends existing approaches for evaluating markers for risk prediction (see Pepe and Janes (2012), Huang et al. (2007), Gu and Pepe (2009)). It also unifies existing methodology for evaluating treatment selection markers. In particular, our preferred marker performance measure has been advocated by Song and Pepe (2004), Brinkley et al. (2010), Janes et al. (2011), Gunter et al. (2011), Qian and Murphy (2011), McKeague and Qian (2013), Zhang et al. (2012).

There are challenges with making inference about the performance measures we propose, similar to problems that have been identified with measures of risk prediction model performance including the area under the ROC curve (Vickers et al. (2011), Pepe et al. (2011), Seshan et al. (2012), Demler et al. (2012)), the integrated discrimination index (Kerr et al. (2011)), and the net reclassification index (Kerr et al. (2013)). The problems may arise when the sample size is modest and marker performance is weak. In particular for the Oncotype DX example, given that the marker is weak and the primary study evaluating its performance by Albain et al. (2010) included just 367 women, our simulation results suggest that the resultant estimate of Θ is likely an over-estimate and that the confidence interval may be conservative. For this reason, we propose testing for non-null marker performance prior to estimating the magnitude of performance. This approach performed reasonably well in our simulation studies, but improved approaches to inference, for the treatment selection as well as risk prediction problem, merit investigation.

The methods described here can and should be extended to accommodate other types of outcomes. Extension to continuous or count outcomes is straight-forward. Specifically, after replacing P(D = 1) with E(D) and using a risk model appropriate to the scale of the outcome, e.g. a linear or log-linear model for a continuous outcome, the analysis proceeds as above. The conceptual framework also applies to time-to-event outcomes, with the task being to predict risk of the outcome by a specified landmark time.

The methods may also be generalized to an observational study setting, or to a setting where data on the two treatments come from two different studies– perhaps historical data are paired with a single-arm trial of T = 1. However the usual concerns about measured and unmeasured confounding in estimating the treatment effect apply. In this setting an analyst would be well-advised to stratify on variables that are potentially associated with treatment provision and outcome. More generally, methods for adjusting for covariates in the evaluation of marker performance warrant further research.

8 Appendix

8.1 Simulation Studies

This section describes a small-scale simulation study that was performed to evaluate the statistical performance of our methods. Data were simulated to reflect the breast cancer RCT example, with T an indicator of chemotherapy in addition to tamoxifen, randomly assigned to half of study participants. Rates of 5-year breast cancer recurrence or death (D) were set to 21% and 24% with and without chemotherapy, respectively, as in SWOG SS8814 (Albain et al. (2010)). We explored the performance of the methods for a weak marker and a strong marker, both of which relate to D via the linear logistic model (1). The weak marker, Y₁, mimics the performance of the Oncotype-DX recurrence score as seen in (Albain et al. (2010)); ${\sqrt{Y}}_1$ is normally distributed with mean 4.8 and standard deviation 1.8. The strong marker, Y₂, follows a standard normal distribution. We used the following procedure to simulate data. We denote the potential outcomes with and without treatment by D(1) and D(0). We specified models for P(D(0),D(1)|Y_j), j = 1,2 that induce marginal linear logistic models as in (1). Specifically, we assumed

$$\begin{array}{l}\text{logit}P(D(0)=1\mid Y_i)={\beta }_0+{\beta }_2{Y}_j\\ \text{logit}P(D(1)=1\mid Y_i)={\beta }_0+{\beta }_1+({\beta }_2+{\beta }_3)Y_j\\ P(D(0)=0,D(1)=1\mid Y_2)=P(D(0)=0\mid Y_2)·P(D(1)=1\mid Y_2)\\ P(D(0)=0,D(1)=1\mid Y_1)=min(k·P(D(0)=1\mid Y_1)·P(D(1)=1\mid Y_1),\\ P(D(0)=1\mid Y_1),P(D(1)=1\mid Y_1)),\end{array}$$ (1a)

where k ensures that

$$\int P(D(0)=0,D(1)=1\mid Y_1)dF(Y_1)=\int P(D(0)=0,D(1)=1\mid Y_2)dF(Y_2)$$

and

$$\sqrt{Y_1}~\mathrm{N}(4.8,1.8)\text{and}{Y}_2~\mathrm{N}(0,1).$$ (2a)

These models fully specify the joint distribution of (D(0),D(1)) given Y_j, j = 1, 2. Note that our measures and estimators depend only on the marginal distributions P(D(0) = 1|Y_j) and P(D(1) = 1|Y_j), j = 1, 2, and hence are invariant to the choice of joint distribution. Next, we used Bayes Theorem to calculate P(Y_j|D(0),D(1)), j =1, 2. We first simulated pairs of potential outcomes (D(0),D(1)) from the multi-nomial distribution induced by (1a) and (2a). Then we simulated independent Y₁ and Y₂ from P(Y_j|D(0),D(1)), j = 1, 2. Treatment assignment, T, was generated independent of potential outcomes and marker values. The observed outcome D was defined as D = D(1)T +D(0)(1−T). True values for the marker performance measures were calculated as the average parameter estimates, using the true risk function (1), across 10 very large datasets (N = 20,000, 000).

We explore the bias and variance of the parameter estimates and false-coverage probabilities of the bootstrap percentile confidence intervals (CIs) for sample sizes ranging from N = 250 to N = 5, 000. A total of 5,000 simulations were performed for each sample size. To explore the impact of our proposed pre-testing strategy, whereby the parameters are not estimated if H₀ : Θ = 0 is not rejected, we evaluate the parameter estimates and confidence intervals marginally and conditionally. Marginal means of parameter estimates include all estimates regardless of H₀ rejection, and conditional means are computed only among datasets where H₀ is rejected. The following probabilities of false coverage of nominal 95% CIs are evaluated: 1. Marginal probability of false coverage, where CIs are calculated regardless of H₀ rejection; 2. Conditional probability of false coverage, computed only among datasets where H₀ is rejected; and 3. Probability of rejecting H₀ and the CI not covering the true value, termed the “false conclusion probability” (Benjamini and Yekuteili (2005)).

8.1.1 Strong Marker

The results for the strong marker are contained in Tables A.1, A.2, and A.3. For this marker, we see that the estimates and CIs have uniformly good performance. Marginal bias is small and false coverage is near nominal; the pre-testing has no impact because of the 100% power to reject H₀ for this marker. There is minimal increase in variance due to using empirical vs. model-based estimators.

8.1.2 Weak Marker

The results for the weak marker are contained in Tables A.4, A.5, and A.6. With N = 250 or 500, conditional on rejecting H₀ the bias in parameter estimates and false-coverage of CIs can be substantial; however rejecting H₀ is unlikely with power 21% or 36%. Marginally, mean parameter estimates are substantially closer to their true values and false-coverage probabilities are generally near-nominal. False conclusion probabilities are less than nominal but sometimes substantially below 0.05 indicating over-conservatism. With N = 1,000 or 5,000, conditional and marginal bias is generally small and false-coverage probabilities are near or below nominal. False conclusion probabilities continue to be less than nominal. This example demonstrates that, for markers with near-null performance, substantial sample sizes are required for accurate inference. We also see that with smaller sample sizes there can be a substantial increase in variability associated with use of empirical vs. model-based estimators.

8.2 Software

We developed a package in the open-source software R called TreatmentSelection that implements our methods for evaluating individual markers and for comparing markers. The software is available at http://labs.fhcrc.org/janes/index.html. The following functions are included:

• trtsel creates a treatment selection object

• eval.trtsel evaluates a treatment selection object, producing estimates and confidence intervals for the summary measures described in Section 4.3

• plot.trtsel plots a treatment selection object, producing risk curves and the treatment effect curve described in Section 4.2

• calibrate.trtsel assesses the calibration of a fitted risk model and treatment effect model using methods described in Section 4.5

• compare.trtsel compares two markers using methods described in Section 5

Case-control and treatment-stratified case-control sampling are accommodated.

Here we illustrate use of the code by showing how the results shown in Figures 1–3 and Table 1 of the main text are produced. First we load the data using the following commands.

> library(TreatmentSelection)
> data(tsdata)
> tsdata[1:10,]
    trt  event      Y1      Y2
1    1     1  39.9120  -0.8535
2    1     0   6.6820  0.2905
3    1     0   6.5820  0.0800
4    0     0   1.3581  1.1925
5    0     0   7.6820  -0.2070
6    0     0  41.1720  -0.0880
7    1     0  19.4920  0.1670
8    1     1  20.8220  -1.0485
9    0     0   6.9620  -0.2435
10   0     0   2.5020  0.2030

Treatment selection objects are created and displayed for Y₁ and Y₂ using the commands

> trtsel.Y1 <- trtsel(event = “event”, trt = “trt”, marker = “Y1”,
   data = tsdata, study.design=”randomized cohort”
)
> trtsel.Y1
Study design: randomized cohort
Model Fit:
  Link function: logit
  Coefficients:
              Estimate    Std. Error      z value       Pr(>|z|)
(Intercept)  -2.51814383  0.235642511  -10.686288  1.179991e-26
trt          0.48938620  0.311762857    1.569739  1.164759e-01
marker      0.04760056  0.006453791    7.375597  1.636104e-13
trt:marker   -0.02318881  0.008324063   -2.785756  5.340300e-03
Derived Data: (first ten rows)
    event  trt   marker   fittedrisk.t0  fittedrisk.t1       trt.effect   marker.neg
1      1   1  39.9120   0.35016583   0.2583742  0.0917916549           0
2      0   1   6.6820   0.09974358   0.1340472  -0.0343036269           1
3      0   1   6.5820   0.09931697   0.1337641  -0.0344471266           1
4      0   0   1.3581   0.07918316   0.1196652  -0.0404820847           1
5      0   0   7.6820   0.10410005   0.1369063  -0.0328062456           1
6      0   0  41.1720   0.36393311   0.2643117   0.0996213622           0
7      0   1  19.4920   0.16933976   0.1746644  -0.0053246137           1
8      1   1  20.8220   0.17843231   0.1793943  -0.0009620341           1
9      0   0   6.9620   0.10094678   0.1348426  -0.0338958439           1
10     0   0   2.5020   0.08324538   0.1226384  -0.0393929781           1
> trtsel.Y2 <- trtsel(event = “event”, trt = “trt”, marker = “Y2”,
   data = tsdata, study.design=”randomized cohort”
)
> trtsel.Y2
Study design: randomized cohort
Model Fit:
  Link function: logit
  Coefficients:
             Estimate    Std. Error       z value       Pr(>|z|)
(Intercept)  -1.2107912   0.1131642    -10.699416  1.024216e-26
trt         -0.5169008   0.1863643     -2.773604  5.543912e-03
marker      0.5779172   0.1148643     5.031305  4.871514e-07
trt:marker   -2.0455033   0.2064547     -9.907756  3.851994e-23
Derived Data: (first ten rows)
   event  trt   marker    fittedrisk.t0   fittedrisk.t1       trt.effect  marker.neg
1     1  1   -0.8535    0.1539379   0.38340813  -0.229470242         1
2     0  1   0.2905    0.2605896   0.10395563   0.156633982          0
3     0  1   0.0800    0.2378401   0.13644937   0.101390712          0
4     0  0   1.1925    0.3724723   0.02995087   0.342521474          0
5     0  0   -0.2070    0.2090899   0.19405065   0.015039232          0
6     0  0   -0.0880    0.2206903   0.16818515   0.052505186          0
7     0  1   0.1670    0.2470740   0.12209072   0.124983277         0
8     1  1   -1.0485    0.1398258   0.45290799   -0.313082172         1
9     0  0   -0.2435    0.2056229   0.20256576   0.003057187          0
10    0  0    0.2030    0.2509647   0.11653995   0.134424710          0

The descriptives shown in Figure 1 are produced using

> plot.trtsel(trtsel.Y1, main = “Y1: Oncotype-DX-like marker”,
   bootstraps = 500,
   trt.names=c(“chemo.”,”no chemo.”
))
> plot.trtsel(trtsel.Y2, main = “Y2: Strong marker”,
   bootstraps = 500,
   trt.names=c(“chemo.”,”no chemo.”
))

Calibration is assessed and displayed as shown in Figure 3 using

> cali.Y1 <- calibrate.trtsel(trtsel.Y1)
> cali.Y1
  Hosmer - Lemeshow test for model calibration
 ---------------------------------------------------------
   No Treatment (trt = 0):
    Test Statistic = 4.496, DF = 8, p value = 0.8098813
   Treated (trt = 1):
    Test Statistic = 4.986, DF = 8, p value = 0.7591213
> cali.Y2 <- calibrate.trtsel(trtsel.Y2)
> cali.Y2
  Hosmer - Lemeshow test for model calibration
 ----------------------------------------------------------
   No Treatment (trt = 0):
     Test Statistic = 8.896, DF = 8, p value = 0.3511235
   Treated (trt = 1):
    Test Statistic = 2.868, DF = 8, p value = 0.9423597
calibrate.trtsel(trtsel.Y1, plot.type = “risk.t0”)
calibrate.trtsel(trtsel.Y2, plot.type = “risk.t0”)
calibrate.trtsel(trtsel.Y1, plot.type = “risk.t1”)
calibrate.trtsel(trtsel.Y2, plot.type = “risk.t1’)
calibrate.trtsel(trtsel.Y1, plot.type = “treatment effect’)
calibrate.trtsel(trtsel.Y2, plot.type = “treatment effect”)

The summary measure estimates and confidence intervals shown in Table 1 are obtained by

> eval.Y1 <- eval.trtsel(trtsel.Y1, bootstraps = 500)
> eval.Y1
  Hypothesis test:
 ----------------------
  H0: No marker-by-treatment interaction
                                 P value = 0.00534
                                 Z statistic = -2.786
  Summary Measure Estimates (with 95% confidence intervals)
 -----------------------------------------------------------------------------
  Decrease in event rate under marker-based treatment (Theta)
    Empirical:    0.013 (-0.01,0.044)
    Model Based: 0.01 (0,0.038)
  Proportion marker negative:
   0.461 (0,0.717)
  Proportion marker positive:
   0.539 (0.283,1)
  Average benefit of no treatment among marker-negatives (B.neg)
    Empirical:    0.029 (-0.07,0.075)
    Model Based: 0.023 (0,0.059)
  Average benefit of treatment among marker-positives (B.pos)
    Empirical:    0.089 (0.014,0.15)
    Model Based:  0.098 (0.04,0.146)
  Variance in estimated treatment effect:
  0.007 (0.001,0.017)
  Total Gain:
  0.066 (0.026,0.1)
  Marker positivity threshold: 21.082
 Event Rates:
 -----------------------
            Treat all    Treat None    Marker-based Treatment
 Empirical:    0.251         0.217         0.204
           (0.210,0.291)  (0.182,0.251)    (0.171,0.241)
 Model Based:  0.257       0.214           0.204
           (0.217,0.295) (0.179,0.248)     (0.169,0.232)
> eval.Y2 <- eval.trtsel(trtsel.Y2, bootstraps = 500)
> eval.Y2
 Hypothesis test:
 -----------------------
 H0: No marker-by-treatment interaction
                                P value = 0
                                Z statistic = -9.908
 Summary Measure Estimates (with 95% confidence intervals)
 ------------------------------------------------------------------------------
 Decrease in event rate under marker-based treatment (Theta)
   Empirical:   0.09 (0.064,0.122)
   Model Based: 0.099 (0.074,0.128)
 Proportion marker negative:
  0.377 (0.306,0.467)
 Proportion marker positive:
  0.623 (0.533,0.694)
 Average benefit of no treatment among marker-negatives (B.neg)
    Empirical:    0.238 (0.173,0.304)
    Model Based: 0.262 (0.211,0.315)
 Average benefit of treatment among marker-positives (B.pos)
    Empirical:    0.203 (0.157,0.266)
    Model Based: 0.211 (0.171,0.259)
 Variance in estimated treatment effect:
   0.08 (0.057,0.108)
 Total Gain:
   0.224 (0.187,0.262)
 Marker positivity threshold: -0.258
 Event Rates:
 --------------------------
            Treat all     Treat None        Marker-based Treatment
 Empirical:     0.251        0.217              0.128
           (0.215,0.290)  (0.186,0.252)        (0.096,0.155)
 Model Based:  0.245         0.212             0.113
           (0.210,0.282)  (0.180,0.245)        (0.090,0.135)

The markers are compared based on summary measures, and visually (as in Figure 2) using

> mycompare <- compare.trtsel(trtsel1 = trtsel.Y1,
                          trtsel2 = trtsel.Y2,
                          bootstraps = 500,
                          plot = TRUE,
                          main=””,
                          marker.names=c(“Y1”,”Y2”))
> mycompare
                    Summary Measure Estimates
                   (with 95% confidence intervals)
               marker 1    |     marker 2   |   difference  (p-value)
 ---------------------------------------------------------------------------------------------
Decrease in event rate under marker-based treatment (Theta)
  Empirical:    0.013      |     0.090     |       -0.076           (< 0.002)
            (-0.007,0.049)  | (0.062,0.124)  |   (-0.111,-0.043)
  Model Based:   0.010     |    0.099      |       -0.088           (< 0.002)
            (0.000,0.039)  | (0.070,0.130)  |    (-0.112,-0.058)
  Proportion marker negative:
                0.461     |    0.377    |       0.084            (0.664)
            (0.000,0.707)  | (0.305,0.471) |   (-0.360,0.258)
Average benefit of no treatment among marker-negatives (B.neg)
  Empirical:      0.029     |    0.238     |     -0.209       (< 0.002)
            (-0.071,0.082)  |  (0.176,0.307)  |  (-0.331,-0.132)
  Model Based:    0.023     |     0.262       |     -0.239        (< 0.002)
             (0.000,0.061)  |  (0.205,0.308)   |  (-0.288,-0.169)
Average benefit of treatment among marker-positives (B.pos)
  Empirical:      0.089        |     0.203     |       -0.114     (0.002)
             (0.007,0.161)    | (0.162,0.266)   |  (-0.201,-0.035)
  Model Based:    0.098        |     0.211     |       -0.113     (< 0.002)
             (0.042,0.162)     | (0.175,0.259)   |    (-0.177,-0.038)
Variance in estimated treatment effect:
               0.007        |     0.080     |         -0.073      (< 0.002)
           (0.001,0.021)     | (0.054,0.110)   |    (-0.103,-0.043)
Total Gain:
              0.066        |     0.224      |       -0.158       (< 0.002)
           (0.027,0.111)     | (0.181,0.266)   |    (-0.214,-0.091)

If instead the dataset with D, Y₁, and T measurements consisted of a case-control sample from within an RCT, given estimates of P(T = 1) and P(D = 1) from the trial cohort (call these “Rand.frac” and “Risk.cohort”) and the size of the trial cohort, N, the only modification would be in creating the treatment selection object:

cctrtsel.Y1 <- trtsel(event = “event”, treatment = “trt”, marker = “Y1”,
   data = tsdata, cohort.attributes = c(N, Rand.frac, Risk.cohort
),
   study.design=”nested case-control”)

Table A.1.

Mean parameter estimates for the strong marker. For Θ, B_neg, and B_pos, results are shown for both empirical and model-based estimators. The probability of rejecting H₀ : Θ = 0 is shown along with marginal and conditional means of parameter estimates. Marginal means include all parameter estimates, regardless of H₀ rejection. Conditional means are only computed among trials for which H₀ was rejected. True parameter values are shown in parentheses.

	N	Prob. Reject H0	Θ (0.110)		Pneg (0.379)	Bneg (0.291)		Bpos (0.228)		VΔ (0.094)	TG (0.245)
			Mod.	Emp.		Mod.	Emp.	Mod.	Emp.
Marginal	250	1	0.113	0.112	0.380	0.295	0.293	0.230	0.229	0.097	0.246
	500	1	0.112	0.112	0.380	0.293	0.293	0.230	0.230	0.096	0.246
	1000	1	0.111	0.111	0.379	0.292	0.292	0.229	0.229	0.095	0.246
	5000	1	0.110	0.110	0.379	0.291	0.291	0.228	0.228	0.094	0.246
Conditional	250	1	0.113	0.112	0.380	0.295	0.293	0.230	0.229	0.097	0.246
	500	1	0.112	0.112	0.380	0.293	0.293	0.230	0.230	0.096	0.246
	1000	1	0.111	0.111	0.379	0.292	0.292	0.229	0.229	0.095	0.246
	5000	1	0.110	0.110	0.379	0.291	0.291	0.228	0.228	0.094	0.246

Table A.2.

False coverage results for the strong marker. For Θ, B_neg, and B_pos, results are shown for both empirical and model-based estimators. Percentile bootstrap confidence intervals (CIs) are evaluated using: Marginal false coverage, the proportion of CIs that do not cover the true value regardless of H₀ rejection; conditional false coverage, the proportion of CIs that do not cover the true value among datasets where H₀ is rejected; and false conclusion probability, the proportion of datasets where H₀ is rejected and the CI does not cover the true value. The probability of rejecting H₀ : Θ = 0 is also shown.

	N	Prob. Reject H0	Θ		Pneg	Bneg		Bpos		VΔ	TG
			Mod.	Emp.		Mod.	Emp.	Mod.	Emp.
Marg. false cov.	250	1	0.059	0.045	0.052	0.056	0.030	0.051	0.034	0.056	0.056
	500	1	0.054	0.043	0.053	0.050	0.031	0.050	0.038	0.054	0.053
	1000	1	0.056	0.055	0.051	0.049	0.044	0.047	0.044	0.055	0.055
	5000	1	0.055	0.051	0.055	0.056	0.048	0.052	0.049	0.053	0.056
Cond. false cov.	250	1	0.059	0.045	0.052	0.056	0.030	0.051	0.034	0.056	0.056
	500	1	0.054	0.043	0.053	0.050	0.031	0.050	0.038	0.054	0.053
	1000	1	0.056	0.055	0.051	0.049	0.044	0.047	0.044	0.055	0.055
	5000	1	0.055	0.051	0.055	0.056	0.048	0.052	0.049	0.053	0.056
False concl.	250	1	0.059	0.045	0.052	0.056	0.030	0.051	0.034	0.056	0.056
	500	1	0.054	0.043	0.053	0.050	0.031	0.050	0.038	0.054	0.053
	1000	1	0.056	0.055	0.051	0.049	0.044	0.047	0.044	0.055	0.055
	5000	1	0.055	0.051	0.055	0.056	0.048	0.052	0.049	0.053	0.056

Table A.3.

Empirical standard deviations of parameter estimates for the strong marker. For Θ, B_neg, and B_pos, results are shown for both empirical and model-based estimators. Calculations are done marginally; all parameter estimates are included regardless of H₀ rejection. True parameter values are shown in parentheses.

N	Θ (0.110)		Pneg (0.379)	Bneg (0.291)		Bpos (0.228)		VΔ (0.094)	TG (0.245)
	Mod.	Emp.		Mod.	Emp.	Mod.	Emp.
250	0.031	0.035	0.072	0.057	0.072	0.045	0.05	0.03	0.042
500	0.022	0.024	0.051	0.039	0.048	0.031	0.036	0.021	0.029
1000	0.016	0.018	0.036	0.028	0.035	0.022	0.025	0.015	0.021
5000	0.007	0.008	0.016	0.012	0.015	0.01	0.011	0.007	0.009

Table A.4.

Mean parameter estimates for the weak marker. For Θ, B_neg, and B_pos, results are shown for both empirical and model-based estimators. The probability of rejecting H₀ : Θ = 0 is shown along with marginal and conditional means of parameter estimates. Marginal means include all parameter estimates, regardless of H₀ rejection. Conditional means are only computed among trials for which H₀ was rejected. True parameter values are shown in parentheses.

	N	Prob. Reject H0	Θ (0.0095)		Pneg (0.439)	Bneg (0.022)		Bpos (0.073)		VΔ (0.005)	TG (0.050)
			Mod.	Emp.		Mod.	Emp.	Mod.	Emp.
Marginal	250	0.217	0.022	0.022	0.423	0.036	0.036	0.090	0.090	0.009	0.060
	500	0.364	0.016	0.015	0.410	0.027	0.026	0.080	0.080	0.007	0.055
	1000	0.63	0.013	0.013	0.405	0.024	0.024	0.076	0.076	0.006	0.054
	5000	0.999	0.010	0.010	0.426	0.022	0.022	0.073	0.073	0.005	0.053
Conditional	250	0.217	0.042	0.041	0.547	0.071	0.069	0.159	0.154	0.022	0.112
	500	0.364	0.026	0.025	0.509	0.046	0.044	0.117	0.117	0.013	0.084
	1000	0.630	0.017	0.017	0.473	0.032	0.032	0.091	0.090	0.008	0.066
	5000	0.999	0.010	0.010	0.426	0.022	0.022	0.073	0.073	0.005	0.053

Table A.5.

False coverage results for the weak marker. For Θ, B_neg, and B_pos, results are shown for both empirical and model-based estimators. Percentile bootstrap confidence intervals (CIs) are evaluated using: Marginal false coverage, the proportion of CIs that do not cover the true value regardless of H₀ rejection; conditional false coverage, the proportion of CIs that do not cover the true value among datasets where H₀ is rejected; and false conclusion probability, the proportion of datasets where H₀ is rejected and the CI does not cover the true value. The probability of rejecting H₀ : Θ = 0 is also shown.

	N	Prob. Reject H0	Θ		Pneg	Bneg		Bpos		VΔ	TG
			Mod.	Emp.		Mod.	Emp.	Mod.	Emp.
Marg. false cov.	250	0.217	0.054	0.030	0.059	0.053	0.023	0.063	0.026	0.034	0.035
	500	0.364	0.043	0.021	0.052	0.034	0.014	0.048	0.022	0.029	0.030
	1000	0.630	0.050	0.026	0.055	0.034	0.015	0.047	0.018	0.052	0.051
	5000	0.999	0.057	0.037	0.058	0.058	0.020	0.058	0.036	0.060	0.058
Cond. false cov.	250	0.217	0.162	0.089	0.102	0.190	0.074	0.248	0.088	0.158	0.161
	500	0.364	0.083	0.043	0.065	0.086	0.032	0.121	0.057	0.081	0.083
	1000	0.630	0.045	0.028	0.043	0.047	0.023	0.061	0.028	0.046	0.044
	5000	0.999	0.056	0.037	0.058	0.057	0.020	0.057	0.035	0.058	0.057
Marg. false concl.	250	0.217	0.035	0.019	0.022	0.041	0.016	0.054	0.019	0.034	0.035
	500	0.364	0.030	0.016	0.024	0.031	0.012	0.044	0.021	0.029	0.030
	1000	0.630	0.028	0.018	0.027	0.030	0.014	0.038	0.018	0.029	0.028
	5000	0.999	0.056	0.037	0.058	0.057	0.020	0.057	0.035	0.058	0.057

Table A.6.

Empirical standard deviations of parameter estimates for the weak marker. For Θ, B_neg, and B_pos, results are shown for both empirical and model-based estimators. Calculations are done marginally; all parameter estimates are included regardless of H₀ rejection. True parameter values are shown in parentheses.

N	Θ (0.0095)		Pneg (0.439)	Bneg (0.022)		Bpos (0.073)		VΔ (0.005)	TG (0.050)
	Mod.	Emp.		Mod.	Emp.	Mod.	Emp.
250	0.025	0.029	0.309	0.032	0.09	0.051	0.083	0.009	0.037
500	0.017	0.02	0.27	0.023	0.061	0.037	0.065	0.006	0.028
1000	0.012	0.014	0.22	0.017	0.045	0.027	0.033	0.004	0.021
5000	0.005	0.007	0.106	0.008	0.013	0.013	0.015	0.002	0.01