Efficient Bayesian mixed model analysis increases association power in large cohorts

Abstract

Linear mixed models are a powerful statistical tool for identifying genetic associations and avoiding confounding. However, existing methods are computationally intractable in large cohorts, and may not optimize power. All existing methods require time cost O(MN²) (where N = #samples and M = #SNPs) and implicitly assume an infinitesimal genetic architecture in which effect sizes are normally distributed, which can limit power. Here, we present a far more efficient mixed model association method, BOLT-LMM, which requires only a small number of O(MN)-time iterations and increases power by modeling more realistic, non-infinitesimal genetic architectures via a Bayesian mixture prior on marker effect sizes. We applied BOLT-LMM to nine quantitative traits in 23,294 samples from the Women’s Genome Health Study (WGHS) and observed significant increases in power, consistent with simulations. Theory and simulations show that the boost in power increases with cohort size, making BOLT-LMM appealing for GWAS in large cohorts.

Linear mixed models are emerging as the method of choice for association testing in genome-wide association studies (GWAS) because they account for both population stratification and cryptic relatedness and achieve increased statistical power by jointly modeling all genotyped markers^1–12. However, existing mixed model methods still have limitations. First, mixed model analysis is computationally expensive. Despite a series of recent algorithmic advances, current algorithms require either O(MN²) or O(M²N) total running time, where M is the number of markers and N is the sample size. This cost is becoming prohibitive for large cohorts, forcing existing methods to subsample the markers so that M<N (ref.⁵). Second, current mixed model methods fall short of achieving maximal statistical power owing to suboptimal modeling assumptions regarding the genetic architectures underlying phenotypes. The standard linear mixed model implicitly assumes that all variants are causal with small effect sizes drawn from independent Gaussian distributions—the “infinitesimal model”—whereas in reality, complex traits are estimated to have roughly a few thousand causal loci^13,14.

Methodologically, efforts to more accurately model non-infinitesimal genetic architectures have followed two general thrusts. One approach is to apply the standard infinitesimal mixed model but adapt the input data. For example, large-effect loci can be explicitly identified and conditioned out as fixed effects⁷, or the mixed model can be applied to only a selected subset of markers^9,11,15,16. A more flexible alternative approach is to adapt the mixed model itself by taking a Bayesian perspective and modeling SNP effects with non-Gaussian prior distributions that better accommodate both small- and large-effect loci. Such methods were pioneered in livestock genetics to improve prediction of genetic values¹⁷ and have been extensively developed in the plant and animal breeding literature for the purpose of genomic selection¹⁸. These techniques are of interest in the association testing setting because models that improve prediction should in theory enable corresponding improvements in association power (via conditioning on other associated loci when testing a candidate marker^9,12). Here, we present an algorithm that performs mixed model analysis in a small number of O(MN)-time iterations and increases power by modeling non-infinitesimal genetic architectures. Our algorithm fits a Gaussian mixture model of SNP effects¹⁹, using a fast variational approximation^20–22 to compute approximate phenotypic residuals, and tests the residuals for association with candidate markers via a retrospective score statistic²³ that provides a bridge between Bayesian modeling for phenotype prediction and the frequentist association testing framework. We calibrate our statistic using an approach based on the recently developed LD Score regression technique²⁴. The entire procedure operates directly on raw genotypes stored compactly in memory and does not require computing or storing a genetic relationship matrix. In the special case of the infinitesimal model, we achieve results equivalent to existing methods at dramatically reduced time and memory cost.

We provide an efficient software implementation of our algorithm, BOLT-LMM, and demonstrate its computational efficiency on simulated data sets of up to 480,000 individuals. Our simulations also show that BOLT-LMM achieves increased association power over standard infinitesimal mixed model analysis of traits driven by a few thousand causal SNPs. We applied BOLT-LMM to perform mixed model analysis of nine quantitative traits in 23,294 samples from the Women’s Genome Health Study (WGHS)²⁵ and observed increased association power equivalent to up to 10% increase in effective sample size. We demonstrate through theory and simulations that the power boost increases with cohort size, making BOLT-LMM a promising approach for large-scale GWAS.

Results

Overview of Methods

The BOLT-LMM algorithm consists of four main steps, each of which require a small number of O(MN)-time iterations. These steps are: (1a) Estimate variance parameters; (1b) Compute infinitesimal mixed model association statistics (denoted BOLT-LMM-inf); (2a) Estimate Gaussian mixture parameters; (2b) Compute Gaussian mixture model association statistics (BOLT-LMM). Step 1a computes results nearly identical to standard variance components analysis but applies a stochastic approximation algorithm^26,27 that reduces time and memory cost by circumventing spectral decomposition, which is expensive for large sample sizes. Instead, the approximation algorithm only requires solving linear systems of mixed model equations, which can be accomplished efficiently using conjugate gradient iteration^28,29. Step 1b likewise circumvents spectral decomposition by introducing a new retrospective mixed model association statistic similar to GRAMMAR-Gamma¹⁰ and MASTOR²³, which we compute—up to a calibration constant—using only solutions to linear systems of equations. We estimate the calibration constant by computing and comparing the new statistic and the standard prospective mixed model statistic at a random subset of SNPs, which can likewise be accomplished efficiently using conjugate gradient iteration. This procedure is similar in spirit to GRAMMAR-Gamma calibration but requires only O(MN)-time iterations.

Steps 2a and 2b are Gaussian mixture parallels of steps 1a and 1b. BOLT-LMM’s non-infinitesimal model amounts to a generalization of the standard mixed model, which from a Bayesian perspective imposes a Gaussian prior distribution on SNP effect sizes. BOLT-LMM relaxes this assumption by using a mixture of two Gaussians as the prior, giving the model greater flexibility to accommodate large-effect SNPs while maintaining effective modeling of genome-wide effects (e.g., ancestry). Exact posterior inference is no longer tractable under the generalized model, so BOLT-LMM instead computes a variational approximation^20–22 that converges after a small number of O(MN)-time iterations. Step 2a applies this method within 5-fold cross-validation to estimate best-fit parameters for the prior distribution (taking into account variance parameters estimated in Step 1a) based on out-of-sample prediction accuracy. If the prediction accuracy of the best-fit Gaussian mixture model exceeds that of the infinitesimal model by at least a specified amount, Step 2b is then run to compute association statistics by testing each SNP against the residual phenotype obtained from the Gaussian mixture model and calibrating the test statistics against the results of Step 1b using LD Score regression²⁴. Otherwise, the BOLT-LMM association statistic is the same as BOLT-LMM-inf. Both Step 1b and Step 2b are performed using a leave-one-chromosome-out (LOCO) scheme to avoid proximal contamination^5,9,12. (The software also supports subdividing chromosomes into more segments; see Online Methods.) The key properties of BOLT-LMM regarding speed and modeling assumptions are compared to existing methods in Table 1.

Table 1.

Comparison of fast mixed model association methods that model all SNPs.

Methoda	Requires O(MN2) time	Avoids proximal contamination	Models non-infinitesimal genetic architecture
EMMAX [3]	X
FaST-LMM [5]	Xb	X
FaST-LMM-Select [9, 11, 15]	Xb	X	Xc
GEMMA [6]	X
GRAMMAR-Gamma [10]	Xd
GCTA-LOCO [12]	X	X
BOLT-LMM		X	X

^aFor methods that have been updated over multiple publications, we cite and list characteristics of the latest published version.

^bIf M<N, FaST-LMM and FaST-LMM-Select can complete in O(M²N) time.

^cFaST-LMM-Select models non-infinitesimal genetic architectures by restricting the mixed model to a subset of SNPs; a caveat of this approach is that it may incur susceptibility to confounding from stratification¹².

^dGRAMMAR-Gamma requires O(MN²) time for only the initial computation of the genetic relationship matrix but not for computing association test statistics. For a detailed breakdown of computational complexity per algorithmic step, see Table 1 of ref.¹².

Computational cost of BOLT-LMM versus existing methods

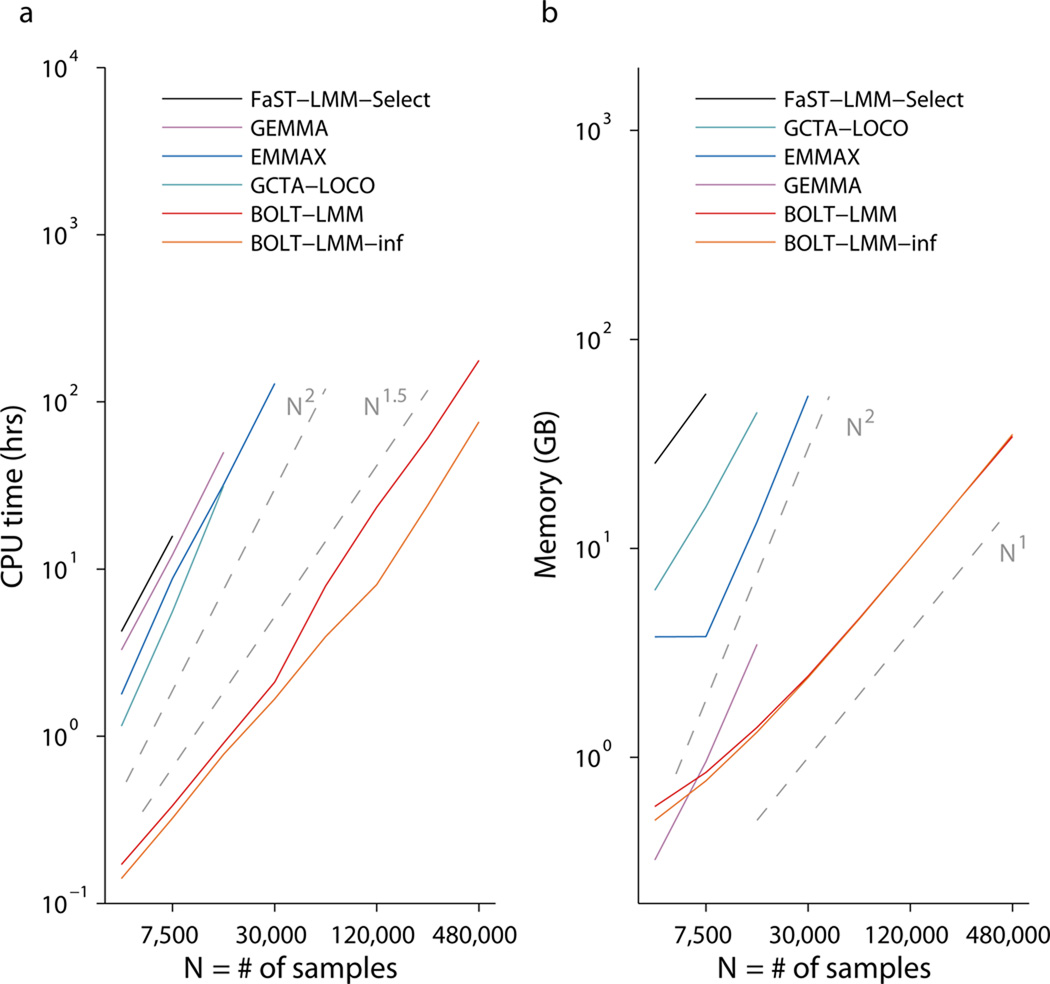
To analyze the computational performance of BOLT-LMM, we simulated data sets of sizes ranging from N=3,750 to 480,000 individuals and M=300,000 SNPs. We used genotypes from the WTCCC2 data set³⁰ analyzed in ref.¹², which contains 15,633 individuals of European ancestry, to form mosaic chromosomes, and we used a phenotype model in which 5,000 SNPs explained 20% of phenotypic variance (Supplementary Note).

We benchmarked BOLT-LMM against existing mixed model association methods, running each method for up to 10 days on machines with 96GB of memory. BOLT-LMM completed all analyses through N=480,000 individuals within these constraints, whereas previous methods could only analyze a maximum of N=7,500–30,000 individuals (Fig. 1 and Supplementary Table 1). All previous methods require O(MN²) running time (for M>N), whereas the running time of BOLT-LMM scales roughly with MN^1.5 (Fig. 1a and Supplementary Fig. 1a). We also observed substantial savings in memory use with BOLT-LMM (Fig. 1b and Supplementary Fig. 1b), which requires little more than the MN/4 bytes of memory needed to store raw genotypes (as in GenABEL software³¹).

Figure 1. Computational performance of mixed model association methods.

Log-log plots of (a) run time and (b) memory as a function of sample size (N). Slopes of the curves correspond to exponents of power-law scaling with N. Benchmarking was performed on simulated data sets in which each sample was generated as a mosaic of genotype data from 2 random “parents” from the WTCCC2 data set (N=15,633, M=360K) and phenotypes were simulated with M_causal=5,000 SNPs explaining h²_causal=0.2 of phenotypic variance. Reported run times are medians of five identical runs using one core of a 2.27 GHz Intel Xeon L5640 processor. We caution that running time comparisons may vary by a small constant factor as a function of computing environment. FaST-LMM-Select (resp. GCTA-LOCO, EMMAX) memory usage exceeded the 96GB available at N=15K (resp. 30K, 60K). GEMMA encountered a runtime error (segmentation fault) at N=30K. Software versions: FaST-LMM-Select, v2.07; GCTA-LOCO, v1.24; EMMAX, v20120210; GEMMA, v0.94. Numerical data are provided in Supplementary Table 1.

The running time of BOLT-LMM depends not only on the cost of matrix arithmetic, which scales linearly with M and N, but also the number of O(MN)-time iterations required for convergence, which empirically scales roughly as N^0.5 (Supplementary Fig. 1) and also varies with heritability, relatedness, and population structure (Supplementary Note and Supplementary Fig. 2). These observations apply both to the full Gaussian mixture modeling performed by BOLT-LMM and to the subset of the computation (Steps 1a and 1b) needed to compute BOLT-LMM-inf infinitesimal mixed model association statistics, which in our benchmarks required ≈40% of the full BOLT-LMM run time (Fig. 1a and Supplementary Fig. 1a). Our results show that even on very large data sets, BOLT-LMM is efficient enough to enable mixed model analysis using a Gaussian mixture prior, which we recommend because of its potential to increase power.

Power and false positive control of BOLT-LMM in simulations

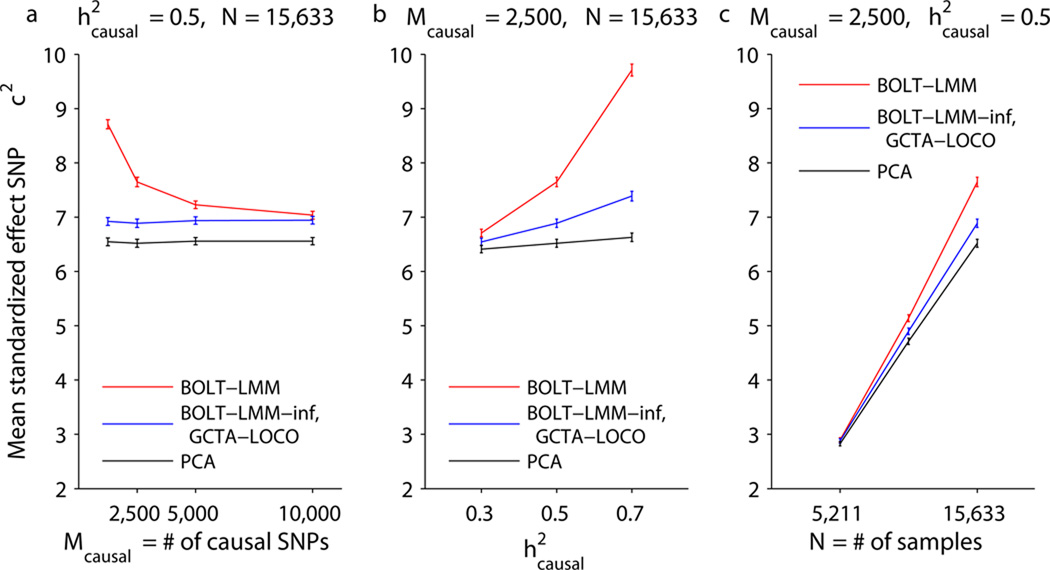
To assess the power of BOLT-LMM to detect associated loci, we performed additional simulations using real genotypes from the WTCCC2 data set, which is an ancestry-stratified sample containing both Northern and Southern European samples. We simulated phenotypes with 1,250–10,000 causal SNPs^13,14 explaining 50% of phenotypic variance and an additional 60 standardized effect SNPs explaining 2% of variance. We included the latter category of SNPs to allow direct power comparisons across different simulation setups, as the 60 standardized effect SNPs always explain the same total amount of variance regardless of other simulation parameters. We further introduced environmental differences in ancestry by including a phenotypic component aligned with the top principal component that explained an additional 1% of variance. (We note that principal component analysis is not part of BOLT-LMM; it is unnecessary to perform PCA when running mixed model association methods¹².) We chose causal SNPs randomly from the first halves of chromosomes, leaving the second halves of chromosomes to contain only non-causal SNPs (Supplementary Note).

We computed χ² association statistics using linear regression with 10 principal components (PCA)³², GCTA-LOCO¹², BOLT-LMM-inf, and BOLT-LMM. We were unable to test FaST-LMM-Select¹⁵ on this data set because of its memory requirements (Fig. 1). For each method, we computed means of its χ² statistics over standardized effect SNPs and compared these means across simulations involving different numbers of causal SNPs (Fig. 2a and Supplementary Table 2). We observed that BOLT-LMM achieved power gains by modeling non-infinitesimal architectures. For the sparsest genetic architecture (1,250 causal SNPs plus 60 standardized effect SNPs), we observed a 25% increase in mean BOLT-LMM χ² statistics at standardized effect SNPs compared to GCTA-LOCO and BOLT-LMM-inf infinitesimal mixed model χ² statistics. This metric is readily interpretable as corresponding to a 25% increase in effective sample size; for completeness, we also computed traditional power curves at two significance thresholds (Supplementary Fig. 3). The power gain of the Gaussian mixture model decreased with increasing numbers of causal SNPs (Fig. 2a). This behavior is expected because the advantage of the Gaussian mixture lies in its ability to more accurately model a small fraction of SNPs with larger effects amid a majority of SNPs with near-zero effects. Larger numbers of causal SNPs explaining a fixed proportion of variance result in smaller effect sizes per causal SNP, giving BOLT-LMM less opportunity for power gain. In contrast, all methods other than BOLT-LMM had performance independent of the number of causal SNPs, consistent with the fact that none of these methods model non-infinitesimal genetic architectures. GCTA-LOCO and BOLT-LMM-inf mean χ² statistics at standardized effect SNPs were essentially identical and slightly exceeded PCA, consistent with theory¹². We also tested EMMAX³ and GEMMA⁶, which are vulnerable to proximal contamination^5,9,12; these methods suffered loss of power relative to PCA (Supplementary Fig. 4a), consistent with theory¹².

Figure 2. BOLT-LMM increases power to detect associations in simulations.

Mean χ² at standardized effect SNPs as a function of (a) number of causal SNPs, (b) proportion of variance explained by causal SNPs, (c) number of samples. Simulations used real genotypes from the WTCCC2 data set (N=15,633, M=360K) and simulated phenotypes with the specified number of causal SNPs explaining the specified proportion of phenotypic variance and 60 more standardized effect SNPs explaining an additional 2% of the variance. Error bars, s.e.m., 100 simulations. We verified on the first 5 simulations that the BOLT-LMM-inf and GCTA-LOCO statistics are nearly identical (Supplementary Table 7). Numerical data are provided in Supplementary Table 2.

To further explore the relationship between the magnitude of Gaussian mixture model power gain and other parameters of the data set, we also varied the proportion of variance explained by causal SNPs (Fig. 2b) and the number of individuals (Fig. 2c). We observed that the power boost of BOLT-LMM over infinitesimal mixed model analysis (GCTA-LOCO, BOLT-LMM-inf) increased with each of these parameters. In further simulations using data sets of size N=30,000 and N=60,000 (Supplementary Note) and simulated phenotypes with M_causal=250–15,000 causal SNPs explaining 15–35% of the variance, we observed that the effectiveness of the Gaussian mixture model is closely tied to h_g²N/M_causal (where h_g² is the heritability parameter estimated by BOLT-LMM; see Online Methods for interpretation); intuitively, this quantity measures the effective number of samples per causal SNP (Supplementary Fig. 5). These results are consistent with theory (Supplementary Note and Supplementary Table 2 of ref.¹²), which explains that even in the absence of confounding, mixed model analysis provides a power gain over marginal regression by conditioning on the estimated effects of other SNPs when testing a candidate SNP^9,12. As sample size increases, the power gain of both methods approaches an asymptote corresponding to an increase in effective sample size of 1/(1−h_g²), but for sparse genetic architectures, the Gaussian mixture model approaches this asymptote much faster.

To verify that BOLT-LMM is correctly calibrated and robust to confounding, we also computed mean χ² statistics across SNPs on the second halves of chromosomes, simulated to all have zero effect (“null SNPs”). Because our simulated phenotypes included an ancestry effect, linear regression without correcting for population stratification suffered 35% inflation. In contrast, the BOLT-LMM and BOLT-LMM-inf statistics were both well-calibrated (Supplementary Fig. 4b, Supplementary Table 3, and Supplementary Table 4). We further verified that Type I error was properly controlled (Online Methods and Supplementary Table 5) and that the distribution of statistics at null SNPs did not deviate noticeably from a 1 d.o.f. chi-squared distribution (Supplementary Fig. 6a,b). Genomic inflation factors³³ for BOLT-LMM and BOLT-LMM-inf exceeded 1 in these simulations (Supplementary Fig. 6c,d), consistent with polygenicity of the simulated phenotype and use of a mixed model statistic that successfully avoids proximal contamination^12,13. In contrast, EMMAX and GEMMA had deflated test statistics (Supplementary Fig. 4b).

To examine the tightness of the variational approximation used by BOLT-LMM for Bayesian model fitting and to enable comparison with FaST-LMM-Select, we ran a small-scale simulation using the same setup as above but only one-third of the samples (N=5,211). We simulated genetic architectures with 1,250 causal SNPs explaining 70% of phenotypic variance (and 60 additional standardized effect SNPs explaining 2% of variance and ancestry explaining 1%, as before). We ran PCA, BOLT-LMM-inf, BOLT-LMM, FaST-LMM-Select, and a modified version of BOLT-LMM in which we replaced the variational iteration of Step 2b with a Markov chain Monte Carlo (MCMC) Gibbs sampler. In the limit of infinite sampling iterations, MCMC would produce exact versions of the posterior approximations computed by BOLT-LMM. In these simulations, the variational iteration (i.e., standard BOLT-LMM) achieved statistically identical results to MCMC (Supplementary Table 6a), supporting the choice of variational Bayes for BOLT-LMM. We also observed that while BOLT-LMM-inf achieved a power gain over PCA and BOLT-LMM achieved a further power gain over BOLT-LMM-inf (consistent with previous simulations), FaST-LMM-Select achieved lower power than BOLT-LMM-inf and BOLT-LMM (Supplementary Table 6a). Upon repeating this experiment with the number of causal SNPs reduced to 500, we observed that FaST-LMM-Select achieved a power gain in between BOLT-LMM-inf and BOLT-LMM (Supplementary Table 6b). Finally, we observed that the LD Score calibration approach used by BOLT-LMM also worked well when applied to FaST-LMM-Select, validating this calibration approach (Supplementary Table 6).

Lastly, we investigated the similarity between the BOLT-LMM-inf mixed model statistic and existing methods at the individual SNP level. Despite its use of an infinitesimal model, the BOLT-LMM-inf statistic is not identical to any existing mixed model statistic because it is an approximate test statistic and avoids proximal contamination (Online Methods and Table 1). Nonetheless, we observed that BOLT-LMM-inf statistics very nearly match GCTA-LOCO statistics (which use the standard prospective model), with R²>0.999 (Supplementary Table 7 and Supplementary Fig. 7).

Application of BOLT-LMM to WGHS phenotypes

To assess the efficacy of Gaussian mixture model analysis for increasing power on real phenotypes, we analyzed nine phenotypes in the Women’s Genome Health Study (N=23,294 samples, M=324,488 SNPs after QC) (Online Methods). These phenotypes consisted of five lipid phenotypes, height, body mass index, and two blood pressure phenotypes; we chose to analyze these phenotypes because of the availability of large-scale GWAS results.

We compared the power of three association tests: linear regression with 10 principal components (PCA)³², infinitesimal mixed model analysis with BOLT-LMM-inf, and Gaussian mixture modeling with BOLT-LMM. Because of memory constraints (Fig. 1), we were unable to run GCTA-LOCO¹², FaST-LMM⁵, or FaST-LMM-Select¹⁵, which are the only previous methods that avoid proximal contamination (Table 1); however, GCTA-LOCO and BOLT-LMM-inf statistics are near-identical (Supplementary Table 7 and Supplementary Fig. 7). To compare power among these methods, we computed two roughly equivalent metrics: mean χ² statistics at known associated loci, a direct but somewhat noisy approach due to having only 19–180 loci for each trait (Supplementary Table 8), and out-of-sample prediction R² (measured in cross-validation) using all SNPs for the mixed model methods and using only PCs for linear regression. For mixed model analysis, the latter metric estimates the ability of the mixed model to condition on effects of other SNPs when testing a candidate SNP, which drives its power (Online Methods)^12,34.

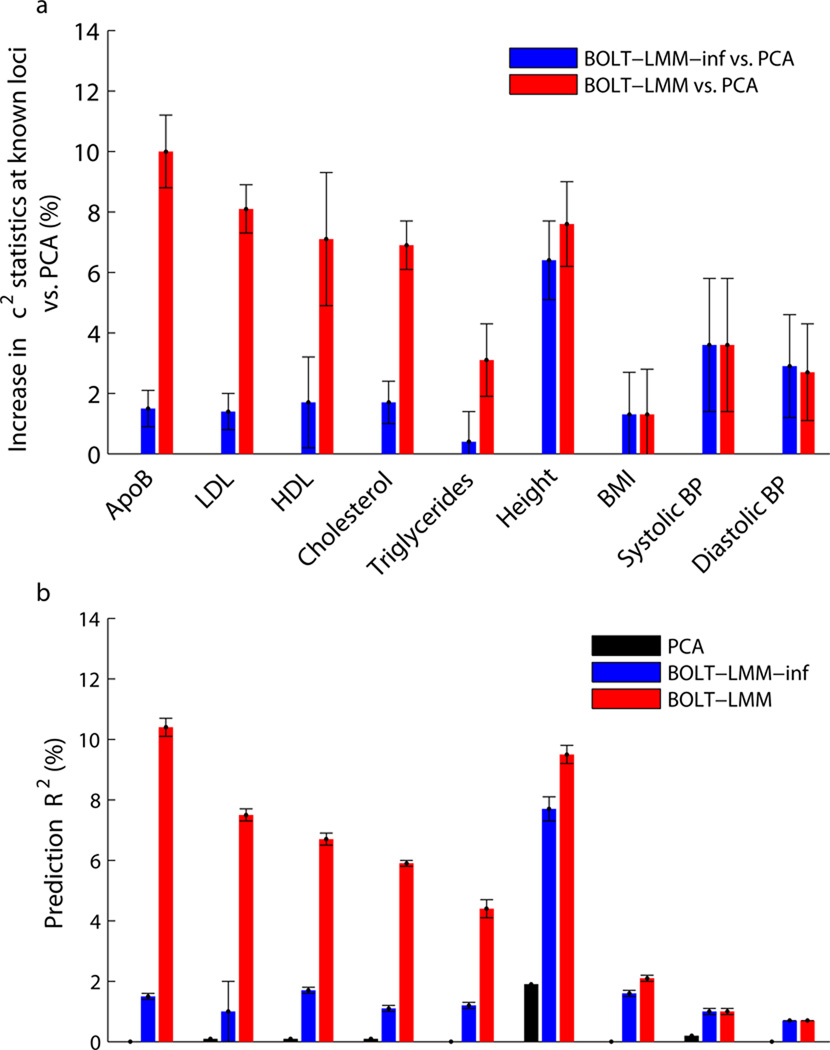
BOLT-LMM achieved higher power than PCA for all traits studied (Fig. 3 and Supplementary Table 9). Most of the increase was due to gains over infinitesimal mixed model analysis, with the magnitude of this power gain increasing with inferred concentration of genetic effects at few loci (Supplementary Table 10). Standard errors of the direct method of assessing improvement (mean χ² at known loci) were somewhat high (0.6–2.2%; Fig. 3a and Supplementary Table 9), so the improvement was statistically significant (p<0.05) for only 6 of 9 traits. According to the prediction R² metric, improvements were statistically significant for all traits (p<0.0002) (Fig. 3b and Supplementary Table 9). The largest gains were achieved for lipid traits; for ApoB, a lipoprotein closely related to LDL cholesterol, BOLT-LMM analysis achieved a 10% increase in mean χ² statistics versus PCA and a 9% increase versus infinitesimal mixed model analysis at known loci. To verify that these increases were not merely driven by a few loci with the largest effects, we also computed flat averages across loci of improvements in χ² statistics (restricting to loci replicating in WGHS with at least nominal p<0.05 significance to reduce statistical noise) and obtained consistent results (Supplementary Table 8). Simulations show that these improvements will increase with sample size (Fig. 2c and Supplementary Fig. 5).

Figure 3. BOLT-LMM increases power to detect associations for WGHS phenotypes.

We compare power (measured using two roughly equivalent metrics) of linear regression using 10 principal components, standard (infinitesimal) mixed model analysis, and BOLT-LMM Gaussian mixture model analysis. (a) Percent increases in χ² statistics across known loci using mixed model methods vs. PCA: ratios of sums of χ² statistics over typed SNPs in highest LD with published associated SNPs. (b) Prediction R² values from 5-fold cross-validation: each fold was left out in turn and predictions were computed by fitting all SNP effects simultaneously (for mixed model methods) or estimating covariate effects (for PCA) using the training folds. (Note that BOLT-LMM-inf is equivalent to BLUP prediction here.) We show PCA in (b) because the small amount of variance that the PCs explain (due to population stratification) provides a baseline that allows translating prediction R² to the power gain of mixed model association vs. regression with PC covariates. That is, the correspondence between association power and prediction accuracy is such that the red bars in (a) roughly correspond to differences between red and black bars in (b), and analogously for blue bars (Online Methods). Error bars, jackknife s.e. over (a) known loci (Supplementary Table 8); (b) 5 cross-validation folds. Numerical data are provided in Supplementary Table 9.

We also observed that infinitesimal mixed model analysis achieved statistically significant power gains over PCA, with the magnitude of the power gains increasing with the heritability parameter h_g² (Fig. 3 and Supplementary Table 9). For height (h_g²=0.47 in WGHS), the moderately large sample size of WGHS (N=23,294) was enough to obtain a 6% increase in BOLT-LMM-inf χ² statistics versus PCA, consistent with theory^12,34. Again, larger sample sizes will enable further gains^12,34.

To verify that BOLT-LMM successfully corrected for confounding from population structure, we computed mean χ² statistics across all typed SNPs and genomic inflation factors for the three methods compared above as well as uncorrected marginal linear regression. We observed that PCA, BOLT-LMM-inf, and BOLT-LMM statistics were consistently calibrated, while uncorrected linear regression statistics were inflated, especially for height (Supplementary Table 11). We further verified that genetic variation at the lactase gene had a false-positive genome-wide significant association with height using uncorrected marginal regression³⁵ which disappeared when using PCA, BOLT-LMM-inf, and BOLT-LMM (Supplementary Table 12).

Discussion

We have described a new algorithm for fast Bayesian mixed model association, BOLT-LMM, and demonstrated that its running time scales only with ≈MN^1.5 and its memory usage is only ≈MN/4 bytes, resulting in orders-of-magnitude improvements in computational efficiency over existing methods for large data sets. We have further shown in simulations and analyses of WGHS phenotypes that the Gaussian mixture modeling capability of BOLT-LMM enables increased association power over standard mixed model analysis while controlling false positives. Among WGHS lipid traits, we observed power increases equivalent to increases in effective sample size of up to 10% over PCA and 9% over standard mixed model analysis.

BOLT-LMM is an advance for two main reasons. First, as sample sizes continue to increase, mixed model analysis is simultaneously becoming more important—in order to correct for population structure and cryptic relatedness in very large data sets—yet less practical with existing methods, all of which have ≥O(MN²) time complexity (for M>N) and high memory requirements. The algorithmic innovations of BOLT-LMM overcome this computational barrier (Fig. 1). (Our implementation uses ≈MN/4 bytes of memory, which is already much less in practice than existing methods. In theory, existing algorithms have a memory complexity of O(N²), while BOLT-LMM’s memory complexity could be reduced to O(M+N) by iteration on data.) Second, the ability of BOLT-LMM to better model non-infinitesimal genetic architectures enables a power gain relative to standard mixed model analysis. Recent methodological progress in this direction includes the multi-locus mixed model (MLMM)⁷, which identifies and conditions out large-effect loci as fixed effects, and FaST-LMM-Select and related methods^{9,11,15,16,36}, which adopt a sparse regression framework that restricts the mixed model to a subset of markers. However, these methods all face the same O(MN²) computational hurdle as standard mixed model analysis.

Bayesian methods have previously been developed that apply non-infinitesimal models to improve the accuracy of genetic risk prediction. These methods extend in principle to association testing, although the Bayes factors and posterior inclusion probabilities that are naturally produced by Bayesian analysis do not directly translate to customary GWAS frequentist test statistics³⁷. The variational Bayes spike regression (vBsr) method³⁸ is a recent step toward addressing this issue, proposing a z-statistic heuristically calibrated by assuming that the vast majority of variants are unassociated (as in genomic control³³), but such a technique is prone to deflation when large sample sizes cause inflation due to polygenicity^13,24. BOLT-LMM sidesteps this difficulty via its hybrid approach of leaving each chromosome out in turn, fitting a Bayesian model on the remaining SNPs, and then applying a retrospective hypothesis test for association of left-out SNPs with the residual phenotype. In contrast to modeling all SNPs simultaneously and assessing evidence for association using Bayesian posterior inference³⁷, our approach generalizes existing mixed model methods that are widely used, and we believe its ability to harness the power of Bayesian analysis while still computing frequentist statistics will be useful to GWAS practitioners. Additionally, such a hybrid approach lends itself readily to efficiently testing millions of imputed SNP dosages for association while including only typed SNPs in the mixed model, which we recommend to limit computational costs.

While BOLT-LMM improves upon existing mixed model association methods in both speed and power, BOLT-LMM still has limitations. First, the power gain that BOLT-LMM offers over existing methods via its more flexible prior on SNP effect sizes is contingent on the true genetic architecture being sufficiently non-infinitesimal and the sample size being sufficiently large (Supplementary Fig. 5). Second, BOLT-LMM, like existing mixed model methods, is susceptible to loss of power when used to analyze large ascertained case-control data sets in diseases of low prevalence¹². We recommend BOLT-LMM for randomly ascertained quantitative traits, ascertained case-control studies of diseases with prevalence ≥5% (Supplementary Table 13)—e.g., type 2 diabetes, heart disease, common cancers, hypertension, asthma—and studies of rarer diseases in large, non-ascertained population cohorts^39,40. For large ascertained case-control studies of rarer diseases, we are developing a method of modeling ascertainment using posterior mean liabilities (LTMLM); applying the techniques of BOLT-LMM to these posterior mean liabilities is an avenue for future research. Third, while mixed model analysis is effective in correcting for many forms of confounding, performing careful data quality control remains critical to avoiding false positives. Fourth, our work does not attempt to estimate the extent to which the heritability parameter estimated by BOLT-LMM (denoted h_g²) may be influenced by population structure or relatedness, nor does it conduct or evaluate genetic prediction in external validation samples from an independent cohort³⁴. Fifth, we have not studied the performance of mixed model methods in data sets dominated by family structure²³. Sixth, the running time of BOLT-LMM scales with the number of phenotypes analyzed; for data sets with a very large number of phenotypes (P), the GRAMMAR-Gamma method¹⁰, which has running time O(MN²+MNP) (reviewed in ref.¹²) may be faster. Seventh, we have only tested BOLT-LMM in human data sets, which have very different patterns of linkage disequilibrium and genetic architectures from plant and animal data. In particular, given that some approximations we make may be violated in non-human data sets (e.g., treating the denominator of the prospective test statistic as near-constant¹⁰), we are unsure whether the BOLT-LMM statistic is valid in these scenarios. Similarly, these assumptions should be viewed with caution when testing very rare variants. Finally, we have developed fast mixed model analysis for a mixed model with one random genetic effect; extending the algorithm to model multiple variance components⁴¹ is a direction for future work.

Online Methods

Standard mixed model association methods

Standard methods employ a model

$$y=x_{\text{test}}{\mathrm{\beta }}_{\text{test}}+g+e,$$ (1)

where y is the phenotype, x_test is the candidate SNP being tested, g is the genetic effect, and e is the environmental effect. We assume for now that all have been mean-centered and there are no covariates; we treat covariates by projecting them out from both genotypes and phenotypes, which is equivalent to including them as fixed effects (Supplementary Note). The genetic and environmental effects are modeled as random effects, while the candidate SNP is modeled as a fixed effect with coefficient β_test, and the goal is to test the null hypothesis β_test=0. Under the standard infinitesimal model, the genetic effect is modeled as

$$g=X_{\mathrm{G}\mathrm{R}\mathrm{M}}{\mathrm{\beta }}_{\mathrm{G}\mathrm{R}\mathrm{M}},$$ (2)

where X_GRM is an N×M_GRM matrix, each column of which contains normalized genotypes corresponding to a SNP included in the model, and β_GRM is an M_GRM-vector of random SNP effect sizes all drawn from the same normal distribution, so that g has a multivariate normal distribution with covariance Cov(g) ∝ X_GRMX_GRM'. Note that in order to avoid proximal contamination^5,9,12, the M_GRM SNPs used in X_GRM should vary depending on which SNP x_test is being tested: the candidate SNP x_test (and SNPs in linkage disequilibrium with it) should be excluded from X_GRM to avoid modeling its effect twice. BOLT-LMM adopts a leave-one-chromosome-out (LOCO) scheme^5,12 in which X_GRM leaves out SNPs on the same chromosome as x_test.

The matrix X_GRMX_GRM'/M_GRM is conventionally called the genetic relationship matrix (GRM) or empirical kinship matrix K, and we write

$$\text{Cov}(g)={{\mathrm{\sigma }}_g}^2{X}_{\mathrm{G}\mathrm{R}\mathrm{M}}{X}_{\mathrm{G}\mathrm{R}\mathrm{M}}\text{'}/M_{\mathrm{G}\mathrm{R}\mathrm{M}}={{\mathrm{\sigma }}_g}^{2}K,$$ (3)

where σ_g² is a variance parameter. Environmental effects are assumed i.i.d. normal, so e is also multivariate normal with

$$\text{Cov}(e)={{\mathrm{\sigma }}_e}^{2}I,$$ (4)

where I denotes the N×N identity matrix and σ_e² is another variance parameter.

In practice, the variance parameters σ_g² and σ_e² are unknown. Several existing methods^3,10,12 therefore take a two-step approach to computing association statistics: first estimate the variance parameters (with the SNP x_test removed from the model) using restricted maximum likelihood (REML), and then compute the prospective chi-squared (1 d.o.f.) test statistic (as previously proposed in family-based tests⁴²)

$${\chi }_{\mathrm{L}\mathrm{M}\mathrm{M}}^2=\frac{{(x_{\text{test}}^{\prime }{V}^{-1}y)}^2}{x_{\text{test}}^{\prime }{V}^{-1}{x}_{\text{test}}},$$ (5)

where

$$V=\text{Cov}(y)={{\mathrm{\sigma }}_g}^{2}K+{{\mathrm{\sigma }}_e}^{2}I,$$ (6)

setting the variance parameters σ_g² and σ_e² to their estimates under the null hypothesis β_test=0. Within a LOCO scheme, the test statistic becomes

$${\chi }_{\mathrm{L}\mathrm{M}\mathrm{M}-\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}}^2=\frac{{(x_{\text{test}}^{\prime }{V}_{\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}}^{-1}y)}^2}{x_{\text{test}}^{\prime }{V}_{\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}}^{-1}{x}_{\text{test}}},$$ (7)

where we have written V_LOCO for V to explicitly indicate that the chromosome containing x_test is left out of the GRM.

Recent computational advances have also enabled computation of exact likelihood ratio test statistics that model the variance parameters while testing the candidate SNP^5,6. While exact statistics are more accurate in situations with very large-effect SNPs, approximate methods produce near-identical results in typical human genetics scenarios^3,10,12.

BOLT-LMM-inf mixed model statistic

The BOLT-LMM-inf infinitesimal mixed model statistic is slightly different:

$${\chi }_{\mathrm{B}\mathrm{O}\mathrm{L}\mathrm{T}-\mathrm{L}\mathrm{M}\mathrm{M}-\text{inf}}^2=\frac{{(x_{\text{test}}^{\prime }{V}_{\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}}^{-1}y)}^2}{c_{\text{inf}}},$$ (8)

where c_inf is a constant calibration factor estimated as

$$c_{\text{inf}}=\frac{\text{Mean}{(x_{\text{test}}^{\prime }{V}_{\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}}^{-1}y)}^2}{\text{Mean}{\chi }_{\mathrm{L}\mathrm{M}\mathrm{M}-\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}}^2}$$ (9)

so that

$$\text{Mean}{\chi }_{\mathrm{B}\mathrm{O}\mathrm{L}\mathrm{T}-\mathrm{L}\mathrm{M}\mathrm{M}-\text{inf}}^2=\text{Mean}{\chi }_{\mathrm{L}\mathrm{M}\mathrm{M}-\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}}^2.$$ (10)

In practice, for computational efficiency, we take means over 30 pseudorandom SNPs not significantly associated with the phenotype (χ²<5 estimated with the GRAMMAR statistic⁴³). We have observed empirically that 30 random SNPs are enough to estimate the calibration factor to within 1% (Supplementary Table 14).

We can view the BOLT-LMM-inf statistic either as an approximation of the standard prospective statistic (which treats phenotypes as random) or as a retrospective statistic (which treats genotypes as random and builds a null model on SNPs). The first perspective is motivated by the observation that in human genetics applications, the denominator of the prospective statistic in equation (5), x_test'V⁻¹x_test, is nearly independent of the SNP x_test being tested¹⁰. From this perspective, BOLT-LMM-inf is similar to GRAMMAR-Gamma¹⁰, with two key differences: (1) BOLT-LMM-inf is computed via much faster algorithms (described below) for performing initial variance parameter estimation and estimating the calibration constant, and (2) BOLT-LMM-inf avoids proximal contamination via LOCO analysis. Alternatively, we can also view BOLT-LMM-inf as a retrospective quasi-likelihood score test similar to T^SCORE–R (ref.⁴⁴) and MASTOR²³ (Supplementary Note).

BOLT-LMM Gaussian mixture model association statistic

We now generalize BOLT-LMM-inf by observing that the vector V_LOCO⁻¹y appearing in equation (8) is a scalar multiple of the residual phenotype vector σ_e²V_LOCO⁻¹y from best linear unbiased prediction (BLUP). Thus, the χ²_BOLT-LMM-inf statistic is equivalent to computing (and then calibrating) squared correlations between SNPs x_test and BLUP residuals. The power of mixed model association is driven by the fact that SNPs x_test are tested against these “de-noised” residual phenotypes from which other SNP effects estimated by the mixed model have been conditioned out^9,12.

We may generalize this approach by defining

$${\chi }_{\mathrm{B}\mathrm{O}\mathrm{L}\mathrm{T}-\mathrm{L}\mathrm{M}\mathrm{M}}^2=\frac{{(x_{\text{test}}^{\prime }{y}_{\text{resid}-\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}})}^2}{c},$$ (11)

where y_resid-LOCO denotes a generalized residual phenotype vector obtained after fitting a Gaussian mixture extension of the standard LMM (using SNPs not on the same chromosome as x_test) and c denotes a calibration factor, estimated so that the LD Score regression intercept²⁴ of χ²_BOLT-LMM matches that of the (properly calibrated) χ²_BOLT-LMM-inf statistic. Under the infinitesimal model, y_resid-LOCO is proportional to V_LOCO⁻¹y, so χ²_BOLT-LMM reduces to χ²_BOLT-LMM-inf. The general χ²_BOLT-LMM statistic can still be interpreted as a retrospective quasi-likelihood score test and is thus asymptotically chi-squared distributed.

To define the Gaussian mixture LMM extension, it is helpful to first frame the standard LMM in a Bayesian formulation. The null model of BOLT-LMM-inf is

$$y=X_{\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}}{\mathrm{\beta }}_{\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}}+e,$$ (12)

where SNP effects β_m (m indexing SNPs not on the left-out chromosome) are independently drawn from the Gaussian prior distribution

$${\mathrm{\beta }}_m~N(0,{{\mathrm{\sigma }}_g}^2)/M_{\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}}$$ (13)

and environmental effects e_n (n indexing samples) are independently drawn from e_n ~ N(0, σ_e²). Performing best linear unbiased prediction amounts to computing the posterior mean of the genetic effect X_LOCOβ_LOCO.

To generalize this model to non-infinitesimal genetic architectures, we replace the Gaussian prior on SNP effect sizes with a more general distribution; this approach has been extensively applied by the “Bayesian alphabet” of genomic prediction methods in the animal breeding literature^17–19. In BOLT-LMM, we use a spike-and-slab mixture of two Gaussians¹⁹ as the prior:

$${\mathrm{\beta }}_m~N(0,{{\mathrm{\sigma }}_{\mathrm{\beta },1}}^2)\text{with probability}\mathrm{p}.{\mathrm{\beta }}_m~N(0,{{\mathrm{\sigma }}_{\mathrm{\beta },2}}^2)\text{with probability}1-\mathrm{p}.$$ (14)

This mixture more flexibly models the heavier-tailed distributions of genetic effects of typical (non-infinitesimal) phenotypes. Explicitly, if p≪1 and σ_β,1² ≫ σ_β,2², the first component of the mixture is a “slab” that models the existence of a small number of relatively large-effect loci, while the second component is a “spike” that models the assumption that most SNPs have near-zero—but not exactly zero—effect on the phenotype. (Note, however, that all SNPs are assigned the same mixture prior; i.e., SNPs are not individually allocated to one or the other component.) It is important that the spike component have nonzero variance so as to capture genome-wide effects on phenotype such as ancestry or relatedness; then, when testing SNPs for association, these genome-wide effects are conditioned out from residual phenotypes, protecting against confounding. The prior could in principle be further generalized; we chose to use a mixture of two Gaussians to keep the model fairly simple and because Gaussian distributions produce convenient analytical formulas during model-fitting.

Under this generalized model, posterior means no longer correspond to BLUP, but we can still approximately fit the Bayesian model (once per left-out chromosome) and obtain residuals

$$y_{\text{resid}-\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}}=y-X_{\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}}{\mathrm{\beta }}_{\mathrm{L}\mathrm{O}\mathrm{C}\mathrm{O}},$$ (15)

where β_LOCO are estimated posterior mean effect sizes. Plugging these residuals into equation (11) gives the BOLT-LMM Gaussian mixture model association test statistic.

Fast iterative algorithm

The BOLT-LMM software performs a four-step computation for mixed model association analysis, stopping after the first two steps when specialized to the infinitesimal model. We outline the algorithm here and provide full details and pseudocode in the Supplementary Note.

Step 1a: Estimate variance parameters

A key feature of BOLT-LMM is estimation of variance parameters σ_g² and σ_e² using only linear-time iterations without building or decomposing any covariance matrices. We use a Monte Carlo REML approach^26,27 that eliminates all O(MN²) and O(N³)-time matrix computations, requiring only the solution of linear systems of mixed model equations. We solve the mixed model equations using conjugate gradient iteration, which requires only O(MN)-time matrix-vector products^28,29 (Supplementary Note).

Step 1b: Compute and calibrate BOLT-LMM-inf statistics

Having variance parameter estimates from Step 1a, it is straightforward to compute (for each LOCO rep) the quantity V_LOCO⁻¹y in the numerator of the BOLT-LMM-inf statistic, equation (8), using conjugate gradient iteration as above. Completing the computation of the numerator of χ²_BOLT-LMM-inf then just amounts to calculating one dot product per SNP x_test, which requires only O(MN) additional cost across all SNPs. Moreover, this computation can easily be performed for additional SNPs not included in the mixed model but at which association statistics are desired; BOLT-LMM handles imputed “dosage” data in this way. To compute the calibration constant c_inf in equation (9), BOLT-LMM rapidly computes the prospective statistic χ²_LMM-LOCO from equation (7) at 30 random SNPs by applying conjugate gradient iteration to compute V_LOCO⁻¹x_test for each of the 30 selected SNPs x_test. Finally, in addition to computing χ² association statistics, BOLT-LMM also computes effect size estimates for all SNPs tested (Supplementary Note).

There is a slight mismatch between the variance parameters estimated in Step 1a, which BOLT-LMM computes once using all SNPs—not leaving any chromosomes out—and the theoretically optimal parameter estimates that would be obtained by refitting once per left-out chromosome. However, we have observed in simulations that slight mis-specification of the variance parameters has a negligible impact (<0.5%) on the calibration of the BOLT-LMM-inf and BOLT-LMM statistics (Supplementary Table 4). Because very slight miscalibration is not a concern for confounding from population stratification at highly differentiated markers (Supplementary Table 12) and has little impact on Type I error (Supplementary Table 5), the BOLT-LMM software does not by default refit variance parameters for each LOCO rep. If extremely precise calibration is desired, we provide a runtime option to refit variance parameters for each LOCO rep, at the cost of a factor of 2–3 in running time. We believe that LOCO strikes a good balance in terms of achieving ≈95% of the potential power gain (by jointly fitting ≈95% of markers that are not in LD with the candidate marker) while keeping run time down¹², but we also provide a runtime option to partition the genome more finely (e.g., into 100 segments rather than 22), again at the cost of a factor of 2–3 in running time.

Step 2a: Estimate Gaussian mixture prior parameters

The first step of BOLT-LMM Gaussian mixture model association analyis is to estimate parameters of the generalized prior on SNP effect sizes. As written in equation (14), this mixture has three parameters: σ_β,1² and σ_β,2², the variances of the two Gaussians, and p, the probability of drawing from the first Gaussian. To reduce the complexity of parameter estimation, we constrain the total variance of the mixture to equal the variance σ_g²/M estimated under the infinitesimal model in Step 1a:

$$p{{\mathrm{\sigma }}_{\mathrm{\beta },1}}^2+(1-\mathrm{p}){{\mathrm{\sigma }}_{\mathrm{\beta },2}}^2={{\mathrm{\sigma }}_g}^2/M.$$ (16)

We reparameterize the remaining two degrees of freedom using the parameters p and f₂, where f₂ denotes the proportion of the total mixture variance within the second Gaussian (the “spike” component that models small genome-wide effects):

$$f_2=\frac{(1-p){\sigma }_{\beta ,2}^2}{p{\sigma }_{\beta ,1}^2+(1-p){\sigma }_{\beta ,2}^2}.$$ (17)

Because the model fit is insensitive to the precise values of the mixture parameters, we test a discrete set of model parameter combinations: f₂∈{0.5,0.3,0.1}, p∈{0.5,0.2.0.1,0.05,0.02,0.01}. Note that f₂=0.5, p=0.5 corresponds to the infinitesimal model: when f₂=1−p, the two Gaussians are identical and the mixture is degenerate. We bound f₂ from below to ensure that at least a small amount (10%) of the mixture variance is assigned to the spike component, protecting against confounding from genome-wide effects. We bound p from below to prevent the model from trying to fit too strongly to a few SNPs, which makes model-fitting computationally difficult and also increases susceptibility to confounding. BOLT-LMM performs model selection among the 18 possible parameter pairs (f₂, p) by performing cross-validation to optimize mean-squared prediction R².

BOLT-LMM uses a variational approximation to fit Bayesian linear regressions with Gaussian mixture priors. Approximation methods are necessary for Bayesian inference in this setting because exact posterior means involve intractable integrals. We apply a fully factored variational approximation^21,22,38 that repeatedly loops through the SNPs, updating the estimated effect size of each SNP with its posterior mean conditional on current estimates of all other SNP effects. This iteration has also previously been termed “iterative conditional expectation (ICE)”²⁰. The variational Bayes framework puts this iteration on a sound theoretical footing as an optimization of an approximate log likelihood function; the iteration monotonically increases this function and is guaranteed to converge⁴⁵. In fact, we show that the optimization can be reformulated as cyclic coordinate descent applied to a penalized regression problem arising from Bayesian linear regression using a transformed prior (Supplementary Note). The approximate log likelihood also serves as a convenient convergence criterion: BOLT-LMM stops the iteration when the increase in approximate log likelihood over one full update cycle drops below 0.01.

While the core variational iteration that BOLT-LMM uses is identical to previous methods^20–22,38 up to the choice of SNP effect size prior, BOLT-LMM uses cross-validation to estimate hyperparameters¹⁵ rather than doing so within the variational iteration^22,38 or based on variational approximate log likelihoods²¹. We found this approach to be more robust to slackness of the variational approximation caused by linkage disequilibrium.

Step 2b: Compute and calibrate BOLT-LMM Gaussian mixture model statistics

After inferring parameters of the mixture prior in Step 2a, BOLT-LMM uses the same variational iteration to estimate posterior mean residuals y_resid-LOCO (independently for each left-out chromosome). The numerators of the BOLT-LMM Gaussian mixture model statistic from equation (11) are then easily obtained as dot products with test SNPs, leaving only the constant calibration factor c in the denominator to be calculated. Unlike the case of the infinitesimal model, here we do not have a prospective statistic to calibrate against, so we instead apply LD Score regression²⁴ (Supplementary Note). In practice, the calibration factor is usually quite close to 1 (e.g., 1.00 to two decimal places for all WGHS traits; see Supplementary Table 15).

WGHS data set

The Women’s Genome Health Study (WGHS) is a prospective cohort of initially healthy, female North American health care professionals. We analyzed 23,294 individuals with self-reported European ancestry with genotyping at 324,488 SNPs after QC (Supplementary Note).

Interpretation of heritability parameter

The heritability parameter (denoted h_g²) estimated by BOLT-LMM may in general include some contribution from cryptic relatedness or population structure⁴⁶, and thus may not strictly correspond to the heritability explained by genotyped SNPs⁴⁷. Ref.³ refers to this parameter as “pseudo-heritability” for this reason. Because the WGHS samples that we primarily analyze here do not contain substantial relatedness or population structure, we have simply used the notation h_g² to avoid complicating the discussion.