Biodemography of Old-Age Mortality in Humans and Rodents

Abstract

The growing number of persons living beyond age 80 underscores the need for accurate measurement of mortality at advanced ages and understanding the old-age mortality trajectories. It is believed that exponential growth of mortality with age (Gompertz law) is followed by a period of deceleration, with slower rates of mortality increase at older ages. This pattern of mortality deceleration is traditionally described by the logistic (Kannisto) model, which is considered as an alternative to the Gompertz model. Mortality deceleration was observed for many invertebrate species, but the evidence for mammals is controversial. We compared the performance (goodness-of-fit) of two competing models—the Gompertz model and the logistic (Kannisto) model using data for three mammalian species: 22 birth cohorts of U.S. men and women, eight cohorts of laboratory mice, and 10 cohorts of laboratory rats. For all three mammalian species, the Gompertz model fits mortality data significantly better than the “mortality deceleration” Kannisto model (according to the Akaike’s information criterion as the goodness-of-fit measure). These results suggest that mortality deceleration at advanced ages is not a universal phenomenon, and survival of mammalian species follows the Gompertz law up to very old ages.

Accurate estimates of mortality at advanced ages are essential for forecasts of population aging and testing the predictions of competing theories of aging. Earlier studies suggest that exponential growth of mortality with age (Gompertz law) is followed by a period of deceleration, with slower rates of mortality increase at extreme old ages (1–6). This mortality deceleration eventually produces the “late-life mortality leveling-off” and “late-life mortality plateaus” at extreme old ages. Greenwood and Irwin (1) provided a detailed description of this phenomenon in humans and even made the first estimates for the asymptotic value of the upper limit to human mortality (see review by Olshansky (7)). The same phenomenon of “almost non-aging” survival dynamics at extreme old ages is detected in other biological species, and in some species, the mortality plateau can occupy a sizable part of their life (8,9).

The phenomenon of late-life mortality leveling-off presents a theoretical challenge to many models and theories of aging. Some researchers believe that the late-life plateau represents a distinct phase of life when the aging slows down or stops (10). Evolutionary biologists believe that aging is a result of declining forces of natural selection with age. When these forces eventually bottom-up at extreme old ages, then the cessation of aging is expected according to this paradigm (11). Population heterogeneity hypothesis is another, even more popular, explanation of mortality deceleration, which was proposed by British actuary Eric Beard in 1959 (12). As George Sacher explained “… sub-populations with the higher injury levels die out more rapidly, resulting in progressive selection for vigour in the surviving populations” (13). This explanation is now considered to be the most common explanation of mortality deceleration phenomenon (2). Another explanation of this phenomenon comes from the reliability theory of aging, which explains mortality leveling-off by an exhaustion of organism’s redundancy (reserves) at extremely old ages, so that every additional random hit of damage results in death (6,14). There is also an opinion that lower (than predicted) risks of death for older people may be due to their less risky behavior (1).

The existence of mortality plateaus is well described for a number of lower organisms, including medfly (8), house fly Musca domestica (9), fruit flies Anastrepha ludens, Anastrepha obliqua, Anastrepha serpentine, parasitoid wasp Diachasmimorpha longiacaudtis (15,16), and bruchid beetle Callosobruchus maculates (17). In the case of mammals, however, data are much more controversial. Some researchers reported short-term periods of mortality deceleration in mice at advanced ages and even used the “mortality deceleration” Perks’ formula in their analyses (13,18,19). However, Austad later argued that rodents do not demonstrate mortality deceleration even in the case of very large samples allowing to study data at very advanced old ages (20). Study of baboons found no mortality deceleration at older ages (21). Longitudinal study of mortality among seven wild primate species failed to find mortality deceleration at older ages (22). The authors came to a conclusion that “none of the age-specific mortality relationships in our non-human primate analyses demonstrated the type of leveling-off that has been shown in human and fly data sets” (22).

Several studies of old-age mortality in humans came to a conclusion that mortality deceleration does exist and starts after age 80 (2–4). It should be noted, however, that analysis of old-age mortality in humans encounters certain methodological problems related to data aggregation and age misreporting among very old. More homogeneous single-year birth cohorts in many countries with good vital statistics have very small numbers of survivors to age 100 that makes estimates of mortality at advanced ages unreliable. On the other hand, aggregation of data for several birth cohorts in order to increase the sample size creates a mixture of different populations. The problem of age misreporting by older people is another important problem affecting estimates of mortality at advanced ages (23–27). It was demonstrated that the age misreporting at older ages results in mortality underestimation (28). Also, it was found that mortality deceleration is more expressed in the case of data with poor quality compared with data with better quality (29). Recent analysis of detailed records from the U.S. Social Security Administration Death Master File (DMF) for several single-year extinct birth cohorts demonstrated that the Gompertz law fits mortality data better than the logistic (Kannisto) model up to ages 105–106 years (29).

With the exception of the most recent study (29), the last systematic studies of mortality trajectories at extreme old ages in humans were conducted more than a decade ago (2,3). Taking into account that the accuracy of age reporting was improving over time (due to better registration and education), one may expect an improvement in age reporting over time leading to lower likelihood of mortality underestimation at older ages. Indeed, it was found that mortality in earlier U.S. cohorts deviated more from the Gompertz model compared with mortality of more recent birth cohorts (29). Thus, it may be reasonable to revisit the question of the shape of mortality trajectories at older ages in humans. Also, in the case of rodents, there were no systematic studies of mortality trajectories using standard methods of model selection.

In this article, we analyze mortality trajectories at advanced ages using data on sufficiently large cohorts of humans and rodents. The study of humans is based on mortality data for the U.S. single-year birth cohorts available in the Human Mortality Database (HMD), which became a traditional resource for demographers (30). Rodent data are represented by individual death records for large cohorts of mice and life tables of rats. Methods of mortality trajectory analysis are based on comparing alternative models of mortality using a standard goodness-of-fit procedure.

Data and Methods

Human Data

Previous studies of mortality trajectories used data of reasonably good quality for European countries and Japan, which had relatively small population sizes compared with the United States. As a result, few individuals in these countries survived to extreme old ages, so the researchers often had to pool together data for as many as 10 calendar years to have a sufficient sample size for the study (2–4). This data pooling is not needed for the United States because it has the largest population size among the advanced economies. The quality of vital statistics in the United States was not considered acceptable when the first comprehensive studies of mortality trajectories have been conducted (2,4,31). However, the quality of U.S. death data was gradually improving over time (32), and now this data can be used in mortality analysis. In this study, we compared two competing models (Gompertz model and Kannisto model) commonly used in mortality studies by analyzing the U.S. cohort mortality data taken from the HMD.

The Human Mortality Database (HMD) was created to provide detailed mortality and population data to researchers, students, journalists, policy analysts, and others interested in the history of human longevity. This is a publicly available data resource, which can be reached at http://www.mortality.org.

We used a set of age-specific death rates for 22 single-year U.S. birth cohorts (men and women born in 1890–1900 range) reported for each year of age. These are raw mortality data not fitted at advanced ages by any parametric formula. We analyzed these single-year U.S. cohort age-specific death rates separately for men and women. Mortality rates of period life tables in HMD are smoothed after age 80 by fitting a logistic function to observed death rates (33), therefore these data are not used in our analyses.

Mortality data are fitted in the age interval 80–106 years because after 106 years of age, the quality of U.S. death data significantly declines (29,34).

Individual death records from the Social Security Administration DMF were used for comparison with mortality data obtained from the HMD. We used DMF full file obtained from the National Technical Information Service. This is the latest available complete version of DMF where the last deaths occurred in September 2011.

Mouse Data

National Institutes of Health Interventions Testing Program Data.—

The National Institute on Aging’s Interventions Testing Program has developed a plan to evaluate agents that are considered plausible candidates for delaying rates of aging. Key features include (a) use of genetically heterogeneous mice (a standardized four-way cross), (b) replication at three test sites (the Jackson Laboratory; University of Michigan; and University of Texas), (c) sufficient statistical power to detect 10% changes in life span.

UM-HET3 mice were produced at each of the three test sites as provided in detail in the special publication (35). The mothers of the test mice were CByB6F1/J, JAX stock # 100009, whose female parents are BALB/cByJ and whose male parents are C57BL/6J. The fathers of the test mice were C3D2F1/J, JAX stock # 100004, whose female parents are C3H/HeJ and whose male parents are DBA/2J.

Mice were examined at least daily for signs of ill health. Mice were euthanized for humane reasons if so severely moribund that they were considered, by an experienced technician, unlikely to survive for more than an additional 48 hours. A mouse was considered severely moribund if it exhibited more than one of the following clinical signs: (a) inability to eat or to drink, (b) severe lethargy, as indicated by reluctance to move when gently prodded with a forceps, (c) severe balance or gait disturbance, (d) rapid weight loss over a period of 1 week or more, or (e) an ulcerated or bleeding tumor (35). The age at which a moribund mouse was euthanized was taken as the best available estimate of its natural life span. Age of mice found dead was also recorded at each daily inspection.

Mortality data are represented by individual records of mice with known birth and death dates and life span measured in days. Only data for mice from the control groups and data from the experiments with no significant effects on life span are used in our analyses of mortality trajectories.

Argonne National Laboratory data.—

A continuous series of large-scale animal studies was conducted between 1970 and 1992 in the Biological and Medical Research Division of the Argonne National Laboratory—a research effort generally referred to as the JANUS program (36,37). From these studies, a large database was compiled on the responses of both sexes of an F1 hybrid mouse, the B6CF (C57BL/6 X BALB/c), to external whole-body irradiation. The detailed documentation of the JANUS experiments is available in a special publication (37).

Argonne National Laboratory mortality data are represented by individual records of mice with known birth and death dates and life span measured in days. Only data for control groups of mice were used in the analyses of mortality trajectories.

For both Interventions Testing Program and Argonne National Laboratory data sets, mortality after 1 year of age was analyzed in order to focus on late-life mortality.

Rat Data

Data on rat mortality were taken from the published life tables. Preference was given to life tables compiled for large samples of laboratory rats. Information on mortality of Wistar rats (38,39), as well as Copenhagen and Fisher lines of rats including backcrosses of the latter two lines (40), was analyzed.

Statistical Methods

Age-specific death rates available in HMD were used as empirical estimates of hazard rates in humans. For mice and rats, age-specific death rates were calculated using Stata command “ltable.” Age-specific death rate is also called an actuarial estimate of hazard rate (5,41) and is calculated in the following way (42):

$${\mu }_x=\frac{2(1-p_x)}{\Delta x(1+p_x)}$$ (1)

where µ_x is hazard rate, p _x is conditional probability of surviving through interval (x, x + Δx), Δx is the length of interval.

This estimate provides nonbiased estimates of hazard rate at old ages in contrast to often used 1-year probability of death, which has a theoretical upper boundary equal to one (29).

In the case of humans, weighted nonlinear regression model was applied to age-specific death rates in the age interval 80–106 years. Age-specific exposure values (person-years) were used as weights (43). Mortality data were fitted by the most frequently used models of adult mortality: the Gompertz model (6,44,45) and the alternative mortality deceleration “logistic” Kannisto model (4).

$$Gompertz:{\mu }_x=a{e}^{bx}$$ (2)

$$Kannisto:{\mu }_x=\frac{a{e}^{bx}}{1+a{e}^{bx}}$$ (3)

Here x designates age and a and b are parameters.

Data for men and women were studied separately.

For mouse data, age-specific death rates are calculated for 10-day age intervals and then adult mortality (after age of 1 year) was fitted using Gompertz and Kannisto models. For rat data, age-specific death rates were calculated for age intervals of 50 days for Wistar rats and 1 month for other rat lines.

Goodness-of-fit for the Gompertz and the Kannisto models was evaluated using the Akaike’s Information Criterion (AIC) (46). This criterion is calculated using the following formula:

$$\text{AIC}=\mathrm{2k}-2\ln (L)$$ (4)

where k is the number of parameters in the statistical model, and L is the maximized value of the likelihood function for the estimated model. AIC is widely used as a measure of the goodness-of-fit of an estimated statistical model, and the best model demonstrates minimal value of AIC. It is not the absolute size of the AIC value, it is the relative values, and particularly the AIC differences (Δ_i), that are important in model selection (47). So, both AIC values for each model and AIC differences have been calculated:

$${\Delta }_i={\text{ AIC}}_i-{\text{AIC}}_{\text{min}}$$ (5)

where Δ_i is the AIC difference for the ith model, AIC_i is the AIC value for the ith model and AIC_min is the AIC value for the best model with minimal AIC.

All calculations were conducted using the Stata statistical software, release 11 (48).

Results

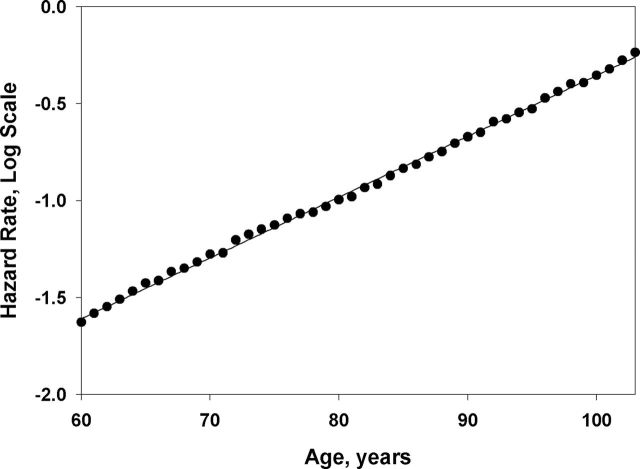
Figure 1 shows age-specific death rates in semi-log scale for 1895 birth cohort of U.S. women. Note that mortality trajectory follows the linear dependence with age in semi-log scale (Gompertz law) up to very advanced ages with no sign of mortality deceleration. In order to quantify this observation, we compared Gompertz and Kannisto models using AIC as a goodness-of-fit measure. The analysis included 11 single-year U.S. birth cohorts (born in 1890–1900 range) and was conducted separately for men and women. The results of this study for men and women are presented in Table 1. Note that in all cases the Gompertz model demonstrates better fit (lower value of AIC) than the “mortality deceleration” Kannisto model for both men and women in the studied age interval 80–106 years. AIC differences (Δ_i) between the best (Gompertz) model and the Kannisto model are higher than 10 for almost all studied birth cohorts. Manuals on model selection suggest that competing models with Δ_i more than 10, compared with the best model with minimal AIC, have little support from empirical data (47). Thus, we may conclude that the Gompertz model is significantly better supported by data on U.S. mortality, compared with the competing mortality deceleration Kannisto model.

Figure 1.

Age-specific hazard rates for U.S. women (1895 birth cohort) fitted by the Gompertz model. Note that mortality fits well with the straight line in semi-log scale, as predicted by the Gompertz model, with no sign of mortality deceleration at extreme old ages.

Table 1.

Testing Two Competing Mortality Models With Human Data

Birth Cohort	Gompertz Model (1)	Kannisto Model (2)	AIC Difference, Δi (2) − (1)
Men
1890	−212.329	−196.489	15.84
1891	−211.914	−189.524	22.39
1892	−218.797	−195.887	22.91
1893	−221.762	−198.028	23.73
1894	−219.283	−200.769	18.51
1895	−232.773	−205.206	27.57
1896	−241.971	−205.407	36.56
1897	−221.926	−198.790	23.14
1898	−237.934	−200.545	37.39
1899	−213.753	−195.510	18.24
1900	−221.477	−193.960	27.52
Women
1890	−212.698	−200.652	12.05
1891	−213.751	−199.934	13.82
1892	−222.666	−199.776	22.89
1893	−219.428	−207.064	12.36
1894	−218.826	−213.570	5.26
1895	−232.062	−212.169	19.89
1896	−236.069	−213.301	22.77
1897	−225.729	−209.820	15.91
1898	−231.468	−210.523	20.95
1899	−216.079	−194.787	21.29
1900	−209.085	−202.302	6.78

Notes: Akaike’s information criterion (AIC) for the Gompertz model and the “mortality deceleration” Kannisto model. Data on U.S. cohort death rates taken from the Human Mortality Database.

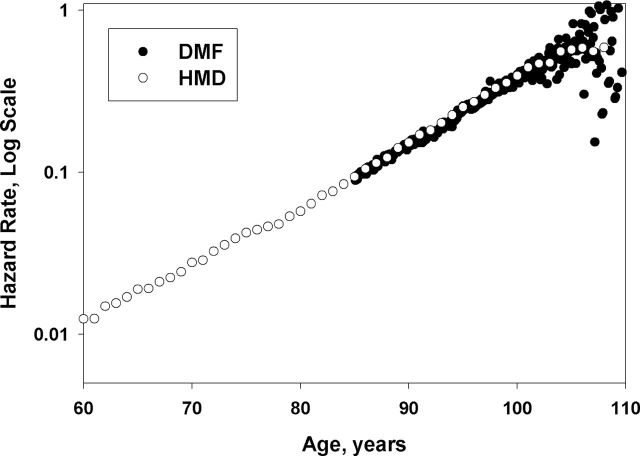
There is a question whether our estimates of mortality based on HMD data are comparable with other sources of the U.S. old-age mortality and whether the slope of mortality trajectories measured at advanced ages is the same as at younger ages. The HMD data are based on the U.S. vital statistics (33). The DMF data are based on the collection of death records available from the Social Security Administration. Figure 2 shows the trajectories of age-specific hazard rates for 1898 birth cohort of women based on data from the HMD and the DMF over a broad age interval starting at 60 years. Note that hazard rate estimates for the DMF birth cohort are practically identical to the age-specific death rates obtained from HMD. Also, note that mortality of DMF birth cohort has the same slope in semi-log coordinates as mortality of HMD birth cohort calculated for much wider age interval. This observation does not support the suggestion about two-stage Gompertz model of mortality with two different slopes at different ages (5,16). Indeed, the maximum likelihood estimation of the Gompertz slope parameter for mortality of 1898 DMF female cohort measured in the interval 85–106 years (0.0946/year, 95% confidence interval: 0.0945–0.0946) does not significantly differ from the slope parameter calculated over the age interval 40–106 years for HMD data: 0.0951/year, 95% confidence interval: 0.0935–0.0968. Thus, we may conclude that the estimates of hazard rates at advanced ages based on individual mortality data (DMF) practically coincide with hazard rate estimates calculated on the basis of age-specific death rates available in HMD.

Figure 2.

Comparison of Social Security Administration Death Master File and Human Mortality Database mortality data for 1898 birth cohort of U.S. women. Note that these two different datasets produce very similar mortality estimates and mortality trajectories in overlapping age interval.

Mouse Data

Figure 3a and 3b show age-specific mortality rates in semi-log scale for male and female mice from the Interventions Testing Program controls. Note the absence of mortality deceleration at advanced ages. Similar results were obtained for the Argonne National Laboratory data on mortality. Table 2 presents values of AIC for the Gompertz and the “mortality deceleration” Kannisto models, which we used to fit mouse mortality data. Note that in all studied mouse populations, AIC for the Gompertz model is lower than that for the Kannisto model, suggesting a better fit for the Gompertz mortality model. Differences in AIC suggest that in five out of eight cases, the Gompertz model has substantially better empirical support, whereas in three cases, both models have a similar data support with AIC differences less than four, still in favor of Gompertz model (47). In the latter three cases, relatively good fit by the Kannisto model can be explained by unusually low mortality at younger ages rather than by mortality deceleration at older ages (see Figure 3b).

Figure 3.

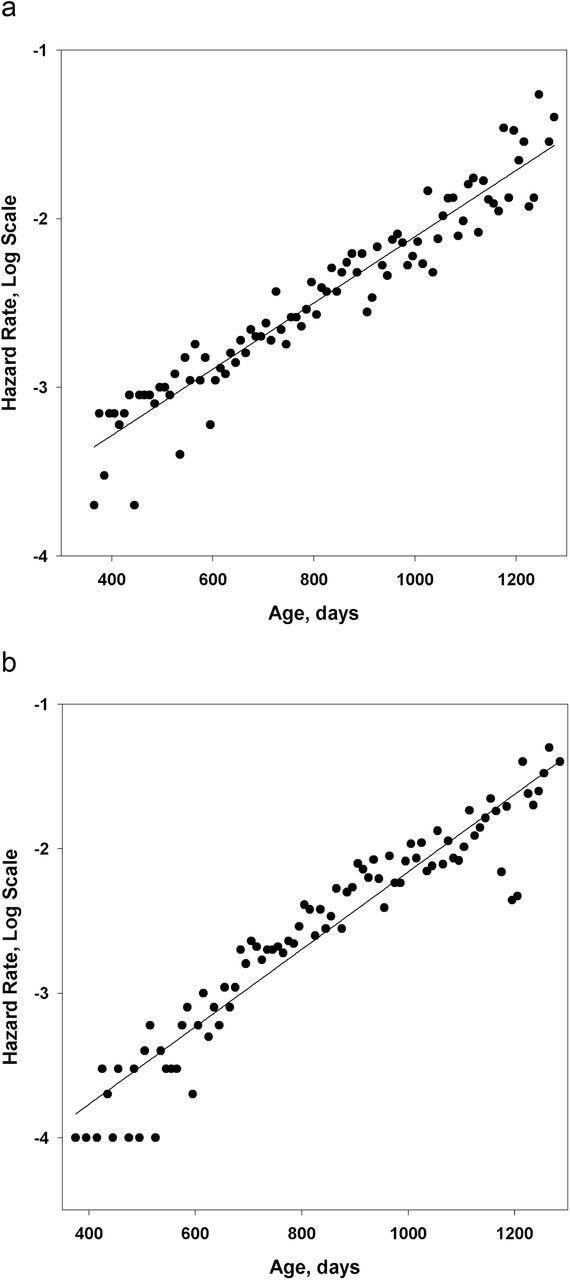
Hazard rate (measured for 10-day age interval) as a function of age. Mouse data, Interventions Testing Program controls. Note that mortality fits well with the straight line in semi-log scale, as predicted by the Gompertz model. (a) Males. (b) Females.

Table 2.

Testing Two Competing Mortality Models Using Data on Mice

Data set	Sex	Cohort Size at 1 Year of Age	AIC		AIC Difference, Δi (2) − (1)
			Gompertz Model (1)	Kannisto Model (2)
ITP data, controls	M	1281	−599.98	−568.12	31.86
	F	1104	−498.95	−497.90	1.05
ITP data, experiments with no significant life extension	M	2181	−663.04	−573.86	89.18
	F	1911	−583.16	−579.73	3.43
ANL data, early controls	M	364	−587.46	−558.79	28.67
	F	431	−568.71	−560.78	7.93
ANL data, late controls	M	487	−642.03	−641.21	0.82
	F	510	−554.43	−550.43	4.00

Note: ITP = Interventions Testing Program; ANL = Argonne National Laboratory. Akaike’s information criterion (AIC) for the Gompertz model and the “mortality deceleration” Kannisto model.

Rat Data

Mortality trajectories for male and female Wistar rats are presented in Figure 4a and 4b. Note the absence of mortality deceleration at older ages in these rat cohorts. The AIC values for the Gompertz and the “mortality deceleration” Kannisto models of rat mortality are presented in Table 3. In all studied rat cohorts, AIC values for the Gompertz model are lower compared with the AIC values for the Kannisto model, demonstrating a better fit of rat mortality by the Gompertz model. Analysis of AIC differences demonstrates substantially better empirical support for the Gompertz model compared with the Kannisto model in all studied cases.

Figure 4.

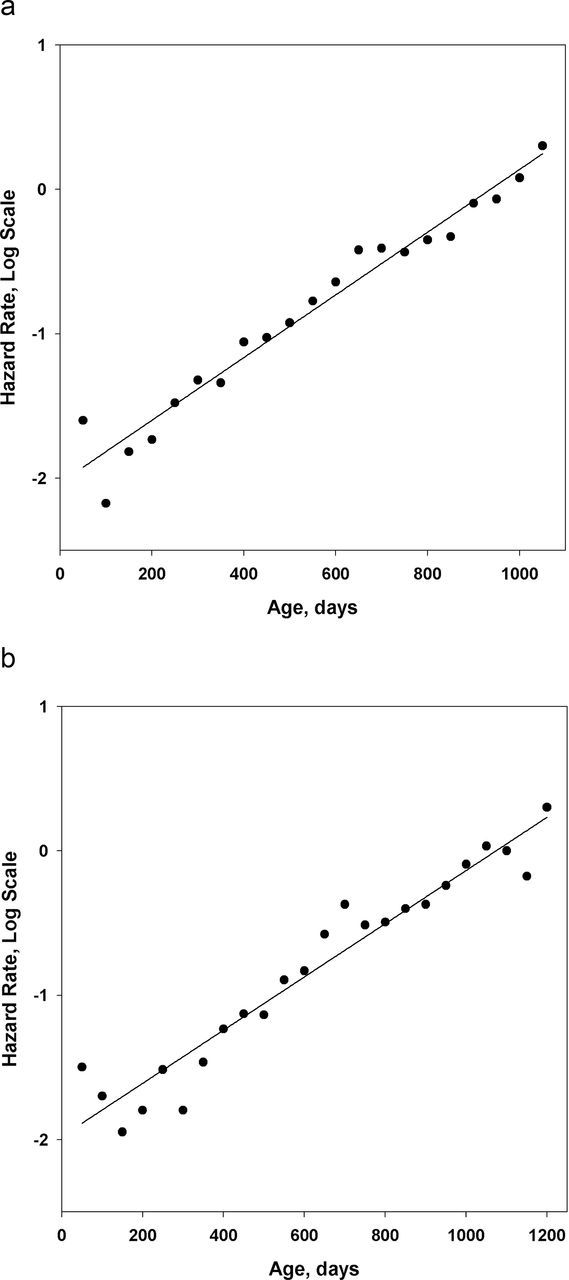
Hazard rate of Wistar rats (measured for 50-day age interval) as a function of age. Data source: Weisner and Sheard (39). Note that mortality fits well with the straight line in semi-log scale, as predicted by the Gompertz model. (a) Males. (b) Females.

Table 3.

Testing Two Competing Mortality Models With Data on Rats

Data set	Sex	Cohort Size at 2 Months of Age	AIC		AIC Difference, Δi (2) − (1)
			Gompertz Model (1)	Kannisto Model (2)
Wistar line (39)	M	1372	−36.38	5.38	41.76
	F	1407	−13.30	3.20	16.50
Wistar line (38)	M	2109	−30.47	2.30	32.77
	F	2035	−56.07	−0.71	55.36
Copenhagen line (40)	M	1328	−14.66	−0.57	14.09
	F	1474	−49.17	−6.61	42.56
Fisher line (40)	M	1076	−19.44	4.43	23.87
	F	2030	−16.19	6.69	22.88
Backcrosses between Copenhagen and Fisher lines (40)	M	585	−21.35	0.99	22.34
	F	672	−41.70	−5.86	35.84

Note: Akaike’s information criterion (AIC) for the Gompertz model and the “mortality deceleration” Kannisto model.

Discussion

We found that the Gompertz model fits adult mortality at older ages (80–106 years) in 22 studied single-year U.S. birth cohorts significantly better than the competing “mortality deceleration” Kannisto model. This result, based on age-specific death rates taken from the HMD, shows that mortality deceleration at advanced ages is negligible up to age of 106 years. Similar results were obtained earlier using mortality data from the Social Security DMF (29). Hazard rate estimates after age 85 obtained from DMF data agree remarkably well with age-specific death rates obtained from the HMD. Some researchers also reported an absence of mortality deceleration at advanced ages for humans, but they did not conduct a systematic study of this phenomenon. For example, Stauffer (49) presents mortality trajectories of German cohorts, which show no mortality deceleration up to 90 years of age. Other researchers found no mortality deceleration at older ages for Canadian cohorts although they hypothesized that this finding may be caused by problems with quality in their data (50). On the other hand, several systematic studies of mortality at older ages conducted in the 1990s came to a conclusion that mortality does decelerate after age 80 (2–4,51).

A number of studies questioned the phenomenon of mortality deceleration at older ages for mammals. Finch and Pike (52) claimed an excellent fit of the Gompertz survival distribution with data from laboratory and domestic mammals. Austad (20) noted that mortality deceleration is not observed for rodents even in the case of very large samples. Similar conclusion was made for mortality of baboons (21) and seven wild primate species (22). Our results demonstrate that mortality deceleration at advanced ages is not a universal phenomenon, which is likely not observed in studied mammalian species. It is interesting that the theoretical maximum life span of humans (121 years) predicted by Finch and Pike (52) on the basis of the Gompertz model is very close to the observed world record of longevity—122 years. This record did not change since 1997 despite significant increase in old-age population. It is also interesting that old-age mortality in the studied U.S. birth cohorts follow the Gompertz model despite substantial improvement of mortality over time. One possible explanation of this puzzling observation may be an assumption of accelerating age pattern of individual mortality rates in excess of the Gompertz model (steeper than the Gompertz mortality trajectory). Right now, accelerating mortality patterns are not observed in human populations, but such patterns may appear after significant improvement in age reporting at older ages.

Some biologists strongly believe that late-life mortality deceleration and mortality plateau (or “aging cessation”) is a universal property of biological systems caused by plateaus in the forces of natural selection (53). Others came to the opposite conclusion. For example, Strehler (54) suggested four criteria of aging process: (a) universality, (b) intrinsicality, (c) progressiveness, and (d) deleteriousness, which do not leave any possibility of aging reversal or cessation.

There are several reasons why earlier studies, including our own research (6,55), reported mortality deceleration and mortality leveling-off at advanced ages (2–4,56,57). First, mortality deceleration in humans may be caused by age misreporting in death data for older persons (26,29). We may expect gradual improvement in age reporting over time and hence less frequent patterns of mortality deceleration in more recent birth cohorts.

Second, mortality deceleration may be a consequence of data aggregation producing a highly heterogeneous sample. Few people survive to advanced ages, and, in standard mortality tables, it is frequently necessary to compile data over an entire decade to obtain a sufficiently large sample. In the case of continuous mortality decline, such aggregation results in highly heterogeneous data. Variability in human data and its effects on the slope of human mortality were discussed some time ago by Strehler and Mildvan (58) using definitions from their mortality model. According to their model, individuals with lower vitality die out first resulting in declining slope of mortality at advanced ages. On the other hand, certain combination of parameters in their model resulted in accelerated trajectory of mortality with age (58). Recently, acceleration of mortality in human populations were also studied by Carnes and Witten (59). Also, Carnes and colleagues demonstrated that the Gompertz model can be extended to lower ages using intrinsic mortality rates (60)

Finally, many empirical estimates of hazard rate (and probability of death in particular) produce biased results (underestimation) at very advanced ages when mortality is particularly high and changes rapidly. Note that the famous Gompertz law was suggested to fit hazard rate (mortality force), rather than probability of death (45). Still many studies of human mortality trajectories use 1-year probabilities of death rather than hazard rate (57,61–65). Estimates of 1-year probability of death and hazard rate are numerically close at younger adult ages when death rates are relatively small and do not change rapidly. However, after 80–85 years of age, probability of death shows a tendency of deviation from the hazard rate, and it has a theoretical upper limit equal to one. In order to get more accurate estimates of hazard rate after 80 years of age, probability of death should be estimated for monthly rather than yearly age interval (29). Researchers often overlook this problem.

Loss of individuals to follow-up in longitudinal study may also be a factor contributing to apparent spurious mortality deceleration at advanced ages (32). It appears that age exaggeration, use of inappropriate estimates of hazard rates, and, perhaps, data aggregation could lead to downward biases in mortality estimates at older ages for humans reported in previous studies.

Some limitations of our study should be acknowledged. First, we studied mortality of only three mammalian species although information on these species is commonly collected in longevity studies. Second, insufficient quality of age reporting for human data prevented us from mortality measurement after 106 years of age. Data on validated international records of longevity beyond 106 years of age do exist and are being collected in the International Database on Longevity (66). This database contains life-span information on more than 600 long-lived persons with validated age from over 11 countries born in 1852–1899. Gampe (62) analyzed mortality after 110 years of age for 224 supercentenarians from International Database on Longevity and obtained almost flat age trajectory for hazard rate. This result can be explained by significant heterogeneity of the studied sample and by applying discrete duration model to hazard rate estimation where hazard rate is treated as probability and hence may be biased downward (67). However, we cannot completely exclude possibility that hazard rates may decelerate at very advanced ages because right now it is not possible to test this hypothesis using high-quality homogeneous data on human mortality after 110 years of age.

Conclusion

We found that mortality at advanced ages in three mammalian species (humans, rats, and mice) follows more closely the Gompertz rather than the “mortality deceleration” Kannisto model. This result suggests that mortality deceleration at older ages is not a universal phenomenon and that mammals in particular demonstrate very weak evidence for mortality plateaus. These findings may represent a challenge to existing theories of aging and longevity, which predict slowing down of mortality growth in the late stages of life (14,15,53). One possible way for reconciliation of the observed phenomenon and the existing theoretical consideration is a possibility of mortality deceleration at very high yet unobservable ages. It should be also recognized that different biological species might have different patterns of mortality at older ages.

Funding

This work was supported in part by the National Institute on Aging (R01 AG028620 to L.G.).