Applications of computational models to better understand microvascular remodelling: a focus on biomechanical integration across scales

Abstract

Microvascular network remodelling is a common denominator for multiple pathologies and involves both angiogenesis, defined as the sprouting of new capillaries, and network patterning associated with the organization and connectivity of existing vessels. Much of what we know about microvascular remodelling at the network, cellular and molecular scales has been derived from reductionist biological experiments, yet what happens when the experiments provide incomplete (or only qualitative) information? This review will emphasize the value of applying computational approaches to advance our understanding of the underlying mechanisms and effects of microvascular remodelling. Examples of individual computational models applied to each of the scales will highlight the potential of answering specific questions that cannot be answered using typical biological experimentation alone. Looking into the future, we will also identify the needs and challenges associated with integrating computational models across scales.

1. Introduction

The design of effective therapeutic strategies aimed at manipulating the microcirculation requires a better understanding of microvascular remodelling, which involves both angiogenesis, defined as the sprouting of new capillaries, and network patterning associated with the organization and connectivity of existing vessels (figure 1). In multiple pathologies, such as cancer, proliferative retinopathies and rheumatoid arthritis, blocking remodelling would be beneficial. In others, such as myocardial infarction, stroke and hypertension, promoting remodelling would be desirable. Development of these types of therapies requires a better understanding of each subprocess involved in microvascular remodelling and, just as important, knowledge of how each subprocess is coordinated across a network. From tissue-level patterns and vessel networks to multiple cell types and spatially patterned molecular cues, microvascular remodelling integrates multiple components across different levels of biological scale (figure 2). A key obstacle to advancing our understanding is the inability to probe the specific component-level effects when biological experiments fall short of providing the necessary spatial and temporal resolution to measure multiple metrics over the time course of a response. So a critical question emerges: How can we gain new information when our experimental observations are often limited by noise and resolution? One answer is computational models.

Figure 1.

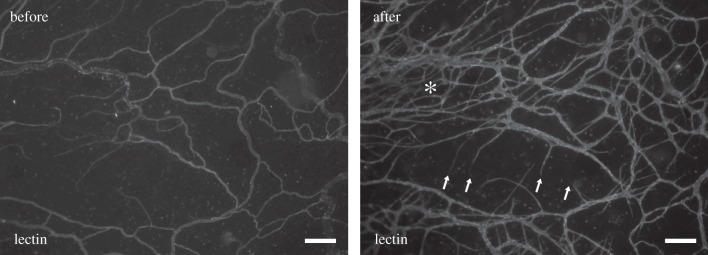
Example of an adult rat mesenteric microvascular network before and after angiogenesis. Time-lapse comparison of images from the same network was obtained using the rat mesentery culture model [1]. Asterisk (*) indicates regions of increased vessel density. Arrows indicate new capillary sprouts. The network-level comparison exemplifies the spatial heterogeneity within a network and the need to investigate local environmental differences within a tissue during microvascular remodelling. Scale bars, 200 μm.

Figure 2.

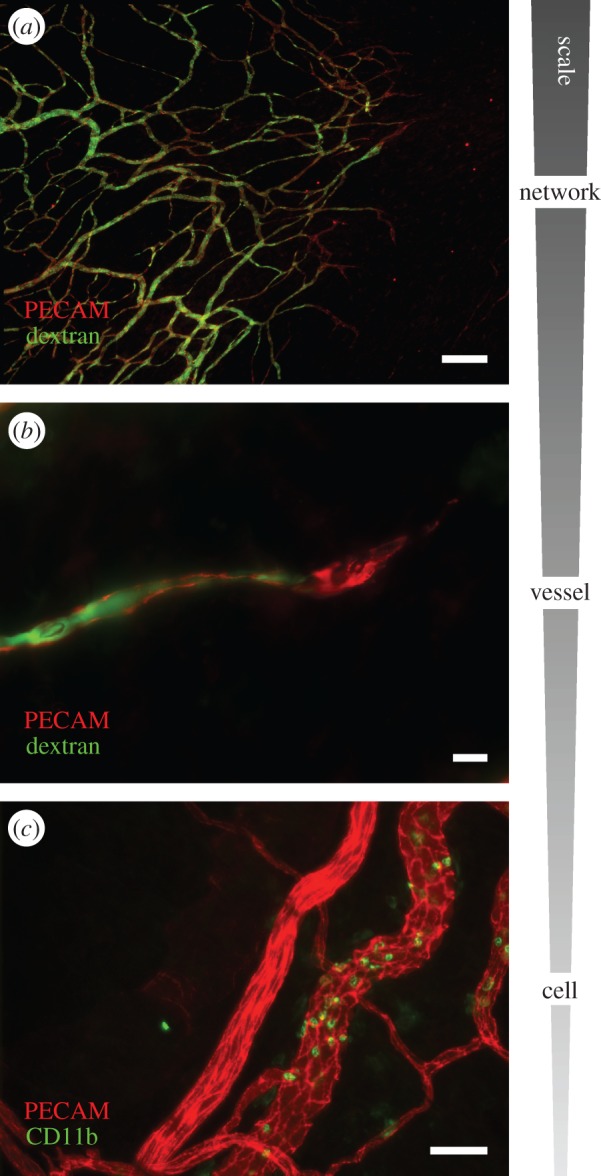
The complexity of microvascular remodelling spans multiple scales. (a) An image of a perfused microvascular network post-angiogenesis. PECAM labelling identifies all the vessels within the network and injected-dextran labelling indicates that even the newest formed vessels are patent. Scale bar, 200 μm. (b) A PECAM-positive capillary sprout perfused with dextran. Scale bar, 10 μm. (c) Example of CD11b-positive monocytes/macrophages along venules versus arterioles in an adult microvascular network. The differential adhesion of WBCs in vessel-specific locations further emphasizes the importance of cell dynamics in vessel- and network-level haemodynamics. Scale bar, 50 μm.

The objective of this article is to present examples of computational applications that have provided new insights at the network, vessel, cellular and molecular levels for advancing our understanding of the underlying mechanisms and effects of microvascular remodelling. By presenting different modelling examples together, a new opportunity becomes obvious—the linking of computational models together in order to span biological scales in a way that is otherwise unachievable using experimental approaches alone. Accordingly, we will also identify the challenges associated with multiscale modelling. In comparison with existing reviews that extensively cover the full scope of modelling [2–5], this article serves to give a snapshot of five important and very different computational modelling approaches that have been developed to answer questions that cannot be answered experimentally. We submit that computational models can create new information and can offer a quantitative interpretation of the literature that guides new directions of research.

2. Multiscale components involved in microvascular remodelling

Microvascular remodelling is a general term which is used to describe an adaptation of the microcirculation at either the network, cellular or even molecular level. Traditionally, microvascular remodelling is delineated into three processes: vasculogenesis, angiogenesis and arteriogenesis [6,7]. Vasculogenesis refers to the formation of blood vessels from undifferentiated precursor cells. This process is most often associated with vascular development during embryonic development, yet recent work has suggested a potential role for the recruitment of vascular precursor cells to either endothelial or pericyte cell locations along neovessels in the adult [8–11]. Angiogenesis is the sprouting of capillaries from pre-existing vessels and involves endothelial cell interactions with the local environment and other cell types, including existing perivascular, circulating and tissue resident precursor cells [12]. The involvement of more than a single cell type in angiogenesis is emphasized by the limited efficacy of using single-molecule approaches in the treatment of myocardial ischaemia [13,14] to promote functional growth of new vessels. Finally, arteriogenesis is a related process that encompasses pericyte recruitment to capillaries, differentiation of pericytes into more mature smooth muscle cells (SMCs) and vessel enlargement [15,16]. In a broad sense, arteriogenesis can also include the subsequent maintenance of arteriole versus venous identity.

Considering the three subprocesses of vasculogenesis, angiogenesis and arteriogenesis, microvascular remodelling can be thought of as involving a host of biological components and processes: endothelial cells, pericytes, SMCs, precursor cells, white blood cells (WBCs), red blood cells (RBCs), macrophages, growth factor production, growth factor receptor–ligand binding, intracellular signalling, cell contraction, mechanotransduction, fluid dynamics, permeability, inflammation, genetic and epigenetic gene regulation and a multitude of others, with the functional targeting of each subprocess, cell or molecule potentially representing a therapeutic strategy.

The complexity of the coordinated orchestra of subprocesses is appreciated when one can observe the cumulative effects of components at the network level. To exemplify this point, let us consider the comparison of the same rat mesenteric network before and after angiogenesis (figure 1). The rat mesentery is a unique tissue that contains three-dimensional networks within a 20–40 µm thick connective tissue, thus enabling visualization of remodelling subprocesses over different spatial locations within a network (figure 2). The observation of new vessel sprouting from specific vessels at discrete regions of a network highlights the importance of understanding how local environments influence network-level behaviour. For example, consider that specific locations of WBC adhesion within different vessel types can impact local haemodynamics at the vessel level. The local haemodynamics can then influence flow patterns at other locations across the network. The complexity of microvascular remodelling can be further appreciated by considering the fate, function and roles of other cell types such as macrophages, fibroblasts and circulating progenitor cells, whose behaviours affect and are affected by the microvascular network. And we cannot neglect that multiple other systems, such as the nervous and lymphatic systems, interact with the vasculature during angiogenesis. Our ability to make sense of how all of these components interact (networks, vessels, cells and molecules) requires us to understand how they are spatially and temporally integrated within a system and across systems. While this review will fall short of providing a comprehensive platform for accomplishing this, we will describe specific questions motivated by experimental observations at different scales across a microvascular network (figure 3) in an attempt to introduce the need for such integration. Undoubtedly, further investigation of each subprocess and specific cell behaviours is warranted, but it will be just as necessary to dynamically integrate our learned understanding, and computational modelling offers an attractive approach—if not the only approach currently to do so.

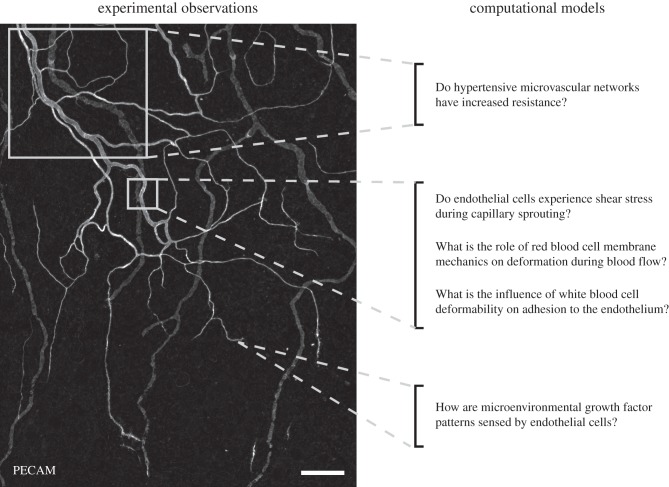
Figure 3.

Consideration of experimental observations across intact microvascular networks motivates physiological questions at the network, vessel, cellular and molecular level. This review article highlights a subset of these questions that are answered with the use of a computational model. The image shown was obtained via PECAM labelling of an adult rat mesenteric network to identify blood and lymphatic vessels. An advantage of this tissue type is that it allows visualization down to the single-cell level at different locations. The spatial heterogeneity and need for considering discrete locations within a network are exemplified by the structural differences in vessel and cellular morphologies along arterioles, venules and capillaries. Scale bar, 200 μm.

3. Computational modelling examples

In this section, we summarize five different computational modelling studies that span the components of the microcirculation (figure 4). In doing so, we will consider the interrelationships between endothelial cell growth factor receptor binding, blood cell biomechanics, flow through a capillary sprout and whole network-level patterning. For each example, we identify the question, physiological motivation, the modelling approach and the gained insights that have come from modelling the biology using mathematical and computational approaches. While our sampling from the literature is incomplete and insufficient for portraying the extensive role that computational modelling has played in helping us to understand microvascular growth and remodelling, the selection of examples we review here attempts to represent the breadth of questions being addressed in different subfields and showcases their interrelated importance.

Figure 4.

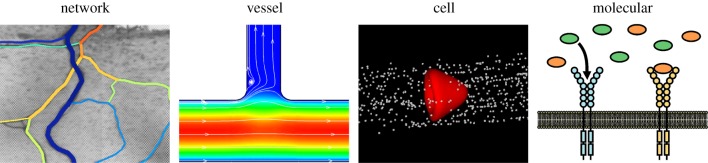
Multiscale components of the microcirculation. Computational modelling applications at the network, vessel, cell and molecular levels provide valuable insights for scenarios in which in vivo experimentation is limited. The differences in modelling theory represent the future challenge in their integration across scales.

3.1. Network level: do hypertensive microvascular networks have increased resistance?

An advantage of computational models is the ability to isolate the contributions of individual parameters to an overall response. In this example, we will examine a case of microvascular alterations during a pathological scenario—hypertension. Hypertension, defined by increased blood pressure, has been clinically linked to an increased risk of stroke, myocardial infarction, heart failure, renal disease and mortality [17]. Furthermore, in animal models, hypertension has been associated with increased oxidative stress, greater numbers of activated circulating leucocytes, elevated capillary flow resistance, impaired selectin-mediated leucocyte adhesion and widespread endothelial cell apoptosis [18–20]. A common characteristic of hypertension is microvascular rarefaction, defined as the anatomical loss of microvessels. Based on the logical assumption that reduced vessel density correlates to a reduced number of parallel resistance pathways, rarefaction is often assumed to contribute to increased network resistance. Yang & Murfee [21] identified that, in adult rat mesenteric networks harvested from spontaneously hypertensive rats, the patterning alterations are more complex than just vessel loss. Compared with normotensive controls, hypertensive networks contained an increased number of arterial/venous connections, which would serve to reduce network resistance by way of low-resistance pathways from the high- to low-pressure sides of the network. Thus, the effects of the hypertension-associated patterning alterations, including both a decrease in the number of vessels and an increase in arterial/venous connections, remained unclear. In light of the experimental challenges of isolating network pattern versus diameter or viscosity changes, computational modelling proved to be a useful tool.

Based on segment lengths, branching locations and an assumed pressure drop, resistance per network was calculated using a simple segmental resistance model previously established by the laboratories of Secomb and Pries to isolate topological details (i.e. vessel patterning or organization) versus geometrical details (i.e. vessel diameters and lengths) [22]. Segment nodal positions were identified across intact adult hypertensive and normotensive networks, which were immunohistochemically labelled and imaged. Then input and output pressures were assigned to the input arterioles and output venules, respectively, and network and segmental flows were calculated assuming a modified Poiseuille flow relationship. For each segment, the apparent viscosity was updated to account for changes in haematocrit in branching vessels based on empirical data reported by Pries and Secomb using intravital microphotometric evaluation and optical density measurements from the rat mesenteric microcirculation [23–25]. Satisfying the conservation of mass at each node, the nodal pressures and flows were determined. The total network resistance was calculated by dividing the total pressure drop by the total flow through the network.

The network resistances in the hypertensive and normotensive networks were not significantly different. Interestingly, only when the arterial/venous shunts were removed from the hypertensive networks was a decrease observed. The results from this study challenge the common paradigm that microvascular patterning changes during hypertension cause increased resistance and highlight the value of applying a simple computational approach to isolate network-level parameters to gain insights that would be highly challenging to evaluate in vivo. Applications of similar models have also proved useful for investigating network-level haemodynamic changes associated with diabetes, exercise and multiple other scenarios [25–29]. And, more recently, Secomb et al. [30] have since extended their classical network-based model to include essential parameters for angiogenesis, allowing for the analysis of endothelial cell sprouting in response to specific growth factors coupled to structural relations and biochemical stimuli. An opportunity to build on this pioneering work is to include local anatomical details that accurately predict vessel- and cell-specific haemodynamics. And it goes without saying, an opportunity with as much impact exists for integrating vessel-level models based on different computational approaches [31–33].

3.2. Vessel level: do endothelial cells experience shear stress during capillary sprouting?

Haemodynamics, and in particular shear stress due to the fluid viscous forces, affects endothelial cell function and differentiation. Based on in vitro flow chamber experiments largely motivated by atherosclerosis scenarios [34,35] and in vivo animal models in which local fluid velocity within individual vessels has been assumed to be increased [36–39], evidence strongly supports that shear stress is a critical regulator of many, if not all, of the endothelial cell dynamics associated with angiogenesis. In recent years, microfluidic angiogenic assays have more directly linked shear stress stimuli to endothelial cell sprouting [40]. However, important questions still remain: Do endothelial cells along a capillary sprout experience a shear stress, and, if so, does the magnitude of shear stress differ depending on the location along the sprouting cell?

These questions are difficult to answer experimentally because of technical challenges associated with intravital measurement of flow profiles within a sprout. Stapor et al. [41] recently used a computational fluid dynamic approach to estimate the shear stress distribution along a blind-ended vessel. Before Stapor et al.'s work, computational/mathematical models had been used to investigate the effects of rigid and elastic spheres in straight tubes and at bifurcations [42–45], but these types of models had not been applied to flow in a blind-ended capillary sprout.

Using a three-dimensional computational fluid dynamic model and a finite volume method, velocity profiles and wall shear stress distributions were determined along blind-ended channels that sprouted off parent vessels. Both the blind-ended and parent vessel geometries were based on geometry measurements made from intact adult microvascular networks. The shear stress and shear stress gradients were simulated for three cases: (i) a non-permeable wall, (ii) a uniformly permeable wall, and (iii) a non-permeable wall with open slots representative of endothelial cell clefts. Shear stresses at the sprout entrance were predicted to range from 8 to 10 dyne cm⁻² and stresses decreased below 0.2 dyne cm⁻² (a value identified as being a physiological threshold for endothelial responses [46]) within the initial 10% of the sprout length. For two cases, shear stresses within the sprout were elevated: at the open slots, representative of interendothelial cell clefts, the shear stress magnitude was 5.9 dyne cm⁻²; and for cases of longer sprouts, shear stress magnitudes remained above 1 dyne cm⁻².

The computational results by Stapor et al. provide a first estimation of shear stress magnitudes and emphasize the value of applying similar approaches to estimating local shear stress distributions due to transmural or interstitial flows over endothelial cells. The application of computational fluid dynamic models offers a method to build intuition that can then be applied to the reductionist in vitro experiments and might give us a better appreciation of what the values of shear stresses in those experiments mean for the context of capillary sprouting. Consider the paradigm of endothelial tip cells versus stalk cells along a capillary sprout—a topic which has recently emerged at the forefront of vascular biology research and consummately been reviewed by others [47–49]. Tip cells are non-proliferative and sense local chemical cues and guide the sprout. Stalk cells are proliferative and in essence are seen as the pushers along a sprout. But—can tip versus stalk cell phenotypic differences be explained by shear stresses? To answer this question, we must first know the shear stress magnitudes that each cell type experiences, and the work by Stapor et al. suggests that the answer depends on sprout length and/or endothelial cell junction details. And, maybe more importantly, consideration of the local mechanical cues sensed by endothelial cells motivates the future opportunity to couple computational fluid dynamic models with other endothelial cell models, such as those concerning tip cell selection [50].

3.3. Cell level: what is the role of red blood cell membrane mechanics on deformation during blood flow?

The estimation of shear stress along capillary sprouts is complicated by including the effects of RBCs. Logically, RBC flow by the entrance of a blind-ended sprout or even within a sprout would impact local shear stress and shear stress gradient magnitudes. Indeed, Stapor et al. [41] suggested that RBC flow within a host vessel resulted in local maximum magnitudes at the sprout entrance. RBC plugging of the sprout served to shorten the effective sprout length and similarly influenced magnitudes depending on the wall permeability scenario. But, the study failed to realistically consider RBC deformability and its effects on blood flow. For this question, we have to move away from microvascular research and enter the areas of biophysics and blood rheology—three research areas that have not historically overlapped with one another.

A single RBC consists of an outer viscoelastic cell membrane and an inner viscous fluid with a non-zero excess surface area, and thus it deforms under the blood flow where the mechanics of the cell membrane plays a major role. Based on the observation of relatively large deformations of RBCs in response to external forces such as those applied by micropipette aspiration, viscous shear flow and optical tweezers, the constitutive equations for the cell membrane have been identified with a set of elastic constants. Another major factor that could determine elastic deformation of the membrane is the zero-stress configuration or natural state. However, as deformations of RBC membranes at the zero-stress configuration are relatively small and difficult to measure in biological experiments, determining the relative contribution of this state requires computational simulations.

An RBC can be modelled as a capsule, defined as a fluid drop encapsulated by a surface membrane with the elastic mechanics of the surface membrane broadly characterized by in-plane shear and area dilatation deformations and out-of-plane bending deformation. For the natural states of the elastic membrane, two configurations have been commonly assumed: a biconcave disc, which is the shape of a normal RBC (i.e. discocyte), and a sphere, which is the shape of a reticulocyte (precursor of a mature RBC). Recently, Tsubota & Wada [51] proposed intermediate shapes between a sphere and biconcave discoid shape determined by linear geometrical interpolation between the two shapes with the spatial non-uniformity parameter α for a model of the membrane's natural state with respect to in-plane shear deformation, while the natural state with respect to out-of-plane bending deformation was assumed to be a flat plane. Tsubota and Wada demonstrated that, given an ideal tank-treading (TT) motion under viscous shear flow of Reynold's number 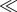1 (i.e. Stokes flow), an additional membrane elastic force generated due to the motion monotonically increases with increasing α of the cell membrane. By using direct numerical simulations with a particle method for a coupled problem between cell membrane deformation and viscous fluid flow [52], Tsubota & Wada [53] confirmed that transition between TT and tumbling (T) motions under viscous shear flow occurs when the additional elastic force during the TT motion is compatible with the viscous fluid force. In addition, Tsubota et al. [54] identified a critical fluid shear force at which a transition between TT and T motions of an RBC occurs in in vitro experiments by using a boundary element method and assuming the experimentally measured elastic moduli. Based on another simulation by Tsubota et al. [54], the moderate non-uniformity of the membrane's natural state is also necessary to maintain a biconcave discoid shape of a normal RBC at an equilibrium state in a stationary fluid, otherwise an RBC takes a cupped shape of a diseased state (i.e. stomatocyte) for a spherical natural state or more flattened discoid shape for a biconcave discoid natural state (α = 1). In simulating the equilibrium shape mechanics, the membrane's bending rigidity at the transition of equilibrium shapes from the biconcave disc to the cup is different by an order of magnitude, depending upon the type of bending model employed, and thus a choice of bending models should be paid great attention [55].

This focus on single RBC mechanics provides valuable insight for understanding blood rheology in capillaries, pre-capillary arterioles and post-capillary venules, where RBCs move in a single-file line. However, blood also consists of RBCs, WBCs and platelets, and the intercellular interactions can be viewed as just as important for influencing local haemodynamics. For example, interactions between multiple RBCs, RBCs and WBCs, and RBCs and platelets have substantial effects on blood rheology [52]. They are responsible for the increased concentration of RBCs near the flow centreline and WBC and platelet margination (cell migration to vessel wall margins) [56–61]. While blood cell dynamics can be qualitatively observed experimentally, the mechanistic contributions to cell mechanics or hydrodynamic interactions remain difficult to evaluate. To this end, a number of computational models have recently been developed to simulate WBC mechanics [62] and the interactions between RBCs and WBCs in microvessels or microchannels [63–68]. These models predict that the high deformability of RBCs is the main reason why RBCs push out WBCs and platelets from the centreline to the vessel walls.

3.4. Cell level: what is the influence of white blood cell deformability on adhesion to the endothelium?

Given the importance of inflammation, macrophages and circulating precursors to the different subprocesses of microvascular remodelling, consideration of blood cell dynamics also warrants additional discussion of WBC adhesion to the endothelium. We know that the adhesion of single WBCs serves to disturb blood flow, substantially increases flow resistance in small vessels, and, of course, plays a critical role in inflammation. Yet, just as in the case of needing computational models to elucidate the influence of RBC mechanics on deformability during flow, computational models are needed to investigate the effects of WBC mechanics on the leucocyte adhesion cascade. To this end, a number of computational models have been proposed to simulate receptor-mediated rolling and adhesion of WBCs to vascular endothelium. Most of them are rigid cell models [64,69–72], applicable to study WBC rolling and adhesion at low, subphysiological shear stresses. In order to more realistically predict the influence of WBC mechanics on rolling and adhesion, three-dimensional models of deformable WBCs have been developed. In these models, a cell is treated as a liquid capsule in which the bulk of the cell has the same properties as the extracellular fluid and cell deformation is controlled by the mechanical properties of its membrane or cortical layer [73,74] or as a compound liquid drop with cortical tension and bulk viscoelasticity of the nucleus and the cytoplasm [75,76].

To understand how WBCs, as well as RBCs and even platelets, contribute to microvascular remodelling, we need to know the mechanical and adhesive properties of these cells during their circulation in vivo [77]. As blood is a highly heterogeneous suspension of cells and there is a significant level of heterogeneity in vascular endothelium, the measurements of the properties of individual cells or a small group of cells from intravital images or related in vivo data remain a big challenge. Computational models integrated with in vivo experiments are one of the most promising ways to extract the in vivo properties of blood cells. A recent achievement in this area of research is the viscoelastic cell adhesion model (VECAM), the first three-dimensional computational algorithm for receptor-mediated deformable leucocyte rolling and adhesion in shear flow that integrates the experimentally tested rheological models of WBC cytoplasm and nucleus, extension and tether pulling from WBC microvilli, cortical tension and stochastic receptor–ligand binding kinetics [78]. VECAM predicts the existence of the critical cytoplasmic viscosity above which circulating WBCs cannot adhere to the endothelium and shows that a decrease in the cytoplasmic viscosity leads to a decrease in the rolling velocity, drag and torque due to the formation of a large, flat area of WBC–endothelium contact [78]. Insights such as these provide valuable information for understanding why WBC and circulating precursor cell trafficking to specific locations in a network might be impaired when cell properties are altered in a given pathological scenario.

3.5. Molecular level: how are microenvironmental growth factor patterns sensed by endothelial cells?

The regulation of network patterning, capillary sprouting, vessel diameter, vessel permeability and other microvascular remodelling dynamics is additionally finely tuned by a complex set of growth factor interactions at the molecular level. As an example of this complexity, we will examine the vascular endothelial growth factor (VEGF) family, members of which communicate a message of hypoxic distress from a parenchymal or stromal cell to the local vasculature [5]. Once secreted by the hypoxic cell, these factors diffuse through the basement membranes and extracellular matrix in the interstitial space, ultimately binding to receptor tyrosine kinases on the ablumenal surface of an endothelial cell.

The complexities of VEGF include the following partial list [79]. First, five VEGF family genes encode dozens of splice isoforms, each with different affinity for the various VEGF receptors. It is necessary to account for them all, as this competition determines the downstream outcome. Second, three genes encode receptor tyrosine kinases—the VEGFRs—that bind the VEGF ligands; plus, two genes encode isoform-specific co-receptors (the neuropilins). This competition among receptors means that relative expression of the receptors, which can be heterogeneous, is key to their response. Third, binding to extracellular matrix proteoglycans can transiently immobilize and store VEGF. This alters VEGF patterning, while immobilized VEGF can also bind VEGF receptors and produce signalling that is different from soluble VEGF. Fourth, VEGF receptors are present on multiple cell types—not just the target endothelial cells, but also stromal cells such as neurons, glia and SMCs, and parenchymal cells in certain tissues including many tumours. These alternative sinks for VEGF provide a clearance path that alters microgradients, while also providing survival signalling to the expressing cell. Fifth, soluble receptors can sequester VEGF and increase cell-receptor-mediated clearance without signalling; these diffusible sinks can also modify local gradients of available VEGF and active receptors.

Understanding the local microenvironment—in this case, the local gradients of VEGF and sFlt1 near blood vessels—is key to understanding what the cells ‘see’, which is to say, what the cell can sense about its environment. Receptor ligation and activation is the first step, and this is controlled by local VEGF concentrations and patterns. But these microgradients are not currently directly measurable using experimental means; while some growth factor gradients have been visualized in situ [80,81], these are monotonic gradients over longer distances. Instead, we need computational models to bridge this experimental gap. One approach is the use of nonlinear partial differential equations to simulate the local gradients of soluble and matrix-bound VEGF and sFlt1 in the interstitial space, and the gradients of ligand-bound, activated VEGF receptors on blood vessels in the region of interest [82–87]. The input data for these models include: a detailed molecular interaction network; cell-type-specific gene expression and secretion rates; cell-type-specific receptor protein expression; and image-based microanatomy. Simulations of VEGF gradients in skeletal muscle have shown that gradients are present even at rest (due to heterogeneity in tissue structure) [82] and are accentuated by exercise [83,84]. The simulations further showed that gradients were driven by receptor density, and this suggests an alternative biomimetic method enhancing angiogenesis: increasing receptor expression [85]. Zooming in on the microenvironment surrounding sprouting vessels, simulations further showed that the differences among VEGF isoforms that contributed to the formation of their distinct gradients were not those expected; in particular, clearance by non-endothelial receptor expression was predicted to be the primary mode of gradient formation [86]. In simulations of vascular development in embryoid bodies, endothelial secretion of soluble VEGF receptor-1 formed a gradient in the opposite direction to VEGF, which decreased VEGFR activation but also altered the gradient of VEGFR activation on the blood vessel surface [87]. These effects were shown to be accentuated by the proximity of vessels to each other, suggesting a possible mechanism for sprout divergence. Overall, these results emphasize the value of using a computational modelling approach to gain insight into underlying molecular mechanisms of microvascular remodelling that we cannot observe experimentally and, perhaps more importantly, the application of such in silico views offers possible explanations for the specific cellular-, vessel- and network-level dynamics which we can observe.

4. Integration of models across scales: future needs and challenges

The five examples described in §3 have proved useful for providing new information, yet each is limited by its necessary simplifying assumptions (as is the case for all computational and mathematical models). The network-level model example accounts for vessel-specific changes in haematocrit, but does not account for the RBC membrane mechanics, the presence of WBCs or transient microdomain changes due to growth factor gradients. It also does not account for flow in blind-ended sprouts, which, as the vessel-level example demonstrates, could be substantial due to growth-factor-mediated cell–cell junction adaptation and increased permeability. And, to really develop a comprehensive model of a microvascular network, do we need to include the role of the glycocalyx shedding [88,89], vascular network metabolism [90], platelet aggregation, vasoreactivity or other dynamic events at different levels of scale (e.g. gene expression)? Additional questions become apparent when one reviews the different models together. Can the effects of WBC or RBC deformation on flow through a vessel impact tip cell recognition of local growth factor gradients? Can vessel organization within a network influence the location or extent of stalk cell proliferation? The answers to these questions are likely to be ‘yes’. However, we lack many of the tools that are necessary for answering these questions experimentally. Perhaps it is possible to leverage computational modelling in order to integrate the necessary complexity by linking models across spatial and temporal scales. Models that integrate phenomena/mechanisms at one level of scale can predict outcomes at higher levels of scale, so intuitively it makes sense that it would be possible to couple different models together to achieve multiscale integration.

When we think about integrating models across scales, an obvious issue is interscale connectivity, which can be pragmatically viewed as intermodel connectivity. In the face of this challenge, the need for integration across spatial and temporal scales has emerged as an emphasis for modelling microvascular remodelling [33], as well as other areas of research outside the vascular system [91,92]. One promising platform is agent-based modelling (ABM), in which discrete cells behave autonomously based on a set of rules. Because each set of rules can be based on biological experiments or outputs from an embedded computational model running either in parallel or iteratively, this approach offers attractive flexibility and is well equipped for linking, or coupling, models at different levels of scale. For the rest of this section, we will focus on ABM, yet we recognize that other modelling platforms based on continuum approaches can prove just as useful in this regard. As one example, Kapela et al. [93] suggest a paradigm for modelling vasoreactivity using continuum models based on finite-element analysis to account for the spatial heterogeneity at each scale, from intracellular and cell membrane dynamics to whole cells. In this article, we chose to focus on ABM because it is particularly well suited for modelling emergent phenomena, such as growth and remodelling of a tissue or microvascular network [94].

ABM can be used to simulate the behaviours of individual cells, such as endothelial cells, SMCs, pericytes, immune cells and stromal cells, as well as their interactions with one another and with the tissue environment [95–99]. As a multi-cell modelling technique situated in-between the scales that are of most interest to the small blood vessel field (nm through mm), ABM has been positioned as a linker that can bridge modelling approaches focused on molecular interactions with modelling approaches that deal with the tissue-level scale [100,101]. The earliest of these multi-scale modelling attempts are being used to study how key molecular signalling pathways in sprouting angiogenesis, such as VEGF and NOTCH-Delta-like ligand-4 (DLL-4), interact to induce endothelial cell behaviours that lead to new vessel formation [94,102,103].

Coupling ABM with other modelling approaches to form a truly unified multiscale computational model poses an additional unique set of challenges. Overcoming these challenges requires both conceptual and computational innovations in model building, evaluation and validation. The logistics of coupling models requires critical decisions about which inputs to and outputs from each model can (or should) be passed back and forth to the other and how this sharing is managed. Java ‘umbrella’ programs, and more recently Matlab ‘interfacing’ programs, have been developed to orchestrate the communication of data between agent-based models and other models [98,104,105]. In passing information back and forth, it is essential that the values and units of shared variables be consistent between the ABM and the modelling approach with which it is coupled. However, this is made challenging by the fact that different data types are typically used to parametrize the two types of models, so internal congruency is not necessarily a given. Hence, it may be necessary to modify the parameters within one or both models to ensure congruency between them [101]. When there is a mismatch in spatial scales between the ABM and the other modelling approach with which it is coupled, as is likely to be the case when constructing a multiscale model, each model will represent the biology with a different degree of granularity. This can further complicate the sharing of information between the models because it may require sampling or averaging the information in the fine-grained model in order to translate it appropriately to the coarse-grained model. And, vice versa, when passing information from the coarse-grained model back to the fine-grained model, there will need to be a strategy for partitioning the information to a finer scale. Another important consideration is the frequency with which information is shared, or passed back and forth, and this is likely to have a considerable effect on computation time. This challenge can be accentuated if the ABM is stochastic (i.e. incorporates a degree of randomness, which is often the case), and multiple simulation runs are required to generate a distribution of outputs for a given parameter set. Strategies to parallelize the multiscale computational model, or at least the ABM simulation runs, can often be helpful in reducing overall computation time.

Evaluating models poses even more challenges. Sensitivity analyses are typically used to explore how altering the parameters, alone or in combination, affects the outputs of the model. However, for a multiscale model that involves ABM coupled with another modelling approach, conducting even a one-dimensional sensitivity analysis can become unwieldy. Furthermore, a multiscale model will inherently have outputs at many different scales, and which parameters to vary and which outputs to measure while doing so may not be obvious. There may be additional confounding issues when considering that the units of the parameters we wish to vary at the respective scales may not be compatible, and we may not know whether we are using comparable levels of perturbation. One approach to help deal with this is to calculate a sensitivity coefficient, S, in which the size of the parameter change, ΔP, is normalized to the initial parameter value P₀. If we also wish to compare different outputs with one another, then we may want to normalize by the original output metric Y₀. This yields a normalized sensitivity coefficient that allows comparison across both changes in parameters and measured outputs

The resulting normalized sensitivity coefficient can be interpreted as follows: if S = 1, this indicates a 1 : 1 relationship between the change in the parameter and the change in the output metric; if S < 1 or S > 1, this indicates lesser or greater sensitivity of the model output to a change in that parameter, respectively. As most models of biology are nonlinear, a change in the level of a given parameter is unlikely to have a linear effect on the output. For example, a 50% increase in a particular model parameter will not necessarily have twice the effect on the output that a 25% parameter increase would have. Therefore, it is good practice to calculate sensitivity coefficients for several relevant parameter perturbation levels to identify nonlinearities in the model. In the cases of nonlinear computational models with multiple unknowns, it might be necessary to perform validation based on experimental data using multiple nonlinear regression analysis. From sensitivity studies, a vector that includes all input parameters can be identified. Using this vector, we can calculate the best-fit values at which the cost function is minimal. This optimization problem can then be solved with a number of algorithms, such as the Levenberg–Marquart method or random search algorithms [106].

To date, there are no formalized strategies for validating multiscale computational models. The current best practices in model validation, regardless of scale, rely on comparing model predictions with independent experimental results. If there is a good match between model prediction and actual data, we conclude that the computational model is ‘valid’. What constitutes a ‘good match’ may be a qualitative judgement or a quantitative assessment backed by statistical analysis—for example, that the predicted data fall within the 95% confidence interval of the actual data (or vice versa). Whether or not it is sufficient to compare a multi-scale model's predictions with independent data at one level of scale has not been determined, but it is likely that validation will be required at multiple levels of scale, especially if important predictions are made at different levels of scale. While the issues of validation remain to be debated, striving for model validation—the act of seeing how a model's output compares with an experimental measurement—is an inherently useful endeavour. When a model falls short of perfectly matching the prediction, we should iterate, refine and try again. That is when important learning happens. And when a model pushes the boundaries and tries to predict something truly new, empirical data against which to compare a model's predictions may not exist. Model validation in this case might be impossible. But, even without validation, models can still be useful—particularly in suggesting new experiments to perform and new hypotheses to pursue. This cycle of model refinement and attempted validation can be particularly useful in leveraging a model's ability to suggest new mechanisms that have not yet been identified or interactions that are currently unknown.

5. Summary

Microvascular remodelling requires the dynamic interplay between molecular signalling, various cell behaviours and tissue-level changes that feedback on one another. The focus of this review was to highlight how different biomechanical dynamics studied at one scale can influence behaviour at another scale. As high-quality and high-throughput biological data at multiple different levels of spatial scale (molecular through tissue) become increasingly available, we are inclined to try to link these data together in order to define the cause-and-effect biological mechanisms that span across spatial scales, and with even greater quantitative detail. Doing so provides an opportunity to probe, for example, how receptor–ligand interactions in the membrane of one endothelial cell impact the migratory behaviours of a neighbouring cell, and, ultimately, whether a new capillary sprout at a specific location within a network will experience shear stress. Similarly, to understand how the branching of a heterogeneous microvascular network affects blood flow and the recruitment of circulating monocytes that coordinate the remodelling of an arteriole through a panoply of cytokine and growth factor secretion requires integration of cause-and-effect relationships across scales. Because these relationships are complex, dynamic and spatially heterogeneous—and usually impossible to assess in vivo using the currently available experimental tools—it becomes useful (if not essential) to employ computational modelling approaches that integrate information across spatial and temporal scales. So what can we do when faced with the obstacle of biological experiments falling short of providing specific, mechanistic and/or quantitative answers? As highlighted by the five examples in this article, valuable information can be gained through the use of computational models, yet a critical question becomes—how can the models be integrated to make the computational space look like what we see under the microscope? While approaches, such as ABM, provide platforms for the necessary integration, caution should be applied to each modelling application to evaluate the required threshold of complexity.

Multiscale computational modelling of microvascular remodelling, or any other complex biological process for that matter, is a new frontier. While the challenges posed to model construction, evaluation, validation and dissemination are only beginning to be identified and addressed, recognition of the need to integrate different types of models across scales represents an exciting opportunity for the future.

Funding statement

This work was supported by the Tulane Center for Aging and NIH 5-P20GM103629–02 to W.L.M.; JSPS Grant-in-Aid for Scientific Research 25630046 to K.T.; American Heart Association 12BGIA12060154, Sloan Research Fellowship and NIH R01HL101200 to F.M.G.; Louisiana Board of Regents LEQSF(2011–2014)-RD-A-24 and National Science Foundation 13012861 to D.K.; NIH EY022063 and NIH HL082838 to S.M.P.