Multiscale models of skeletal muscle reveal the complex effects of muscular dystrophy on tissue mechanics and damage susceptibility

Abstract

Computational models have been increasingly used to study the tissue-level constitutive properties of muscle microstructure; however, these models were not created to study or incorporate the influence of disease-associated modifications in muscle. The purpose of this paper was to develop a novel multiscale muscle modelling framework to elucidate the relationship between microstructural disease adaptations and modifications in both mechanical properties of muscle and strain in the cell membrane. We used an agent-based model to randomly generate new muscle fibre geometries and mapped them into a finite-element model representing a cross section of a muscle fascicle. The framework enabled us to explore variability in the shape and arrangement of fibres, as well as to incorporate disease-related changes. We applied this method to reveal the trade-offs between mechanical properties and damage susceptibility in Duchenne muscular dystrophy (DMD). DMD is a fatal genetic disease caused by a lack of the transmembrane protein dystrophin, leading to muscle wasting and death due to cardiac or pulmonary complications. The most prevalent microstructural variations in DMD include: lack of transmembrane proteins, fibrosis, fatty infiltration and variation in fibre cross-sectional area. A parameter analysis of these variations and case study of DMD revealed that the nature of fibrosis and density of transmembrane proteins strongly affected the stiffness of the muscle and susceptibility to membrane damage.

1. Introduction

Skeletal muscle has a complex hierarchical structure consisting of long contractile muscle cells (fibres) embedded within a connective tissue matrix. The importance of the interaction between contractile muscle cells and the extracellular matrix (ECM) has received significant attention over the past two decades [1–5]. In particular, the ECM is thought to play a critical role in enabling force transmission from fibres to tendons and in the protection of muscle cells from excessive damage during muscle contractions.

Muscle cells, ECM and their transmembrane connections have all been implicated in muscle disease. For example, Duchenne muscular dystrophy (DMD) is an X-linked recessive disorder caused by a mutation in the DMD gene, resulting in the incomplete translation of the transmembrane protein dystrophin [6–10]. It is the most common neuromuscular disease of childhood and is responsible for dramatically impaired muscle function and progressive muscle wasting [6,11]. Boys born with DMD become very weak at an early age, need wheelchairs by their teens and die of respiratory or cardiac failure by their third decade of life [12,13]. There is no cure for DMD, despite extensive experimental research regarding the pathophysiology of the disease. While the current standard treatment is corticosteroids, it is merely palliative to prolong ambulation [14–16]. Several animal models of the disease have been developed—including zebrafish [17,18], mouse [19,20] and canine [21,22]; however, there are still unanswered questions regarding the role of dystrophin in muscle function and how this leads to progressive muscle wasting in DMD. How does the protein protect the cell membrane from mechanical damage? How does the protein affect muscle properties? How do secondary changes in the muscle—such as fibrosis and fatty infiltration—influence the function of the muscle? In this paper, we posit that multiscale computational models can provide a quantitative, mechanistic approach to investigate the influence of muscle diseases, like DMD, on muscle function. These scientific underpinnings provide a new framework to generate hypotheses regarding treatment targets moving forward.

Computational models of skeletal muscle have advanced significantly over the last two decades. While historically models of muscle have simplified the architecture of muscle into a lumped-parameter representation [23], there has been a movement towards tissue-level models that represent muscle tissue as a fibre-reinforced composite. These tissue-level models make use of ‘phenomenological’ constitutive models that do an excellent job of accounting for the underlying structure of muscle [24,25]. However, muscle cells and connective tissue are not explicitly defined in these models, which limits their capacity to relate molecular and cellular underpinnings and reveal insights into disease-related muscle changes. Recently, micromechanical models of muscle have been developed to derive tissue-level constitutive properties from the muscle microstructure [26]. This work provided a framework for multiscale analysis of muscle; however, the models were not created to study or incorporate the influences of disease-associated modifications in muscle.

The overall goal of this paper was to develop a multiscale muscle modelling framework to elucidate the relationship between microstructural disease adaptations and modifications in both mechanical properties of muscle and strain in the cell membrane. To achieve this goal, we developed a novel approach for randomly generating muscle fascicle geometries, enabling us to explore disease-related changes by altering muscle fibre and ECM volume fractions, variance in fibre cross-sectional area (CSA), amount of fat infiltration and fibre–ECM transmembrane protein density. We used the models to reveal the trade-offs between mechanical properties and damage susceptibility in the context of DMD-associated changes in muscle.

2. Material and methods

2.1. Random generation of fascicle cross sections from an agent-based model

We used an agent-based model of muscle to generate new fascicle cross sections with the agent-based modelling platform Netlogo (http://ccl.northwestern.edu/netlogo/). A unique cross section of one muscle fascicle was generated from 14 ‘seed’ fibres within a two-dimensional discretized grid. The grid dimensions were: 130 × 130 elements, with each element 3 × 3 µm. Fibres were grown in a stepwise function according to their defined mean and variance of the fibre CSA. The unused elements were prescribed as boundary elements.

In order to determine the input parameters necessary to model structural changes in musculoskeletal disease, we determined the most prevalent pathological variations seen in DMD (figure 1). These variations include: density of transmembrane proteins, variation of fibre CSA and pseudohypertrophy which manifests as an increase of fibrosis and fat infiltration within the muscle [11,28]. To enable the agent-based model to simulate these pathological variations, we modified the mean and variance of the fibre CSA and added additional capabilities to increase the amount of fibrosis or change muscle fibre into fat tissue. In addition, by defining the variance of fibre CSA, we used the agent-based model to randomly create new fascicle cross sections. Each simulation had a unique set of muscle fibre shapes and sizes, accounting for physiological variability. Through manipulation of these input parameters, we generated fascicle geometries that account for both structural changes seen in disease and variability inherent in muscle tissue (figure 2). The generation of new fascicle geometries was completed under the assumption of constant physiological conditions (e.g. pH, temperature and electrolyte composition).

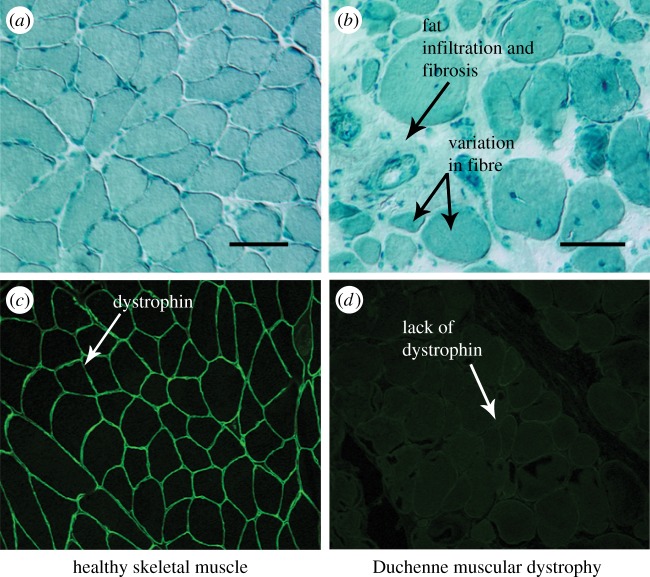
Figure 1.

Histological comparison of healthy (a) and DMD (b) muscle reveals common pathological variations seen in musculoskeletal disease, including increased variation in fibre CSA, fibrosis and fat infiltration. Scale bar, 60 µm. (Adapted from [3].) Immunofluorescence staining of healthy (c) and DMD (d) muscle samples show a lack of dystrophin expression in the DMD muscle compared with the healthy muscle. (Adapted from [27].) (Online version in colour.)

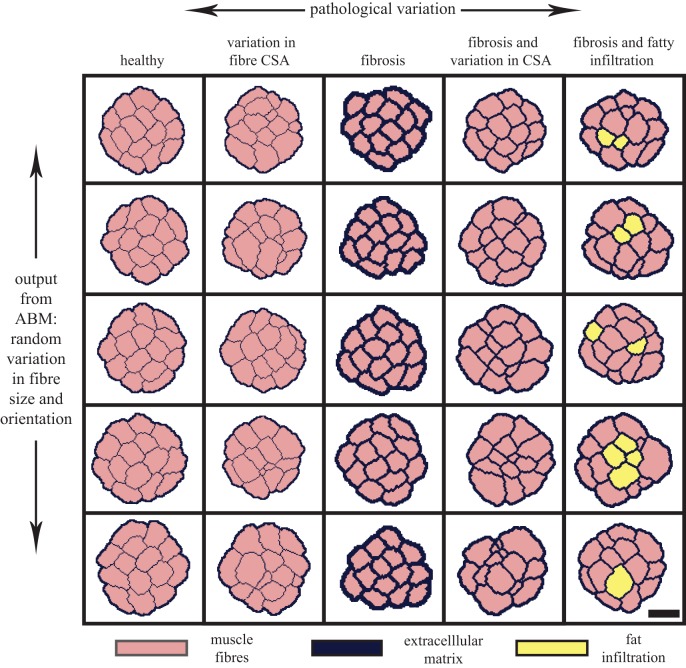
Figure 2.

An agent-based model (ABM) is used to generate a variety of new fascicle cross-section geometries for different pathological variations commonly seen in musculoskeletal disease. The horizontal axis represents the different pathological conditions modelled, including: variation in fibre CSA, fibrosis and fatty infiltration. These symptoms are manifested as pseudohypertrophy in DMD patients where the total muscle volume increases due to increased fibrosis and fat infiltration. The vertical axis represents the variation in fascicle geometry created by the ABM's randomized generation of fascicle cross sections with differing fibre shapes and sizes. Scale bar, 100 µm. (Online version in colour.)

2.2. Conversion from agent-based model to micromechanical model

We mapped the material elements from the agent-based model's discretized grid onto an initialized finite-element mesh that represents the cross section of a single muscle fascicle (figure 3). The mesh density was increased and a smoothing algorithm was applied to eliminate any ill-conditioned elements in narrow portions of the ECM. An initialized mesh, the size of the agent-based model grid, was created using TrueGrid (XYZ Scientific Applications). The hexahedral element mesh dimensions were: 390 × 390 elements in the cross-section plane and one element thick. Additional simulations were completed with a three-element-thick hexahedral mesh and the calculated shear modulus was within 0.5% of the one-element-thick mesh; therefore a one-element-thick mesh was used to decrease computational time.

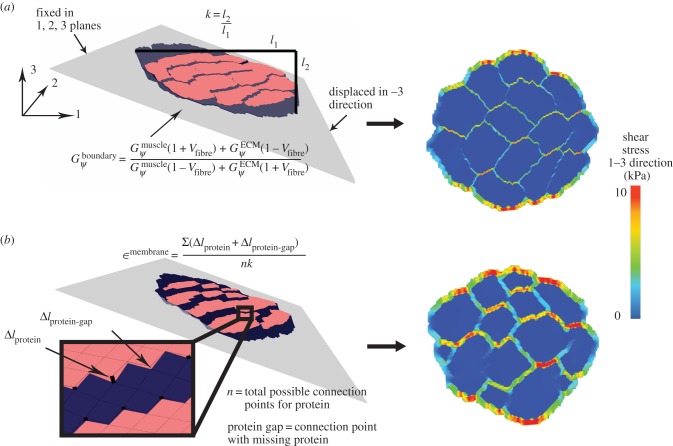
Figure 3.

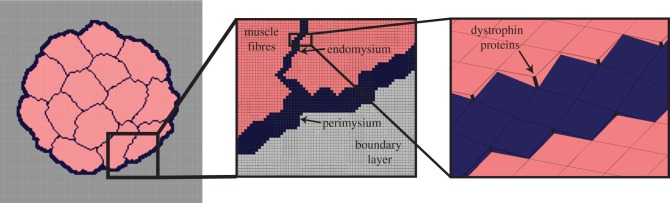
Components of the finite-element micromechanical model, including material types for ECM (endomysium and perimysium), muscle fibres, boundary layer and springs representing transmembrane proteins. (Online version in colour.)

As muscle fibre force is known to be transmitted laterally through shearing of the endomysium, we were interested in analysing the muscle in shear [4,26]. We assigned the boundary conditions to prescribe simple shear deformation, representing the shear displacement of muscle fibres and fascicles relative to each other. The elements on one face were constrained in all directions and the opposite face was displaced in the −3 direction, creating a shear displacement in the 1–3 direction. All elements were constrained in the 1 and 2 directions.

2.3. Definition of constitutive model and material parameters

We used a transversely isotropic, nearly incompressible, hyperelastic constitutive model to represent the muscle fibres, ECM and boundary layer. The deformation gradient (F) and right Cauchy–Green deformation tensor (C) are defined, respectively, as

where x represents the deformed vector and X represents the reference vector. The stresses are derived from the strain energy density function (W), and the second Piola–Kirchoff stress (S) is defined as

This constitutive model uses an uncoupled form of the strain energy density function to enforce the incompressible behaviour of the connective and muscle tissue. The strain energy density function separates the dilatational and deviatoric response of the muscle, resulting in the following strain energy density function [24]:

where λ is the along-fibre stretch, ψ is along-fibre shear, β is cross-fibre shear and J is the relative change in volume of the tissue. The fibre direction is defined along the axis of transverse isotropy. In this model, it is assumed to run along the path of the muscle for both ECM and muscle fibres. Physically based strain invariants were used to relate material parameters to experimentally quantifiable measurements [29]. W_λ(λ) is a piecewise function representing the passive material properties of the tissue, dependent on the fibre length. W_ψ, W_β and W_J, were defined as follows:

where G_ψ is the along-fibre shear modulus, G_β is cross-fibre shear modulus and K is the bulk modulus [24]. Fat infiltration was modelled as a simple incompressible, hyperelastic, neo-Hookean material with a single material parameter representing Young's modulus of the material. Currently, there are no known measurements for the along-fibre shear modulus of muscle and ECM, 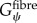, , 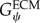however previous studies have shown that the ratio of 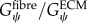is the critical factor in determining the contribution of structural variation on tissue-level properties [26]. Furthermore, there remains a debate in the literature as to whether muscle fibres are more or less stiff than the ECM [2–4]. Therefore, in order to explore the implications of these possible scenarios, 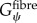was held constant during simulations and 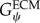was adjusted to be both stiffer and more compliant in shear than the muscle fibres.

2.4. Definition of boundary material properties

Our method requires initialization of a finite-element mesh so that only the material type for each element needs to be defined based on the output of the agent-based model. The boundary layer surrounding the muscle fascicle within the agent-based model grid allows for a unique opportunity to pre-allocate the mesh properties, boundary conditions and applied displacements for the initialized finite-element mesh (figure 4). In order to prevent the boundary layer from adversely affecting the model, its material properties were adjusted so that its behaviour simulated the macroscopic shear properties of the muscle fascicle. Using rules of mixtures, the along-fibre shear properties of the boundary were defined as follows:

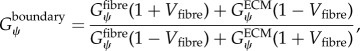where V_fibre is the volume fraction of fibres within the muscle fascicle. This created a homogenized, macroscopically representative material to which boundary conditions and displacements can be pre-imposed and used for all the unique fascicle geometries used in this study.

Figure 4.

Finite-element model in shear for healthy (a) and diseased (b) muscle fascicles reveals variable shear stress profiles. The boundary layer properties were defined based on rules of mixtures to simulate macroscopic-fascicle properties. Fascicle displacement, k, was calculated as the fascicle displacement in the 3 direction (l₂), divided by the width of the fascicle (l₁). The displacement, k, and the shear stress in the 1–3 direction were used to calculate the fascicle shear modulus. Membrane strain is the average change in length between fibre and ECM nodes at both proteins and inter-protein regions, normalized by k. (Online version in colour.)

2.5. Inclusion of transmembrane proteins

To analyse the effect of transmembrane proteins, such as dystrophin, we identified all nodes connecting the muscle fibres and ECM within the micromechanical model, added a node at that point, and then connected the two nodes with a spring. The transmembrane protein was modelled as a nonlinear elastic spring [30–32]. To represent a loss of proteins in the diseased state, a random number generator was used to randomly delete a specified quantity of the springs (ranging between 0% and 80%).

2.6. Determination of macroscopic along-fibre shear properties

Simulations were run using the nonlinear finite-element solver NIKE3D [33]. The macroscopic along-fibre shear properties of the muscle fascicle were calculated based on the displacement and shear stress of the micromechanical model fascicle, excluding the boundary layer. The average shear stress (1–3 plane) in the fascicle was calculated using the post-processing software Postview [34]. The shear displacement of the fascicle, k, was also calculated in Postview, as the maximum 3-plane displacement across the fascicle, divided by the width of the fascicle at that point. The macroscopic along-fibre shear modulus was then calculated as follows:

2.7. Analyses

To initially validate the approach for defining geometries and boundary conditions, we performed simulations with a muscle to ECM shear modulus ratio ranging from 0.01 to 500 for a healthy muscle fascicle; the results replicated those found by Sharafi & Blemker [26]. The micromechanical model was then used in a parameter analysis to test the individual effect of a number of variations in microstructures prevalent in musculoskeletal disease. We explored the effects of volume fraction of fibres, the density of transmembrane proteins, variance in fibre CSA and volume fraction of fatty infiltration, all of which are structural variations that have been observed in DMD muscle. The agent-based model was used to generate new fascicle cross sections for each simulation so that all analyses were completed with a unique geometry, accounting for typical variability seen in muscle fibres.

Because there is debate in the literature on whether muscle fibres are stiffer than the ECM or the ECM is stiffer than muscle fibres, all parameter analyses were repeated at two ratios of 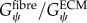: one in which the muscle is 75 times stiffer than the ECM [26], and one in which the ECM is 25 times stiffer than the muscle [3]. Total finite-element simulation time was 8 min on a 32 GB eight-processor IBM Linux workstation.

2.8. A case study investigating muscle disease

We performed a simulated case study of DMD in which the muscle fascicle was analysed for healthy muscle and at three stages of disease. The early stage of the disease included only a loss of dystrophin proteins, the middle stage included loss of proteins, fibrosis and an increase in variance of fibre CSA, and the late stage included loss of proteins, increased fibrosis, fatty infiltration and large variations in fibre CSA [6,28]. The macroscopic along-fibre shear moduli and ECM shear moduli were normalized by the muscle fibre modulus in order to simplify the presentation of the results. A second parameter, membrane strain, was used to analyse the potential for damage at the membrane. Membrane strain was calculated as the average change in length between fibre and ECM nodes at both proteins and inter-protein gaps, normalized by the macro-scale shear displacement factor, k.

3. Results

3.1. Parameter analysis

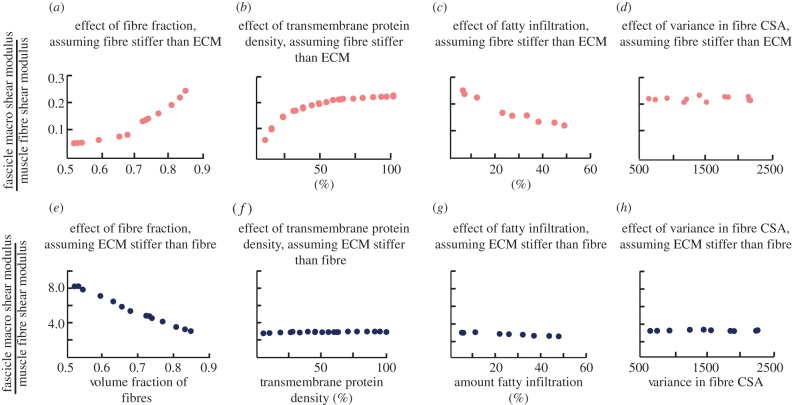
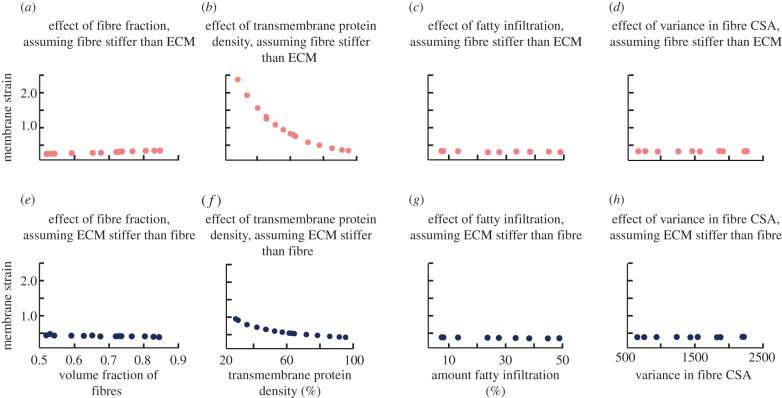
The effect of microstructural variations differs depending on whether the ECM is stiffer than the fibres or the fibres are stiffer than the ECM. When the muscle fibres are stiffer than the ECM, increasing the volume fraction of fibres (figure 5a) and the density of transmembrane proteins (figure 5b) both led to a significant increase in the macroscopic shear modulus of the fascicle. Incorporation of fatty infiltration decreased the shear stiffness of the muscle (figure 5c), while variability in the fibre CSA had no effect on stiffness (figure 5d). Conversely, when the ECM was stiffer than the muscle, only the volume fraction of fibres affected the tissue-level properties of the muscle, with an increasing volume fraction of fibres leading to a decrease in the macroscopic shear modulus (figure 5e). All other parameters had minimal effect on shear stiffness when the ECM was stiffer.

Figure 5.

Macroscopic shear modulus is affected by stiffness of ECM, volume fraction of fibres, density of transmembrane proteins and amount of fatty infiltration. When the muscle fibres are stiffer than the ECM (a–d), both increasing the volume fraction of fibres (a) and increasing the density of transmembrane proteins (b) increase stiffness, while increasing fatty infiltration (c) decreases stiffness. When ECM is stiffer than muscle fibres (e–h), only the volume fraction of fibres (e) has an effect, with an increase in volume fraction of fibres leading to a decrease in stiffness. (Online version in colour.)

Regardless of the assumption of the relative stiffness of the fibres and the ECM, the density of transmembrane proteins had the most significant effect on membrane strain predictions, as compared with the other variations. However, in the case where the fibre was stiffer than the ECM, the protein density had a much more dramatic effect (figure 6b). These results highlight the fact that both protein density (which is decreased in DMD) and ECM properties contribute to the damage susceptibly of muscle.

Figure 6.

Membrane strain in the muscle fascicle is only affected by stiffness of ECM and density of transmembrane proteins. When the muscle is stiffer than the ECM (a–d), increasing the density of transmembrane proteins (b) decreases the strain on the membrane. When the ECM is stiffer than the muscles (e–h), increasing the density of transmembrane proteins (f) also decreases the strain on the membrane, but the effect is less significant. (Online version in colour.)

3.2. Case study: Duchenne muscular dystrophy

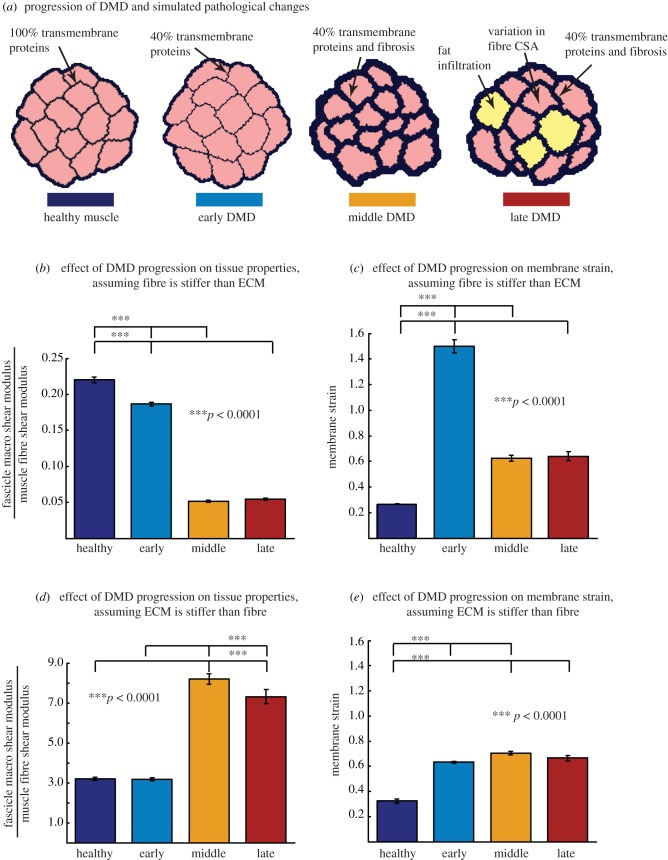
The case study analysis demonstrated that pathological alterations associated with DMD progression influence both tissue properties and damage susceptibility, and the relative stiffness of the fibre and ECM dramatically influence the predicted results. In the case where the ECM remains more compliant than the fibre, tissue stiffness would decrease significantly over time (figure 7b). However, membrane strain initially increases (i.e. more damage susceptibility) but then decreases with fibrosis and fatty infiltration (figure 7c). When the ECM is stiffer than the fibres, the stiffness increases significantly in the middle and last stages (figure 7d), while the membrane strain increases less dramatically but remains elevated through the middle and late stages of disease progression (figure 7e).

Figure 7.

Fascicle geometries (a) for healthy, early, middle and late stage DMD muscle. Pseudohypertrophy of muscle is represented in the middle and late stages of DMD with fibrosis and fatty infiltration (a). When the muscle fibre is stiffer than the ECM (b,c), the macroscopic shear modulus decreases significantly during progression of disease (b) and the membrane strain increases significantly during the early stage, then decreases at the middle and late stages (c). When the ECM is stiffer than the fibre (d,e), the macroscopic shear modulus increases significantly in the middle stage and decreases slightly at the late stage (d), while the membrane strain increases less significantly throughout progression of the disease with a slight decrease at the late stage (e). (Online version in colour.)

4. Discussion

The goal of this work was to develop a computational framework to investigate how disease-related changes in the muscle influence the tissue-level mechanical properties and susceptibly to membrane damage. By using an agent-based model to generate geometries and mapping it to an initialized mesh, this novel modelling framework eliminates the cumbersome task of creating unique finite-element meshes for each analysis and allows for an unprecedented quantity of simulations to be run in a short amount of time. Additionally, the agent-based model generated new fascicle cross sections with varying muscle fibre shapes and sizes for each simulation, which incorporated architectural variability commonly seen in vivo. This automation enabled us to explore a wide range of pathological variations commonly seen in muscle disease to first understand their influence independently and to then analyse their compounding effects in a case study of DMD.

Analysing the compounding effects of microstructural variations in the DMD case study revealed the importance of understanding fibrosis in DMD. The stiffness of the ECM relative to the fibre significantly affected the degree to which disease progression influenced the fascicle stiffness and membrane strain. Interestingly, other studies focusing on fibrosis in DMD have asserted that fibrosis not only exacerbates disease progression, but may also prevent the success of many targeted gene therapies [20,35,36]. Further, the mechanical properties of fibrosis are likely altered throughout the course of disease, as its stiffness has been correlated with both the amount of collagen and the number of cross-links [5,37,38]. Together, these results emphasize the complexity of fibrosis, and the need to better understand its development in DMD.

The model is also consistent with the theory that the transmembrane proteins protect the muscle cell from damage [32,39–41] because deletion of membrane proteins resulted in increased strains in the membrane. However, the study further reveals that the function of the proteins is significantly affected by the nature of fibrosis. In the early stage DMD model, a 60% deletion of transmembrane proteins increased the membrane strain significantly (twofold and fivefold) under both stiffness assumptions, with only a minimal effect on the stiffness of the muscle. This implies that even if there is not a measurable difference in stiffness at the beginning of the disease, which is supported in experimental studies [42], the protein-deficient muscle membrane may still be withstanding considerably elevated strains. The subsequent onset of fibrosis and fatty infiltration in the middle and late stages then either alleviates the membrane strain (muscle stiffer than ECM), or slightly increases it (ECM stiffer than muscle). This differential effect of fibrosis reveals a potential trade-off between functional preservation and protection of the membrane. When fibrosis decreases membrane strain the muscle stiffness also decreases, and when fibrosis increases membrane strain the muscle stiffness is increased. These insights further support the significance of understanding the nature of fibrosis.

Previous studies have predicted that damage to the muscle membrane is likely to be seen at the inter-protein regions where the dystrophin proteins are missing [32,39,40]. We accounted for this effect in our predictions of membrane strain by determining the strain between the nodes across the entire border between muscle fibres and ECM, which included regions where dystrophin proteins existed as well as inter-protein gaps. Interestingly, when the muscle was stiffer than the ECM, there were higher strains at the inter-protein regions than within the transmembrane proteins. When the ECM was stiffer than the fibre, the membrane strain was distributed more evenly between the protein and inter-protein regions.

Our predictions are consistent with recent studies which determined the influence of transmembrane protein density and stiffness on lateral force transmission [30]. Supporting that study, we found that the stiffness of the protein had minimal effect on the fascicle shear modulus, while the density of proteins significantly affected the fascicle shear modulus. Interestingly, our analysis also revealed that, in the situation in which the ECM is stiffer than the fibres, the influence of protein density on tissue stiffness and membrane damage is diminished.

It is important to consider a number of limitations to the models presented here. First, the ECM was considered to be a continuous structure for both the endomysium and perimysium, and the same constitutive model was used for both components. However, it is known that these two layers have distinct structural compositions and may have different material parameters [2,43]. Additionally, we did not account for the varying collagen directions seen in the ECM, though studies have postulated that the collagen direction in the endomysium does not have an effect on the shear properties [2]. In our representation of fibrosis, we varied only the volume fraction of ECM while keeping the mechanical properties constant and homogeneous across the sample. This simplification allowed us to focus on the effect of the volume fraction of ECM. However, this approach ignores the fact that the ECM stiffness is affected by additional factors, such as the amount of collagen within the ECM, the number of collagen cross-links and the architectural structure of the collagen (e.g. fibre orientation) [5,37,38]. Indeed, increasing the volume fraction of ECM could be paired with changes in collagen content and architecture, which would also influence the tissue-level properties and potential damage sensitivity of the membrane. Further, the mechanical properties of the transmembrane proteins were represented using a continuous nonlinear curve [30], although physiological models often represent it as a piecewise function due to the unfolding of the protein [31,32].

The analyses presented in this paper focused on the behaviour of muscle in simple shear. We focused on shearing of the fascicle because it is the dominant mode of lateral force transmission in muscle, and the behaviour in shear cannot be simply inferred from the microstructure (as opposed to along-fibre tensile behaviour). However, we acknowledge that simple shear does not fully represent physiological loading patterns [2,4,44]. In the future, coupling these models with macro-scale tissue-level models [45] would enable us to study the behaviour of the microstructures in the context of real physiological deformations. Additionally, we only effectively analysed the passive mechanics of the muscle, whereas membrane damage primarily occurs during active lengthening contractions [46,47]. While the effects of activation on the shear properties of fibres are currently unknown, we would reason that muscle activation would further increase the stiffness of the muscle relative to the ECM. Therefore, we expect that the membrane damage profiles would be similar to the stiff fibre results in the DMD analysis (figure 7c) with potentially even greater membrane damage for a given level of shear deformation.

One of the critical challenges in creating multiscale muscle models is the limited availability of experimental data for input parameters and validation of the model predictions. For this reason, the presented study focused on analysing the effects of microstructural variations, given the uncertainty of specific parameters (such as the relative stiffness of the ECM and muscle fibres). We therefore used the presented analysis as a series of in silico experiments to explore the mechanics of DMD-associated modifications in microstructure and to generate hypotheses that drive new experiments.

Future research to determine the shear properties of the ECM (and effect of pathological changes) would allow more focused analysis of disease progression. Additionally, correlations between the amount of collagen cross-links and the stiffness of the muscle have revealed potential mechanisms through which disease may alter the mechanical properties of muscle, so it is critical to study how ECM properties differ in healthy and diseased populations. It is also important to understand the structural differences between the endomysium and perimysium within the ECM. Recent studies have developed novel methods for imaging the perimysium structure and could be used to highlight these differences [48].

The modelling framework presented here can also be extended through a full coupling of the agent-based and micromechanical models to allow for the predictive analysis of DMD disease progression. As the components of muscle are mechanosensitive, it would be informative to link the strain results of the micromechanical model with the agent-based model to predict the progression of DMD within a mechanical environment. Additionally, a fruitful area of future exploration would be to model the effects of pharmacological interventions on changes in DMD microstructure, such as the current standard-of-care, corticosteroids. Corticosteroids are known to reduce gene expression and inhibit myofibroblast activity, which potentially suppresses collagen production [28]. Based on the findings in our DMD analysis, suppression of collagen production would have a differential effect on damage and function depending on the stiffness of the ECM. The integrated models would help reveal these mechanisms through which the corticosteroid's decreased collagen production prolongs ambulation; likewise, they could be extended to predict other critical structure–function relationships of muscle.

Data accessibility

The datasets supporting this article have been uploaded as part of the electronic supplementary material.

Author contributions

K.V. participated in design of the study, carried out all the simulations, performed the data analysis and drafted the manuscript. K.M. developed the agent-based model, participated in the design of the study and edited the manuscript. S.P. participated in the design of the study and edited the manuscript. S.B. participated in the design of the study and drafted the manuscript. All authors gave final approval for publication.

Funding statement

This study was funded by the National Science Foundation, grant no. 1235224.

Conflict of interests

We have no competing interests.